The Study of the Surface Plasmon Polaritons at the Interface Separating Nanocomposite and Hypercrystal
Abstract
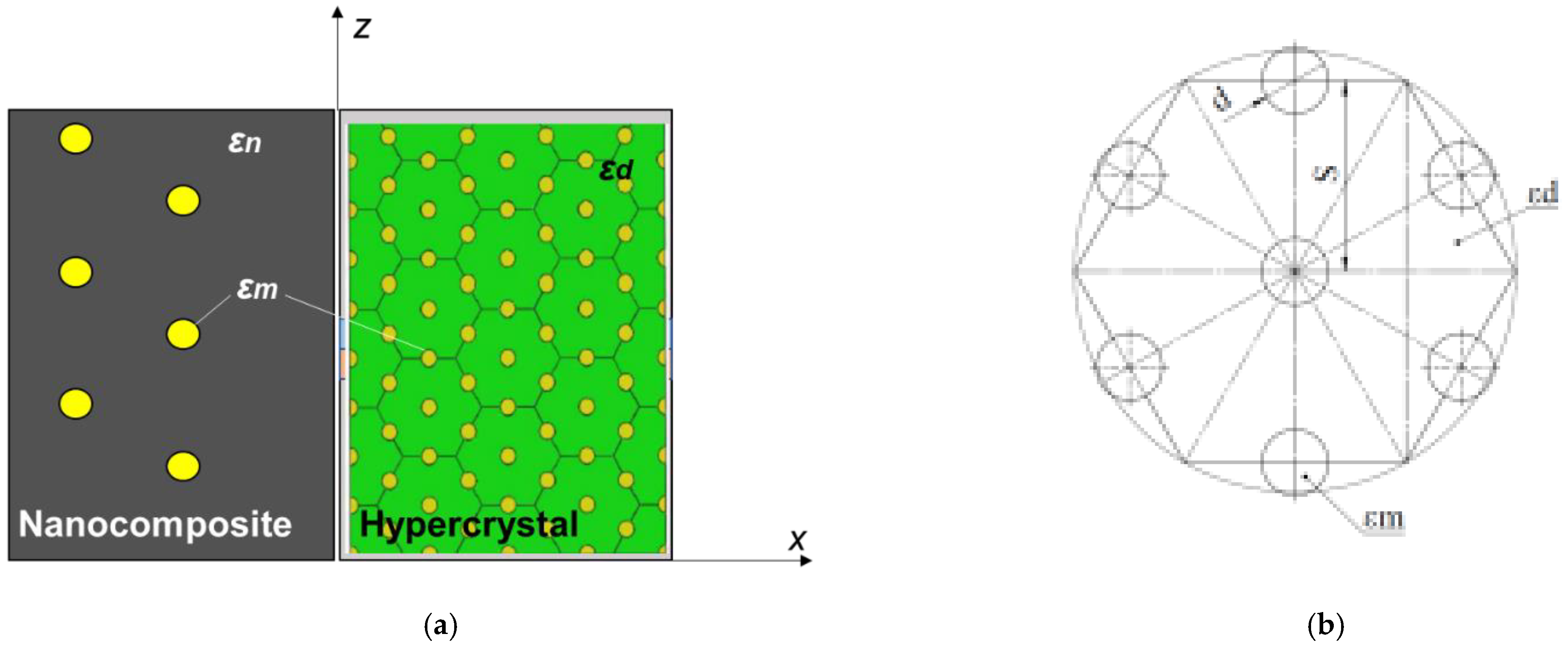
:1. Introduction
2. Materials and Methods
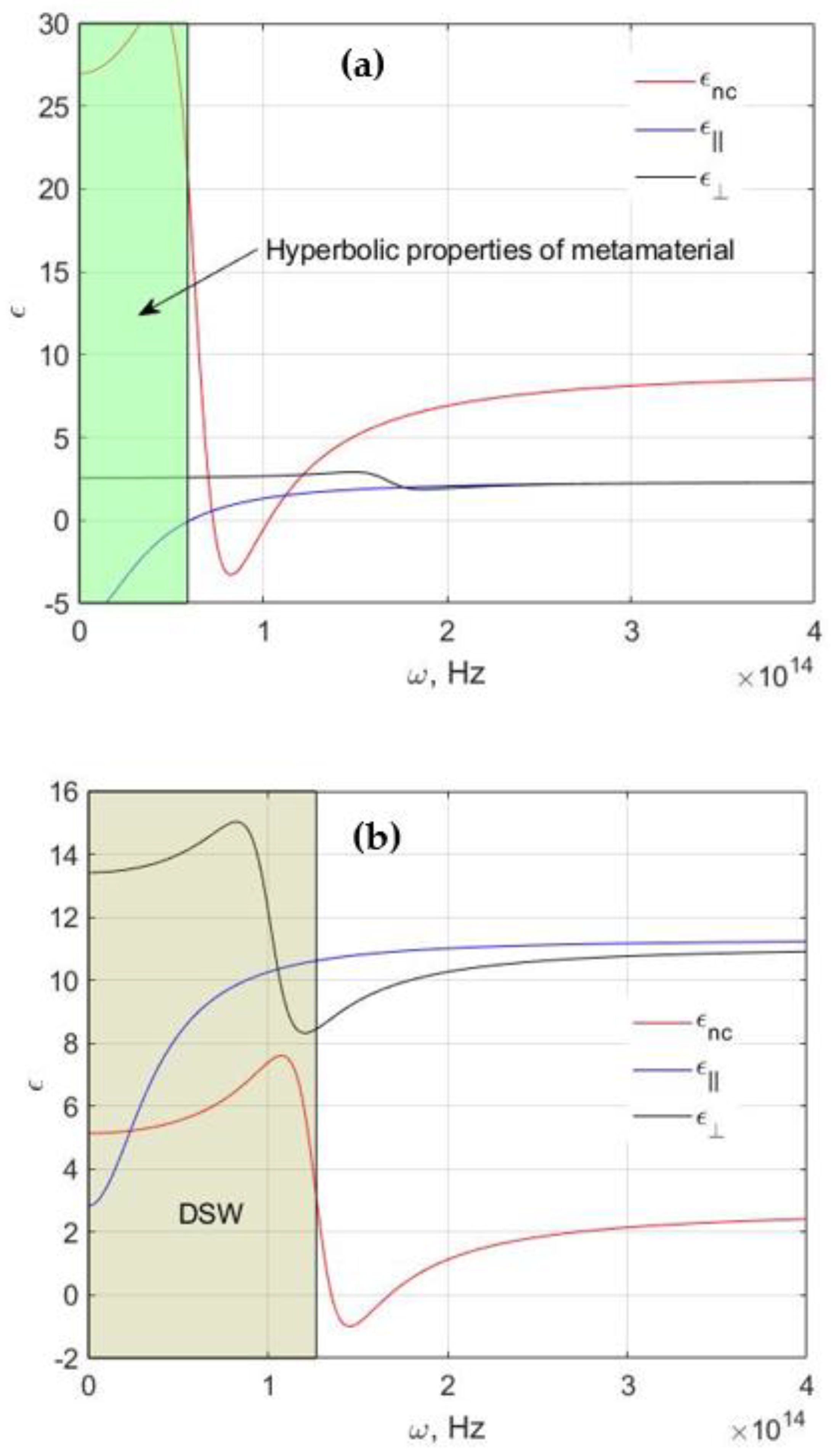
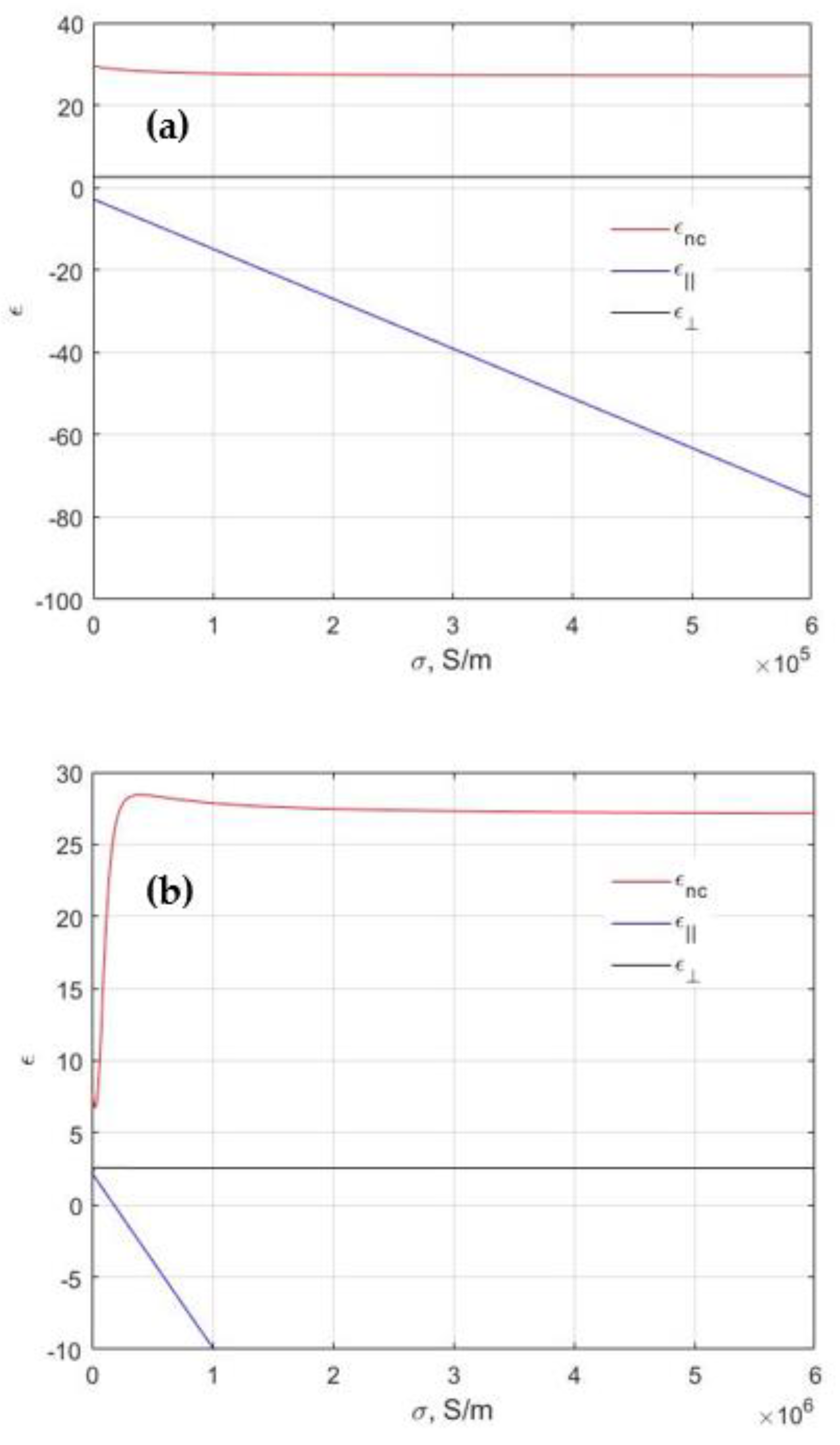
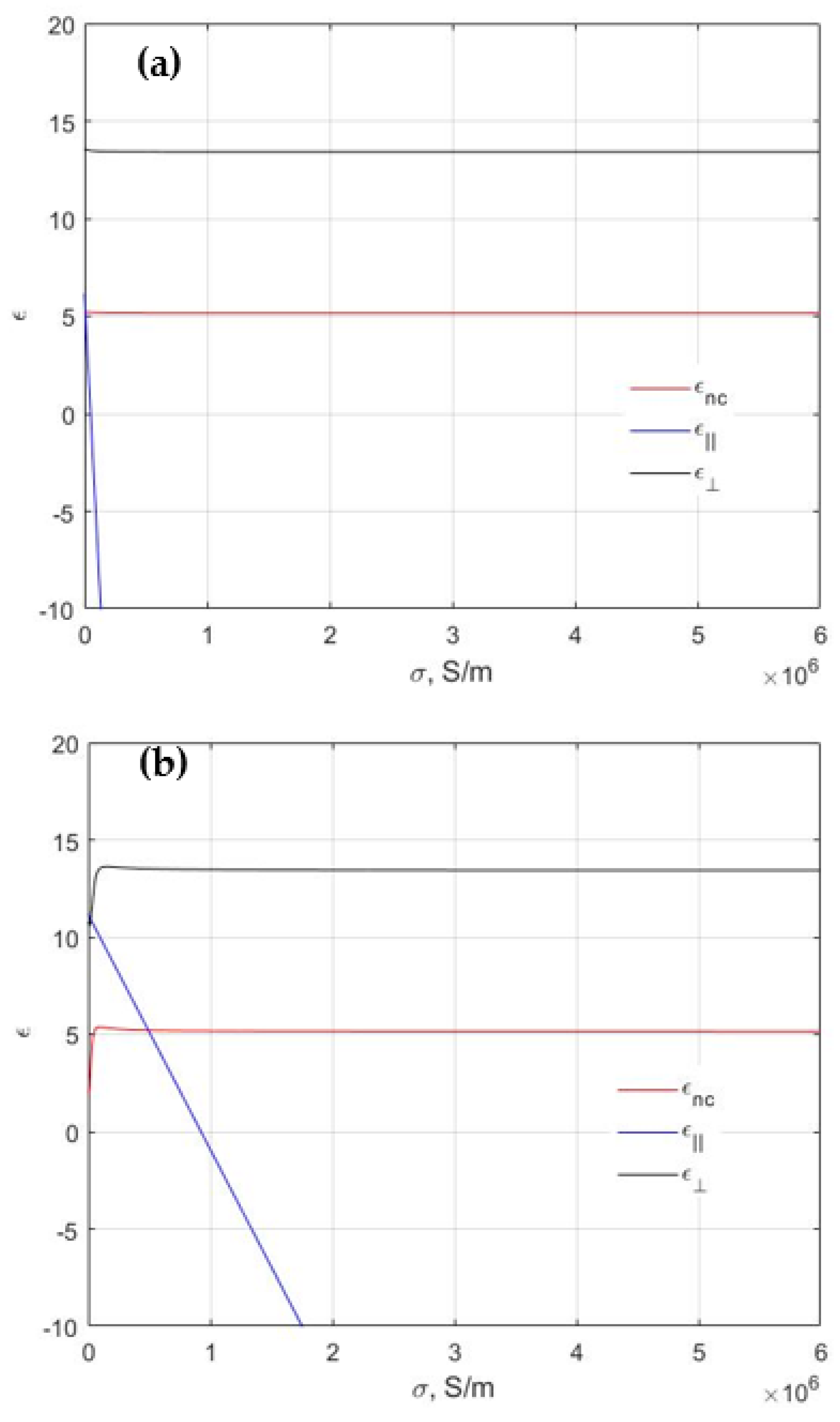
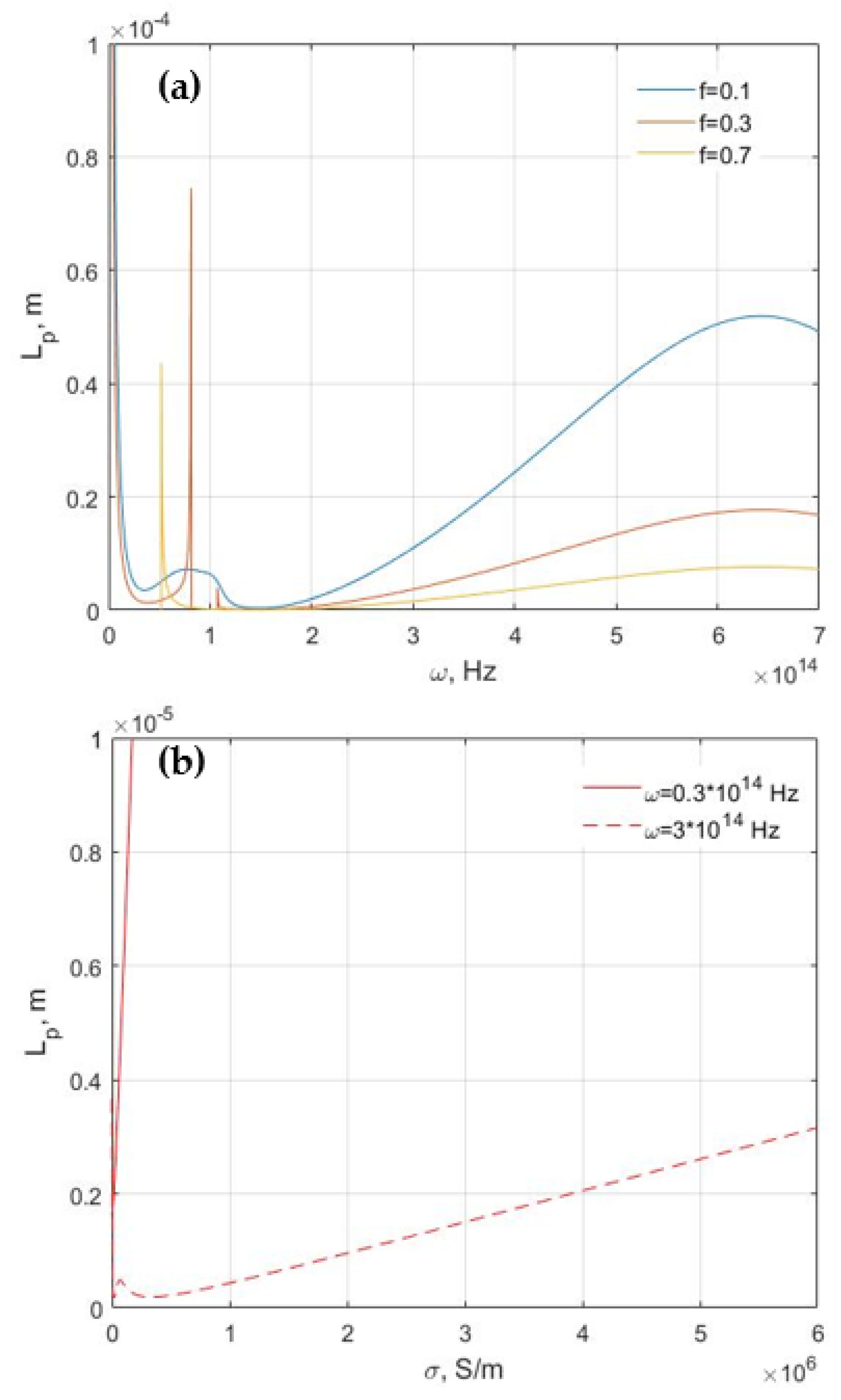
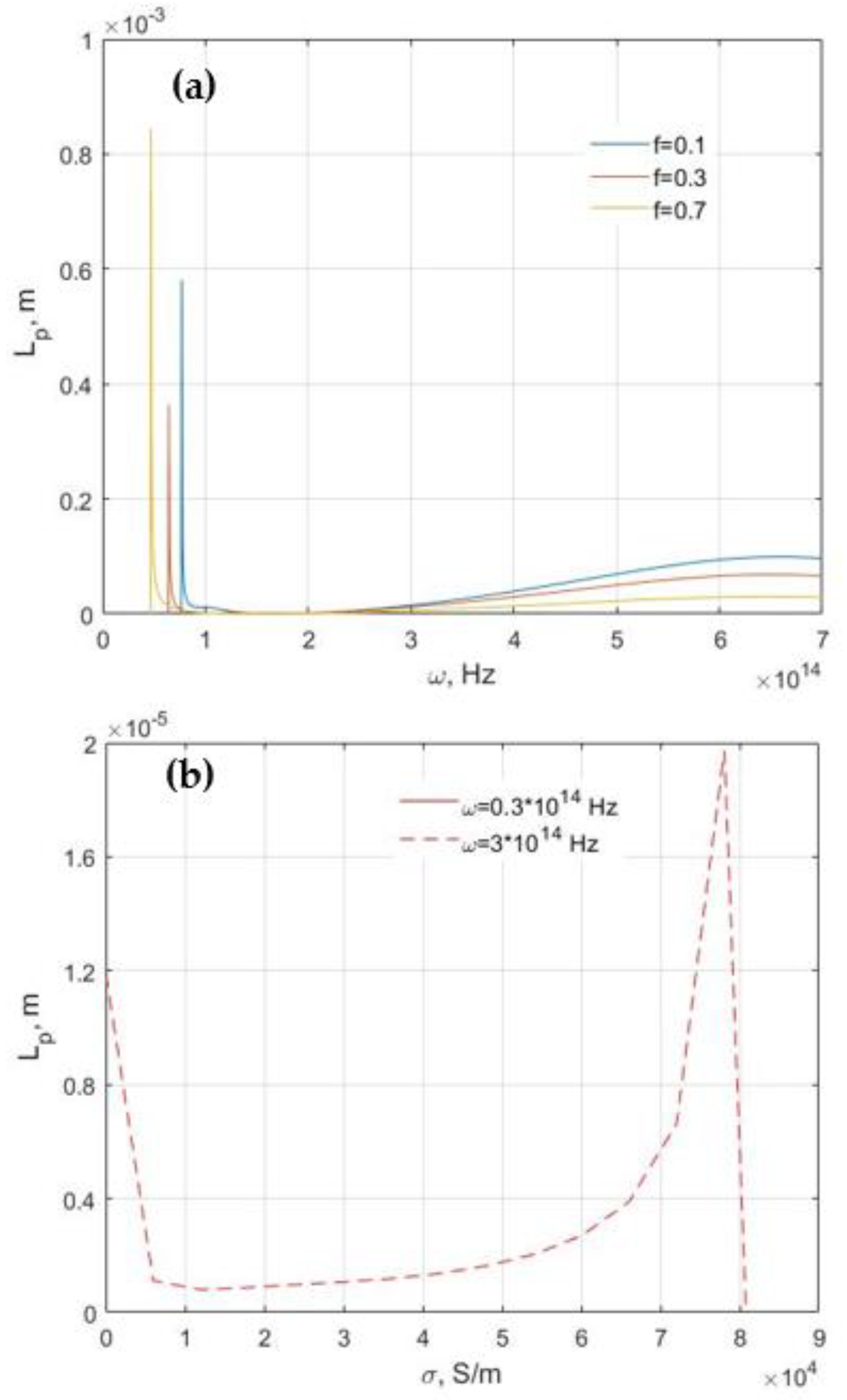
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Kneipp, K. Surface-enhanced Raman scattering. Phys. Today 2007, 60, 40–45. [Google Scholar] [CrossRef] [Green Version]
- Juan, M.L.; Righini, M.; Quidant, R. Plasmon nanooptical tweezers. Nat. Photonics 2011, 5, 349. [Google Scholar] [CrossRef]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Luo, Y.; Aubry, A.; Pendry, J.B. Electromagnetic contribution to surface-enhanced Raman scattering from rough metal surfaces: A transformation optics approach. Phys. Rev. B Condens. Matter Mater. Phys. 2011, 83, 155422. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Ye, J.; Chen, C.; Hermans, L.; Verellen, N.; Ryken, J.; Jans, H.; Van Roy, W.; Moshchalkov, V.V.; Lagae, L.; et al. Biosensing using diffractively coupled plasmonic crystals: The figure of merit revisited. Adv. Opt. Mater. 2015, 3, 176–181. [Google Scholar] [CrossRef]
- Li, X.; Ren, X.; Xie, F.; Zhang, Y.; Xu, T.; Wei, B.; Choy, W.C.H. High-performance organic solar cells with broadband absorption enhancement and reliable reproducibility enabled by collective plasmonic effects. Adv. Opt. Mater. 2015, 3, 1220–1231. [Google Scholar] [CrossRef]
- Giannini, V.; Fernández-Domínguez, A.I.; Heck, S.C.; Maier, S.A. Plasmonic nanoantennas: Fundamentals and their use in controlling the radiative properties of nanoemitters. Chem. Rev. 2011, 111, 3888–3912. [Google Scholar] [CrossRef]
- Stiens, J.; Vounckx, R.; Veretennicoff, I. Slab plasmon polaritons and waveguide modes in four-layer resonant semiconductor waveguides. J. Appl. Phys. 1997, 81, 1–4. [Google Scholar] [CrossRef]
- Singh, M.R.; Racknor, C. Nonlinear energy transfer in quantum dot and metallic nanorod nanocomposites. J. Opt. Soc. Am. B 2015, 32, 2216–2222. [Google Scholar] [CrossRef]
- Singh, M.R.; Brassem, G.; Yastrebov, S. Enhancement of Radiative and Nonradiative Emission in Random Lasing Plasmonic Nanofibers. Annalen Physik 2021, 533, 2000558. [Google Scholar] [CrossRef]
- Singh, M.R. A Review of Many-Body Interactions in Linear and Nonlinear Plasmonic Nanohybrids. Symmetry 2021, 13, 445. [Google Scholar] [CrossRef]
- Naik, G.V.; Shalaev, V.M.; Boltasseva, A. Alternative plasmonic materials: Beyond gold and silver. Adv. Mater. 2013, 25, 3264–3294. [Google Scholar] [CrossRef]
- Feigenbaum, E.; Diest, K.; Atwater, H.A. Unity-Order Index Change in Transparent Conducting Oxides at Visible Frequencies. Nano Lett. 2010, 10, 2111. [Google Scholar] [CrossRef]
- Das, S.; Salandrino, A.; Wu, J.Z.; Hui, R. Near-infrared electro-optic modulator based on plasmonic graphene. Opt. Lett. 2015, 40, 1516. [Google Scholar] [CrossRef]
- Das, S.; Fardad, S.; Kim, I.; Rho, J.; Hui, R.; Salandrino, A. Nanophotonic modal dichroism: Mode-multiplexed modulators. Opt. Lett. 2016, 41, 4394. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, A.; Alekseyev, L.; Howard, S.; Franz, K.; Wasserman, D.; Podolskiy, V.; Narimanov, E.; Sivco, D.; Gmachl, C. Negative refraction in semiconductor metamaterials. Nat. Mater. 2007, 6, 946–950. [Google Scholar] [CrossRef]
- Feng, J.; Chen, Y.; Blair, J.; Kurt, H.; Hao, R.; Citrin, D.S.; Summers, C.J.; Zhou, Z. Fabrication of annular photonic crystals by atomic layer deposition and sacrificial etching. J. Vac. Sci. Technol. B Microelectron. Nanometer Struct. 2009, 27, 568. [Google Scholar] [CrossRef]
- Peragut, F.; Cerutti, L.; Baranov, A.; Hugonin, J.P.; Taliercio, T.; de Wilde, Y.; Greffet, J.J. Hyperbolic metamaterials and surface plasmon polaritons. Optica 2017, 4, 1409–1415. [Google Scholar] [CrossRef]
- Ali, K.; Ullah, M.; Bacha, B.A.; Jabar, M.S.A. Complex conductivity-dependent two-dimensional atom microscopy. Eur. Phys. J. Plus 2019, 134, 618. [Google Scholar] [CrossRef]
- Khan, N.; Bacha, N.B.A.; Iqba, A.; Rahman, A.U.; Afaq, A. Gain-assisted superluminal propagation and rotary drag of photon and surface plasmon polaritons. Phys. Rev. A. 2017, 96, 013848. [Google Scholar] [CrossRef]
- Shekhar, P.; Atkinson, J.; Jacob, Z. Hyperbolic metamaterials: Fundamentals and applications. Nano Converg. 2014, 1, 14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Starko-Bowes, R.; Atkinson, J.; Newman, W.; Hu, H.; Kallos, T.; Palikaras, G.; Fedosejevs, R.; Pramanik, S.; Jacob, Z. Optical characterization of Epsilon Near Zero, Epsilon Near Pole and hyperbolic response in nanowire metamaterials. J. Opt. Soc. Am. B 2015, 32, 2074–2080. [Google Scholar] [CrossRef] [Green Version]
- Gric, T.; Hess, O. Surface plasmon polaritons at the interface of two nanowire metamaterials. J. Opt. 2017, 19, 085101. [Google Scholar] [CrossRef]
- Iorsh, I.; Orlov, A.; Belov, P.; Kivshar, Y. Interface modes in nanostructured metal-dielectric metamaterials. Appl. Phys. Lett. 2011, 99, 151914. [Google Scholar] [CrossRef] [Green Version]
- Ioannidis, T.; Gric, T.; Rafailov, E. Controlling surface plasmon polaritons propagating at the interface of low-dimensional acoustic metamaterials. Waves Random Complex Media 2021, submitted. [Google Scholar]
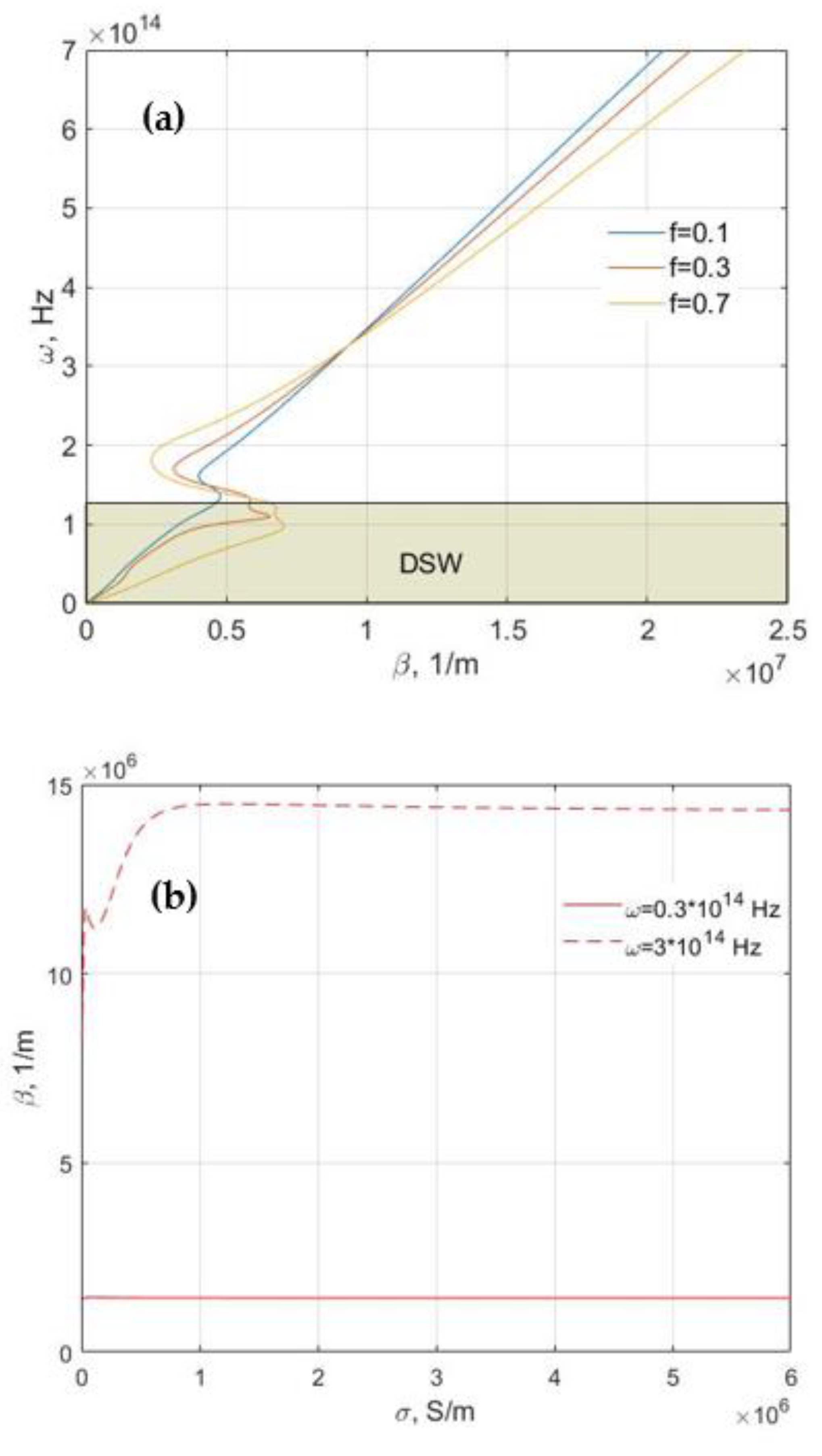
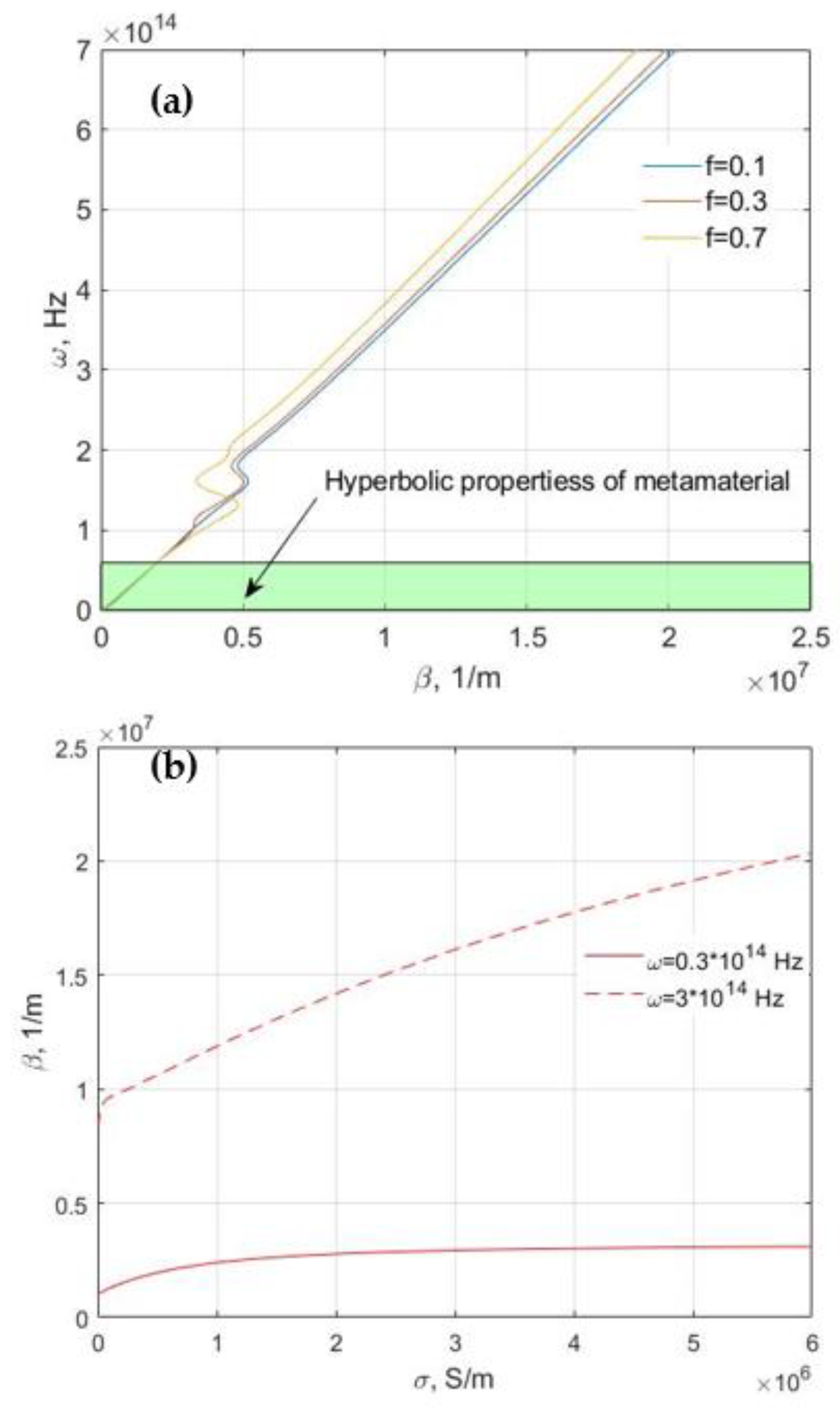
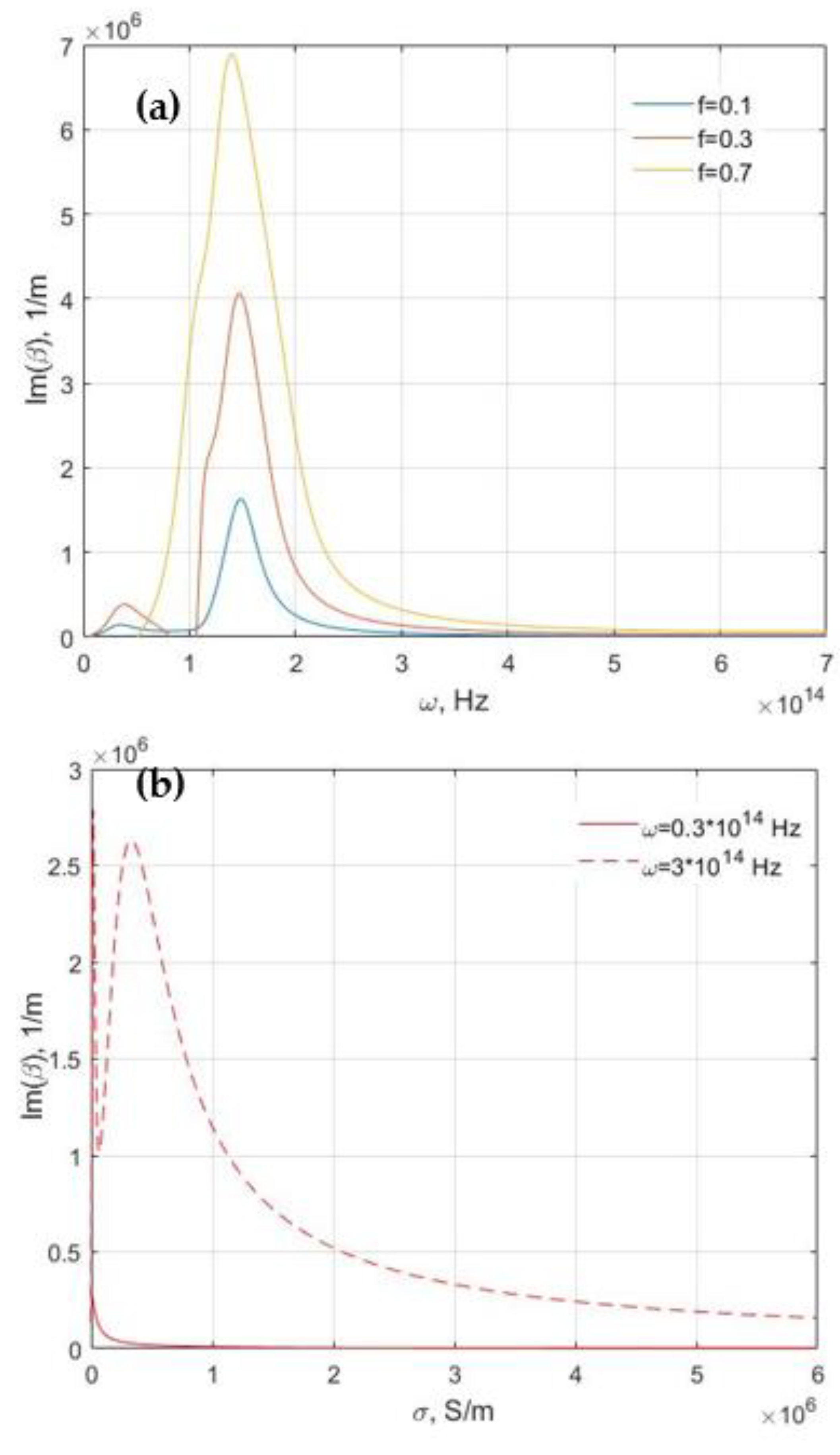
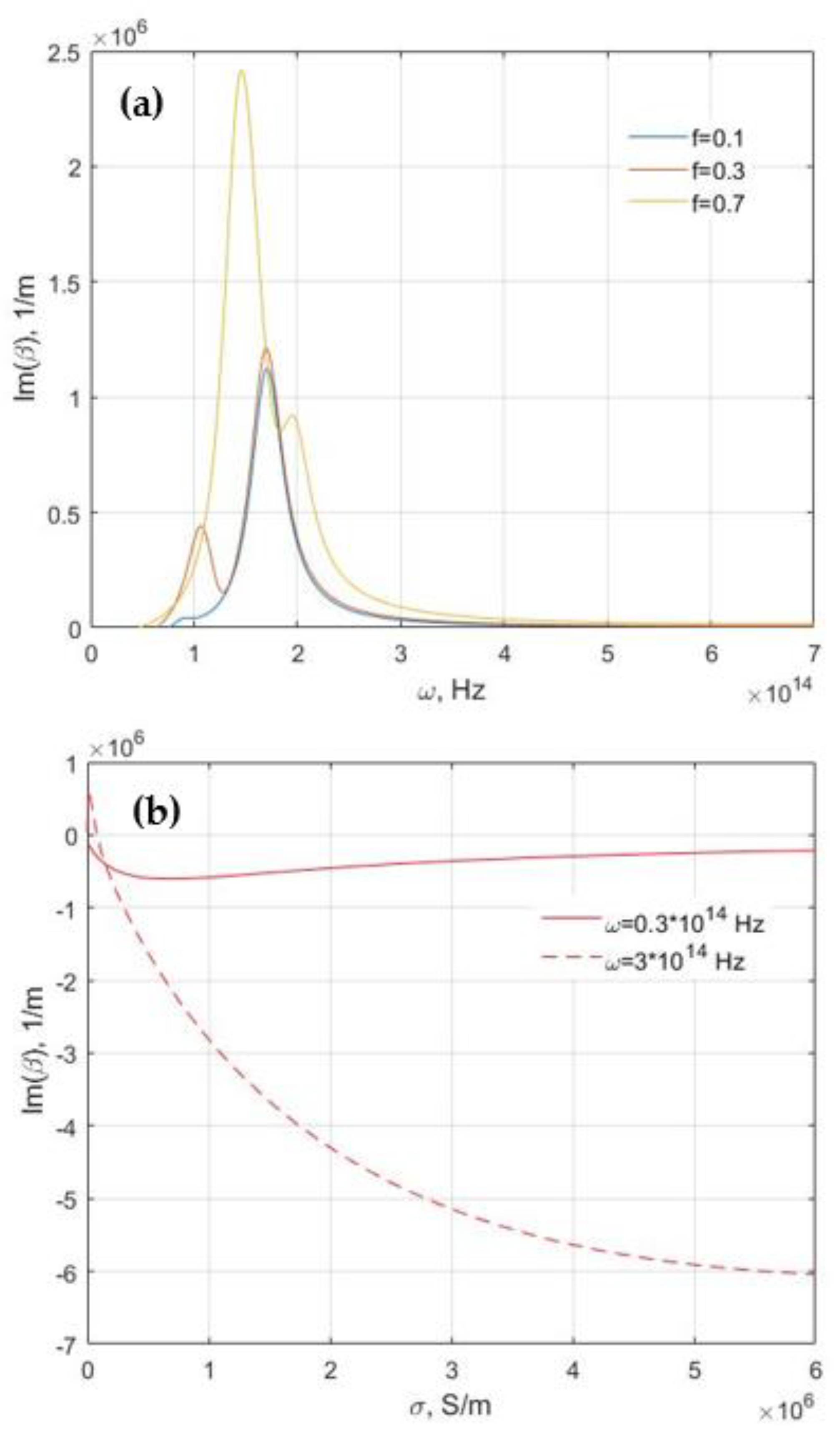
| AZO | GZO | ITO | TiN (Deposited at 800 °C) | TiN (Deposited at 500 °C) | ZrN | |
|---|---|---|---|---|---|---|
| εb | 3.54 | 3.23 | 3.53 | 4.86 | 2.49 | 3.47 |
| ωp (eV) | 1.75 | 1.99 | 1.78 | 7.93 | 5.95 | 8.02 |
| γp (eV) | 0.04 | 0.12 | 0.16 | 0.18 | 0.51 | 0.52 |
| f1 | 0.51 | 0.39 | 0.39 | 3.29 | 2.04 | 2.45 |
| ω1 (eV) | 4.29 | 4.05 | 4.21 | 4.22 | 3.95 | 5.48 |
| γ1 (eV) | 0.10 | 0.09 | 0.09 | 2.03 | 2.49 | 1.74 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ioannidis, T.; Gric, T.; Rafailov, E. The Study of the Surface Plasmon Polaritons at the Interface Separating Nanocomposite and Hypercrystal. Appl. Sci. 2021, 11, 5255. https://doi.org/10.3390/app11115255
Ioannidis T, Gric T, Rafailov E. The Study of the Surface Plasmon Polaritons at the Interface Separating Nanocomposite and Hypercrystal. Applied Sciences. 2021; 11(11):5255. https://doi.org/10.3390/app11115255
Chicago/Turabian StyleIoannidis, Thanos, Tatjana Gric, and Edik Rafailov. 2021. "The Study of the Surface Plasmon Polaritons at the Interface Separating Nanocomposite and Hypercrystal" Applied Sciences 11, no. 11: 5255. https://doi.org/10.3390/app11115255
APA StyleIoannidis, T., Gric, T., & Rafailov, E. (2021). The Study of the Surface Plasmon Polaritons at the Interface Separating Nanocomposite and Hypercrystal. Applied Sciences, 11(11), 5255. https://doi.org/10.3390/app11115255








