Vibration and Derailment Analyses of Trains Moving on Curved and Cant Rails
Abstract
:1. Introduction
2. Finite Element Simulation of Trains Moving on Curved Rails
2.1. Illustration of Coordinate Systems
2.2. Finite Element Procedures for Moving Trains on Curved Rails
2.3. A frictional Contact Finite Element for Two Wheels Moving on Curved Rails
3. Simple Theoretical Method for Wheel Forces, Wheel Sliding, and Car Overturning
3.1. Illustration of the Simple Theoretical Equations
3.2. Summary of the Proposed Simple Theoretical and Finite Element Methods
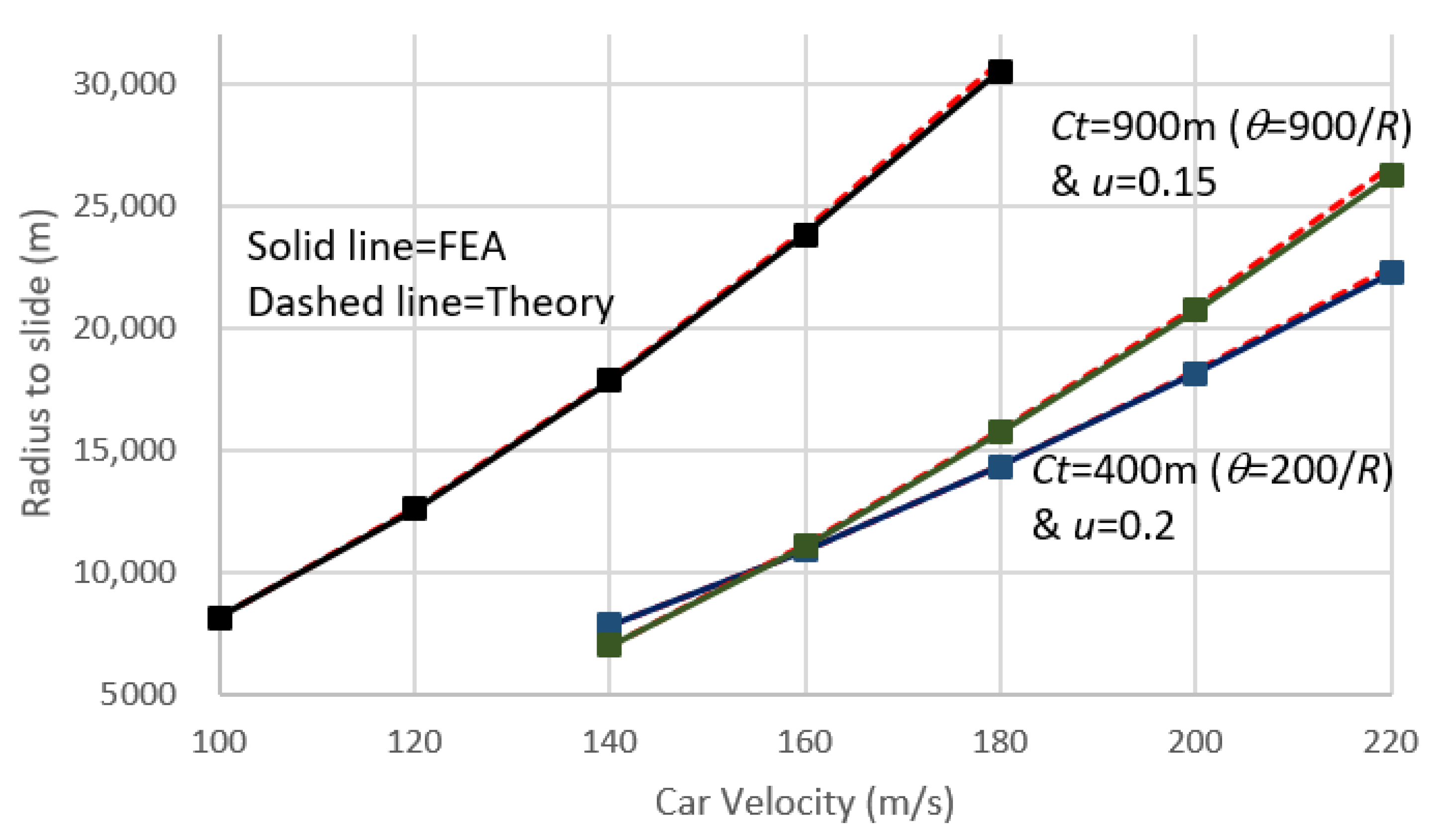
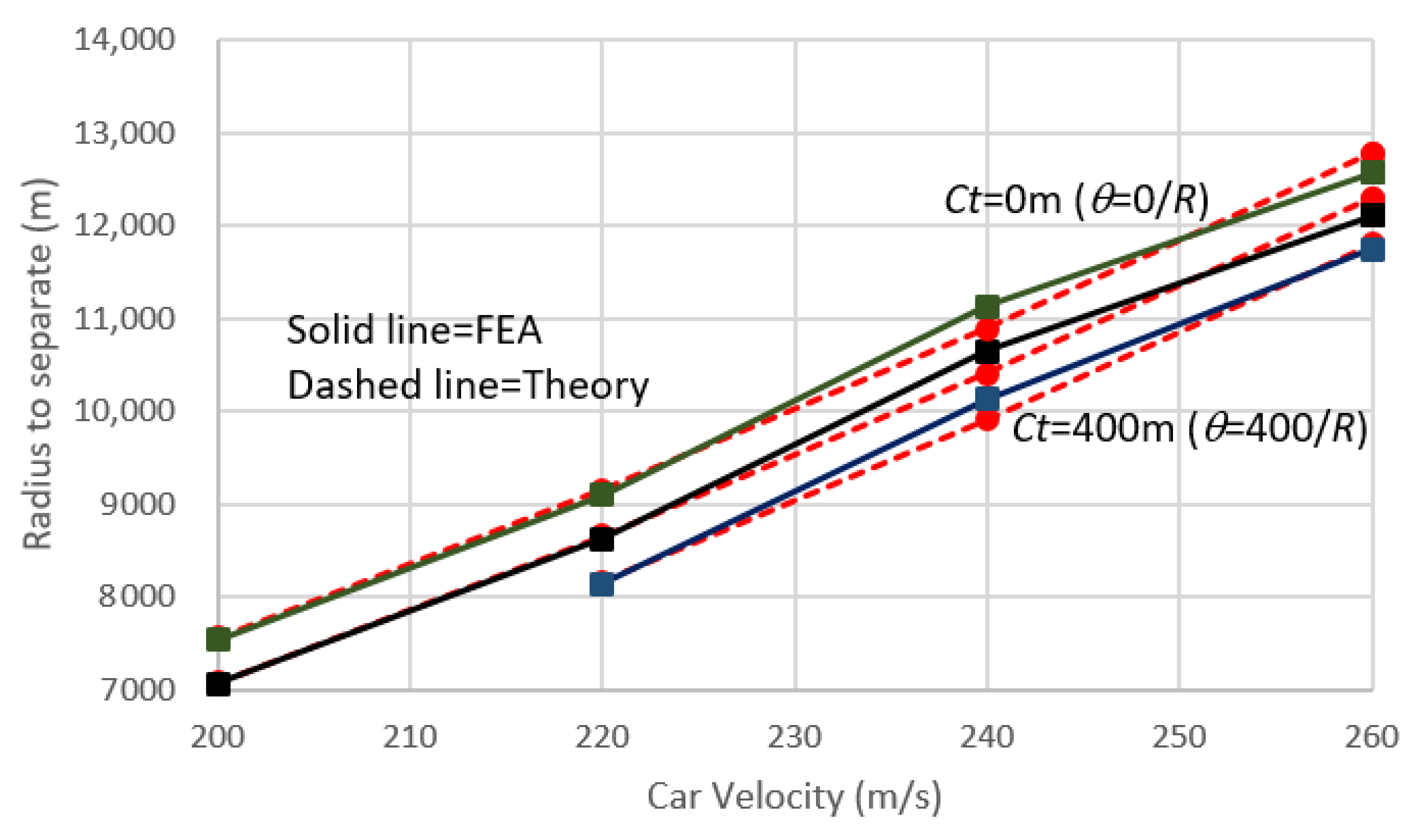
- For the use of the proposed simple theoretical method, Equation (24) can be used to check the sliding of the carriage, Equations (25) and (26) can be used to find the normal and shear forces of each wheel, and Equation (25) can be used to check the overturning of the carriage. We validate the finite element results based on the formulations in Section 4 using these equations. Moreover, all the data of the comparison of the next section were computed by the computer automatically.
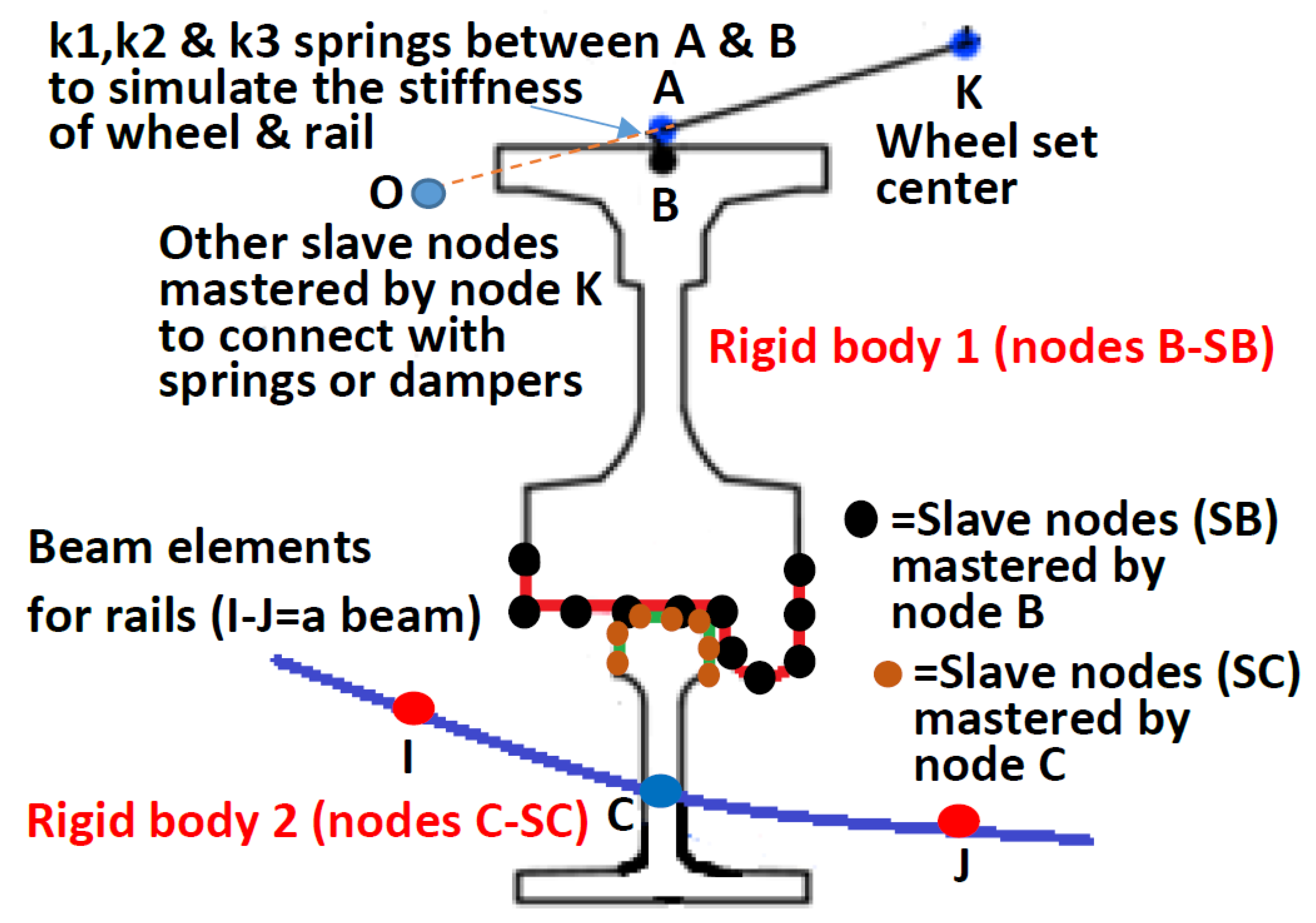
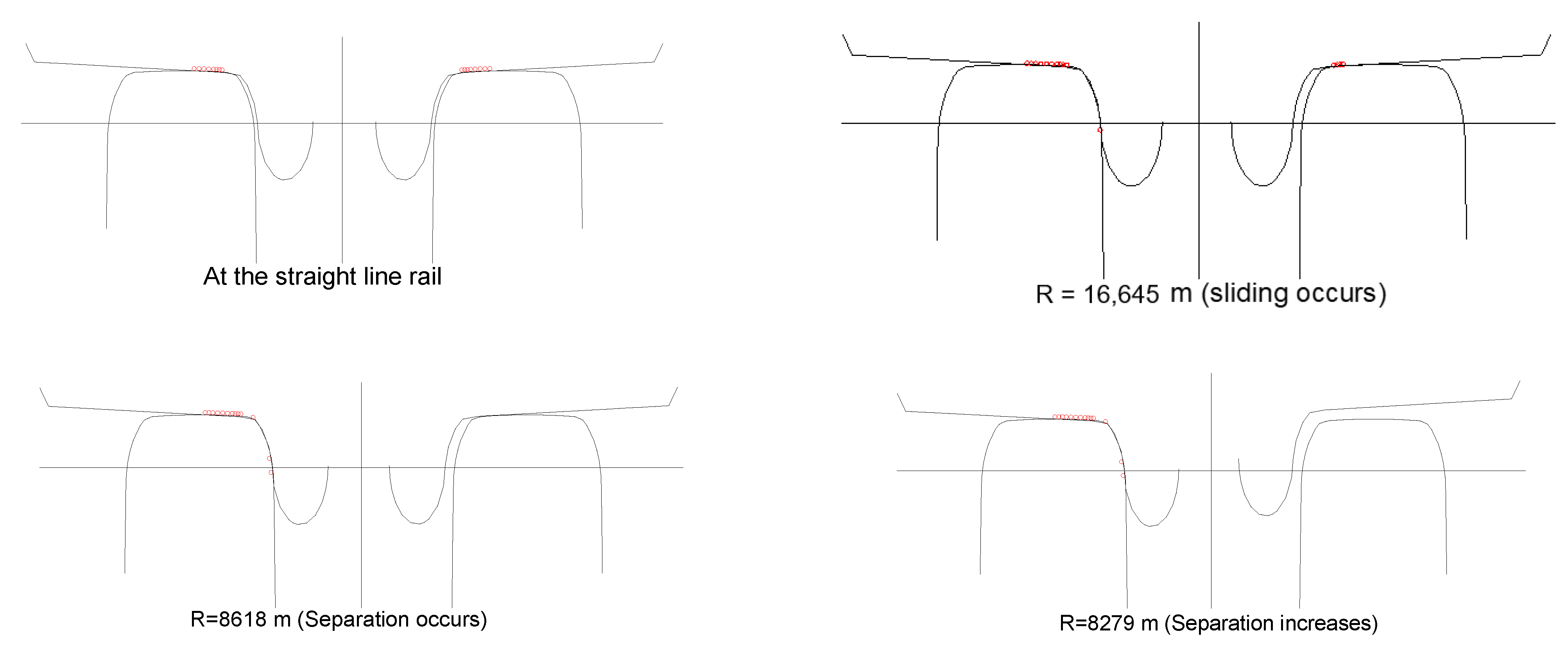
- As shown in Figure 4, the proposed moving wheel axis element requires to input the possible contact wheel and rail profiles, where slave nodes SB are mastered by node B, and slave nodes SC are mastered by node C. Thus, there are two rigid bodies contacting together according to the Mohr–Coulomb’s friction law mentioned in Section 2.3. Then, k1, k2, and k3, as shown in Figure 2 and Figure 4 are used to simulate the stiffness of the wheel and rail profiles, where k1 and k2 are constant in the lateral and longitudinal directions and k3 is set as the power low (Equation (15)) in the vertical direction. Those parameters can be obtained using the 3D static contact finite element analysis of the actual wheel and rail. Thus, the proposed moving wheel axis element can simulate the sticking, sliding, separation, and multi-point contact behavior between wheels and rails.
- The element contains 21 DOFs, where six DOFs with three translations and three rotations are set to node I, J, and K, and three translation DOFs are set to node B. The three rotation DOFs of node B and the six DOFs of node A are mastered by node K, while the purpose of the two nodes are used to arrange the location of stiffness k1, k2, and k3, and they will not connect to other elements. Nodes I and J should be connected to a beam element to simulate rails where the wheel is located between that beam. Node K is located at the wheel axle center, and springs and dampers can be connected to it using slave nodes (such as node O). For example, as shown in Figure 5, nodes 301 and 401 are mastered by node 1210 of the wheel axle center, and springs and dampers are then connected between these two nodes to link with the wheel set.
- Curved rails should be modeled using a number of beam elements, where the known position of the wheel can be used to automatically find the beam element to be located, so that a moving axis element is formed easily. Since the vibration of the train is highly dependent on a smooth rail, the curve rail system should include the straight-line, clothoid, and circular segments for the calculation of the wheel position. The centrifugal forces of the train are directly calculated from Equation (5), but not from the finite element computation, so they are exact without errors.
- A sub-program of the proposed moving wheel axis element (Figure 4) can be established using the equations in Section 2. This finite element can then be used in combination with other elements to simulate a train traveling on a curved track system, in which only the standard Newmark’s and the Newton–Raphson methods are required in the finite element main program. One may use the beam element to simulate rails and bridges, the plate element to simulate the reinforce concrete slab track system, the soil spring to simulate the ballast track system, the rigid link and lumped mass to simulate trains, and any other element to simulate the certain function of the railway. Finally, using the proposed moving wheel axis element with the above finite element mesh, one can simulate train moving on complicated railway systems without difficult.
- The simulation error is highly dependent on the used time step length (dt), where the vibration frequency of the analyzed domain larger than 1/(6dt) Hz may cause large errors. It is noted that we assume that a certain frequency vibration can be modeled appropriately at least using six time steps. Thus, one should use an appropriate time step length to perform the proposed finite element analysis.
4. Validations of the Proposed Finite Element Simulations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Pieringer, A. A numerical investigation of curve squeal in the case of constant wheel/rail friction. J. Sound Vib. 2014, 333, 4295–4313. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Dimitrakopoulos, E.G. A three-dimensional dynamic analysis scheme for the interaction between trains and curved railway bridges. Comput. Struct. 2015, 149, 43–60. [Google Scholar]
- Zeng, Q.; Dimitrakopoulos, E.G. Seismic response analysis of an interacting curved bridge–train system under frequent earthquakes. Earthq. Eng. Struct. Dyn. 2016, 45, 1129–1148. [Google Scholar] [CrossRef]
- Zeng, Q.; Yang, Y.B.; Dimitrakopoulos, E.G. Dynamic response of high-speed vehicles and sustaining curved bridges under conditions of resonance. Eng. Struct. 2016, 114, 61–74. [Google Scholar] [CrossRef]
- Han, J.; He, Y.; Xiao, X.; Sheng, X.; Zhao, G.; Jin, X. Effect of Control Measures on Wheel/Rail Noise When the Vehicle Curves. Appl. Sci. 2017, 7, 1144. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Q.; Dimitrakopoulos, E.G. Vehicle–bridge interaction analysis modeling derailment during earthquakes. Nonlinear Dyn. 2018, 93, 2315–2337. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Ngamkhanong, C.; Liu, X. Spectro-Temporal responses of curved railway tracks with variable radii of arc curves. Int. J. Struct. Stab. Dyn. 2019, 19, 1950044. [Google Scholar] [CrossRef]
- Ma, L.X.; Ouyang, H.J.; Sun, C.; Zhao, R.T.; Wang, L. A curved 2.5D model for simulating dynamic responses of coupled track-tunnel-soil system in curved section due to moving loads. J. Sound Vib. 2019, 451, 1–31. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, Y.Y.; Clarke, D.B.; Peng, Q.Y.; Dong, C.J. An innovative method for calculating diagonal lashing force of cargo on railway wagons in a curve alignment. Veh. Syst. Dyn. 2019. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Z. Numerical modeling of wheel-rail squeal-exciting contact. Int. J. Mech. Sci. 2019, 153, 490–499. [Google Scholar] [CrossRef] [Green Version]
- Li, T.; Su, Q.; Kaewunruen, S. Saturated Ground Vibration Analysis Based on a Three-Dimensional Coupled Train-Track-Soil Interaction Model. Appl. Sci. 2019, 9, 4991. [Google Scholar] [CrossRef] [Green Version]
- Ma, M.; Xu, L.H.; Du, L.L.; Wu, Z.Z.; Tan, X.Y. Prediction of building vibration induced by metro trains running in a curved tunnel. J. Vib. Control 2020. [Google Scholar] [CrossRef]
- Pan, B.; Zhang, W.; Zheng, S.; Zhou, M.L.; Zhao, C.F.; Spencer, B.F. Modelling ambient vibration responses induced by operation of metro train on curved rail segment with small curvature radius. Math. Probl. Eng. 2020, 2020, 1–17. [Google Scholar] [CrossRef] [Green Version]
- Lai, V.V.; Chiello, O.; Brunel, J.F.; Dufrenoy, P. The critical effect of rail vertical phase response in railway curve squeal generation. Int. J. Mech. Sci. 2020, 167, 105281. [Google Scholar] [CrossRef]
- Lulu, G.B.; Chen, R.; Wang, P.; Xu, J.M.; Chen, J.Y.; Fang, J.S. Random vibration analysis of tram-track interaction on a curve due to the polygonal wheel and track irregularity. Veh. Syst. Dyn. 2020. [Google Scholar] [CrossRef]
- Ju, S.H. A frictional contact finite element for wheel/rail dynamic simulations. Nonlinear Dyn. 2016, 85, 365–374. [Google Scholar] [CrossRef]
- Kalker, J.J. Variational and non-variational theory of frictionless adhesive contact between elastic bodies. Wear 1987, 119, 63–76. [Google Scholar] [CrossRef]
- Sichani, M.S. Wheel-Rail Contact Modelling in Vehicle Dynamics Simulation. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2013. [Google Scholar]
- Ju, S.H.; Rowlands, R.E. A three-dimensional frictional contact element whose stiffness matrix is symmetric. J. Appl. Mech. 1999, 66, 460–467. [Google Scholar] [CrossRef]
- Ju, S.H. A cubic-spline contact element for frictional contact problems. J. Chin. Inst. Eng. 1998, 21, 119–128. [Google Scholar] [CrossRef]
- Ju, S.H. A simple finite element for nonlinear wheel/rail contact and separation simulations. J. Vib. Control 2014, 20, 330–338. [Google Scholar] [CrossRef]
- Ro, T.-I. Study on Wheel-Rail Interaction of Moving Trains in Curved Railways. Master’s Thesis, National Cheng-kung University, Tainan, Taiwan, 2020. [Google Scholar]





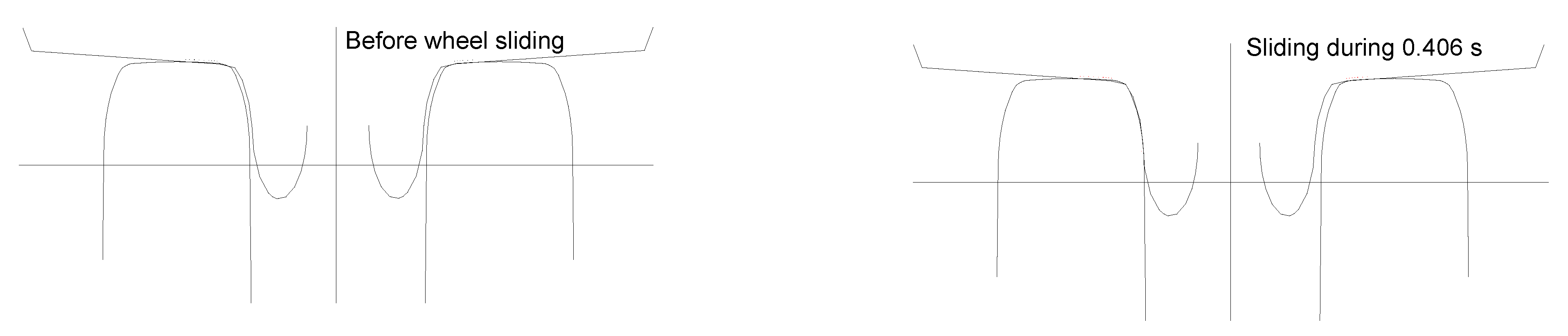

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ju, S.-H.; Ro, T.-I. Vibration and Derailment Analyses of Trains Moving on Curved and Cant Rails. Appl. Sci. 2021, 11, 5106. https://doi.org/10.3390/app11115106
Ju S-H, Ro T-I. Vibration and Derailment Analyses of Trains Moving on Curved and Cant Rails. Applied Sciences. 2021; 11(11):5106. https://doi.org/10.3390/app11115106
Chicago/Turabian StyleJu, Shen-Haw, and Ti-Iaw Ro. 2021. "Vibration and Derailment Analyses of Trains Moving on Curved and Cant Rails" Applied Sciences 11, no. 11: 5106. https://doi.org/10.3390/app11115106
APA StyleJu, S.-H., & Ro, T.-I. (2021). Vibration and Derailment Analyses of Trains Moving on Curved and Cant Rails. Applied Sciences, 11(11), 5106. https://doi.org/10.3390/app11115106






