Seismic Design and Performance Assessment of Frame Buildings Reinforced by Dual-Phase Steel
Abstract
1. Introduction
2. Mechanical Properties of Tempcore Steel and Dual-Phase Steel DPD2
3. Mathematical Modelling of Cyclic Response of Columns Reinforced with B500B and DPD2
3.1. Description of Code-Based Mathematical Modelling of Seismic Response of RC Columns
- For the steel bar in tension
- For the (unconfined) concrete
- For the steel bar in tension
- For the confined concrete core inside the steel ties
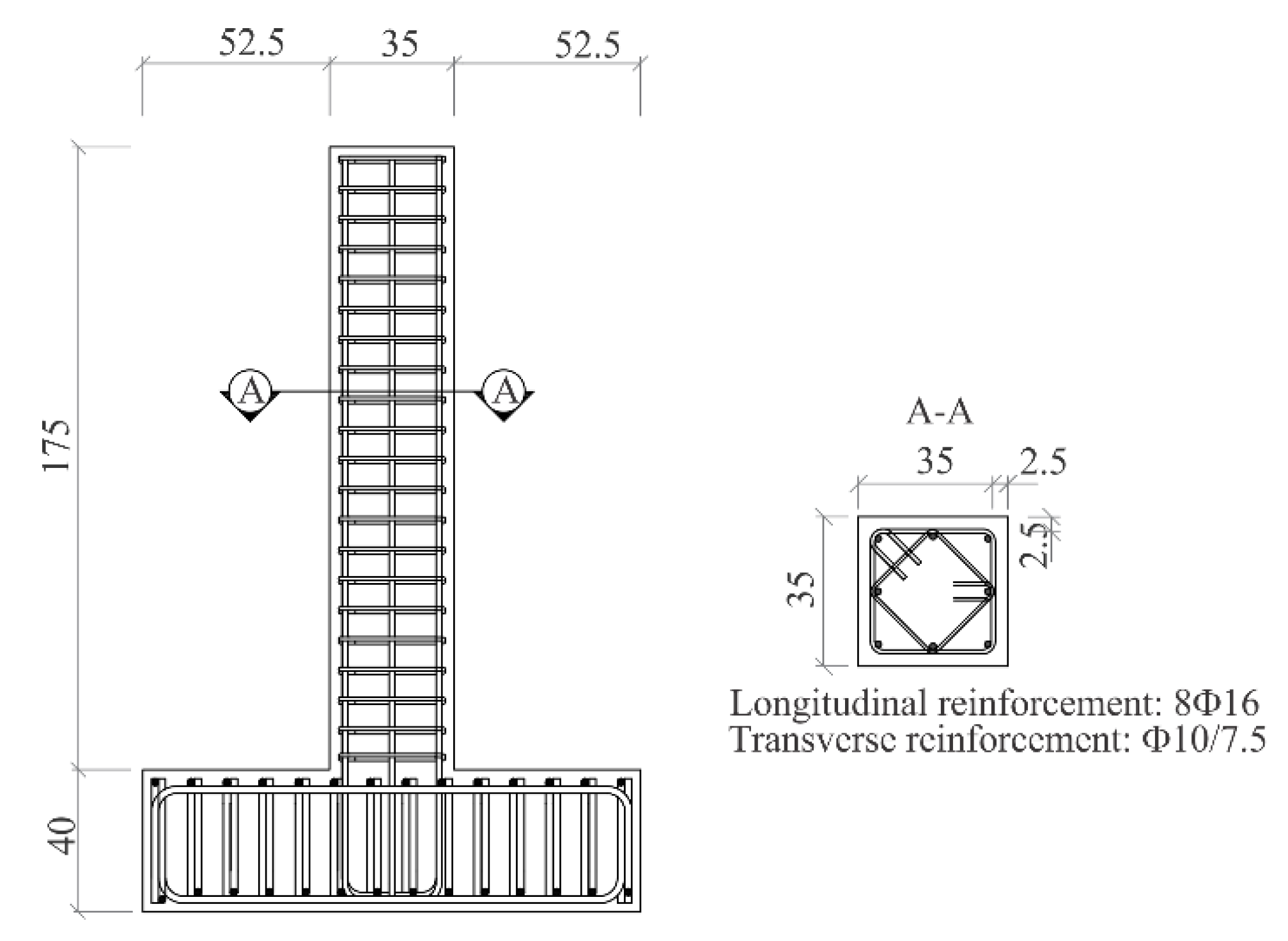
3.2. Numerical Simulation of Cyclic Test of Column Reinforced with B500B
3.3. Numerical Simulation of Cyclic Test of Column Reinforced with DPD2
4. Design and Seismic Performance Assessment of DPD2 and B500B Buildings
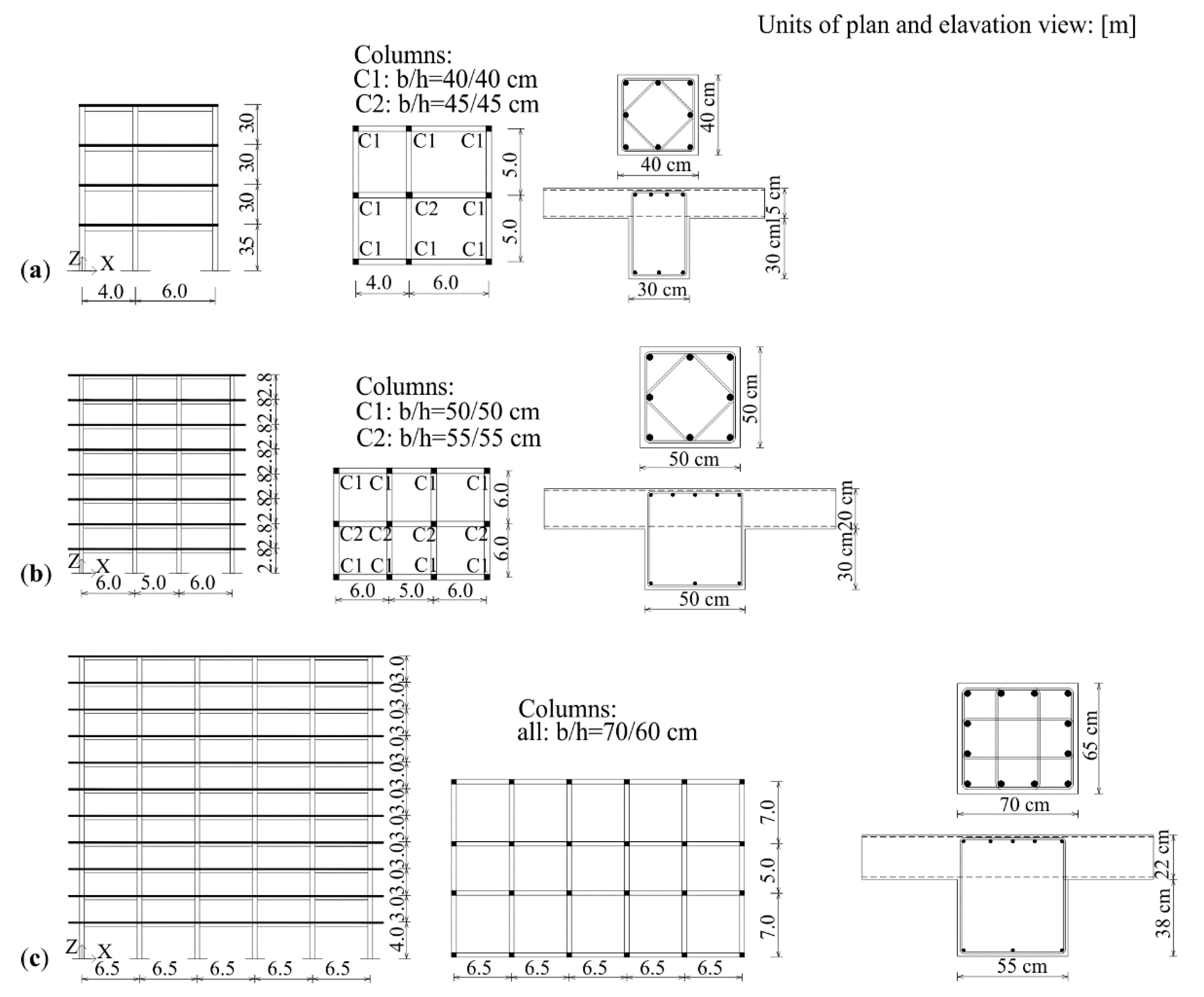
4.1. Description of Analysed Buildings
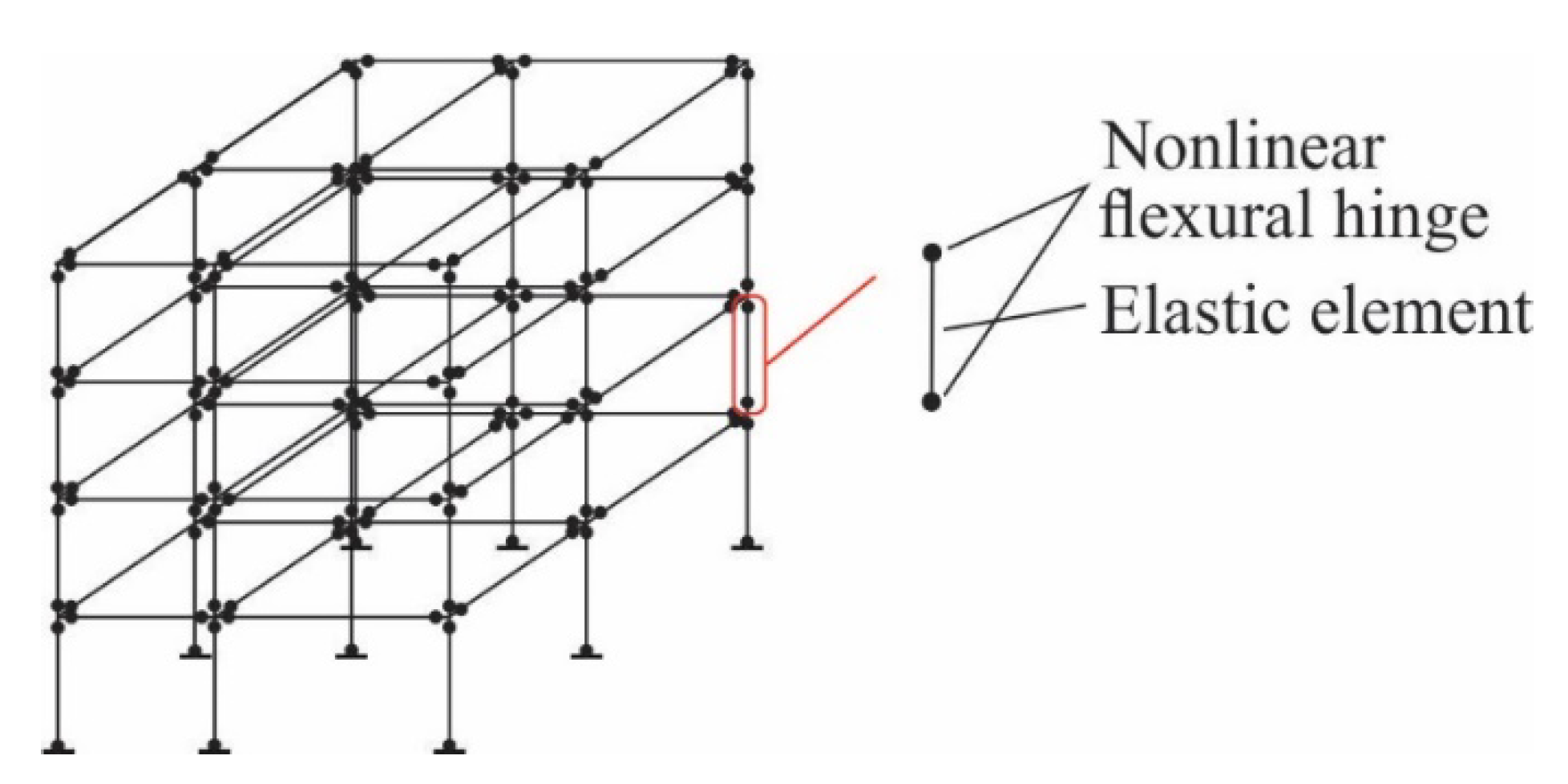
4.2. Description of Mathematical Model for Nonlinear Seismic Analysis of RC Frame Building
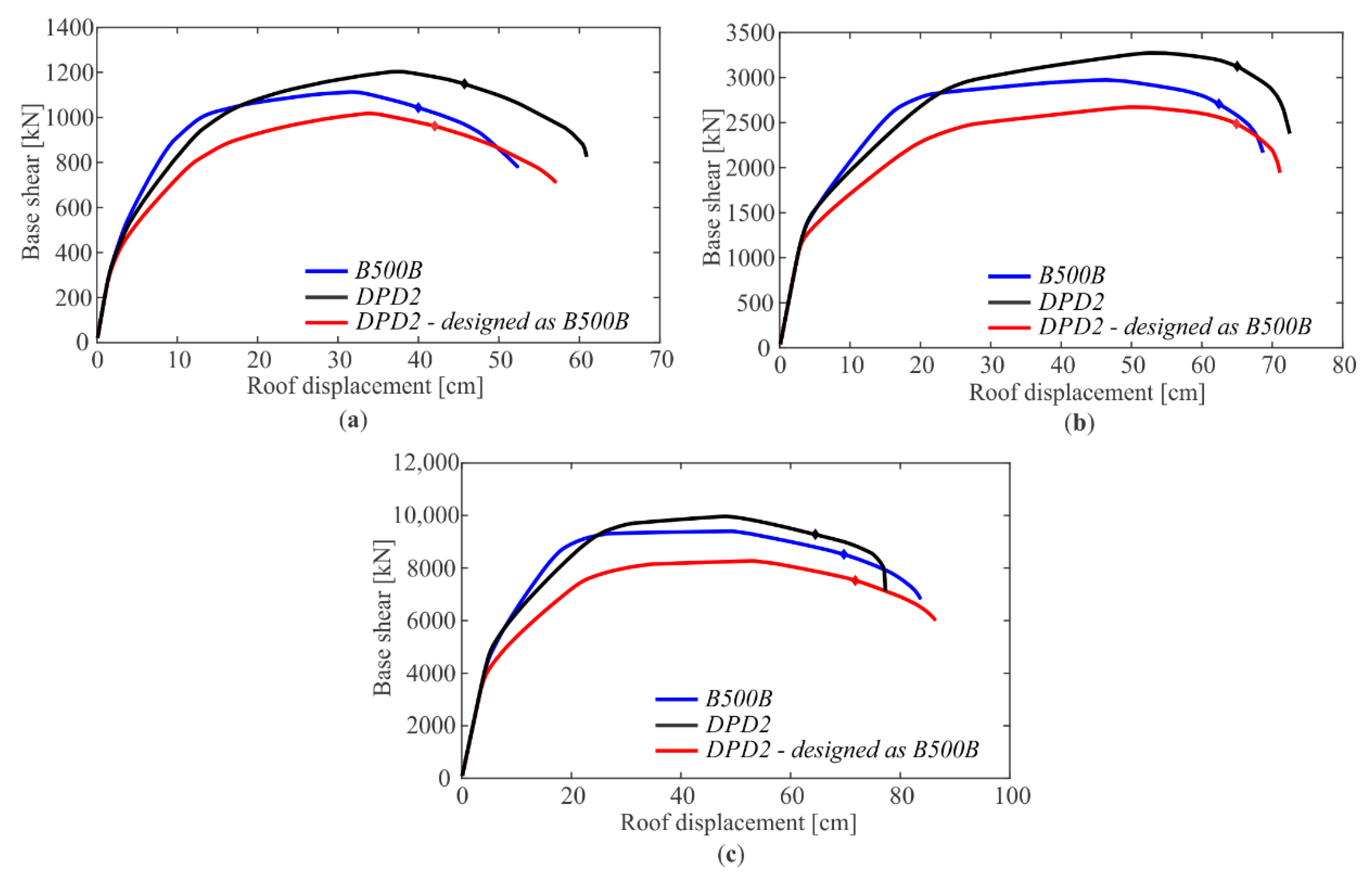
4.3. Pushover Analyses
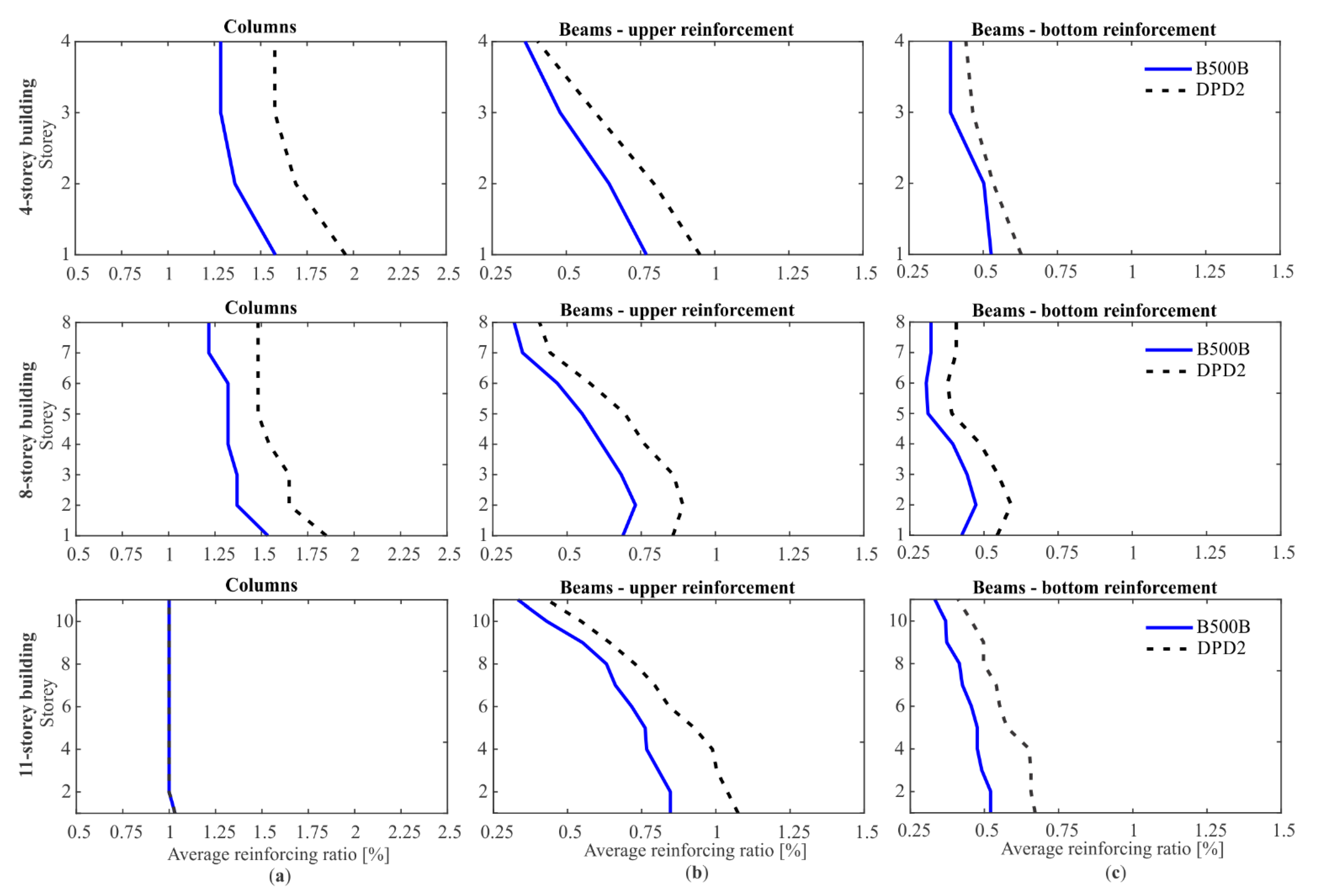
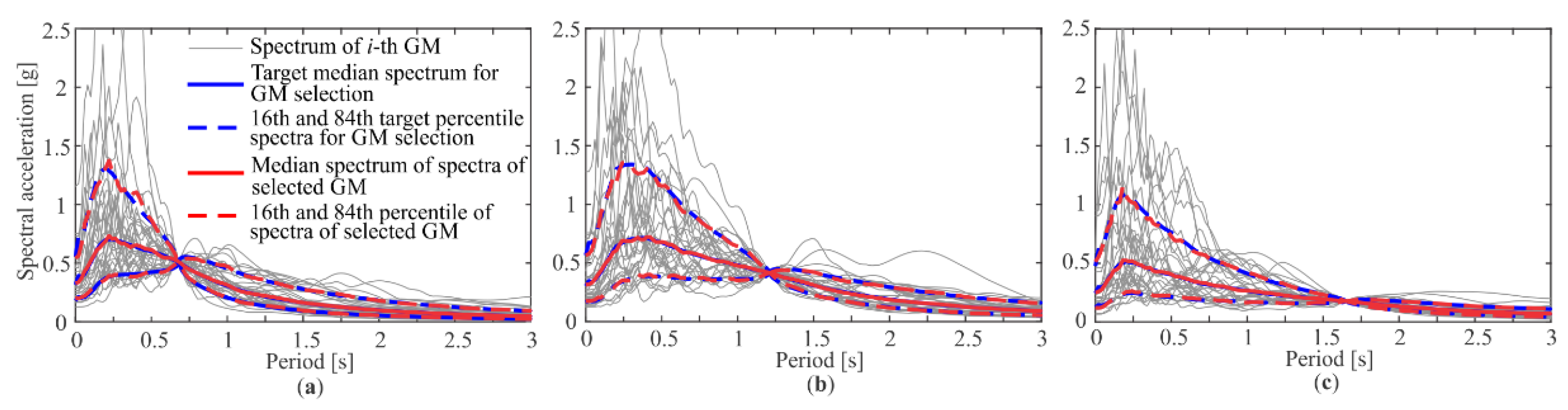
4.4. Results of Seismic Performance Assessment
5. Conclusions
- Only the yield rotation of Eurocode empirical regression models had to be calibrated to adequately simulate the moment–rotation relationship from the cyclic tests of particular columns. However, it is suggested that the modelling uncertainty is investigated further at the level of DPD2 buildings, for example, by performing a pseudo-dynamic test using the full-scale building;
- For the majority of DPD2 buildings, the maximum lateral strength (6–10%), deformation capacity (up to 15%) and seismic intensity causing a near-collapse limit state (up to 13%) were observed to be improved in comparison to B500B buildings;
- Because the seismic performance of DPD2 buildings is better than that of B500B buildings if they are designed by Eurocode 8, it can be concluded that the DPD2 reinforcing steel can be used for the construction of DPD2 buildings designed by Eurocode 8;
- The reinforcement quantity of DPD2 buildings is increased in the design primarily because of the smaller yield strength of DPD2 steel. However, this is not a prevailing source of the improved lateral strength of DPD2 buildings;
- The improved performance of the DPD2 building in terms of strength is attributed to substantial strain hardening of the DPD2 steel after the yielding point, which is not the case for the Tempcore steel with a typical yielding plateau;
- DPD2 reinforcing steel improves seismic resistance and resistance against corrosion, but also increases the amount of reinforcement required. However, some modifications to the existing design rules may also be introduced in the future, aiming to decrease the required amount of reinforcement and to modify the minimum required amount of reinforcement.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| B500B | Tempcore reinforcing steel with B500B characteristics |
| DPD2 | Dual phase reinforcing steel type D2 |
| DPF2 | Dual phase reinforcing steel type F2 |
| DPD2 | Dual phase reinforcing steel type D2 |
| CP1-CP3 | three characteristic points of three-linear backbone |
| CR | characteristic point of the moment-rotation relationship associated with cracking of cross-section |
| M | characteristic point of the moment-rotation relationship associated with a maximum moment of cross-section |
| NC | near collapse limit state/characteristic point of the moment-rotation relationship associated with the near-collapse limit state of an element |
| RC | reinforced concrete |
| Y | characteristic point of the moment-rotation relationship associated with yielding of cross-section |
| Ac | cross-sectional area |
| Agt | deformation at a maximum strength of reinforcing steel |
| Asw | area of the transverse reinforcement bars of cross-section |
| A5 | deformation of rupture of the bar |
| Ec | elastic modulus of concrete |
| EI | product of elastic modulus of concrete and moment of inertia of the cross-section |
| Fb | design base shear |
| Fmax | maximum base shear |
| K | confinement factor |
| Lpl | length of the plastic hinge |
| LV | length between the plastic hinge and the point of zero moment |
| MCR | moment at cracking of cross-section |
| MM | maximum moment of cross-section |
| MNC | moment corresponding to near-collapse limit state, which was defined at 80% of MM |
| MY | moment at yielding od cross-section |
| N | axial force, which is considered to be positive for compression |
| Nb,compr | number of bars near the extreme compression fibres |
| PC,a | target (acceptable) annual probability of collapse |
| Se,D(T1) | spectral acceleration corresponding to first vibration mode from the elastic spectrum |
| Se,C | median spectral accelerations at the first vibration period causing the collapse of the structure |
| Se,NC | median spectral accelerations at first vibration period causing a near-collapse limit state |
| Se,NC,a | risk-targeted spectral acceleration causing NC of structure |
| Se,2475 | spectral acceleration for a return period of 2475 years |
| T1 | first fundamental period |
| W | weight of the structure |
| agD,R | design peak ground acceleration |
| aVz | tension shift of the bending moment diagram |
| db | bar diameter |
| dbl | (mean) diameter of the tension reinforcement |
| bi | i-th centreline spacing between longitudinal bars laterally restrained by a stirrup corner or hook |
| bw | width of the cross-section |
| bo | width of the rectangular of the confined concrete measured to the centreline of the perimeter bar |
| dNC | roof displacement at near-collapse limit state |
| fc | concrete compressive strength of (unconfined) concrete |
| fcc | confined concrete maximum compressive strength |
| fct | axial tensile strength of concrete |
| fu | mean value of the maximum tensile strength of reinforcing steel |
| fyd,DPD2 | design yield strength of the DPD2 reinforcing steel |
| fyd,B500B | design yield strength of the B500B reinforcing steel |
| fy,k | characteristic yield strength of reinforcing steel |
| fy,m | mean yield strength |
| fy | yield strength of the steel |
| fyw | mean yield strength of transverse steel |
| h | depth of the rectangular cross-section/the depth of the unspalled section |
| ho | depth of the rectangular of the confined concrete measured to the centreline of the perimeter bar |
| k | hardening ratio of reinforcing steel |
| n | number of longitudinal bars laterally restrained along the perimeter of the cross-section |
| rCM | ratio between θC and θM |
| sw | spacing of the stirrups measured from the centreline. |
| vs,30 | shear-wave velocity at last 30 m |
| Δθu,slip | post-yield fixed-end rotation due to yield penetration |
| θC | rotation at zero moment |
| θM | rotation at maximum moment |
| θNC | rotation at near-collapse limit state |
| θY | yield rotation |
| ϕ | diameter of bar |
| α | confinement effectiveness factor |
| βSe,C | dispersion of the spectral acceleration causing collapse |
| γls | limit-state reduction factor |
| εcu | ultimate compressive strain of unconfined concrete. |
| εcu,c | ultimate compressive strain of confined concrete |
| εc0 | compressive strain in the concrete at maximum strength |
| εc0,c | strain at the confined concrete maximum compressive strength |
| εsu | ultimate tension strain of bar |
| εsu,nom | uniform elongation at tensile strength in a standard steel coupon test |
| εsy | yield strain of the steel |
| εt | tensile strain at fct |
| ν | normalised axial force |
| ρsv | volumetric ratio of transverse reinforcement defined as the volume of confining hoops over the volume of a concrete core |
| ρsw | ratio of transverse reinforcement |
| φy | yield curvature of a cross-section |
| φu | ultimate curvature of a cross-section |
References
- Berto, L.; Caprili, S.; Saetta, A.; Salvatore, W.; Talledo, D. Corrosion effects on the seismic response of existing rc frames designed according to different building codes. Eng. Struct. 2020, 216, 110397. [Google Scholar] [CrossRef]
- Val, D.V.; Stewart, M.G. Reliability Assessment of ageing reinforced concrete structures–Current situation and future challenges. Struct. Eng. Int. 2009, 19, 211–219. [Google Scholar] [CrossRef]
- Anoop, M.B.; Rao, K.B. Seismic damage estimation of reinforced concrete framed structures affected by chloride-induced corrosion. Earthq. Struct. 2015, 9, 851–873. [Google Scholar] [CrossRef]
- Yuksel, I.; Coskan, S. Earthquake response of reinforced concrete frame structures subjected to rebar corrosion. Earthq. Struct. 2013, 5, 321–341. [Google Scholar] [CrossRef]
- Apostolopoulos, C.A. Mechanical behavior of corroded reinforcing steel bars S500s tempcore under low cycle fatigue. Constr. Build. Mater. 2007, 21, 1447–1456. [Google Scholar] [CrossRef]
- Caprili, S.; Salvatore, W. Cyclic behaviour of uncorroded and corroded steel reinforcing bars. Constr. Build. Mater. 2015, 76, 168–186. [Google Scholar] [CrossRef]
- Meda, A.; Mostosi, S.; Rinaldi, Z.; Riva, P. Experimental evaluation of the corrosion influence on the cyclic behaviour of RC columns. Eng. Struct. 2014, 76, 112–123. [Google Scholar] [CrossRef]
- Celarec, D.; Vamvatsikos, D.; Dolšek, M. Simplified estimation of seismic risk for reinforced concrete buildings with consideration of corrosion over time. Bull. Earthq. Eng. 2011, 9, 1137–1155. [Google Scholar] [CrossRef]
- Xiong, C.; Deng, X.; Liang, Y.; Li, Q.; Huang, J.; Lin, X.; Li, D. Regional seismic damage simulation of corroded RC frame structures: A case study of Shenzhen City. Appl. Sci. 2020, 10, 4818. [Google Scholar] [CrossRef]
- Lavorato, D.; Fiorentino, G.; Pelle, A.; Rasulo, A.; Bergami, A.V.; Briseghella, B.; Nuti, C. A corrosion model for the interpretation of cyclic behavior of reinforced concrete sections. Struct. Concr. 2020, 21, 1732–1746. [Google Scholar] [CrossRef]
- Maraveas, C. Durability issues and corrosion of structural materials and systems in farm environment. Appl. Sci. 2020, 10, 990. [Google Scholar] [CrossRef]
- Al-Obaidi, S.; Bamonte, P.; Ferrara, L.; Luchini, M.; Mazzantini, I. Durability-based design of structures made with ultra-high-performance/ultra-high-durability concrete in extremely aggressive scenarios: Application to a geothermal water basin case study. Infrastructures 2020, 5, 102. [Google Scholar] [CrossRef]
- CEN. EN1992-1-1, Eurocode 2: Design of Concrete Structures–Part 1-1: General Rules and Rules for Buildings; European Committee for Standardisation: Brussels, Belgium, 2004. [Google Scholar]
- Lollini, F.; Carsana, M.; Gastaldi, M.; Redaelli, E. Corrosion behaviour of stainless steel reinforcement in concrete. Corros. Rev. 2019, 37, 3–19. [Google Scholar] [CrossRef]
- Gu, L.; Meng, X.H. Review on research and application of stainless steel reinforced concrete. In Proceedings of the International Conference on Mechatronics, Manufacturing and Materials Engineering (MMME 2016), Hong Kong, China, 11–12 June 2016. [Google Scholar]
- Maffei, B.; Salvatore, W.; Valentini, R. Dual-phase steel rebars for high-ductile r.c. structures, Part 1: Microstructural and mechanical characterization of steel rebars. Eng. Struct. 2007, 29, 3325–3332. [Google Scholar] [CrossRef]
- Salvatore, W.; Buratti, G.; Maffei, B.; Valentini, R. Dual-phase steel re-bars for high-ductile r.c. structures, Part 2: Rotational capacity of beams. Eng. Struct. 2007, 29, 3333–3341. [Google Scholar] [CrossRef]
- Lorusso, H.; Burgueño, A.; Egidi, D.; Svoboda, H. Application of dual phase steels in wires for reinforcement of concrete structures. Procedia Mater. Sci. 2012, 1, 118–125. [Google Scholar] [CrossRef][Green Version]
- Caprili, S.; Salvatore, W.; Valentini, R.; Ascanio, C.; Luvarà, G. A new generation of high-ductile dual-phase steel reinforcing bars. Constr. Build. Mater. 2018, 179, 66–79. [Google Scholar] [CrossRef]
- Caprili, S.; Mattei, F.; Salvatore, W.; Ascanio, C.; Luvarà, G. Industrial and techno-economic feasibility of concrete structures reinforced with DP rebars. Constr. Build. Mater. 2021, 283, 122793. [Google Scholar] [CrossRef]
- Caprili, S.; Salvatore, W.; Valentini, R.; Ascanio, C.; Luvarà, G. Dual-phase steel reinforcing bars in uncorroded and corroded conditions. Constr. Build. Mater. 2019, 218, 162–175. [Google Scholar] [CrossRef]
- Bautista, A.; Pomares, J.C.; González, M.N.; Velasco, F. Influence of the microstructure of TMT reinforcing bars on their corrosion behavior in concrete with chlorides. Constr. Build. Mater. 2019, 229, 116899. [Google Scholar] [CrossRef]
- CEN. EN1998-1, Eurocode 8: Design of Structures for Earthquake Resistance–Part 1: General Rules, Seismic Actions and Rules for Buildings; European Committee for Standardisation: Brussels, Belgium, 2004. [Google Scholar]
- Dolšek, M.; Kramar, M.; Gams, M.; Bohinc, U.; Anžlin, A.; Lajkovič, G.; Mihelčič, F.; Požonec, V. Poročilo o preizkusih armiranobetonskih stebrov za ARRS projekt J2-5461; Slovenian National Building and Civil Engineering Institute: Ljubljana, Slovenija, 2016. (In Slovenian) [Google Scholar]
- Caprili, S.; Chellini, G.; Mattei, F.; Romis, F.; Salvatore, W. NEWREBAR Research Project: Deliverable, D.4.1: Report on Design, Execution and Results of Tests on Full-Scale Prototypes; University of Pisa, Department of Civil and Industrial Engineering: Pisa, Italy, 2019. [Google Scholar]
- Apostolopoulos, C.A.; Papadakis, V.G. Consequences of steel corrosion on the ductility properties of reinforcement bar. Constr. Build. Mater. 2008, 22, 2316–2324. [Google Scholar] [CrossRef]
- Salvatore, W.; Caprili, S.; Braconi, A.; Finetto, M.; Bianco, L.; Ascanio, C.; Moersch, J.; Apostolopoulos, C.; Ferreira Pimenta, G. Effects of Corrosion on Low-Cycle Fatigue (Seismic) Behaviour of High-Strength Steel Reinforcing Bars (RUSTEEL); Publications Office of the European Union: Luxembourg, 2014. [Google Scholar]
- Colla, V.; De Sanctis, M.; Dimatteo, A.; Lovicu, G.; Solina, A.; Valentini, R. Strain hardening behavior of dual-phase steels. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2009, 40, 2557–2567. [Google Scholar] [CrossRef]
- Caprili, S.; Salvatore, W.; Valentini, R.; Apostolopoulos, C.; Drakakaki, I.; Cabral, A.M.; Reis, S. NEWREBAR research project: Deliverable, D.2.1: Report on Mechanical, Micro-Structural and Corrosion Properties of Reinforcing Selected DP Steel Rebars; University of Pisa, Department of Civil and Industrial Engineering: Pisa, Italy, 2019. [Google Scholar]
- McKenna, F.; Fenves, G.L. Open System for Earthquake Engineering Simulation (OpenSees). Available online: http://opensees.berkeley.edu (accessed on 14 March 2018).
- Ferreira, T.M.; Costa, A.A.; Vicente, R.; Varum, H. A simplified four-branch model for the analytical study of the out-of-plane performance of regular stone URM walls. Eng. Struct. 2015, 83, 140–153. [Google Scholar] [CrossRef]
- OpenSees Concrete04 Material. Available online: http://opensees.berkeley.edu/OpenSees/manuals/usermanual/1626.htm (accessed on 20 January 2021).
- CEN. wdEN1998-3 NEN SC8 PT3, Eurocode 8: Design of Structures for Earthquake Resistance–Part 3: Assessment and Retrofitting of Buildings and Bridges; CEN European Committee for Standardisation: Brussels, Belgium, 2018. [Google Scholar]
- Wang, P.; Shi, Q.; Wang, F.; Wang, Q. Seismic behaviour of concrete columns with high-strength stirrups. Earthq. Struct. 2020, 18, 15–25. [Google Scholar] [CrossRef]
- OpenSees MultiLinear Material. Available online: http://opensees.berkeley.edu/wiki/index.php/MultiLinear_Material (accessed on 20 January 2021).
- CEN. EN1998-3, Eurocode 8: Design of Structures for Earthquake Resistance–Part 3: Assessment and Retrofitting of Buildings; European Committee for Standardisation: Brussels, Belgium, 2005. [Google Scholar]
- Dolsek, M. Development of computing environment for the seismic performance assessment of reinforced concrete frames by using simplified nonlinear models. Bull. Earthq. Eng. 2010, 8, 1309–1329. [Google Scholar] [CrossRef]
- Liu, Z.; Li, S. Development of an ANN-based lumped plasticity model of RC columns using historical pseudo-static cyclic test data. Appl. Sci. 2019, 9, 4263. [Google Scholar] [CrossRef]
- Taylor, A.W.; Kuo, C.; Wellenius, K.; Chung, D. A Summary of Cyclic Lateral Load Tests on Rectangular Reinforced Concrete Columns; Building and Fire Research Laboratory, National Institute of Standards and Technology: Gaithersburg, MA, USA, 1997. [Google Scholar]
- Rasulo, A.; Pelle, A.; Lavorato, D.; Fiorentino, G.; Nuti, C.; Briseghella, B. Finite element analysis of reinforced concrete bridge piers including a flexure-shear interaction model. Appl. Sci. 2020, 10, 2209. [Google Scholar] [CrossRef]
- Žižmond, J.; Dolšek, M. Evaluation of factors influencing the earthquake-resistant design of reinforced concrete frames according to Eurocode 8. Struct. Infrastruct. Eng. 2016, 12, 1323–1341. [Google Scholar] [CrossRef]
- Žižmond, J.; Dolšek, M. Modeliranje efektivne širine pasnice grede za nelinearno analizo armiranobetonske okvirne stavbe (Modelling of effective flange width of beam for nonlinear analysis of reinforced concrete frame building). Gradb. Vestn. 2014, 63, 26–39. (In Slovenian) [Google Scholar]
- Rasulo, A.; Pelle, A.; Lavorato, D.; Fiorentino, G.; Nuti, C.; Briseghella, B. Seismic assessment of reinforced concrete frames: Influence of shear-flexure interaction and rebar corrosion. In International Conference on Computational Science and Its Applications; Gervasi, O., Murgante, B., Misra, S., Garau, C., Blečić, I., Taniar, D., Apduhan, B.O., Rocha, A.M.A.C., Tarantino, E., Torre, C.M., et al., Eds.; Springer: Cham, Switzerland, 2020; pp. 463–478. [Google Scholar]
- Lazar Sinković, N.; Brozovič, M.; Dolšek, M. Risk-based seismic design for collapse safety. Earthq. Eng. Struct. Dyn. 2016, 45, 1451–1471. [Google Scholar] [CrossRef]
- Zoubek, B.; Isakovic, T.; Fahjan, Y.; Fischinger, M. Cyclic failure analysis of the beam-to-column dowel connections in precast industrial buildings. Eng. Struct. 2013, 52, 179–191. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Baker, J.W. Conditional mean spectrum: Tool for ground-motion selection. J. Struct. Eng. 2011, 137, 322–331. [Google Scholar] [CrossRef]
- Woessner, J.; Laurentiu, D.; Giardini, D.; Crowley, H.; Cotton, F.; Grünthal, G.; Valensise, G.; Arvidsson, R.; Basili, R.; Demircioglu, M.B.; et al. The 2013 European seismic hazard model: Key components and results. Bull. Earthq. Eng. 2015, 13, 3553–3596. [Google Scholar] [CrossRef]
- Chiou, B.; Darragh, R.; Gregor, N.; Silva, W. NGA project strong-motion database. Earthq. Spectra 2008, 24, 23–44. [Google Scholar] [CrossRef]
- Akkar, S.; Sandikkaya, M.A.; Şenyurt, M.; Azari Sisi, A.; Ay, B.O.; Traversa, P.; Douglas, J.; Cotton, F.; Luzi, L.; Hernandez, B.; et al. Reference database for seismic ground-motion in Europe (RESORCE). Bull. Earthq. Eng. 2014, 12, 311–339. [Google Scholar] [CrossRef]
- Žižmond, J.; Dolšek, M. Formulation of risk-targeted seismic action for the force-based seismic design of structures. Earthq. Eng. Struct. Dyn. 2019, 48, 1406–1428. [Google Scholar] [CrossRef]
- ATC. FEMA P695, Quantification of Building Seismic Performance Factors; Federal Emergency Management Agency: Washington, DC, USA, 2009. [Google Scholar]
- Dolšek, M.; Lazar Sinković, N.; Žižmond, J. IM-based and EDP-based decision models for the verification of the seismic collapse safety of buildings. Earthq. Eng. Struct. Dyn. 2017, 46, 1–18. [Google Scholar] [CrossRef]
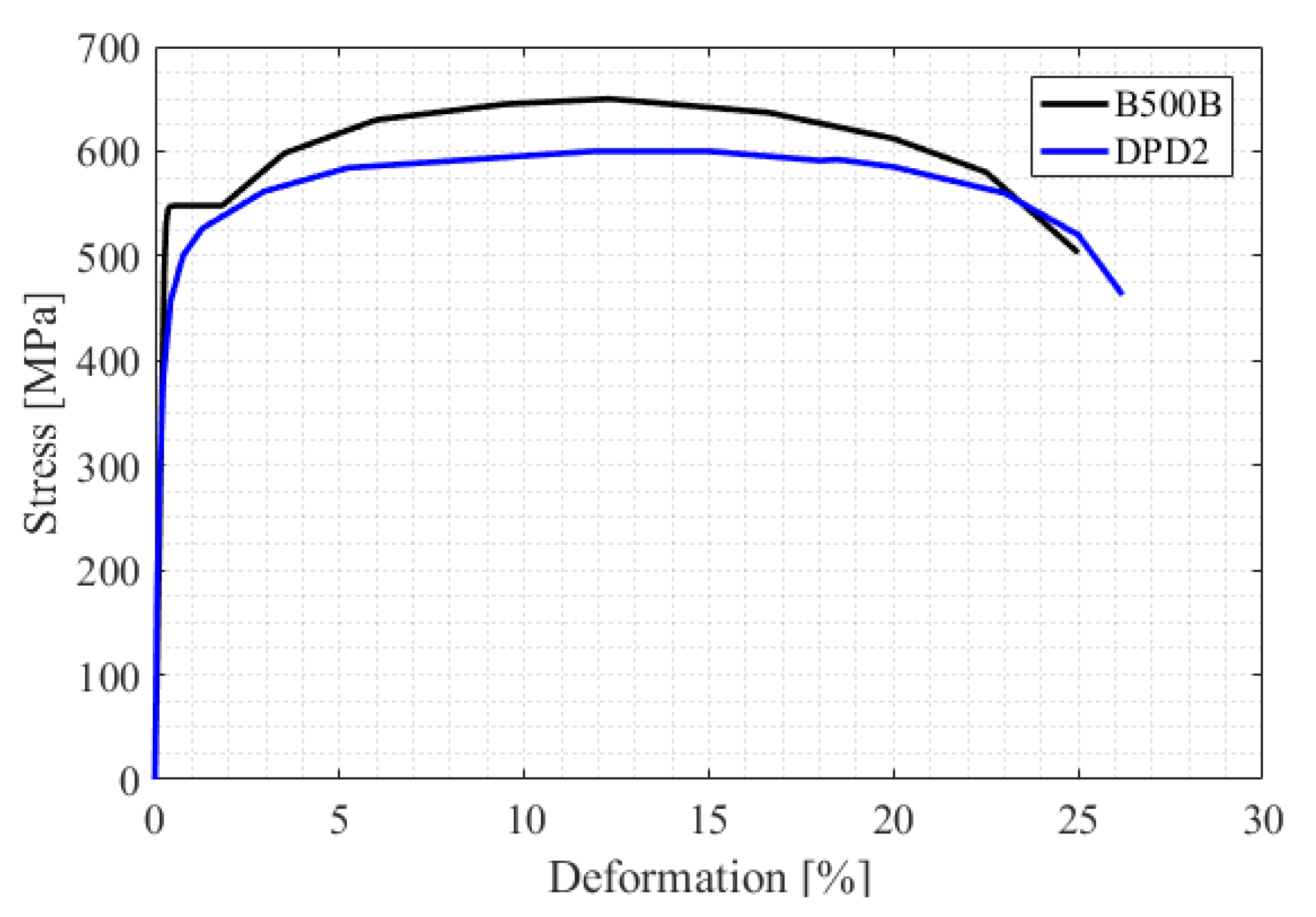

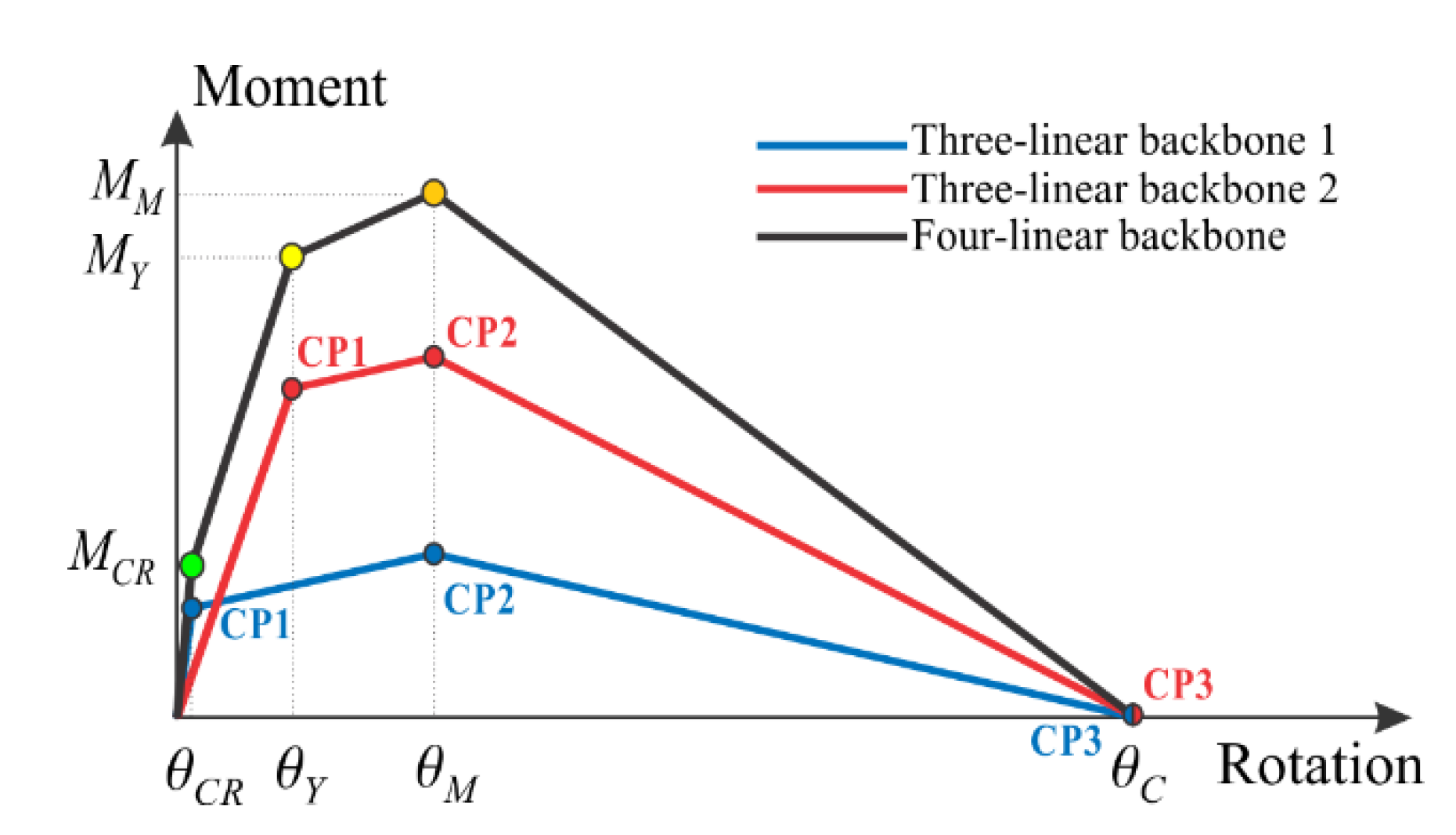
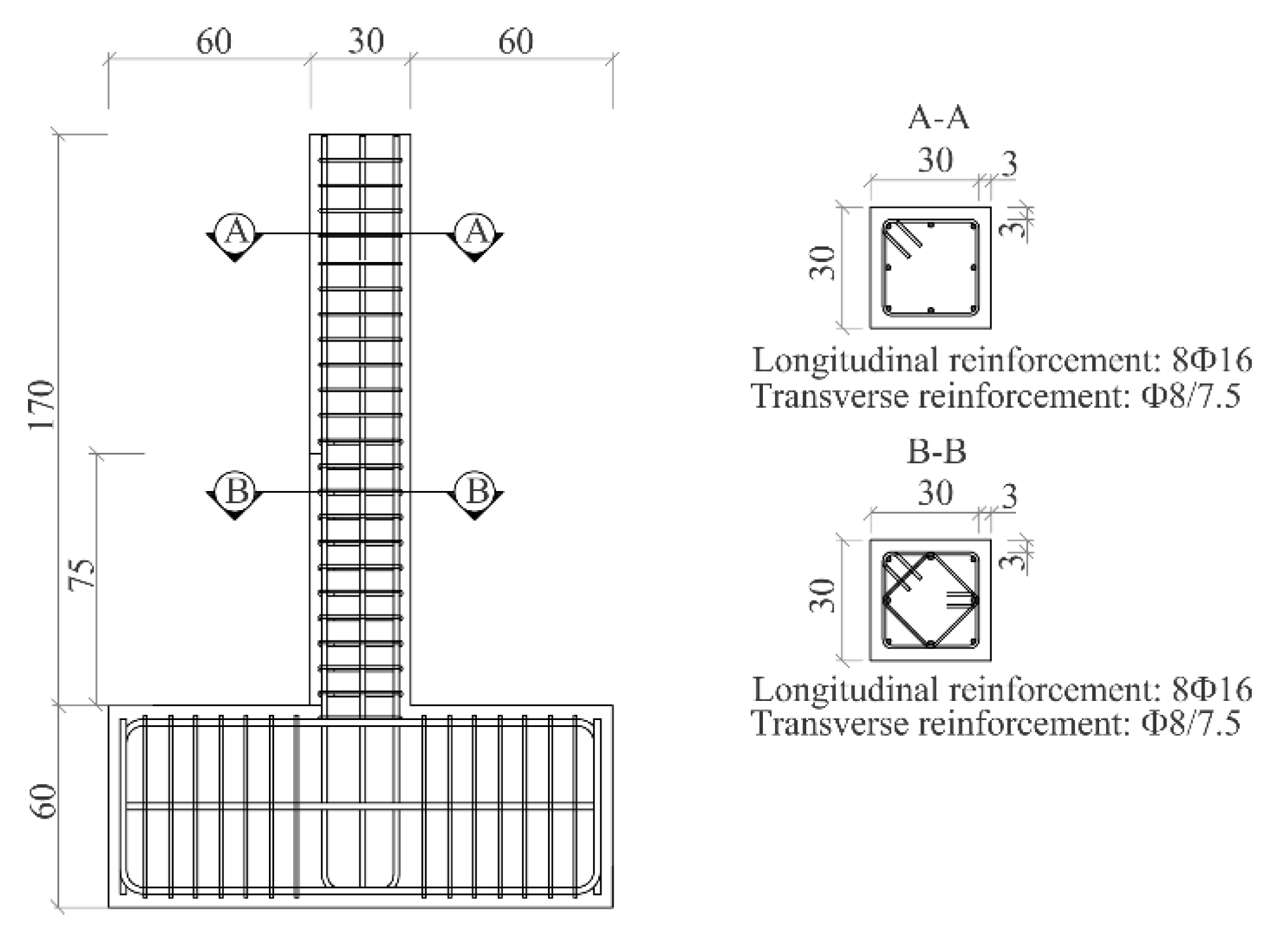
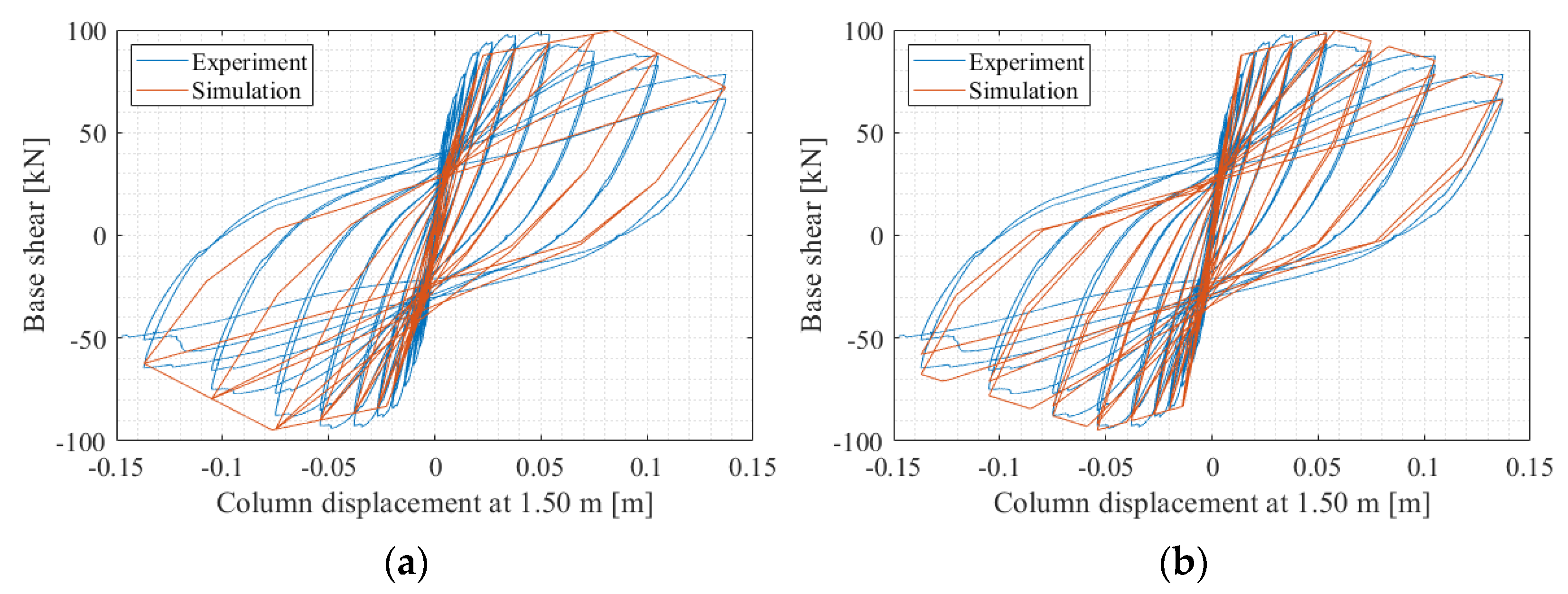


| Steel Grade | fy,k [MPa] | fy,m [MPa] | fu [MPa] | Agt | A5 | k |
|---|---|---|---|---|---|---|
| B500B | 500 | 548 | 650 | 12.3% | 25.0% | 1.19 |
| DPD2 | 400 | 461 | 590 | 11.9% | 26.2% | 1.28 |
| Unconfined Concrete | Confined Concrete | |
|---|---|---|
| fc [MPa] | 41.2 | 56.8 |
| εc0 [‰] | 2.22 | 6.41 |
| εcu [‰] | 3.50 | 19.66 |
| fct [MPa] | 3.1 | 3.1 |
| εt [‰] | 0.086 | 0.086 |
| Ec [MPa] | 3.6·104 | 3.6·104 |
| Unconfined Concrete | Confined Concrete | |
|---|---|---|
| fc [MPa] | 21.1 | 35.7 |
| εc0 [‰] | 1.80 | 8.04 |
| εcu [‰] | 3.50 | 23.28 |
| fct [MPa] | 1.7 | 3.1 |
| εt [‰] | 0.056 | 0.086 |
| Ec [MPa] | 3.0·104 | 3.0·104 |
| Building | Total Mass (t) | Period T1 [s] | agD,R [g] | Soil Factor | Se,D(T1) [g] | Fb/W |
|---|---|---|---|---|---|---|
| 4-storey | 339 | 0.68 | 0.30 | 1.2 | 0.66 | 15.5% |
| 8-storey | 2338 | 1.21 | 0.25 | 1.15 | 0.36 | 7.7% |
| 11-storey | 10,221 | 1.67 | 0.25 | 1.2 | 0.23 | 5.2% |
| Building | Designed According to | Fmax [kN] | dNC [cm] | Se,NC [g] |
|---|---|---|---|---|
| 4-storey | B500B | 1113 | 40.0 | 2.84 |
| DPD2 | 1203 | 45.7 | 3.20 | |
| DPD2—designed as B500B | 1018 | 42.0 | 2.89 | |
| 8-storey | B500B | 2974 | 62.4 | 1.48 |
| DPD2 | 3273 | 65.0 | 1.49 | |
| DPD2—designed as B500B | 2672 | 64.9 | 1.42 | |
| 11-storey | B500B | 9402 | 69.7 | 0.91 |
| DPD2 | 9968 | 64.5 | 0.83 | |
| DPD2—designed as B500B | 8272 | 71.8 | 0.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Žižmond, J.; Dolšek, M. Seismic Design and Performance Assessment of Frame Buildings Reinforced by Dual-Phase Steel. Appl. Sci. 2021, 11, 4998. https://doi.org/10.3390/app11114998
Žižmond J, Dolšek M. Seismic Design and Performance Assessment of Frame Buildings Reinforced by Dual-Phase Steel. Applied Sciences. 2021; 11(11):4998. https://doi.org/10.3390/app11114998
Chicago/Turabian StyleŽižmond, Jure, and Matjaž Dolšek. 2021. "Seismic Design and Performance Assessment of Frame Buildings Reinforced by Dual-Phase Steel" Applied Sciences 11, no. 11: 4998. https://doi.org/10.3390/app11114998
APA StyleŽižmond, J., & Dolšek, M. (2021). Seismic Design and Performance Assessment of Frame Buildings Reinforced by Dual-Phase Steel. Applied Sciences, 11(11), 4998. https://doi.org/10.3390/app11114998






