Multiscale Post-Seismic Deformation Based on cGNSS Time Series Following the 2015 Lefkas (W. Greece) Mw6.5 Earthquake
Abstract
:1. Introduction
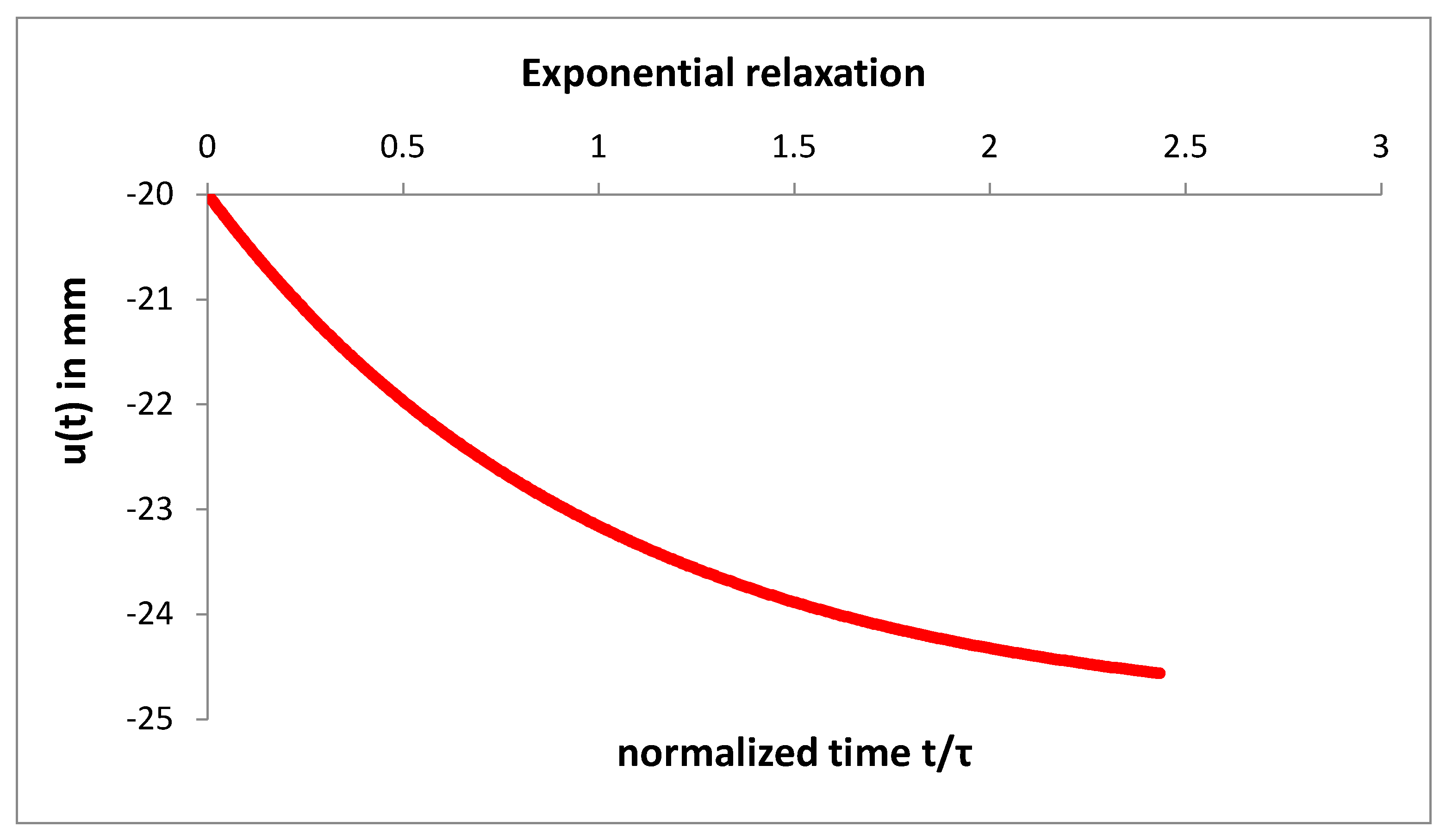
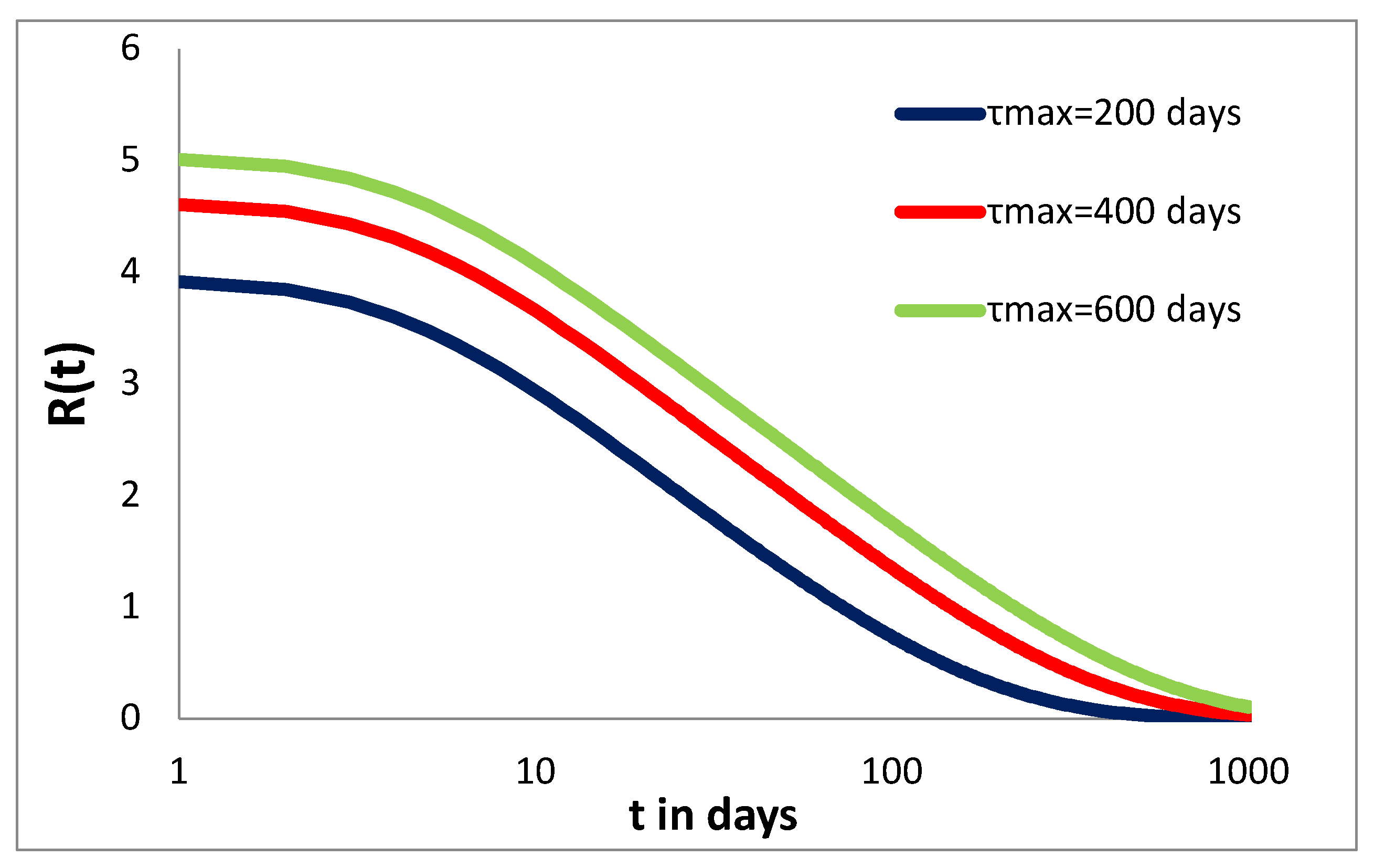
2. A Thermodynamic Model of Post Seismic Relaxation
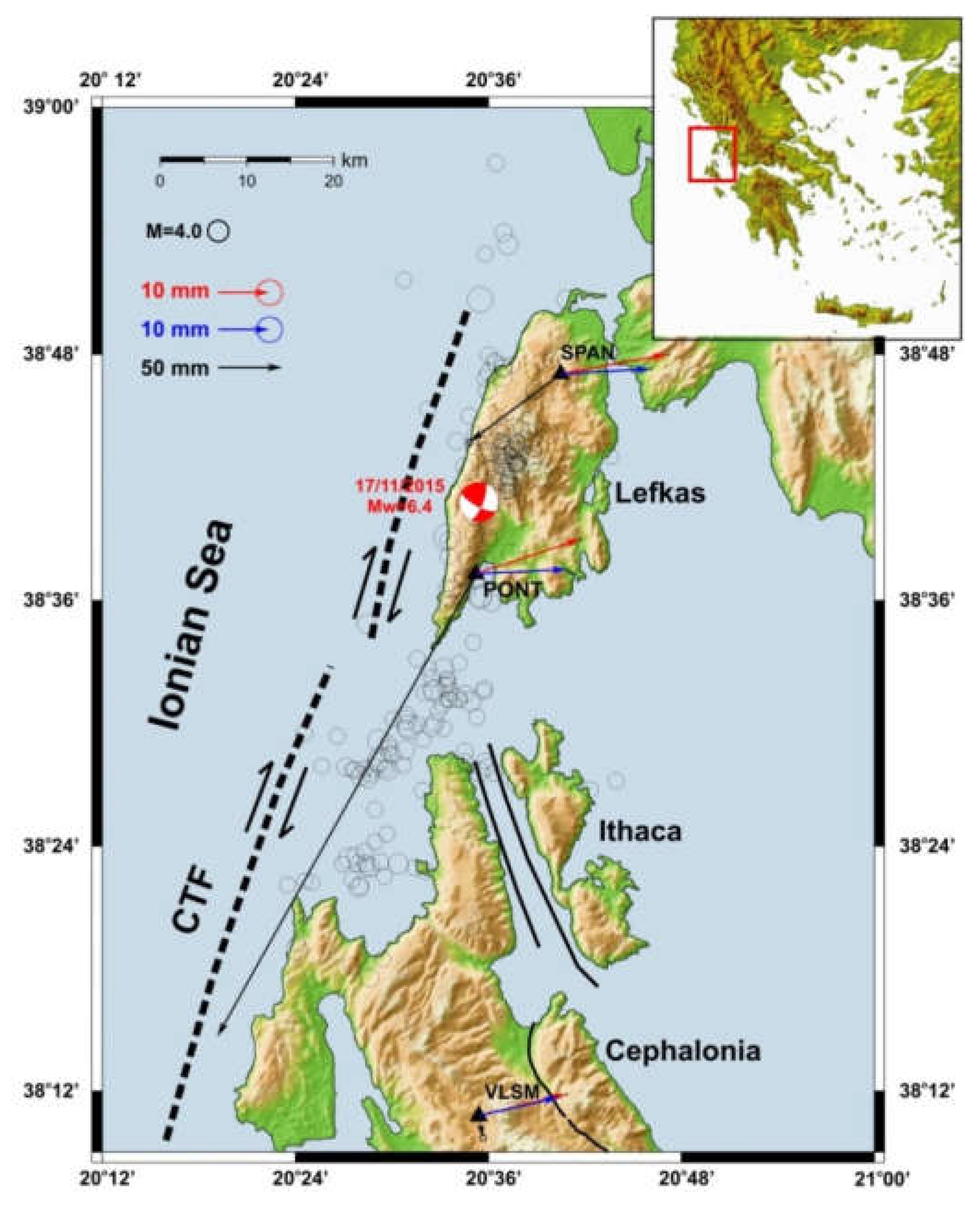
3. Seismotectonic Setting, Data Selection, and Analysis
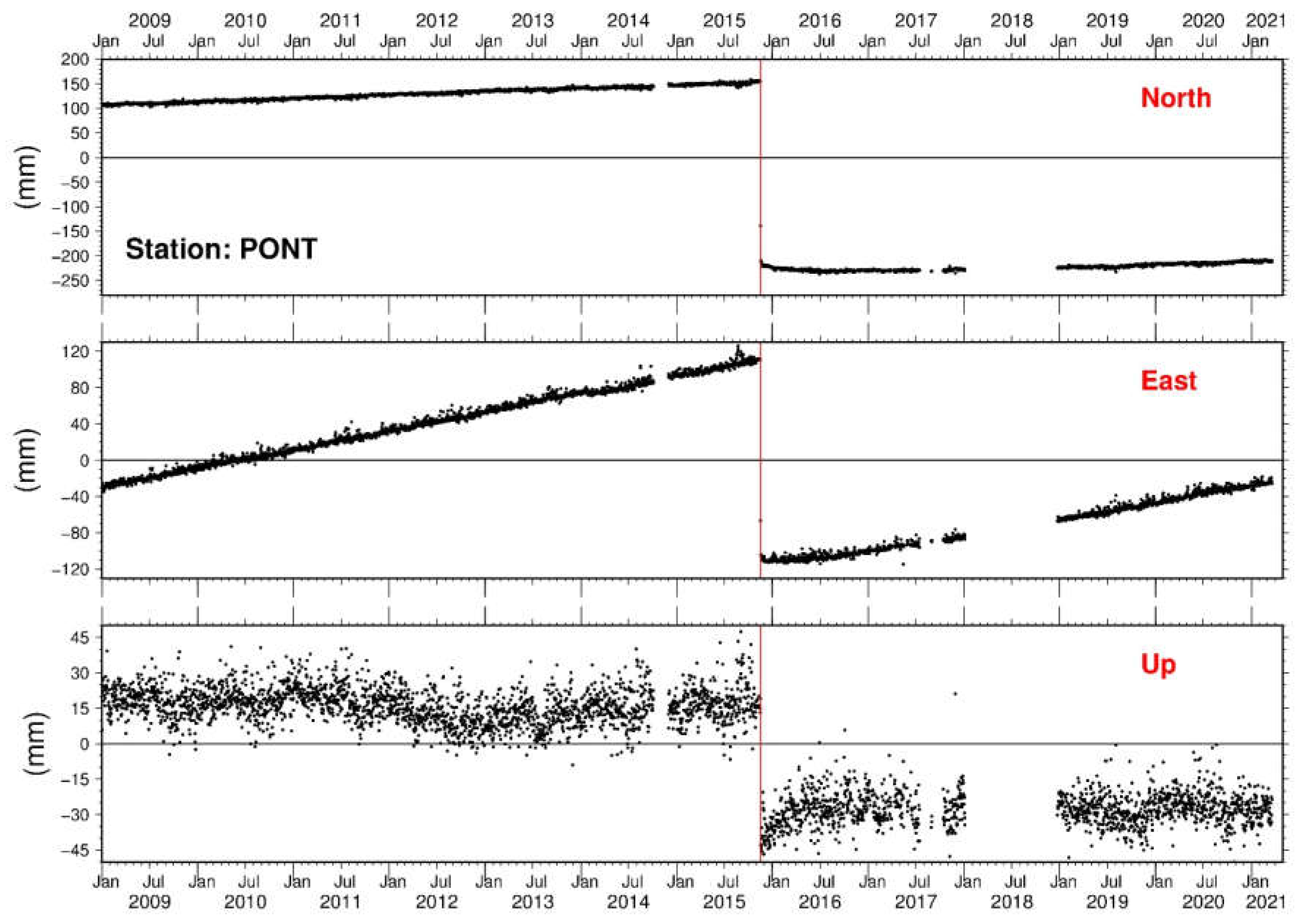
3.1. GNSS Data Analysis
3.2. Post Seismic Time Series Analysis
4. Discussion
5. Concluding Remarks
- A multiscale post-seismic relaxation mechanism based on the existence of a distribution in relaxation time is presented.
- Assuming an Arrhenius dependence of the relaxation time with the uniform distributed activation energy in a mesoscopic scale, we conclude there is a generic logarithmic type relaxation on a macroscopic scale.
- The hierarchically constrained dynamics model could be used to understand the evolution of post seismic relaxation.
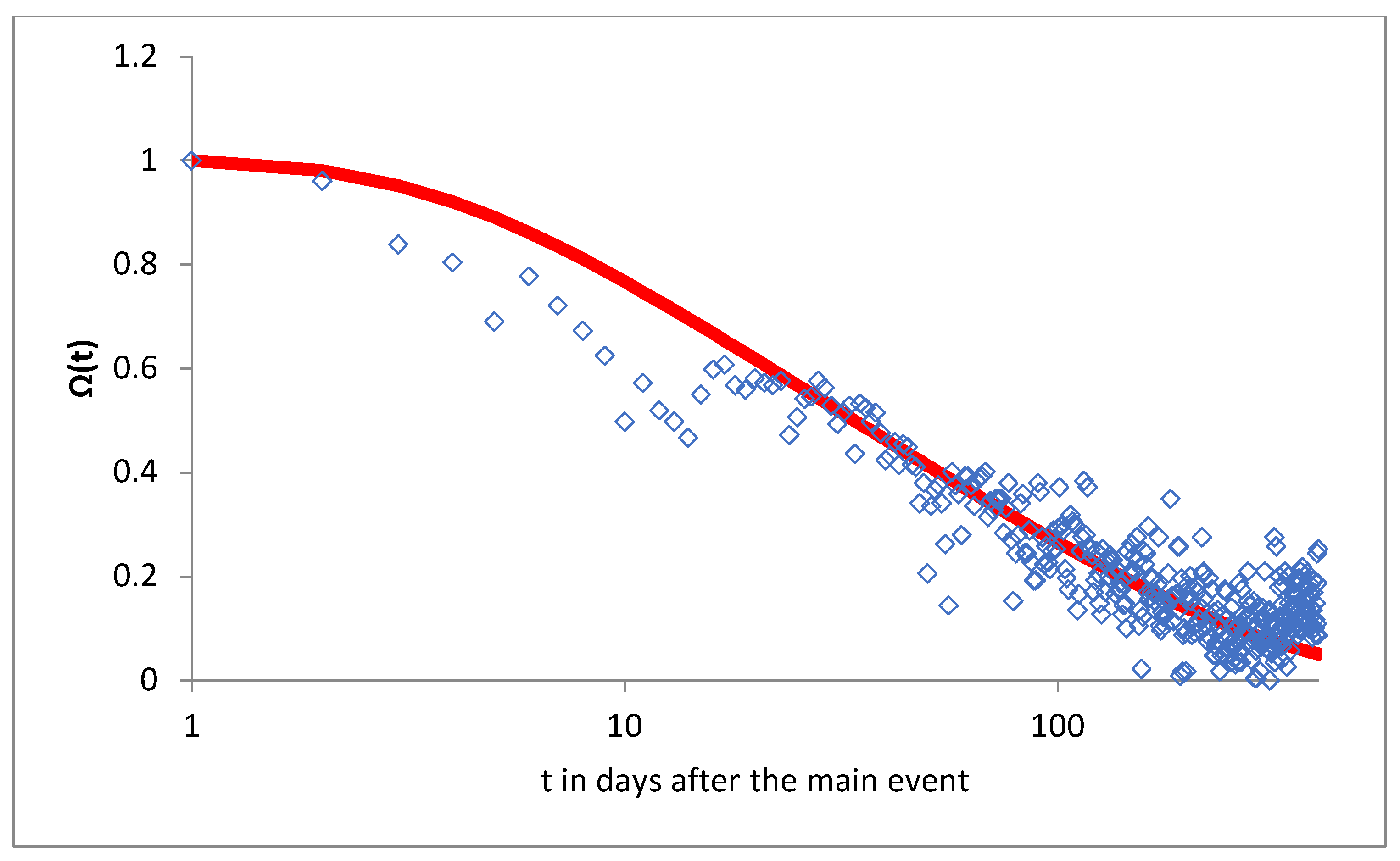
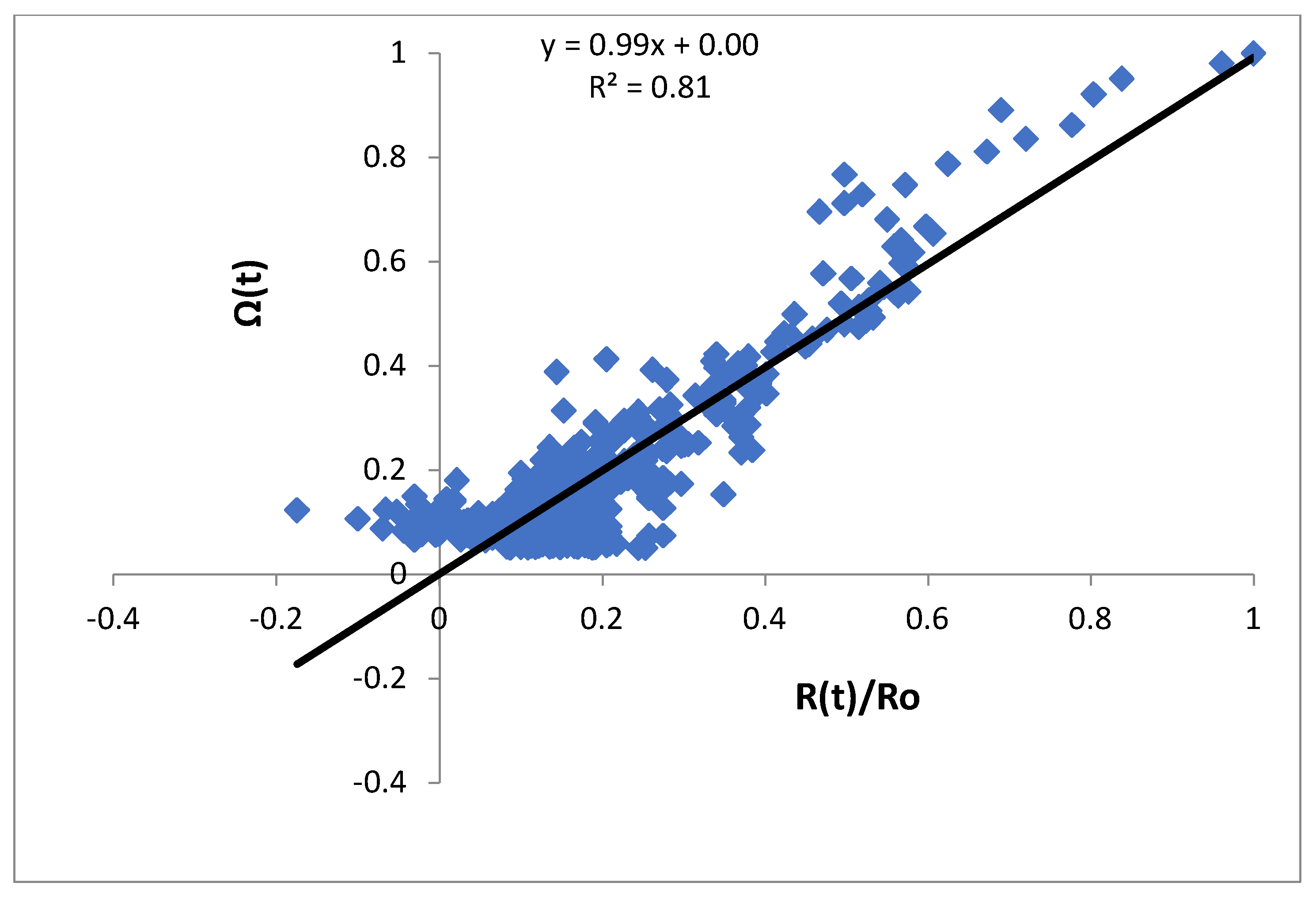
- The model was applied in the case of 2015 Lefkas (Greece) Mw6.5 earthquake, where cGNSS time series were recorded in a station located in the vicinity of the epicentral area. The application of the present approach to the Lefkas event fits the observed displacements, implying a distribution of relaxation times in the range τmin ≈ 3.5 days to τmax ≈ 350 days.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hearn, E.H. What can GPS data tell us about the dynamics of post-seismic deformation? Geophys. J. Int. 2003, 155, 753–777. [Google Scholar] [CrossRef]
- Nur, A.; Byerlee, J.D. An effective stress law for elastic deformation of rocks with fluids. J. Geophys. Res. 1971, 76, 414–419. [Google Scholar] [CrossRef]
- Wang, H.F. Theory of Linear Poroelasticity with Applications to Geomechanics and Hydrogeology; Princeton University Press: Princeton, NJ, USA, 2000; Volume 2, p. 276. [Google Scholar]
- Marone, C.J.; Scholtz, C.H.; Bilham, R. On the mechanics of earthquake afterslip. J. Geophys. Res. 1991, 96, 8441–8452. [Google Scholar] [CrossRef]
- Pollitz, F.F.; Bürgmann, R.; Segall, P. Joint estimation of afterslip rate and postseismic relaxation following the 1989 Loma Prieta earthquake. J. Geophys. Res. 1998, 103, 26975–26992. [Google Scholar] [CrossRef] [Green Version]
- Montési, L.G.J. Controls of shear zone rheology and tectonic loading on postseismic creep. J. Geophys. Res. 2004, 109, B10404. [Google Scholar] [CrossRef] [Green Version]
- Marone, C.; Raleigh, C.B.; Scholz, C.H. Frictional behavior and constitutive modeling of simulated fault gouge. J. Geophys. Res. 1990, 95, 7007–7025. [Google Scholar] [CrossRef]
- Hetland, E.A.; Hager, B.H. The effects of rheological layering on post-seismic deformation. Geophys. J. Int. 2006, 166, 277–292. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.; Hainzl, S.; Sinan Özeren, M.; Ben-Zion, Y. Postseismic deformation induced by brittle rock damage of aftershocks. J. Geophys. Res. 2010, 115, B10422. [Google Scholar] [CrossRef] [Green Version]
- Ingleby, T.; Wright, T.J. Omori-like decay of postseismic velocities following continental earthquakes. Geophys. Res. Lett. 2017, 44, 3119–3130. [Google Scholar] [CrossRef]
- Perfettini, H.; Avouac, J.-P. Postseismic relaxation driven by brittle creep: A possible mechanism to reconcile geodetic measurements and the decay rate of aftershocks, application to the Chi-Chi earthquake, Taiwan. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef]
- Mallick, N.; Ciliberto, S.; Roux, S.G.; Di Stephano, P.; Vanel, L. Aftershocks in thermally activated rupture of indented glass. In Proceedings of the 12th International Conference on Fracture, ICF-12, Ottawa, ON, Canada, 12–17 July 2009; Volume 6, pp. 4564–4572. [Google Scholar]
- Bürgmann, R.; Segall, P.; Lisowski, M.; Svarc, J. Postseismic strain following the 1989 Loma Prieta earthquake from GPS and leveling measurements. J. Geophys. Res. 1997, 102, 4933–4955. [Google Scholar] [CrossRef] [Green Version]
- Yu, S.B.; Kuo, L.C.; Hsu, Y.J.; Su, H.H.; Liu, C.C.; Hou, C.; Lee, J.F.; Shin, T.C. Preseismic deformation and coseismic displacements associated with the 1999 Chi-Chi, Taiwan, earthquake. Bull. Seismol. Soc. Am. 2001, 91, 995–1012. [Google Scholar] [CrossRef]
- Hearn, E.H.; Bürgmann, R.; Reilinger, R.E. Dynamics of İzmit earthquake postseismic deformation and loading of the Düzce earthquake hypocenter. Bull. Seismol. Soc. Am. 2002, 92, 172–193. [Google Scholar] [CrossRef] [Green Version]
- Takahashi, H.; Nakao, S.; Okazaki, N.; Koyama, J.; Sagiya, T.; Ito, T.; Ohya, F.; Sato, K.; Fujita, Y.; Hashimoto, M.; et al. GPS observation of the first month of postseismic crustal deformation associated with the 2003 Tokachi-oki earthquake (MJMA 8.0), off southeastern Hokkaido. Earth Planets Space 2004, 56, 377–382. [Google Scholar] [CrossRef] [Green Version]
- Anugrah, B.; Meilano, I.; Gunawan, E.; Efendi, J. Estimation of postseismic deformation parameters from continuous GPS data in northern Sumatra after the 2004 Sumatra-Andaman earthquake. Earthq. Sci. 2015, 28, 347–352. [Google Scholar] [CrossRef] [Green Version]
- Tobita, M. Combined logarithmic and exponential function model for fitting postseismic GNSS time series after 2011 Tohoku-Oki earthquake. Earth Planets Space 2011, 68, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Marone, C. Laboratory-derived friction laws and their application to seismic faulting. Annu. Rev. Earth Planet. Sci. 1998, 26, 643–696. [Google Scholar] [CrossRef] [Green Version]
- Kawada, Y.; Nagahama, H.; Hara, H. Irreversible thermodynamic and viscoelastic model for power-law relaxation and attenuation of rocks. Tectonophysics 2006, 427, 255–263. [Google Scholar] [CrossRef]
- Brantut, N.; Heap, M.; Baud, P.; Meredith, P. Mechanisms of time-dependent deformation in porous limestone. J. Geophys. Res. 2014, 119, 5444–5463. [Google Scholar] [CrossRef]
- Bocquet, L.; Charlaix, E.; Ciliberto, S.; Crassous, A. Moisture-induced ageing in granular media and the kinetics of capillary condensation. Nature 1998, 396, 735–737. [Google Scholar] [CrossRef]
- Renard, F.; Dysthe, D.; Feder, J.; Meakin, P.; Morris, S.; Jamtveit, B. Pattern formation during healing of fluid-filled cracks: An analog experiment. Geofluids 2009, 9, 365–372. [Google Scholar] [CrossRef]
- Ten Cate, J.A.; Shankland, T.J. Slow dynamics in the nonlinear elastic response of Berea sandstone. Geophys. Res. Lett. 1996, 21, 3019–3022. [Google Scholar] [CrossRef] [Green Version]
- Gibbs, M.; Evetts, J.; Leake, J. Activation energy spectra and relaxation in amorphous materials. J. Mater. Sci. 1983, 18, 278–288. [Google Scholar] [CrossRef]
- Shaknhovich, E.; Gutin, A. Relaxation to equilibrium in the random energy model. Eurphys. Lett. 1989, 9, 569–574. [Google Scholar] [CrossRef]
- Ten Cate, J.; Smith, E.; Guyer, R. Universal slow dynamics in granular solids. Phys. Rev. Lett. 2000, 85, 1020–1023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brey, J.; Prados, A. Slow logarithmic relaxation in models with hierarchically constrained dynamics. Phys. Rev. E 2001, 63, 21108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amir, A.; Oreg, Y.; Imry, Y. On relaxations and aging of various glasses. Proc. Natl. Acad. Sci. USA 2012, 109, 1850–1855. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zaitsev, V.; Gusev, V.; Tournat, V.; Richard, P. Slow relaxation and aging phenomena at the nanoscale in granular materials. Phys. Rev. Lett. 2014, 112, 108302. [Google Scholar] [CrossRef] [Green Version]
- Varotsos, P.; Alexopoulos, C. Thermodynamics of Point Defects and Their Relation with the Bulk Properties; Amelinckx, S., Gevers, R., Nihoul, J., Eds.; Elsevier: Amsterdam, The Netherlands, 1986. [Google Scholar]
- Ganas, A.; Drakatos, G.; Rontogianni, S.; Tsimi, C.; Petrou, P.; Papanikolaou, M.; Argyrakis, P.; Boukouras, K.; Melis, N.; Stavrakakis, G. NOANET: The new permanent GPS network for Geodynamics in Greece. Geophys. Res. Abstr. 2008, 10, EGU2008–A–04380. [Google Scholar]
- Snieder, R.; Sens-Schönfelder, C.; Wu, R. The time dependence of rock healing as a universal relaxation process, a tutorial. Geophys. J. Int. 2017, 208, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Ranalli, G. Rheology of the Earth; Allen and Unwin Inc.: Winchester, MA, USA, 1987. [Google Scholar]
- Ergintav, S.; Bürgmann, R.; McClusky, S.; Çakmak, R.; Reilinger, R.E.; Lenk, O.; Barka, A.; Özener, H. Postseismic deformation near the İzmit earthquake (17 August 1999, M 7.5) rupture zone. Bull. Seismol. Soc. Am. 2002, 92, 194–207. [Google Scholar] [CrossRef]
- Pollitz, F.F. Transient rheology of the uppermost mantle beneath the Mojave Desert, California. Earth Planet. Sci. Lett. 2003, 215, 89–104. [Google Scholar] [CrossRef]
- Pollitz, F.F. Transient rheology of the upper mantle beneath central Alaska inferred from the crustal velocity field following the 2002 Denali earthquake. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef] [Green Version]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Dover Books on Mathematics: Dover, NY, USA, 1965. [Google Scholar]
- Papazachos, B.C. Seismicity of the Aegean and surrounding area. Tectonophysics 1009, 178, 287–308. [Google Scholar]
- Louvari, E.; Kiratzi, A.A.; Papazachos, B.C. The Cephalonia transform fault and its extension to western Lefkada island (Greece). Tectonophysics 1999, 308, 223–236. [Google Scholar] [CrossRef]
- Le Pichon, X.; Chamot Rooke, N.; Lallemant, S.; Noomen, R.; Veis, G. Geodetic determination of the kinematics of central Greece with respect to Europe: Implications for eastern Mediterranean tectonics. J. Geophys. Res. 1995, 100, 12675–12690. [Google Scholar] [CrossRef]
- Kokinou, E.; Papadimitriou, E.; Karakostas, V.; Kamberis, E.; Vallianatos, F. The Kefalonia Transform Zone (offshore Western Greece) with special emphasis to its prolongation towards the Ionian Abyssal Plain. Mar. Geophys. Res. 2006, 27, 241–252. [Google Scholar] [CrossRef]
- Van Hinsbergen, D.J.J.; van der Meer, D.G.; Zachariasse, W.J.; Meulenkamp, J.E. Deformation of western Greece during Neogene clockwise rotation and collision with Apulia. Int. J. Earth Sci. 2006, 95, 463–490. [Google Scholar] [CrossRef]
- Vassilakis, E.; Royden, L.; Papanikolaou, D. Kinematic links between subduction along the Hellenic trench and extension in the Gulf of Corinth, Greece: A multidisciplinary analysis. Earth Planet. Sci. Lett. 2011, 303, 108–120. [Google Scholar] [CrossRef]
- Lekkas, E.; Mavroulis, S.; Carydis, P.; Alexoudi, V. The 17 November 2015 Mw 6.4 Lefkas (Ionian Sea, Western Greece) Earthquake: Impact on Environment and Buildings. Geotech. Geol. Eng. 2018, 36, 2109–2142. [Google Scholar] [CrossRef]
- Karastathis, V.; Mouzakiotis, E.; Ganas, A.; Papadopoulos, G.A. High-precision relocation of seismic sequences above a dipping Moho: The case of the January–February 2014 seismic sequence on Cephalonia island (Greece). Solid Earth 2015, 6, 173–184. [Google Scholar] [CrossRef] [Green Version]
- Karakostas, V.; Papadimitriou, E.; Papazachos, C.B. Properties of the 2003 Lefkada, Ionian Islands, Greece, earthquake seismic sequence and seismicity triggering. Bull. Seismol. Soc. Am. 2004, 94, 1976–1981. [Google Scholar] [CrossRef] [Green Version]
- Papadimitriou, P.; Kaviris, G.; Makropoulos, K. The Mw = 6.3 2003 Lefkada Earthquake (Greece) and induced stress transfer changes. Tectonophysics 2006, 423, 73–82. [Google Scholar] [CrossRef]
- Lagios, E.; Sakkas, V.; Papadimitriou, P.; Damiata, B.N.; Parcharidis, I.; Chousianitis, K.; Vassilopoulou, S. Crustal deformation in the Central Ionian Islands (Greece): Results from DGPS and DInSAR analyses (1995–2006). Tectonophysics 2007, 444, 119–145. [Google Scholar] [CrossRef]
- Saltogianni, V.; Stiros, S. A two-fault model of the 2003 Leucas (Aegean Arc) earthquake based on topological inversion of GPS data. Bull. Seismol. Soc. Am. 2015, 105, 2510–2520. [Google Scholar] [CrossRef]
- Papadopoulos, G.A.; Karastathis, V.; Koukouvelas, I. The Cephalonia, Ionian Sea (Greece), sequence of strong earthquakes of January-February (2014): A first report. Res. Geophys. 2015, 4, 5441. [Google Scholar] [CrossRef] [Green Version]
- Karakostas, V.; Papadimitriou, E.; Mesimeri, M.; Gkarlaouni, C.; Paradisopoulou, P. The 2014 Kefalonia doublet (Mw6.1 and Mw6.0) central Ionian Islands, Greece: Seismotectonic implications along the Kefalonia transform fault zone. Acta Geophys. 2015, 63, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Chousianitis, K.; Konca, A.O.; Tselentis, G.-A.; Papadopoulos, G.A.; Gianniou, M. Slip model of the 17 November 2015 M=6.5 Lefkada earthquake from the joint inversion of geodetic and seismic data. Geophys. Res. Lett. 2016, 43, 7973–7981. [Google Scholar] [CrossRef] [Green Version]
- Papadimitriou, E.; Karakostas, V.; Mesimeri, M.; Chouliaras, G.; Kourouklas, C. The Mw6.5 17 November 2015 Lefkada (Greece) Earthquake: Structural Interpretation by Means of the Aftershock Analysis. Pure Appl. Geophys. 2017, 174, 3869–3888. [Google Scholar] [CrossRef]
- Bernese GNSS Software Version 5.2. User Manual; Dach, R.; Lutz, S.; Walser, P.; Fridez, P. (Eds.) Astronomical Institute, University of Bern; Bern Open Publishing: Bern, Switzerland, 2015; ISBN 978-3-906813-05-9. [Google Scholar] [CrossRef]
- Niell, A.E. Global mapping functions for the atmosphere delay at radio wavelengths. J. Geophys. Res. 1996, 101, 3227–3246. [Google Scholar] [CrossRef]
- Saastamoinen, I.I. Contribution to the theory of atmospheric refraction. Bull. Géodésique 1972, 105, 279–298. [Google Scholar] [CrossRef]
- Ray, R.D.; Ponte, R.M. Barometric tides from ECMWF operational analyses. Ann. Geophys. 2003, 21, 1897–1910. [Google Scholar] [CrossRef] [Green Version]
- Tsallis, C. Some open points in nonextensive statistical mechanics. Int. J. Bifurc. Chaos 2012, 22, 1230030. [Google Scholar] [CrossRef] [Green Version]
- Savage, J.C.; Svarc, J.L. Post seismic deformation associated with the 1992 Mw = 7.3 Landers earthquake, southern California. J. Geophys. Res. 1997, 102, 7565–7577. [Google Scholar] [CrossRef]
- Savage, J.; Svarc, J.; Yu, S.-B. Postseismic relaxation and transient creep. J. Geophys. Res. 2005, 110, B11402. [Google Scholar] [CrossRef]
- Ten Cate, J. Slow dynamics of earth materials: An experimental overview. Pure Appl. Geophys. 2011, 168, 2211–2219. [Google Scholar] [CrossRef]
- Vallianatos, F.; Chatzopoulos, G. A Complexity View into the Physics of the Accelerating Seismic Release Hypothesis: Theoretical Principles. Entropy 2018, 20, 754. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tarasov, A.; Titov, K. Relaxation time distribution from time domain induced polarization measurements. Geophys. J. Int. 2007, 170, 31–43. [Google Scholar] [CrossRef] [Green Version]
- Zaitsev, V.; Gusev, V.; Castagnede, B. Thermoelastic mechanism for logarithmic slow dynamics and memory in elastic wave interactions with individual cracks. Phys. Rev. Lett. 2003, 90, 75501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ostrovsky, L.; Lebedev, A.; Riviere, J.; Shokouhi, P.; Wu, C.; Stuber Geesey, M.A.; Johnson, P.A. Long-Time Relaxation Induced by Dynamic Forcing in Geomaterials. J. Geophys. Res. 2019, 124, 5003–5013. [Google Scholar] [CrossRef]
- Brouers, F.; Sotolongo-Costa, O. Universal relaxation in nonextensive systems. Eurphys. Lett. 2003, 62, 808–814. [Google Scholar] [CrossRef] [Green Version]
- Brouers, F.; Sotolongo-Costa, O. Relaxation in heterogeneous systems: A rare events dominated phenomenon. Phys. A Stat. Mech. Appl. 2005, 356, 359–374. [Google Scholar] [CrossRef]
- Vallianatos, F. On the non-extensive nature of the Isothermal Depolarization relaxation Currents in cement mortars. J. Phys. Chem. Solid 2012, 73, 550–553. [Google Scholar] [CrossRef]
- Huisman, B.; Fasolino, A. Logarithmic relaxation due to minimization of interactions in the Burridge-Knopoff model. Phys. Rev. E 2006, 74, 26110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Persson, B.N.J. Theory of friction: Stress domains, relaxation and creep. Phys. Rev. B 1995, 51, 13568–13585. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vallianatos, F.; Sakkas, V. Multiscale Post-Seismic Deformation Based on cGNSS Time Series Following the 2015 Lefkas (W. Greece) Mw6.5 Earthquake. Appl. Sci. 2021, 11, 4817. https://doi.org/10.3390/app11114817
Vallianatos F, Sakkas V. Multiscale Post-Seismic Deformation Based on cGNSS Time Series Following the 2015 Lefkas (W. Greece) Mw6.5 Earthquake. Applied Sciences. 2021; 11(11):4817. https://doi.org/10.3390/app11114817
Chicago/Turabian StyleVallianatos, Filippos, and Vassilis Sakkas. 2021. "Multiscale Post-Seismic Deformation Based on cGNSS Time Series Following the 2015 Lefkas (W. Greece) Mw6.5 Earthquake" Applied Sciences 11, no. 11: 4817. https://doi.org/10.3390/app11114817
APA StyleVallianatos, F., & Sakkas, V. (2021). Multiscale Post-Seismic Deformation Based on cGNSS Time Series Following the 2015 Lefkas (W. Greece) Mw6.5 Earthquake. Applied Sciences, 11(11), 4817. https://doi.org/10.3390/app11114817






