Next Article in Journal
Efficient Implementation of PRESENT and GIFT on Quantum Computers
Previous Article in Journal
Design of a Multimodal Imaging System and Its First Application to Distinguish Grey and White Matter of Brain Tissue. A Proof-of-Concept-Study
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Applied Sciences
Volume 11
Issue 11
10.3390/app11114778
applsci-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Review

Model-Based Dynamic Toll Pricing: An Overview

by
Claudio Lombardi
1,2,*,
Luís Picado-Santos
1,* and
Anuradha M. Annaswamy
2,*
1
CERIS, Instituto Superior Técnico, Universidade de Lisboa, Av. Rovisco Pais 1, 1049-001 Lisboa, Portugal
2
Active Adaptive Control Laboratory, Department of Mechanical Engineering, Massachusetts Institute of Technology, 77 Massachusetts Avenue, Cambridge, MA 02139, USA
*
Authors to whom correspondence should be addressed.
Appl. Sci. 2021, 11(11), 4778; https://doi.org/10.3390/app11114778
Submission received: 2 April 2021 / Revised: 3 May 2021 / Accepted: 9 May 2021 / Published: 23 May 2021
(This article belongs to the Section Computing and Artificial Intelligence)
Browse Figures
Review Reports Versions Notes

Abstract

:
In this paper, we review some of the most recent research regarding design, simulation, implementation and evaluation of dynamic tolling schemes. Analyzing the structure of the reviewed studies, we identify the common elements and the differences in the approaches chosen by different authors, presenting an overview of the methods for price definition and of the simulation techniques as well as a discussion on the newest technology applications in the field. Optimization revealed to be the dominant price definition method, while control-based algorithms are notably employed for managed lanes toll pricing schemes. Regarding traffic and driver behavior simulation we observed a great variety of solutions throughout the reviewed papers, with a prevalence of macroscopic models for the former and logit models for the latter. Still few papers include models for externalities quantification, while AI paradigms are gaining importance in the field.

1. Introduction

During the last decades, the technique of dynamic pricing has started to play a key-role in manifold domains of Intelligent Transportation Systems, such as fare pricing, charging/discharging pricing for electric vehicles, parking pricing and congestion pricing [1]. This technique entails the variation of prices according to market conditions, in response to the demand-supply imbalance. Dynamic toll pricing is a variant of congestion pricing [1] where tolls vary in real-time as a function of current traffic conditions, as opposed to flat tolls, which stay constant over time, and scheduled tolls, where tolls vary by time of day, day of the week or season following a predetermined schedule [2].
The idea of traffic congestion pricing was introduced in the 1920s by the pioneering work of Pigou [3], but its first implementation was only in 1975 with the Singapore Area Licensing Scheme [4]. Congestion pricing can be applied at different scales, from single lanes to large scale networks.
In Figure 1, we can see the distribution by scope of the dynamic toll pricing studies analyzed in this review, revealing the predominance of studies concerning managed lanes, followed by networks and, eventually, general tolled facilities.
Managed lanes, i.e., High Occupancy Toll (HOT) and Express lanes facilities constitute one of the few examples of congestion toll pricing operating schemes; as of January 2019, dynamic toll pricing is implemented on at least 13 managed lanes facilities in the United States [5] and their schemes are considered to be the closest to pure dynamic toll [6], while, at the moment, there are no implemented dynamic city tolling systems [7]. Although most of the adopted dynamic toll pricing strategies are simple and heuristic [8], some of the existing schemes showed to have better performances than fixed tolls [9,10], encouraging researchers to develop new schemes.
To present a brief overview of the research efforts carried out worldwide on dynamic toll pricing, we evaluated the studies published to date. This analysis was based on the Scopus search engine (www.scopus.com, (accessed on 3 May 2021)). The query string was written to find documents matching the keywords ‘dynamic’ AND ‘toll’ AND ’pricing’ in the title, the abstract or the keywords. This query provided 209 references in all, spanning from 1992 to 2021. For comparison, we show the results of other query runs (Table 1), using different combinations in pairs of the same keywords.
The analysis of the outcomes of the query indicates that dynamic toll pricing embraces a very diverse group of subject areas with a prevalence of engineering, social science, computer science and mathematics, as appears in Table 2. A classification of the documents by year, in Figure 2, suggests an overall increase of the research efforts on dynamic toll pricing during the last decades, with a peak of published documents in 2018. In this review, we will focus in particular on the research efforts carried out since 2008 when existing research on pricing algorithms for HOT operations was considered to be in its early stage [11]. Sorting of the documents by country (Figure 3) revealed that the USA and China are the countries that have contributed the most to the number of documents published on dynamic toll pricing.
In almost all approaches evaluated in this survey, the overall structure consists of a pricing strategy followed by a simulation study that evaluates the pricing strategy. This simulation study is carried out using a socio-technical model that combines a driver behavior model and a traffic flow model [12], with some papers also including quantification of traffic externalities.
A list of the main reviewed dynamic toll pricing studies described by reference, year of publication, scope, main pricing rule principle, traffic simulation basis, driver behavior model and recent technology application is presented in Table 3. All the quantitative considerations about the popularity of different scopes and methods presented in this paper are determined based on the papers mentioned in Table 3.
In Section 2, we introduce an overview of the most relevant methods for price definition, in Section 3, we review some of the adopted simulation techniques, in Section 4, we carry out a discussion about the interactions of the newest technology applications with dynamic toll pricing, and in Section 5 we present our conclusions with some insights about future research perspectives.

2. Overview of Dynamic Toll Price Definition Methods

The dynamic tolling operations schemes currently in force in the managed lanes facilities in the United States are proprietary, and therefore not available to the public [63]. A notable exception is the algorithm employed to compute MnPASS dynamic toll is published [64]; MnPASS was one of the first managed lanes facilities to become dynamically tolled in 2005 [65] creating a congestion-free lane for both single occupancy vehicles whose drivers are willing to pay the toll and high occupancy vehicles [66]. During the morning and evening peak hours, the toll rate for a particular entry point of the MnPASS express lanes is a function of the maximum density downstream of the entry point: variations of this density define a specific variation of the toll based on lookup tables [64] with a 3-min tolling interval [13].
Two operational objectives are identified for HOT lanes in [49]: (i) to keep free-flow conditions to ensure travel time reliability; and (ii) to maximize the tolled lanes’ throughput in order to minimize the system’s total delay. The most relevant methods for dynamic toll price definition explored in literature that we present in the remainder of this section are usually built to pursue one of these two objectives or a combination of both. We can say that control-based approaches are more focused on the former objective, while optimization algorithms usually pursue the latter or the maximization of another performance index of the tolled infrastructure. Figure 4 displays the distribution of the analyzed studies categorized by scope and main price definition method. We note that optimization (OPT) is the predominant price definition method, especially for studies regarding networks (NW) and tolled facilities (TF). For managed lanes studies (ML), which include also research concerning HOT lanes, express lanes and general toll lanes, control-based algorithms (C) are adopted in almost as many cases as optimization-based ones. We also stress that optimal control, which may be considered an application of both optimization and control theories, is implemented in two papers relating to managed lanes, one relating to network and one relating to toll facilities and we counted these algorithms in the control-based groups. Three approaches that are not attributable either to optimization or control theory, identified with label OTH, are employed for networks.
In what follows, Section 2.1 is dedicated to control-based algorithms and Section 2.2 to optimization-based approaches.

2.1. Control-Based Algorithms

The general topic of traffic modeling and control has been studied at length in the literature (ex. [67]). Broadly speaking, traffic control can be classified as either road-based or vehicle-based. Road-based traffic control includes ramp management via methods such as ramp metering [68,69], posting of variable speed limits so as to homogenize speeds and avoid stop-and-go waves [70,71], average speed enforcement [72,73], lane control redirecting vehicles to different lanes [74], Route Guidance and Information Systems (RGIS) communicated to drivers through various messaging methods [75,76]. A fairly large literature exists on vehicle-based control, which pertain to Vehicle-to-Infrastructure (V2I) based communication strategies and Connected and Automated Vehicles (CAVs) based coordination strategies [77]. In addition to the above methods, one can consider a dynamic toll-pricing based approach, which may be viewed as either road-based or vehicle-based, where the toll price is messaged to the driver (either through a message posted on the road or directly to the vehicle), and the driver makes a decision in turn whether to enter the highway or not [17,22]. Viewing real-time traffic information data as a sensor and the toll based on these data as a control input, the underlying traffic congestion problem is posed as a control problem, where the driver can be viewed as an actuator. The concept of transactive control, a feedback control strategy enabled through economic contracts to incentivize and enable flexible consumption, is eliciting significant attention of late [78], with multiple applications in dynamic toll pricing.
A simple feedback digital control law for on-ramp metering called ALINEA was proposed in [79] as in (1):
r ( k ) = r ( k − 1 ) + k p · [ o r e f − o ( k ) ] .
The metering rate at time k, r ( k ) (in equivalent passenger vehicles/hour, or veh/h), is defined by the product of a proportional gain k p with the difference between the desired value of an occupancy parameter o r e f and its current value o ( k ) (in % km/km), which, in turn, is related to traffic density ρ ( k ) (in equivalent passenger vehicles/km, or veh/km) by Equation (2):
ρ ( k ) = η · o ( k ) ,
where η is defined as in (3):
η = ν 100 · l ,
with ν equal to the number of lanes on the mainstream and l (in km/veh) equal to the mean effective vehicles length in km.
A principle similar to ALINEA was applied in [13] to build a toll pricing controller, given by Equation (4):
π ( k + 1 ) = π ( k ) + k p · [ o ( k ) − o r e f ] ,
where the toll price π ( k ) (in monetary units) is defined by a controller, being the control variable an occupancy parameter. A similar concept was applied in [11], where the optimal HOT flow ratio to set the dynamic toll is defined by a control-based piecewise linear function, in [50] and in [52]. Also in [14,15,16] the control mechanism is based on a piecewise linear function but with variable revenue-maximizing optimal gains.
In [17], desired flow into the HOT at time t (in veh/h), indicated with y ( t ) , is computed through a proportional derivative (PD) analog controller with a feedforward additive component (5):
y ( t ) = k p · e ( t ) + k d · e ˙ ( t ) + k f f · ρ r e f ,
where k p , k d and k f f represent proportional, derivative and feedforward gains, respectively, and e ( t ) is an error signal, given by the difference between the desired density ρ r e f and the current density ρ ( t ) (in veh/km).
In [18], in turns, a proportional integral (PI) controller defines time-dependent tolls for road networks based on the congestion level of the network (proportional part) and on users’ adaption to the tolls (integral part). A PI feedback control for toll pricing extendable to time-dependent pricing for a large scale dynamic traffic network is presented in [19] and a PI adaptive controller computes desired HOT flow rates in [20].
The HOT dynamic pricing algorithm proposed in [21] embeds a proportional integral derivative (PID) controller that considers the time delay between the tollbooth and the exit of HOT lanes.
In [80] we propose a dynamic toll pricing scheme based on feedback control theory, similar to the approach in [17,22], for a freeway segment with multiple access locations.
Cascaded feedback control is employed to build a discrete-time dynamic tolling computation algorithm that later was successfully implemented in a HOT between Ben Gurion Airport and Tel Aviv, in Israel [23]. Without going into the details of the equations, the inner loop is a PD controller which computes the toll rate increment having the inflow to the HOT as feedback signal, while the outer loop is given by a PI controller that calculates the inflow reference value with the average velocity on the HOT lane as the feedback signal.
In optimal control, the control gains are optimized so that some performance measure of the system, function of its current and past states and inputs, is maximized. Hamilton-Jacobi-Bellman equation is used to design feedback optimal control laws that utilize real-time traffic information for defining dynamic tolls of lanes or routes in [24,25,26]. The extended Kalman filtering technology is employed in [27] for a stochastic optimal control based algorithm to execute a freeway traffic management mechanism that integrates dynamic toll and ramp control.

2.2. Optimization-Based Algorithms

While control-based dynamic toll pricing approaches described in Section 2.1 usually focus on keeping free-flow conditions, optimization-based algorithms are built around the maximization of some performance index of the system. Road managers may be interested in implementing strategies that, as they deal with congestion on the managed road, satisfy some objectives as maximization of revenue, social welfare, freeway throughput, or a combination of them [48]. A general formulation of the unconstrained optimization problem for the definition of such strategies is given by Equation (6):
π ( n ) = argmax π ( n ) ∑ k = n n + N g ( π ( k ) ) ,
where the toll price for tolling interval n + 1 , π ( n + 1 ) is the one that maximizes the accumulation of a performance index g ( π ( k ) ) , chosen according to the strategy objectives, over a certain period of time, called rolling horizon, corresponding to the following N intervals. The complete formulation of the optimization problem is given by (6) with appropriate constraints. Manifold single-objective pricing strategies with similar formulations are presented in literature: revenue-maximizing problems are described in [28,29,30,46], a throughput maximizing problem is formulated in [31], and an average-flow maximizing toll is presented in [8]. In [8,30,31], penalty methods are applied, replacing the constraints to ensure free-flow with penalty functions added to the objective function.
As is intuitive, strategies obtained via the maximization of a performance indicator associated with a single objective may not satisfy other possible objectives: for example, total system travel time minimization and revenue maximization are found to conflict in [40]; multi-objective approaches in literature aim to design tolls from a compromise among multiple objectives, seeking Pareto optimum, a solution characterized by the fact that “no other feasible solutions can improve at least one objective without deteriorating another” [60]. A bi-objective optimization approach is proposed in [33], where the objective function γ is defined as the weighted sum of the system cost c (in monetary units) and time τ (in time units) (7):
γ = c + w · ξ ¯ · τ ,
where ξ ¯ is the weighted average value of time (VOT), to convert time units in monetary units, and w is a non-negative weighting parameter, called Pareto parameter. The obtained toll expression reduces to a minimum cost scheme for w = 0 and to a minimum time scheme, in case of w → ∞ . The authors of [60] propose a toll defined by a bi-objective program for a tollable vehicular network, seeking to minimize both total delays and emissions, formulating the problem as a mathematical programming with complementarity constraints (MPCC) and solving it with a quadratic penalty-based gradient projection algorithm. A Pareto-improving queue-eliminating dynamic toll is proposed in [34].
Dynamic toll pricing problems are generally particularly difficult because of their fundamental bi-level form, where the upper level is the one picking the optimal tolls, which are subject to route-choice constraints that constitute the lower-level dynamic traffic assignment [81]. The computational complexity of the toll design problem is known to be NP-hard [81,82,83], even when the formulation is not explicitly dynamic [37,84,85,86,87]. As a consequence, these problems are typically solved through heuristics or meta-heuristics [81]. In [35], a bi-level dynamic second-best toll pricing model is solved through a relaxation scheme consisting in the conversion of the bi-level formulation into a single level nonlinear programming problem, which is then solved iteratively. In [36], the genetic algorithm and the method of successive average are used to solve a two-layer network dynamic congestion pricing problem. In [37], a hybrid self-adaptive gradient projection (SAGP) and artificial bee colony (ABC) algorithm are employed to solve a bi-level dynamic congestion tolling problem, with the SAGP solving the lower level and ABC for the upper one. In [38], bi-level cellular particle swarm optimization is applied to a dynamic optimal toll problem with equilibrium constraints under demand uncertainty. Optimal dynamic pricing problems have also been formulated as Markov Decision Process and solved through approximate dynamic programming via state space aggregation [39], value function approximation with different initializations [40], a multiagent reinforcement learning algorithm [41] and policy gradient methods with tolls determined via a feedforward neural network [42].
The bi-level nature of dynamic toll pricing problems can also be described from a game theory perspective, where drivers and road managers are identified as players. At the lower level, drivers choose their paths pursuing their travel costs minimization without considering the impact of their choices on the other network users [88]. The traffic assignment resulting from drivers’ selfish choices is a Nash equilibrium called user equilibrium (UE) or Wardrop equilibrium [39,89,90]. User equilibrium traffic assignment may not coincide with the socially best solution, identified as System Optimum (SO), which is characterized by minimization of the total system travel cost [86]. In this context, road managers can introduce congestion pricing at the upper level as a cooperation mechanism to minimize total system costs [91], driving a user equilibrium pattern toward a System Optimum. A Stackelberg game occurs between the road operators who act as leaders due to their dominating role in the decision process and the users who act as followers, whereas a Nash game occurs between competing road operators [92]. Dynamic toll pricing algorithms based on Stackelberg game theory are presented in [43,45].
According to [93], dynamic marginal cost tolls can stabilize transportation networks around their social optimum traffic assignment. In [94], the system optimal traffic flow pattern is obtained through piecewise linear tolls on a subset of the network links. In [51], marginal costs-based dynamic pricing strategies are showed to eliminate all the delays and minimize the total schedule deviation cost experienced by users. A dynamic toll pricing scheme to achieve system optimum on a day-to-day basis is explored in [95].
The authors of [96], analyzing a morning commute problem, compared a conventional system optimum corresponding to the minimization of the total system travel cost taking into account user heterogeneity with a time-based system optimum, where the total travel time is minimized and found that the latter is Pareto-improving compared to the former.
In summary, in this Section, we have described the main dynamic toll pricing rules proposed in the literature, classifying them depending on whether they are based on feedback control (Section 2.1) or on optimization theory (Section 2.2). The following Section is dedicated to the simulation methods that can be employed to test the pricing rules.

3. Overview of Simulations

The pricing rules described in Section 2 represent possible interventions on transportation networks to improve operating achievements. Real-life drivers are informed of the toll value and decide whether to pay the toll to use the tolled facility or choose an alternative transportation solution. Data about the traffic formed by the users who accepted to pay the toll are usually collected through sensors, then elaborated and used as inputs for the definition of the toll. Nevertheless, since real-life experiments are challenging to perform in the transportation engineering field, there is a need for a simulation environment that can model drivers’ choices and their effects on traffic in order to test the performance of new pricing strategies in a closed-loop framework. This section is dedicated to reviewing the main simulation frameworks presented in the most recent dynamic toll pricing literature. Traffic and Driver Behavior Models are presented in Section 3.1 and Section 3.2, respectively. In view of the ever-growing ecologic concerns, recent researches frequently include emissions models to simulate vehicle-driven environmental deterioration. We dedicated Section 3.3 to the discussion of these models.

3.1. Traffic Simulation

The traffic model is an essential part of dynamic tolling design studies; it aims to quantify some traffic characteristics corresponding to each transport alternative, depending on the traffic volumes choosing that particular transport solution. A comprehensive survey on traffic state estimation can be found in [97]. According to the scale, traffic flow models can be classified as macroscopic, mesoscopic or microscopic, with an increasing level of detail:
  • macroscopic models are usually based on the analogy of traffic with fluid dynamics, thus traffic is described by the value of a few synthetic variables (flow, density and speed);
  • microscopic models focus on the single vehicles’ trajectories, and mesoscopic models share both the previously mentioned families’ elements.
In terms of formulation in a macroscopic model, traffic state is described by vector (8):
H ( x , t ) = v ( x , t ) ρ ( x , t ) q ( x , t ) ,
where v ( x , t ) is velocity (in km/h), ρ ( x , t ) is density (in veh/km) and q ( x , t ) is flow (in veh/h), all function of time t and location x on the infrastructure. Traffic flow is modeled locally through a system of partial differential equations inspired by hydrodynamics, as the system given by (9):
∂ q ( x , t ) ∂ x + ∂ ρ ( x , t ) ∂ t = 0 q ( x , t ) = q ( ρ ( x , t ) ) .
The first equation of the system is a conservation law, whereas the second equation, expressing flow rate in function of density, is called fundamental diagram.
The Lighthill-Whitham-Richards (LWR) kinematic wave model [98,99], characterized by the fundamental relation (10):
q ( x , t ) = v ( x , t ) · ρ ( x , t ) .
This relation is considered pioneering in macroscopic traffic flow modeling [97]. This model is used to characterize traffic flow evolution on the HOT lane in [20]. A stochastic macroscopic traffic flow model built by [47] on the classical LWR model is adopted in [46] for managed lanes. An accumulator model consisting in an aggregate, lumped-parameter model, based on the LWR model, is proposed in references [17,22]. The Cell Transmission Model (CTM) [100,101] and its derivatives, which are based on the discretization of the differential equations of the LWR model, are broadly used in traffic flow modeling for dynamic tolling design. In [40,48], traffic dynamics on managed lanes is modeled through CTM. Lou [8] adopts a multi-lane hybrid CTM proposed by [32] to describe traffic dynamics in HOT facilities.
The Macroscopic fundamental diagram, also called Network Fundamental Diagram, introduced by [102] to model networks traffic dynamics on an aggregate level by considering relations between space-mean traffic flow and density in urban regions, is adopted in [18,19,36,50,51].
In microscopic models, on the contrary, traffic is described at a disaggregated level by single-vehicle trajectories as given by (11):
x i = x i ( t ) .
In (11), x i ( t ) identifies the position of vehicle i at time t. Microscopic modeling is at the base of simulation platforms that have been often used in dynamic toll pricing studies at the network level: car-following-based VISSIM [11,14,15,16,23,36], Paramics [21,27], CORSIM [29,52] and MITSIM [30]. A mesoscopic modeling-based simulator, DynusT, is employed in [53] and a regional mesoscopic dynamic traffic assignment simulation environment is adopted in [54,56]. DynaMIT, a mesoscopic dynamic traffic simulator is applied in [30] toghether with microscopic simulation. Usually, these platforms can model both traffic and driver behavior.
In some studies, where the considered situation is analyzed as a bottleneck, traffic modeling is limited to a delay operator: in [13,49] traffic dynamics are described through the point-queue concept [103], assuming that the average travel time is given by the sum of a congestion-independent cruise time and a queuing delay. In [45] delays derive from the comparison between arrivals and departures curves, and a similar approach is followed in [57]. BPR (Bureau of Public Roads) volume-delay functions are adopted in [58,59]. Queuing theory is used in [24,25]. Arnott’s bottleneck model is finally employed in [43]. For more details on traffic modeling, we refer the reader to [67].
As shown in Figure 5, traffic simulation is quantitatively dominated by macroscopic models, delay operators and microscopic models, which together cover almost three fourths of the analyzed methods with similar percentages, between 20% and 30%.

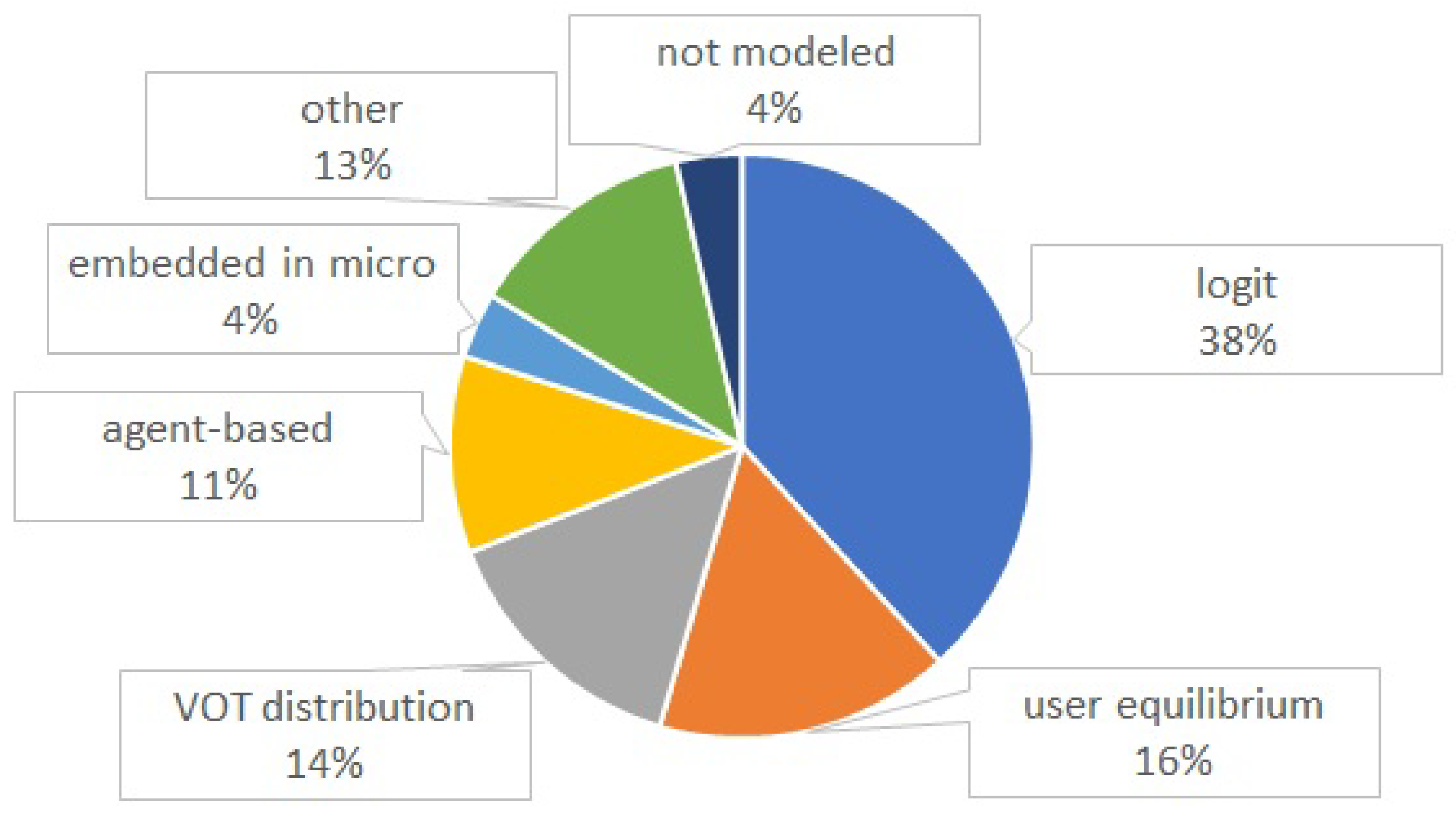
3.2. Driver Behavior

A User Behavior Model reproduces people’s choices among different transportation alternatives based on the alternatives’ and the users’ characteristics. Drivers’ choices between two alternatives may be described through binary logit models, where the utility of each alternative is a function of its current travel time and toll [6,8,11,13,16,17,20,22,24,25,28,31,46,48,49]. In such cases, general utility function U j ( t ) for an alternative j is formulated as in (12):
U j ( t ) = δ · π j ( t ) + ϵ · τ j ( t ) + ζ ,
where δ and ϵ represent the weighting of travel time and toll price, respectively, and ζ is an offset term used to take into account other unobservables. π j ( t ) and τ j ( t ) are respectively toll price and travel time of alternative j at time t. Other factors may be taken into account besides toll and travel time, for instance in [14], the utility is also a function of travel time reliability, which, in some cases, has been even found to be more valued than travel time savings [104]. Once defined a utility function, the probability of choosing alternative j in a binary logit model is expressed by (13):
p j ( t ) = 1 1 + e Δ U ( t ) ,
where Δ U ( t ) represents the difference in the utility function values of the two alternatives at time t.
Binary choices between a tolled and an untolled alternative may also be modeled through the cumulative distribution function of drivers’ VOT F ( ξ ) . The users whose VOT exceeds a particular limit, called the critical VOT ξ c r ( t ) , are assumed to choose the tolled alternative. The critical VOT is defined as the ratio of the toll price π ( t ) and the difference in travel times Δ τ ( t ) between the two alternatives at time t, as in (14):
ξ c r ( t ) = π ( t ) Δ τ ( t ) .
Indicating with p ( t ) the proportion of drivers choosing the tolled alternative we can formulate the model as in (15):
p ( t ) = p ( ξ c r ( t ) ) = 1 − F ( x c r ( t ) ) .
Different distribution functions are considered in the literature: a log-normal distribution is proposed in [45]; Weibull distribution is chosen for fitting in [29]; the authors of [12] adopt a simplified variant of the Burr distribution; the authors of [40] employ a discrete distribution of users’ VOT; Gutman [23] assumes a Gaussian drivers’ VOT probability distribution. We note that multinomial logit models may also be considered for modeling choices with more than two alternatives, whereas the driver behavior model described by (14) and (15) cannot be used in such cases. This last model, in turn, can consider drivers’ heterogeneity in VOT.
Drivers choices can also be modeled through user equilibrium considerations. As mentioned in Section 2.2, the user equilibrium is a Nash equilibrium derived from drivers’ selfish choices that operate to pursue travel costs minimization. In [57] the user equilibrium condition between tolled and untolled alternative for users all characterized by the same VOT is formulated as given by (16):
τ u n t o l l e d ( t ) = τ t o l l e d ( t ) + π t o l l e d ( t ) ,
where τ t o l l e d ( t ) and τ u n t o l l e d ( t ) indicate the travel time on the tolled alternative and on the untolled alternative at time t, respectively, and π t o l l e d ( t ) is the toll price of the tolled alternative at time t. Condition (16) holds when both alternatives are used; otherwise, only the less expensive alternative is used.
Modeling the case of large networks is typically more complex than for two-alternative cases: a route-choice model usually models driver behavior in association with a departure-time-choice model. The authors of [60] present a dynamic user equilibrium, where travelers engage in a Nash-like game choosing routes and departure times aiming to minimize selfishly their travel costs, which account for travel time, early/late arrival penalties and tolls. The authors of [54,56] adopt an econometric model considering drivers’ socio-economic characteristics and the network level-of-service to capture the drivers’ departure time choice in consequence of the toll. In [30], a path-size logit model is used for route choice, considering the similarities between overlapping paths.
While most models assume homogeneous drivers, agent-based models may be used to take into account drivers’ heterogeneity, as in [14,15,18,21,50].
In Figure 6 we may observe that logit models are quantitatively prevailing in driver behavior simulation, with user equilibrium, VOT distribution and agent-based models all present in over 10% of the studies and choice models embedded in micro-simulation traffic models (label: embedded in micro) in about 4% of the studies.

3.3. Externalities Quantification

Drivers are responsible for additional costs imposed upon other users and society, such as congestion, accidents, pollutants emissions and noise. These costs, called externalities, can be internalized through road charging [4]. As referred in Section 2.2, social welfare improvement, and maximization are among the objectives of dynamic pricing schemes, thus, together with the quantification of travel times, which is usually done through traffic assignment and reflects congestion, some studies include models for the quantification of other externalities.
Vehicular pollutants emissions include carbon dioxide (CO 2 ), nitrous oxides (NO x ), volatile organic compounds (VOC), carbon monoxide (CO), and particulate matter (PM 10 ) [105,106]. The emission may be estimated through emission factors (in gram/km), as in [107], or modeled in function of traffic conditions. Emission models are classified by [60] into three categories: microscopic, macroscopic and mesoscopic. In microscopic approach, the emission rates e i ( t ) of single vehicles i (in gram/m/s), are modeled as a function of the vehicular velocity v i ( t ) (in km/h) and, possibly, acceleration a i ( t ) (in m/s 2 ), as in (17):
e i ( t ) = f ( v i ( t ) , a i ( t ) ) ,
while in macroscopic emission models, the average emission rate e ¯ ( t ) (in gram/m/s) on a road segment is expressed as a function of the average density ρ ¯ ( t ) in (veh/km) and average velocity v ¯ ( t ) (in km/h) in that segment as in (18):
e ¯ ( t ) = g ( ρ ¯ ( t ) , v ¯ ( t ) ) .
Finally, mesoscopic models combine elements of the two previous approaches.
In [86], carbon dioxide emissions are quantified through a microscopic model as a velocity function only. In [108], emission rate is calculated at a macro level as a function of average segment velocity and vehicle type.
A noise emissions model is presented in [109]: noise emission levels are calculated on a macro level for each road segment due to traffic volume, heavy-duty vehicles share and maximum speeds. A grid of receivers is considered for calculating noise immission levels, which allow the quantification of the noise damages to be internalized.
The authors of [110] recently observed that when more than one externality is considered for marginal cost pricing, there exist correlation between the externalities, and it should be taken into account with proper correction factors.
Not only are externalities considered for dynamic toll schemes design, but they are also part of evaluation criteria, as in the Benefit-cost analysis of variable pricing projects in [105,106].
In summary, in this section we have presented the main components of the traffic simulation frameworks adopted in literature, grouping them into traffic models (Section 3.1), driver behavior models (Section 3.2) and externalities quantification models (Section 3.3). We now briefly discuss the most recent technology applications in the dynamic toll pricing field.

4. Interactions with Recent Technology Applications

The development of new communication and transportation technology is having various positive effects on road toll pricing, making it faster, easier, cheaper and more reliable [111]. In particular, connected traffic sensors enable the collection and storage of big amounts of data, which can be processed and mined to support real-time decision making [59], including dynamic toll pricing definition. Self-learning techniques have been proposed to gradually learn the parameters of the driver behavior model by the mining of the recorded traffic data [8,13,31], enabling a more accurate representation of the users’ preferences, which is fundamental for price definition. Reinforcement learning algorithms for optimization of dynamic pricing strategies are employed in [41,42] and random forest predictions are included in [62].
Connected drivers and vehicles allow the definition of user-specific strategies, where toll authorities can guide users’ mode and routing choices with user-dependent advice and dynamic pricing [109,112,113,114].

5. Conclusions

In this paper, we have reviewed recent literature about dynamic toll pricing focusing in particular on the studies published since 2008. We have identified the main objectives of dynamic toll pricing in keeping free-flow conditions, minimizing travel times and reducing externalities. We have observed that control-based price definition rules focus more on satisfying the first objective, while optimization-based algorithms, which represent the prevalent method, are built upon the maximization of some performance index of the system. We have identified a common structure in dynamic toll pricing studies, formed by a price definition rule together with a simulation framework composed by a model of the driver behavior, a traffic flow model and, possibly, externalities quantification models.
The scope of dynamic toll pricing varies from single infrastructures, as in the case of managed lanes facilities, where in some cases it is already implemented, to large scale networks, for which there are no known implementations at present. Managed lanes constitute the scope of most of the dynamic toll pricing schemes reviewed in this paper, followed by networks and tolled facilities.
Implemented dynamic toll pricing schemes are indeed still very few worldwide but the evolution of information technology, which allows increasingly fast and massive exchange of information, together with the progress in computation capabilities and the advancement of AI paradigms are certainly paving the way to the ideation of more complex and efficient dynamic toll pricing schemes and to new implementations, as dynamic pricing keeps emerging as a practice in multiple domains of Intelligent Transportation Systems.

Funding

C.L. would like to acknowledge the support of the Fundação para a Ciência e a Tecnologia (FCT), IP - Portugal for the Ph.D. Grant PD/BD/128137/2016. A.M.A. would like to acknowledge the support of the Ford-MIT Alliance.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

Data available within the article. All the quantitative considerations about the popularity of different scopes and methods presented in this article are determined based on the papers mentioned in Table 3.

Conflicts of Interest

The authors declare no conflict of interest.

Abbreviations

Abbreviations used specifically in Table 3 are referred in its caption. The following abbreviations are used in the rest of this manuscript:
AIartificial intelligence
HOTHigh Occupancy Toll
VOTValue of Time
ABCArtificial Bee Colony
vehequivalent passenger vehicles
hhour
kmkilometer
LWRLighthill-Whitham-Richards
CTMCell Transmission Model

References

  1. Saharan, S.; Bawa, S.; Kumar, N. Dynamic pricing techniques for Intelligent Transportation System in smart cities: A systematic review. Comput. Commun. 2020, 150, 603–625. [Google Scholar] [CrossRef]
  2. de Palma, A.; Lindsey, R. Traffic congestion pricing methodologies and technologies. Transp. Res. Part C Emerg. Technol. 2011, 19, 1377–1399. [Google Scholar] [CrossRef]
  3. Pigou, A.C. The Economics of Welfare; Macmillan: London, UK, 1920. [Google Scholar]
  4. Seik, F.T. An advanced demand management instrument in urban transport. Electronic road pricing in Singapore. Cities 2000, 17, 33–45. [Google Scholar] [CrossRef]
  5. Managed Lanes Project Database. Available online: https://managedlanes.wordpress.com/category/projects (accessed on 16 November 2020).
  6. Figueiras, P.; Gonçalves, D.; Costa, R.; Guerreiro, G.; Georgakis, P.; Jardim-Gonçalves, R. Novel Big Data-supported dynamic toll charging system: Impact assessment on Portugal’s shadow-toll highways. Comput. Ind. Eng. 2019, 135, 476–491. [Google Scholar] [CrossRef]
  7. Bracher, B.; Bogenberger, K. A dynamic prizing scheme for a congestion charging zone based on a network fundamental diagram. In Proceedings of the 5th IEEE International Conference on Models and Technologies for Intelligent Transportation Systems, MT-ITS 2017—Proceedings, Naples, Italy, 26–28 June 2017; pp. 669–674. [Google Scholar] [CrossRef]
  8. Lou, Y. A unified framework of proactive self-learning dynamic pricing for high-occupancy/toll lanes. Transp. A Transp. Sci. 2013, 9, 205–222. [Google Scholar] [CrossRef] [Green Version]
  9. Supernak, J.; Steffey, D.; Kaschade, C. Dynamic value pricing as instrument for better utilization of high-occupancy toll lanes: San Diego I-15 case. Transp. Res. Rec. 2003, 1839, 55–64. [Google Scholar] [CrossRef]
  10. Systematics, C. I-394 MnPASS Technical Evaluation: Final Report; Minnesota Department of Transportation: St. Paul, MN, USA, 2006. [Google Scholar]
  11. Zhang, G.; Wang, Y.; Wei, H.; Yi, P. A Feedback-Based Dynamic Tolling Algorithm for High-Occupancy Toll Lane Operations. Transp. Res. Rec. J. Transp. Res. Board 2008, 2065, 54–63. [Google Scholar] [CrossRef] [Green Version]
  12. Gardner, L.M.; Bar-gera, H.; Boyles, S.D. Development and comparison of choice models and tolling schemes for high-occupancy/toll (HOT) facilities. Transp. Res. Part B Methodol. 2013, 55, 142–153. [Google Scholar] [CrossRef]
  13. Yin, Y.; Lou, Y. Dynamic Tolling Strategies for Managed Lanes. J. Transp. Eng. 2009, 135, 45–52. [Google Scholar] [CrossRef]
  14. Li, W.; Cheng, D.; Bian, R.; Ishak, S.; Osman, O.A. Accounting for travel time reliability, trip purpose and departure time choice in an agent-based dynamic toll pricing approach. IET Intell. Transp. Syst. 2018, 12, 58–65. [Google Scholar] [CrossRef]
  15. Cheng, D.; Li, W.; Ishak, S. Accounting for travel time reliability and trip purpose in an agent-based approach to toll pricing with dynamic feedback control: Case study on 1-95 managed-lanes corridor. Transp. Res. Rec. 2014, 2470, 131–141. [Google Scholar] [CrossRef]
  16. Cheng, D.; Ishak, S. Maximizing toll revenue and level of service on managed lanes with a dynamic feedback-control toll pricing strategy. Can. J. Civ. Eng. 2015, 43, 18–27. [Google Scholar] [CrossRef]
  17. Phan, T.; Annaswamy, A.M.; Yanakiev, D.; Tseng, E. A model-based dynamic toll pricing strategy for controlling highway traffic. In Proceedings of the American Control Conference, Boston, MA, USA, 6–8 July 2016; pp. 6245–6252. [Google Scholar] [CrossRef]
  18. Zheng, N.; Rérat, G.; Geroliminis, N. Time-dependent area-based pricing for multimodal systems with heterogeneous users in an agent-based environment. Transp. Res. Part C Emerg. Technol. 2016, 62, 133–148. [Google Scholar] [CrossRef] [Green Version]
  19. Gu, Z.; Shafiei, S.; Liu, Z.; Saberi, M. Optimal distance- and time-dependent area-based pricing with the Network Fundamental Diagram. Transp. Res. Part C Emerg. Technol. 2018, 95, 1–28. [Google Scholar] [CrossRef] [Green Version]
  20. Zhang, G.; Ma, X.; Wang, Y. Self-adaptive tolling strategy for enhanced high-occupancy toll lane operations. IEEE Trans. Intell. Transp. Syst. 2014, 15, 306–317. [Google Scholar] [CrossRef]
  21. Zou, G.; Alvaro, G.; Kulkarni, R. Dynamic Pricing Algorithm with Embedded Controller for High Occupancy Toll Lanes. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, Gran Canaria, Spain, 15–18 September 2015; pp. 2384–2389. [Google Scholar] [CrossRef]
  22. Annaswamy, A.M.; Guan, Y.; Tseng, H.E.; Zhou, H.; Phan, T.; Yanakiev, D. Transactive Control in Smart Cities. Proc. IEEE 2018, 106, 518–537. [Google Scholar] [CrossRef]
  23. Gutman, P.O. Dynamic Pricing for Toll Lanes - a Case Study. IFAC-PapersOnLine 2016, 49, 25–30. [Google Scholar] [CrossRef]
  24. Kachroo, P.; Gupta, S.; Agarwal, S.; Ozbay, K. Optimal Control for Congestion Pricing: Theory, Simulation, and Evaluation. IEEE Trans. Intell. Transp. Syst. 2017, 18, 1234–1240. [Google Scholar] [CrossRef]
  25. Kachroo, P.; Özbay, K.M. Feedback routing via congestion pricing. In Feedback Control Theory for Dynamic Traffic Assignment; Springer International Publishing AG: Cham, Switzerland, 2018; Chapter 10; pp. 249–266. [Google Scholar] [CrossRef]
  26. Agarwal, S.; Kachroo, P. On the Economic Control of Cyber-physical Systems. In Proceedings of the 2017 IEEE 7th Annual International Conference on CYBER Technology in Automation, Control, and Intelligent Systems, CYBER 2017, Honolulu, HI, USA, 31 July–4 August 2017; pp. 86–90. [Google Scholar] [CrossRef]
  27. Sheu, J.B.; Yang, H. An integrated toll and ramp control methodology for dynamic freeway congestion management. Phys. A Stat. Mech. Its Appl. 2008, 387, 4327–4348. [Google Scholar] [CrossRef]
  28. Hassan, A.; Abdelghany, K.; Semple, J. Dynamic road pricing for revenue maximization. Transp. Res. Rec. 2013, 2345, 100–108. [Google Scholar] [CrossRef]
  29. El Khoury, J.; Srour, F.J. Value of Dynamic Revenue-Maximizing Congestion Pricing in a Highly Congested Corridor. J. Transp. Eng. 2015, 141, 04015029-1–04015029-11. [Google Scholar] [CrossRef]
  30. Zhang, Y.; Atasoy, B.; Akkinepally, A.; Ben-akiva, M. Dynamic Toll Pricing using Dynamic Traffic Assignment System with Online Calibration. Transp. Res. Rec. 2019, 2673, 532–546. [Google Scholar] [CrossRef]
  31. Lou, Y.; Yin, Y.; Laval, J.A. Optimal dynamic pricing strategies for high-occupancy/toll lanes. Transp. Res. Part C Emerg. Technol. 2011, 19, 64–74. [Google Scholar] [CrossRef]
  32. Laval, J.A.; Daganzo, C.F. Lane-changing in traffic streams. Transp. Res. Part B Methodol. 2006, 40, 251–264. [Google Scholar] [CrossRef]
  33. Tan, Z.; Yang, H.; Guo, R.Y. Dynamic congestion pricing with day-to-day flow evolution and user heterogeneity. Transp. Res. Part C Emerg. Technol. 2015, 61, 87–105. [Google Scholar] [CrossRef]
  34. Xiao, F.; Zhang, H.M. Pareto-improving and self-sustainable pricing for the morning commute with nonidentical commuters. Transp. Sci. 2014, 48, 159–169. [Google Scholar] [CrossRef]
  35. Ban, X.; Liu, H.X. A link-node discrete-time dynamic second best toll pricing model with a relaxation solution algorithm. Netw. Spat. Econ. 2009, 9, 243–267. [Google Scholar] [CrossRef]
  36. Wei, B.; Sun, D. A Two-Layer Network Dynamic Congestion Pricing Based on Macroscopic Fundamental Diagram. J. Adv. Transp. 2018, 2018. [Google Scholar] [CrossRef] [Green Version]
  37. Cheng, Q.; Liu, Z.; Szeto, W.Y. Transportmetrica B: Transport Dynamics A cell-based dynamic congestion pricing scheme considering travel distance and time delay. Transp. B Transp. Dyn. 2019, 7, 1286–1304. [Google Scholar] [CrossRef]
  38. Chung, B.D.; Yao, T.; Friesz, T.L.; Liu, H. Dynamic congestion pricing with demand uncertainty: A robust optimization approach. Transp. Res. Part B Methodol. 2012, 46, 1504–1518. [Google Scholar] [CrossRef]
  39. Rambha, T.; Boyles, S.D. Dynamic pricing in discrete time stochastic day-to-day route choice models. Transp. Res. Part B Methodol. 2016, 92, 104–118. [Google Scholar] [CrossRef]
  40. Pandey, V.; Boyles, S.D. Dynamic pricing for managed lanes with multiple entrances and exits. Transp. Res. Part C Emerg. Technol. 2018, 96, 304–320. [Google Scholar] [CrossRef]
  41. Pandey, V.; Boyles, S.D. Multiagent Reinforcement Learning Algorithm for Distributed Dynamic Pricing of Managed Lanes. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, Maui, HI, USA, 4–7 November 2018; pp. 2346–2351. [Google Scholar] [CrossRef]
  42. Pandey, V.; Wang, E.; Boyles, S.D. Deep reinforcement learning algorithm for dynamic pricing of express lanes with multiple access locations. Transp. Res. Part C Emerg. Technol. 2020, 119, 102715. [Google Scholar] [CrossRef]
  43. Kang, W.; Liu, X.; Li, L. Study on traffic congestion pricing for large scale multimodal networks in city. Adv. Mater. Res. 2013, 779, 805–809. [Google Scholar] [CrossRef]
  44. Jang, K.; Song, M.K.; Choi, K.; Kim, D.K. A bi-level framework for pricing of high-occupancy tool lanes. Transport 2014, 29, 317–325. [Google Scholar] [CrossRef] [Green Version]
  45. Jang, K.; Chung, K.; Yeo, H. A dynamic pricing strategy for high occupancy toll lanes. Transp. Res. Part A Policy Pract. 2014, 67, 69–80. [Google Scholar] [CrossRef]
  46. Yang, L.; Saigal, R.; Zhou, H. Distance-based dynamic pricing strategy for managed toll lanes. Transp. Res. Rec. 2012, 2283, 90–99. [Google Scholar] [CrossRef]
  47. Chu, K.C.; Yang, L.; Saigal, R.; Saitou, K. Validation of stochastic traffic flow model with microscopic traffic simulation. In Proceedings of the IEEE 7th International Conference on Automation Science and Engineering, Trieste, Italy, 24–27 August 2011. [Google Scholar] [CrossRef]
  48. Toledo, T.; Mansour, O.; Haddad, J. Simulation-based Optimization of HOT Lane Tolls. Transp. Res. Procedia 2015, 6, 189–197. [Google Scholar] [CrossRef] [Green Version]
  49. Jin, W.L.; Wang, X.; Lou, Y. Stable dynamic pricing scheme independent of lane-choice models for high-occupancy-toll lanes. Transp. Res. Part B Methodol. 2020, 140, 64–78. [Google Scholar] [CrossRef]
  50. Zheng, N.; Waraich, R.A.; Axhausen, K.W.; Geroliminis, N. A dynamic cordon pricing scheme combining the Macroscopic Fundamental Diagram and an agent-based traffic model. Transp. Res. Part A Policy Pract. 2012, 46, 1291–1303. [Google Scholar] [CrossRef]
  51. Amirgholy, M.; Gao, H.O. Modeling the dynamics of congestion in large urban networks using the macroscopic fundamental diagram: User equilibrium, system optimum, and pricing strategies. Transp. Res. Part B Methodol. 2017, 104, 215–237. [Google Scholar] [CrossRef]
  52. Michalaka, D.; Yin, Y.; Hale, D. Simulating high-occupancy toll lane operations. Transp. Res. Rec. 2013, 2396, 124–132. [Google Scholar] [CrossRef]
  53. He, X.; Chen, X.; Xiong, C.; Zhu, Z.; Zhang, L. Optimal time-varying pricing for toll roads under multiple objectives: A simulation-based optimization approach. Transp. Sci. 2017, 51, 412–426. [Google Scholar] [CrossRef]
  54. Aboudina, A.; Abdelgawad, H.; Abdulhai, B.; Nurul Habib, K. Time-dependent congestion pricing system for large networks: Integrating departure time choice, dynamic traffic assignment and regional travel surveys in the Greater Toronto Area. Transp. Res. Part A Policy Pract. 2016, 94, 411–430. [Google Scholar] [CrossRef]
  55. Small, K.A.; Verhoef, E.T. The Economics of Urban Transportation; Routledge: Abingdon, UK, 2007. [Google Scholar]
  56. Aboudina, A.; Abdulhai, B. A bi-level distributed approach for optimizing time-dependent congestion pricing in large networks: A simulation-based case study in the Greater Toronto Area. Transp. Res. Part C 2017, 85, 684–710. [Google Scholar] [CrossRef]
  57. Laval, J.A.; Cho, H.W.; Muñoz, J.C.; Yin, Y. Real-time congestion pricing strategies for toll facilities. Transp. Res. Part B Methodol. 2015, 71, 19–31. [Google Scholar] [CrossRef]
  58. Hong, K.S.; Lee, C.; Lee, K. Dynamic toll pricing model for an intelligent transportation system with individual high occupancy toll lanes. In Proceedings of the 2015 5th International Conference on IT Convergence and Security, ICITCS 2015—Proceedings, Kuala Lumpur, Malaysia, 24–27 August 2015. [Google Scholar] [CrossRef]
  59. Figueiras, P.; Costa, R.; Guerreiro, G.; Antunes, H.; Rosa, A.; Jardim-Gonçalves, R. User interface support for a big ETL data processing pipeline an application scenario on highway toll charging models. In Proceedings of the 2017 International Conference on Engineering, Technology and Innovation (ICE/ITMC), Madeira Island, Portugal, 27–29 June 2017; pp. 1437–1444. [Google Scholar] [CrossRef]
  60. Friesz, T.L.; Han, K.; Liu, H.; Yao, T. Dynamic Congestion and Tolls with Mobile Source Emission. Procedia-Soc. Behav. Sci. 2013, 80, 818–836. [Google Scholar] [CrossRef] [Green Version]
  61. Friesz, T.L.; Bernstein, D.; Smith, T.E.; Tobin, R.L.; Wie, B.W. A Variational Inequality Formulation of the Dynamic Network User Equilibrium Problem. Oper. Res. 1993, 41, 179–191. [Google Scholar] [CrossRef]
  62. Zhang, K.; Zhou, Z.; Qi, Y.; Wang, Y. Dynamic pricing strategy for high occupancy toll lanes based on random forest and nested model. IET Intell. Transp. Syst. 2019, 13, 636–643. [Google Scholar] [CrossRef]
  63. Nikolic, G.; Pringle, R.; Jacob, C.; Mendonca, N.; Bekkers, M.; Torday, A.; Rinelli, P. Dynamic tolling of HOT lanes through simulation of expected traffic conditions. In Proceedings of the Conference of the Transportation Association of Canada, Montreal, ON, Canada, 28 September–1 October 2014; pp. 2188–2205. [Google Scholar]
  64. Hourdos, J.; Janson, M.; Levinson, D.; Parikh, G. MnPASS Modeling and Pricing Algorithm Enhancement; Technical Report May; Minnesota Department of Transportation: St. Paul, MN, USA, 2015. [Google Scholar]
  65. Buckeye, K.R. Performance evaluation of I-394 MnPASS express lanes in Minnesota. Transp. Res. Rec. 2012, 2278, 153–162. [Google Scholar] [CrossRef]
  66. Buckeye, K.R. Express lanes performance evaluation: Interstate 35W in Minnesota. Transp. Res. Rec. 2014, 2450, 36–43. [Google Scholar] [CrossRef]
  67. Ferrara, A.; Sacone, S.; Siri, S. Freeway Traffic Modelling and Control; Springer International Publishing AG: Cham, Switzerland, 2018. [Google Scholar]
  68. Papageorgiou, M.; Kotsialos, A. Freeway Ramp Metering: An Overview. IEEE Trans. Intell. Transp. Syst. 2002, 3, 271–281. [Google Scholar] [CrossRef]
  69. Horowitz, R.; Sun, X.; Muñoz, L.; Zhang, M. Design, Field Implementation and Evaluation of Adaptive Ramp Metering Algorithms. California PATH Research Report UCB-ITS-PRR-2005-2; Technical Report January; University of California: Berkeley, CA, USA, 2005. [Google Scholar]
  70. Papageorgiou, M.; Kosmatopoulos, E.; Papamichail, I. Effects of variable speed limits on motorway traffic flow. Transp. Res. Rec. 2008, 2047, 37–48. [Google Scholar] [CrossRef]
  71. Soriguera, F.; Martínez, I.; Sala, M.; Menéndez, M. Effects of low speed limits on freeway traffic flow. Transp. Res. Part C Emerg. Technol. 2017, 77, 257–274. [Google Scholar] [CrossRef] [Green Version]
  72. Soole, D.W.; Watson, B.C.; Fleiter, J.J. Effects of average speed enforcement on speed compliance and crashes: A review of the literature. Accid. Anal. Prev. 2013, 54, 46–56. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  73. Vanlommel, M.; Houbraken, M.; Audenaert, P.; Logghe, S.; Pickavet, M.; De Maeyer, P. An evaluation of section control based on floating car data. Transp. Res. Part C Emerg. Technol. 2015, 58, 617–627. [Google Scholar] [CrossRef]
  74. Jenior, P.; Dowling, R.; Nevers, B.; Neudorff, L. Use of Freeway Shoulders for Travel—Guide for Planning, Evaluating, and Designing Part-Time Shoulder Use as a Traffic Management Strategy; Technical Report; U.S. Department of Transportation—Federal Highway Administration: Washington, DC, USA, 2016.
  75. Ben-Akiva, M.; Bottom, J.; Ramming, M.S. Route guidance and information systems. Proc. Inst. Mech. Eng. Part I 2001, 215, 317–324. [Google Scholar] [CrossRef]
  76. Schmitt, E.J.; Jula, H. Vehicle route guidance systems: Classification and comparison. In Proceedings of the IEEE Intelligent Transportation Systems Conference, Toronto, ON, Canada, 17–20 September 2006; pp. 242–247. [Google Scholar] [CrossRef]
  77. Baskar, L.D.; De Schutter, B.; Hellendoorn, J.; Papp, Z. Traffic control and intelligent vehicle highway systems: A survey. IET Intell. Transp. Syst. 2011, 5, 38–52. [Google Scholar] [CrossRef] [Green Version]
  78. Annaswamy, A.M.; Malekpour, A.R.; Baros, S. Emerging research topics in control for smart infrastructures. Annu. Rev. Control 2016, 42, 259–270. [Google Scholar] [CrossRef] [Green Version]
  79. Papageorgiou, M.; Hadj-Salem, H.; Blosseville, J.M. ALINEA: A Local Feedback Control Law for On-Ramp Metering. Transp. Res. Rec. J. Transp. Res. Board 1991, 1320, 58–64. [Google Scholar] [CrossRef]
  80. Lombardi, C.; Annaswamy, A.; Picado Santos, L. Model-based dynamic toll pricing scheme for a congested suburban freeway with multiple access locations. (unpublished).
  81. Sharon, G.; Hanna, J.P.; Rambha, T.; Levin, M.W.; Albert, M.; Boyles, S.D.; Stone, P. Real-time Adaptive Tolling Scheme for Optimized Social Welfare in Traffic Networks. In Proceedings of the 16th International Conference on Autonomous Agents and Multiagent Systems (AAMAS 2017), São Paulo, Brazil, 8–12 May 2017; pp. 828–836. [Google Scholar]
  82. Staňková, K.; Olsder, G.J.; Bliemer, M.C. Comparison of different toll policies in the dynamic second-best optimal toll design problem: Case study on a three-link network. Eur. J. Transp. Infrastruct. Res. 2009, 9, 331–346. [Google Scholar] [CrossRef]
  83. Li, H.; Bliemer, M.C.; Bovy, P.H. Network reliability-based optimal toll design. J. Adv. Transp. 2008, 42, 311–332. [Google Scholar] [CrossRef]
  84. Yu, B.; Zhang, L.; Guan, F.; Peng, Z.; Yao, B. Equity based congestion pricing: Considering the constraint of alternative path. Oper. Res. 2017, 17, 313–337. [Google Scholar] [CrossRef]
  85. Grandoni, F.; Rothvoß, T. Pricing on paths: A ptas for the highway problem. SIAM J. Comput. 2016, 45, 675–684. [Google Scholar] [CrossRef]
  86. Wen, L.; Eglese, R. Minimizing CO2e emissions by setting a road toll. Transp. Res. Part D Transp. Environ. 2016, 44, 1–13. [Google Scholar] [CrossRef] [Green Version]
  87. Stefanello, F.; Buriol, L.S.; Hirsch, M.J.; Pardalos, P.M.; Querido, T.; Resende, M.G.C.; Ritt, M. On the minimization of traffic congestion in road networks with tolls. Ann. Oper. Res. 2017, 249, 119–139. [Google Scholar] [CrossRef]
  88. Shirazi, M.; Aashtiani, H.Z.; Quadrifoglio, L. Estimating the minimal revenue tolls in large-scale roadway networks using the dynamic penalty function method. Comput. Ind. Eng. 2017, 107, 120–127. [Google Scholar] [CrossRef]
  89. John, N. Non-cooperative games. Ann. Math. 1951, 54, 286–295. [Google Scholar]
  90. Glen, W.J. Some theoretical aspect of road traffic research. Proc. Inst. Civ. Eng. Part II 1952, 1, 352–362. [Google Scholar]
  91. Levinson, D. Micro-foundations of congestion and pricing: A game theory perspective. Transp. Res. Part A Policy Pract. 2005, 39, 691–704. [Google Scholar] [CrossRef] [Green Version]
  92. Zhou, J.; Chen, X.g.; Yang, H.w. Control Strategy on Road Toll Pricing under a BOT Scheme. Syst. Eng.-Theory Pract. 2009, 28, 148–151. [Google Scholar] [CrossRef]
  93. Maggistro, R.; Como, G. Stability and optimality of multi-scale transportation networks with distributed dynamic tolls. In Proceedings of the IEEE Conference on Decision and Control, Nice, France, 11–13 December 2019; pp. 211–216. [Google Scholar] [CrossRef] [Green Version]
  94. Shen, W.; Zhang, H.M. On the morning commute problem in a corridor network with multiple bottlenecks: Its system-optimal traffic flow patterns and the realizing tolling scheme. Transp. Res. Part B Methodol. 2009, 43, 267–284. [Google Scholar] [CrossRef] [Green Version]
  95. Han, L.; Wang, D.Z.; Lo, H.K.; Zhu, C.; Cai, X. Discrete-time day-to-day dynamic congestion pricing scheme considering multiple equilibria. Transp. Res. Part B Methodol. 2017, 104, 1–16. [Google Scholar] [CrossRef]
  96. Liu, Y.; Nie, Y.M. Morning commute problem considering route choice, user heterogeneity and alternative system optima. Transp. Res. Part B Methodol. 2011, 45, 619–642. [Google Scholar] [CrossRef]
  97. Seo, T.; Bayen, A.M.; Kusakabe, T.; Asakura, Y. Traffic state estimation on highway: A comprehensive survey. Annu. Rev. Control 2017, 43, 128–151. [Google Scholar] [CrossRef] [Green Version]
  98. Lighthill, M.; Witham, G. On Kinematic Waves. I. Flow Model- ing in Long Rivers. II. A Theory of Traffic Flow on Long Crowded Roads. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1955, 229, 317–345. [Google Scholar]
  99. Richards, P. Shockwaves on the Highway. Oper. Res. 1956, 4, 42–51. [Google Scholar] [CrossRef]
  100. Daganzo, C.F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp. Res. Part B Methodol. 1994, 28B, 269–287. [Google Scholar] [CrossRef]
  101. Daganzo, C.F. The cell transmission model, part II: Network traffic. Transp. Res. Part B Methodol. 1995, 29B, 79–93. [Google Scholar] [CrossRef]
  102. Daganzo, C.F. Urban gridlock: Macroscopic modeling and mitigation approaches. Transp. Res. Part B Methodol. 2007, 41, 49–62. [Google Scholar] [CrossRef]
  103. Kuwahara, M.; Akamatsu, T. Decomposition of the reactive dynamic assignments with queues for a many-to-many origin-destination pattern. Transp. Res. Part B Methodol. 1997, 31, 1–10. [Google Scholar] [CrossRef]
  104. Brent, D.A.; Gross, A. Dynamic road pricing and the value of time and reliability. J. Reg. Sci. 2018, 58, 330–349. [Google Scholar] [CrossRef]
  105. Burris, M.; Asce, M.; Sullivan, E.; Asce, M. Benefit-Cost Analysis of Variable Pricing Projects: QuickRide HOT Lanes. J. Transp. Eng. 2006, 132, 183–190. [Google Scholar] [CrossRef] [Green Version]
  106. Sullivan, E.; Burris, M. Benefit-cost analysis of variable pricing projects: SR-91 express lanes. J. Transp. Eng. 2006, 132, 191–198. [Google Scholar] [CrossRef] [Green Version]
  107. Kickhöfer, B.; Nagel, K. Towards High-Resolution First-Best Air Pollution Tolls: An Evaluation of Regulatory Policies and a Discussion on Long-Term User Reactions. Netw. Spat. Econ. 2016, 16, 175–198. [Google Scholar] [CrossRef]
  108. Wu, K.; Chen, Y.; Ma, J.; Bai, S.; Tang, X. Traffic and emissions impact of congestion charging in the central Beijing urban area: A simulation analysis. Transp. Res. Part D Transp. Environ. 2017, 51, 203–215. [Google Scholar] [CrossRef]
  109. Kaddoura, I.; Kröger, L.; Nagel, K. User-specific and Dynamic Internalization of Road Traffic Noise Exposures. Netw. Spat. Econ. 2017, 17, 153–172. [Google Scholar] [CrossRef] [Green Version]
  110. Agarwal, A.; Kickhöfer, B. The correlation of externalities in marginal cost pricing: Lessons learned from a real-world case study. Transportation 2018, 45, 849–873. [Google Scholar] [CrossRef] [Green Version]
  111. Iseki, H.; Demisch, A. Examining the linkages between electronic roadway tolling technologies and road pricing policy objectives. Res. Transp. Econ. 2012, 36, 121–132. [Google Scholar] [CrossRef]
  112. Bui, K.T.; Huynh, V.A.; Frazzoli, E. Dynamic traffic congestion pricing mechanism with User-Centric considerations. In Proceedings of the IEEE Conference on Intelligent Transportation Systems, Proceedings, ITSC, Anchorage, AK, USA, 16–19 September 2012; pp. 147–154. [Google Scholar] [CrossRef] [Green Version]
  113. Wu, L.; Zhang, L.; Ge, H. Pricing strategy of public and individual competition transportation system. Appl. Mech. Mater. 2012, 209-211, 861–865. [Google Scholar] [CrossRef]
  114. Shukla, A.; Bhattacharya, P.; Tanwar, S.; Kumar, N.; Guizani, M. DwaRa: A Deep Learning-Based Dynamic Toll Pricing Scheme for Intelligent Transportation Systems. IEEE Trans. Veh. Technol. 2020, 69, 12510–12520. [Google Scholar] [CrossRef]
Applsci 11 04778 g001 550
Figure 1. Distribution of the analyzed dynamic toll pricing studies by scope.
Figure 1. Distribution of the analyzed dynamic toll pricing studies by scope.
Applsci 11 04778 g001
Applsci 11 04778 g002 550
Figure 2. Evolution of the number of publications on dynamic toll pricing.
Figure 2. Evolution of the number of publications on dynamic toll pricing.
Applsci 11 04778 g002
Applsci 11 04778 g003 550
Figure 3. Distribution of the published documents on dynamic toll pricing by country.
Figure 3. Distribution of the published documents on dynamic toll pricing by country.
Applsci 11 04778 g003
Applsci 11 04778 g004 550
Figure 4. The distribution of the analyzed studies categorized by scope (inner circle) and main price definition method (outer circle). Labels: ML = Managed Lanes, NW = Networks, TF = Tolled Facilities, OPT = Optimization, C = Control, OTH = Other.
Figure 4. The distribution of the analyzed studies categorized by scope (inner circle) and main price definition method (outer circle). Labels: ML = Managed Lanes, NW = Networks, TF = Tolled Facilities, OPT = Optimization, C = Control, OTH = Other.
Applsci 11 04778 g004
Applsci 11 04778 g005 550
Figure 5. The distribution of the analyzed studies sorted by traffic simulation method.
Figure 5. The distribution of the analyzed studies sorted by traffic simulation method.
Applsci 11 04778 g005
Applsci 11 04778 g006 550
Figure 6. The distribution of the analyzed studies sorted by driver behavior model.
Figure 6. The distribution of the analyzed studies sorted by driver behavior model.
Applsci 11 04778 g006
Table
Table 1. Results of three different runs of the keywords search in title, abstract or keywords of documents on the Scopus search engine, characterized by different keywords combinations.
Table 1. Results of three different runs of the keywords search in title, abstract or keywords of documents on the Scopus search engine, characterized by different keywords combinations.
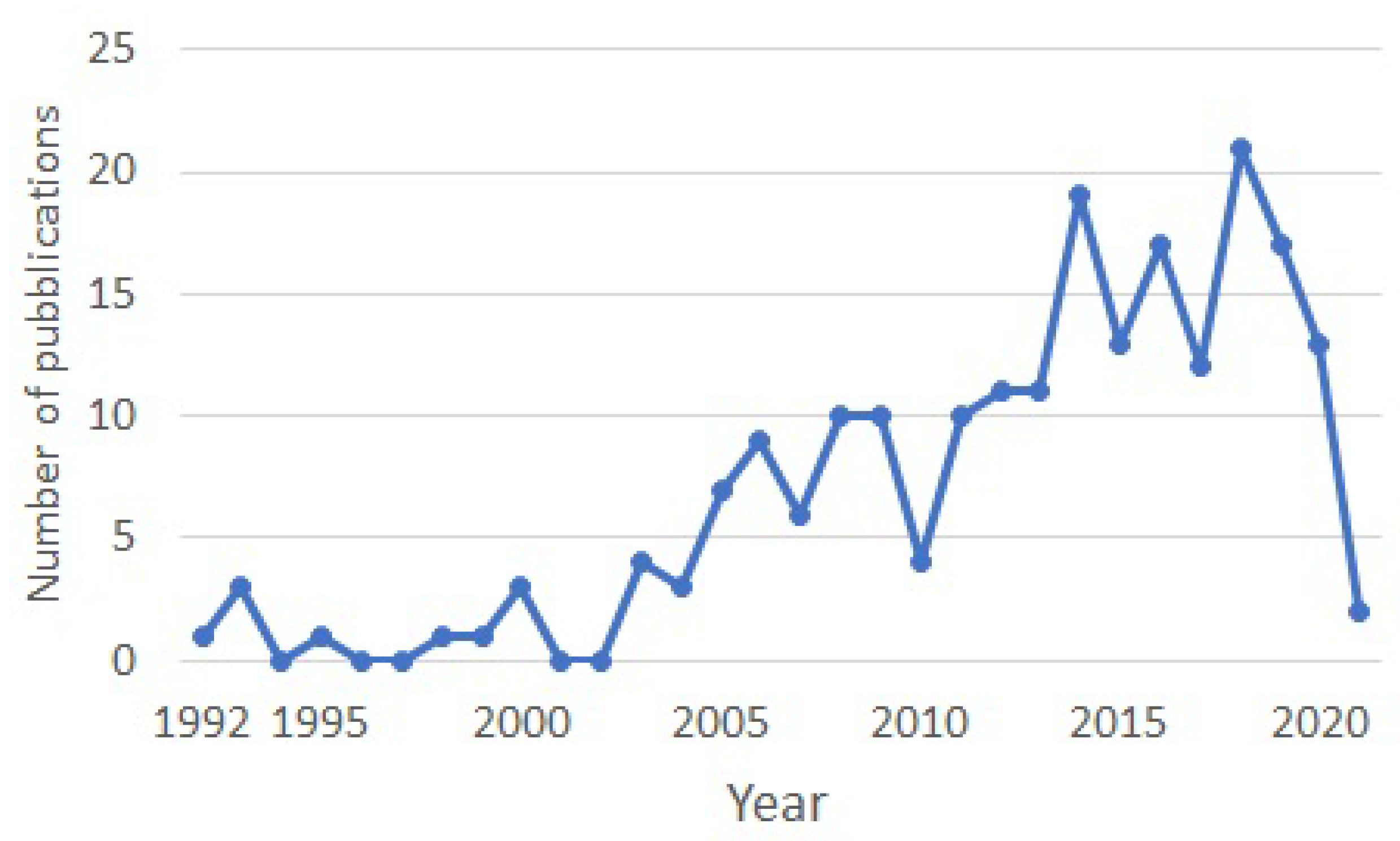
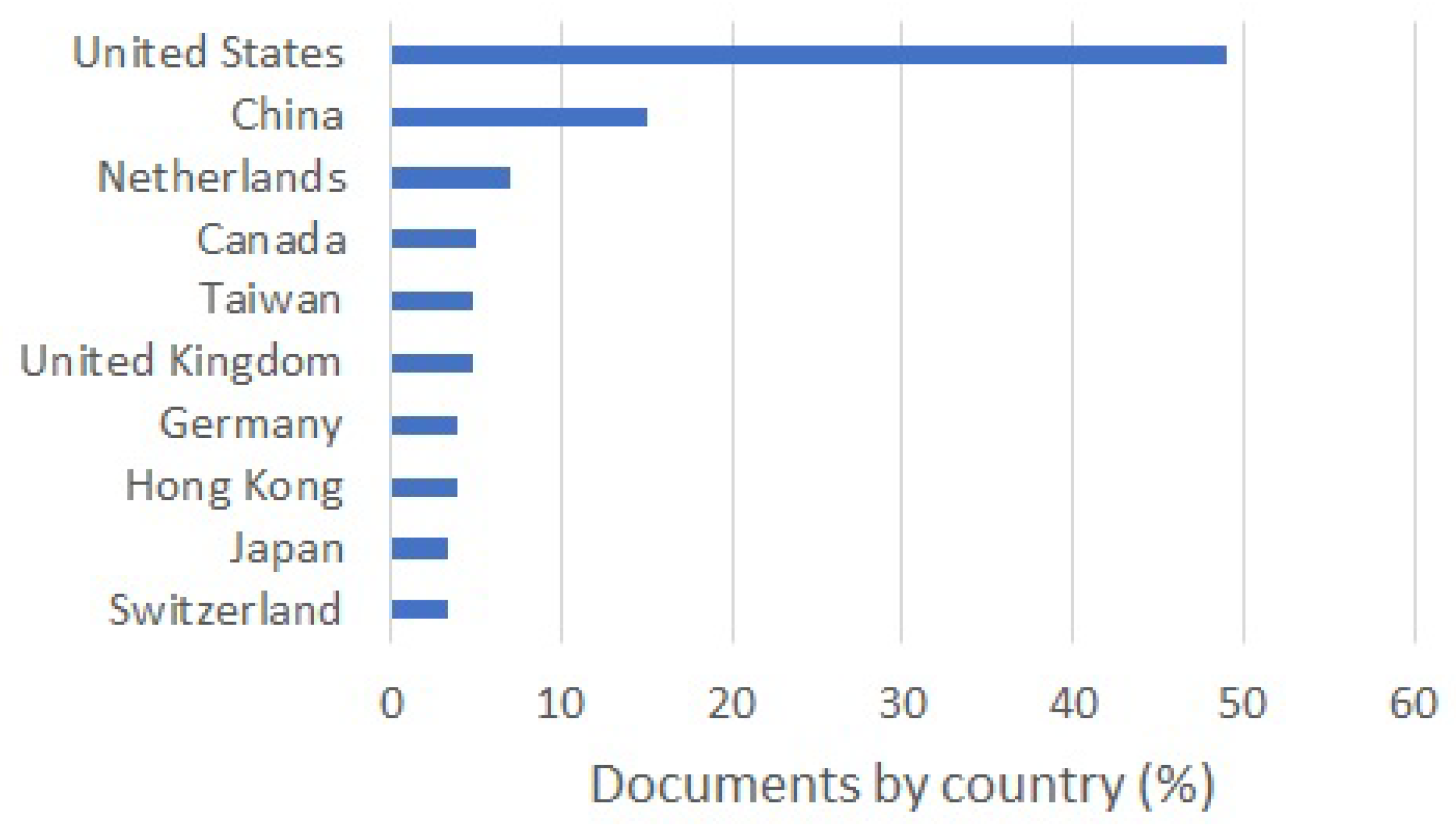
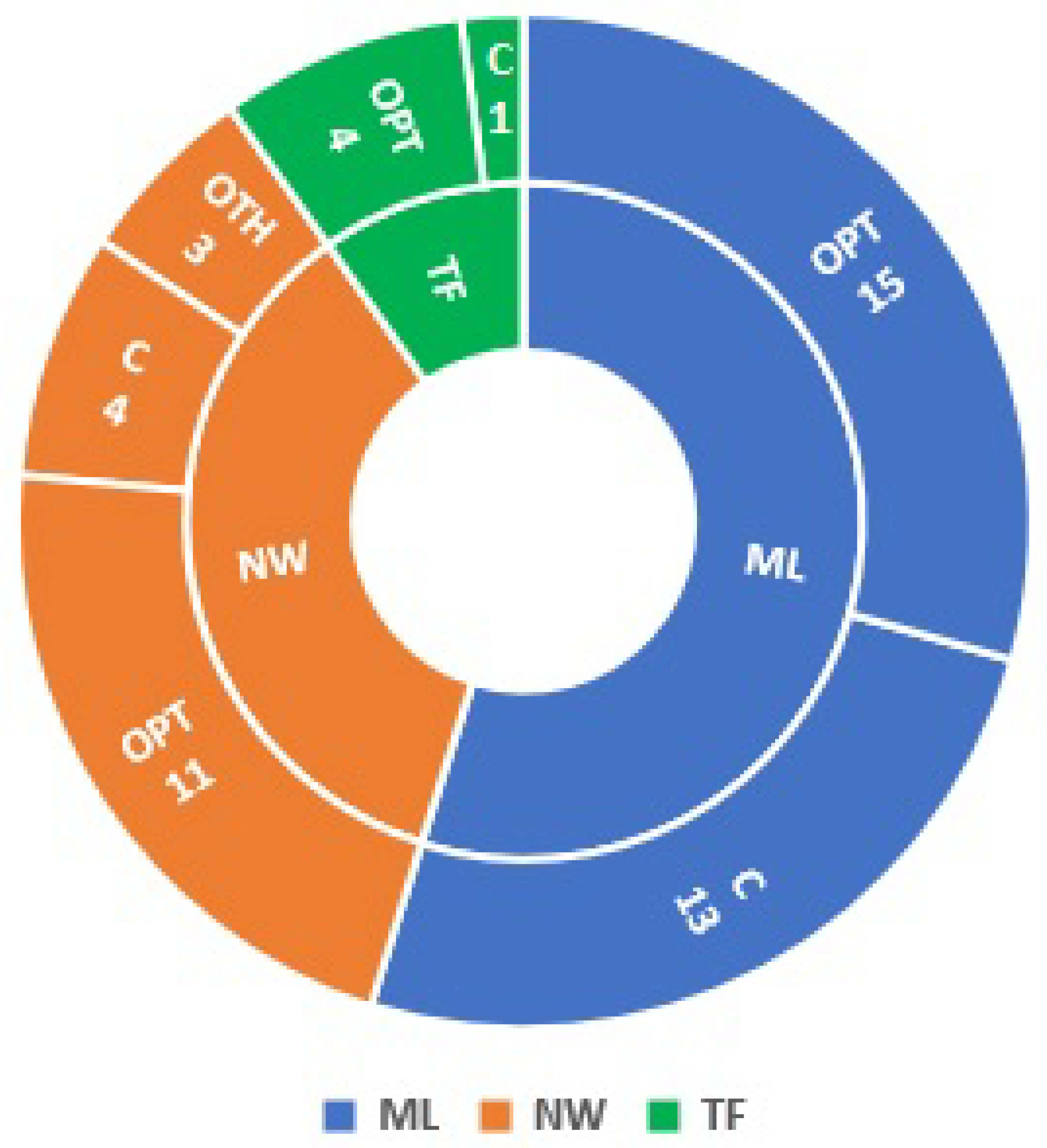
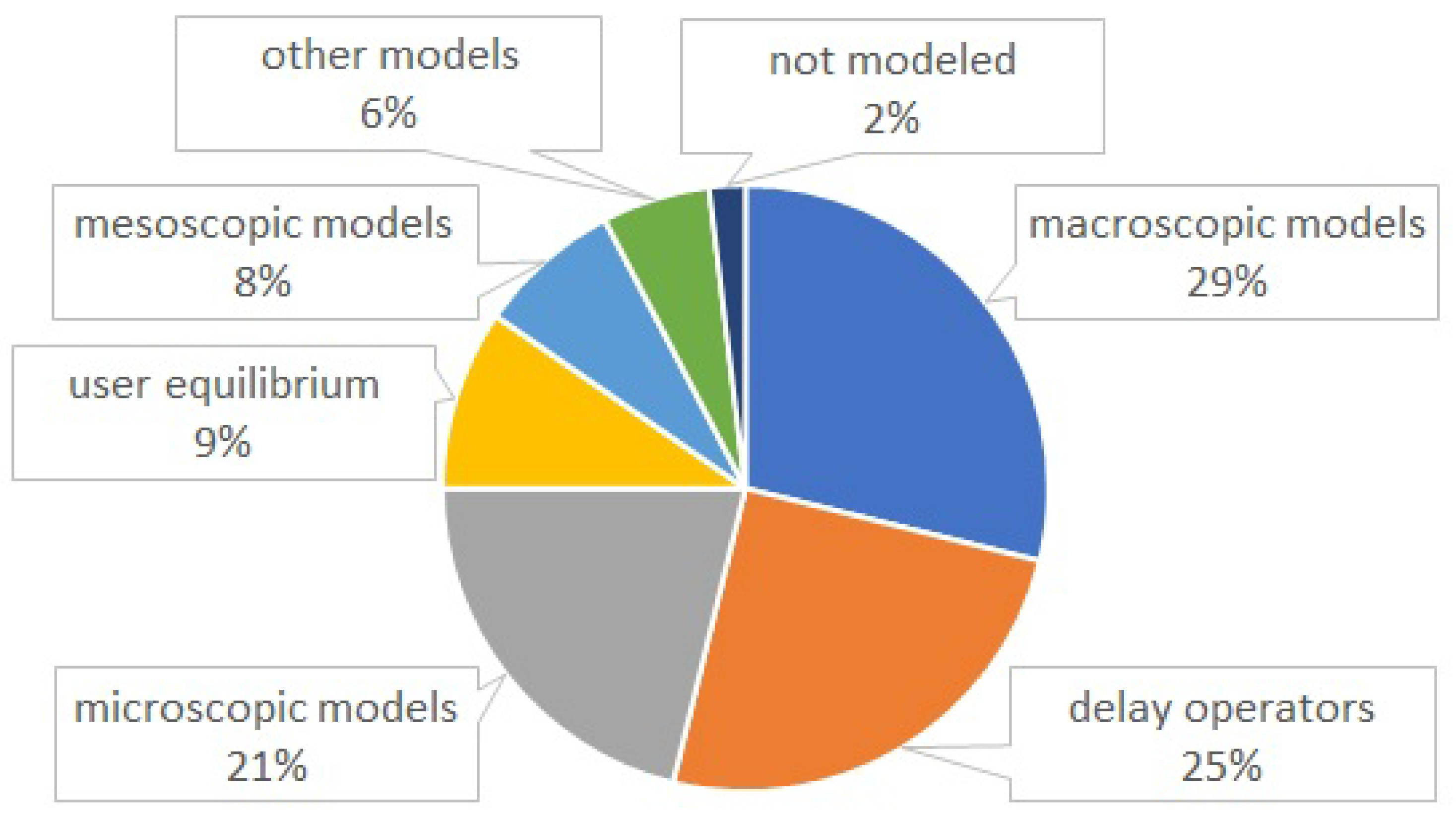
KeywordsReferencesYears (Since)
dynamic AND toll AND pricing2091992
dynamic AND toll15031973
dynamic AND pricing88941967
Table
Table 2. Analysis of the search results in terms of subject areas, from Scopus.
Table 2. Analysis of the search results in terms of subject areas, from Scopus.
Subject AreaDocuments
Engineering151
Social Sciences111
Computer Science72
Mathematics21
Environmental Science12
Economics, Econometric and Finance11
Decision Sciences9
Business, Management and Accounting6
Physics and Astronomy5
Energy4
Earth and Planetary Science3
Arts and Humanities1
Chemical Engineering1
Materials Science1
Table
Table 3. A list of the main reviewed studies described by reference (Ref.), year of publication, scope, main pricing rule principle, traffic simulation basis, driver behavior model and recent technology application. We included in the table also some studies which do not give a complete pricing scheme, but are limited to the presentation of some tool which can be combined with other models in order to obtain a complete pricing scheme. The following abbreviations are adopted in this table: AD = Arrivals-Departures, adj. = adjustable, av. = average, bottl. = bottleneck, CTM = Cell Transmission Model, D2D = Day-to-day, discr. = discrete, distr. = distribution, DTC = departure time choice, DUE = Dynamic User Equilibrium, emb. = embedded, enh. = enhanced, fac. = facilities, Gauss. = Gaussian, infl. = inflow, log-n. = log-normal, LS = large scale, LWR = Lighthill-Witham-Richards, macro = macroscopic, max. = maximizing, MC = multiclass, meso = mesoscopic, MFD = macroscopic fundamental diagram, micro = microscopic, min. = minimizing, MM = multi-modal, MN = multinomial, na. = national, NW = networks, obj. = objective, op. = optimal, oper. = operator, opt. = optmization, P = proportional, PD = porportional derivative, PI = Proportional Integral, PQ = Point-Queue concept, PWcontr. = piece-wise linear control, PID = Proportional Integral Derivative, rd = road, RF = random forest, RL = reinforcement learning, sens. = sensitivity, SRDC = simultaneous route-and-departure choice, syst. = system, TDGP = total delay on general purpose lanes, TE = total emissions, throughp. = throughput, transp. = transportation, TTC = total travel cost, TTT = total travel time, TTTC = total travel time cost, UE = User Equilibrium, unt. = untolled, urb. = urban, vehic. = vehicular, VOT = value of time, Weib. = Weibull.
Table 3. A list of the main reviewed studies described by reference (Ref.), year of publication, scope, main pricing rule principle, traffic simulation basis, driver behavior model and recent technology application. We included in the table also some studies which do not give a complete pricing scheme, but are limited to the presentation of some tool which can be combined with other models in order to obtain a complete pricing scheme. The following abbreviations are adopted in this table: AD = Arrivals-Departures, adj. = adjustable, av. = average, bottl. = bottleneck, CTM = Cell Transmission Model, D2D = Day-to-day, discr. = discrete, distr. = distribution, DTC = departure time choice, DUE = Dynamic User Equilibrium, emb. = embedded, enh. = enhanced, fac. = facilities, Gauss. = Gaussian, infl. = inflow, log-n. = log-normal, LS = large scale, LWR = Lighthill-Witham-Richards, macro = macroscopic, max. = maximizing, MC = multiclass, meso = mesoscopic, MFD = macroscopic fundamental diagram, micro = microscopic, min. = minimizing, MM = multi-modal, MN = multinomial, na. = national, NW = networks, obj. = objective, op. = optimal, oper. = operator, opt. = optmization, P = proportional, PD = porportional derivative, PI = Proportional Integral, PQ = Point-Queue concept, PWcontr. = piece-wise linear control, PID = Proportional Integral Derivative, rd = road, RF = random forest, RL = reinforcement learning, sens. = sensitivity, SRDC = simultaneous route-and-departure choice, syst. = system, TDGP = total delay on general purpose lanes, TE = total emissions, throughp. = throughput, transp. = transportation, TTC = total travel cost, TTT = total travel time, TTTC = total travel time cost, UE = User Equilibrium, unt. = untolled, urb. = urban, vehic. = vehicular, VOT = value of time, Weib. = Weibull.
Ref.YearScopePricing RuleTraffic SimulationDriver BehaviorRecent Technology
[13]2009managed lanesP controldelay operator (PQ)binary logitself-learning
[11]2008HOT lanesPWcontr.micro (VISSIM)binary logit-
[14]2018managed lanesPWcontr. op. gainsmicro (VISSIM)agent-based-
[15]2014managed lanesPWcontr. op. gainsmicro (VISSIM)agent-based-
[16]2015managed lanesPWcontr. op. gainsmicro (VISSIM)binary logit-
[17]2016HOT lanesPD controlmacro (LWR-based)binary logit-
[18]2016MM urb. NWPI controlmacro (MFD)agent-based-
[19]2018LS NWPI controlmacro (MFD)C-logit-
[20]2014HOT lanesPI controlmacro (LWR)binary logit-
[21]2015HOT lanesPID controlmicro (Paramics)agent-based-
[22]2018HOT lanesPD controlmacro (LWR-based)binary logit-
[23]2016HOT lanescascaded controlmicro (VISSIM)VOT distr. (Gauss.)-
[24]2017toll lanesoptimal controlqueuing theorybinary logit-
[25]2018toll lanesoptimal controlqueuing theorybinary logit-
[26]2018LS systemoptimal controldiscretized modelUE-
[27]2008freewaysoptimal controlmicro (Paramics)emb. in Paramics-
[28]2013toll facilitiesrevenue-max. opt.linear functionbinary logit-
[29]2015tolled routerevenue-max. opt.micro (CORSIM)VOT distr. (Weib.)-
[30]2019managed lanesrevenue-max. opt.micro (MITSIM)path-size logit-
meso (DynaMIT)
[31]2011HOT lanesthroughp.-max. opt.macro (CTM [32])binary logitself-learning
[8]2013HOT lanesav.flow-max. opt.macro (CTM [32])binary logitself-learning
[33]2015toll. NW (D2D)bi-objective opt.UEUE-
[34]2014transp. NWsyst.cost-min.delay operatorVOT distr.-
[35]2009general NWbi-level opt.UEUE-
[36]2018two-layer NWbi-level opt.macro (MFD)UE-
micro (VISSIM)
[37]2019NWbi-level opt.DUEDUE-
[38]2012NWbi-level opt.DUEDUE-
[39]2016NW (D2D)Markov DPMarkovianpath-size logit-
[40]2018managed lanesMarkov DPmacro (CTM)VOT distr. (disc.)-
[41]2018managed lanesMarkov DPmacro (CTM)agent-basedMA RL
[42]2020express lanesMarkov DPmacro (CTM)MC binary logitdeep RL
MC decision route
[43]2013LS MM NWgame theorydelay oper. (ABM)Nash Equilibrium-
[44]2014HOT lanesgame theorydelay operator (AD)VOT distr. (log-n.)-
[45]2014HOT lanesmulti-obj. opt.delay operator (AD)VOT distr. (log-n.)-
[46]2012managed lanesrevenue-max. opt.macro [47]binary logit-
[48]2015HOT lanesopt. (any objective)macro (CTM)binary logit-
[49]2020HOT lanesthroughp.-max. opt.delay operator (PQ)MN logit-
UE VOT distr.
general lane-choice
[50]2012urb. NWP controlmacro (MFD)binary logit-
agent-based-
[51]2017large urb. NWoutflow-max. opt.macro (MFD)UE-
[52]2013HOT lanesP controlmicro (CORSIM)emb. in CORSIM-
[53]2017toll roadsmulti-obj. opt.meso (DynusT)--
[54]2016large NWbottl. model [55]mesoeconometric DTC-
[56]2017large NWTTT-min. opt.mesoeconometric DTC-
[57]2015toll vs. unt. fac.various obj. opt.delay operator (AD)UE-
[58]2015HOT lanesTTTC-min. opt.delay opertor (BPR)time and price sens.-
TTT-min. opt.
[59]2017urb./na. rd NWshifting obj.--big data mining
[6]2019urb./na. rd NWshifting obj. (adj.)delay opertor (BPR)binary logit-
[12]2013HOT lanesHOT infl.-max. opt.delay operator (AD)VOT distr. (Burr)-
[60]2013toll. vehic. NWTTC&TE-min. opt.SRDC (DUE)[61]SRDC (DUE)[61]-
[62]2019HOT lanesTDGP-min. opt.delay operator (AD)RF predictionsRF predictions

Short Biography of Authors

Applsci 11 04778 i001Claudio Lombardi, 29, received the B.S. degree in Civil Engineering from Politecnico di Milano, Milan, Italy, in 2014 and the M.S. degree in Civil Engineering from Instituto Superior Técnico and from Politecnico di Milano in 2016. He has been a visiting student in the Active-Adaptive Control Laboratory, Department of Mechanical Engineering at Massachusetts Institute of Technology during 2018–2020. He is currently pursuing the Ph.D. degree in Transportation Systems in CERIS, Instituto Superior Técnico, Lisbon, Portugal, working on dynamic toll pricing for freeways.
Applsci 11 04778 i002Luís Picado-Santos, 60, PhD, is a Full Professor of Transport and Infrastructures. He was President of the research centre CERIS (2019–2020). Luís is Director of the Doctoral Program in Transportation Systems, initiated under the MIT-Portugal joint collaboration program. He is Director of the Highways and Transport Experimental Laboratory. He is working in an international IR&D project and several short-term IR&D projects. Also supervises five PhD students. Since 1995, Luís supervised 22 concluded PhD and 63 MSc dissertations on pavement mechanics, asset management, dynamic traffic management, and road safety. In the same period, he was in charge of research and technology transfer to industry projects (14 and 20 respectively). He is the author of more than 300 international publications, including 60 articles on international peer reviewed journals (ISI and/or SCOPUS). For more than 25 years, he has had an intense consultancy activity with international and local agencies and the private sector.
Applsci 11 04778 i003Anuradha M. Annaswamy is Founder and Director of the Active-Adaptive Control Laboratory in the Department of Mechanical Engineering at MIT. Her research interests span adaptive control theory and its applications to aerospace, automotive, and propulsion systems as well as cyber physical systems such as Smart Grids, Smart Cities, and Smart Infrastructures. Her research team of 15 students and post-docs is supported at present by the US Air-Force Research Laboratory, US Department of Energy, Boeing, Ford-MIT Alliance, and NSF. She has received best paper awards (Axelby; CSM), Distinguished Member and Distinguished Lecturer awards from the IEEE Control Systems Society (CSS) and a Presidential Young Investigator award from NSF. She is the author of a graduate textbook on adaptive control, co-editor of two vision documents on smart grids as well as two editions of the Impact of Control Technology report, and a member of the National Academy of Sciences Committee that published a report on the Future of Electric Power in the United States in 2021. She is a Fellow of IEEE and IFAC. She was the President of CSS in 2020.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Lombardi, C.; Picado-Santos, L.; Annaswamy, A.M. Model-Based Dynamic Toll Pricing: An Overview. Appl. Sci. 2021, 11, 4778. https://doi.org/10.3390/app11114778

AMA Style

Lombardi C, Picado-Santos L, Annaswamy AM. Model-Based Dynamic Toll Pricing: An Overview. Applied Sciences. 2021; 11(11):4778. https://doi.org/10.3390/app11114778

Chicago/Turabian Style

Lombardi, Claudio, Luís Picado-Santos, and Anuradha M. Annaswamy. 2021. "Model-Based Dynamic Toll Pricing: An Overview" Applied Sciences 11, no. 11: 4778. https://doi.org/10.3390/app11114778

APA Style

Lombardi, C., Picado-Santos, L., & Annaswamy, A. M. (2021). Model-Based Dynamic Toll Pricing: An Overview. Applied Sciences, 11(11), 4778. https://doi.org/10.3390/app11114778

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop