Wind-Resistant Capacity Modeling for Electric Transmission Line Towers Using Kriging Surrogates and Its Application to Structural Fragility
Abstract
Featured Application
Abstract
1. Introduction
2. Tower Capacity
2.1. Wind Loading
2.2. Limit Capacity
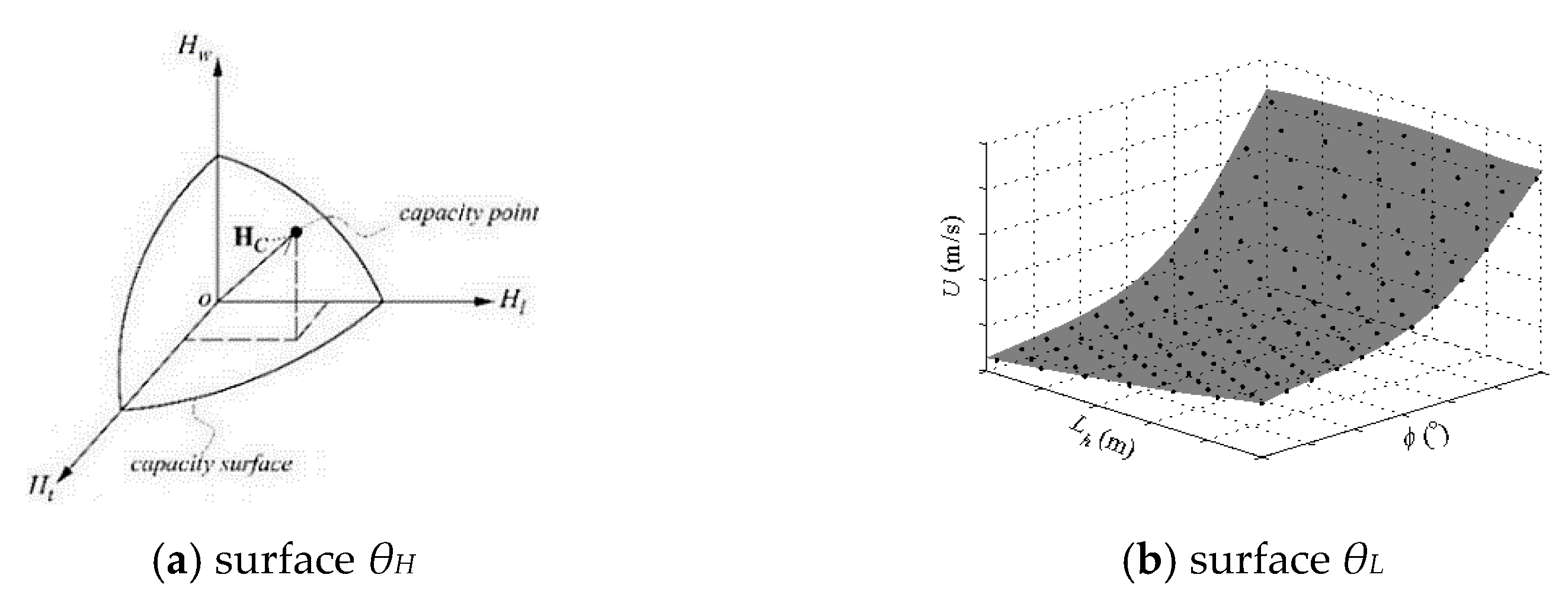
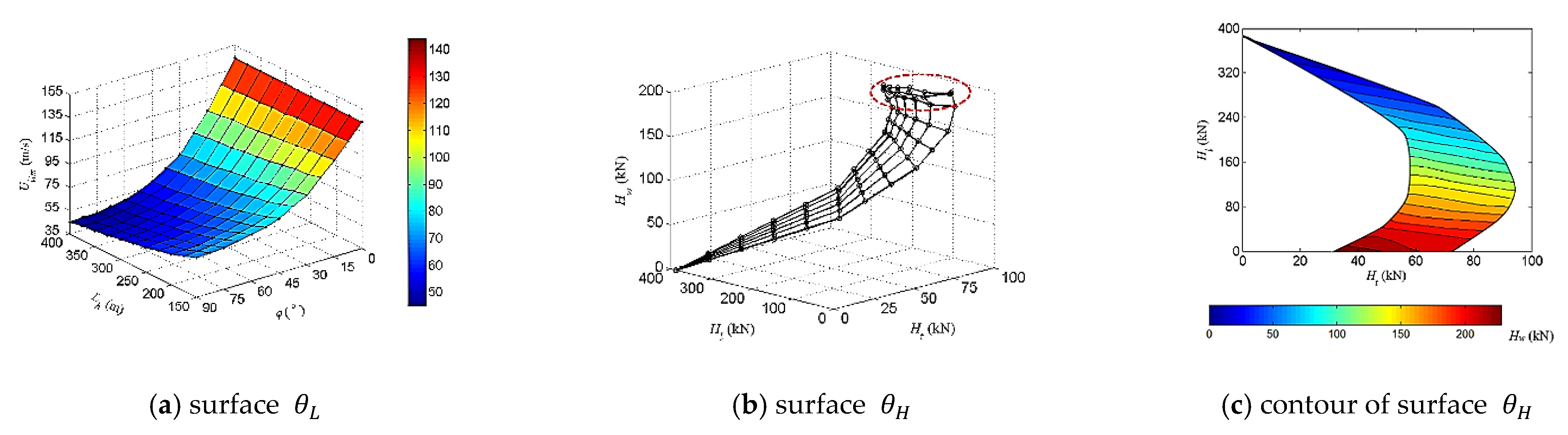
2.2.1. Capacity Surface
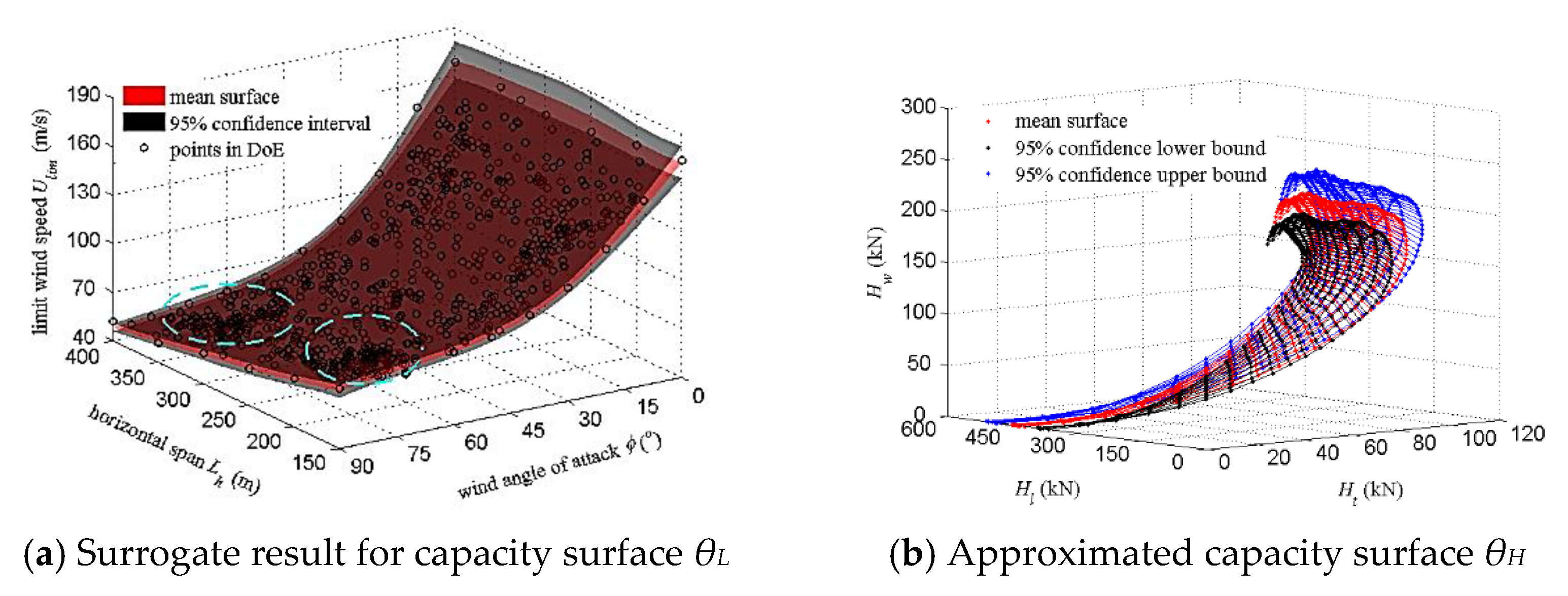
2.2.2. Example
2.2.3. Discussion
3. Kriging-Based Adaptive Surrogate Modeling for Limit Capacity of the Tower
3.1. Kriging Method
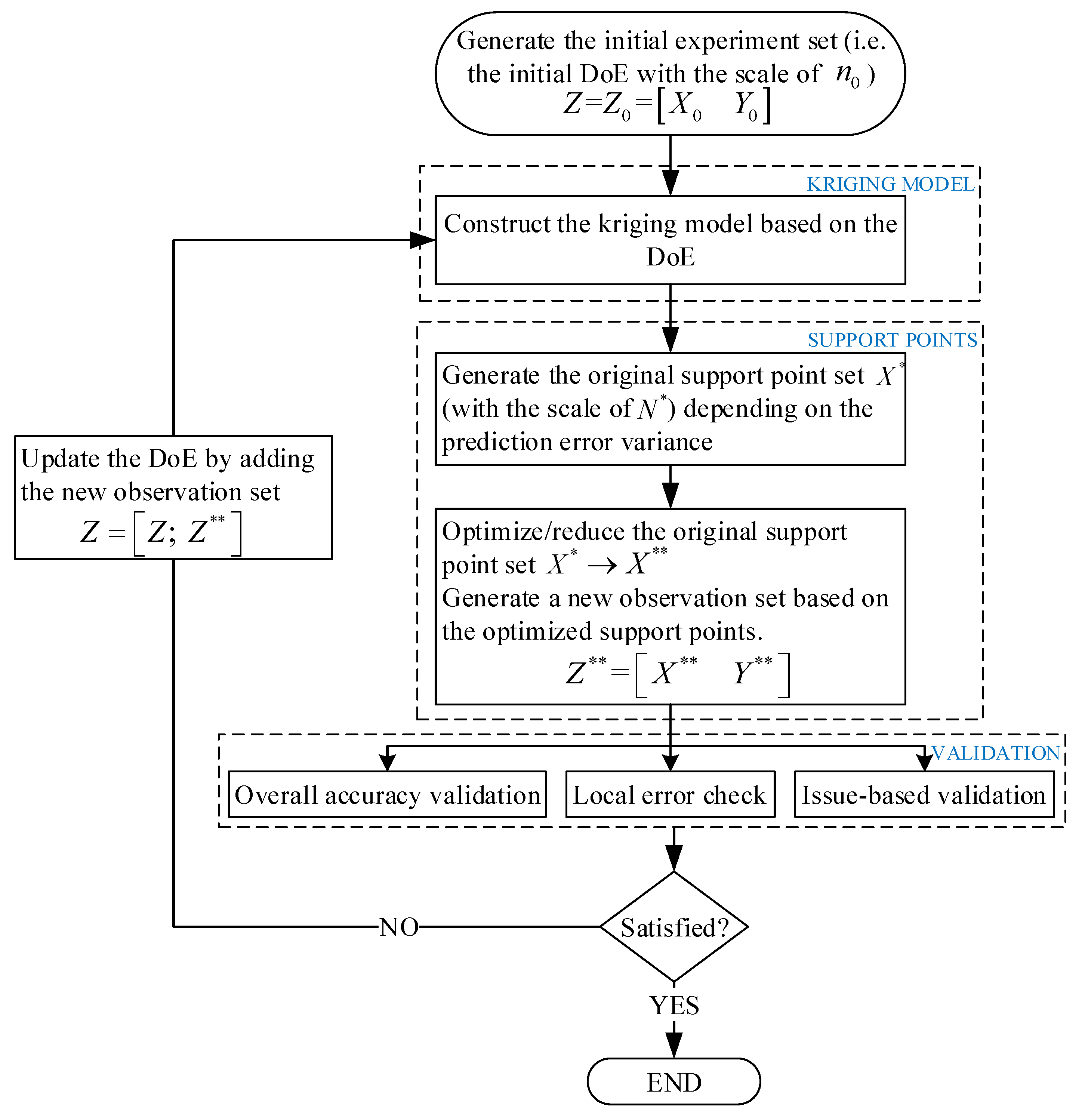
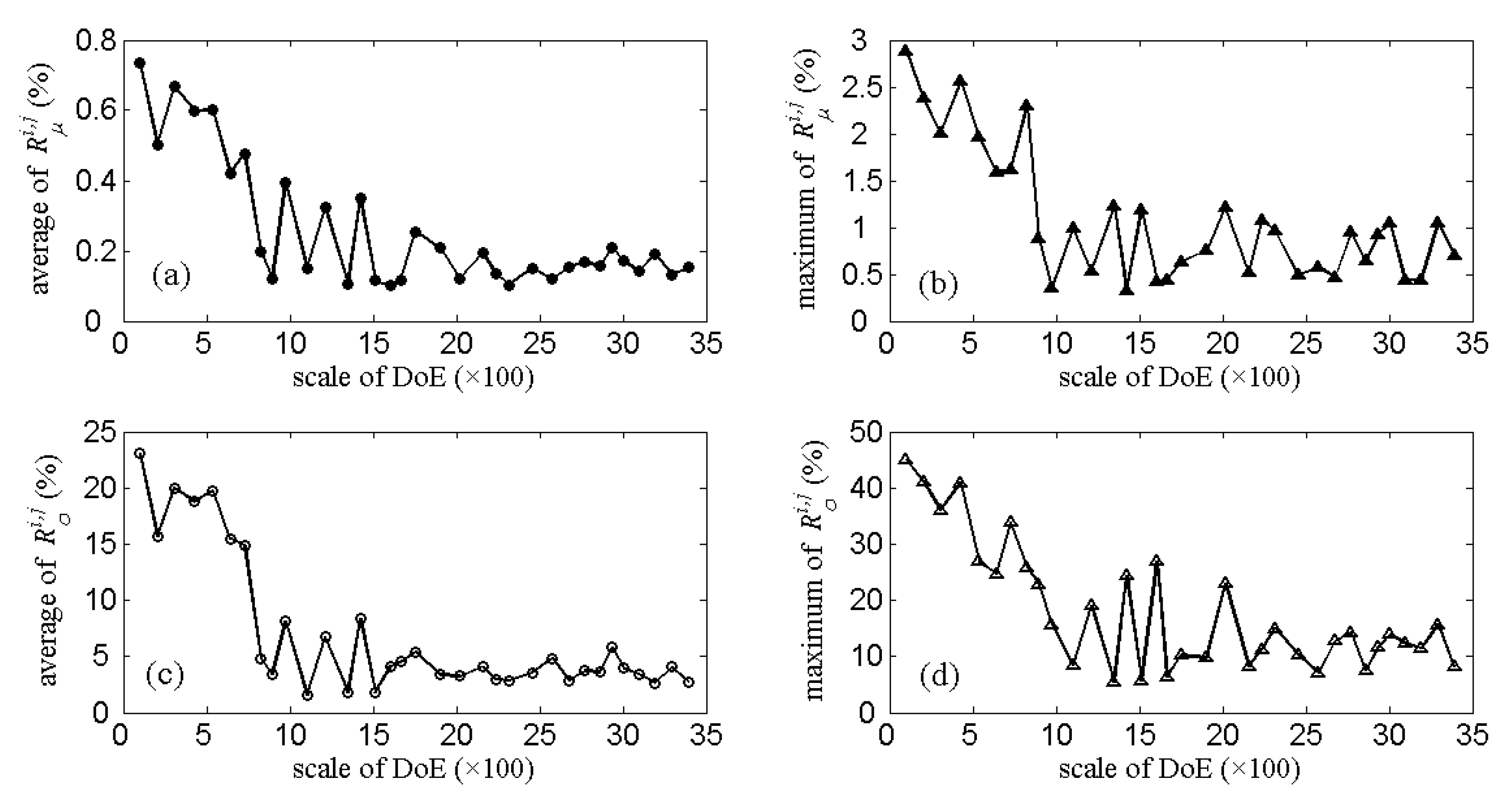
3.2. An Adaptive Modeling Framework
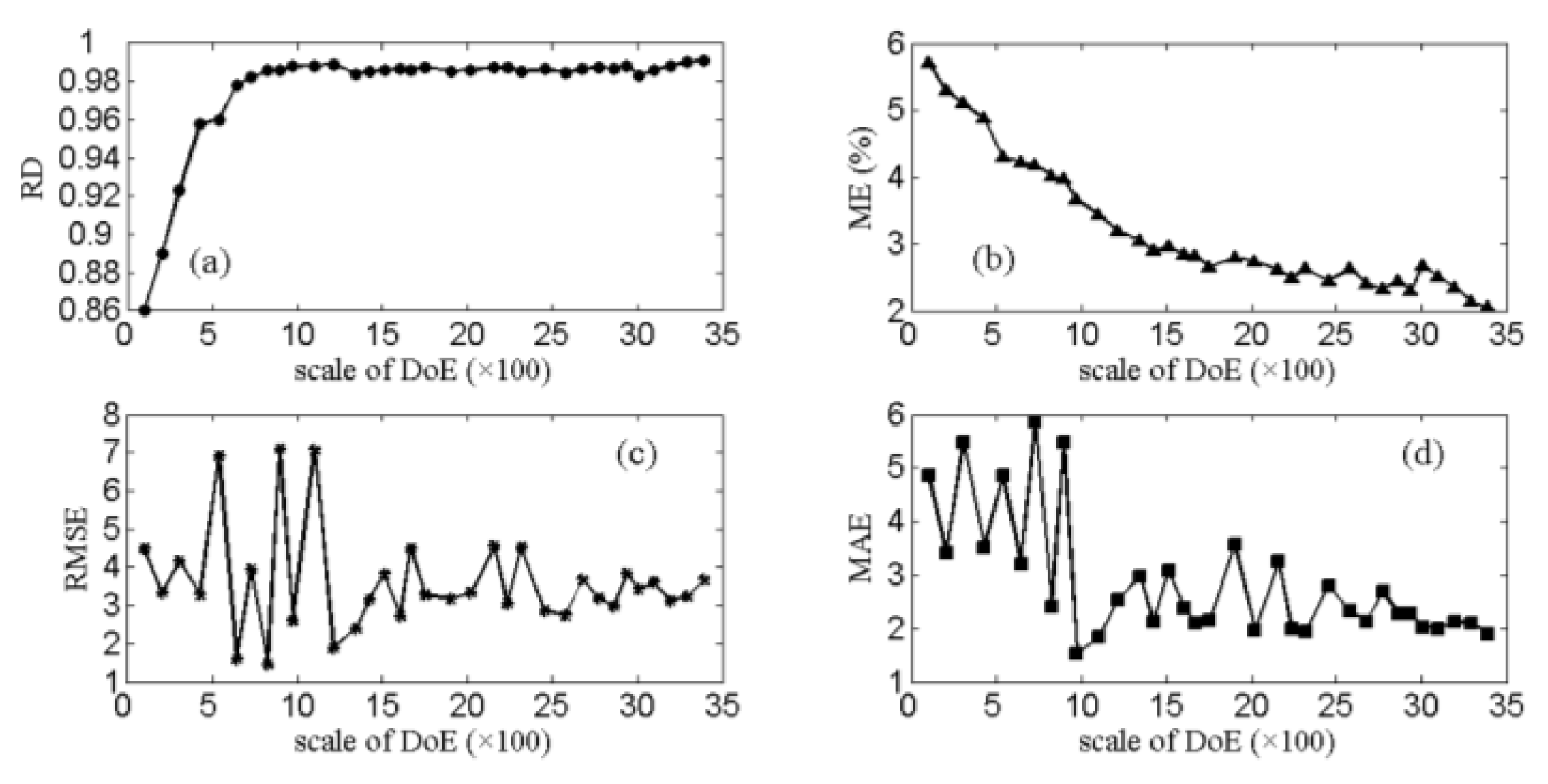
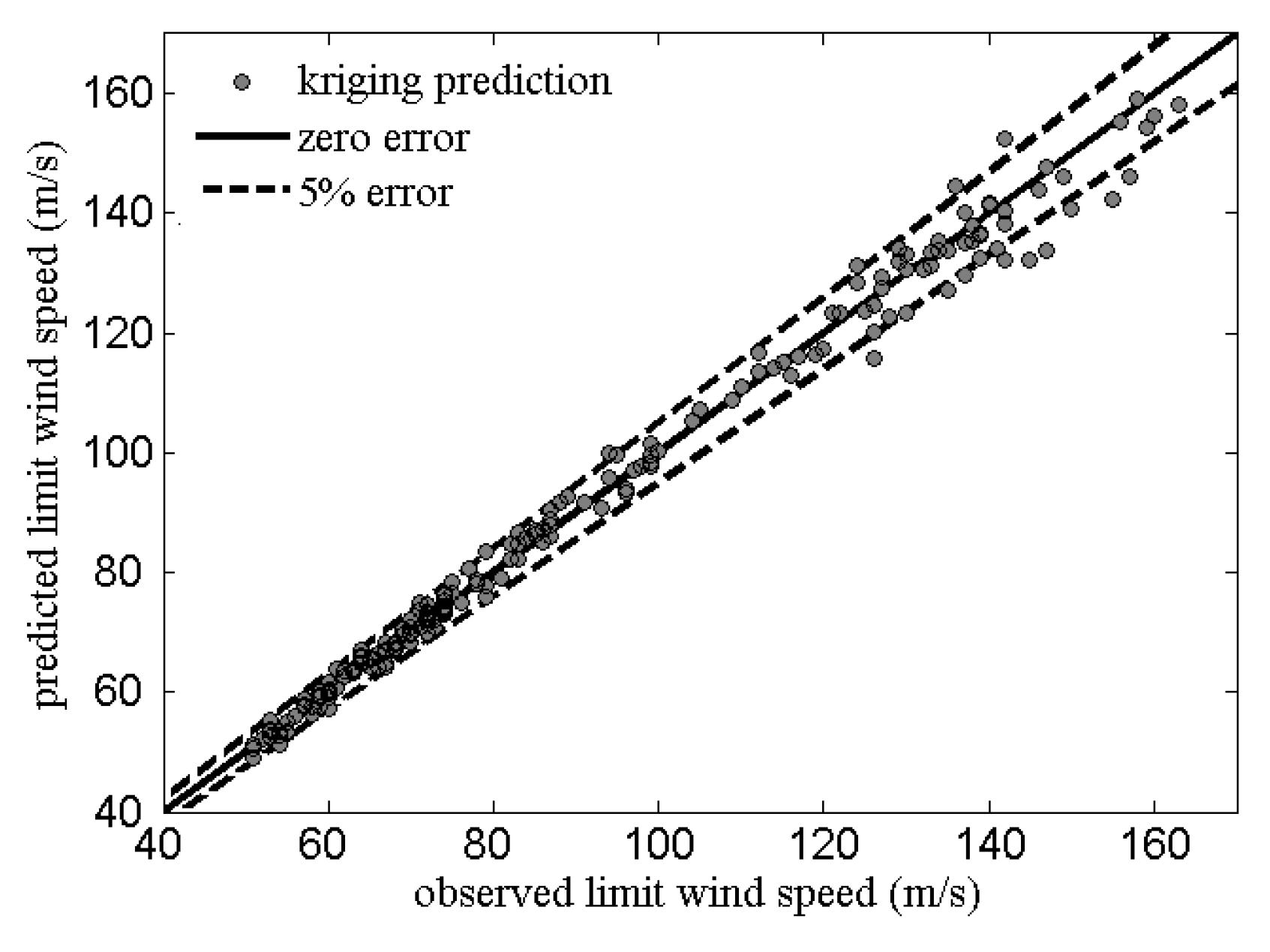
3.3. Example Study
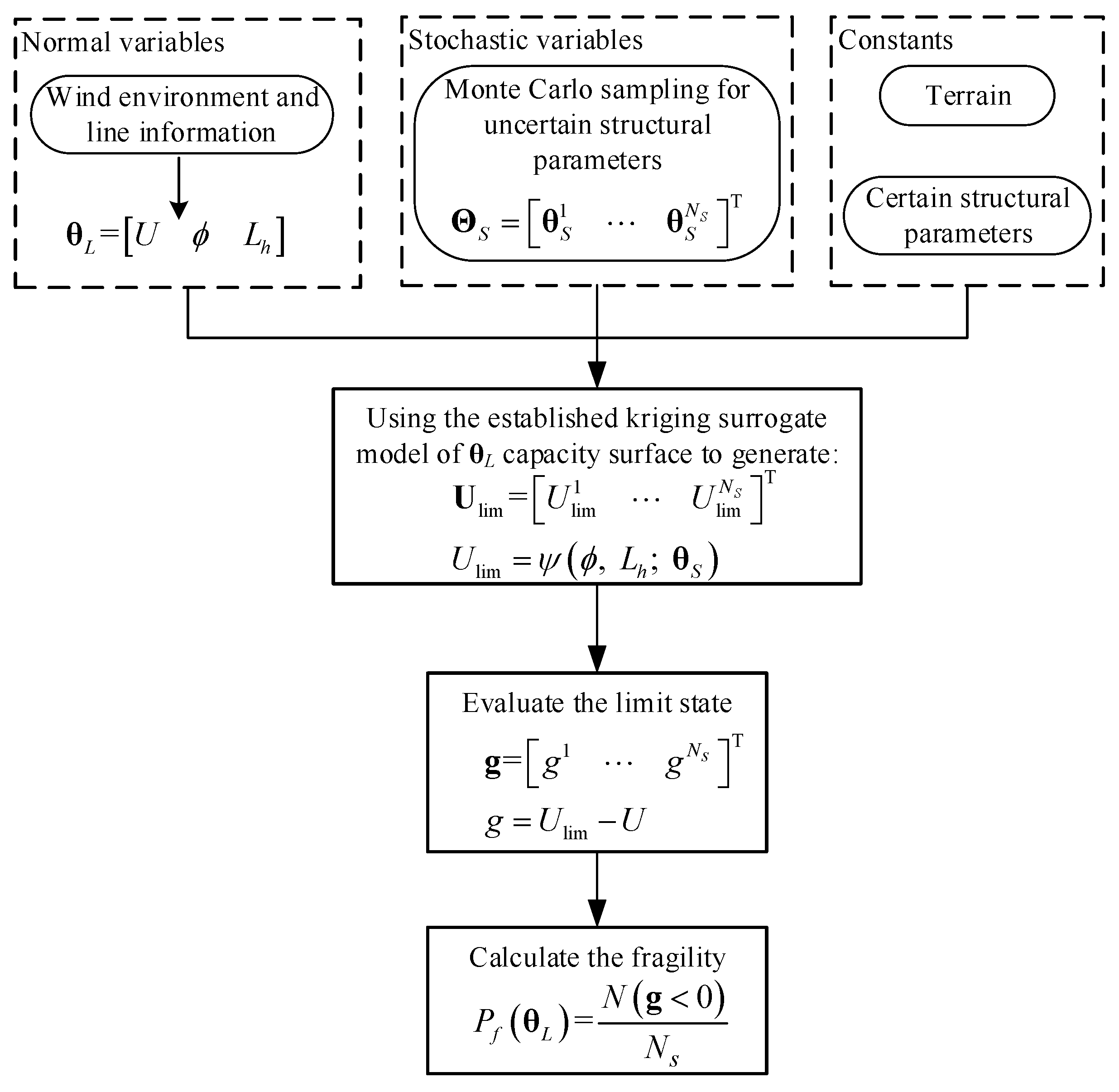
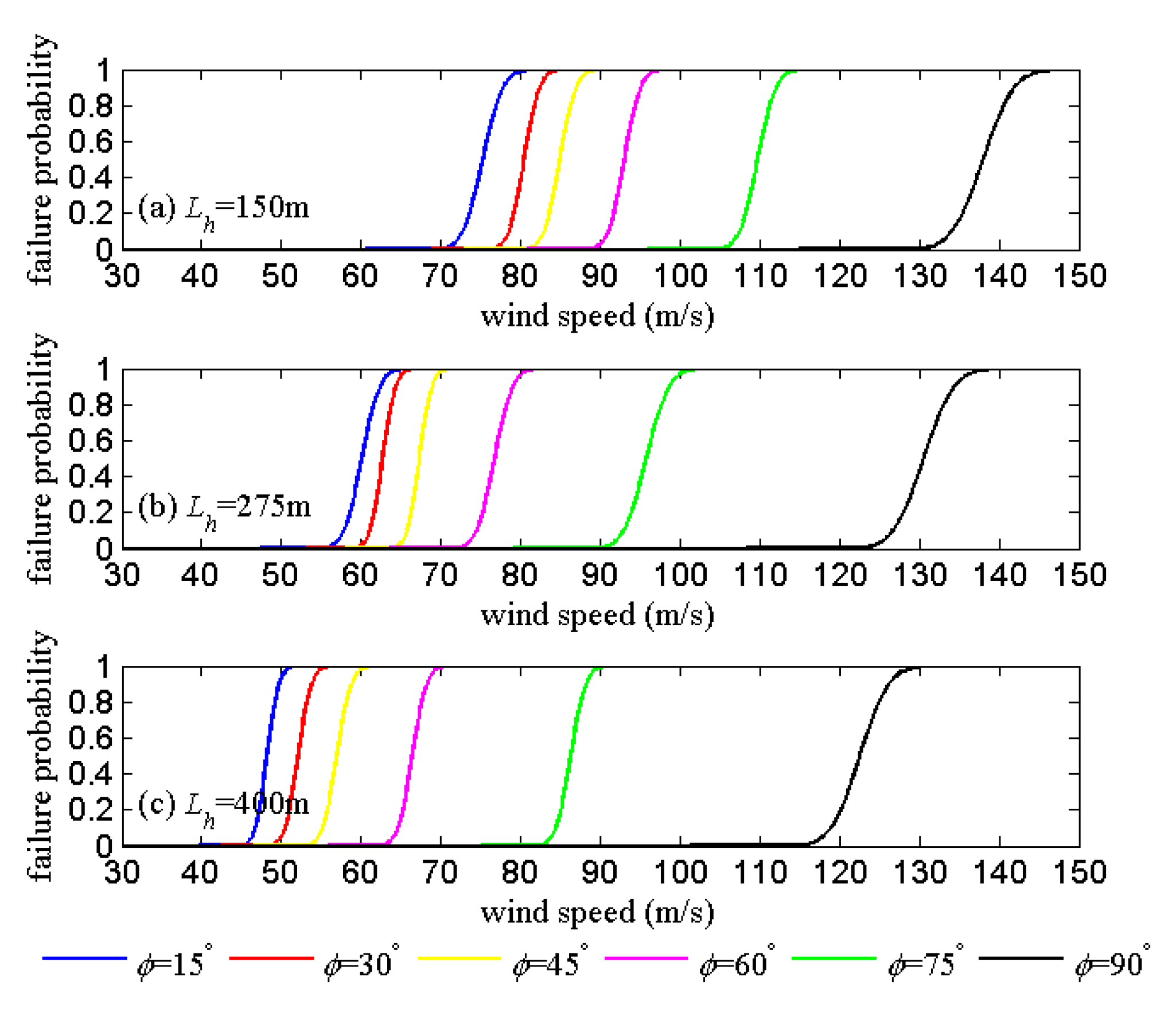
4. Application to the Structural Fragility Assessment on a Transmission Line
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Interaction between the Wind and the Transmission Line Towers
| Parameters | Tower Structure | Transmission Wires | Remarks |
|---|---|---|---|
| Combined wind factor [21] | The power law is adopted here. z is the height of concern, z0 is the reference height taken to be 10 m, and α0 is the roughness exponent. | ||
| Gust response factor [37] | Iz is the turbulence intensity of winds, B (including Bt and Bw) is the background component of the structural response, Ls is the integral scale of turbulence of winds, z is the height of the tower section, and S is the span of line. | ||
| Shape factor [38] | If d < 17 mm, μs,w = 1.2 If d ≥ 17 mm, μs,w = 1.1 | As and A are the projected area and the area of the outer profile of the tower section, respectively, η is the geometrical factor of the tower section, and d is the outer diameter of the wire. | |
| Span factor [39] | - | U < 20 m/s, α = 1.00; 20 m/s ≤ U < 27 m/s, α = 0.85; 27 m/s ≤ U < 31.5 m/s, α = 0.75; U ≥ 31.5 m/s, α = 0.70. | U is the 10-min-averaged wind speed at 10 m over the ground. |
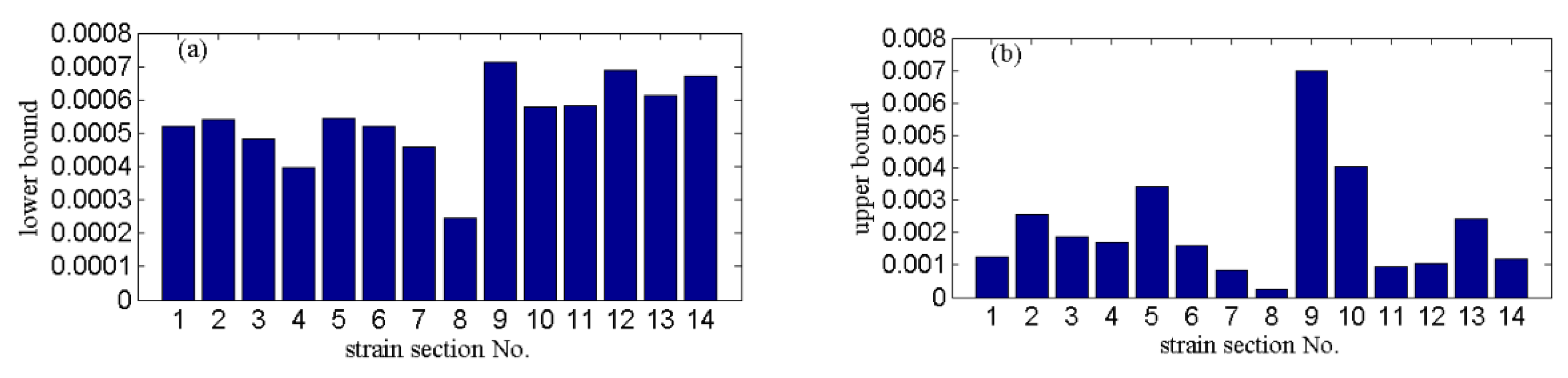
Appendix B. Simulation Results of the Limit Capacity of Transmission Towers under Winds
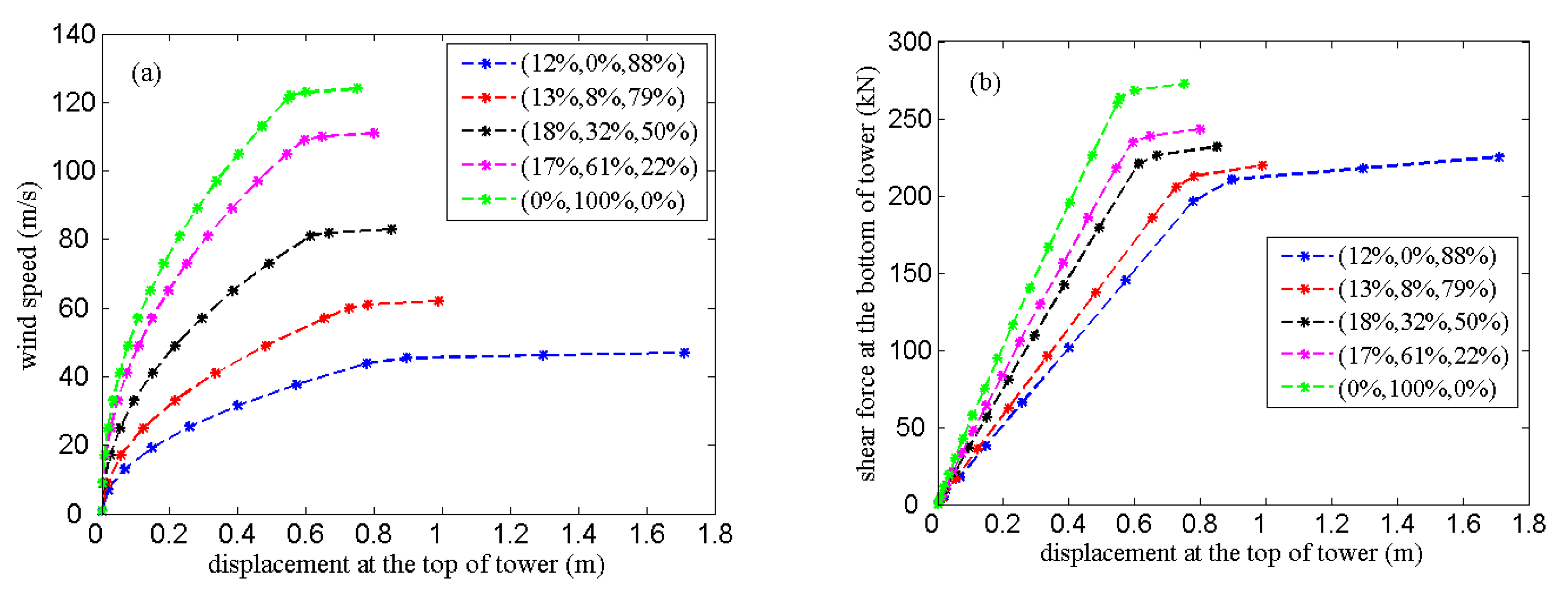
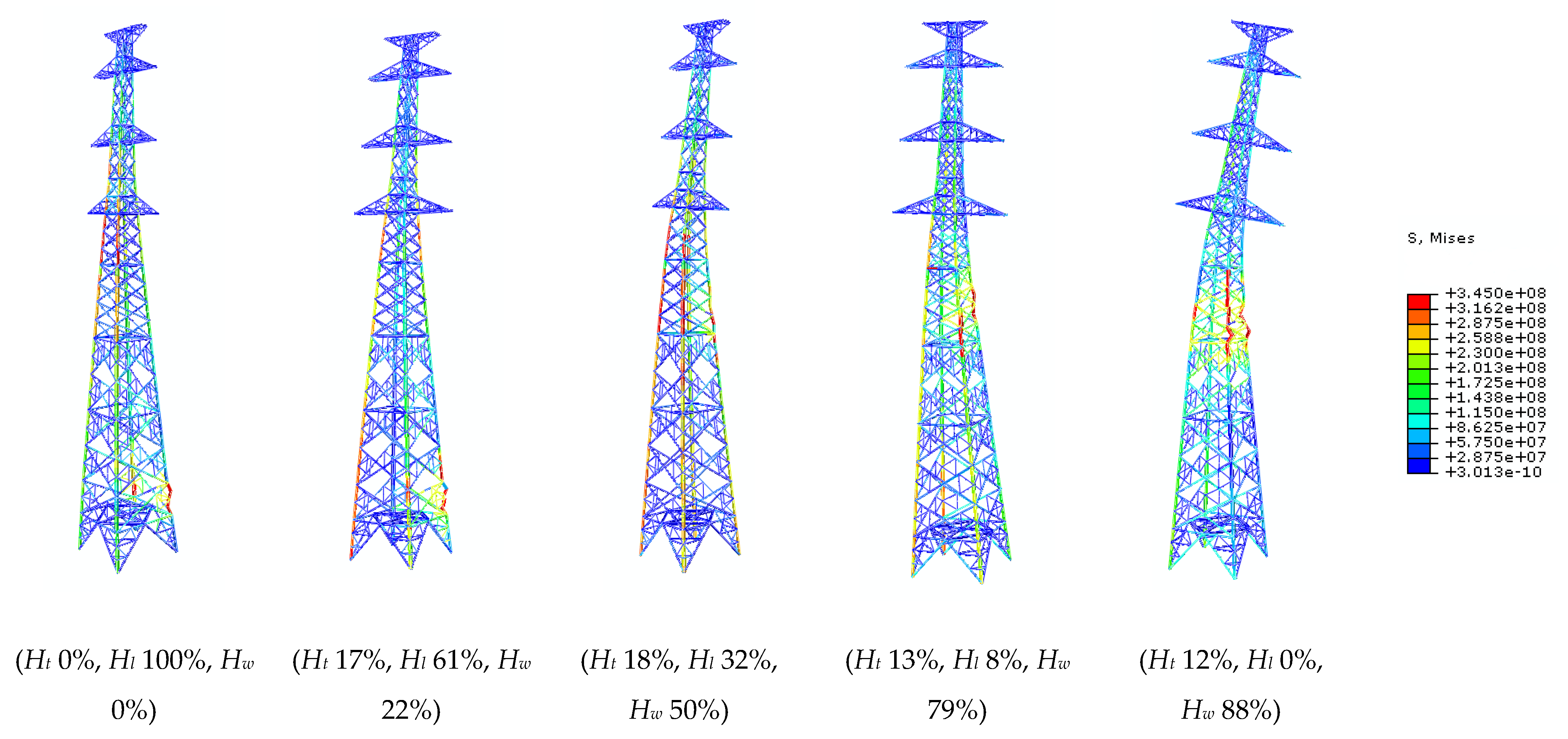
References
- Liu, Y.; Singh, C. Reliability evaluation of composite power systems using Markov cut-set method. IEEE Trans. Power Syst. 2010, 25, 777–785. [Google Scholar] [CrossRef]
- Vaiman, M.; Bell, K.; Chen, Y.; Chowdhury, B.; Dobson, I.; Hines, P.; Zhang, P. Risk assessment of cascading outages: Methodologies and challenges. IEEE Trans. Power Syst. 2012, 27, 631–641. [Google Scholar] [CrossRef]
- Panteli, M.; Mancarella, P. Influence of extreme weather and climate change on the resilience of power systems: Impacts and possible mitigation strategies. Elect. Power Syst. Res. 2015, 127, 259–270. [Google Scholar] [CrossRef]
- Panteli, M.; Pickering, C.; Wilkinson, S.; Dawson, R.; Mancarella, P. Power system resilience to extreme weather: Fragility modelling, probabilistic impact assessment, and adaptation measures. IEEE Trans. Power Syst. 2017, 32, 3747–3757. [Google Scholar] [CrossRef]
- Tao, T.; Shi, P.; Wang, H. Spectral modelling of typhoon winds considering nexus between longitudinal and lateral components. Renew. Energy 2020, 162, 2019–2030. [Google Scholar] [CrossRef]
- Tao, T.; Wang, H. Modelling of longitudinal evolutionary power spectral density of typhoon winds considering high-frequency subrange. J. Wind Eng. Ind. Aerod. 2019, 193, 103957. [Google Scholar] [CrossRef]
- Tao, T.; Shi, P.; Wang, H. Short-term prediction of downburst winds: A double-step modification enhanced approach. J. Wind Eng. Ind. Aerod. 2021, 211, 104561. [Google Scholar] [CrossRef]
- Alam, M.J.; Santhakumarj, A.R. System reliability analysis of transmission line towers. Comput. Struct. 1994, 53, 343–350. [Google Scholar] [CrossRef]
- Natarajan, K.; Santhakumar, A. Reliability-based optimization of transmission line towers. Comput. Struct. 1995, 55, 387–403. [Google Scholar] [CrossRef]
- Fenton, G.A.; Sutherland, N. Reliability-based transmission line design. IEEE Trans. Power Deliv. 2011, 26, 596–606. [Google Scholar] [CrossRef]
- Prasad, R.N.; Knight, G.M.S.; Mohan, S.J.; Lakshmanan, N. Studies on failure of transmission line towers in testing. Eng. Struct. 2012, 35, 55–70. [Google Scholar] [CrossRef]
- Qiang, X.; Li, S. Experimental study on the mechanical behavior and failure mechanism of a latticed steel transmission tower. J. Struct. Eng. 2013, 139, 1009–1018. [Google Scholar]
- Tapia-Hernández, E.; Ibarra-González, S.; De-León-Escobedo, D. Collapse mechanism of power towers under wind loading. Struct. Infrastruct. Eng. 2017, 13, 766–782. [Google Scholar] [CrossRef]
- Albermani, F.; Kitipornchai, S.; Chan, R.W.K. Failure analysis of transmission towers. Eng. Fail. Anal. 2009, 16, 1922–1928. [Google Scholar] [CrossRef]
- Yang, S.C.; Hong, H.P. Nonlinear inelastic responses of transmission tower-line system under downburst wind. Eng. Struct. 2016, 123, 490–500. [Google Scholar] [CrossRef]
- Fu, X.; Li, H.N.; Li, G. Fragility analysis and estimation of collapse status for transmission tower subjected to wind and rain loads. Struct. Safety 2016, 58, 1–10. [Google Scholar] [CrossRef]
- Fu, X.; Li, H.N. Uncertainty analysis of the strength capacity and failure path for a transmission tower under a wind load. J. Wind Eng. Ind. Aerod. 2018, 173, 147–155. [Google Scholar] [CrossRef]
- Fu, X.; Li, H.N.; Tian, L.; Wang, J.; Cheng, H. Fragility analysis of transmission line subjected to wind loading. J. Perform. Constr. Fac. 2019, 33, 04019044. [Google Scholar] [CrossRef]
- Cai, Y.Z.; Xie, Q.; Xue, S.T.; Hu, L.; Kareem, A. Fragility Modelling Framework for Transmission Line Towers under Winds. Eng. Struct. 2019, 191, 686–697. [Google Scholar] [CrossRef]
- DL/T 5154-2012. Technical Code for the Design of Tower and Pole Structures of Overhead Transmission Line (Industrial Standard); Electric Power Planning & Engineering Institute: Beijing, China, 2012. [Google Scholar]
- IEC 60826. Design Criteria of Overhead Transmission Lines, 3rd ed.; International Electro-technical Commission: Geneva, Switzerland, 2003. [Google Scholar]
- Mara, T.G.; Hong, H.P. Effect of wind direction on the response and capacity surface of a transmission tower. Eng. Struct. 2013, 57, 493–501. [Google Scholar] [CrossRef]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and analysis of computer experiments. Stat. Sci. 1989, 4, 409–435. [Google Scholar] [CrossRef]
- Dubourg, V.; Sudret, B.; Bourinet, J.M. Reliability-based design optimization using kriging surrogates and subset simulation. Struct. Multidisc. Optim. 2011, 44, 673–690. [Google Scholar] [CrossRef]
- Irfan, K. Application of kriging method to structural reliability problems. Struct. Safety 2005, 27, 133–151. [Google Scholar]
- Ioannis, G.; Alexandros, A.T.; George, P.M. Kriging metamodeling in seismic risk assessment based on stochastic ground motion models. Earthq. Eng. Struct. Dyn. 2015, 44, 2377–2399. [Google Scholar]
- Robert, C.P.; Casella, G. Monbte Carlo Statistical Methods, 2nd ed.; Springer: New York, NY, USA, 2004. [Google Scholar]
- Hartigan, J.A.; Wong, M.A. Algorithm AS 136: A K-means clustering algorithm. J. R. Stat. Soc. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Kovaleva, E.V.; Mirkin, B.G. Bisecting k-means and 1D projection divisive clustering: A unified framework and experimental comparison. J. Classif. 2015, 32, 414–442. [Google Scholar] [CrossRef]
- Meckesheimer, M.; Booker, A.J.; Barton, R.R.; Simpson, T.W. Computationally inexpensive metamodel assessment strategies. AIAA J. 2002, 40, 2053–2060. [Google Scholar] [CrossRef]
- Takeuchi, M.; Maeda, J.; Ishida, N. Aerodynamic damping properties of two transmission towers estimated by combining several identification methods. J. Wind Eng. Ind. Aerod. 2010, 98, 872–880. [Google Scholar] [CrossRef]
- JCSS. Probabilistic Model Code–Part 3-Material Properties. JCSS. 2001. Available online: https://www.jcss-lc.org/jcss-probabilistic-model-code/ (accessed on 1 January 2021).
- Google Earth Pro V7.3.3.7786. Zhanjiang, Guangzhou Province, China. 21°16′13″ N 110°21′33″ E, Eye alt 45 km. Available online: https://www.google.com/earth/ (accessed on 10 September 2017).
- Ying, M.; Zhang, W.; Yu, H.; Lu, X.; Feng, J.; Fan, Y.; Zhu, Y.; Chen, D. An overview of the China Meteorological Administration tropical cyclone database. J. Atmos. Ocean Technol. 2014, 31, 287–301. [Google Scholar] [CrossRef]
- Lu, X.Q.; Yu, H.; Yang, X.M.; Li, X.F. Estimating Tropical Cyclone Size in the Northwestern Pacific from Geostationary Satellite Infrared Images. Remote Sens. 2017, 9, 728. [Google Scholar] [CrossRef]
- Cai, Y.Z. Typhoon Fragility for Electric Transmission Line Based on the Failure of Transmission Towers. Ph.D. Thesis, Tongji University, Shanghai, China, 2019. [Google Scholar]
- Bowman, A.W.; Azzalini, A. Applied Smoothing Techniques for Data Analysis; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- ASCE. Guidelines for Electrical Transmission Line Structural Loading, 3rd ed.; ASCE Manuals and Reports on Engineering Practice No. 74; ASCE: Reston, VA, USA, 2010. [Google Scholar]
- GB 50009-2012. Load Code for the Design of Building Structures (National Standard); Ministry of Construction of the People’s Republic of China: Beijing, China, 2012.
- GB 50545-2010. Code for Design of 110 kV~750 kV Overhead Transmission Line (National Standard); China Electricity Council: Beijing, China, 2010. [Google Scholar]
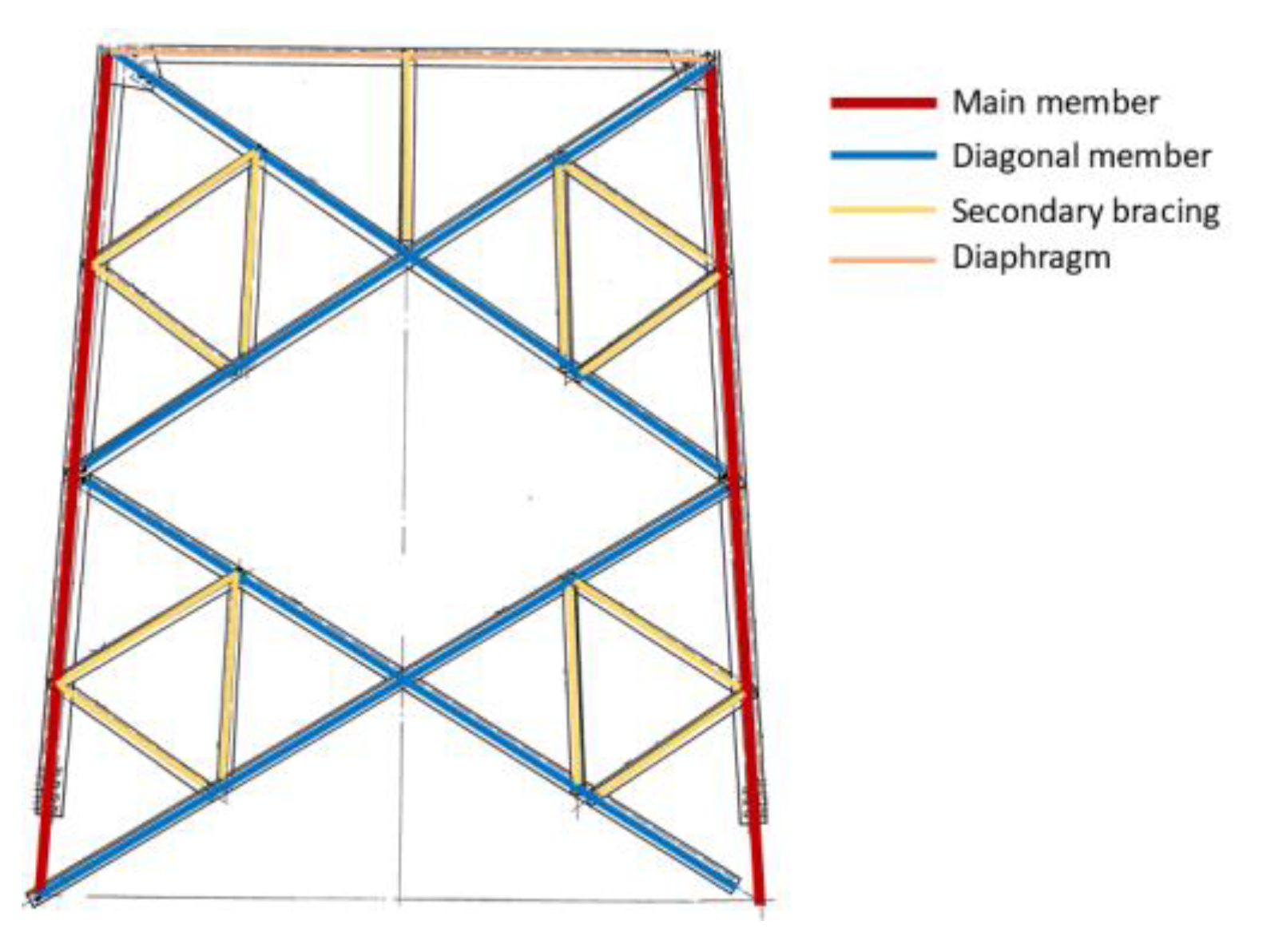

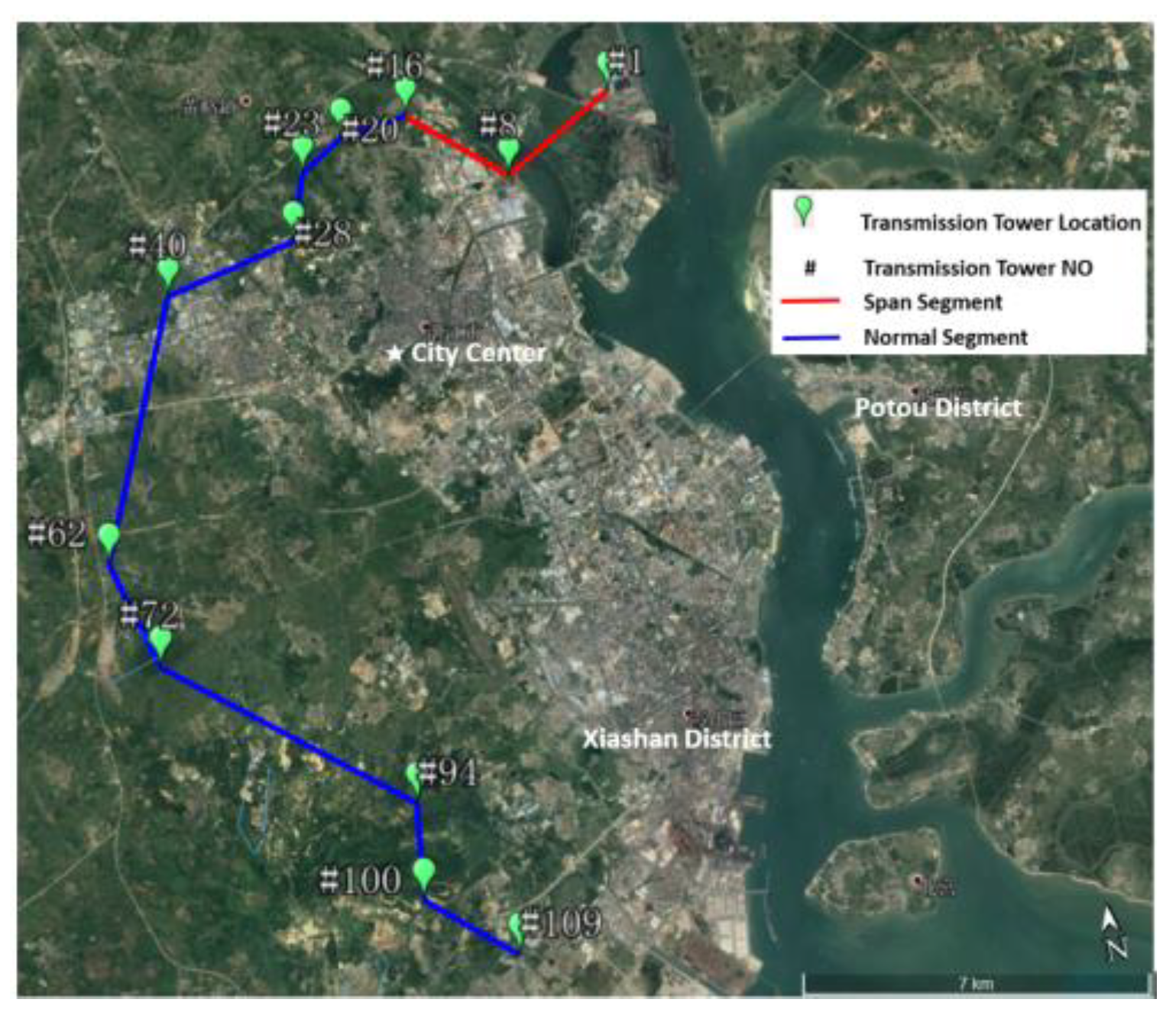
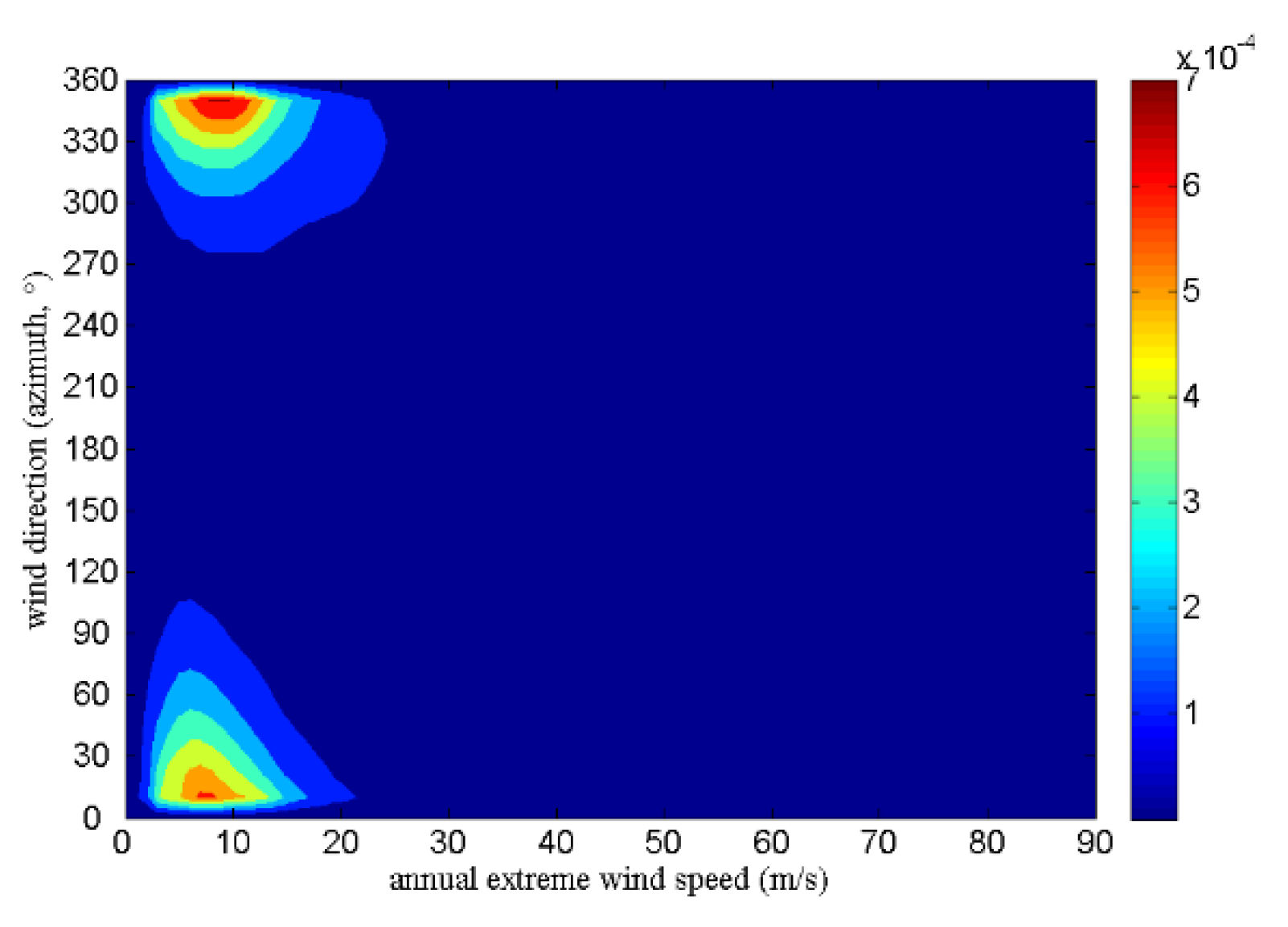
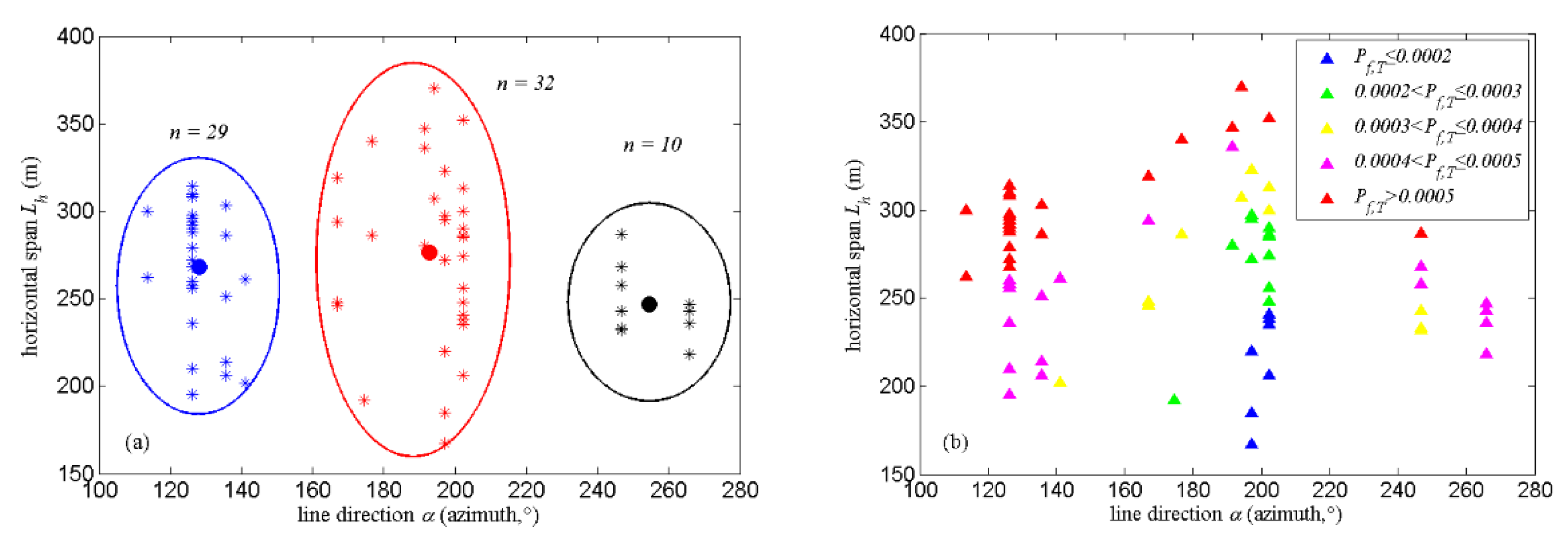
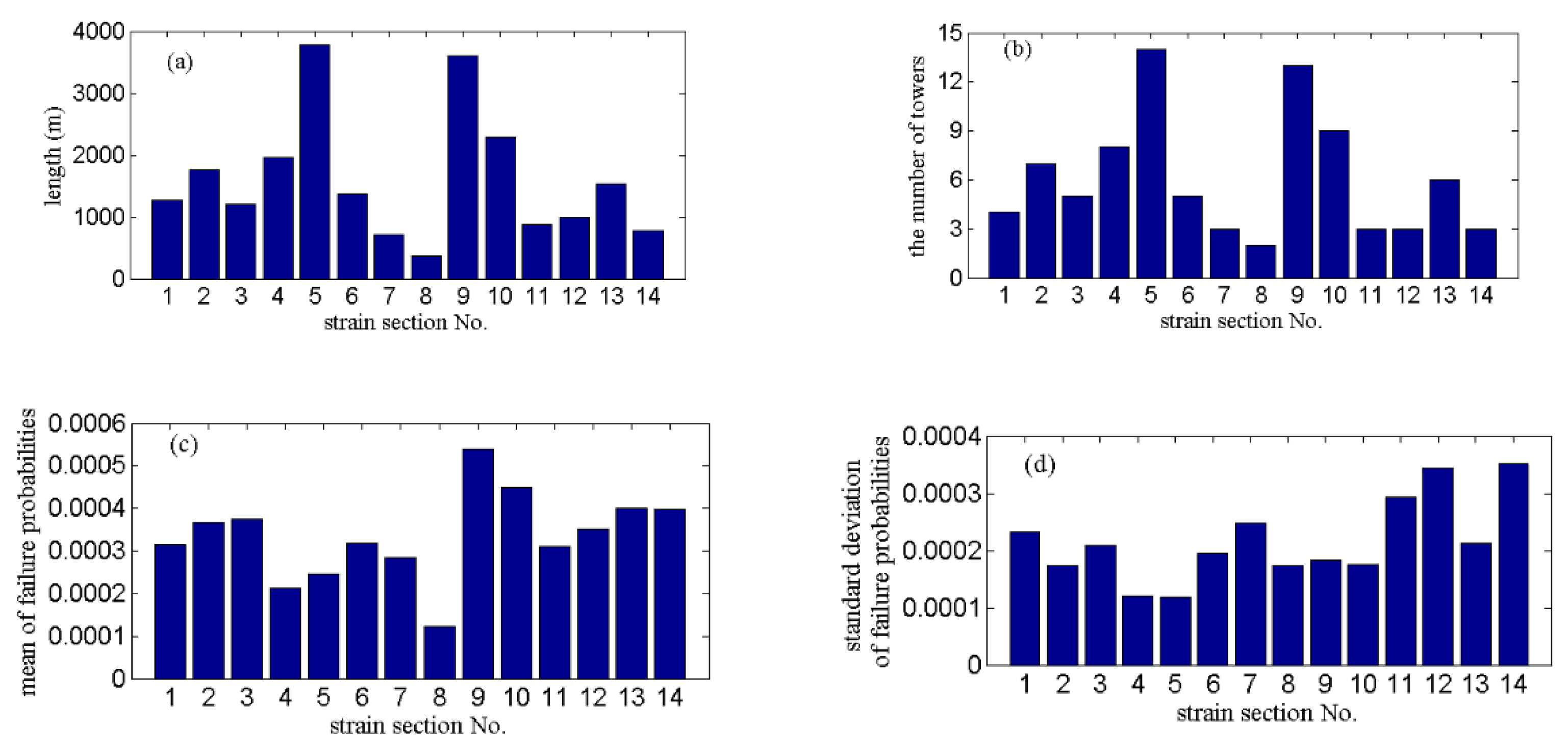
| Tower ZY | |
|---|---|
| Type | Double-Circuit Angle-Steel Lattice Suspension Tower |
| Total height (m) | 45.5 |
| Body height (m) | 30 |
| Steel type | Q345, Q235 [14] |
| Foot distance (m) | 6.4 |
| Natural frequency (Hz) | 2.037 (transverse), 2.047 (longitudinal) |
| Damping ratio | 0.01 |
| Transmission wires (conductors and ground wires) | |
| Type | LGJQ-300/40 (two-bundle conductors) LGJQ-95/55 (ground wires) |
| Linear density (kg/m) | 2.2660 (conductors), 0.7077 (ground wires) |
| Effective diameters (mm) | 47.88 (conductors), 16 (ground wires) |
| Transmission line | |
| Horizontal span (m) | maximum 370/minimum 127/average 275 |
| Direction (azimuth, °) | maximum 265.82/minimum 113.49/average 181.08 |
| Terrain | Open (C exposure) |
| Material [32] | Mean (μ) | C.O.V (δ) | Distribution |
|---|---|---|---|
| Yield strength (fy,Q345) | 387 MPa | 0.07 | Lognormal |
| Yield strength (fy,Q235) | 264 MPa | 0.07 | Lognormal |
| Elastic modulus (Es) | 206,000 MPa | 0.03 | Lognormal |
| Poisson ratio (ν) | 0.3 | 0.03 | Lognormal |
| Geometry [17] | Mean */standard deviation (μ/σ) | C.O.V (δ) | Distribution |
| Thickness of angle steel members (t) | 0.985 | 0.032 | Normal |
| Length of angle steel members (l) | 1.001 | 0.008 | Normal |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Wan, J. Wind-Resistant Capacity Modeling for Electric Transmission Line Towers Using Kriging Surrogates and Its Application to Structural Fragility. Appl. Sci. 2021, 11, 4714. https://doi.org/10.3390/app11114714
Cai Y, Wan J. Wind-Resistant Capacity Modeling for Electric Transmission Line Towers Using Kriging Surrogates and Its Application to Structural Fragility. Applied Sciences. 2021; 11(11):4714. https://doi.org/10.3390/app11114714
Chicago/Turabian StyleCai, Yunzhu, and Jiawei Wan. 2021. "Wind-Resistant Capacity Modeling for Electric Transmission Line Towers Using Kriging Surrogates and Its Application to Structural Fragility" Applied Sciences 11, no. 11: 4714. https://doi.org/10.3390/app11114714
APA StyleCai, Y., & Wan, J. (2021). Wind-Resistant Capacity Modeling for Electric Transmission Line Towers Using Kriging Surrogates and Its Application to Structural Fragility. Applied Sciences, 11(11), 4714. https://doi.org/10.3390/app11114714





