A Novel Shape Finding Method for the Main Cable of Suspension Bridge Using Nonlinear Finite Element Approach
Abstract
Featured Application
Abstract
1. Introduction
2. Shape Finding of the Main Cable with Eulerian Description
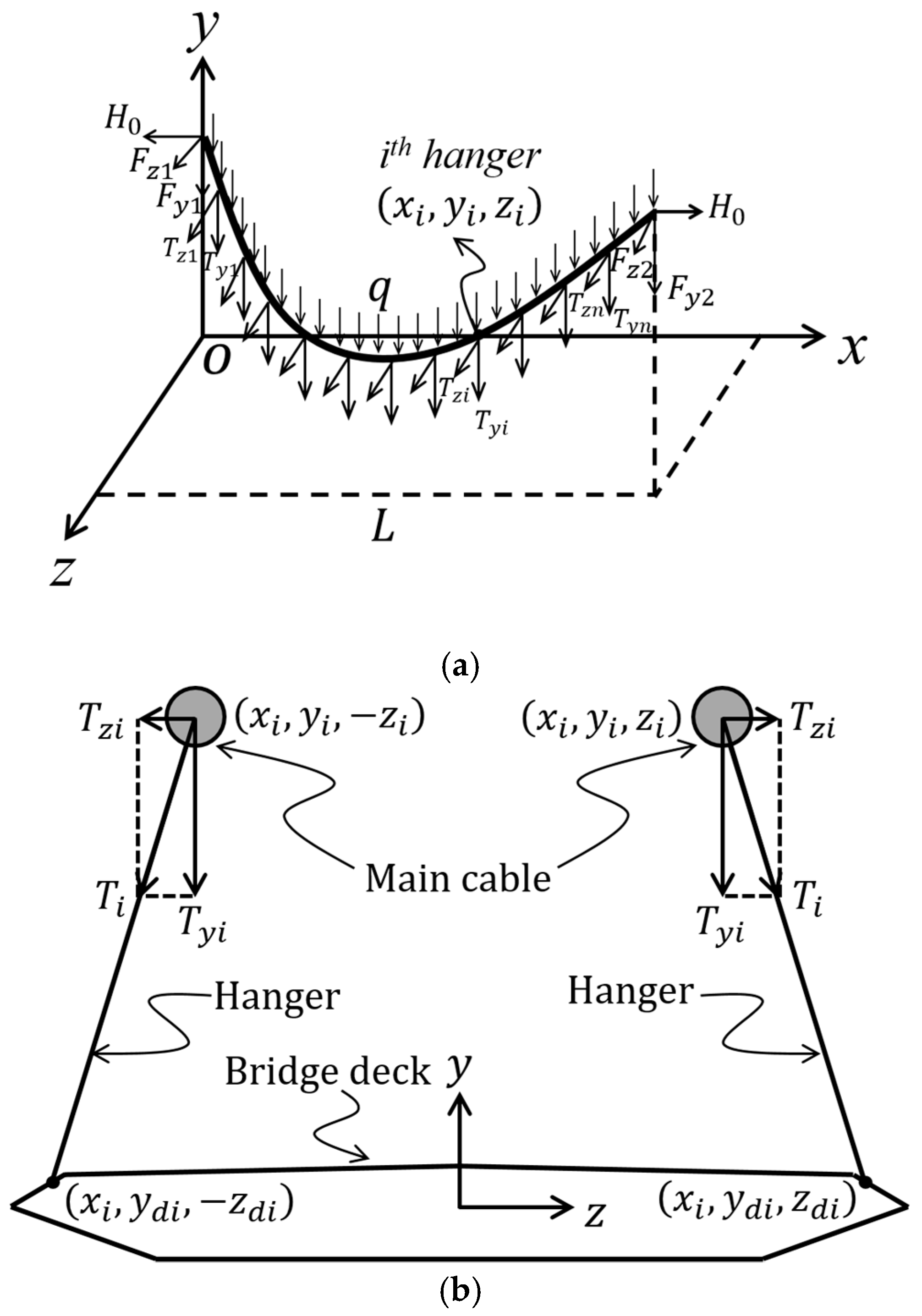
2.1. Governing Equations of Spatial Main Cable
- (1)
- The main cable of the suspension bridge is ideally flexible and unable to bear any bending moment. Only the axial tension is considered for the main cable.
- (2)
- The axial deformation of the main cable is tiny such that the area of the cross section for the main cable remains unchanged and the cable weight per unit length is a constant.
- (3)
- The linear elastic assumption for all materials is adopted.
- (4)
- All the loadings on the main cable are parallel to the y-o-z plane. The tension in the x-direction of the main cable is constant and defined as .
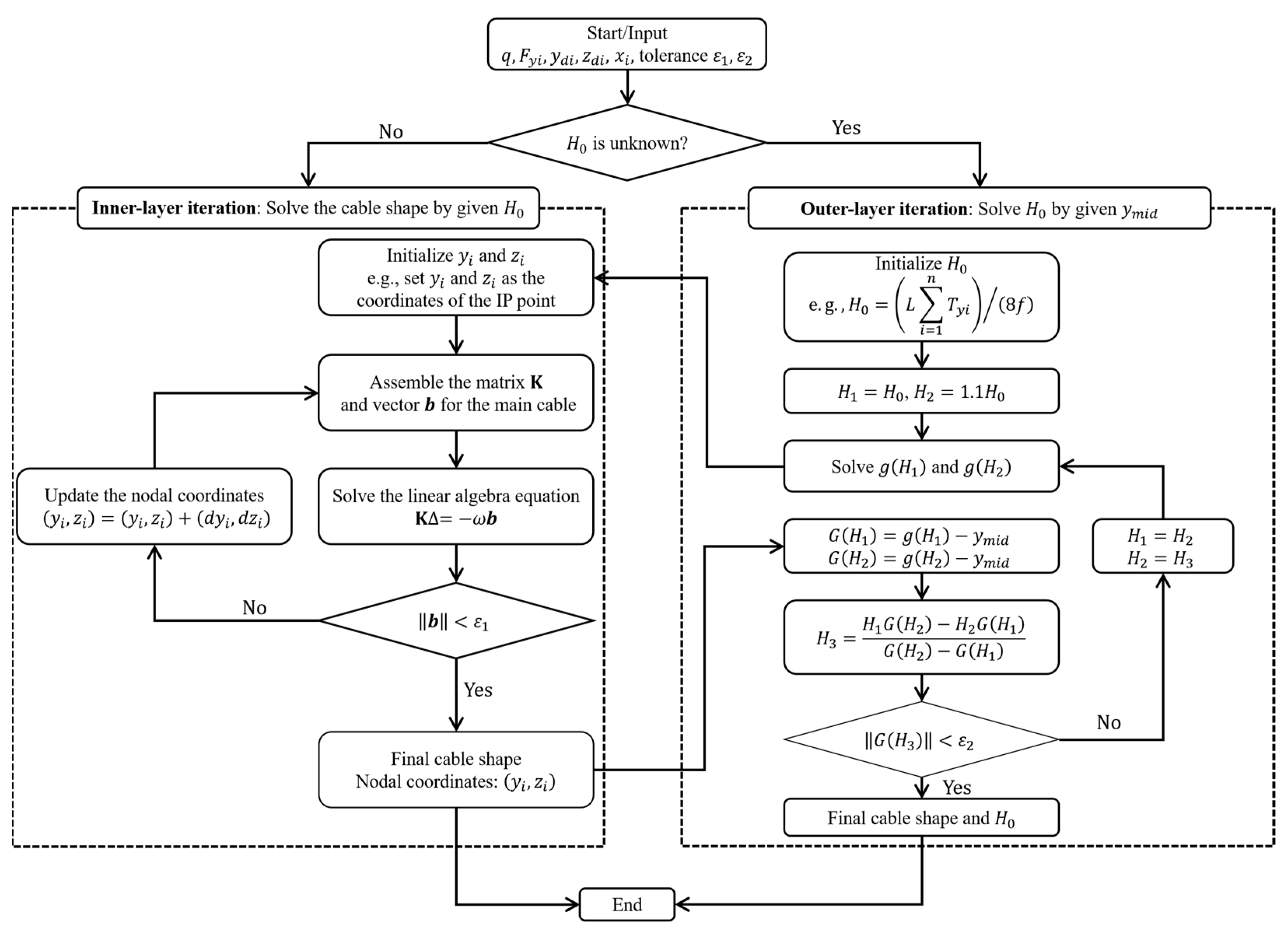
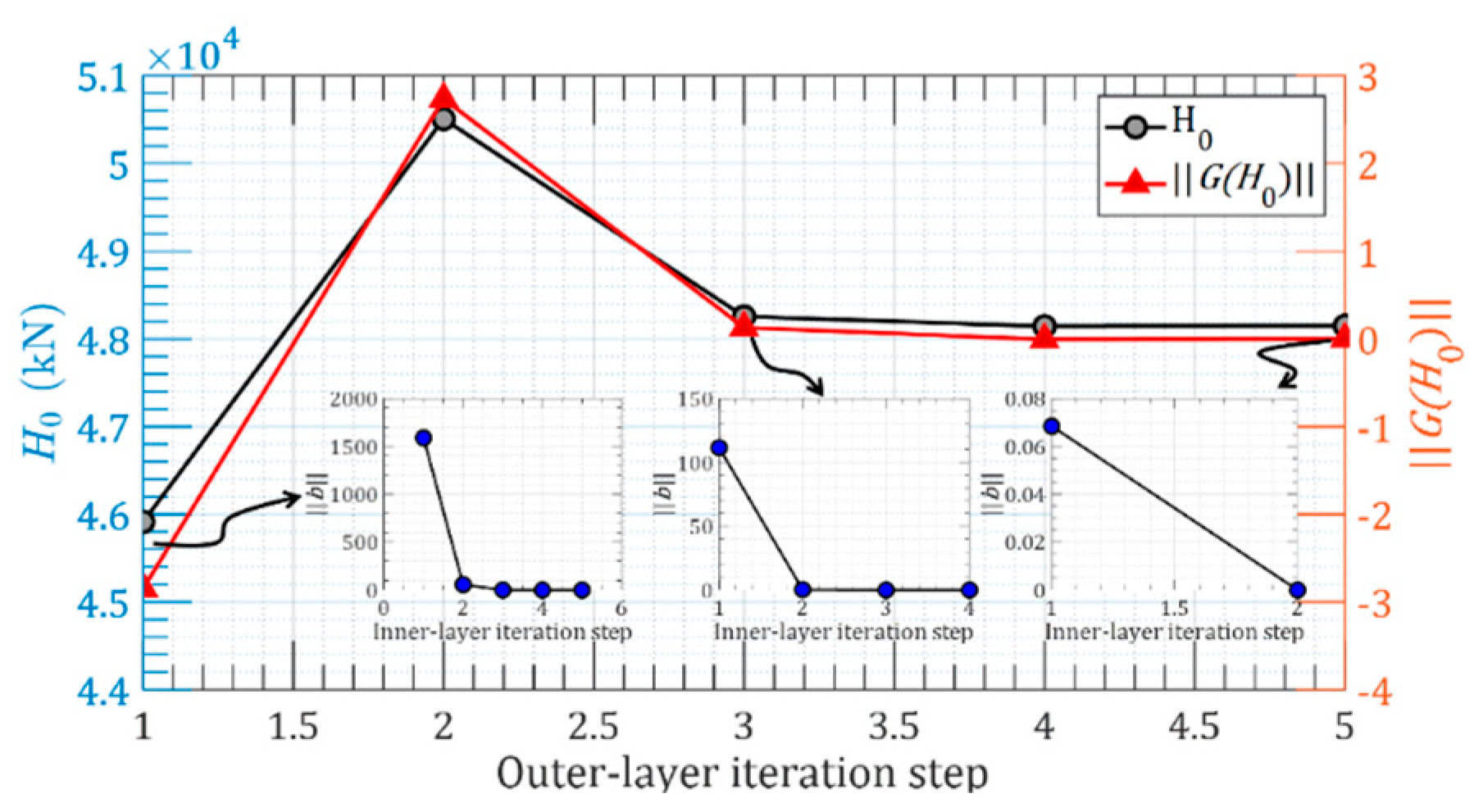
2.2. Nonlinear FEM Solution for the Cable Shape
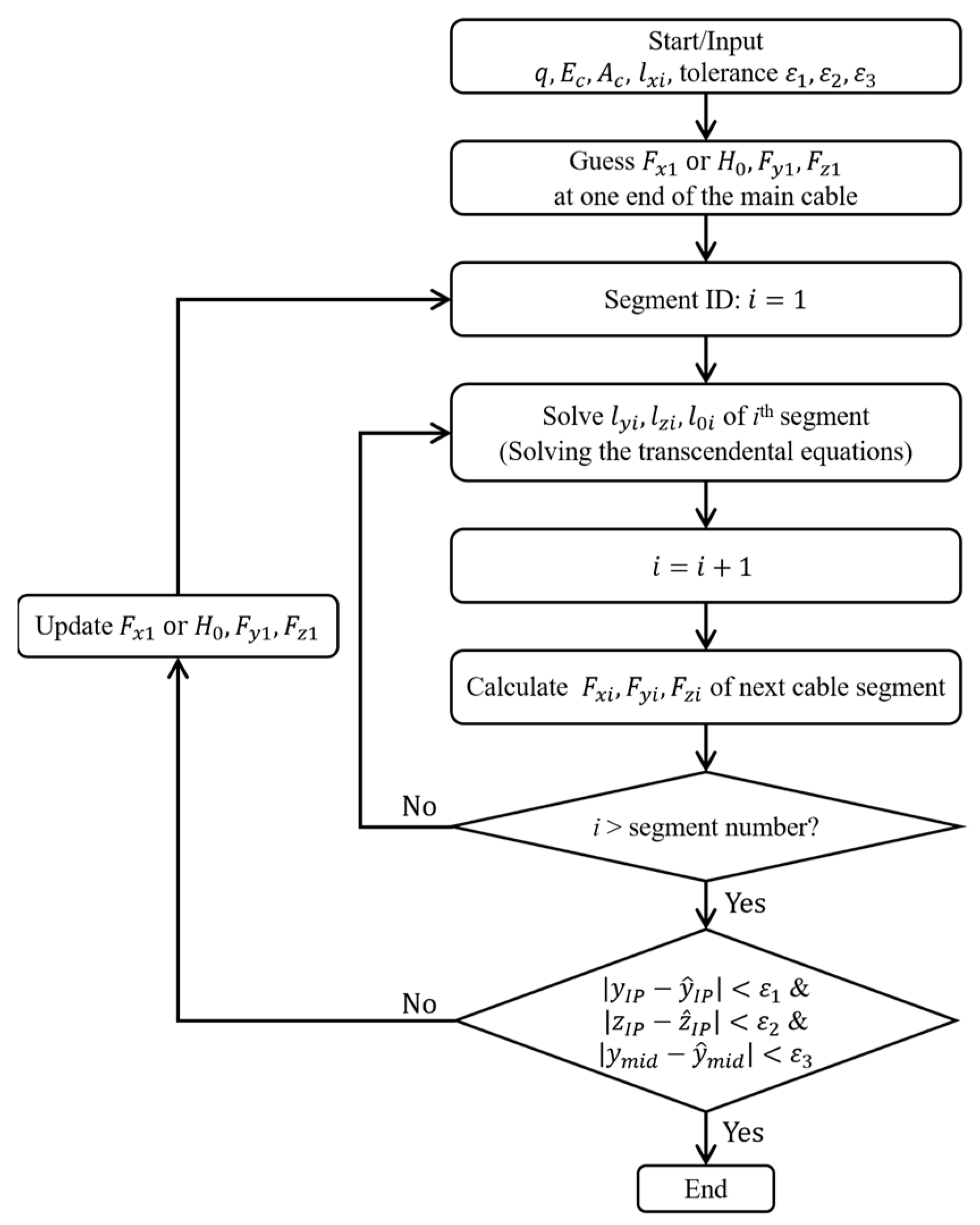
2.3. Comparison with the Segmental Catenary Method
3. Cases Study
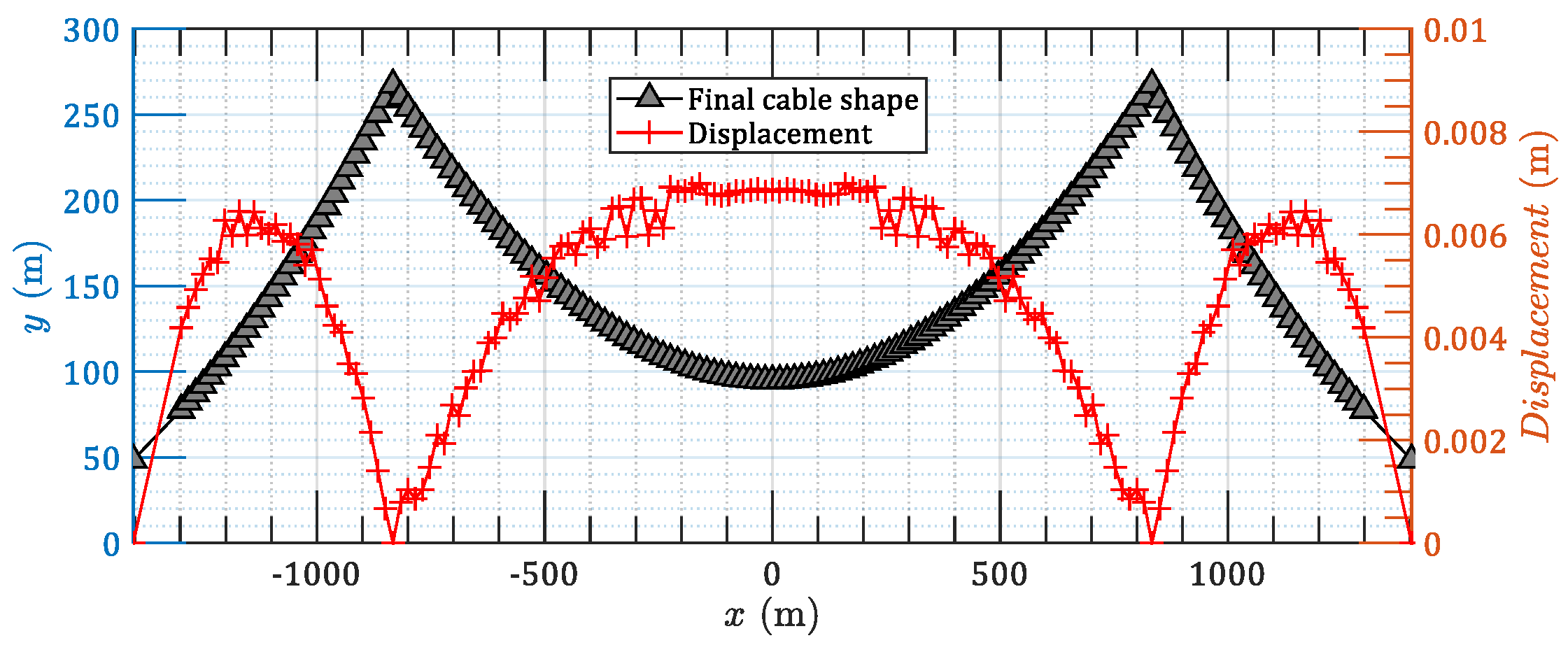
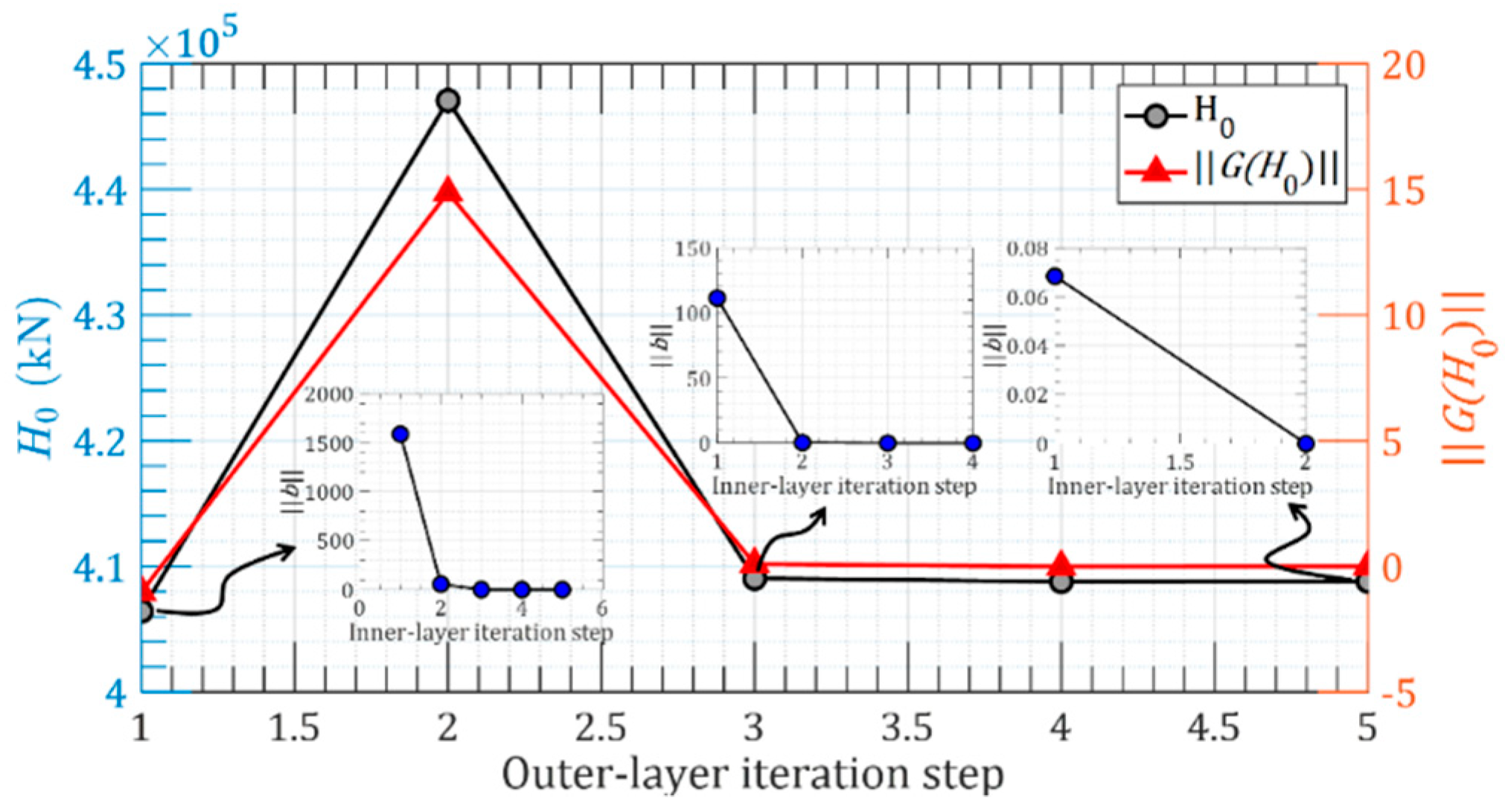
3.1. Case 1: 2D Parallel Main Cables of an Earth-Anchored Suspension Bridge
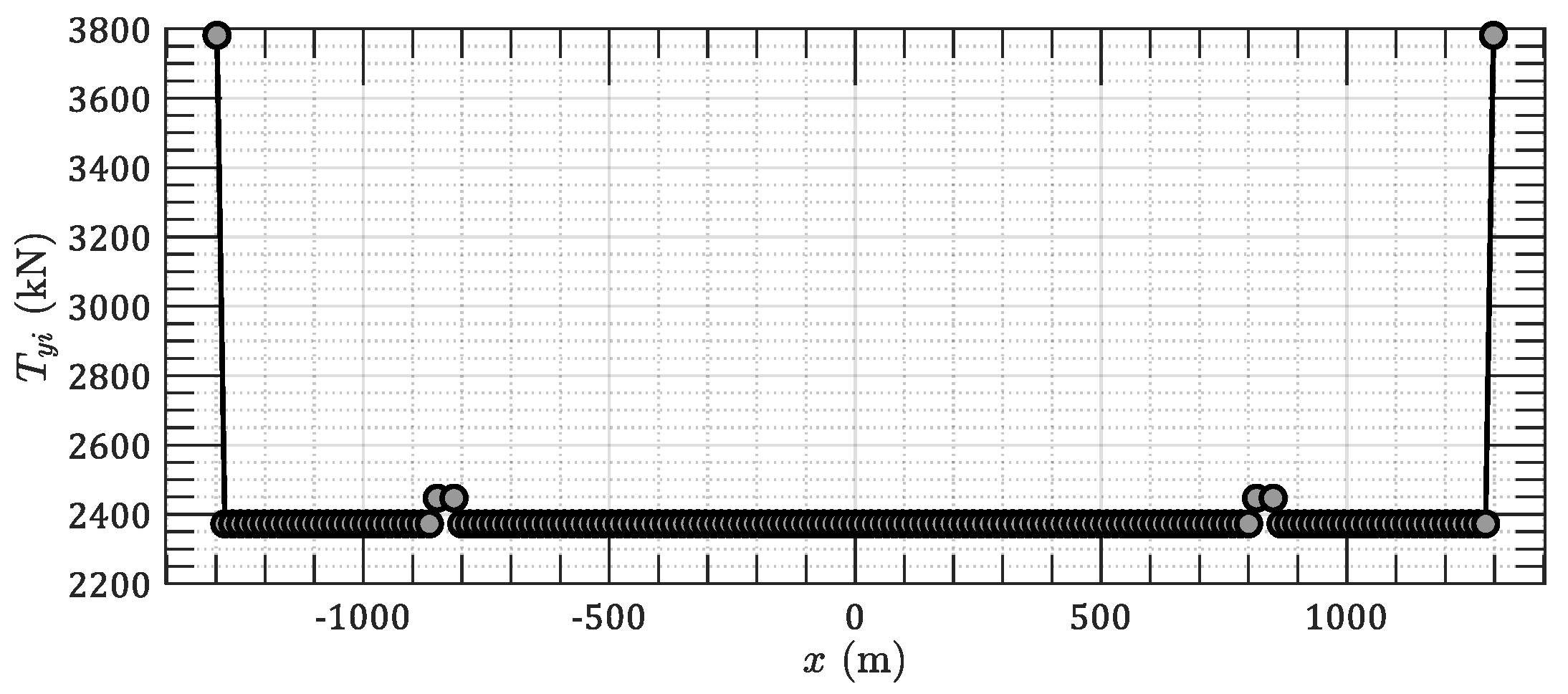
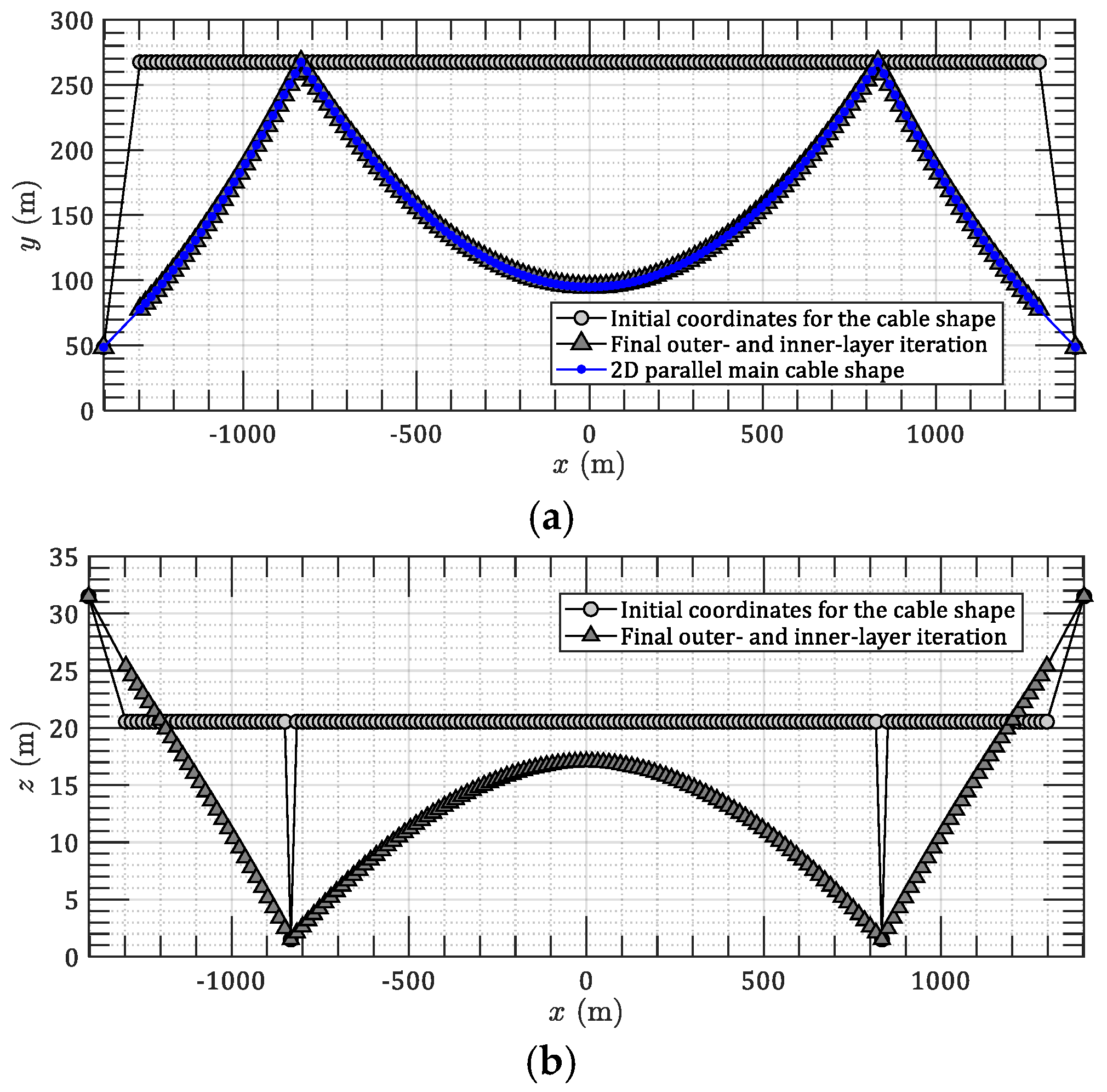
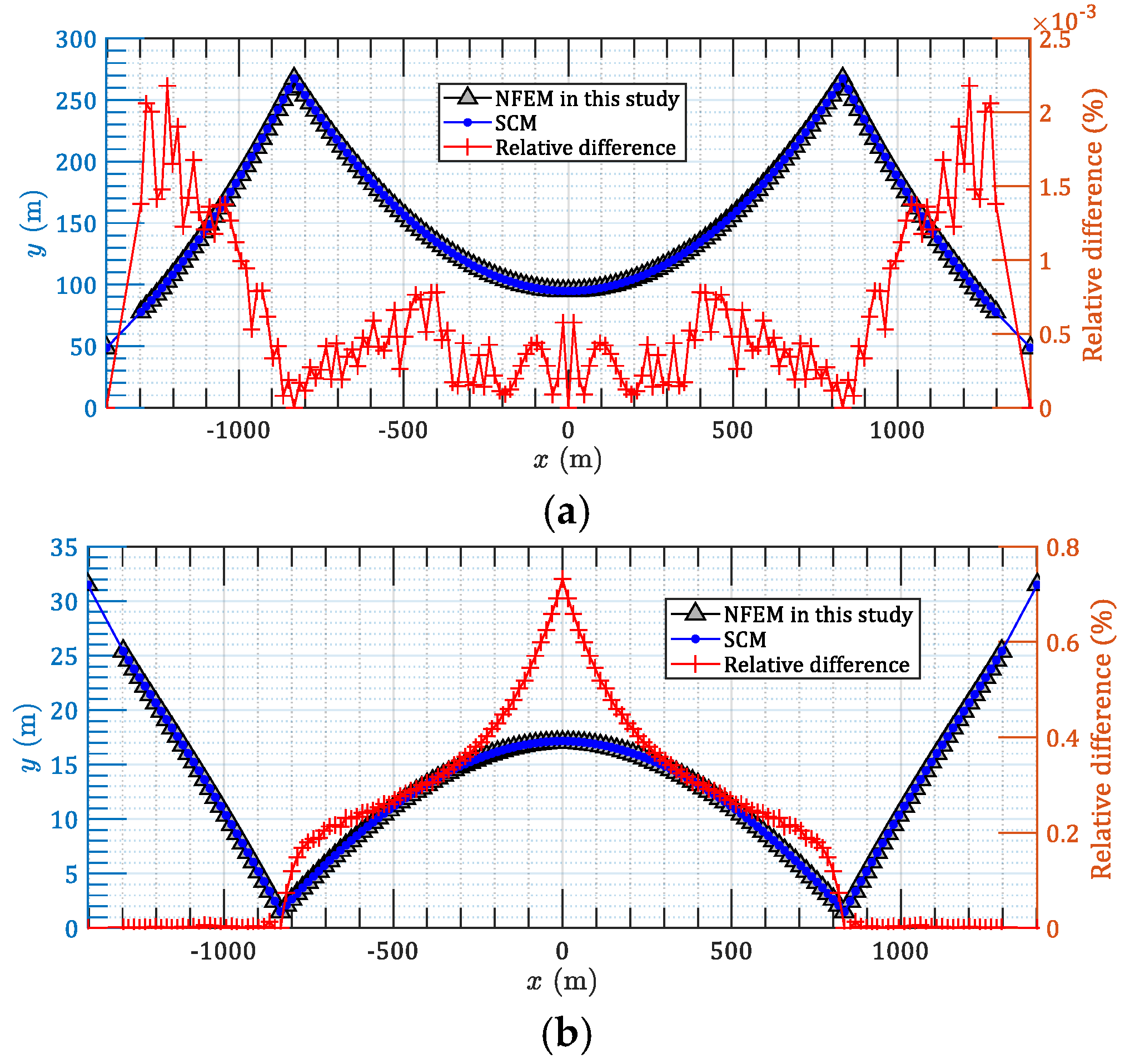
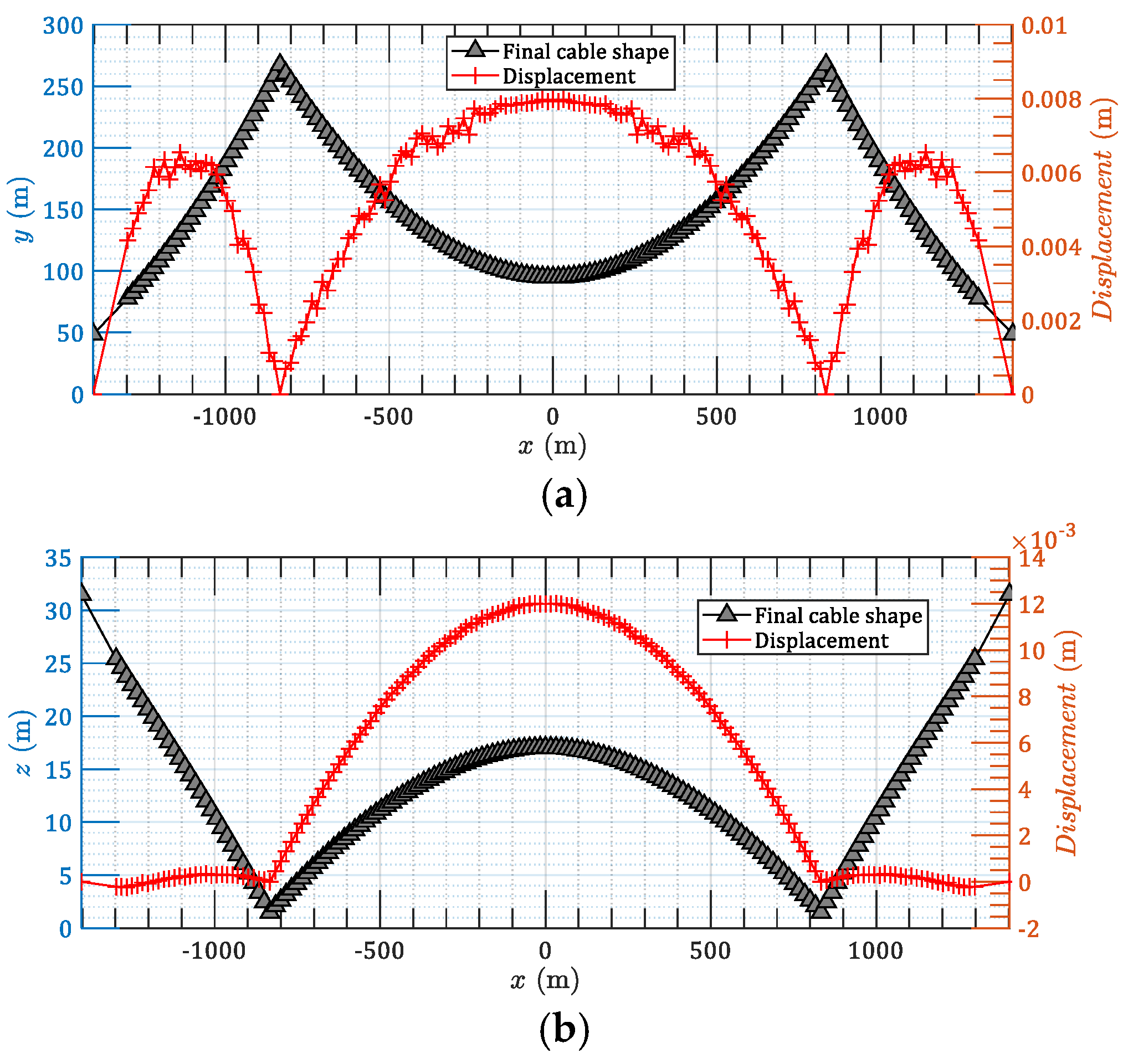
3.2. Case 2: 3D Spatial Main Cables of an Earth-Anchored Suspension Bridge
3.3. Case 3: 3D Spatial Main Cables of a Self-Anchored Suspension Bridge
4. Conclusions
- (1)
- The proposed shape finding technique enables an efficient and accurate estimation of the target configuration of the main cable for the suspension bridge.
- (2)
- The present NFEM performs the form-finding for the whole cable in the Eulerian coordinate system using a few iteration steps without any information of the cable material or cross area as compared with the commonly used SCM. The unstrained cable length can also be calculated by subtracting the elongation from the final length of the cable.
- (3)
- Both the SCM and the present NFEM methods have enough efficiency and accuracy for finding final cable shape of the suspension bridge. The proposed technique provides an alternative to be used by the bridge designers and engineers for the rapid estimation of both 2D parallel and 3D spatial cable curves in the preliminary design stage.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xiang, H.F.; Ge, Y.J. Aerodynamic challenges in span length of suspension bridges. Front. Archit. Civ. Eng. China 2005, 1, 153–162. [Google Scholar] [CrossRef]
- Atmaca, B.; Ates, S. Construction stage analysis of three-dimensional cable-stayed bridges. Steel. Compos. Struct. 2012, 5, 413–426. [Google Scholar] [CrossRef]
- Zhang, W.M.; Li, T.; Shi, L.Y.; Liu, Z.; Qian, K.R. An iterative calculation method for hanger tensions and the cable shape of a suspension bridge based on the catenary theory and finite element method. Adv. Struct. Eng. 2019, 22, 1566–1578. [Google Scholar] [CrossRef]
- Gimsing, N.J.; Georgakis, C.T. Cable Supported Bridges; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2012; Volume 3. [Google Scholar]
- Wu, Z.Q.; Wei, J. Nonlinear Analysis of Spatial Cable of Long-Span Cable-Stayed Bridge considering Rigid Connection. KSCE J. Civ. Eng. 2019, 23, 148–215. [Google Scholar] [CrossRef]
- Yuan, X.; Dong, S. A two-node curved cable element for nonlinear analysis. Eng. Mech. 1999, 4, 007. (In Chinese) [Google Scholar]
- Yang, M.; Chen, Z. Nonlinear analysis of cable structures using a two-node curved cable element of high precision. Eng. Mech. 2003, 20, 42–47. (In Chinese) [Google Scholar]
- Kwan, A. A new approach to geometric nonlinearity of cable structures. Comput. Struct. 1998, 67, 243–252. [Google Scholar] [CrossRef]
- Ever, C.; Leonardo, F. Nonlinear analysis of structures cable-truss. Int. J. Eng. Technol. Sci. 2015, 7, 160–169. [Google Scholar]
- Ahmad, A.M.S.; Ahmad, S.; Vahab, E.; Alireza, N.R. Nonlinear analysis of cable structures under general loadings. Finite Elem. Anal. Des. 2013, 73, 11–19. [Google Scholar]
- Andreu, A.; Gil, L.; Roca, P. A new deformable catenary element for the analysis of cable net structures. Comput. Struct. 2006, 84, 1882–1890. [Google Scholar] [CrossRef]
- Li, C.X.; He, J.; Zhang, Z.; Liu, Y.; Ke, H.J.; Dong, C.W.; Li, H. An Improved Analytical Algorithm on Main Cable System of Suspension Bridge. Appl. Sci. 2018, 8, 1358. [Google Scholar] [CrossRef]
- Chen, Z.; Cao, H.; Zhu, H.; Hu, J.; Li, S. A simplified structural mechanics model for cable-truss footbridges and its implications for preliminary design. Eng. Struct. 2014, 68, 121–133. [Google Scholar] [CrossRef]
- Irvine, H.M. Cable Structures; MIT Press: Cambridge, MA, USA, 1981. [Google Scholar]
- Xiao, R.C.; Xiang, H.F. Research on method and program system for determining ideal state of suspension bridge with large span. East China Highw. 1998, 11, 42–50. (In Chinese) [Google Scholar]
- Kim, H.K.; Lee, M.J.; Chang, S.P. Non-linear shape-finding analysis of a self-anchored suspension bridge. Eng. Struct. 2002, 24, 1547–1559. [Google Scholar] [CrossRef]
- Tang, M.L. Spatial Geometric Nonlinear Analysis and Software Development of Long Span Suspension Bridges. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2003. (In Chinese). [Google Scholar]
- Zhang, W.M.; Yang, C.Y.; Wang, Z.W.; Liu, Z. An analytical algorithm for reasonable central tower stiffness in the three-tower suspension bridge with unequal-length main spans. Eng. Struct. 2019, 199, 109595. [Google Scholar] [CrossRef]
- Kim, K.S.; Lee, H.S. Analysis of target configurations under dead loads for cable-supported bridges. Comput. Struct. 2001, 79, 2681–2692. [Google Scholar] [CrossRef]
- Kim, M.Y.; Kim, D.Y.; Jung, M.R.; Attard, M.M. Improved methods for determining the 3-dimensional initial shapes of cable-supported bridges. Int. J. Steel. Struct. 2014, 14, 83–102. [Google Scholar] [CrossRef]
- Kim, M.Y.; Jung, M.R.; Attard, M.M. Unstrained length-based methods determining an optimized initial shape of 3-dimensional self-anchored suspension bridges. Comput. Struct. 2019, 217, 18–35. [Google Scholar] [CrossRef]
- Sun, Y.; Zhu, H.P.; Dong, X. New method for shape finding of self-anchored suspension bridges with three-dimensionally curved cables. J. Bridge Eng. 2015, 20, 04014063. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D. Static perturbation analysis of inclined shallow elastic cables under general 3D-loads. Curved. Layer. Struct. 2016, 5, 250–259. [Google Scholar] [CrossRef]
- Luongo, A.; Zulli, D. Statics of shallow inclined elastic cables under general vertical loads: A perturbation approach. Mathematics 2018, 6, 24. [Google Scholar] [CrossRef]
- Tang, M.L.; Qiang, S.Z.; Shen, R.Z. Segmental catenary method of calculating the cable curve of suspension bridge. J. China Railw. Soc. 2003, 25, 87–91. (In Chinese) [Google Scholar]
- Luo, X.H.; Xiao, R.C.; Xiang, H.F. Cable shape analysis of suspension bridge with spatial cables. J. Tongji Univ. 2004, 32, 1349–1354. (In Chinese) [Google Scholar]
- Wang, S.R.; Zhou, Z.X.; Huang, Y.Y.; Gao, Y.M. Analytical calculation method for the preliminary analysis of self-anchored suspension bridges. Math. Probl. Eng. 2015, 3, 1–12. [Google Scholar] [CrossRef]
- Zhou, Y.F.; Chen, S. Iterative Nonlinear Cable Shape and Force Finding Technique of Suspension Bridges Using Elastic Catenary Configuration. J. Eng. Mech. 2019, 145. [Google Scholar] [CrossRef]
- Li, T.; Liu, Z. A Recursive Algorithm for Determining the Profile of the Spatial Self-anchored Suspension Bridges. KSCE J. Civ. Eng. 2019, 23, 1283–1292. [Google Scholar] [CrossRef]
- Xiao, R.C.; Chen, M.H.; Sun, B. Determination of the reasonable state of suspension bridges with spatial cables. J. Bridge Eng. 2017, 22, 04017060. [Google Scholar] [CrossRef]
- Song, C.L.; Xiao, R.C.; Sun, B. Improved Method for Shape Finding of Long-Span Suspension Bridges. Int. J. Steel Struct. 2020, 20, 247–258. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method; McGraw-Hill: London, UK, 1967; Volume 3. [Google Scholar]
- Cheney, E.; Kincaid, D. Numerical Mathematics and Computing; Nelson Education: Toronto, ON, Canada, 2012. [Google Scholar]

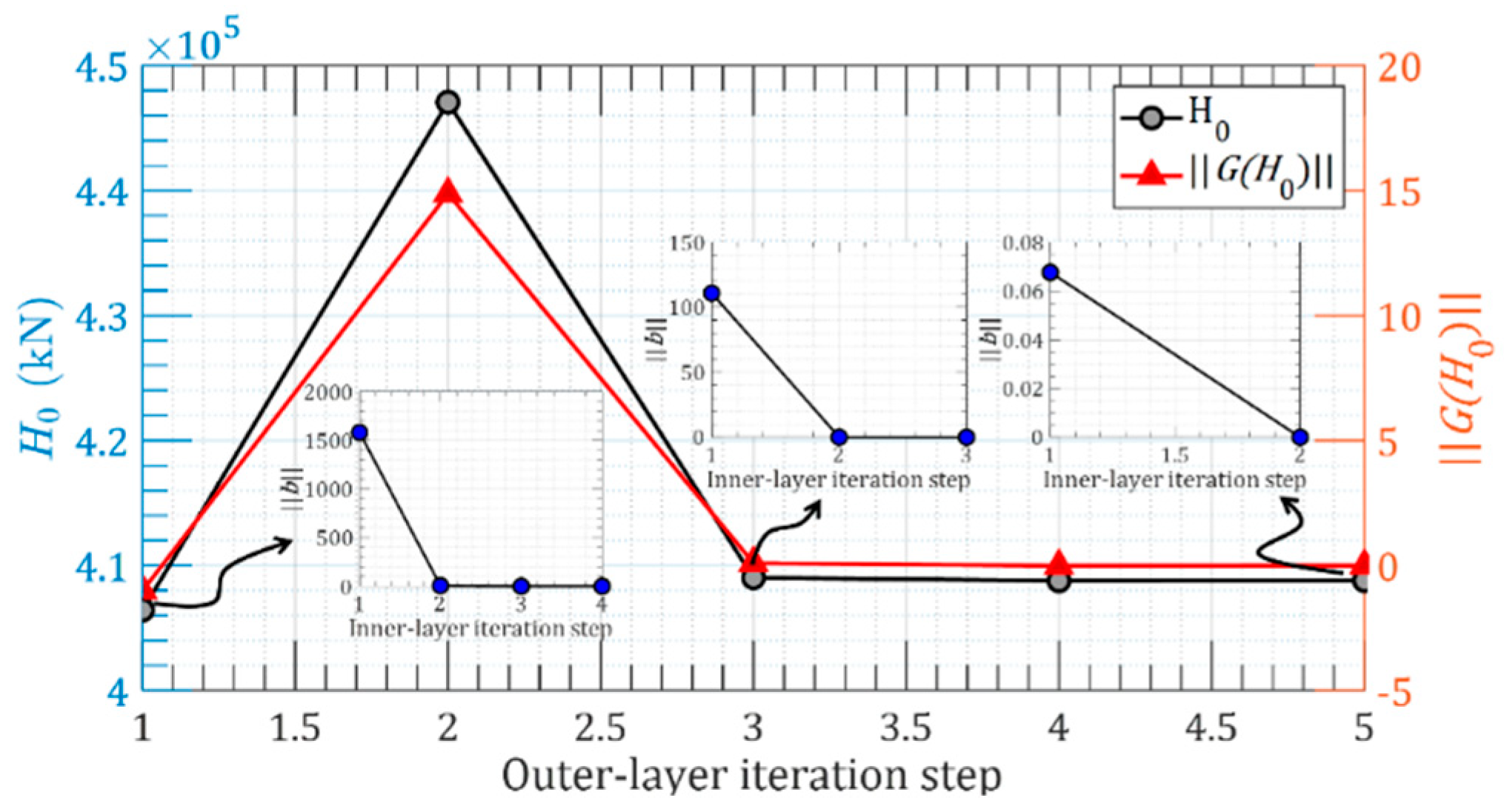
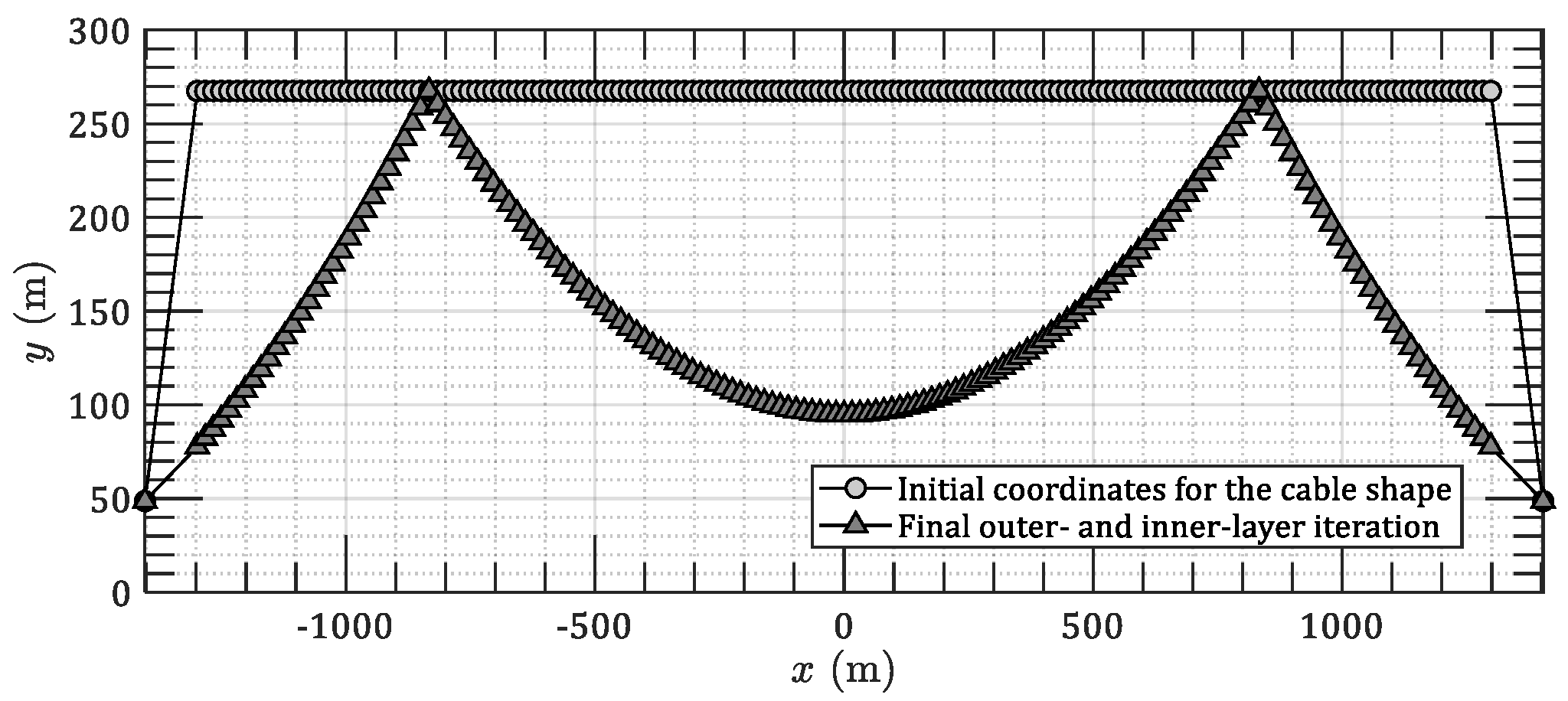
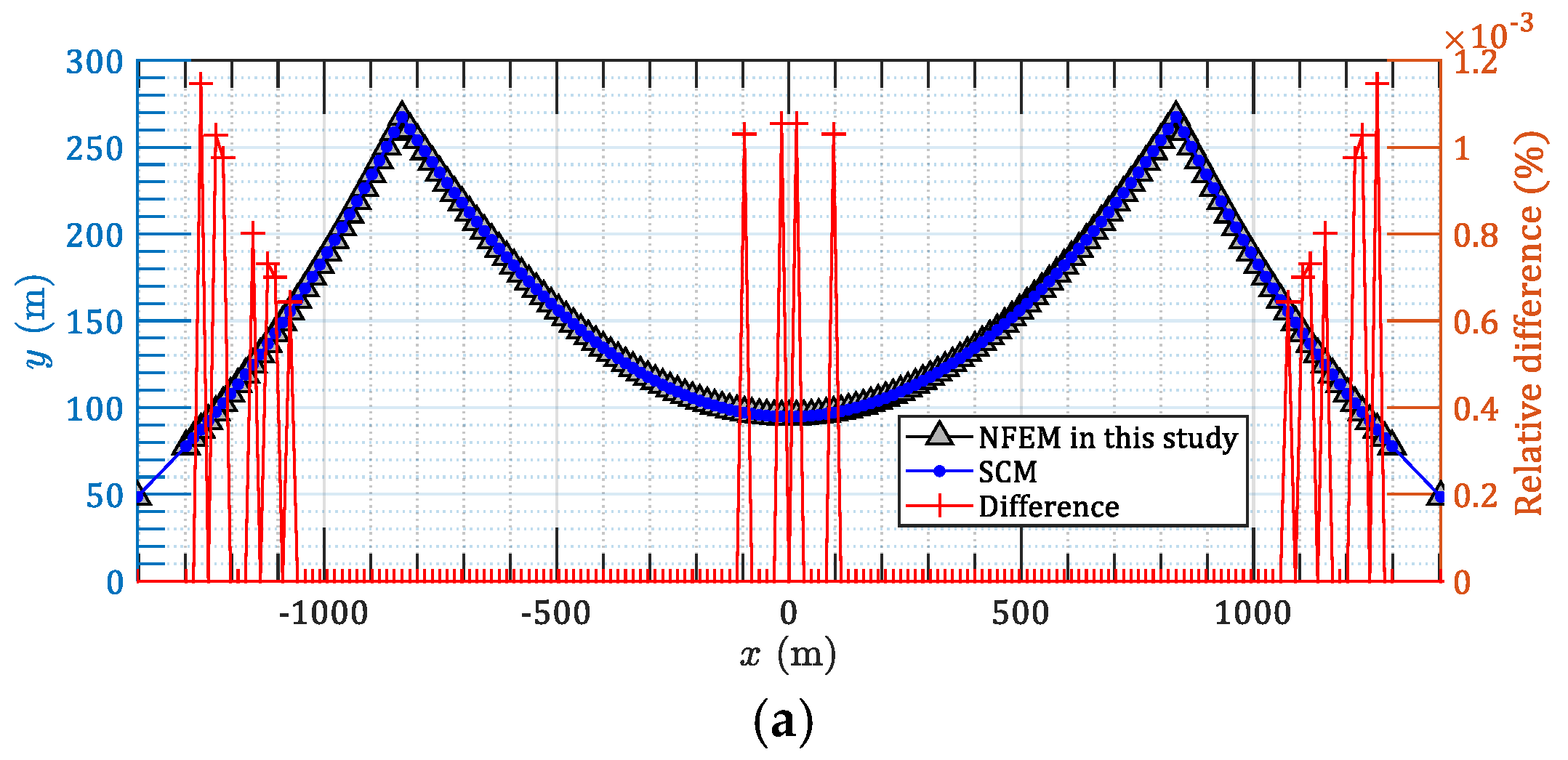
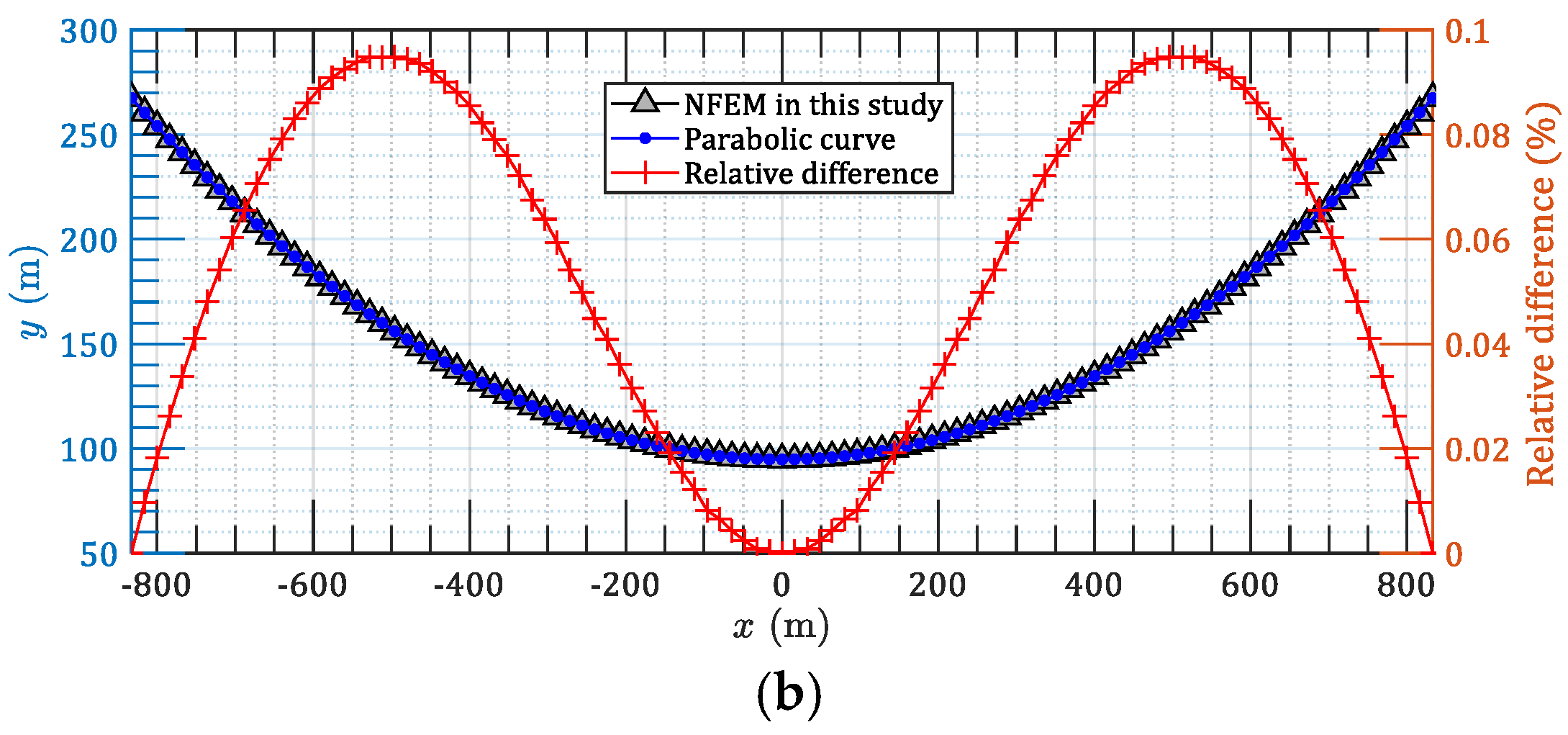


| Method | Object | Coordinate System | Governing Equations | Axis Stiffness of Cable |
|---|---|---|---|---|
| entry 1 | Cable segment | Lagrangian (with respect to l0) | Algebraic equations | Yes |
| entry 2 | Whole cable | Eulerian (with respect to x) | Differential equations | No |
| x (m) | (m) | (m) |
|---|---|---|
| 125.000 | 48.870 | 15.960 |
| 137.500 | 48.994 | 15.960 |
| 150.000 | 49.108 | 15.960 |
| 162.500 | 49.210 | 15.960 |
| 175.000 | 49.302 | 15.960 |
| 187.500 | 49.383 | 15.960 |
| 200.000 | 49.453 | 15.960 |
| 212.500 | 49.512 | 15.960 |
| 225.000 | 49.561 | 15.960 |
| 237.500 | 49.599 | 15.960 |
| 250.000 | 49.626 | 15.960 |
| 262.500 | 49.642 | 15.960 |
| 275.000 | 49.647 | 15.960 |
| x(m) | Kim et al. (2002) (A) | Luo et al. (2004) (B) | This Study (C) | A vs. C (%) | B vs. C (%) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| y (m) | z (m) | y (m) | z (m) | y (m) | z (m) | (yA − yC)/yA | (zA − zC)/zA | (yB − yC)/yB | (zB − zC)/zB | |
| 125.000 | 114.573 | 1.500 | 113.763 | 1.681 | 114.573 | 1.500 | - | - | - | - |
| 137.500 | 104.938 | 3.632 | 104.968 | 3.625 | 104.927 | 3.644 | 0.010 | −0.330 | 0.039 | −0.524 |
| 150.000 | 96.160 | 5.586 | 96.180 | 5.576 | 96.141 | 5.605 | 0.020 | −0.340 | 0.041 | −0.520 |
| 162.500 | 88.230 | 7.360 | 88.243 | 7.350 | 88.208 | 7.382 | 0.025 | −0.299 | 0.040 | −0.435 |
| 175.000 | 81.147 | 8.955 | 81.155 | 8.944 | 81.125 | 8.976 | 0.027 | −0.235 | 0.037 | −0.358 |
| 187.500 | 74.905 | 10.369 | 74.910 | 10.357 | 74.885 | 10.386 | 0.027 | −0.164 | 0.033 | −0.280 |
| 200.000 | 69.502 | 11.601 | 69.505 | 11.590 | 69.485 | 11.612 | 0.024 | −0.095 | 0.029 | −0.190 |
| 212.500 | 64.935 | 12.650 | 64.937 | 12.639 | 64.923 | 12.654 | 0.018 | −0.032 | 0.022 | −0.119 |
| 225.000 | 61.201 | 13.514 | 61.203 | 13.504 | 61.194 | 13.510 | 0.011 | 0.030 | 0.015 | −0.044 |
| 237.500 | 58.300 | 14.191 | 58.301 | 14.183 | 58.296 | 14.179 | 0.007 | 0.085 | 0.009 | 0.028 |
| 250.000 | 56.228 | 14.678 | 56.230 | 14.671 | 56.227 | 14.661 | 0.002 | 0.116 | 0.005 | 0.068 |
| 262.500 | 54.985 | 14.973 | 54.987 | 14.966 | 54.987 | 14.951 | −0.004 | 0.147 | 0.000 | 0.100 |
| 275.000 | 54.573 | 15.071 | 54.573 | 15.065 | 54.573 | 15.049 | 0.000 | 0.146 | 0.000 | 0.106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, W.; Ge, Y.; Fang, G.; Cao, J. A Novel Shape Finding Method for the Main Cable of Suspension Bridge Using Nonlinear Finite Element Approach. Appl. Sci. 2021, 11, 4644. https://doi.org/10.3390/app11104644
Zhu W, Ge Y, Fang G, Cao J. A Novel Shape Finding Method for the Main Cable of Suspension Bridge Using Nonlinear Finite Element Approach. Applied Sciences. 2021; 11(10):4644. https://doi.org/10.3390/app11104644
Chicago/Turabian StyleZhu, Weiliang, Yaojun Ge, Genshen Fang, and Jinxin Cao. 2021. "A Novel Shape Finding Method for the Main Cable of Suspension Bridge Using Nonlinear Finite Element Approach" Applied Sciences 11, no. 10: 4644. https://doi.org/10.3390/app11104644
APA StyleZhu, W., Ge, Y., Fang, G., & Cao, J. (2021). A Novel Shape Finding Method for the Main Cable of Suspension Bridge Using Nonlinear Finite Element Approach. Applied Sciences, 11(10), 4644. https://doi.org/10.3390/app11104644







