Slope Stability Analysis to Correlate Shear Strength with Slope Angle and Shear Stress by Considering Saturated and Unsaturated Seismic Conditions
Abstract
Featured Application
Abstract
1. Introduction
2. Materials and Methods
Sampling and Testing
3. Results
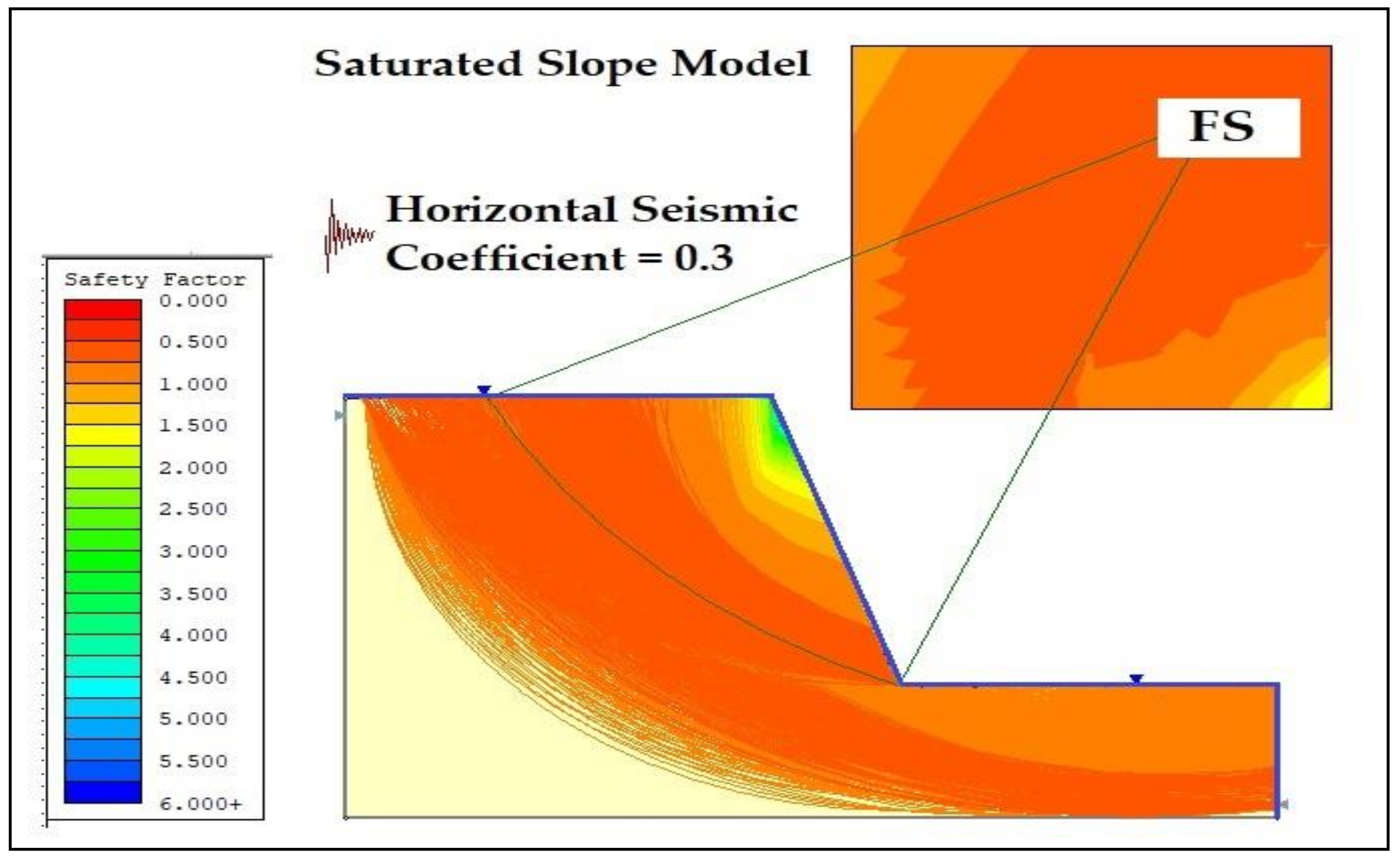
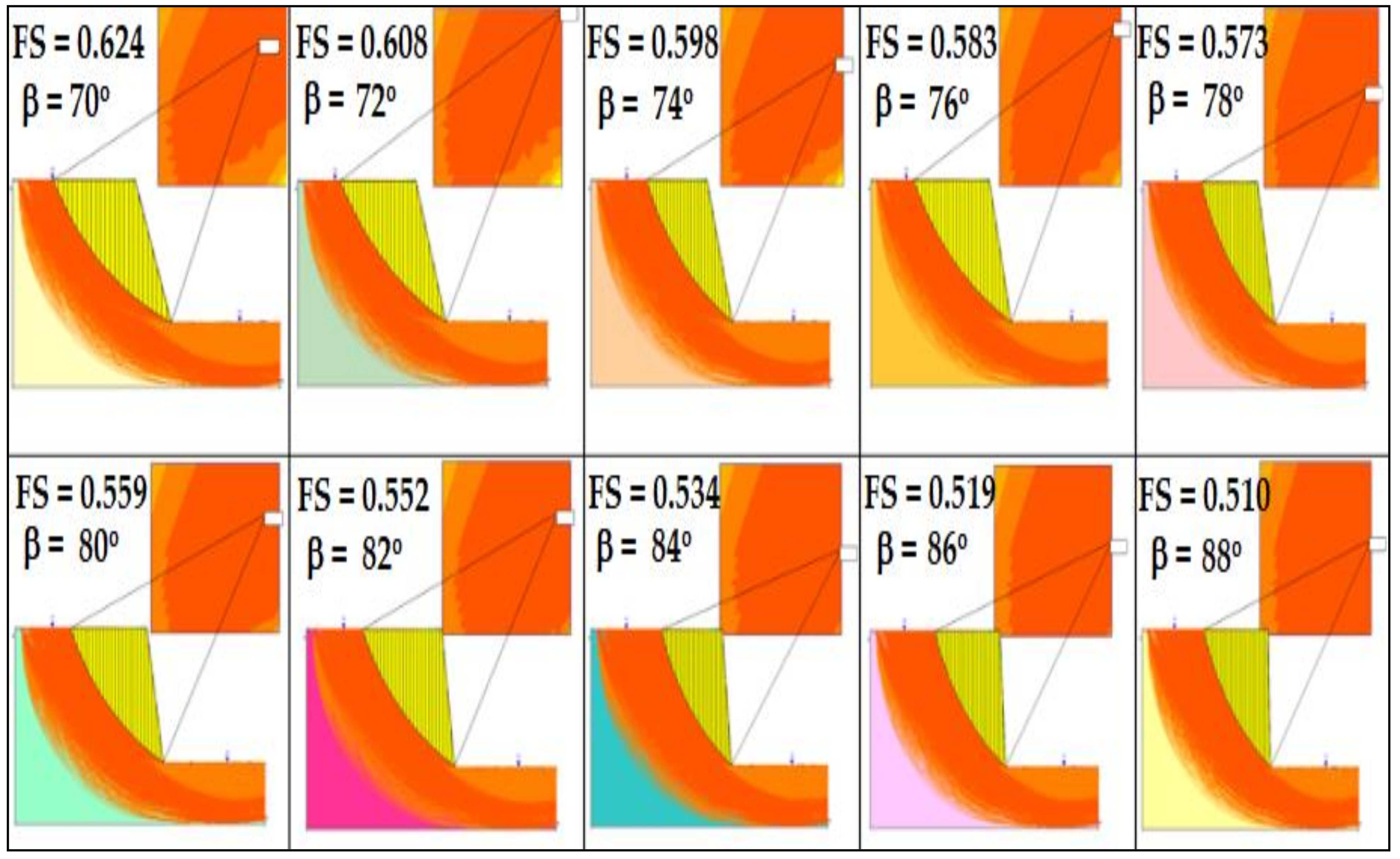
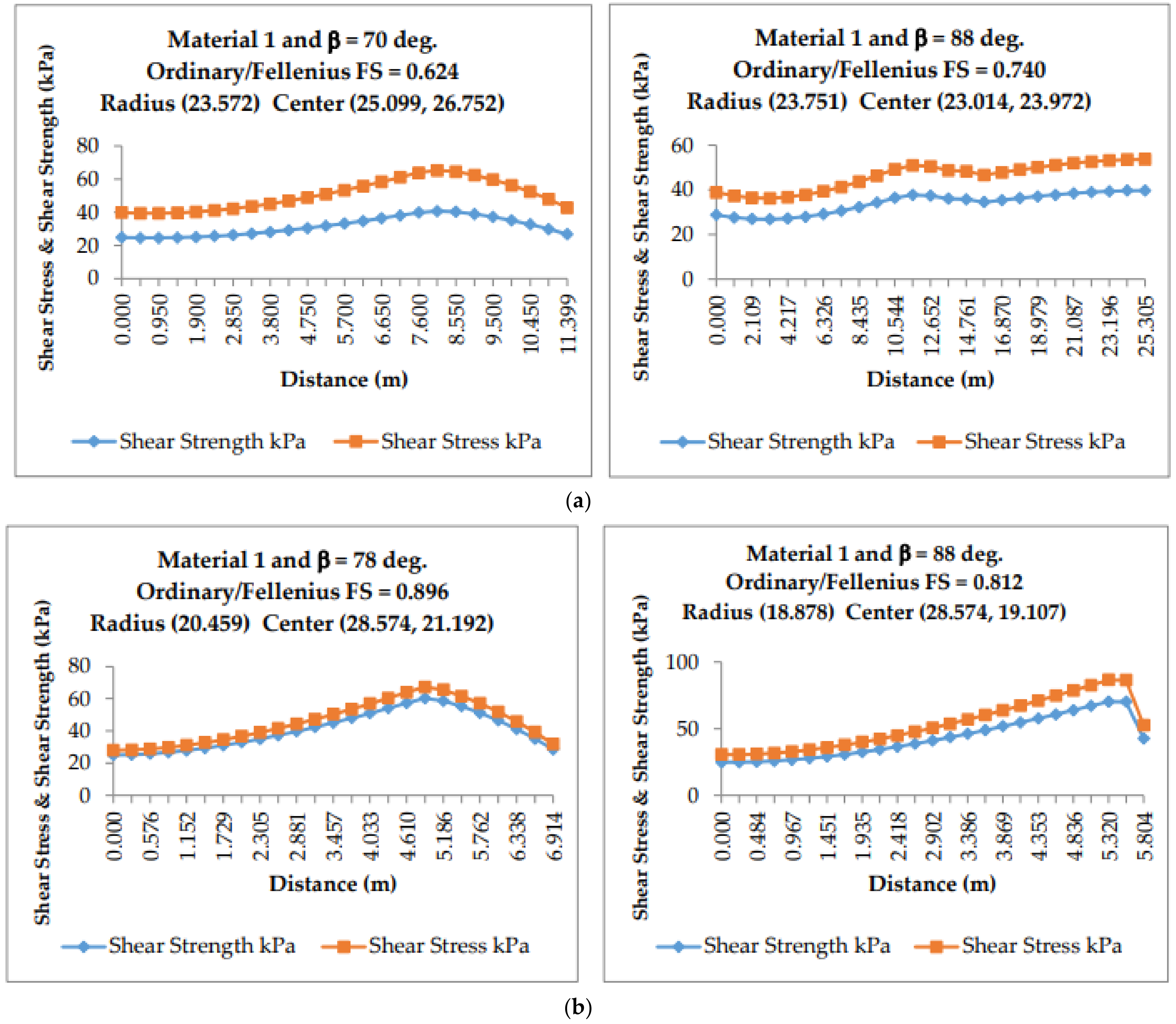
3.1. Saturated Seismic Analysis
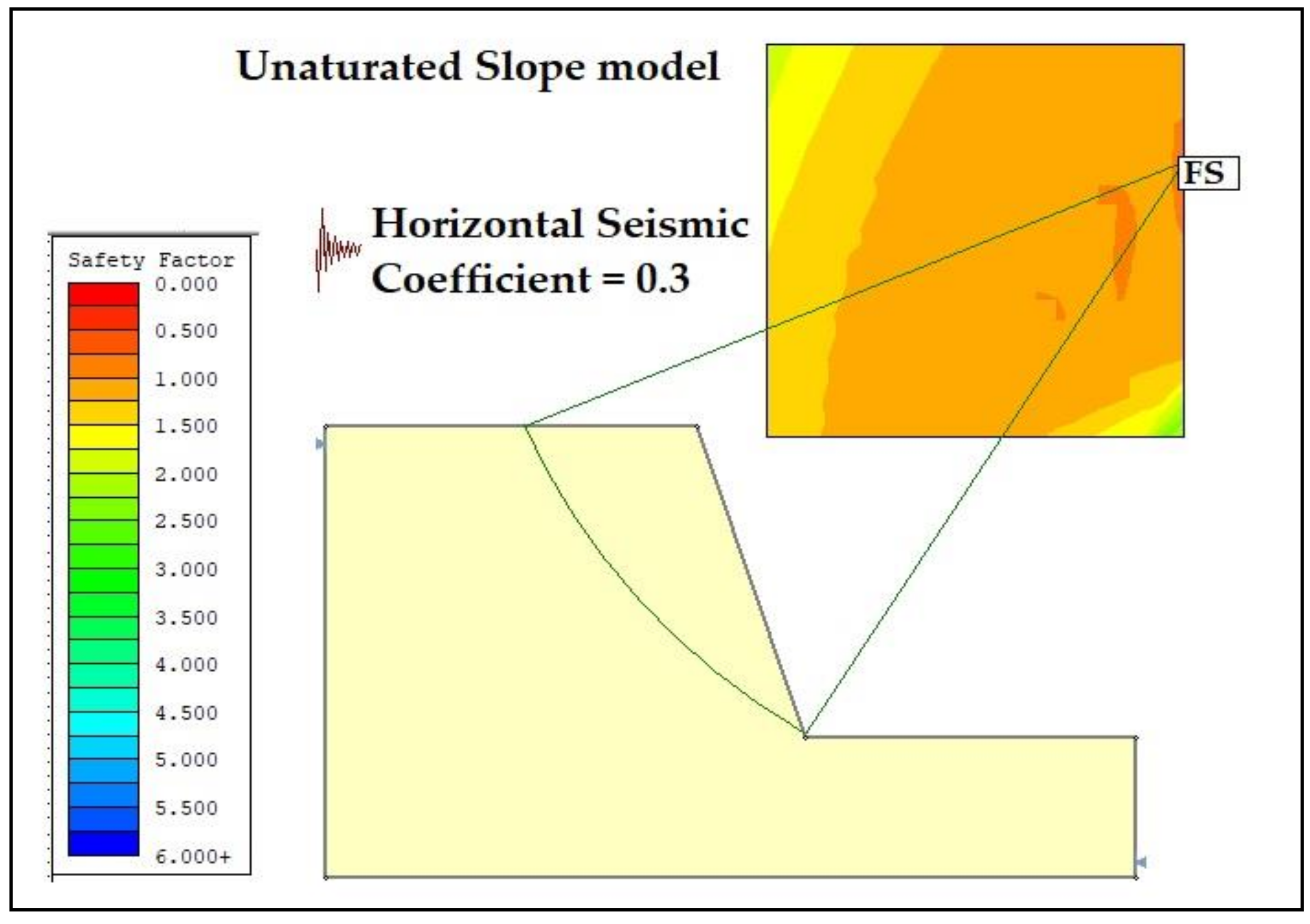
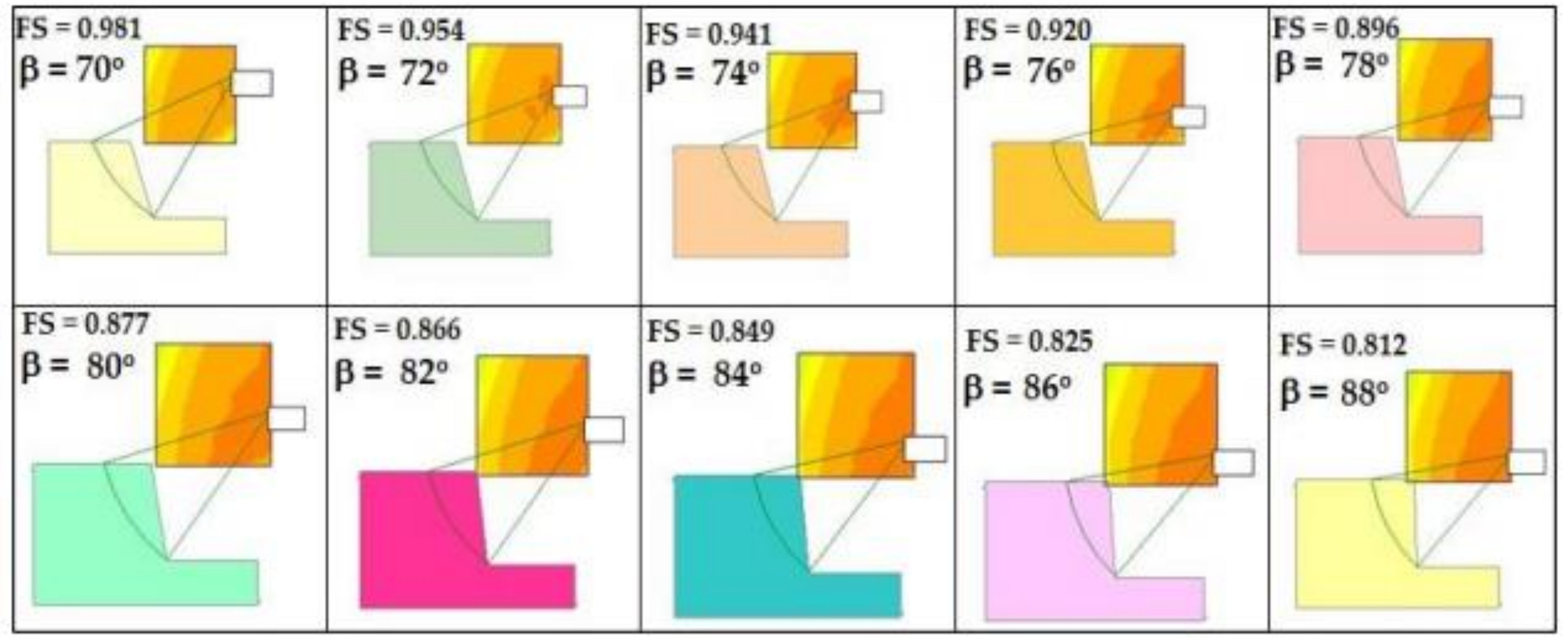
3.2. Unsaturated Seismic Analysis
4. Discussions
5. Conclusions
- From Equations (9) and (10), it is clear that the higher the value of β and σ, the value of τ will be lower. The relationship could be checked for any slope stability case. For any other slope stability project, the shear strength can be obtained by simply applying Equations (9) and (10). The factor of safety can also be obtained by dividing shear strength by shear stress. These equations can be used to compute the shear strength of any soil slope in the given material properties range.
- The applicability of Equations (9) and (10) is above 99 percent.
- The same equations can be extended to other material types with the same procedure of analysis. If a material’s properties exist between the specified values, then the shear strength can be calculated with interpolation. The same work can be extended to analyze the seismic condition by also considering the vertical seismic coefficient to get a clearer idea of the shear strength variation in complex conditions.
- In future work, the correlation of shear strength, factor of safety and slope angle with the variation of the width of an embankment will be studied.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| FS | Factor of safety |
| τ | Shear strength of soil |
| β | Slope angle |
| σ | Shear stress of soil |
| c | Cohesion of soil |
| Φ | Soil friction angle |
| SPSS | Statistical package for social sciences (Software) |
| SI | System international |
References
- Conte, E.; Pugliese, L.; Troncone, A. Post-failure analysis of the Maierato landslide using the material point method. Eng. Geol. 2020, 277, 105788. [Google Scholar] [CrossRef]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Iverson, R.M.; George, D.L.; Allstadt, K.; Reid, M.E.; Collins, B.D.; Vallance, J.W.; Schilling, S.P.; Godt, J.W.; Cannon, C.M.; Magirl, C.S.; et al. Landslide mobility and hazards: Implications of the 2014 Oso disaster. Earth Planet. Sci. Lett. 2015, 412, 197–208. [Google Scholar] [CrossRef]
- Troncone, A.; Pugliese, L.; Lamanna, G.; Conte, E. Prediction of rainfall-induced landslide movements in the presence of stabilizing piles. Eng. Geol. 2021, 288, 106143. [Google Scholar] [CrossRef]
- Bandara, S.; Ohtsuka, S.; Fukumoto, Y. Identification of shear strength and seismic coefficient by back analyzing surficial slides in the 2004 Mid-Niigata prefecture earthquake. Landslides 2018, 15, 2255–2266. [Google Scholar] [CrossRef]
- White, J.A.; Singham, D.I. Slope stability assessment using stochastic rainfall simulation. Procedia Comput. Sci. 2012, 9, 699–706. [Google Scholar] [CrossRef]
- Suradi, M.; Fourie, A.B.; Saynor, M.J. An experimental and numerical study of a landslide triggered by an extreme rainfall event in northern Australia. Landslides 2016, 13, 1125–1138. [Google Scholar] [CrossRef]
- Li, W.C.; Lee, L.M.; Cai, H.; Li, H.J.; Dai, F.C.; Wang, M.L. Combined roles of saturated permeability and rainfall characteristics on surficial failure of homogeneous soil slope. Eng. Geol. 2013, 153, 105–113. [Google Scholar] [CrossRef]
- Wu, L.Z.; Liu, G.G.; Wang, L.C.; Zhang, L.M.; Li, B.E.; Li, B. Numerical analysis of 1D coupled infiltration and deformation in layered unsaturated porous medium. Environ. Earth Sci. 2016, 75, 761. [Google Scholar] [CrossRef]
- Tsai, T.L. Influences of soil water characteristic curve on rainfall-induced shallow landslides. Environ. Earth Sci. 2011, 64, 449–459. [Google Scholar] [CrossRef]
- Lenti, L.; Martino, S. The interaction of seismic waves with step-like slopes and its influence on landslide movements. Eng. Geol. 2012, 126, 19–36. [Google Scholar] [CrossRef]
- Fotopoulou, S.D.; Pitilakis, K.D. Predictive relationships for seismically induced slope displacements using numerical analysis results. Bull. Earthq. Eng. 2015, 13, 3207–3238. [Google Scholar] [CrossRef]
- Martino, S.; Bigarre, P.; Coccia, S.; Bourdeau, C.; Lenti, L.; Ozel, O.; Yalcinkaya, E. Integrated engineering-geological and numerical approach applied to the large Büyükçekmece (Turkey) landslide for evaluating earthquake-induced effects. In Landslides and Engineered Slopes. Experience, Theory and Practice; CRC Press: Boca Raton, FL, USA, 2016; pp. 1375–1382. [Google Scholar]
- Dai, F.C.; Xu, C.; Yao, X.; Xu, L.; Tu, X.B.; Gong, Q.M. Spatial distribution of landslides triggered by the 2008 Ms 8.0 Wenchuan earthquake, China. J. Asian Earth Sci. 2011, 40, 883–895. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, L.M.; Glade, T. Characteristics of earthquake-and rain-induced landslides near the epicenter of Wenchuan earthquake. Eng. Geol. 2014, 175, 58–73. [Google Scholar] [CrossRef]
- Ding, M.; Hu, K. Susceptibility mapping of landslides in Beichuan County using cluster and MLC methods. Nat. Hazards 2014, 70, 755–766. [Google Scholar] [CrossRef]
- Guo, D.; Hamada, M. Qualitative and quantitative analysis on landslide influential factors during Wenchuan earthquake: A case study in Wenchuan County. Eng. Geol. 2013, 152, 202–209. [Google Scholar] [CrossRef]
- Zhou, J.W.; Cui, P.; Fang, H. Dynamic process analysis for the formation of Yangjiagou landslide-dammed lake triggered by the Wenchuan earthquake, China. Landslides 2013, 10, 331–342. [Google Scholar] [CrossRef]
- Fan, G.; Zhang, J.; Wu, J.; Yan, K. Dynamic response and dynamic failure mode of a weak intercalated rock slope using a shaking table. Rock Mech. Rock Eng. 2016, 49, 3243–3256. [Google Scholar] [CrossRef]
- Martino, S.; Lenti, L.; Bourdeau, C. Composite mechanism of the Büyükçekmece (Turkey) landslide as conditioning factor for earthquake-induced mobility. Geomorphology 2018, 308, 64–77. [Google Scholar] [CrossRef]
- Wang, L.; Pu, X.; Wu, Z.; Xu, X.; Liu, K. Shaking table tests on dynamic response of loess slopes under coupling effects of earthquakes and rainfalls. Chin. J. Geotech. Eng. 2018, 40, 1287–1293. [Google Scholar]
- Liu, H.; Xu, Q.; Zhou, F. Shaking table test for seismic responses of slopes with a weak interlayer. Chin. J. Rock Mech. Eng. 2015, 5, 994–1005. [Google Scholar]
- Crosscut, N.B. As Landslides Close Roads, Washington’s Remote Towns Deal with Isolation. 2020. Available online: https://crosscut.com/2020/02/landslides-close-roads-washingtons-remote-towns-deal-isolation (accessed on 18 February 2020).
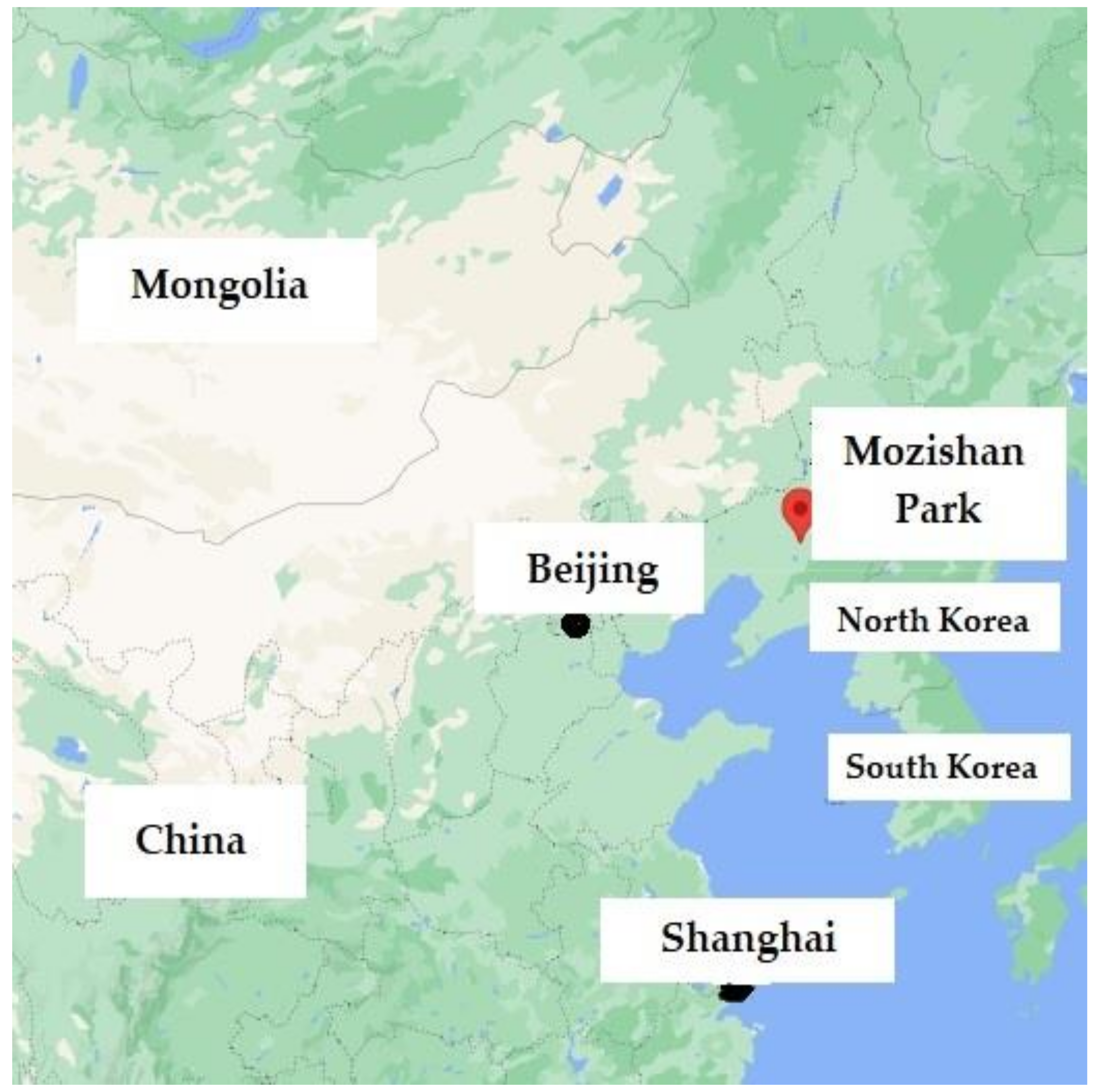
- Google Maps. Available online: https://google.com/maps/place/Mozis/han+Park,+Hunnan+Qu,+Shenyang+Shi,+China/@41.6671333,123.4773671,209m/ (accessed on 14 May 2021).
- Dafalias, Y.F. An anisotropic critical state soil plasticity model. Mech. Res. Commun. 1986, 13, 341–347. [Google Scholar] [CrossRef]
- Amorosi, A.; Rollo, F.; Houlsby, G.T. A nonlinear anisotropic hyperelastic formulation for granular materials: Comparison with existing models and validation. Acta Geotech. 2020, 15, 179–196. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Taiebat, M. Anatomy of rotational hardening in clay plasticity. Géotechnique 2013, 63, 1406–1418. [Google Scholar] [CrossRef]
- Kavvadas, M.; Amorosi, A. A constitutive model for structured soils. Géotechnique 2000, 50, 263–273. [Google Scholar] [CrossRef]
- Wheeler, S.J.; Näätänen, A.; Karstunen, M.; Lojander, M. An anisotropic elastoplastic model for soft clays. Can. Geotech. J. 2003, 40, 403–418. [Google Scholar] [CrossRef]
- Anandarajah, A.; Dafalias, Y.F. Bounding surface plasticity. III: Application to anisotropic cohesive soils. J. Eng. Mech. 1986, 112, 1292–1318. [Google Scholar] [CrossRef]
- Banerjee, P.K.; Yousif, N.B. A plasticity model for the mechanical behaviour of anisotropically consolidated clay. Int. J. Numer. Anal. Methods Geomech. 1986, 10, 521–541. [Google Scholar] [CrossRef]
- Slebi-Acevedo, C.J.; Zuluaga-Astudillo, D.A.; Ruge, J.C.; Castro-Fresno, D. Influence of the Diatomite Specie on the Peak and Residual Shear Strength of the Fine-Grained Soil. Appl. Sci. 2021, 11, 1352. [Google Scholar] [CrossRef]
- Delgado, J.; Galiana-Merino, J.J.; García-Tortosa, F.J.; Garrido, J.; Lenti, L.; Martino, S.; Peláez, J.A.; Rodríguez-Peces, M.J.; de Galdeano, C.S.; Soler-Llorens, J.L. Ambient Noise Measurements to Constrain the Geological Structure of the Güevéjar Landslide (S Spain). Appl. Sci. 2021, 11, 1452. [Google Scholar] [CrossRef]
- Segoni, S.; Piciullo, L.; Gariano, S.L. A review of the recent literature on rainfall thresholds for landslide occurrence. Landslides 2018, 15, 1483–1501. [Google Scholar] [CrossRef]
- Sengani, F.; Mulenga, F. Influence of Rainfall Intensity on the Stability of Unsaturated Soil Slope: Case Study of R523 Road in Thulamela Municipality, Limpopo Province, South Africa. Appl. Sci. 2020, 10, 8824. [Google Scholar] [CrossRef]
- Dai, Z.; Guo, J.; Luo, H.; Li, J.; Chen, S. Strength Characteristics and Slope Stability Analysis of Expansive Soil with Filled Fissures. Appl. Sci. 2020, 10, 4616. [Google Scholar] [CrossRef]


| Material Number | Cohesion (kPa) | Friction Angle (Degrees) | Unit Weight (kN/m3) |
|---|---|---|---|
| 1 | 25 | 36 | 16.5 |
| 2 | 25.8 | 35.5 | 16.2 |
| 3 | 26 | 35 | 15.9 |
| 4 | 26.3 | 34.6 | 15.5 |
| 5 | 26.9 | 34.2 | 15.1 |
| 6 | 27.4 | 33.7 | 14.8 |
| 7 | 28 | 33.2 | 14.4 |
| 8 | 28.5 | 31.8 | 14 |
| 9 | 29 | 31.4 | 13.6 |
| 10 | 29.4 | 30.9 | 13.1 |
| Slope Angle | Material 1 | Material 2 | Material 3 | Material 4 | Material 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | |
| 70 | 40.68 | 65.24 | 0.624 | 40.11 | 62.68 | 0.640 | 38.99 | 60.47 | 0.646 | 37.69 | 57.68 | 0.654 | 38.05 | 56.82 | 0.670 |
| 72 | 38.58 | 63.46 | 0.608 | 38.17 | 61.07 | 0.625 | 37.20 | 59.01 | 0.630 | 36.09 | 56.40 | 0.640 | 35.33 | 53.77 | 0.657 |
| 74 | 35.39 | 59.20 | 0.598 | 38.96 | 63.33 | 0.615 | 37.88 | 61.09 | 0.620 | 36.65 | 58.26 | 0.629 | 38.65 | 60.01 | 0.644 |
| 76 | 40.21 | 69.02 | 0.583 | 39.63 | 66.24 | 0.598 | 38.50 | 63.85 | 0.603 | 37.20 | 60.84 | 0.611 | 36.24 | 57.80 | 0.627 |
| 78 | 36.27 | 63.30 | 0.573 | 40.83 | 69.13 | 0.591 | 40.20 | 67.59 | 0.595 | 39.39 | 65.44 | 0.602 | 38.28 | 62.19 | 0.616 |
| 80 | 40.17 | 71.86 | 0.559 | 39.56 | 68.82 | 0.575 | 39.88 | 68.80 | 0.580 | 38.45 | 65.44 | 0.588 | 37.37 | 62.02 | 0.603 |
| 82 | 41.21 | 74.72 | 0.552 | 40.57 | 71.59 | 0.567 | 39.38 | 68.93 | 0.571 | 38.74 | 66.87 | 0.579 | 38.83 | 65.43 | 0.593 |
| 84 | 35.82 | 67.09 | 0.534 | 35.46 | 64.18 | 0.553 | 40.04 | 71.71 | 0.558 | 38.59 | 68.09 | 0.567 | 37.50 | 64.42 | 0.582 |
| 86 | 38.92 | 75.04 | 0.519 | 38.38 | 71.68 | 0.535 | 37.29 | 68.86 | 0.541 | 36.02 | 65.34 | 0.551 | 35.09 | 61.79 | 0.568 |
| 88 | 40.30 | 79.05 | 0.510 | 39.67 | 75.44 | 0.526 | 38.49 | 72.42 | 0.531 | 37.12 | 68.67 | 0.541 | 36.10 | 64.86 | 0.557 |
| Slope Angle | Material 6 | Material 7 | Material 8 | Material 9 | Material 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | |
| 70 | 37.33 | 54.69 | 0.683 | 36.42 | 52.02 | 0.700 | 37.12 | 52.01 | 0.714 | 38.38 | 52.61 | 0.730 | 39.64 | 53.59 | 0.740 |
| 72 | 34.77 | 51.78 | 0.672 | 38.91 | 56.55 | 0.688 | 37.36 | 53.37 | 0.700 | 36.30 | 50.67 | 0.716 | 39.61 | 54.01 | 0.733 |
| 74 | 37.83 | 57.61 | 0.657 | 36.85 | 54.70 | 0.674 | 37.12 | 54.08 | 0.686 | 36.13 | 51.45 | 0.702 | 36.05 | 50.18 | 0.718 |
| 76 | 35.54 | 55.51 | 0.640 | 34.68 | 52.70 | 0.658 | 33.73 | 50.02 | 0.674 | 36.08 | 52.21 | 0.691 | 34.61 | 48.88 | 0.708 |
| 78 | 37.46 | 59.72 | 0.627 | 36.42 | 56.64 | 0.643 | 35.10 | 53.44 | 0.657 | 34.14 | 50.68 | 0.674 | 32.78 | 47.39 | 0.692 |
| 80 | 36.58 | 59.44 | 0.615 | 35.56 | 56.23 | 0.632 | 35.90 | 55.41 | 0.648 | 34.85 | 52.47 | 0.664 | 33.38 | 48.99 | 0.681 |
| 82 | 38.94 | 64.41 | 0.605 | 38.48 | 62.14 | 0.619 | 36.86 | 58.37 | 0.632 | 35.69 | 55.16 | 0.647 | 34.07 | 51.36 | 0.663 |
| 84 | 36.68 | 61.65 | 0.595 | 37.88 | 62.01 | 0.611 | 37.55 | 60.32 | 0.623 | 36.99 | 58.11 | 0.637 | 35.18 | 54.04 | 0.651 |
| 86 | 34.42 | 59.12 | 0.582 | 38.52 | 64.56 | 0.597 | 36.88 | 60.52 | 0.609 | 39.60 | 64.77 | 0.611 | 35.47 | 55.35 | 0.641 |
| 88 | 35.35 | 62.00 | 0.570 | 34.39 | 58.47 | 0.588 | 39.36 | 65.51 | 0.601 | 37.93 | 61.78 | 0.614 | 36.01 | 57.38 | 0.628 |
| Material Number | Shear Strength (kPa) |
|---|---|
| 1 | 34.572 − 0.434*β + 0.559*σ |
| R2 = 99.4% | |
| 2 | 33.791 − 0.412*β + 0.562*σ |
| R2 = 98.9% | |
| 3 | 31.792 − 0.455*β + 0.648*σ |
| R2 = 99.2% | |
| 4 | 30.325 − 0.415*β + 0.633*σ |
| R2 = 99.6% | |
| 5 | 29.162 − 0.388*β + 0.634*σ |
| R2 = 99.8% | |
| 6 | 28.600 − 0.355*β + 0.613*σ |
| R2 = 99.8% | |
| 7 | 28.849 − 0.353*β + 0.622*σ |
| R2 = 99.5% | |
| 8 | 28.884 − 0.360*β + 0.645*σ |
| R2 = 99.9% | |
| 9 | 30.500 − 0.325*β + 0.579*σ |
| R2 = 99.1% | |
| 10 | 28.343 − 0.349*β + 0.670*σ |
| R2 = 99.9% |
| Slope Angle | Material 1 | Material 2 | Material 3 | Material 4 | Material 5 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | |
| 70 | 62.49 | 63.71 | 0.981 | 61.94 | 61.68 | 1.004 | 63.15 | 62.33 | 1.013 | 61.98 | 60.12 | 1.031 | 63.44 | 60.04 | 1.057 |
| 72 | 61.31 | 64.24 | 0.954 | 60.80 | 62.16 | 0.978 | 59.73 | 60.42 | 0.988 | 58.69 | 58.25 | 1.007 | 57.99 | 55.99 | 1.036 |
| 74 | 64.41 | 68.43 | 0.941 | 63.78 | 66.17 | 0.964 | 65.27 | 67.04 | 0.974 | 64.02 | 64.61 | 0.991 | 66.14 | 65.06 | 1.017 |
| 76 | 59.89 | 65.12 | 0.920 | 59.43 | 62.89 | 0.945 | 58.41 | 61.07 | 0.956 | 57.42 | 58.80 | 0.977 | 65.39 | 65.16 | 1.004 |
| 78 | 60.24 | 67.24 | 0.896 | 59.77 | 64.92 | 0.921 | 58.73 | 63.02 | 0.932 | 57.73 | 60.66 | 0.952 | 65.81 | 67.15 | 0.980 |
| 80 | 67.21 | 76.60 | 0.877 | 66.49 | 73.93 | 0.899 | 65.20 | 71.76 | 0.909 | 63.95 | 69.05 | 0.926 | 63.03 | 66.22 | 0.952 |
| 82 | 70.91 | 81.90 | 0.866 | 70.06 | 79.00 | 0.887 | 68.64 | 76.65 | 0.896 | 67.25 | 73.73 | 0.912 | 66.20 | 70.66 | 0.937 |
| 84 | 69.13 | 81.45 | 0.849 | 68.33 | 78.46 | 0.871 | 66.98 | 76.05 | 0.881 | 65.66 | 73.08 | 0.899 | 72.99 | 79.11 | 0.923 |
| 86 | 67.18 | 81.41 | 0.825 | 66.46 | 78.33 | 0.848 | 65.17 | 75.87 | 0.859 | 63.92 | 72.85 | 0.877 | 63.00 | 69.67 | 0.904 |
| 88 | 70.24 | 86.52 | 0.812 | 69.41 | 83.25 | 0.834 | 68.02 | 80.63 | 0.844 | 66.65 | 77.41 | 0.861 | 65.63 | 74.02 | 0.887 |
| Slope Angle | Material 6 | Material 7 | Material 8 | Material 9 | Material 10 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | τ (kPa) | σ (kPa) | FS | ττ (kPa) | σ (kPa) | FS | |
| 70 | 62.55 | 58.17 | 1.075 | 61.55 | 55.83 | 1.103 | 59.41 | 53.21 | 1.117 | 58.56 | 51.06 | 1.147 | 57.32 | 48.51 | 1.182 |
| 72 | 57.30 | 54.22 | 1.057 | 63.49 | 58.40 | 1.087 | 63.58 | 57.87 | 1.099 | 64.51 | 57.28 | 1.126 | 64.48 | 55.73 | 1.157 |
| 74 | 65.14 | 62.96 | 1.035 | 66.30 | 62.49 | 1.061 | 63.78 | 59.44 | 1.073 | 62.74 | 56.97 | 1.101 | 61.26 | 54.04 | 1.134 |
| 76 | 64.42 | 63.04 | 1.022 | 66.27 | 63.24 | 1.048 | 66.00 | 62.27 | 1.060 | 64.86 | 59.65 | 1.087 | 64.92 | 58.09 | 1.118 |
| 78 | 67.38 | 67.52 | 0.998 | 66.16 | 64.62 | 1.024 | 65.33 | 63.06 | 1.036 | 64.22 | 60.39 | 1.064 | 62.67 | 57.23 | 1.095 |
| 80 | 62.15 | 63.99 | 0.971 | 61.18 | 61.23 | 0.999 | 59.06 | 58.11 | 1.016 | 58.23 | 55.63 | 1.047 | 66.44 | 61.46 | 1.081 |
| 82 | 65.20 | 68.25 | 0.955 | 64.09 | 65.27 | 0.982 | 61.75 | 61.88 | 0.998 | 60.79 | 59.19 | 1.027 | 59.43 | 56.04 | 1.060 |
| 84 | 71.73 | 76.39 | 0.939 | 70.32 | 73.02 | 0.963 | 67.48 | 69.18 | 0.975 | 66.28 | 66.14 | 1.002 | 64.61 | 62.57 | 1.033 |
| 86 | 70.16 | 75.98 | 0.923 | 68.82 | 72.55 | 0.949 | 72.60 | 75.53 | 0.961 | 74.28 | 78.95 | 0.941 | 69.24 | 68.28 | 1.014 |
| 88 | 64.65 | 71.35 | 0.906 | 63.56 | 68.07 | 0.934 | 69.25 | 72.93 | 0.950 | 73.63 | 75.52 | 0.975 | 71.55 | 71.41 | 1.002 |
| Material Number | Shear Strength (kPa) |
|---|---|
| 1 | 54.625 − 0.714 *β + 0.911 *σ |
| R2 = 99.8% | |
| 2 | 52.408 − 0.660 *β + 0.906 *σ |
| R2 = 99.8% | |
| 3 | 51.614 − 0.650 *β + 0.916 *σ |
| R2 = 99.8% | |
| 4 | 49.580 − 0.606 *β + 0.913 *σ |
| R2 = 99.8% | |
| 5 | 49.891 − 0.645 *β + 0.980 *σ |
| R2 = 99.6% | |
| 6 | 49.295 − 0.631 *β + 0.992 *σ |
| R2 = 99.7% | |
| 7 | 48.733 − 0.598 *β + 0.988 *σ |
| R2 = 99.5% | |
| 8 | 47.371 − 0.573 *β + 0.990 *σ |
| R2 = 99.8% | |
| 9 | 46.726 − 0.432 *β + 0.841 *σ |
| R2 = 98.6% | |
| 10 | 46.128 − 0.550 *β + 1.036 *σ |
| R2 = 99.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khan, M.I.; Wang, S. Slope Stability Analysis to Correlate Shear Strength with Slope Angle and Shear Stress by Considering Saturated and Unsaturated Seismic Conditions. Appl. Sci. 2021, 11, 4568. https://doi.org/10.3390/app11104568
Khan MI, Wang S. Slope Stability Analysis to Correlate Shear Strength with Slope Angle and Shear Stress by Considering Saturated and Unsaturated Seismic Conditions. Applied Sciences. 2021; 11(10):4568. https://doi.org/10.3390/app11104568
Chicago/Turabian StyleKhan, Muhammad Israr, and Shuhong Wang. 2021. "Slope Stability Analysis to Correlate Shear Strength with Slope Angle and Shear Stress by Considering Saturated and Unsaturated Seismic Conditions" Applied Sciences 11, no. 10: 4568. https://doi.org/10.3390/app11104568
APA StyleKhan, M. I., & Wang, S. (2021). Slope Stability Analysis to Correlate Shear Strength with Slope Angle and Shear Stress by Considering Saturated and Unsaturated Seismic Conditions. Applied Sciences, 11(10), 4568. https://doi.org/10.3390/app11104568






