Influence of Wind Power on Modeling of Bidding Strategy in a Promising Power Market with a Modified Gravitational Search Algorithm

Abstract

It is expected that large-scale producers of wind energy will become dominant players in the future electricity market. However, wind power output is irregular in nature and it is subjected to numerous fluctuations. Due to the effect on the production of wind power, producing a detailed bidding strategy is becoming more complicated in the industry. Therefore, in view of these uncertainties, a competitive bidding approach in a pool-based day-ahead energy marketplace is formulated in this paper for traditional generation with wind power utilities. The profit of the generating utility is optimized by the modified gravitational search algorithm, and the Weibull distribution function is employed to represent the stochastic properties of wind speed profile. The method proposed is being investigated and simplified for the IEEE-30 and IEEE-57 frameworks. The results were compared with the results obtained with other optimization methods to validate the approach.

1. Introduction

Nowadays, the electric industries are reforming and implementing a deregulated business policy, which generates competition among power trading firms. The electric companies are more concerned with profit maximization in this dynamic electricity market. The electric utility companies have engaged in competitive bidding in order to achieve a strong profit margin. The benefit of electricity producing companies is fully reliant on the price of marginal cost (MCP), playing an important role in the dynamic energy market. The value of MCP is determined by the system operator (SO) using curves of supply and demand. To calculate the value of the next unit of power produced, MCP uses the process used in market clearing strategy [1]. A feasible approach to the optimum bidding problem can be achieved by using this mechanism. Renewable electricity sources, such as wind energy, have been an inseparable component of the current power grid. In contrast to other non-renewable energy sources, wind energy sources are an option prior to power generation. Due to the unpredictability of this renewable energy supply, several restrictions exist in the market in support of power dealings [2]. The key objective of this situation is to create a bidding approach representation for optimizing the benefit of producing utilities in a deregulated setting, using a single-sided bidding setup. The effect of the wind source on the bidding model is being investigated using uncertainty modelling.

First, in a restructured power market setting, for traditional power traders, the optimum bidding problem was solved with the help of a complex programming approach [3]. Furthermore, for the purpose of resolving power sector bidding strategy considering variables that influence the bidding strategy challenge, such as generation costs, market restrictions, and competitor bidding behavior, many researchers have used numerous mathematical approaches, e.g., Monte Carlo simulation [4], particle swarm optimization algorithms (PSO) [5], genetic algorithms (GA) [6], bat inspired techniques [7], krill herd algorithms (KHA) [8], gravitational search algorithms [9], etc. In the above-mentioned works, the action of competitors is first explained using the normal probability distribution function (PDF), followed by the solution of the benefit maximization problem. Moreover, the issue was only addressed for traditional power sources.

In open bidding procedures, traditional renewable generation (RES) companies participate in the bidding procedures. In the deregulated electric industry, it ensures market fairness and improved RES use [10]. Of all forms of renewable energy sources, the most popular source of renewable energy is wind because of its low cost, and the use of wind energy is rapidly increasing these days [11]. The development of strategic bidding when considering the involvement of wind power suppliers has been the subject of extensive research. The biggest drawback of wind energy generation is the unpredictability and volatility of wind speed, which always results in deviations from the actual power output in real time [12]. The existence of volatility makes bidding more difficult for market participants in the restructured energy marketplace [13]. There has been a concerted effort in previous decades to address issues that have arisen in the field of wind energy sources in a global environment. The bidding issue is solved, with the aim of minimizing running costs by only considering wind sources [10,11,12,13], whereas the problem has been addressed with RESs for dispatching and scheduling of generating services by taking into account the overestimation and underestimation costs that are correlated with RE production surpluses and shortfalls [14,15]. Uncertain wind power generation raises the cost of imbalance and the fines that come with wind turbines. As a result, income for wind energy providers is reduced. Therefore, accurate wind power modelling is needed to reduce the uncertainty and maximize benefit [16].

According to the literature review, there are many optimization strategies that can be applied to the issue of bidding approach and optimize supplier benefit. Heuristic optimization techniques such as the particle swarm optimization algorithm (PSO) [5], genetic algorithm (GA) [6], bat inspired technique (BIT) [7], krill herd algorithm (KHA) [8], gravitational search algorithm [9] have main limitations in their sensitivity to the choice of parameters, such as the inertia weight and learning factors in PSO, crossover and mutation probabilities in GA, the requirement of parameter tuning, a poor control strategy the and lack of exploration capability in BIT, poor exploitation capability in KHM, and population initialization in GSA.

Tuning of parameters determines the effectiveness of heuristic tailored strategies. The methods with fewer parameters tuned have the highest precision. Thereby, Rashedi et al. [17] propose a new heuristic solution a called gravitational search algorithm (GSA) that focuses on the gravitational law and mass exchanges. GSA is based on Newton’s theorem, which states that any particle in the space attracts every other particle with a force equal to the product of their masses and inversely proportional to the square of their separation. Moreover, GSA is straightforward, scalable, and fast to adopt as compared to other evolutionary methods, and it can also find global optimal solutions. However, GSA has the downside of premature convergence, which will greatly reduce the algorithm’s global search ability, and hence GSA’s performance needs to be improved. In [18], Tizhoosh proposed the principle of opposition-based learning (OBL). The key theory behind OBL is to consider estimation and its inverse estimate (i.e., guess and opposite guess) at the same time in order to improve the calculation for the current candidate explanation. The population initialization in GSA is random, and the operation approach with various parameters is also random. Convergence can be reached easily when the guess made at random is not that far off the desired outcome. On the other hand, the random guess could be far from the best outcome. This bad scenario will result in more time spent looking for the best solution, or, in the worst-case scenario, a non-optimal solution. Without possessing some prior knowledge of the case, it is difficult to make the right initial estimate. Therefore, the method should logically be searching at all potential alternatives or, to be more precise, it should also search in the opposite direction. Therefore, the OBL has been used to speed up the convergence rate of the GSA in this article. As a result, our suggested method is known as the opposition-based gravitational search algorithm (OGSA).

Is it possible to integrate the opposite number concept during population initialization as well as the generation of new populations during the GSA evolutionary phase described in [17]? Is it possible to draw a rational conclusion based on the proposed algorithm’s performance on a set of power system optimization problems, such as strategic bidding? In light of the above, the aim of this study is to test the proposed algorithm’s optimizing efficiency on some real-world power system optimization problems, such as the solution of strategic bidding for optimizing generating utilities’ benefit in a dynamic electricity sector. To optimize benefit value for generating utilities, a considered bidding technique is devised that includes wind power. In order to quantify the total benefit, a composite market clearing price for traditional and wind power supplies is taken into account. An actual modeling of wind uncertainty was developed using Weibull pdf in order to reduce forecasted error while retaining the benefit. Furthermore, the wind power probabilities were normalized to represent real-world scenarios. In addition, the Weibull pdf provided wind power scenarios are reduced using the forward-reduction algorithm. To calculate the anomalies of wind power, cost functions for underestimation and overestimation were used. The proposed bidding model is tested on IEEE-30 and 57 bus test systems, respectively, and is solved using OGSA. The procedure is clearly applicable in this regard and appropriate due to its effectiveness. The rest of the paper is presented as follows: Section 2 describes the statistical modeling of bidding strategy problem; methods and materials are given in Section 3; Section 4 presents the main results and the discussion of them; finally, the main conclusions are given in Section 5.

2. Statistical Modeling of Bidding Strategy Problem

It is supposed that every power supplier (PS) is needed to send a bid to POOL as a non-decreasing linear supply feature in a single-sided POOL-based energy market, and the running cost function of any generating unit is given by Equation (1)

$$P{C}_m(P{g}_m)=a_{m}P{g}_m+b_{m}P{g}_m^2$$

(1)

where: m is the number of PS; bid constraints of the mth PS are $a_m$ and $b_m$; and $P{g}_m$ is the real power quantity of the mth PS.

In a single-side bid model, the mth PS is submit the linear supply bid function which is non-decreasing according to Equation (2),

$$C{P}_m(P{g}_m)={\pi }_m+{\varphi }_{m}P{g}_m,m=1,2,\dots \dots ,\mathrm{CPS}$$

(2)

where ${\pi }_m$ and ${\varphi }_m$ are bid parameters that are required to be non-negative.

If the PS offers have been completed and submitted to ISO, the ISO compares the power supply with the overall demand of the system. After the matching, ISO decided the market clearing price (MCP) and cleared the marketplace. The bid function, power balance constraint, and power inequality constraint of the mth PS are given by Equations (3)–(5).

$${\pi }_m+{\varphi }_{m}P{g}_m=R$$

(3)

$${\displaystyle \sum _{m=1}^{cps}P{g}_m+{\displaystyle \sum _{n=1}^{wg}W{g}_n}=Q(R)}$$

(4)

$$P{g}_{\min ,\mathrm{m}}\le P{g}_m\le P{g}_{\max ,\mathrm{m}}$$

(5)

where: $W{g}_n$ is the forecasted wind power generation output for bidding in MW, n is the number of wind power suppliers, $P{g}_{\min ,\mathrm{m}}$ and $P{g}_{\max ,\mathrm{m}}$ are the minimum and maximum active power generation by the mth power supplier, the MCP is R, and the projected load by the market operator is $Q(R)$. It is assumed that $Q(R)$ is given by Equation (6)

$$Q(R)=L_c-K\ast R$$

(6)

where: $L_c$ is constant; K = 0 is non-negative load price elasticity.

For deciding MCP and calculation of the amount of bid power, ISO considered Equations (3) and (4) and ignored Equation (5). The MCP and amount of bid power are calculated by Equations (7) and (8), respectively.

$$R=\frac{L_c-{\displaystyle \sum _{n=1}^{wg}W{g}_n}+{\displaystyle \sum _{m=1}^{cps}\frac{{\pi }_m}{{\varphi }_m}}}{k+{\displaystyle \sum _{m=1}^{cps}\frac{1}{{\varphi }_m}}}$$

(7)

$$P{g}_m=\frac{R-{\pi }_m}{{\varphi }_m}$$

(8)

If the amount of bid power in Equation (8) exceeds its limits, it will be fixed by Equation (5).

After the calculation of MCP and the amount of bid power, the profit of the mth PS can be calculated. Therefore, in this work, the main objective is to increase the earnings of the mth PS in the presence of renewable PS according to Equation (9)

$$\mathrm{Maximize}:F({\pi }_m,{\varphi }_m)=R\times P{g}_m-P{C}_m(P{g}_m)+R\times W{g}_n-IMC(W{g}_n)$$

(9)

Here, $IMC(W{g}_n)$ is the imbalance cost related to wind power in USD/MW.

The cost function of all thermal generating utilities is given by Equation (1). The underestimation and overestimation costs make up the running costs of an mth wind power generation utility. Due to its intermittent existence, wind sources are susceptible to both overestimation and underestimation. The expenditure task of wind power suppliers is given by Equation (10):

$$IMC(W{g}_n)=O_c(w_g)+U_c(w_g)$$

(10)

where, $O_c(w_g)$ and $U_c(w_g)$ are the overestimation and underestimation cost related to wind power in USD.

The penalty cost for overestimation is represented by the first term, and the penalty cost for underestimation is represented by the second term, which are given by Equations (11) and (12):

$$O_c(w_g)=K_o\ast {\displaystyle \underset{0}{\overset{W_g}{\int }}(W_g-W_a)\ast f_{W_a}}(W_a)\ast d{W}_a$$

(11)

where $K_o$ is the penalty coefficient for overestimating power.

$$U_c(w_g)=K_u\ast {\displaystyle \underset{W_g}{\overset{W_{\max }}{\int }}(W_a-W_g)\ast f_{W_a}}(W_a)\ast d{W}_a$$

(12)

where $K_u$ is a fine for the lack of situational advantages per USD/kWh owing to underestimation of the capacity.

3. Methods for Solving Proposed Bidding Strategy

This section is provided the different methods that are utilized to solve the proposed bidding strategy. Section 3.1 gives the probabilistic modeling of interrelated bidding coefficients behavior. Section 3.2 and Section 3.3 are provided the uncertainty modeling of the wind power source. In Section 3.4 is presented the OGSA technique for the solution of the proposed bidding strategy.

3.1. Probabilistic Strategy

Generally, in the sealed bidding process, the bidding information is kept confidential, but bidding information of previous bidding processes can be obtained. In the light of this information, PS’s can guess about the market clearing and estimate the MCP. Therefore, each PS tries to guess the bidding method and behaviour of other suppliers. However, they face the problems when they try to guess the behaviour of the rival. Due to the interrelation of bid parameters, PS’s used the joint probability distribution function (PDF) according to Equation (13) for guessing the behaviour of the rival.

$$\begin{array}{l}\mathrm{pdf}({\pi }_m,{\varphi }_m)=\frac{1}{{2\pi \sigma }_m{}^{\left(\pi \right)}{\sigma }_m{}^{\left(\varphi \right)}\sqrt{{1-\rho }_m^2}}\times \exp \{-\frac{1}{2\left({1-\rho }_m^2\right)}\\ [{\left(\frac{{\pi }_m{-\mu }_m^{\left(\pi \right)}}{{\sigma }_m^{\left(\pi \right)}}\right)}^2+\left(\frac{{\varphi }_m{-\mu }_m^{\left(\varphi \right)}}{{\sigma }_m^{\left(\varphi \right)}}\right)-\frac{{2\rho }_m\left({\pi }_m{-\mu }_m{}^{\left(\pi \right)}\right)\left({\varphi }_m{-\mu }_m{}^{\left(\varphi \right)}\right)}{{\sigma }_m^{\left(\pi \right)}{\sigma }_m^{\left(\varphi \right)}}]\}\end{array}$$

(13)

This PDF can be displayed in a compact form by Equation (11)

$$({\pi }_m,{\varphi }_m)\sim N\{\left[\begin{array}{c}{\mu }_m^{(\pi )}\\ {\mu }_m^{(\varphi )}\end{array}\right],\left[\begin{array}{cc}{({\sigma }_m^{(\pi )})}^2& {\rho }_m{\sigma }_m^{(\pi )}{\sigma }_m^{(\varphi )}\\ {\rho }_m{\sigma }_m^{(\pi )}{\sigma }_m^{(\varphi )}& {({\sigma }_m^{(\varphi )})}^2\end{array}\right]\}$$

(14)

Here, the collective distribution parameters are ${\mu }_m^{(\pi )}$, ${\mu }_m^{(\varphi )}$, ${\sigma }_m^{(\pi )}$ and ${\sigma }_m^{(\varphi )}$, the coefficient of correlation between ${\pi }_m$ and ${\varphi }_m$ is ${\rho }_m$. ${\mu }_m^{(\pi )}$ and ${\mu }_m^{(\varphi )}$ are the mean and ${\sigma }_m^{(\pi )}$ and ${\sigma }_m^{(\varphi )}$ are the standard deviations of the ${\pi }_m$ and ${\varphi }_m$, respectively.

3.2. Modeling of Wind Energy Sources

Given the existence of wind, to contend with fair bidding, the instability associated with wind speed needs to be handled. Instability with wind speed is usually represented by utilizing a two-parametric function called Weibull PDF. The meanings are given by Equation (15):

$$W_{pdf}=\frac{k}{c}{\left(\frac{v}{c}\right)}^{\left(k-1\right)}\left(exp{\left(-\frac{v}{c}\right)}^k\right)$$

(15)

where: k and c are the shape and scale factors, respectively; v is the wind speed in meters per second. These parametric standards can be estimated using the known mean $\left({\mu }_{hws}\right)$ and standard deviation $\left({\sigma }_{std}\right)$ by Equations (16) and (17)

$$k={\left(\frac{{\sigma }_{std}}{{\mu }_{hws}}\right)}^{\left(-1.086\right)}$$

(16)

$$c=\left(\frac{{\mu }_{hws}}{\Gamma \left(1+\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$k$}\right.\right)\right)}\right)$$

(17)

Diverse scenarios are produced by utilizing wind velocity data, which are collected from anemometers. Anemometers are used to measured wind speed in selected wind farm locations at different heights. To analyse similar patterns, first, 1000 scenarios are generated randomly using the Weibull distribution, which are further changed into corresponding power scenarios to adequate hub heights. In certain cases, the heights of the center and the anemometers are not equivalent. In these conditions, the wind speed is estimated by Equation (18)

$$v\left(h_{est}\right)=v\left(h_{rkh}\right){\left(\frac{h_g}{h_{kah}}\right)}^{\left(\gamma \right)}$$

(18)

where: $v\left(h_{est}\right)$ is estimated wind speed at an appropriate turbine hub height; $v\left(h_{rkh}\right)$ is traced wind speed at acknowledged hub altitudes; $h_g$ is generator wind turbine base height (m); $h_{kah}$ is anemometer in place height; and $\gamma$ is the shear coefficient parameter governing the irregularity and environment circumstance of the surface.

The measured wind velocities are changed into wind energy with the wind turbine energy curve. The energy curve is a relationship between wind speed and wind power given by Equation (19)

$$W_a\left(v\right)=\{\begin{array}{ll}0& v\le v_{in}\\ \frac{1}{2}{\eta }_p\left(v\right)\rho A_s{v}^3 & v_{in}\le v\le v_r\\ W_r& v_r\le v\le v_o\\ 0& v\ge v_o\end{array}$$

(19)

where ${\eta }_p\left(v\right)$, $W_r$ and $W_a\left(v\right)$ are efficiency, rated output and available power at a given wind speed of wind producers, respectively; $\rho$ is the air density (kg/m³); $A_s$ is the swept field of a wind turbine’s rotor. Additionally, $v_{in}$, $v_r$ and $v_o$ are the cut in, rated and cut out wind speed limits.

The produced inconsistent wind energy can be integrated into the distribution by means of the power curve to predict the likelihood of wind power in a range of working zones.

Linear wind output probability can be defined as

$$f_w\left(v_{in}\le v\le v_r\right)=\left(\frac{kz{v}_{in}}{c{W}_r}\right)\left[\frac{(1+z{W}_a/W_r)v_{in}}{c}\right]\times \left\{-{\left[\frac{(1+z{W}_a/W_r)v_{in}}{c}\right]}^k\right\}$$

(20)

where $z=\frac{\left(v_r-v_{in}\right)}{v_{in}}$

The probability of zero wind production can be given by Equation (21)

$$f_w\left[(v\le v_{in})\mathrm{and}(v\ge v_o)\right]=1-\exp \left[-{\left(\frac{v_{in}}{c}\right)}^k\right]+\exp \left[-{\left(\frac{v_o}{c}\right)}^k\right]$$

(21)

Finally, the rated wind output probability is calculated by Equation (22)

$$f_w{(v}_r\le v\le v_o)=\exp \left[-{\left(\frac{v_r}{c}\right)}^k\right]+\exp \left[-{\left(\frac{v_o}{c}\right)}^k\right]$$

(22)

3.3. Characterization of Uncertainty of Wind

There are 1000 wind scenarios formed. However, the possibility of some events may be extremely low. In addition, the odds of some situations may be the same. Subsequently, scrutinizing the scenarios is necessary to achieve a substantial smaller number of scenarios, while showing outstanding scenarios of lesser and the same possibility. The diminution will be such that it does not change the stochastic properties. The number of decreased scenarios builds upon the form and complexity of the difficulty to be optimized and should be concentrated to or below one-quarter of the possibilities produced [19].

The Kantorovich Distance Matrix (KDM) is employed for the scenario reduction [19]. KDM is based on the difference between the Euclidian possibilities and their related probabilities. It reduces the nearest and lowest-probability scenarios. The following steps are employed to measure the KD matrix.

Step I: For every case, measure the Euclidian distance to other imaginable circumstances. Of any two separate possibilities ${\upsilon }^i$ and ${\upsilon }^j$, the distance is calculated by Equation (23)

$$KD\left({\upsilon }^i,{\upsilon }^j\right)={\left({\displaystyle \sum _{l=0}^{{\eta }_l}{\left(v_l^i-v_l^j\right)}^2}\right)}^{\frac{1}{2}}$$

(23)

Step II: Locate the nearest minimum detachment $\min \left\{KD\left({\upsilon }^i,{\upsilon }^j\right)\right\}$ for each possibility ${\upsilon }^i$ to the possibility ${\upsilon }^j,\mathrm{j}\ne \mathrm{i}$.

Step III: Reproduce or multiply with corresponding probability obtained in Step II.

$$\min \left\{KD\left({\upsilon }^i,{\upsilon }^j\right)\right\}\times P\left[{\upsilon }^i\right]$$

(24)

Step IV: Reduce the smallest gap and the least possible scenario. Then, apply the likelihood of the eliminated scenario to the next closest scenario.

Step V: Complete Steps II–IV again until the criterion of stoppage has been reached.

KDM is utilized to obtain the expected wind $(W_g)$ energy, and the correct probability is determined by Equation (25)

$$W_g={\displaystyle \sum _{i=1}^{{\upsilon }_i}{W}_{ai}\times {\mathrm{prob}}_i}$$

(25)

where ${\mathrm{prob}}_i$ is the possibility of decreased ith generated scenario.

3.4. Oppositional Gravitational Search Algorithm

Authors proposed a new heuristic solution GSA to solve non-differentiable and non-linear optimization problems in [17]. Each driving force in GSA offers a healthier approach to the difficulty. In the shape of a flowchart, Figure 1 shows the solution protocol.

3.4.1. Population Initialization

Given a structure consisting of N agents (masses), the kth agent place can be defined by Equation (26)

$${\lambda }_k=({\lambda }_k^1,\dots \dots ,{\lambda }_k^D,\dots \dots ,{\lambda }_k^M)\mathrm{For}k=1,2,\dots \dots ,N$$

(26)

where: ${\lambda }_k^D\in [L_k^D,U_k^D]$, $D=1,2\dots \dots ,M,$ is the kth agent place in the Dth aspect; M is the aspect of the search space; $L_k^D,U_k^D$ are the lesser limit and higher bound limits of kth agents in the Dth aspect.

3.4.2. Modification in GSA

The theory of opposition-based learning was defined by Tizhoosh [18]. The author took into account both the current and conflicting agents in sequence to provide a clearer estimate of the contemporary representative result. In comparison to random agent solutions, it is inferred that a conflicting agent has healthier optimal solutions. The positions of the conflicting agent $(O{\lambda }_k)$ are fully established by the components of ${\lambda }_k$ according to Equation (27)

$$O{\lambda }_k=[O{\lambda }_k^1,\dots \dots ,O{\lambda }_k^D,\dots \dots ,O{\lambda }_k^M]$$

(27)

where $O{\lambda }_k^D=L_k^D+U_k^D-{\lambda }_k^D$ with $O{\lambda }_k^D\in [L_k^D,U_k^D]$ is the kth opposite location of the agent in the Dth aspect of the oppositional community

3.4.3. Fitness Function

The best solution of Equation (9) is used as the fitness purpose in this case. When OGSA begins an iterative procedure, a combined inhabitant $\{\lambda ,O\lambda \}$ is created, where it meets all of the constraints. From the created current population $\{\lambda ,O\lambda \}$, assortment strategies are used to pick the N number of most fitting agents $\lambda$ according to Equation (28).

$${\lambda }_k(i)=\{\begin{array}{l}\begin{array}{ccc}O{\lambda }_k(i) & if & fit(O{\lambda }_k(i)>fit({\lambda }_k(i))\end{array}\\ \begin{array}{cc}{\lambda }_k(i) & otherwise\end{array}\end{array}$$

(28)

The algorithm judges the power of an agent and its opposing agent at the same time. The agent with the higher fitness score is used for further calculations, while the additional agent is useless.

3.4.4. Agents Acceleration

The strength assessment is used in GSA to determine each agent’s mass. The mass of each agent is intended as follows:

$$M_k(i)=\frac{m_k(i)}{{\displaystyle \sum _{l=1}^N{m}_l(i)}}$$

(29)

being $m_k(i)=\frac{fi{t}_k(i)-worst(i)}{best(i)-worst(i)}$

where: $M_k(i)$ is the normalized mass of kth agent at the ith iteration; $worst(i)$, $best(i)$ are the worst and best fitness of all agents, respectively, at the ith iteration. The acceleration $a_k^D(i)$ acting on the kth agent at iteration i is evaluated by Equation (30)

$$a_k^D(i)={\displaystyle \sum _{\begin{array}{l}l\in Gbest,\\ l\ne k\end{array}}\begin{array}{cc}ran{d}_l& G(i)\frac{M_k(i)}{R_{kl}(i)+E}({\lambda }_l^D(i)-{\lambda }_l^D(i))\end{array}}$$

(30)

where: the position of the first 2% of agents is $Gbest$ with the best assessment of fitness; extreme mass $ran{d}_l$ is the standardized random number between interval [0, 1]; $R_{kl}(i)$ is the Euclidean detachment linking two agents kth and lth at the ith iteration; $E$ is a diminutive optimistic constant. The gravitational function G(j) is communicated by Equation (31)

$$G(i)=G\times \left(1-\frac{iteration}{\begin{array}{cc}Total& iteration\end{array}}\right)$$

(31)

being $G=c\underset{D\in \{1,2,\dots \dots ,M\}}{\max }\left(|{\lambda }_U^D-{\lambda }_L^D|\right)$, and c is exploration limitation.

3.4.5. Position and Velocity Updating of the Agents

The location and velocity of the agents are determined by Equation (30) in the next (i + 1) iteration.

$$\{\begin{array}{c}{v}_k^D(i+1)=ran{d}_k\times v_k^D(i)+a_k^D(i)\\ {\lambda }_k^D(i+1)={\lambda }_k^D(i)+v_k^D(i+1)\end{array}$$

(32)

where $ran{d}_k$ is a random number linking space [0, 1]; $v_k^D(i)$ is the velocity of kth agent at Dth aspect during the ith iteration; ${\lambda }_k^D(i)$ is the location of kth agent at the Dth aspect during the ith iteration.

3.4.6. Solution Process of OGSA

The following are the key steps of the OGSA for the bidding strategy problem:

• Set the parameters of the proposed OGSA and the input data of the considered test systems for the bidding strategy.
• Create an initial population $\lambda$ as random for ${\varphi }_m$ in the interval between [$b_m$, $M\times b_m$], and value of M is assumed to be 10.
• Calculate the market clearing price and dispatch for each generating unit.
• Calculate each generator’s benefit after setting power generation limits and balancing the system load.
• Create opposite population $O\lambda$. Therefore, determine the market clearing price and dispatch for each generating unit.
• Calculate each generator’s benefit after setting power generation limits and balancing the system load.
• Assess the fitness function for both random and oppositional populations.
• As the actual population, choose the N most fitting agents from the current and opposing populations.
• Calculate the mass of each agent as well as the gravitational constant.
• Determine the acceleration of agents.
• Update the agent’s velocity and location, respectively.
• Proceed to Step 3 if the full number of iterations has not been reached; otherwise, the process should be terminated and the best bidding technique printed.

4. Results and Discussion

The IEEE- 30 bus [16] and IEEE-57 bus [16] have been used to model the bidding strategy in an emerging power market. The load demands for 30-bus and 57-bus networks are 500 and 1500 MW, respectively. The bidding technique is first devised on a standard evaluation bus scheme. Second, it is analyzed using an updated framework that takes into account one renewable energy source, wind power, with a capacity of 200 MW. The suggested strategy was tested in a MATLAB R-2014a environment with 4 GB of RAM and an i5 Core Processor. The OGSA is put to the test with a search agent that prefers 1000 iterations. The number of individual runs was set to one hundred.

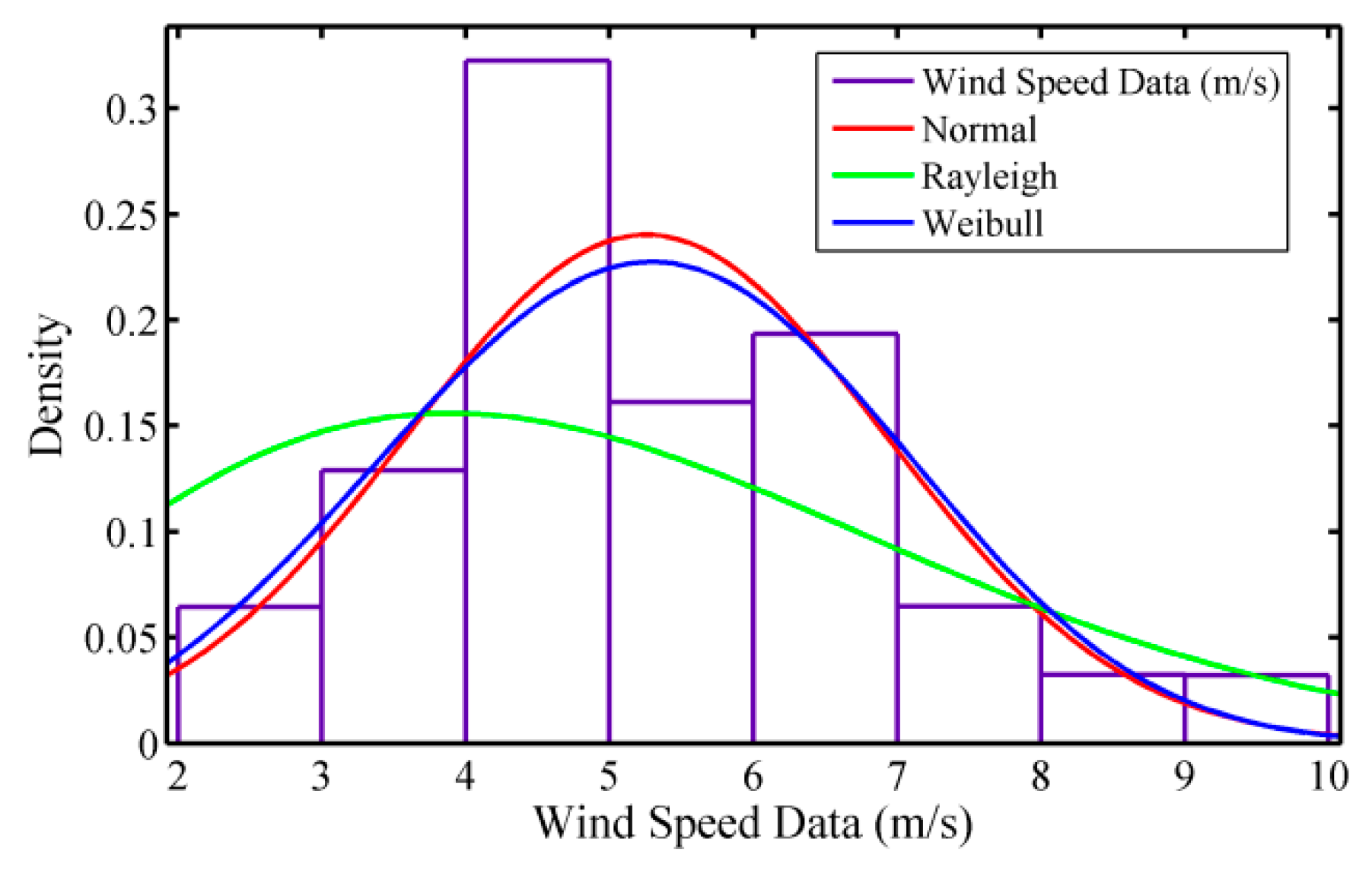
An average wind speed for 1 (12:00–13:00) hour in August 2005 in Barnstable city, USA [20], was used to estimate renewable wind supply, with a hub height of 39 m. In this proposed work, the average wind speed capacity curve for a VENSIS-100 wind turbine with 2.50 MW and 100 m hub height [21] was used to calculate wind power. The density of the air was 1.242 kg/m². Using past data of a specified wind speed, demonstration of wind speed is possible with various potential PDFs (Normal, Weibull, and Rayleigh), as seen in Figure 2, and the Weibull PDF is considered to be the most suitable since the statistics are better suited to the distribution, as seen in

Table 1. Variance, mean, and log likelihood values for different probability distribution functions of wind speed.

	Rayleigh PDF	Weibull PDF	Normal PDF
Variance	6.4984	2.84011	2.7568
Mean	4.87676	5.25439	5.25484
Log Likelihood	−65.3438	−59.1945	−59.2052

. The shape and scale parameters for 100 m hub height were found to be 3.49 and 8.13, respectively, and are given in

Table 2. Parameters values of wind speed.

Height of Hub	k	c (m/s)
39 m	3.49	5.84
100 m	3.49	8.13

, having calculated the mean and variance of the wind speed.

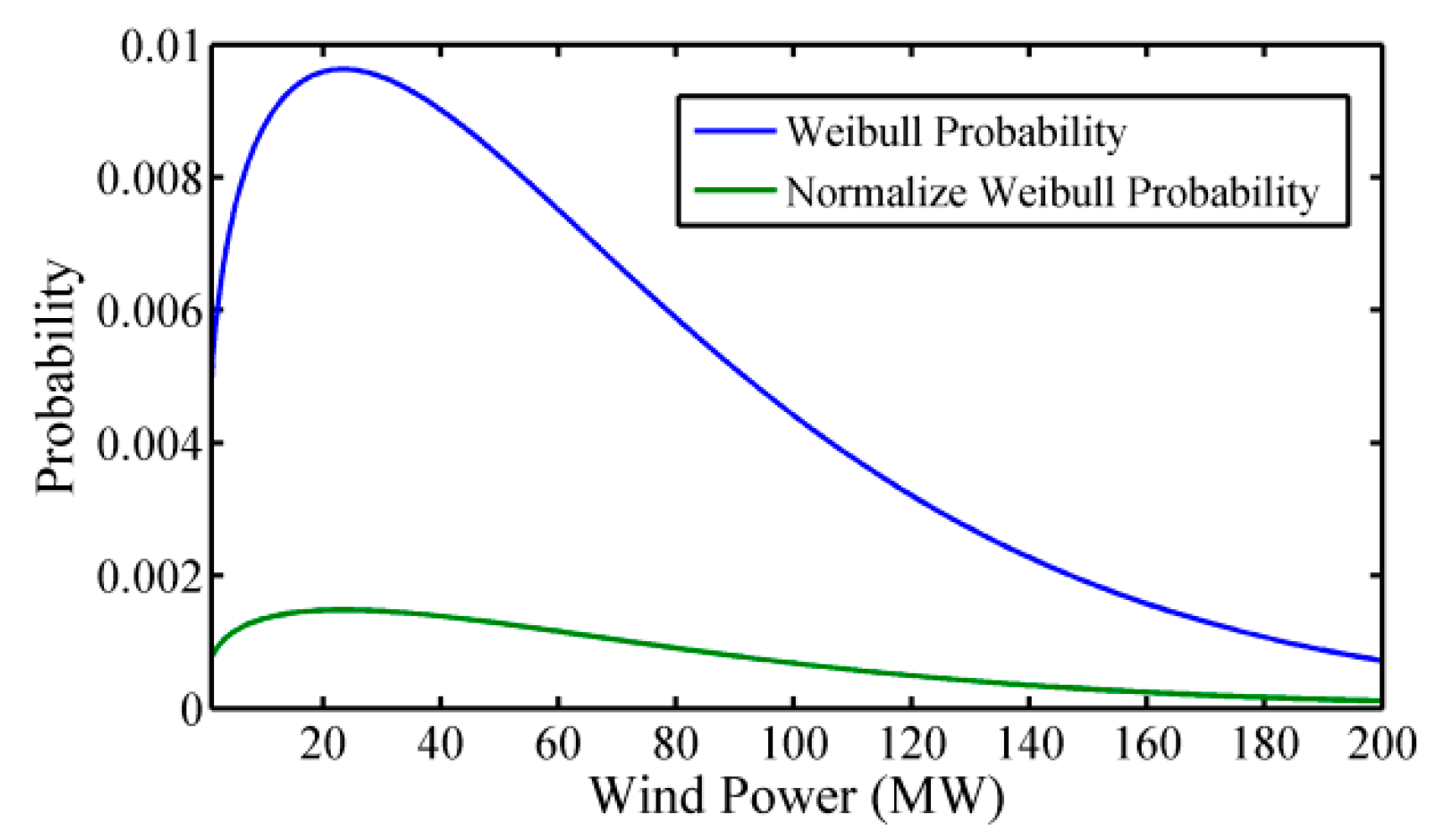
For precision, 1000 wind speed scenarios were developed and translated to power scenarios at the appropriate hub height. Weibull probability densities for the generated power scenarios are shown in Figure 3. Following scenario generation, scenario reduction was carried out using the likelihood distance method known as the Kantorovich distance [19] to construct a wind power model that takes into account uncertainty. Initially, 1000 scenarios were developed, from which 10 reduced scenarios were derived using likelihood distance [19].

Table 3. Power outputs of wind and their cooresponding probabilities for a smaller number of 10 scenarios.

Concentrated Scenario	Wind Power (MW)	Probability of Incidence
1	10.56	0.142
2	28.65	0.283
3	54.86	0.325
4	81.43	0.144
5	103.5	0.049
6	121.7	0.029
7	136.7	0.013
8	155.8	0.01
9	178.3	0.002
10	191.2	0.002

shows the associated diminished scenario performance as well as the likelihood of its occurrence. Equation (25) is used to calculate the possible wind power from this decreased situation, which is 51.95 MW.

For the first case, input data of the IEEE 30-bus system were taken from reference [16]. In a dynamic power market, bidding criteria are primarily used to develop bidding strategies. As a result, it is measured with the help of a joint PDF (Equation (13)) and optimized by the proposed OGSA methodology. For generating utilities, these bidding coefficients cannot be chosen individually in order to maximize profits. Therefore, each utility was given ${\pi }_m$ of bidding, and ${\varphi }_m$ is estimated using OGSA in the range (b_m, 10b_m). Then, using the optimized bidding parameters, MCP is calculated. The net benefit of generating electricity and overall power dispatch for this case is estimated using the calculated MCP.

Table 4. Optimal bidding results for the IEEE standard 30-bus without including wind power.

PSs	${\mathit{\pi }}_{\mathit{m}}$	GA [22]			PSO [23]			GSA [16]			OGSA
		${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit
1	2.0	0.044090	160	1592.4	0.042666	160	1645.73	0.049231	160	1815.32	0.049984	160	1848.47
2	1.75	0.19429	75.05	712.19	0.211031	74.81	735.14	0.224134	77.45	839.65	0.223528	78.68	867.49
3	1.0	0.300167	57.94	459.54	0.436374	49.28	433.95	0.722945	40.95	425.33	0.680919	42.5	446.15
4	3.25	0.094465	100	846.85	0.103585	100	880.18	0.097653	100	986.18	0.099466	100	1006.9
5	3.0	0.280553	53.50	439.52	0.275273	57.95	488.96	0.289934	60.80	573.06	0.307913	59.41	574.36
6	3.0	0.280553	53.50	439.52	0.275273	57.95	488.96	0.289934	60.80	573.06	0.307913	59.41	574.36
MCP		12.55			12.89			13.9458			14.15
Profit		4490.02			4672.93			5212.6			5317.72
Total PG		500			500			500			500

summarizes the results of various optimization techniques, such as OGA, GSA [16], GA [22], and PSO [23]. In addition to other strategies, Table 4 indicates that the overall benefit of the method has risen to USD 5317.72 for OGSA. As opposed to MCP prices of USD 12.55/MW, USD 12.89/MW, and USD 13.94/MW achieved by GA, PSO and GSA, the market is now open at MCP value USD 14.15/MW by OGSA, which is the largest value. As a result, the proposed OGSA methodology outperforms the algorithms described above.

To determine the impact of RESs on the bidding strategy model, wind energy was studied along with thermal power plants. Due to the presence of alternative energy sources, the MO modifies the current demand of the system by eliminating wind power generation. The MCP value and bidding parameters are adapted for the adjusted system demand for wind. The cost of a wind energy source is measured by taking into account the uncertainty of the source.

The coefficients k_o and k_u were taken from reference [16] to calculate the cost of overestimation and underestimation.

Table 5. Optimal bidding outcomes with wind power for the IEEE standard 30-bus.

PSs	${\mathit{\pi }}_{\mathit{m}}$	GA [22]			PSO [23]			GSA [16]			OGSA
		${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit
1	2.0	0.043369	160	1429.56	0.048167	160	1464.98	0.049575	160	1572.05	0.049242	160	1632.5
2	1.75	0.195359	63.36	549.71	0.197386	61.51	549.30	0.215113	59.69	574.8	0.189561	70.19	689.57
3	1.0	0.561368	32.04	273.38	0.596858	28.84	258.24	0.453362	35.26	325.15	0.647421	30.11	298.72
4	3.25	0.088848	100	745.08	0.084439	100	767.22	0.104385	97.96	818.8	0.109269	99.31	866.43
5	3.0	0.258245	46.32	341.72	0.230275	48.85	368.05	0.251243	47.57	391.8	0.303061	44.22	384.64
6	3.0	0.258245	46.32	341.72	0.230275	48.85	368.05	0.251243	47.57	391.8	0.303061	44.22	384.64
MCP		11.53			11.76			12.4253			12.80
Total Profit for TPS		3681.16			3775.86			4074.4			4256.5
Total PG for TPS		448.05			448.05			448.05			448.05
$Wg$		51.95			51.95			51.95			51.95
$O_c(w_g)$		38.1026			38.8627			41.0612			42.2995
$U_c(w_g)$		335.4122			342.1030			361.4568			372.3570
$IMC(W{g}_n)$		373.5148			380.9656			402.5180			414.6565
Profit for WPS		225.4687			229.9664			242.9763			250.3035

shows the optimal strategic bidding outcomes using GSA [16], GA [22], PSO [23], and OGSA on the standard test scheme with wind power. OGSA outperforms the other algorithms in this case as well. Table 5 shows that MCP in the presence of a wind source is USD 12.80/MW. This MCP value is lower than the previous value of USD 14.15/MW obtained from Table 4, which was calculated using OGSA without a wind source. The MCP, net benefit for TPS, and WPS using OGSA are USD 12.80/MW, USD 4256.5, and USD 250.3035, respectively. Table 5 shows that when, wind energy is taken into account, the amount of electricity that needs to be dispatched from thermal generation sources decreased to 448.05 MW. Taking into account the uncertainty, the cost of a wind supply is estimated to be USD 414.6565. Since the cost of overestimation USD 42.2995 is smaller than the cost of underestimation USD 372.3570, utilities that have wind energy sources would be allowed to compete for more electricity.

After that, the usefulness of the suggested technique was put to the test on a standard IEEE 57-bus system. The data for the IEEE-57 bus system used were taken from reference [16]. The bidding strategy was simulated with and without a wind source. In this case, the MCP is determined first in a dynamic power market using an optimal bidding parameter. The net benefit of generating electricity, as well as the dispatching of overall capacity, are then calculated and input into

Table 6. Optimal bidding results for the IEEE standard 57-bus without including wind power.

PSs	${\mathit{\pi }}_{\mathit{m}}$	GA [22]			PSO [23]			GSA [16]			OGSA
		${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit
1	1.7365	0.019718	530.23	5065.65	0.020393	520.21	5058.66	0.021819	510.26	5238.34	0.022239	505.16	5241.2
2	10	0.095015	23.07	45.23	0.098836	23.73	50.02	0.092598	30.99	79.34	0.076760	38.7	99.99
3	7.1429	0.078495	64.32	295.35	0.082602	62.98	299.48	0.081198	70.53	368.62	0.088860	65.58	351.7
4	10	0.095015	23.07	45.23	0.098836	23.73	50.02	0.092598	30.99	79.34	0.076760	38.7	99.99
5	1.8	0.020843	498.08	4724.32	0.021487	490.3	4732.82	0.02278	485.52	4945.47	0.023240	480.23	4944.7
6	10	0.095015	23.07	45.23	0.098836	23.73	50.02	0.092598	30.99	79.34	0.076760	38.7	99.99
7	2.4390	0.028839	338.18	3023.63	0.02788	355.3	3216.81	0.030615	340.71	3275.32	0.031635	332.92	3240.2
MCP		12.19			12.35			12.87			12.97
Total Profit		13,244.65			13,457.81			14,065.79			14,077.77
Total PG		1500			1500			1500			1500

. Table 6 shows that the demand finished at an MCP value of USD 12.97/MW, generating utilities benefit is USD 14,077.77 when using OGSA without wind, which are the largest as compared to GSA [16], GA [22], and PSO [23].

When a wind supplier is included in the IEEE 57-bus system to model a bidding plan, SO modifies the current demand of the system by subtracting wind power output from real demand. Changed demand is used to calculate bidding coefficients and MCP value. The cost of a wind energy source is determined by estimating overestimation and underestimation costs.

Table 7. Optimal bidding outcomes with wind power for the IEEE standard 57-bus.

PSs	${\mathit{\pi }}_{\mathit{m}}$	GA [22]			PSO [23]			GSA [16]			OGSA
		${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit	${\mathit{\varphi }}_{\mathit{m}}$	PG	Profit
1	1.7365	0.020926	481.97	4466.11	0.022242	460.8	4367.64	0.021140	503.3	4923.36	0.021315	510.02	5102.39
2	10	0.093054	19.58	31.85	0.085062	23.34	40.90	0.095375	24.9	52.94	0.118167	22.07	52.68
3	7.1429	0.055503	84.31	344.03	0.070490	68.70	299.17	0.089745	58.3	280.91	0.086831	62.94	315.82
4	10	0.093054	19.58	31.85	0.085062	23.34	40.90	0.095375	24.9	52.94	0.118167	22.07	52.68
5	1.81	0.021983	455.45	4186.68	0.020178	504.3	4573.59	0.021931	481.7	4671.9	0.023482	459.83	4584.5
6	10	0.093054	19.58	31.85	0.085062	23.24	40.90	0.09375	24.9	52.94	0.118167	22.07	52.68
7	2.4390	0.025527	367.57	3124.72	0.027791	344.3	344.26	0.030105	330.1	3017.93	0.029132	349.05	3257.04
MCP		11.82			11.99			12.38			12.61
Total Profit for TPS		12,217.07			12,459.12			13,052.93			13,417.84
Total PG for TPS		1448.05			1448.05			1448.05			1448.05
$Wg$ (MW)		51.95			51.95			51.95			51.95
$O_c(w_g)$		39.0609			39.6227			40.9115			41.6716
$U_c(w_g)$		343.8484			348.7938			360.1390			366.8298
$IMC(W{g}_n)$		382.9093			388.4165			401.0505			408.5014
Profit for WPS		231.1397			234.4640			242.0905			246.5881

shows that, when the wind power is mixed with thermal power, the MCP value drops to USD 12.61 per MW, relative to USD 12.97 per MW without wind power and the corresponding net benefits for TPS and WPS using OGSA are USD 13,417.84, and USD 246.5881, respectively. Moreover, the estimated overestimation expense is USD 48.78, which is less than the underestimation cost of USD 356.54 for wind. It is evident from Table 7 that OGSA provides better results for the IEEE 57-bus system compared to GSA [16], GA [22], and PSO [23].

Findings for IEEE 30- and 57-buses indicates that inclusion of the wind energy in the bidding process has a significant impact on MCP, individual generation dispatch, and complete generation dispatch for conventional power supplies. The utilization of wind power reduces the MCP, thus benefiting the traditional generators. Moreover, when KDM is involved for handling uncertainty related to wind power, overestimation of uncertainty is much lower than underestimation of wind power generation. If the underestimation is positive, this would enable wind power providers to bid the extra power into the real-time market. Furthermore, the bidding strategy proposed in this paper by utilizing OGSA is better suited to obtaining power suppliers’ profits in comparison to the GSA [16], GA [22], and PSO [23] techniques.

Through comparing simulation outcomes with GSA, PSO and GA, the superiority of the OGSA algorithm is shown. The success of evolutionary algorithms cannot be judged by the outcome of a single run due to their randomness. To draw a clear conclusion about the success of the algorithms, several trials with various initializations should be run. It should be noted that an algorithm is only called stable if it can provide suitable results under a variety of operating conditions, since the algorithms OGSA, GSA, PSO, and GA are all random. Therefore, for each method, the bidding data were run 20 times.

Table 8. Comparative analysis of the results of various techniques for robustness of the OGSA method for IEEE standard 30-bus and 57-bus.

Takings	IEEE 30-Bus				IEEE 57-Bus
	GA [22]	PSO [23]	GSA [16]	OGSA	GA [22]	PSO [23]	GSA [16]	OGSA
Best	4490.02	4672.93	5212.59	5317.719	13,244.65	13,457.81	14,065.79	14,077.77
Worst	3941.41	4253.56	4798.86	4944.638	11,448.63	12,009	12,982.51	13,212.03
Mean	4187.19	4395.08	4944.70	5046.50	11,927.7	12,509.51	13,446.45	13,590.17
SD	155.87	124.91	109.75	94.66	415.5907	386.71	350.59	262.77

provides a comparative analysis of the results of various techniques for robustness and validation of the OGSA method. It can be deduced that the standard deviation is lowest for the OGSA technique in comparison to others for the IEEE 30-bus and IEEE 57-bus methods, respectively. Moreover, OGSA produces better outcomes in terms of best, worst, and mean. Therefore, the accuracy of the proposed method is better and allows producers to earn a higher profit by utilizing OGSA. According to the result analysis, the OGSA technique is more effective, accurate, and modeling the bidding technique is possible for the IEEE30-bus and IEEE 57-bus systems, respectively.

Discussion

This research focuses solely on bidding techniques that combined renewable energy sources while minimizing the uncertainties and disadvantages associated with wind energy. In addition, a statistical model for calculating the market clearing price (MCP) in the presence of wind energy sources is proposed. The Weibull distribution of probability is used to tackle wind speed uncertainties, which are then converted into wind power. Furthermore, the KDM process is used to reduce the number of wind power measurements. Moreover, the variability of renewable energy is calculated in terms of overestimation and underestimation. This task is accomplished using the OGSA optimization technique. The model and method introduced in this study provide a comprehensive approach to investigating the issue of supplier profit maximization. These protocols can assist electricity market participants in successful implementation of bidding policies and maximization of their individual profits by enhancing their strategic advantage in electricity markets.

5. Conclusions

This research presents a novel OGSA to model the best bidding approach in a dynamic energy market, taking into account the renewable energy sources and market constraints. The exploration and exploitation phases of the above optimization algorithm are modified by properly adapting them. The proposed OGSA methodology is put to the test using certain common benchmark functions in order to equate its results to that of other techniques, being the most superior one for the current business strategy shifts scenario. Furthermore, the uncertainties of the wind source are modelled using the Weibull distribution function. The bidding plan is planned with and without wind power. Normal PDF is used to find the benefit maximization of each utility when taking into account the information of competitors. The effect of wind energy on bidding strategies lowers thermal power generation and lowers the market clearing price. For the IEEE 30-bus and IEEE 57-bus systems, optimal bidding strategies have been developed. When compared to GA, PSO, and GSA techniques, the proposed OGSA technique produces the best results in terms of accuracy and viability for optimizing the benefit of the generation utilities. While the algorithms have the potential to incorporate certain regulatory limitations, the theoretical implementation has been based primarily on a price-driven economic competition model. The theory and algorithm demonstrated how a provider could decide the rates at which a given volume of generation could be offered to the grid system, taking into account competitor prediction behaviour, wind power volatility, and planned system specifications. Allowances for variability in these variables were successfully included, which is a key aspect of the model. Furthermore, the current work only considers symmetrical information, allowing the ith supplier’s conclusions about the jth, and vice versa, to be symmetrical. For further studies we will extend this study for unsymmetrical information, because this model is not appropriate for unsymmetrical details, which helps some suppliers to make better estimates than others.