Long-Term Numerical Analysis of Subsurface Delamination Detection in Concrete Slabs via Infrared Thermography
Abstract
1. Introduction
2. Experimental Section
2.1. Concrete Sample
2.2. Infrared Thermography Measurements
3. Finite Element Method (FEM)
3.1. Heat Transfer Theory
3.2. Material Properties
3.3. Boundary Conditions
3.4. Development of the FEM Model
4. Results and Discussion
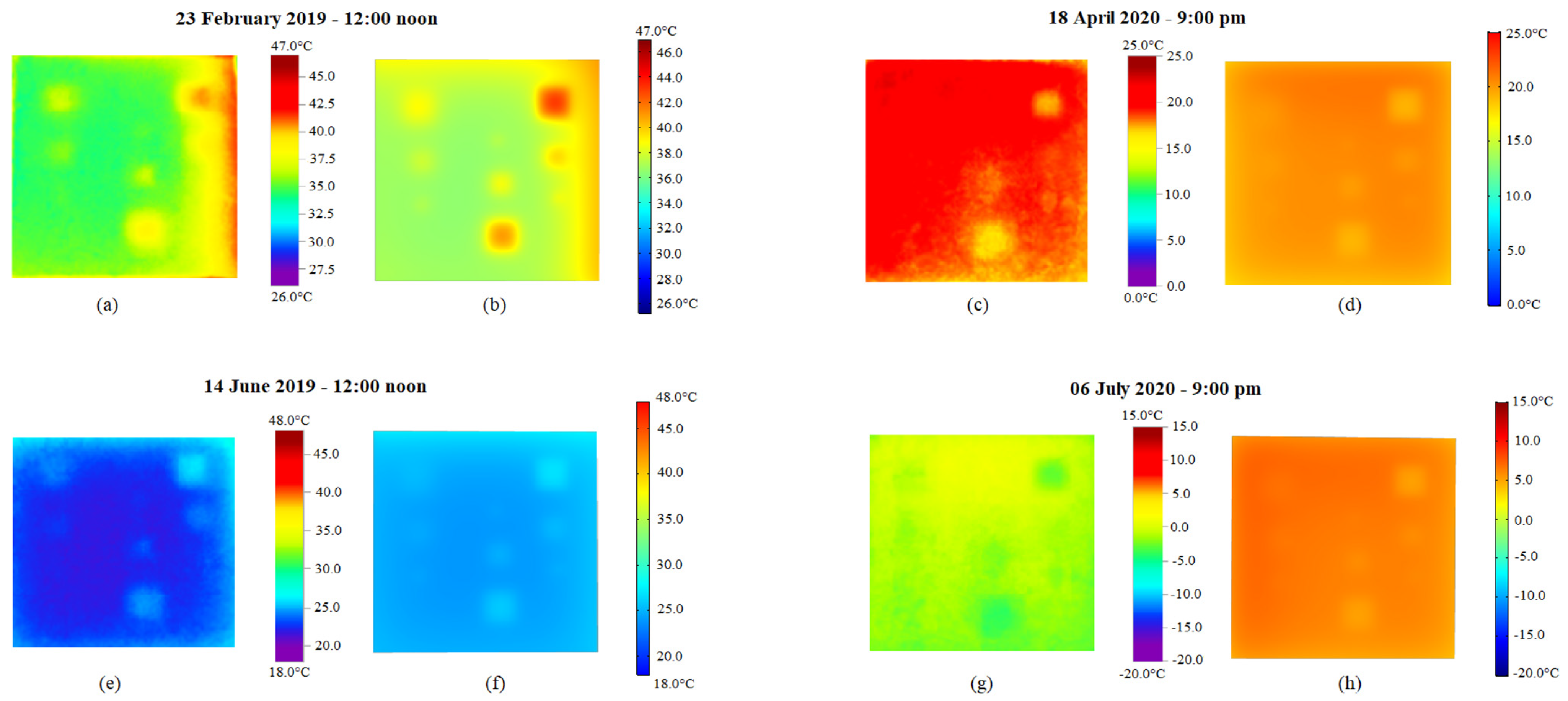
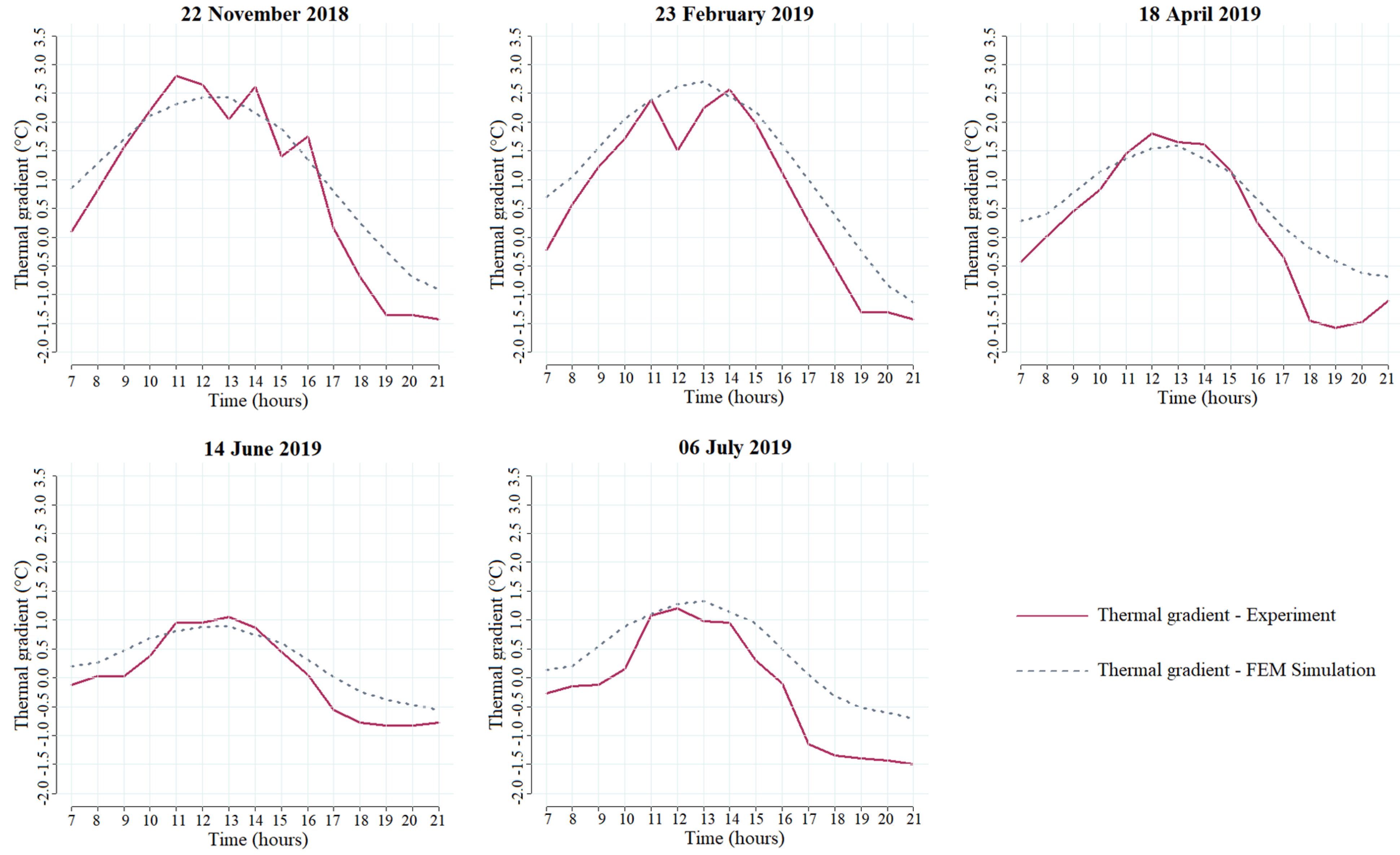
4.1. Comparison of Experimental and Simulated Results
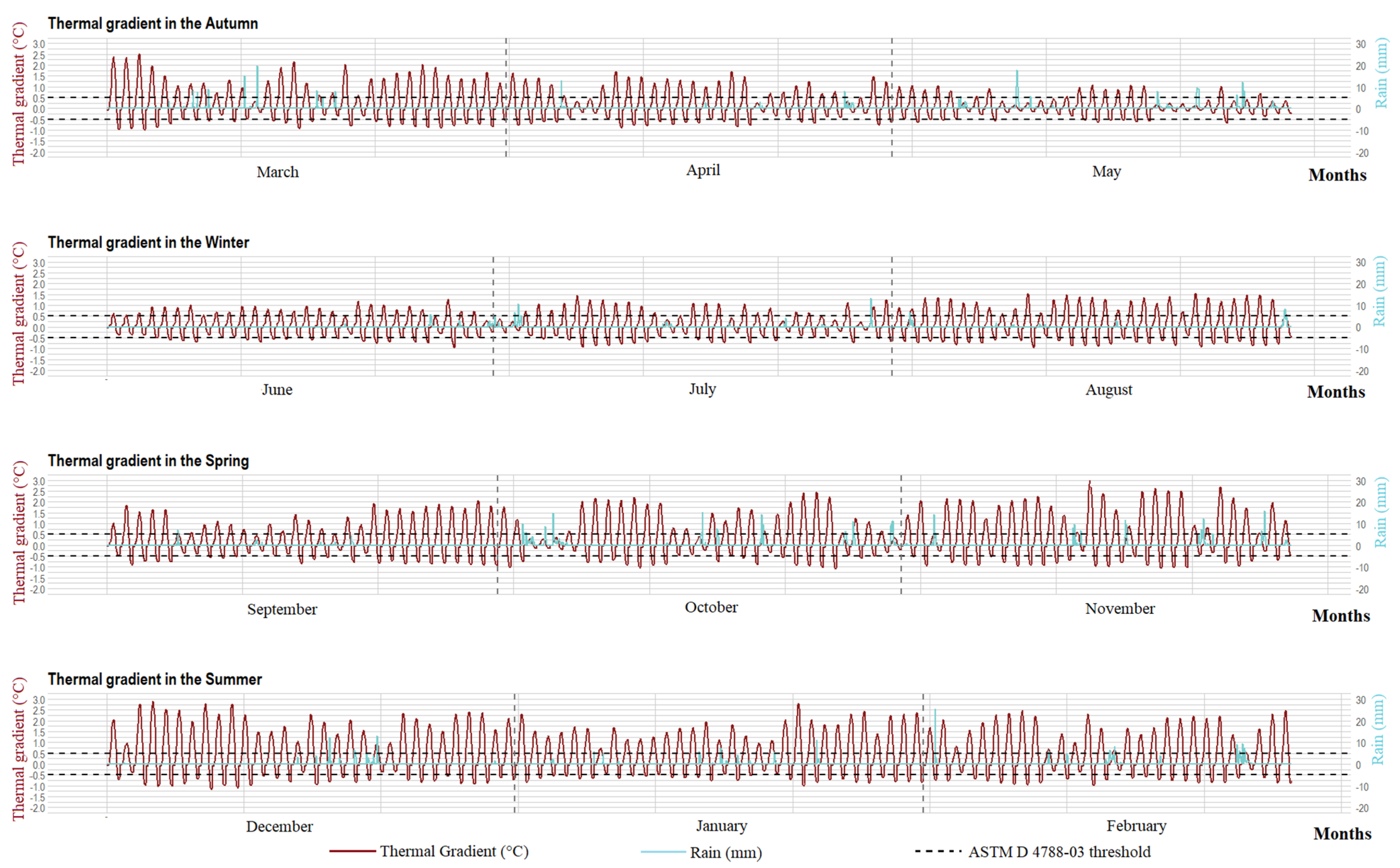
4.2. Discussion on Appropriate Periods for IRT Inspection of Concrete Bridge Slabs Based on Long-Term Fem Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- American Road and Transportation Builders Association (ARTBA). “Bridge Report. 2020”. 2020. Available online: https://artbabridgereport.org/ (accessed on 14 October 2020).
- HAQ, G.; Ortega Hortelano, A.; Tsakalidis, A.; Gkoumas, K.; Pekár, F.; Balen, M.; Grosso, M.; Marques Dos Santos, F.L. Research and Innovation in Bridge. Maintenance, Inspection and Monitoring: A European Perspective Based on the Transport. Research and Innovation Monitoring and Information System (TRIMIS); EUR 29650 EN.; Publications Office of the European Union: Luxembourg, 2019. [Google Scholar]
- Oliveira, C.B.L.; Greco, M.; Bittencourt, T.N. Analysis of the brazilian federal bridge inventory. Rev. IBRACON Estrut. Mater. 2019, 12, 1–3. [Google Scholar] [CrossRef]
- European Commission. “Discussion Paper-State of Infrastructure Maintenance”. 2019. Available online: https://ec.europa.eu/growth/sectors/construction/observatory (accessed on 4 October 2020).
- Garrido, I.; Lagüela, S.; Otero, R.; Arias, P. Thermographic methodologies used in infrastructure inspection: A review—data acquisition procedures. Infrared Phys. Technol. 2020, 111, 103481. [Google Scholar] [CrossRef]
- Chang, P.C.; Liu, S.C. Recent Research in Nondestructive Evaluation of Civil Infrastructures. J. Mater. Civ. Eng. 2003, 15, 298–304. [Google Scholar] [CrossRef]
- Zinno, R.; Artese, S.; Clausi, G.; Magarò, F.; Meduri, S.; Miceli, A.; Venneri, A. Structural Health Monitoring (SHM). In The Internet of Things for Smart Urban Ecosystems; Cicirelli, F., Guerrieri, A., Mastroianni, C., Spezzano, G., Vinci, A., Eds.; Springer International Publishing: Cham, Switzerland, 2019; pp. 225–249. [Google Scholar]
- Ibarra-Castanedo, C.; Sfarra, S.; Genest, M.; Maldague, X. Infrared Vision: Visual Inspection beyond the Visible Spectrum. In Integrated Imaging and Vision Techniques for Industrial Inspection: Advances and Applications; Liu, Z., Ukida, H., Ramuhalli, P., Niel, K., Eds.; Springer: Berlin, Germany, 2015; Volume 11, pp. 42–57. [Google Scholar]
- Maldague, X. Theory and Practice of Infrared Technology for Nondestructive Testing; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar]
- Maldague, X. Nondestructive Evaluation of Materials by Infrared Thermography, 1st ed.; Springer: London, UK, 1993. [Google Scholar]
- Gucunski, N.; Romero, R.; Kruschwitz, S.; Feldmann, R.; Parvardeh, H. Comprehensive Bridge Deck Deterioration Mapping of Nine Bridges by Nondestructive Evaluation Technologies; Final Report; Iowa Department of Transportation: Ames, IA, USA, 2011.
- Aggelis, D.; Kordatos, E.; Soulioti, D.; Matikas, T. Combined use of thermography and ultrasound for the characterization of subsurface cracks in concrete. Constr. Build. Mater. 2010, 24, 1888–1897. [Google Scholar] [CrossRef]
- Khan, F.; Bartoli, I. Detection of delamination in concrete slabs combining infrared thermography and impact echo techniques: A comparative experimental study. Struct. Health Monit. Insp. Adv. Mater. Aerosp. Civ. Infrastruct. 2015, 9437, 94370I. [Google Scholar] [CrossRef]
- Omar, T.; Nehdi, M.L. Remote sensing of concrete bridge decks using unmanned aerial vehicle infrared thermography. Autom. Constr. 2017, 83, 360–371. [Google Scholar] [CrossRef]
- Vaghefi, K.; Ahlborn, T.T.; Harris, D.K.; Brooks, C.N. Combined Imaging Technologies for Concrete Bridge Deck Condition Assessment. J. Perform. Constr. Facil. 2015, 29, 04014102. [Google Scholar] [CrossRef]
- Pozzer, S.; Azar, E.R.; Rosa, F.D.; Pravia, Z.M.C. Semantic Segmentation of Defects in Infrared Thermographic Images of Highly Damaged Concrete Structures. J. Perform. Constr. Facil. 2021, 35, 04020131. [Google Scholar] [CrossRef]
- McLaughlin, E.; Charron, N.; Narasimhan, S. Automated Defect Quantification in Concrete Bridges Using Robotics and Deep Learning. J. Comput. Civ. Eng. 2020, 34, 04020029. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Sfarra, S.; Klein, M.; Maldague, X. Solar loading thermography: Time-lapsed thermographic survey and advanced thermographic signal processing for the inspection of civil engineering and cultural heritage structures. Infrared Phys. Technol. 2017, 82, 56–74. [Google Scholar] [CrossRef]
- Yçengel, A.; Ghajar, A.J. Heat and Mass Transfer: Fundamentals & Applications, 5th ed.; McGraw Hill Education: New York, NY, USA, 2015. [Google Scholar]
- Kleinfeld, J.M. Applying FEA to Perform Heat Transfer Calculations to Increase the Utility of IR Thermography. In IR INFO; Kleinfeld Technical Services, Inc.: Bronx, NY, USA, 2002. [Google Scholar]
- Rodríguez, F.L.; Nicolau, V.D.P. Inverse heat transfer approach for IR image reconstruction: Application to thermal non-destructive evaluation. Appl. Therm. Eng. 2012, 33–34, 109–118. [Google Scholar] [CrossRef]
- Chowdhury, R.; Attanayaka, A.M.U.B.; Aktan, H.M. Heat Transfer Fundamentals Applicable to Infrared Thermography of Concrete Structures. AIP Conf. Proc. 2004, 700, 1042–1049. [Google Scholar] [CrossRef]
- Hiasa, S.; Birgul, R.; Matsumoto, M.; Catbas, F.N. Experimental and numerical studies for suitable infrared thermography implementation on concrete bridge decks. Measurement 2018, 121, 144–159. [Google Scholar] [CrossRef]
- Hiasa, S.; Birgul, R.; Catbas, F.N. Investigation of effective utilization of infrared thermography (IRT) through advanced finite element modeling. Constr. Build. Mater. 2017, 150, 295–309. [Google Scholar] [CrossRef]
- Cheng, T.-Y.; Sakagami, T.; Kubo, S. Determination of delamination depth in concrete structure based on inverse analysis of thermography data. SPIE Def. Secur. Sens. 2010, 7661, 76610E. [Google Scholar] [CrossRef]
- Belattar, S.; Rhazi, J.; El Ballouti, A. Non-destructive testing by infrared thermography of the void and honeycomb type defect in the concrete. Int. J. Microstruct. Mater. Prop. 2012, 7, 235. [Google Scholar] [CrossRef]
- Khan, F.; Bolhassani, M.; Kontsos, A.; Hamid, A.; Bartoli, I. Modeling and experimental implementation of infrared thermography on concrete masonry structures. Infrared Phys. Technol. 2015, 69, 228–237. [Google Scholar] [CrossRef]
- Belattar, S. The Finite Element Method and Infrared Thermography Applied to the Characterization of Defects in a Chimney Structure. Quant. Infrared Thermogr. Asia 2015. [Google Scholar] [CrossRef]
- Dragan, R.G.; Roșca, I.C.; Cazangiu, D.; Leonte, A.S. Thermal Response for a Reinforced Concrete Slab Analyzed with Active Infrared Thermography and Comsol Multiphysics. Appl. Mech. Mater. 2015, 760, 627–632. [Google Scholar] [CrossRef]
- Cotič, P.; Kolarič, D.; Bosiljkov, V.B.; Bosiljkov, V.; Jagličić, Z. Determination of the applicability and limits of void and delamination detection in concrete structures using infrared thermography. NDT E Int. 2015, 74, 87–93. [Google Scholar] [CrossRef]
- Naik, M.; Hegde, G.; Giri, L.I. Optimization of Infrared Thermography for Damage Detection in Concrete Structures Using Finite Element Modelling. In Recent Trends in Civil Engineering; Springer: Singapore, 2021; pp. 177–188. [Google Scholar]
- Rumbayan, R.; Washer, G.A. Modeling of Environmental Effects on Thermal Detection of Subsurface Damage in Concrete. Res. Nondestruct. Eval. 2014, 25, 235–252. [Google Scholar] [CrossRef]
- Güray, E.; Birgül, R. Determination of Favorable Time Window for Infrared Inspection by Numerical Simulation of Heat Propagation in Concrete. In Proceedings of the 3rd International Sustainable Buildings Symposium (ISBS 2017), Dubai, United Arab Emirates, 15–17 March 2017; Fırat, S., Kinuthia, J., Abu-Tair, A., Eds.; Springer International Publishing: Cham, Switzerland, 2018; Volume 7, pp. 577–591. [Google Scholar]
- Hiasa, S.; Birgul, R.; Catbas, F.N. A data processing methodology for infrared thermography images of concrete bridges. Comput. Struct. 2017, 190, 205–218. [Google Scholar] [CrossRef]
- Hiasa, S.; Birgul, R.; Catbas, F.N. Effect of Defect Size on Subsurface Defect Detectability and Defect Depth Estimation for Concrete Structures by Infrared Thermography. J. Nondestruct. Eval. 2017, 36, 57. [Google Scholar] [CrossRef]
- Vitório, J.A.P. Uma Contribuição ao Estudo da Avaliação da Segurança de Pontes Existentes. J. Nondestruct. Eval. 2017, 36, 1–21. [Google Scholar]
- Pozzer, S.; Pravia, Z.M.C.; Azar, E.R.; Rosa, F.D. Statistical analysis of favorable conditions for thermographic inspection of concrete slabs. J. Civ. Struct. Health Monit. 2020, 10, 609–626. [Google Scholar] [CrossRef]
- Watase, A.; Birgul, R.; Hiasa, S.; Matsumoto, M.; Mitani, K.; Catbas, F.N. Practical identification of favorable time windows for infrared thermography for concrete bridge evaluation. Constr. Build. Mater. 2015, 101, 1016–1030. [Google Scholar] [CrossRef]
- Raja, B.N.K.; Miramini, S.; Duffield, C.; Sofi, M.; Mendis, P.; Zhang, L. The influence of ambient environmental conditions in detecting bridge concrete deck delamination using infrared thermography (IRT). Struct. Control Health Monit. 2020, 27. [Google Scholar] [CrossRef]
- Washer, G.; Fenwick, R.; Bolleni, N. Effects of Solar Loading on Infrared Imaging of Subsurface Features in Concrete. J. Bridg. Eng. 2010, 15, 384–390. [Google Scholar] [CrossRef]
- INMET. Estação Meteorológica de Observação de Superfície Automática. Available online: https://tempo.inmet.gov.br/TabelaEstacoes/83914# (accessed on 14 August 2020).
- Sharples, S.; Charlesworth, P. Full-scale measurements of wind-induced convective heat transfer from a roof-mounted flat plate solar collector. Sol. Energy 1998, 62, 69–77. [Google Scholar] [CrossRef]
- COMSOL. Parasol and Solar Irradiation. 2019. Available online: https://www.comsol.com/model/sun-s-radiation-effect-on-two-coolers-placed-under-a-parasol-12825 (accessed on 10 October 2020).
- Gothäll, H. How to Inspect Your Mesh in COMSOL Multiphysics. COMSOL 2017. Available online: https://www.comsol.com/blogs/how-to-inspect-your-mesh-in-comsol-multiphysics/ (accessed on 21 September 2020).
- Urquhart, B.; Ghonima, M.; Nguyen, D.; Kurtz, B.; Chow, C.W.; Kleissl, J. Chapter 9-Sky-Imaging Systems for Short-Term Forecasting. In Solar Energy Forecasting and Resource Assessment; Kleissl, J., Ed.; Academic Press: Boston, MA, USA, 2013; pp. 195–232. [Google Scholar]
- American Society for Testing and Materials. ASTM D4788–03: Standard Test Method for Detecting Delaminations in Bridge Decks Using Infrared Thermography; American Society for Testing and Materials: West Conshohocken, PA, USA, 2013. [Google Scholar]
- Al Gharawi, M.; Adu-Gyamfi, Y.; Washer, G. A framework for automated time-lapse thermography data processing. Constr. Build. Mater. 2019, 227, 116507. [Google Scholar] [CrossRef]
- Ibarra-Castanedo, C.; Khodayar, F.; Klein, M.; Sfarra, S.; Maldague, X.; Helal, H.; Tayoubi, M.; Marini, B.; Barré, J.C. Infrared vision for artwork and cultural heritage NDE studies: Principles and case studies. Insight Non-Destr. Test. Cond. Monit. 2017, 59, 243–248. [Google Scholar] [CrossRef]
- Omar, T.; Nehdi, M.L. Condition Assessment of Reinforced Concrete Bridges: Current Practice and Research Challenges. Infrastructures 2018, 3, 36. [Google Scholar] [CrossRef]
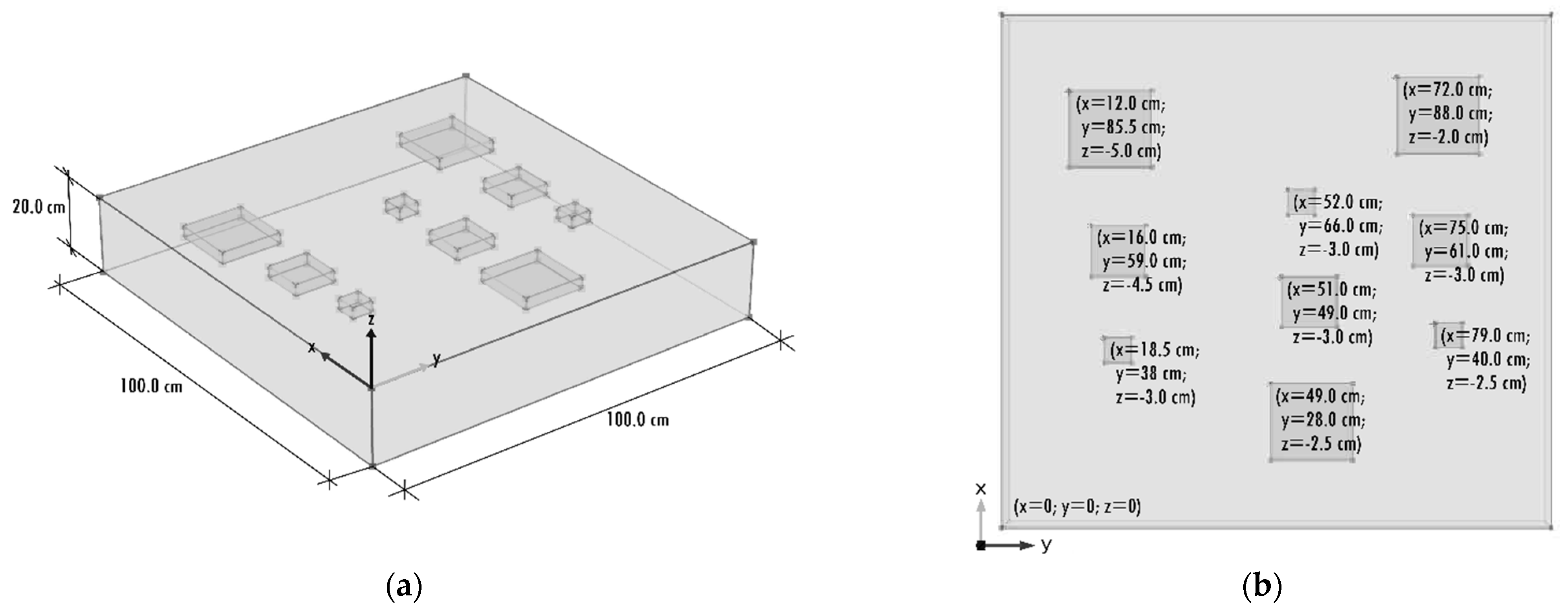

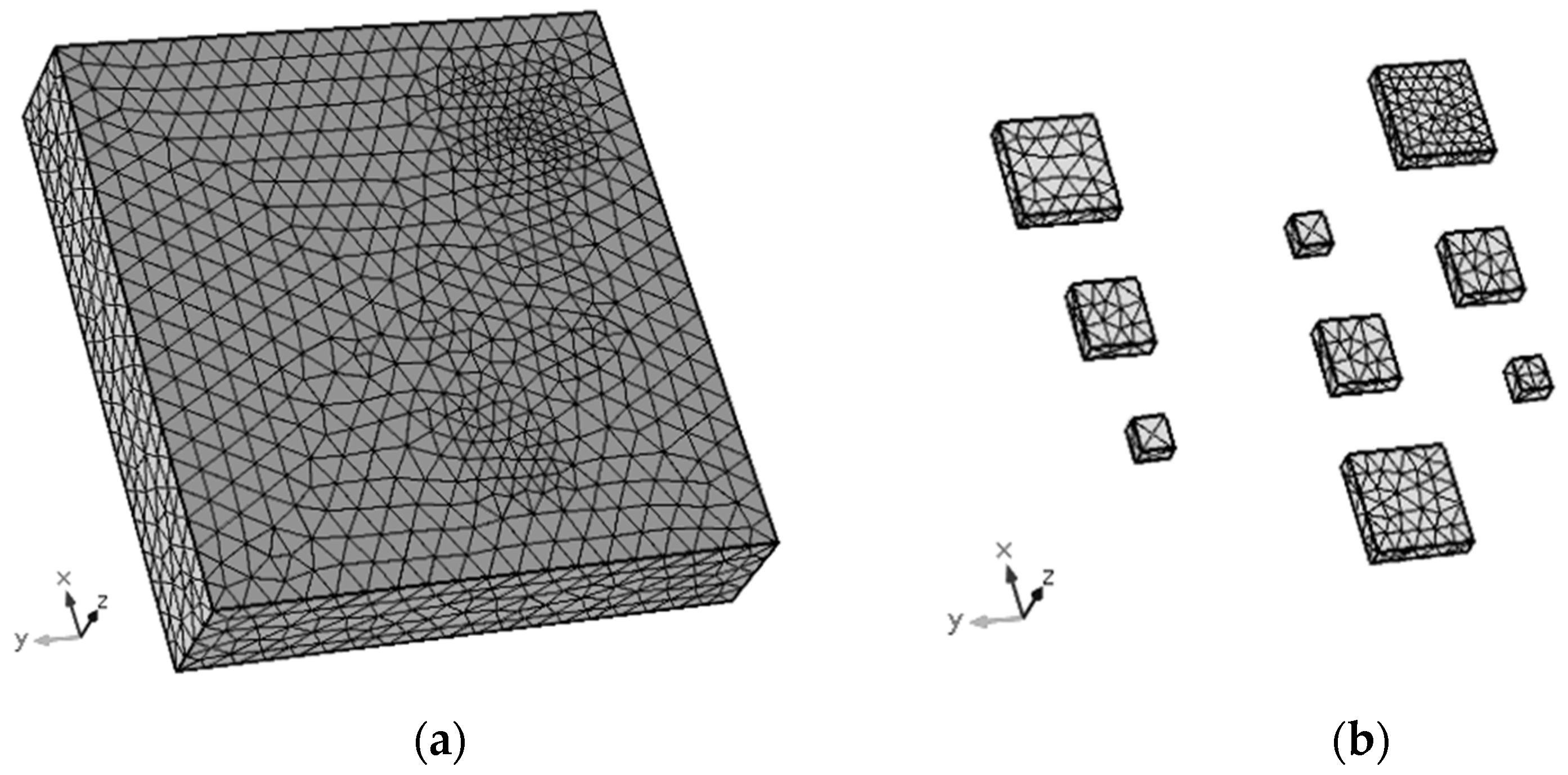


| Month | Day of Inspection | Duration of the Inspection | Solar Radiation (W/m²·s) | Wind Speed (m/s) | Average Temperature (°C) | Half Diurnal Temperature Variation (°C) |
|---|---|---|---|---|---|---|
| November | 22 November 2018 | 7 h to 21 h | 574.02 | 3.21 | 23.95 | 6.90 |
| February | 23 February 2019 | 7 h to 21 h | 524.14 | 1.30 | 27.00 | 8.85 |
| April | 18 April 2019 | 7 h to 21 h | 464.19 | 1.71 | 17.55 | 5.80 |
| June | 14 June 2019 | 7 h to 21 h | 276.48 | 2.85 | 20.28 | 5.60 |
| July | 06 July 2019 | 7 h to 21 h | 408.58 | 1.38 | 3.81 | 6.35 |
| Material Properties | Unit of Measure | Concrete | Styrofoam |
|---|---|---|---|
| Density | kg/m³ | 2400 | 25 |
| Specific heat | J/(kg·K) | 1008 | 1130 |
| Thermal conductivity | W/(m·K) | Temperature dependent | 0.027 |
| Emissivity | - | 0.9 | - |
| Experiment | Healthy Area Temperature | Damaged Area Temperature | Thermal Gradient | ||||||
|---|---|---|---|---|---|---|---|---|---|
| R | MBE (°C) | MAE (°C) | R | MBE (°C) | MAE (°C) | R | MBE (°C) | MAE (°C) | |
| 22 November 2018 | 0.98 | 0.02 | 3.07 | 0.98 | 0.31 | 3.37 | 0.97 | 0.29 | 0.51 |
| 23 February 2019 | 0.97 | 0.20 | 2.17 | 0.97 | 0.63 | 2.46 | 0.97 | 0.48 | 0.51 |
| 18 April 2019 | 0.99 | −0.93 | 4.21 | 0.99 | −0.55 | 4.36 | 0.98 | 0.38 | 0.47 |
| 14 June 2019 | 0.96 | 2.51 | 2.78 | 0.97 | 2.73 | 2.96 | 0.97 | 0.22 | 0.29 |
| 6 July 2019 | 0.98 | 3.24 | 3.95 | 0.98 | 3.82 | 4.38 | 0.97 | 0.58 | 0.58 |
| Season | Month | N° of Detections | N° of Simulations | Monthly Detection Percentage (%) | Season Detection Percentage (%) | 6-Months Detection Percentage (%) |
|---|---|---|---|---|---|---|
| Autumn | March | 367 | 744 | 49.33 | 35.46 | 35.87 |
| April | 275 | 720 | 38.19 | |||
| May | 141 | 744 | 18.95 | |||
| Winter | June | 227 | 720 | 31.53 | 36.28 | |
| July | 216 | 744 | 29.03 | |||
| August | 358 | 744 | 48.12 | |||
| Spring | September | 326 | 720 | 45.28 | 48.08 | 53.29 |
| October | 325 | 744 | 43.68 | |||
| November | 399 | 720 | 55.42 | |||
| Summer | December | 456 | 744 | 61.29 | 58.56 | |
| January | 428 | 744 | 57.53 | |||
| February | 381 | 672 | 56.70 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pozzer, S.; Dalla Rosa, F.; Pravia, Z.M.C.; Rezazadeh Azar, E.; Maldague, X. Long-Term Numerical Analysis of Subsurface Delamination Detection in Concrete Slabs via Infrared Thermography. Appl. Sci. 2021, 11, 4323. https://doi.org/10.3390/app11104323
Pozzer S, Dalla Rosa F, Pravia ZMC, Rezazadeh Azar E, Maldague X. Long-Term Numerical Analysis of Subsurface Delamination Detection in Concrete Slabs via Infrared Thermography. Applied Sciences. 2021; 11(10):4323. https://doi.org/10.3390/app11104323
Chicago/Turabian StylePozzer, Sandra, Francisco Dalla Rosa, Zacarias Martin Chamberlain Pravia, Ehsan Rezazadeh Azar, and Xavier Maldague. 2021. "Long-Term Numerical Analysis of Subsurface Delamination Detection in Concrete Slabs via Infrared Thermography" Applied Sciences 11, no. 10: 4323. https://doi.org/10.3390/app11104323
APA StylePozzer, S., Dalla Rosa, F., Pravia, Z. M. C., Rezazadeh Azar, E., & Maldague, X. (2021). Long-Term Numerical Analysis of Subsurface Delamination Detection in Concrete Slabs via Infrared Thermography. Applied Sciences, 11(10), 4323. https://doi.org/10.3390/app11104323








