A Simple Technique for Studying Chaos Using Jerk Equation with Discrete Time Sine Map
Abstract
1. Introduction
2. Problem Description
3. Proposed Methodology
4. Eigenvalue Analysis
5. Numerical Simulation & Results
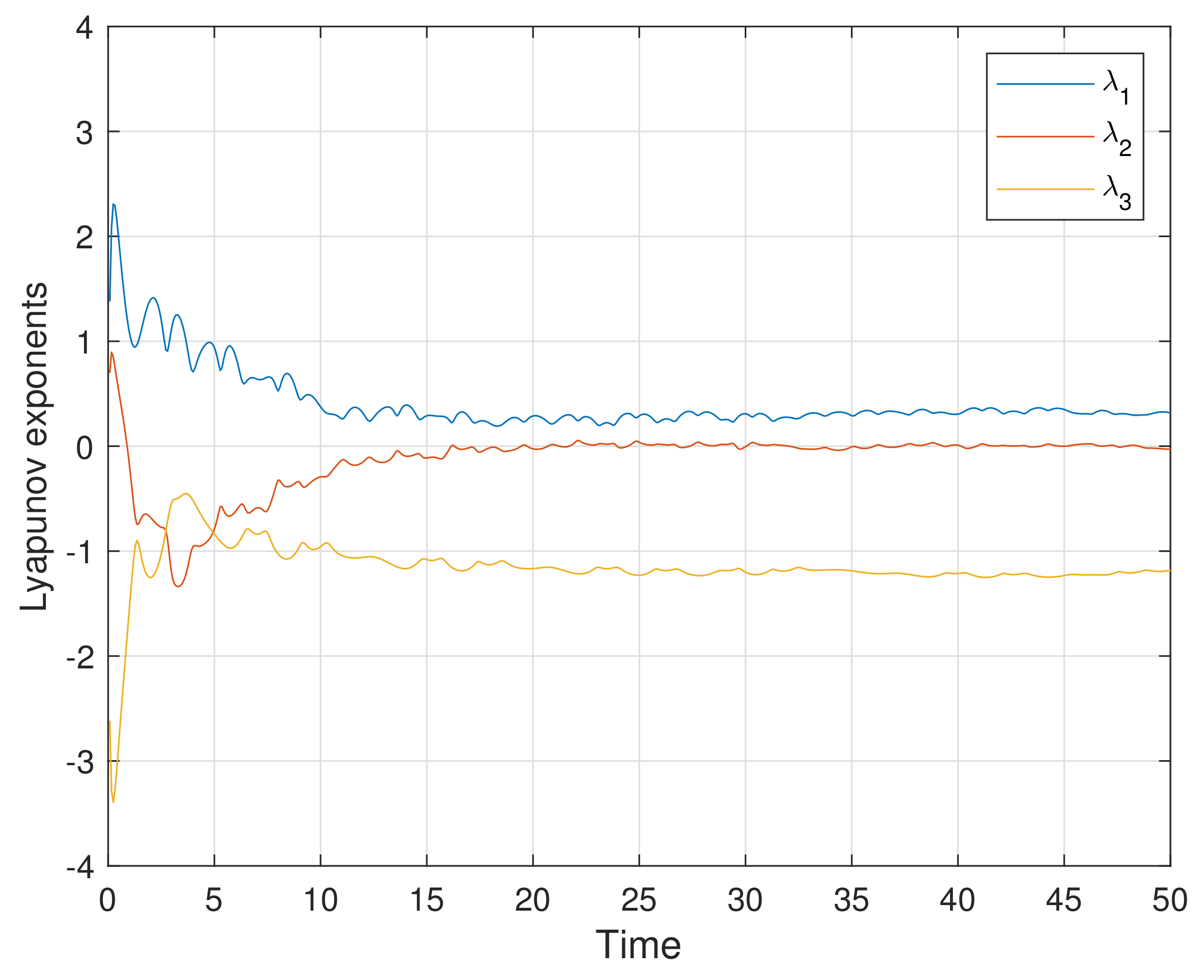
5.1. Lyapunov Exponent Test
5.2. Bifurcation Diagram
5.3. Correlation Dimension
5.4. Frequency Spectra
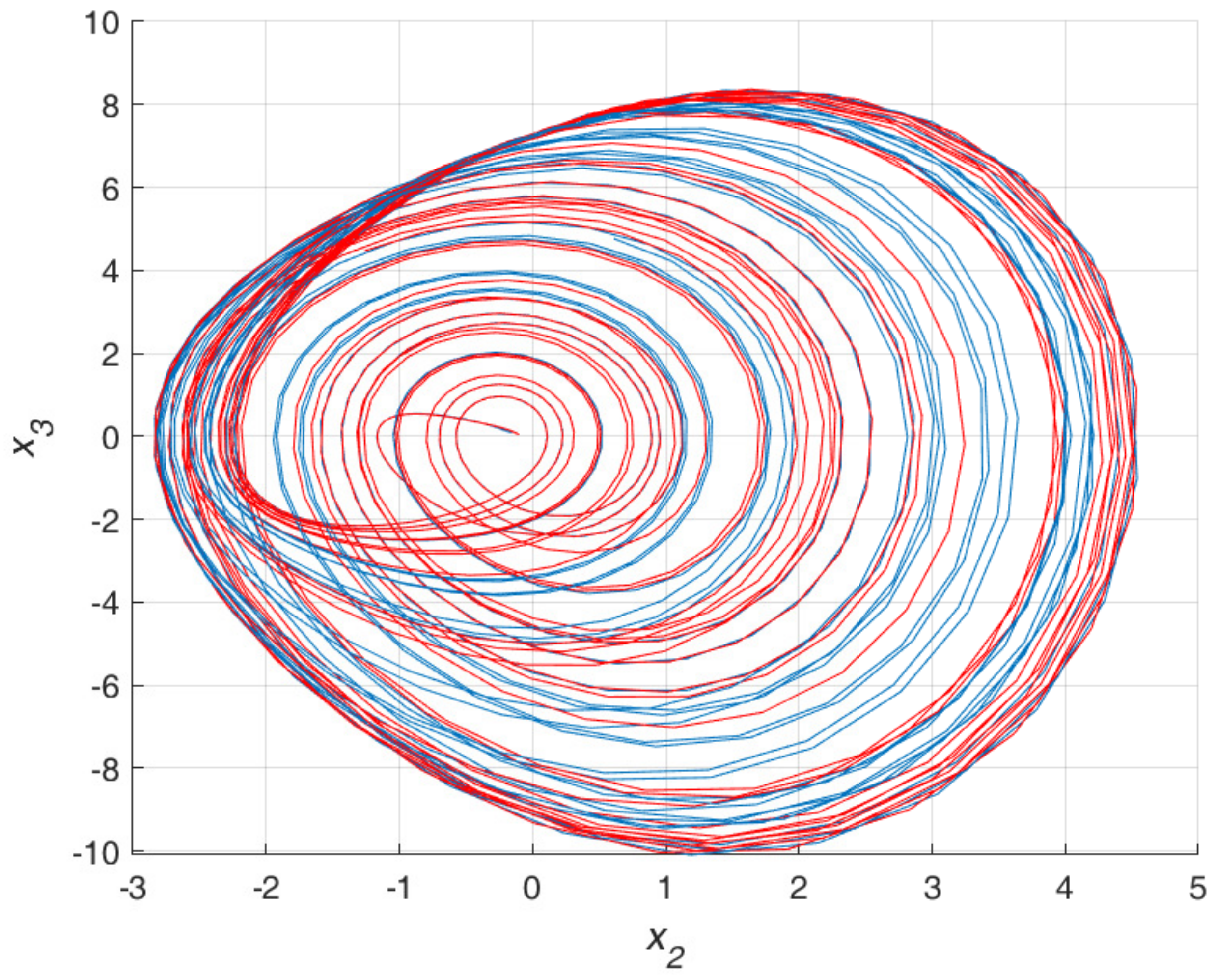
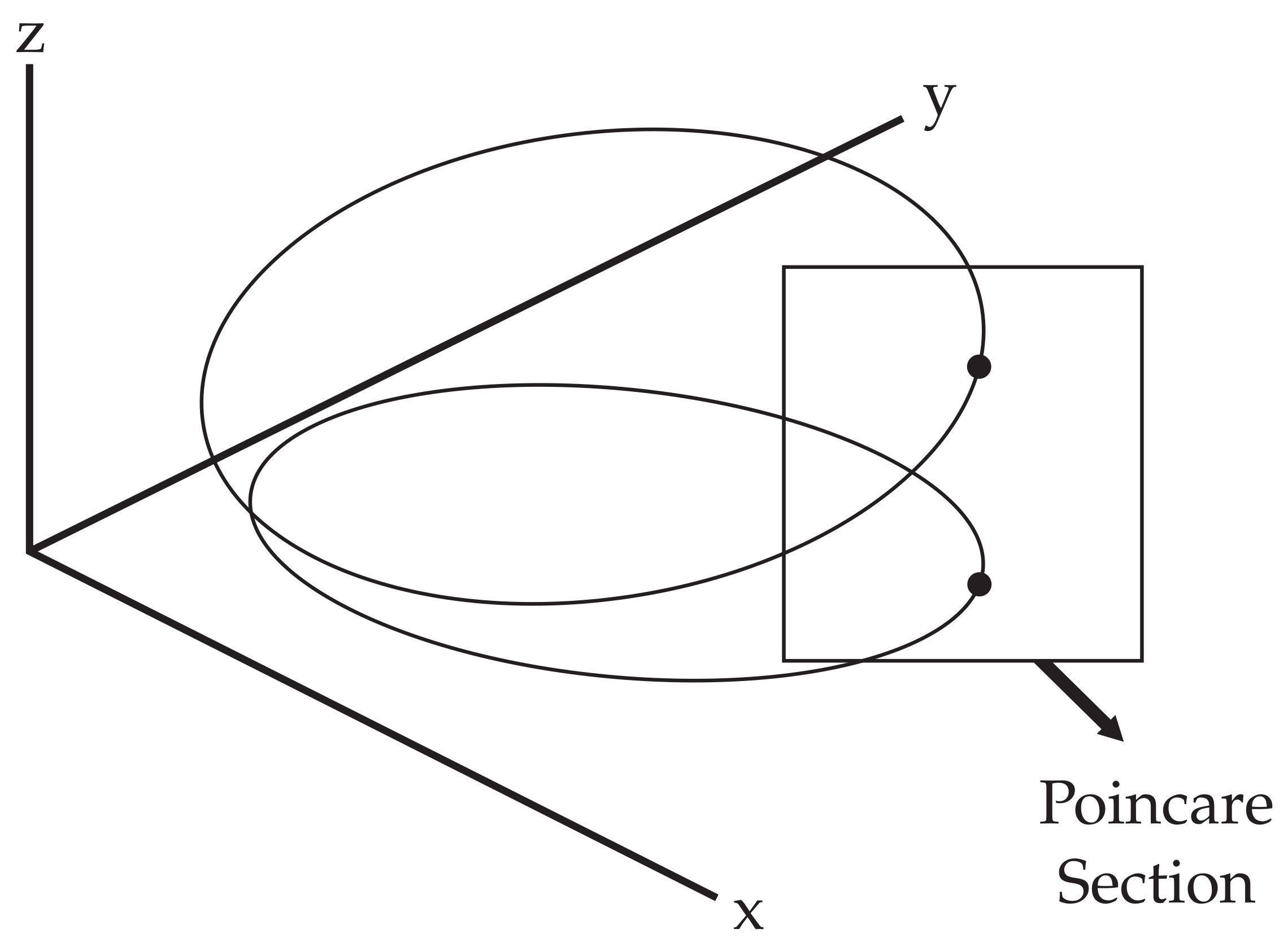
5.5. Poincare Section for Different Attractors
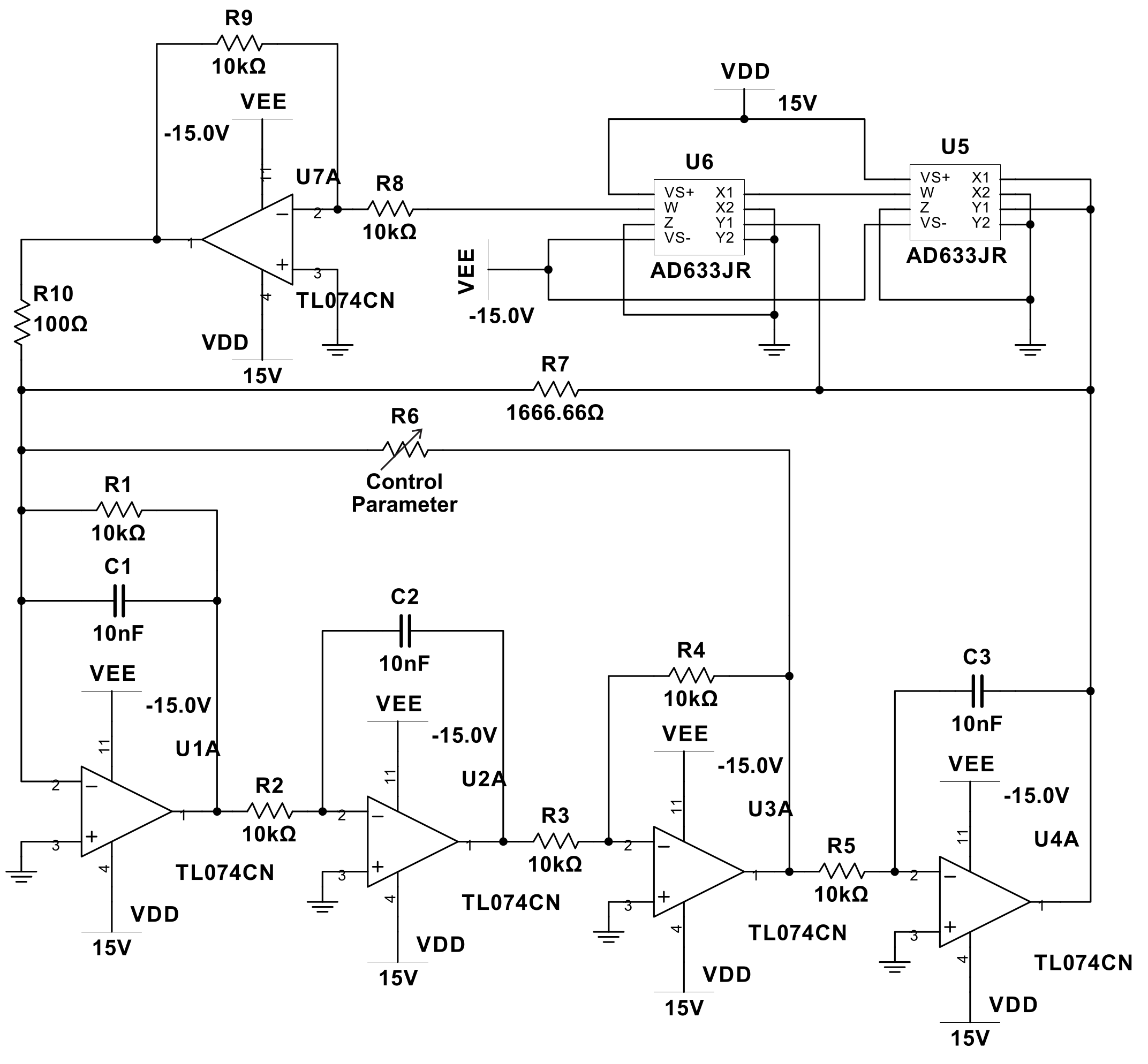
6. Experimental Setup
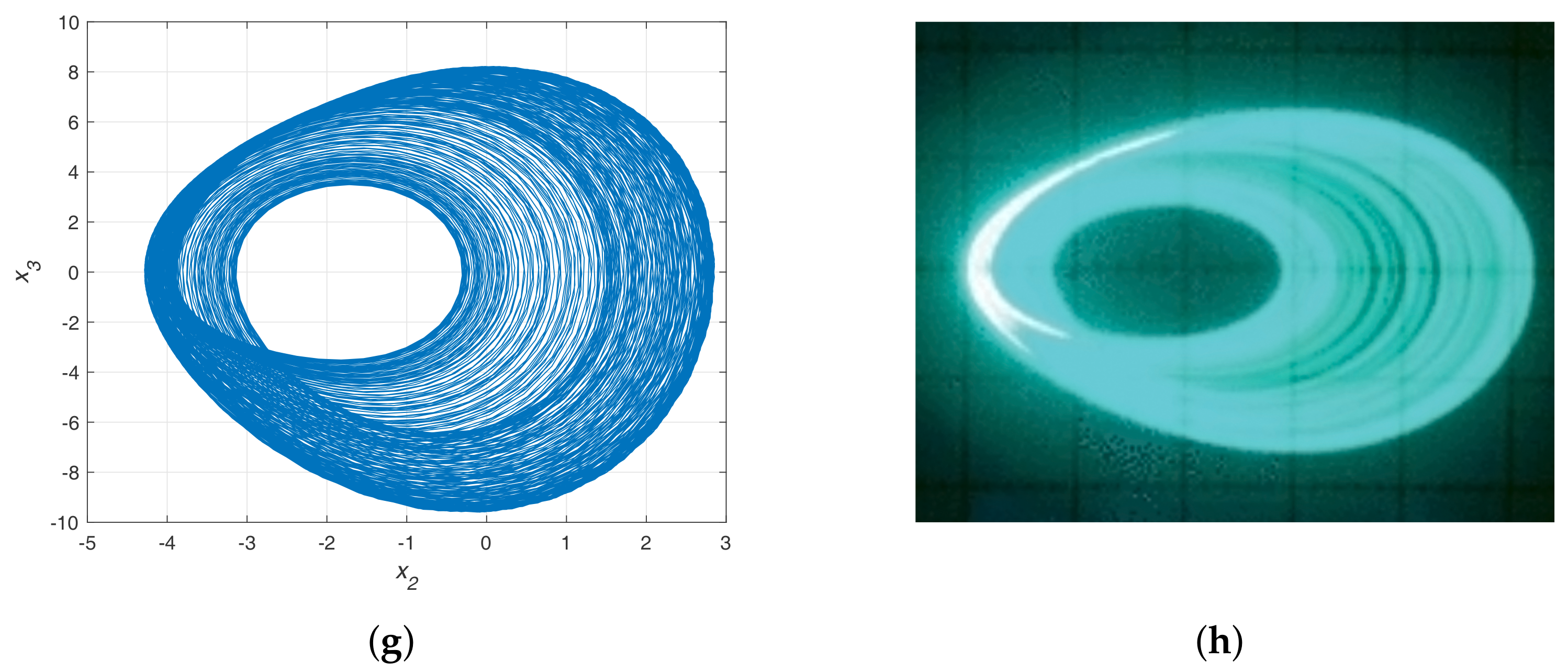
Experimental Verification
7. Discussion
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| MLE | Maximum Lyapunov Exponent |
| ODE | Ordinary differential equation |
| SNFS | Saturated Nonlinear Function Series |
| DOF | Degree of freedom |
| H.O.T. | Higher-order terms |
| DSR | Deanship of Scientific Research |
| K. A. CARE | King Abdullah City of Atomic & Renewable Energy |
References
- Li, T.Y.; Yorke, J.A. Period Three Implies Chaos. Am. Math. Mon. 1975, 82, 985–992. [Google Scholar] [CrossRef]
- Oestreicher, C. A History of Chaos Theory. Dialogues Clin. Neurosci. 2007, 9, 279. [Google Scholar] [PubMed]
- Sundar, S.; Minai, A.A. Synchronization of Randomly Multiplexed Chaotic Systems with Application to Communication. Phys. Rev. Lett. 2000, 85, 5456. [Google Scholar] [CrossRef] [PubMed]
- Kotulski, Z.; Szczepański, J.; Górski, K.; Paszkiewicz, A.; Zugaj, A. Application of Discrete Chaotic Dynamical Systems in Cryptography—DCC Method. Int. J. Bifurc. Chaos 1999, 9, 1121–1135. [Google Scholar] [CrossRef]
- Krysko, A.; Awrejcewicz, J.; Zhigalov, M.; Pavlov, S.; Krysko, V. Nonlinear behaviour of different flexible size-dependent beams models based on the modified couple stress theory. Part 2. Chaotic dynamics of flexible beams. Int. J. Non-Linear Mech. 2017, 93, 106–121. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Krysko, A.; Kutepov, I.; Zagniboroda, N.; Dobriyan, V.; Krysko, V. Chaotic dynamics of flexible Euler-Bernoulli beams. Chaos Interdiscip. J. Nonlinear Sci. 2013, 23, 043130. [Google Scholar] [CrossRef]
- Arshad, M.H.; Kassas, M. A Chaos Based SVPWM technique for B4 Inverter fed Two-Phase Symmetric Induction Motor for THD & EMI improvement at Low Modulation Index. In Proceedings of the 2019 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 7–8 February 2019; pp. 1–6. [Google Scholar]
- Ian, S. Does God Play Dice?: The Mathematics of Chaos; Blackwell Publishing: Hoboken, NJ, USA, 1989; p. 393. [Google Scholar]
- Sayed, W.S.; Radwan, A.G.; Fahmy, H.A. Chaotic Systems Based on Jerk Equation and Discrete Maps with Scaling Parameters. In Proceedings of the IEEE 2017 6th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 4–6 May 2017; pp. 1–4. [Google Scholar]
- Eckmann, J.P.; Ruelle, D. Ergodic Theory of Chaos and Strange Attractors. In The Theory of Chaotic Attractors; Springer: Berlin/Heidelberg, Germany, 1985; pp. 273–312. [Google Scholar]
- Sprott, J. Some Simple Chaotic Jerk Functions. Am. J. Phys. 1997, 65, 537–543. [Google Scholar] [CrossRef]
- Kennedy, M.P. Experimental Chaos from Autonomous Electronic Circuits. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1995, 353, 13–32. [Google Scholar]
- Lakshmanan, M.; Murali, K. Experimental Chaos from Non-Autonomous Electronic Circuits. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1995, 353, 33–46. [Google Scholar]
- Linsay, P.S. Period Doubling and Chaotic Behavior in a Driven Anharmonic Oscillator. Phys. Rev. Lett. 1981, 47, 1349. [Google Scholar] [CrossRef]
- Newcomb, R.; Sathyan, S. An RC Op-Amp Chaos Generator. IEEE Trans. Circuits Syst. 1983, 30, 54–56. [Google Scholar] [CrossRef]
- Matsumoto, T.; Chua, L.; Komuro, M. The Double Scroll Bifurcations. Int. J. Circuit Theory Appl. 1986, 14, 117–146. [Google Scholar] [CrossRef]
- Azzouz, A.; Duhr, R.; Hasler, M. Transition to Chaos in a Simple Nonlinear Circuit Driven by a Sinusoidal Voltage Source. IEEE Trans. Circuits Syst. 1983, 30, 913–914. [Google Scholar] [CrossRef]
- Kennedy, M.P. Chaos in the Colpitts Oscillator. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 1994, 41, 771–774. [Google Scholar] [CrossRef]
- Tekam, R.B.W.; Kengne, J.; Kenmoe, G.D. High Frequency Colpitts’ Oscillator: A Simple Configuration for Chaos Generation. Chaos Solitons Fractals 2019, 126, 351–360. [Google Scholar] [CrossRef]
- Madan, R.N. Chua’s Circuit: A Paradigm for Chaos; World Scientific Publishing Co.: Singapore, 1993. [Google Scholar]
- Prebianca, F.; Marcondes, D.W.; Albuquerque, H.A.; Beims, M.W. Exploring an Experimental Analog Chua’s Circuit. Eur. Phys. J. B 2019, 92, 134. [Google Scholar] [CrossRef]
- Tchitnga, R.; Nguazon, T.; Fotso, P.H.L.; Gallas, J.A. Chaos in a Single Op-Amp–based Jerk Circuit: Experiments and Simulations. IEEE Trans. Circuits Syst. II Express Briefs 2015, 63, 239–243. [Google Scholar] [CrossRef]
- Chiu, R.; López-Mancilla, D.; Castañeda, C.E.; Orozco-López, O.; Villafaña-Rauda, E.; Sevilla-Escoboza, R. Design and Implementation of a Jerk Circuit using a Hybrid Analog–Digital System. Chaos Solitons Fractals 2019, 119, 255–262. [Google Scholar] [CrossRef]
- Radwan, A.; Soliman, A.M.; Elwakil, A.S. 1-D Digitally-Controlled Multiscroll Chaos Generator. Int. J. Bifurc. Chaos 2007, 17, 227–242. [Google Scholar] [CrossRef]
- Bao, B.; Zhou, G.; Xu, J.; Liu, Z. Multiscroll Chaotic Attractors from a Modified Colpitts Oscillator Model. Int. J. Bifurc. Chaos 2010, 20, 2203–2211. [Google Scholar] [CrossRef]
- Zidan, M.A.; Radwan, A.G.; Salama, K.N. Controllable V-shape multiscroll butterfly attractor: System and circuit implementation. Int. J. Bifurc. Chaos 2012, 22, 1250143. [Google Scholar] [CrossRef]
- Sánchez-López, C.; Trejo-Guerra, R.; Munoz-Pacheco, J.; Tlelo-Cuautle, E. N-Scroll Chaotic Attractors from Saturated Function Series Employing CCII+ s. Nonlinear Dyn. 2010, 61, 331–341. [Google Scholar] [CrossRef]
- Sánchez López, C. A 1.7 MHz Chua’s Circuit using VMs and CF+ s. Rev. Mex. De Física 2012, 58, 86–93. [Google Scholar]
- Ortega-Torres, E.; Sánchez-López, C.; Mendoza-López, J. Frequency Behavior of Saturated Nonlinear Dunction Series Based on Opamps. Rev. Mex. Física 2013, 59, 504–510. [Google Scholar]
- Sprott, J.C. A New Class of Chaotic Circuit. Phys. Lett. A 2000, 266, 19–23. [Google Scholar] [CrossRef]
- Komuro, M. Birth and Death of the Double Scroll. In Proceedings of the 1985 24th IEEE Conference on Decision and Control, Fort Lauderdale, FL, USA, 11–13 December 1985; pp. 456–460. [Google Scholar]
- Matsumoto, T.; Chua, L.; Komuro, M. Birth and Death of the Double Scroll. Phys. D Nonlinear Phenom. 1987, 24, 97–124. [Google Scholar] [CrossRef]
- Patidar, V.; Sud, K. Bifurcation and Chaos in Simple Jerk Dynamical Systems. Pramana 2005, 64, 75–93. [Google Scholar] [CrossRef]
- Kengne, J.; Njikam, S.; Signing, V.F. A Plethora of Coexisting Strange Attractors in a Simple Jerk System with Hyperbolic Tangent Nonlinearity. Chaos Solitons Fractals 2018, 106, 201–213. [Google Scholar] [CrossRef]
- Kengne, J.; Mogue, R.L.T.; Fozin, T.F.; Telem, A.N.K. Effects of Symmetric and Asymmetric Nonlinearity on the Dynamics of a Novel Chaotic Jerk Circuit: Coexisting Multiple Attractors, Period Doubling Reversals, Crisis, and Offset Boosting. Chaos Solitons Fractals 2019, 121, 63–84. [Google Scholar] [CrossRef]
- Tagne, R.M.; Kengne, J.; Negou, A.N. Multistability and chaotic dynamics of a simple Jerk system with a smoothly tuneable symmetry and nonlinearity. Int. J. Dyn. Control 2019, 7, 476–495. [Google Scholar] [CrossRef]
- Giakoumis, A.; Volos, C.K.; Stouboulos, I.N.; Kyprianidis, I.M.; Nistazakis, H.E.; Tombras, G.S. Implementation of a Laboratorybased Educational Tool for Teaching Nonlinear Circuits and Chaos. In Advances and Applications in Chaotic Systems; Springer: Berlin/Heidelberg, Germany, 1995; pp. 379–407. [Google Scholar]
- Chen, C.T. Linear System Theory and Design; Oxford University Press, Inc.: Oxford, UK, 1998. [Google Scholar]
- Tancredi, G.; Sánchez, A.; Roig, F. A Comparison Between Methods to Compute Lyapunov Exponents. Astron. J. 2001, 121, 1171. [Google Scholar] [CrossRef]
- Greiner, W. Lyapunov Exponents and Chaos. In Classical Mechanics: Systems of Particles and Hamiltonian Dynamics; Springer: Berlin/Heidelberg, Germany, 2010; pp. 503–516. [Google Scholar]
- Sprott, J.C. Chaos and Time-Series Analysis; Oxford University Press, Inc.: Oxford, UK, 2003; Volume 69. [Google Scholar]
- Awrejcewicz, J.; Krysko, A.; Soldatov, V.; Krysko, V. Analysis of the nonlinear dynamics of the Timoshenko flexible beams using wavelets. J. Comput. Nonlinear Dyn. 2012, 7, 011005. [Google Scholar] [CrossRef]
- Seshadri, H.; Verma, K. The Embedding Theorems of Whitney and Nash. Resonance 2016, 21, 815–826. [Google Scholar] [CrossRef]
- May, R.M. Simple Mathematical Models with very Complicated Dynamics. In The Theory of Chaotic Attractors; Springer: Berlin/Heidelberg, Germany, 2004; pp. 85–93. [Google Scholar]
- Strogatz, S.H. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]








| Parameter | Value | Unit |
|---|---|---|
| R1–R5, R8–R9 | 10 k | |
| 1.67 k | ||
| 100 | ||
| C1–C3 | 10 n | F |
| 15 | V | |
| –15 | V |
| Sr. No. | Value of R6 | Attractor Type |
|---|---|---|
| 1 | 1112 | Period 1 |
| 2 | 1667 | Period 2 |
| 3 | 1715 | Period 4 |
| 4 | 1807 | Chaotic Attractor |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshad, M.H.; Kassas, M.; Hussein, A.E.; Abido, M.A. A Simple Technique for Studying Chaos Using Jerk Equation with Discrete Time Sine Map. Appl. Sci. 2021, 11, 437. https://doi.org/10.3390/app11010437
Arshad MH, Kassas M, Hussein AE, Abido MA. A Simple Technique for Studying Chaos Using Jerk Equation with Discrete Time Sine Map. Applied Sciences. 2021; 11(1):437. https://doi.org/10.3390/app11010437
Chicago/Turabian StyleArshad, Muhammad Haseeb, Mahmoud Kassas, Alaa E. Hussein, and Mohammad A. Abido. 2021. "A Simple Technique for Studying Chaos Using Jerk Equation with Discrete Time Sine Map" Applied Sciences 11, no. 1: 437. https://doi.org/10.3390/app11010437
APA StyleArshad, M. H., Kassas, M., Hussein, A. E., & Abido, M. A. (2021). A Simple Technique for Studying Chaos Using Jerk Equation with Discrete Time Sine Map. Applied Sciences, 11(1), 437. https://doi.org/10.3390/app11010437







