Quantum Features of Atom–Field Systems in the Framework of Deformed Fields
Abstract
1. Introduction
2. Deformed Spin Algebra
3. Deformed Schrödinger Cat Spin Coherent States
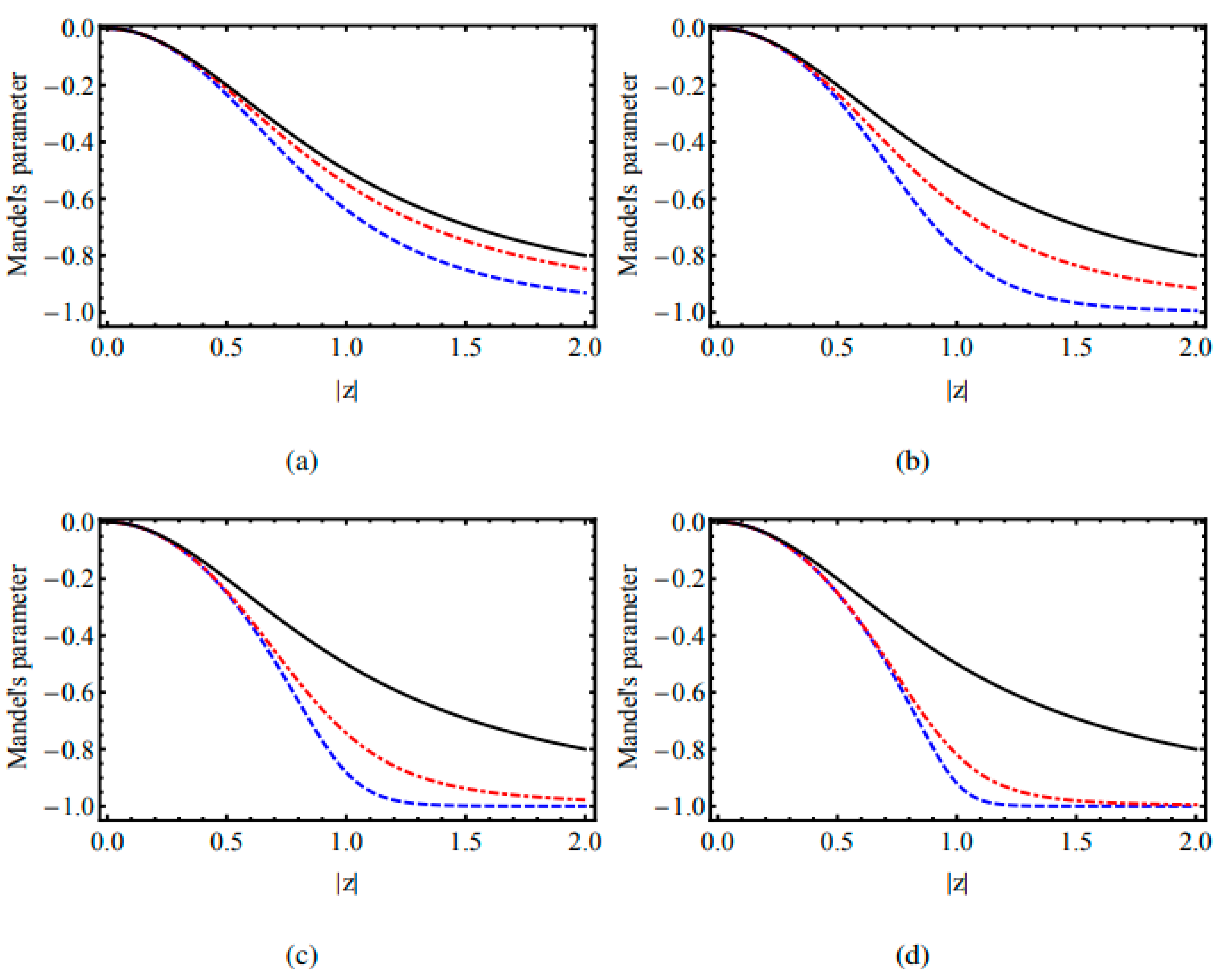
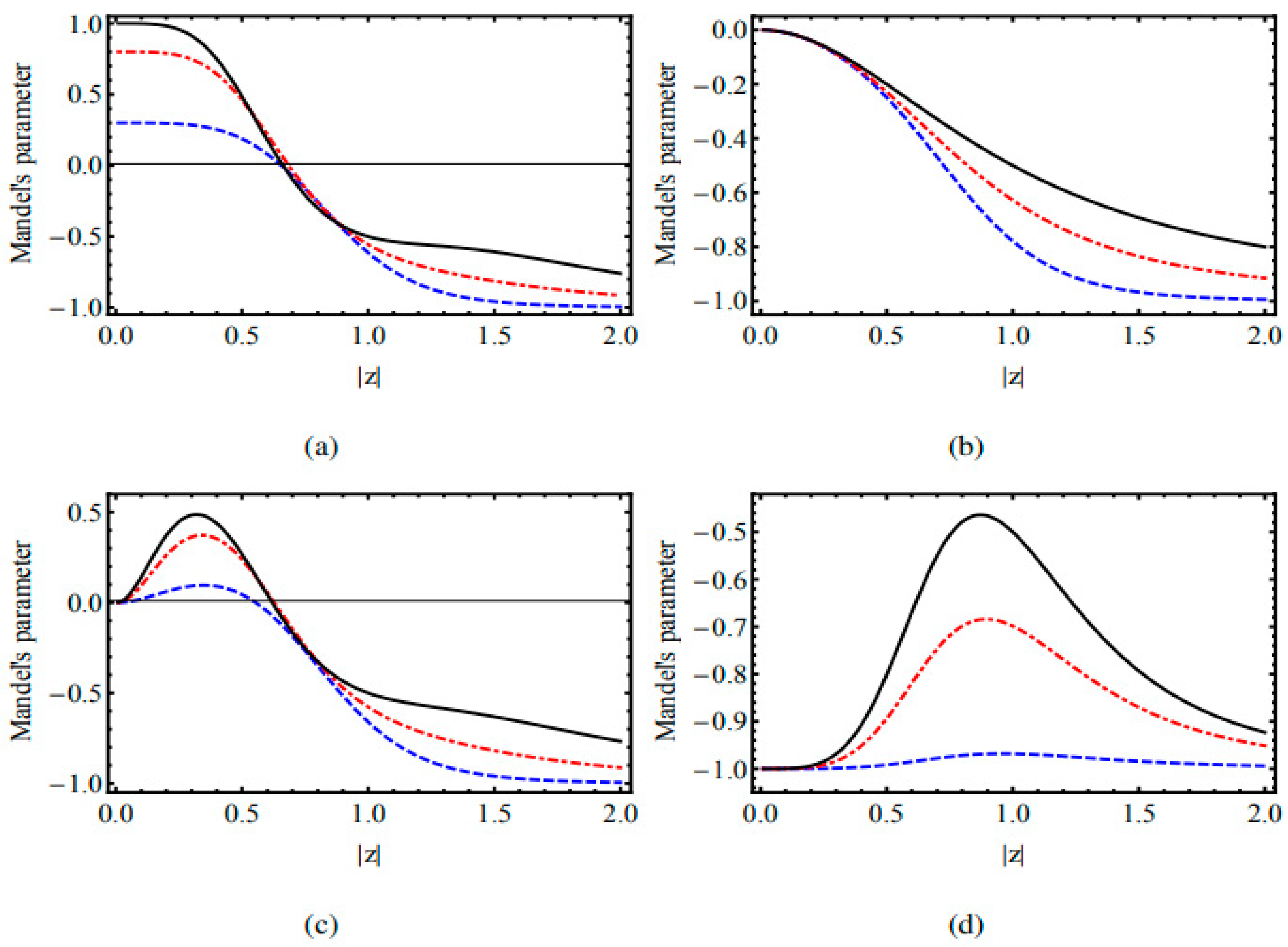
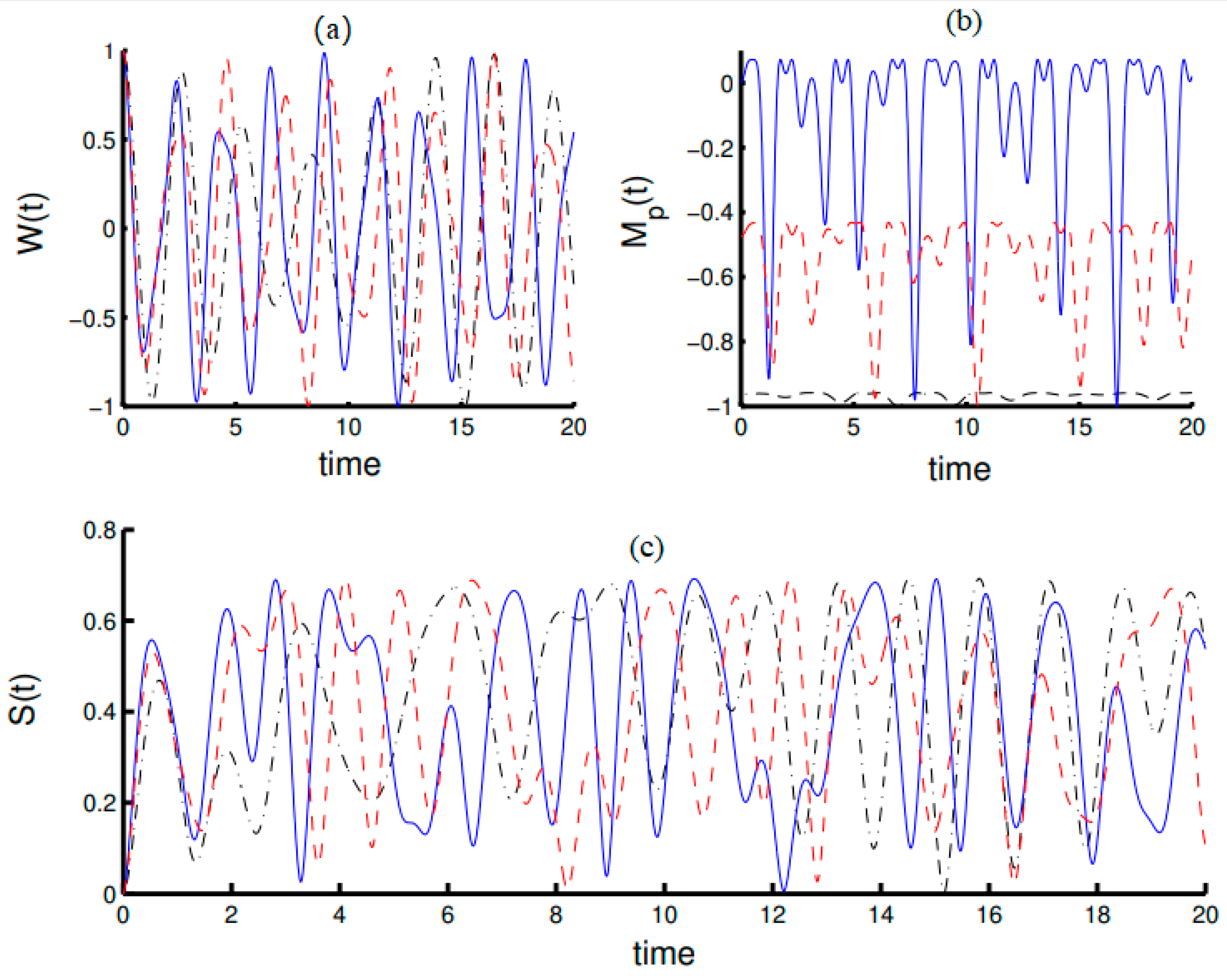
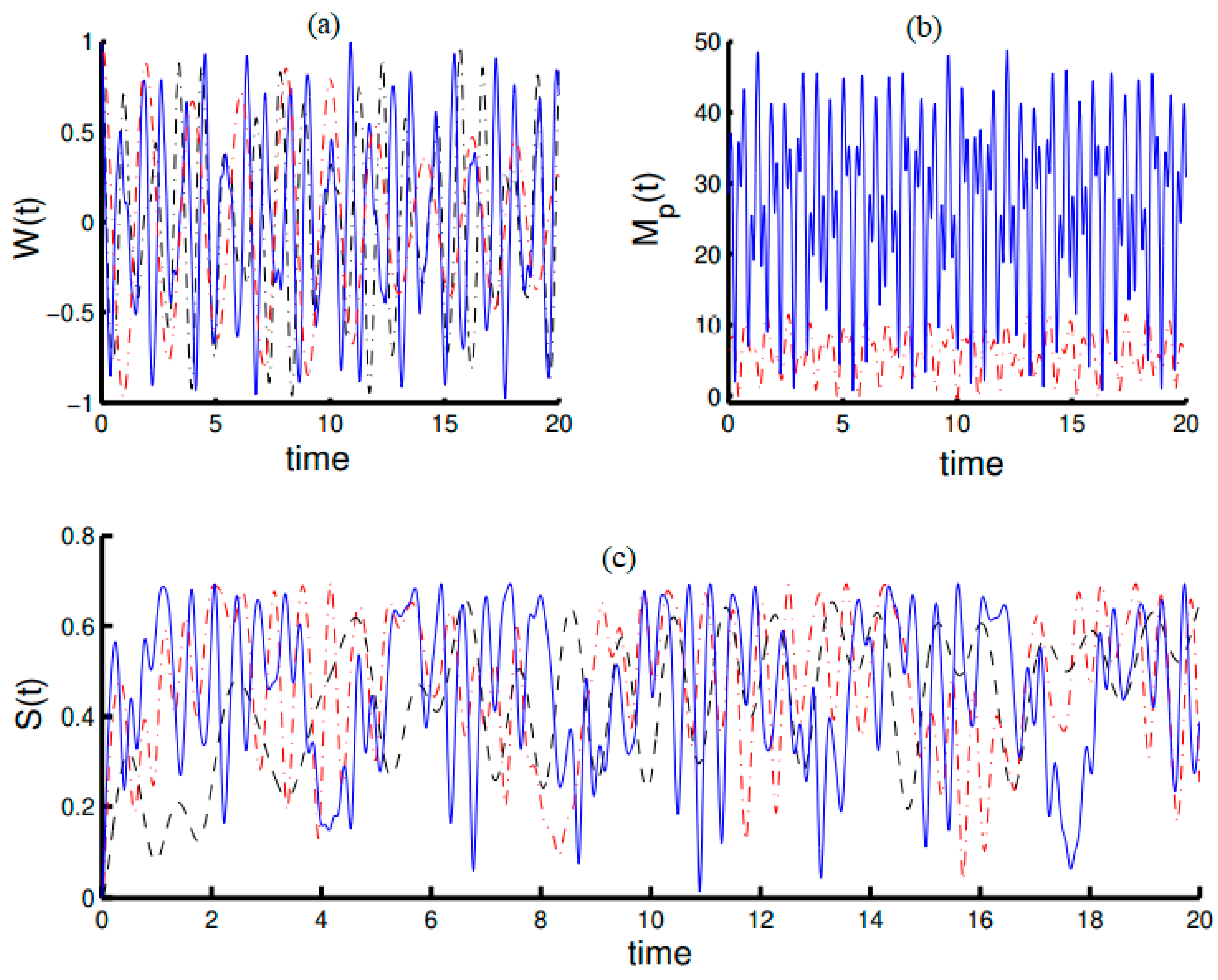
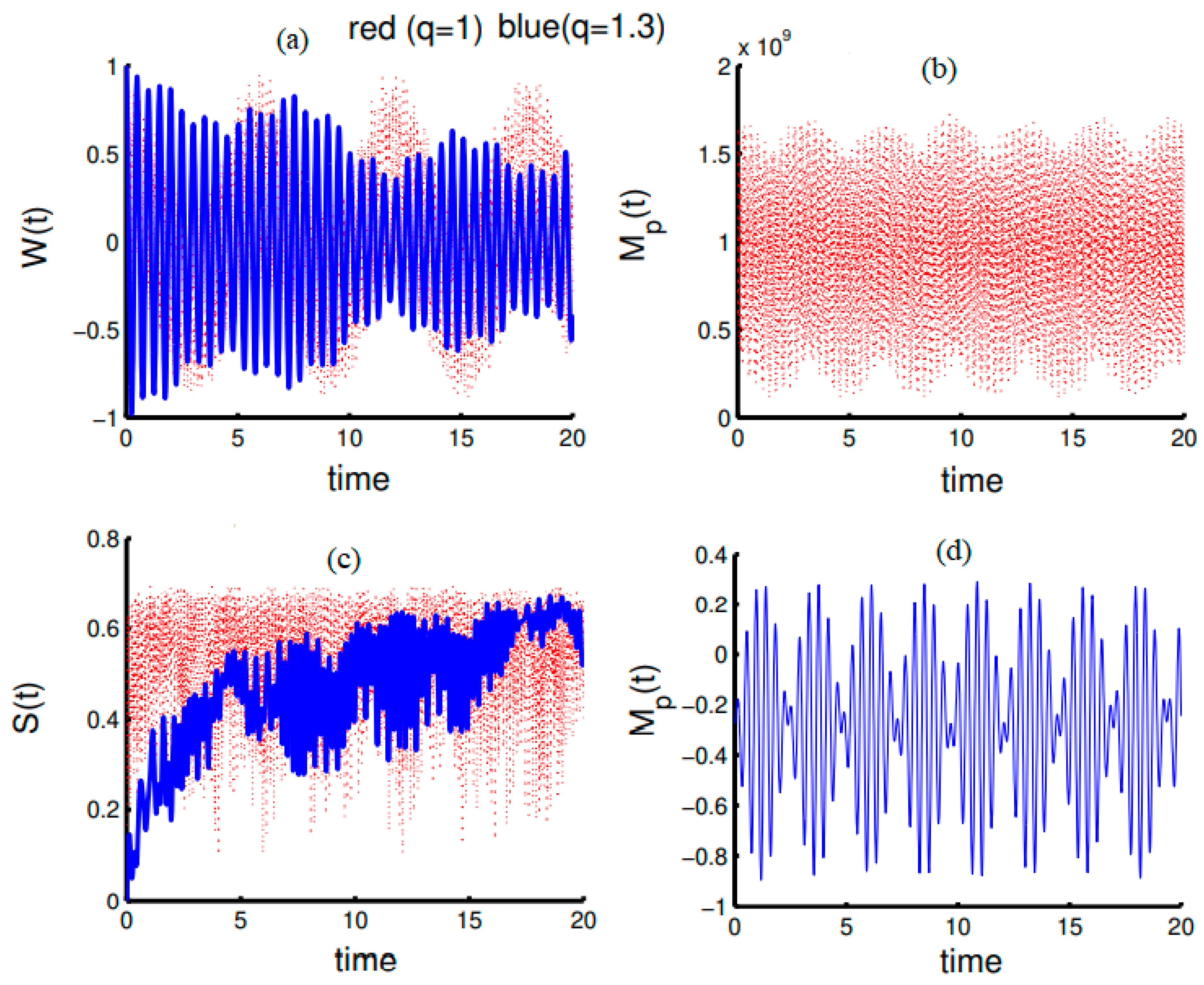
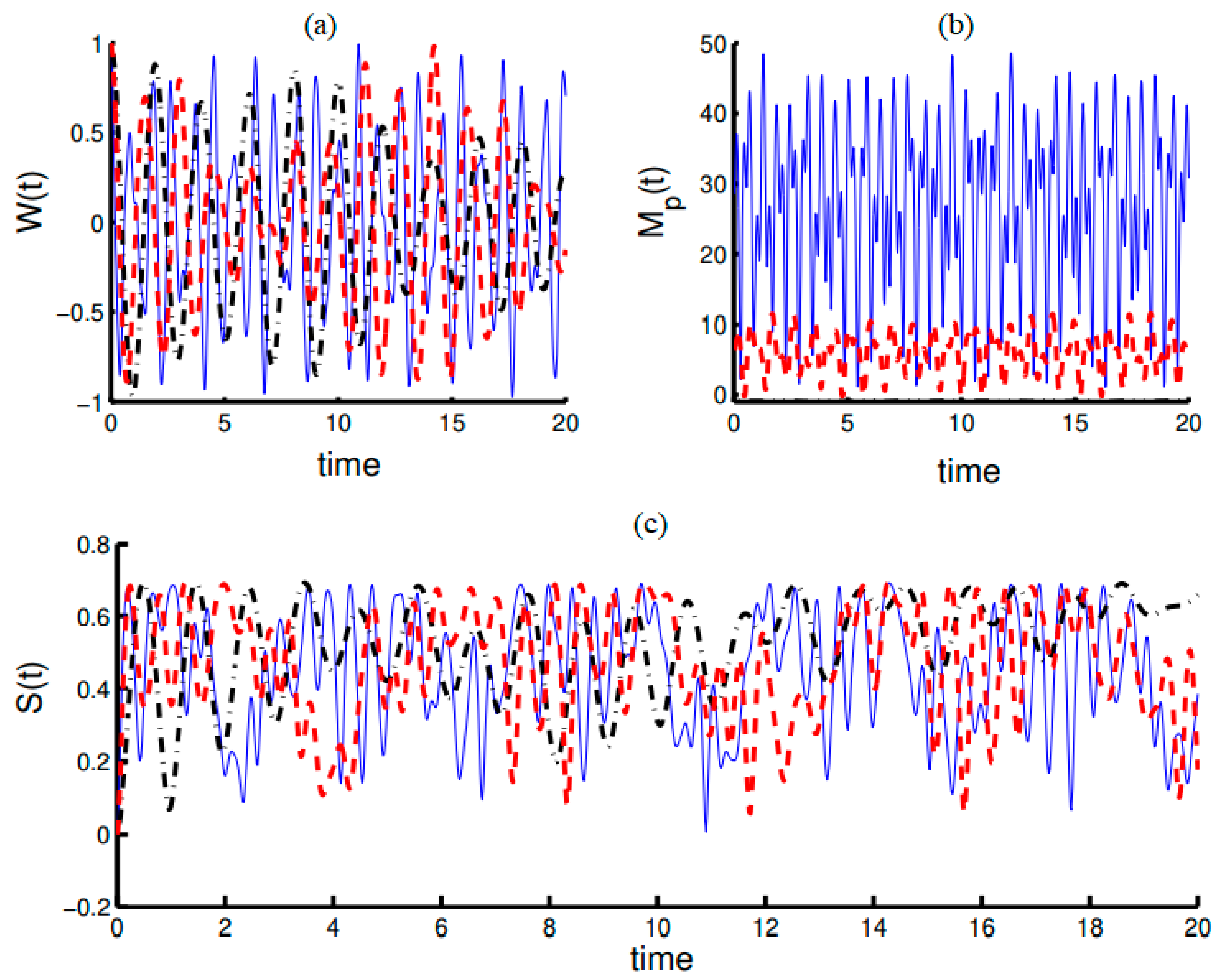
4. Interactions of a Two-Level Atom with a Field in the Framework of Algebra
5. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schrodinger, E. Der stetigeÜbergang von der Mikro-zurMakromechanik. Naturwissenscahften 1926, 14, 664. [Google Scholar] [CrossRef]
- Glauber, R. The quantum theory of optical coherence. Phys. Rev. 1963, 130, 2529. [Google Scholar] [CrossRef]
- Glauber, R. Coherent and incoherent states of radiation field. J. Phys. Rev. 1963, 131, 2766. [Google Scholar] [CrossRef]
- Klauder, J.R. Continuous representation theory. I. Postulates of continuous representation theory. J. Math. Phys. 1963, 4, 1055. [Google Scholar] [CrossRef]
- Klauder, J.R. Generalized relation between quantum and classical dynamics. J. Math. Phys. 1963, 4, 1058. [Google Scholar] [CrossRef]
- Klauder, J.R.; Skagertan, B.-S. Coherent States; World Scientifique: Singapore, 1985. [Google Scholar]
- Perelomov, A.M. Generalized Coherent States and Their Applications; Springer: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Ali, S.T.; Antoine, J.-P.; Gazeau, J.P. Coherent States, Wavelets and Their Generalizations; Springer: New York, NY, USA, 2000. [Google Scholar]
- Gilmore, R. Geometry of symmetrized states. Ann. Phys. 1972, 74, 391. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S. Entanglement of atom–field interaction for nonlinear optical fields. PhysicaE 2011, 44, 628–634. [Google Scholar] [CrossRef]
- Berrada, K.; Abdel-Khalek, S.; Ooi, C.H.R. Quantum metrology with entangled spin-coherent states of two modes. Phys. Rev. A 2012, 86, 033823. [Google Scholar] [CrossRef]
- Berrada, K. Quantum metrology with SU (1, 1) coherent states in the presence of nonlinear phase shifts. Phys. Rev. A 2013, 88, 013817. [Google Scholar] [CrossRef]
- Abdel-Khalek, S.; Berrada, K.; Ooi, C.H.R. Beam splitter entangler for nonlinear bosonic fields. Laser Phys. 2012, 22, 1449–1454. [Google Scholar] [CrossRef]
- Jimbo, M. A q-difference analogue of U (g) and the Yang-Baxter equation. Lett. Math. Phys. 1985, 10, 63. [Google Scholar] [CrossRef]
- Berrada, K.; Eleuch, H. Noncommutative deformed cat states under decoherence. Phys. Rev. D 2019, 100, 016020. [Google Scholar] [CrossRef]
- Juro, B. On coherent states for the simplest quantum groups. Lett. Math. Phys. 1991, 21, 51. [Google Scholar] [CrossRef]
- Ellinas, D. Path integrals for quantum algebras and the classical limit. J. Phys. A 1993, 26, L543. [Google Scholar] [CrossRef][Green Version]
- Ellinas, D. On coherent states and q-deformed algebras. In Proceedings of the International Symposium on Coherent States: Past, Present and Future, Oak Ridge, TN, USA, 14–17 June 1993. [Google Scholar]
- Scarfone, A.M.; Narayana Swamy, P. An interacting ensemble of particles in the context of quantum algebra. J. Stat. Mech. 2009, 2009, 1–13. [Google Scholar] [CrossRef]
- Chaturvedi, S.; Kappoor, A.K.; Sandhya, R.; Srinivasan, V. Generalized commutation relations for a single-mode oscillator. Phys. Rev. A 1991, 43, 4555. [Google Scholar] [CrossRef]
- Chiu, S.H.; Gray, R.W.; Nelson, C.A. The q-analogue quantized radiation field and its uncertainty relations. Phys. Lett. A 1992, 164, 237–242. [Google Scholar] [CrossRef]
- Katriel, J.; Solomon, A.I. Lasers, nonclassical light, and deformed photon states. Phys. Rev. A 1994, 49, 5149. [Google Scholar] [CrossRef]
- Si-Cong, J.S.; Hong-Yi, F. q-deformed binomial state. Phys. Rev. A 1994, 49, 2277. [Google Scholar] [CrossRef]
- Yurke, B.; Stoler, D. Generating quantum mechanical superpositions of macroscopically distinguishable states via amplitude dispersion. Phys. Rev. Lett. 1986, 57, 13. [Google Scholar] [CrossRef]
- De Matos Filho, R.L.; Vogel, W. Even and odd coherent states of the motion of a trapped ion. Phys. Rev. Lett. 1996, 76, 608. [Google Scholar] [CrossRef] [PubMed]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89–109. [Google Scholar] [CrossRef]
- Joshi, A.; Puri, R.R. Characteristics of Rabi oscillations in the two-mode squeezed state of the field. Phys. Rev. A 1990, 42, 4336. [Google Scholar] [CrossRef] [PubMed]
- Yeazell, J.A.; Mallalieu, M.; Stroud, C.R., Jr. Observation of the collapse and revival of a Rydberg electronic wave packet. Phys. Rev. Lett. 1990, 64, 2007. [Google Scholar] [CrossRef]
- Eberly, J.H.; Narozhny, N.B.; Sanchez Mondragon, J.J. Periodic spontaneous collapse and revival in a simple quantum model. Phys. Rev. Lett. 1980, 44, 1383. [Google Scholar] [CrossRef]
- Knight, P.L.; Radmore, P.M. Quantum revivals of a two-level system driven by chaotic radiation. Phys. Lett. A 1982, 90, 342–346. [Google Scholar] [CrossRef]
- Short, R.; Mandel, L. Observation of sub-poissonian photon statistics. Phys. Rev. Lett. 1983, 51, 384. [Google Scholar] [CrossRef]
- Abdalla, M.S.; Obada, A.S.F.; Abdel-Khalek, S. Entropy squeezing of time dependent single-mode Jaynes–Cummings model in presence of non-linear effect. Chaos Solitons Fractals 2008, 36, 405–417. [Google Scholar] [CrossRef]
- Arvinda, P.K.; Guanhui, H. Influence of initial conditions on squeezing and anti-bunching in the Jaynes—Cummings model. Phys. C 1988, 150, 427–439. [Google Scholar] [CrossRef]
- Li, X.S.; Lin, D.L.; George, T.F.; Liu, Z.D. Squeezing of atomic variables in the one-photon and two-photon Jaynes—Cummings model. Phys. Rev. A 1989, 40, 2504. [Google Scholar] [CrossRef]
- Ekert, A.K. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 1991, 67, 661. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Brassard, G.; Mermin, N.D. Quantum cryptography without Bell’s theorem. Phys. Rev. Lett. 1992, 68, 557. [Google Scholar] [CrossRef] [PubMed]
- Bennett, C.H.; Bessette, F.; Brassard, G.; Salvail, L.; Smolin, J. Experimental quantum cryptography. J. Cryptol. 1992, 5, 3–28. [Google Scholar] [CrossRef]
- Honjo, T.; Nam, S.W.; Takesue, H.; Zhang, Q.; Kamada, H.; Nishida, Y.; Tadanaga, O.; Asobe, M.; Baek, B.; Hadfield, R.; et al. Long-distance entanglement-based quantum key distribution over optical fiber. Opt. Express 2008, 16, 19118–19126. [Google Scholar] [CrossRef] [PubMed]
- Ekert, A.; Jozsa, R. Quantum computation and Shor’s factoring algorithm. Rev. Mod. Phys. 1996, 68, 733. [Google Scholar] [CrossRef]
- Bennett, C.H.; Brassard, G.; Crepeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar] [CrossRef]
- Takesue, H.; Shellee, D.D.; Stevens, M.J.; Verma, V.; Mirin, R.P.; Nam, S.W. Quantum teleportation of an optical qutrit. Opt. Express 2015, 2, 832–835. [Google Scholar]
- Berrada, K.; Abdel-Khalek, S.; Ooi, C.H.R. Geometric phase and entanglement for a single qubit interacting with deformed-states superposition. Quantum Inf. Process. 2013, 12, 2177–2188. [Google Scholar] [CrossRef]
- Wootters, W.K. Entanglement of formation of an arbitrary state of two qubits. Phys. Rev. Lett. 1998, 80, 2245. [Google Scholar] [CrossRef]
- Uhlmann, A. Fidelity and concurrence of conjugated states. Phys. Rev. A 2000, 62, 032307. [Google Scholar] [CrossRef]
- Bennett, C.H.; Bernstein, S.; Popescu, H.J.; Schumacher, B. Concentrating partial entanglement by local operations. Phys. Rev. A 1996, 53, 2046. [Google Scholar] [CrossRef] [PubMed]
- Popescu, S.; Rohrlich, D. Concentrating partial entanglement by local operations. Phys. Rev. A 1997, 56, R3319. [Google Scholar] [CrossRef]
- Bose, S.; Vedral, V. Mixedness and teleportation. Phys. Rev. A 2000, 61, 040101. [Google Scholar] [CrossRef]
- Wei, T.C.; Nemoto, K.; Goldbart, P.M.; Kwiat, P.G.; Munro, W.J.; Verstraete, F. Maximal entanglement versus entropy for mixed quantum states. Phys. Rev. A 2003, 67, 022110. [Google Scholar] [CrossRef]
- Sklyanin, E.K. Some algebraic structures connected with the Yang-Baxter equation. Funct. Anal. Appl. 1982, 16, 26–270. [Google Scholar]
- De Boer, J.; Harmsze, F.; Tjin, T. Non-linear finite W-symmetries and applications in elementary systems. Phys. Rep. 1996, 272, 139. [Google Scholar] [CrossRef]
- Schwinger, J. On the Quantum Theory of Angular Momentum; Biedenharn, L.C., van Dam, H., Eds.; Academic Press: New York, NY, USA, 1965. [Google Scholar]
- Jordan, P. Der Zusammenhang der symmetris chenunelinearen Gruppen und das Mehrkorper poblem Z. Physik 1935, 94, 531. [Google Scholar] [CrossRef]
- Holstein, T.; Primakoff, H. Field dependence of the intrinsic domain magnetization of a ferromagnet. Phys. Rev. 1940, 58, 1098. [Google Scholar] [CrossRef]
- Bonatsos, D.; Daskaloyannis, C.; Kolokotronis, P. Generalized deformed SU (2) algebra. J. Phys. A Math. Gen. 1993, 26, L871. [Google Scholar] [CrossRef]
- Berrada, K.; El Baz, M.; Hassouni, Y. Generalized spin coherent states: Construction and some physical properties. J. Stat. Phys. 2011, 142, 510. [Google Scholar] [CrossRef]
- Mandel, L.; Wolf, E. Optical Coherence and Quantum Optics; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdel-Khalek, S.; Berrada, K.; Altowyan, A.S. Quantum Features of Atom–Field Systems in the Framework of Deformed Fields. Appl. Sci. 2021, 11, 408. https://doi.org/10.3390/app11010408
Abdel-Khalek S, Berrada K, Altowyan AS. Quantum Features of Atom–Field Systems in the Framework of Deformed Fields. Applied Sciences. 2021; 11(1):408. https://doi.org/10.3390/app11010408
Chicago/Turabian StyleAbdel-Khalek, Sayed, Kamal Berrada, and Abeer S. Altowyan. 2021. "Quantum Features of Atom–Field Systems in the Framework of Deformed Fields" Applied Sciences 11, no. 1: 408. https://doi.org/10.3390/app11010408
APA StyleAbdel-Khalek, S., Berrada, K., & Altowyan, A. S. (2021). Quantum Features of Atom–Field Systems in the Framework of Deformed Fields. Applied Sciences, 11(1), 408. https://doi.org/10.3390/app11010408



