Parametric Analysis of the Shear Lag Effect in Tube Structural Systems of Tall Buildings
Abstract
1. Introduction
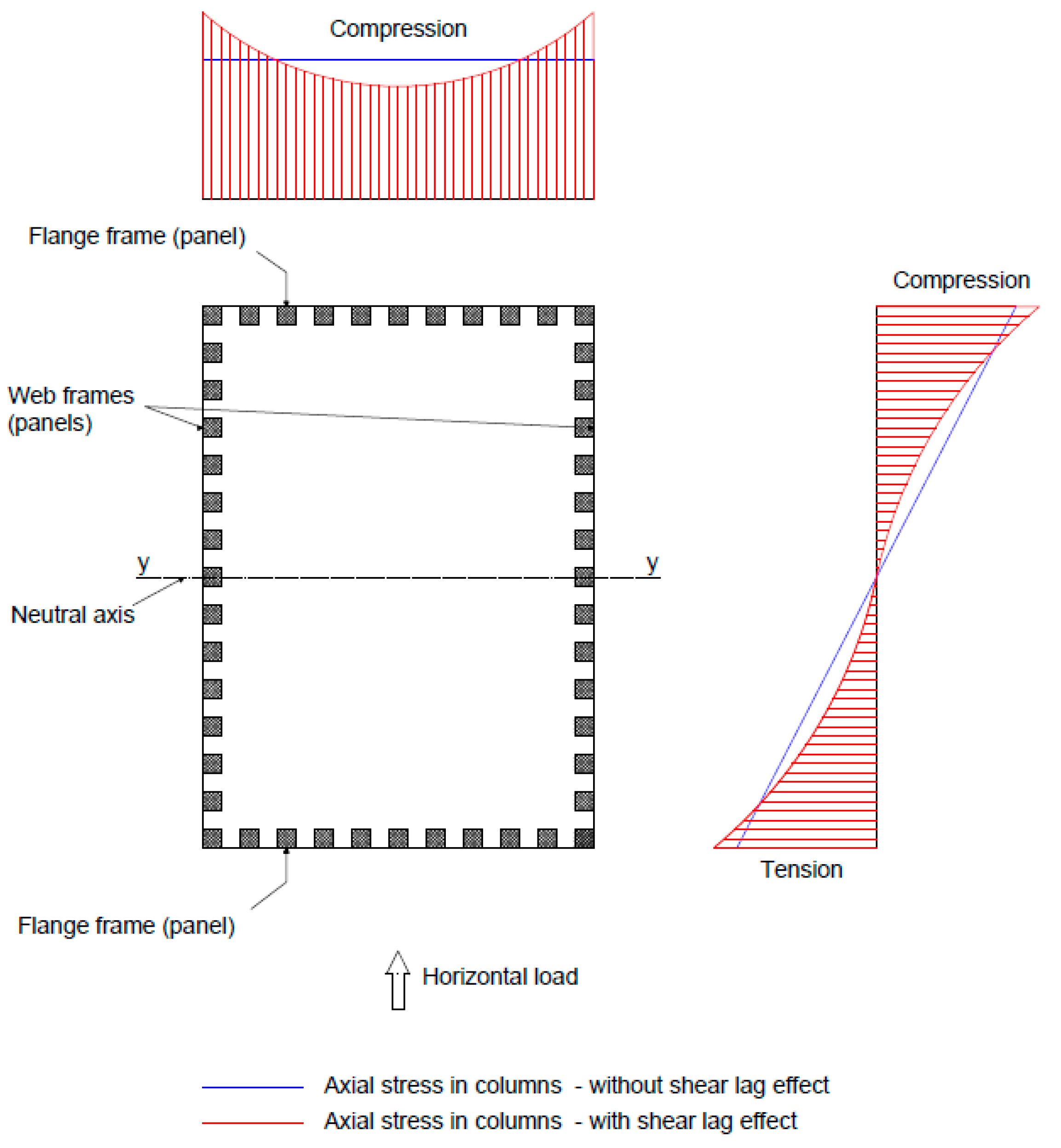
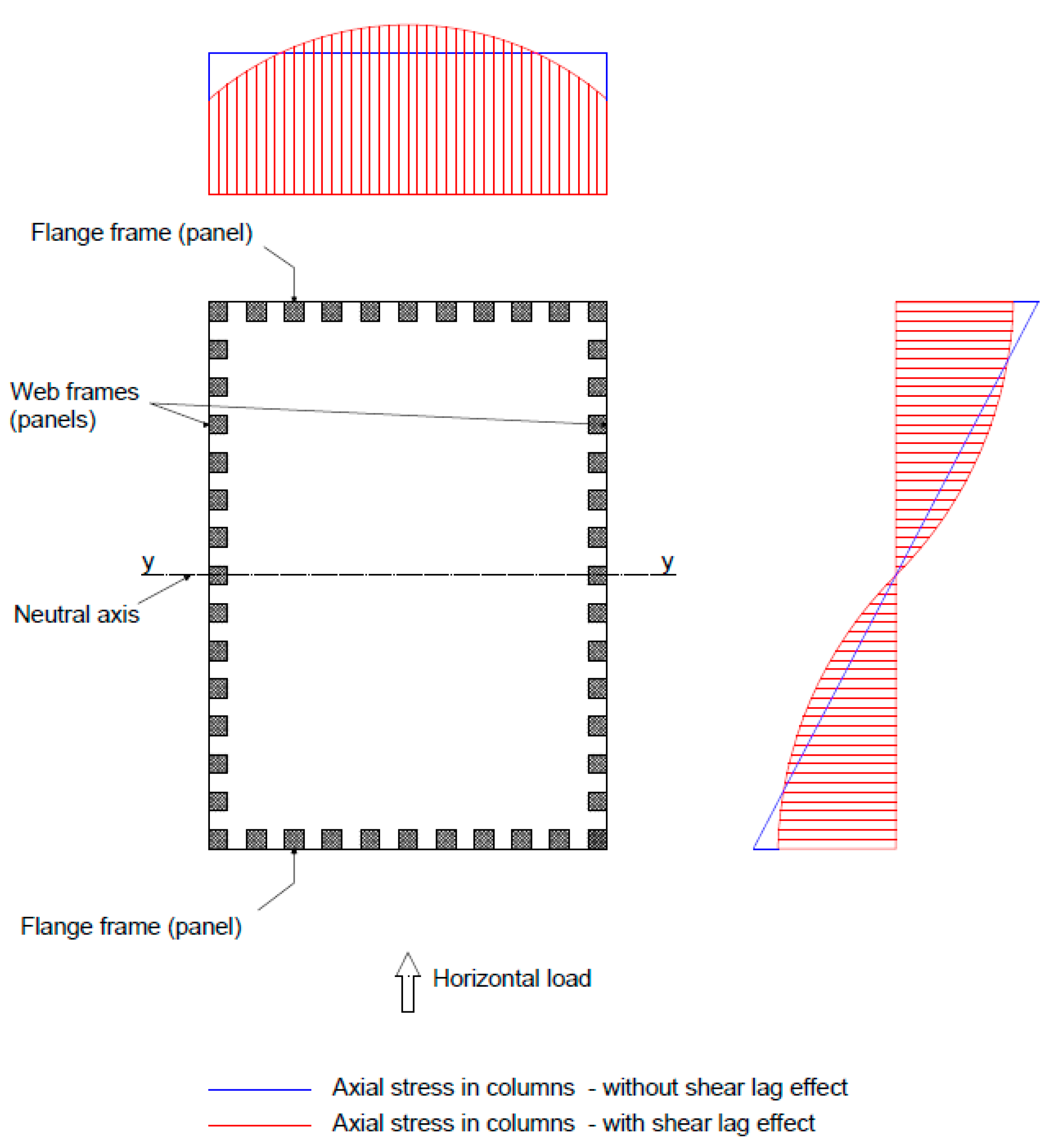
2. Shear Lag Effect in Tube Structural Systems
3. Overview of the Existing Tall Buildings with Tube Structural System
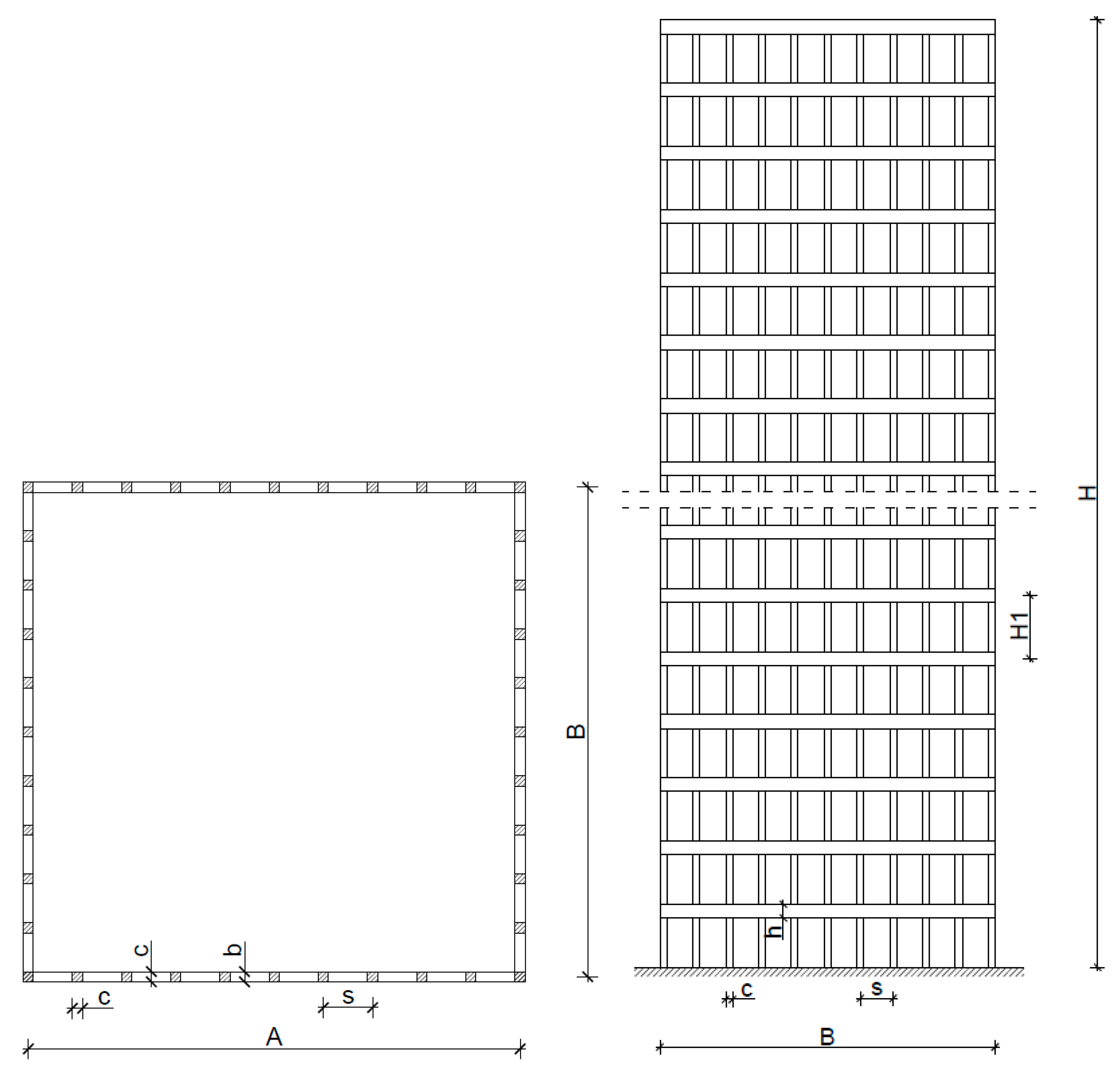
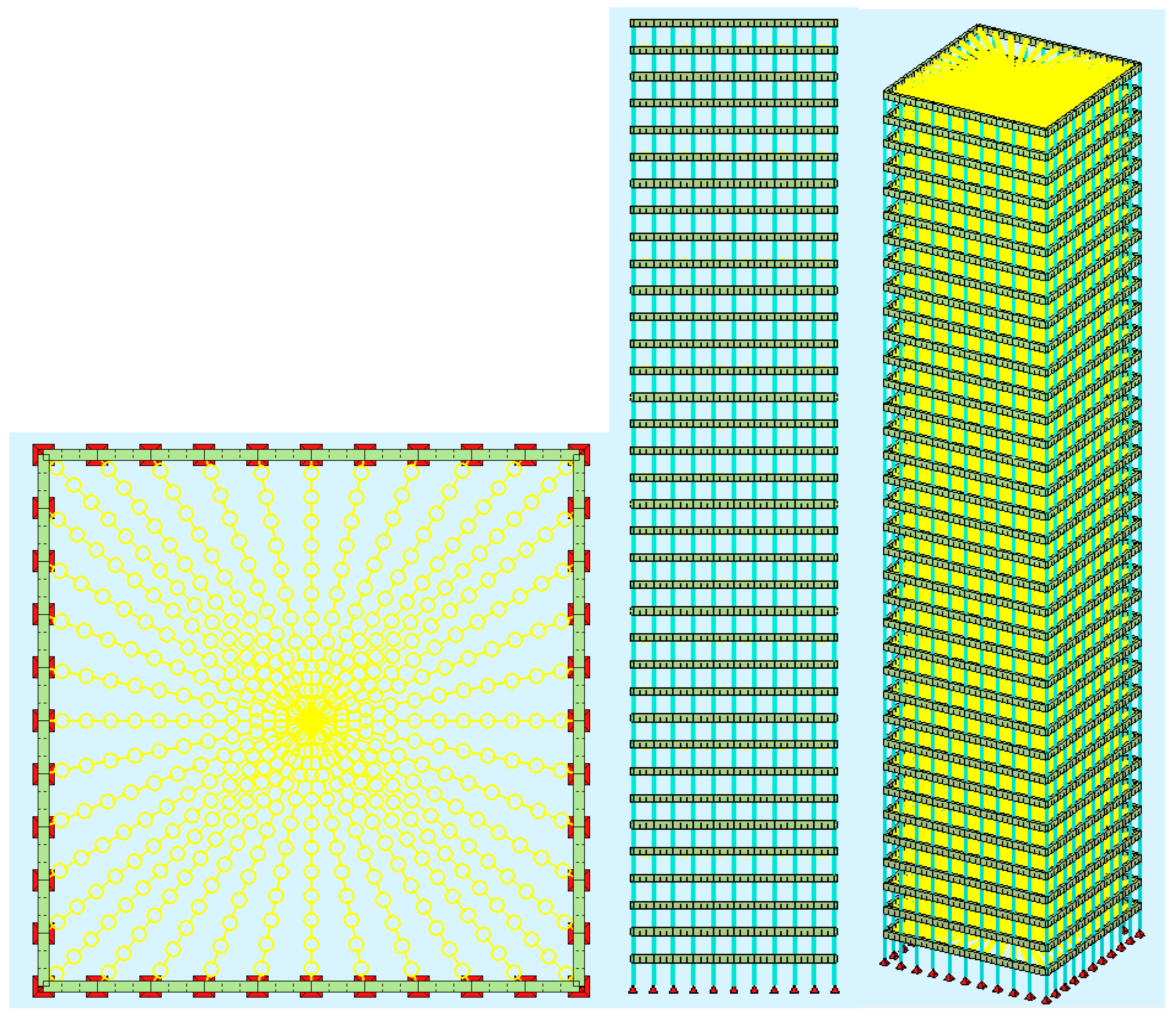
4. Computer-Based Model of the Tube Structure
- -
- Layout dimensions of the building: A/B = 24 m/24 m
- -
- Connecting beam dimensions: b/h = 0.5 m/1.0 m
- -
- Square column edge dimension: c = 0.5 m
- -
- Column spacing: s = 2.4 m
- -
- Storey height: H1 = 3.5 m
- -
- Building height: H = 126.0 m
- -
- Number of storeys: 36
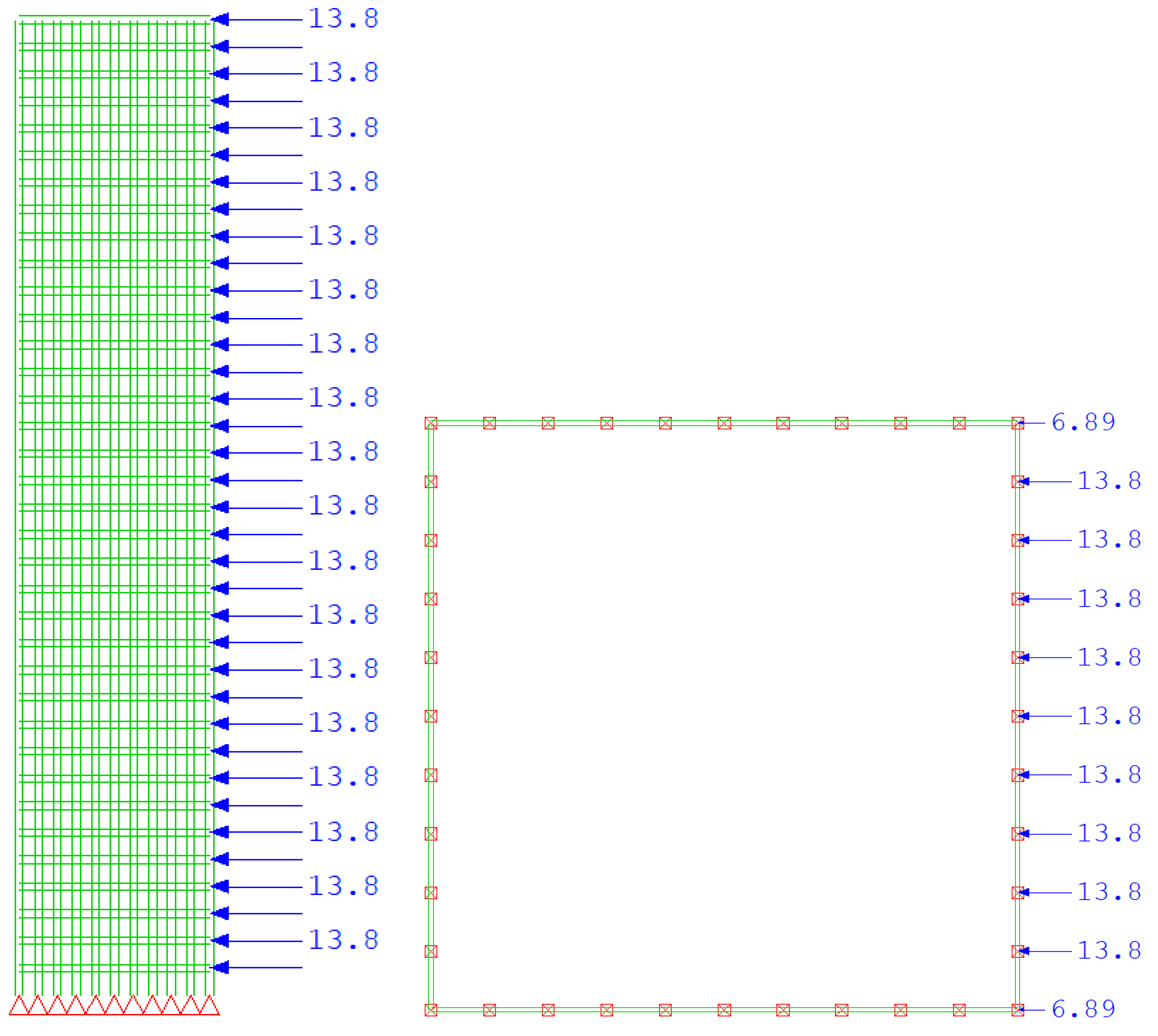
5. Parametric Analysis
- (1)
- s/c—the ratio of column spacing perpendicular to the horizontal load direction and column dimension, ranging from 4 to 6, in every next model variation one column is removed to maintain a constant building layout)
- (2)
- H1/h—the ratio of storey height and beam height (ranging from 2.9 to 4.4 with the increment of 0.1 m)
- (3)
- A/B—the ratio of building layout dimensions (ranging from 0.55 to 1.0, in each step two columns are removed on the side of the building perpendicular to the horizontal load to maintain constant column spacing
- (4)
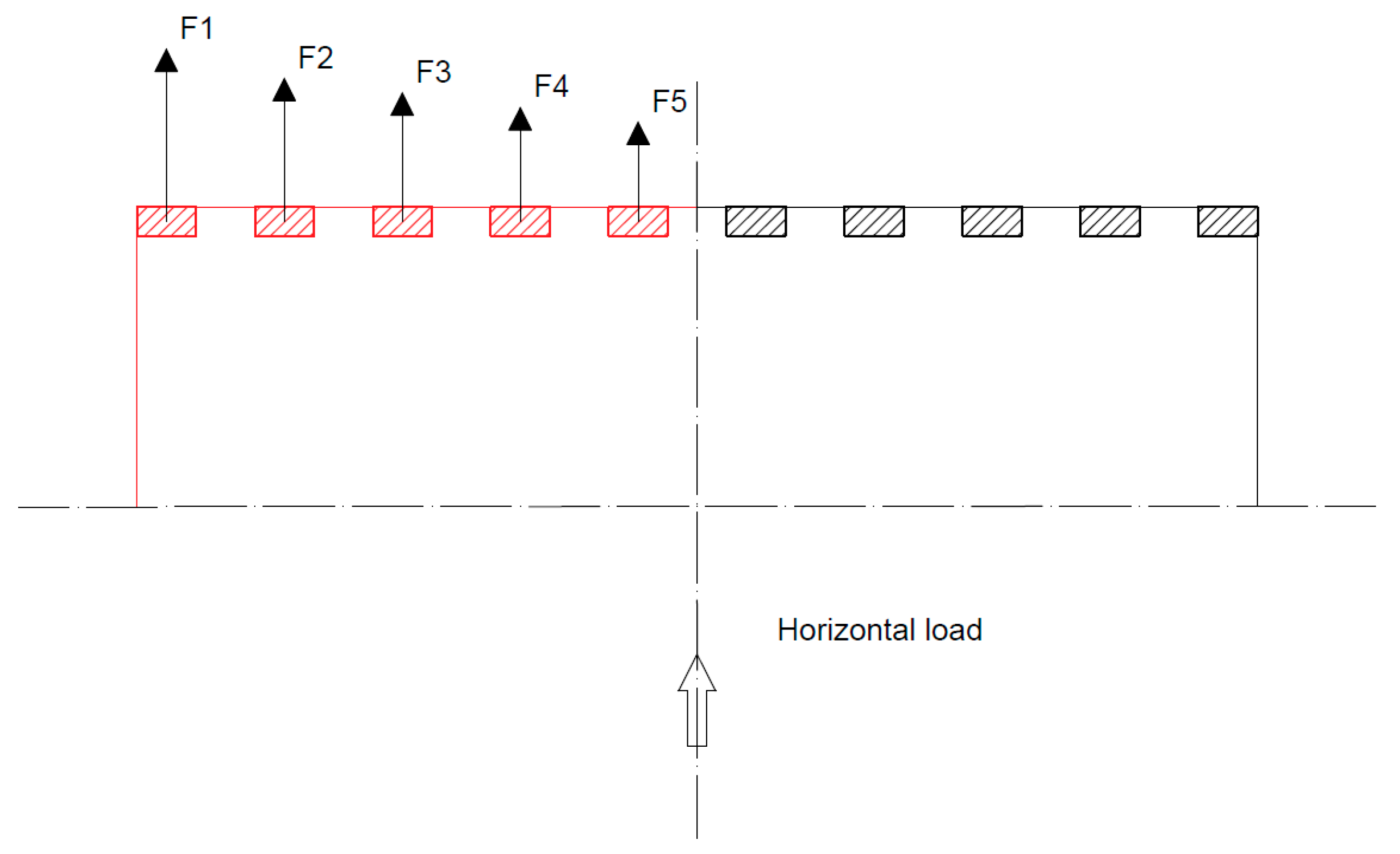
- horizontal load profile
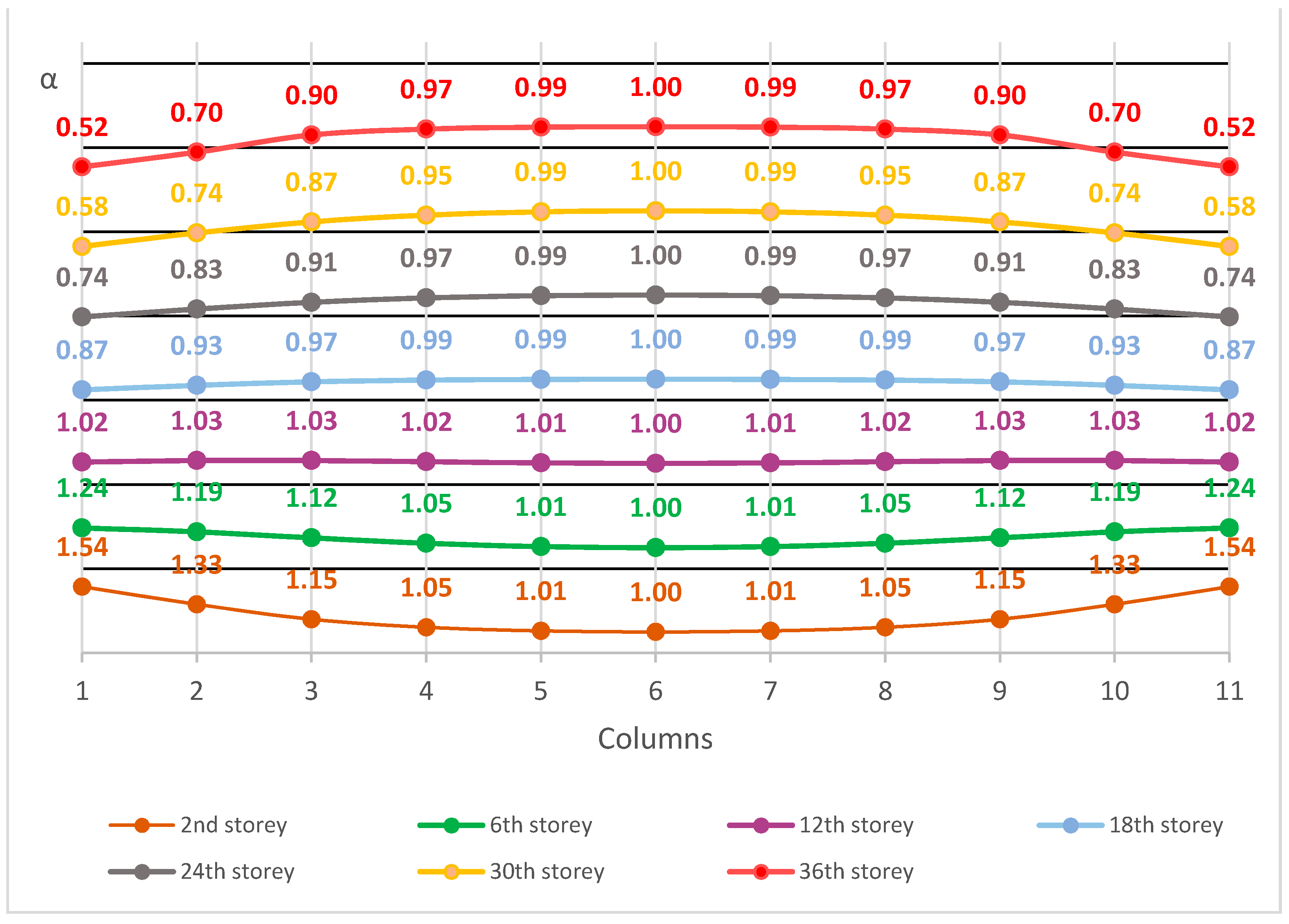
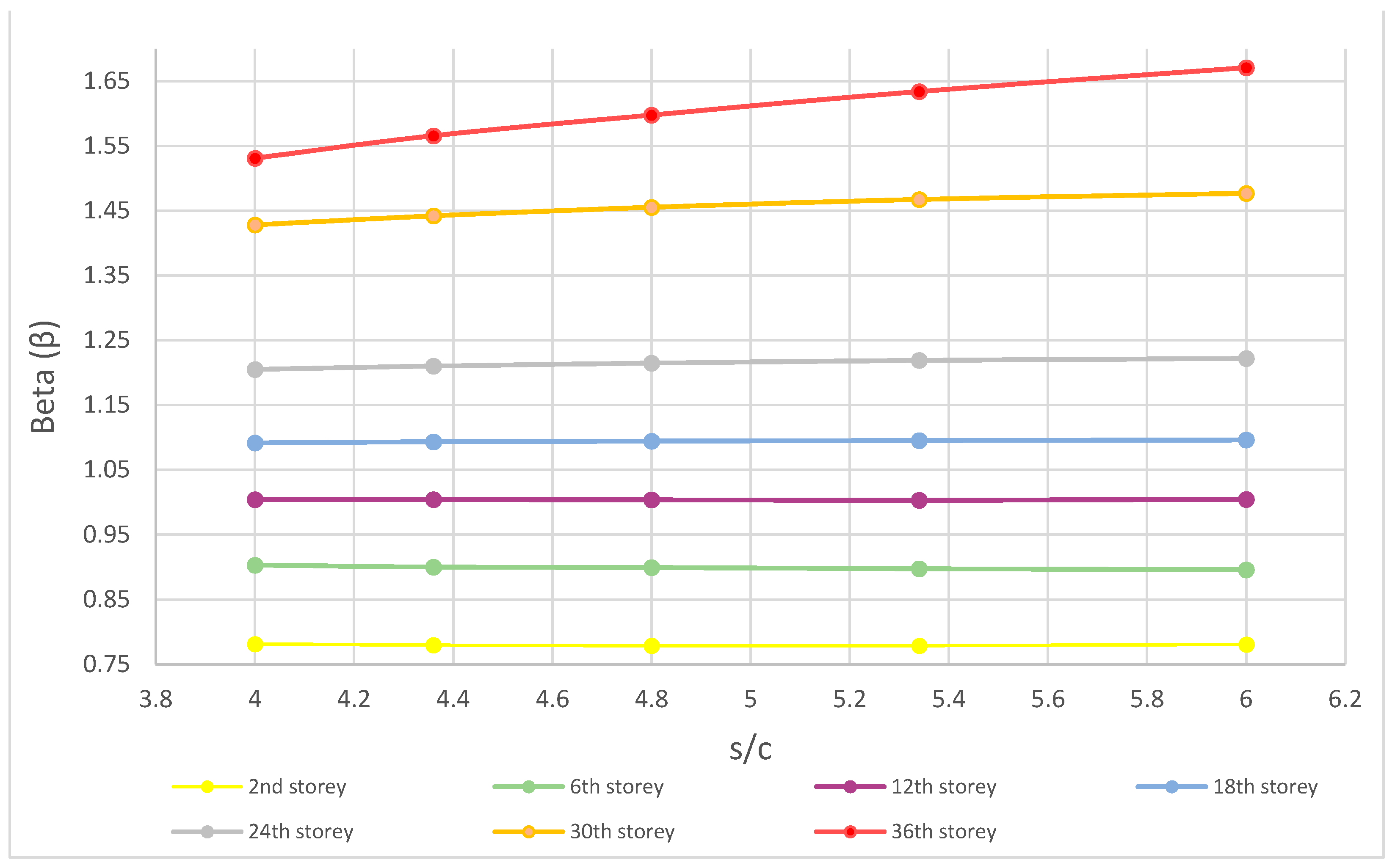
5.1. The Impact of Column Spacing on the Shear Lag Effect
- (1)
- All storeys bellow the 12th storey are in the positive shear lag effect area (β < 1). It is also clear that the column spacing for these storeys has no meaningful impact on the positive shear lag effect (the value of β for the 2nd, 6th and 12th storey is not changing).
- (2)
- The transition from the positive to the negative shear lag effect area for all column spacing variants is at the 12th storey (β = 1), which is approximately at 33% of the building height measured from the ground.
- (3)
- All storeys above the 12th storey are in the negative shear lag effect area (β > 1). It is also clear that the column spacing for these storeys has some impact on the negative shear lag effect. As the building rises, so does the coefficient β. Furthermore, the increase of coefficient β in one storey due to the variation of column spacing is more and more prominent as the building rises. While on the 18th storey this increase is mild, on the 36th storey the increase of coefficient β with the increase of column spacing is quite notable.
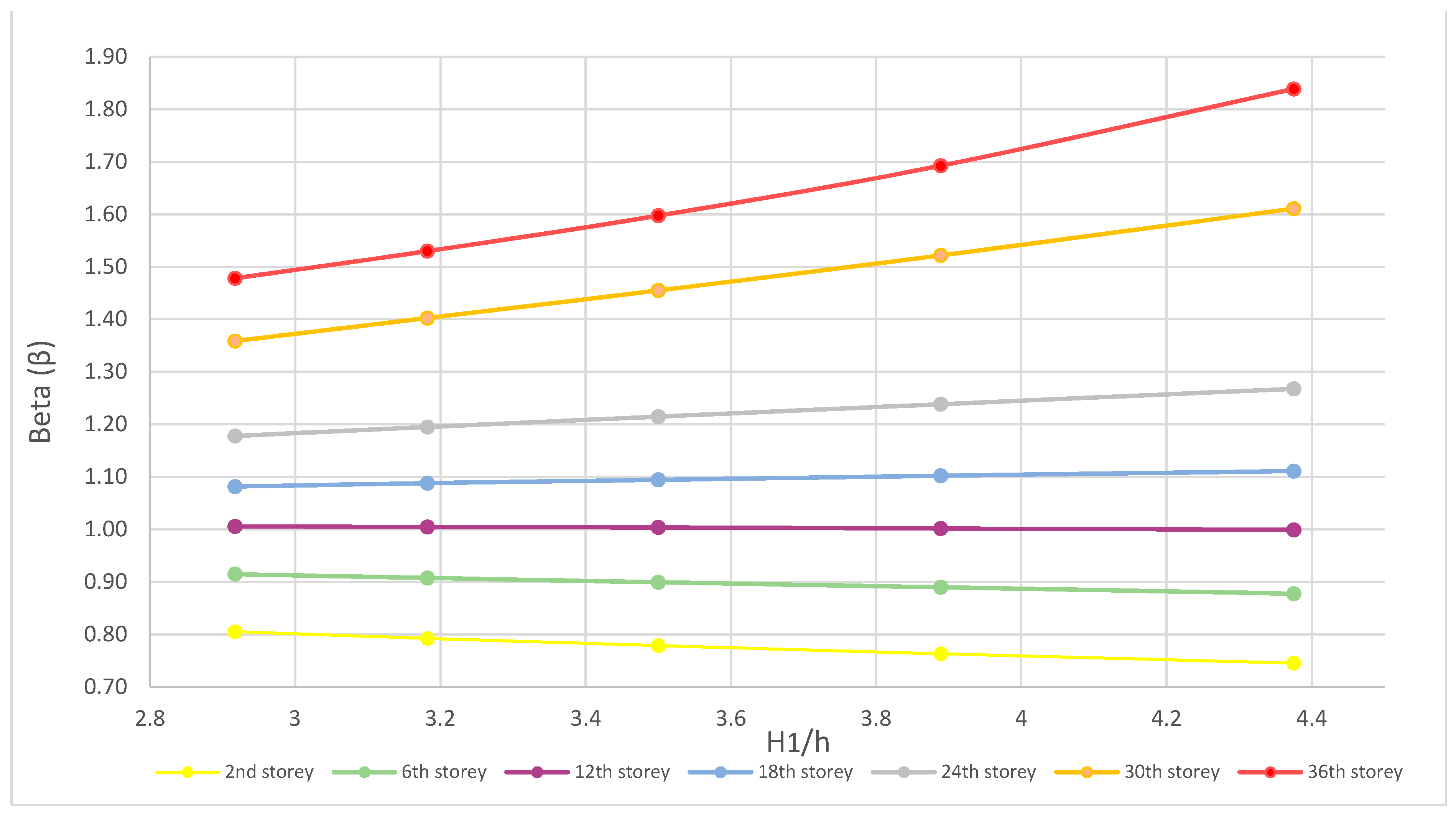
5.2. The Impact of Beam Height on the Shear Lag Effect
- (1)
- All storeys bellow the 12th storey are in the positive shear lag effect area (β < 1). For these storeys, by decreasing the beam height, the positive shear lag effect increases. Examining the curves in Figure 10 it can be concluded that the positive shear lag effect is more prominent for lower storeys of the building and that coefficient β is smallest for the ground storey.
- (2)
- The transition from the positive to the negative shear lag effect area for all beam height variants is at the 12th storey (β = 1), which is approximately at 33% of the building’s height measured from the ground.
- (3)
- All storeys above the 12th storey can be found in the negative shear lag effect area (β > 1). As the building rises, so does the coefficient β. Furthermore, the increase of coefficient β in one storey due to the variation of beam height is more and more prominent as the building rises. While on the 18th storey this increase is mild, on the 36th storey the increase of coefficient β with the decrease of beam height is quite notable.
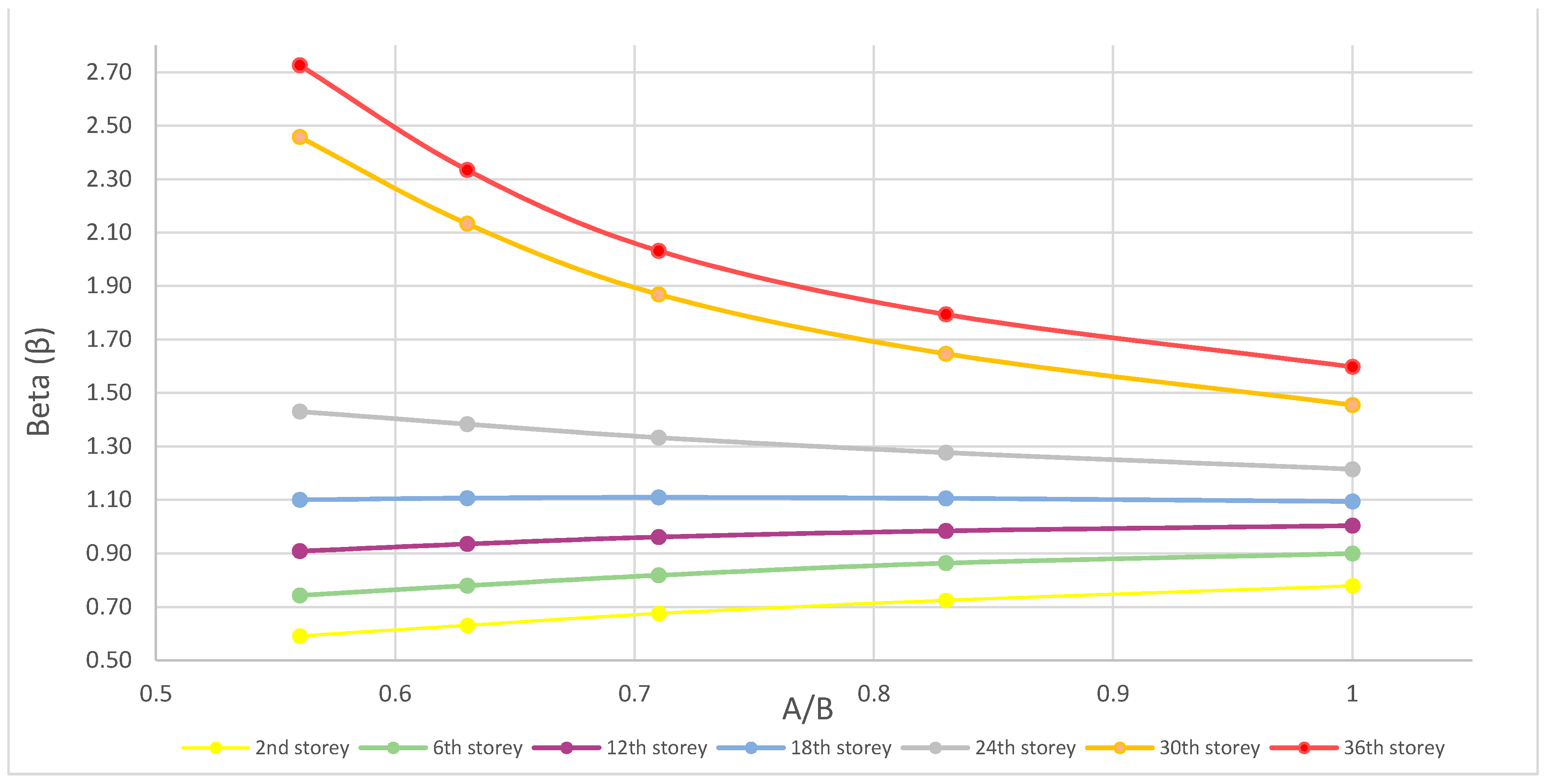
5.3. The Impact of Layout Dimensions on the Shear Lag Effect
- (1)
- The 2nd, 6th and 12th storey are in the positive shear lag effect area (β < 1). It can be concluded that the largest impact of the positive shear lag effect (lowest β) is seen in the rectangular shaped building with the ratio of floor dimensions of A/B = 0.56 and the smallest impact (highest β) is seen in the square shaped building with the ratio of floor dimensions of A/B = 1.0. In this area the positive shear lag effect is largest in the lowest storey of the building and change (increase) of coefficient β in one storey is more prominent at the lower parts of the building.
- (2)
- The transition from the positive to the negative shear lag effect area is no longer unambiguously determined with one location (12th storey in prior analyses). For the square shape of the building the value of coefficient β = 1 is reached at the 12th storey, while for the rectangular shape of the building this does not apply. The value of β = 1 for this type of floor dimensions is reached at higher storeys of the building.
- (3)
- The negative shear lag effect is largest for the building with the layout dimension ratio of A/B = 0.56 and the smallest for the ratio of A/B = 1.0. Furthermore, the change of coefficient β in one storey due to the variation of layout dimensions in the negative shear lag effect area is more and more prominent as the building rises.
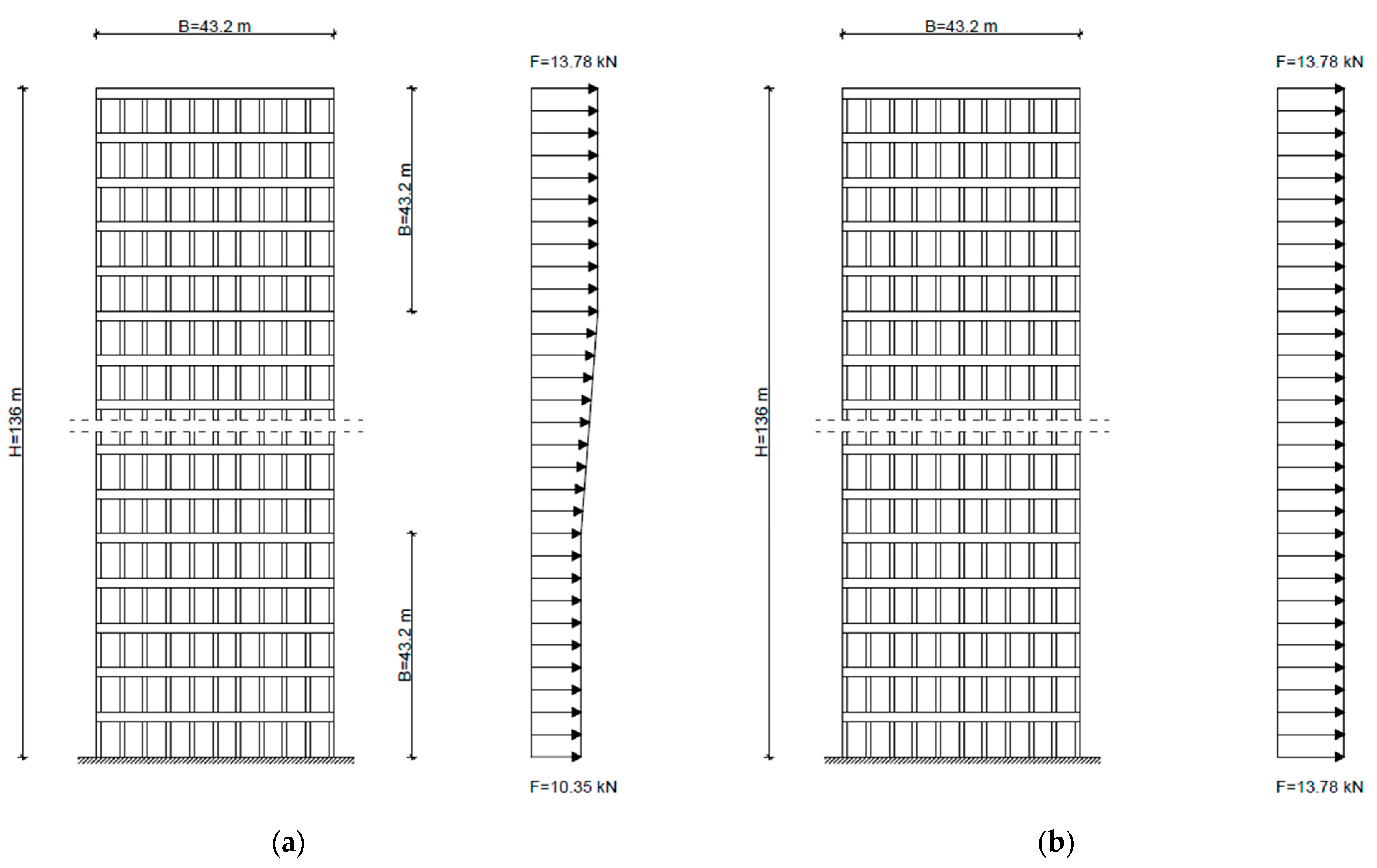
5.4. The Impact of Wind Load Type on the Shear Lag Effect
- (1)
- The 2nd, 6th and 12th storey are found in the positive shear lag effect area (β < 1). In this area the shear lag effect is more significant (smaller β) for the constant value (C) of the wind load which is most clearly seen on the 2nd storey of the building. As the building rises the gap between two wind load profiles regarding the positive shear lag effect diminishes with the positive shear effect being more prominent for the actual wind load profile on the 12th storey.
- (2)
- All storeys above the 12th storey are found in the negative shear lag effect area (β > 1). In this area the shear lag effect is more significant (larger β) for the constant value (C) of the wind load than for the actual wind load profile. As the building rises, the gap between two wind load profiles regarding the negative shear lag effect increases until the 30th storey after which the gap slightly diminishes to the buildings top.
6. Conclusions
- (1)
- The positive shear lag effect is characteristic for the lower storeys of the structure and as the structure rises, the positive shear lag decreases and gradually transforms into negative shear lag which then increases to the buildings top. This transformation usually happens at around 33% of the building height measured from the bottom to the top except in the case of the variation of the layout dimensions where the transformation happens at 50% of the building height.
- (2)
- The increase of column spacing, with the layout dimensions of the building staying the same, has no major impact on the positive shear lag effect that is characteristic for the lower storeys of the building. The position of the change from the positive to the negative shear lag is also not conditioned by the column spacing. In upper storeys, where negative shear lag appears, with the increase in column spacing the negative shear lag increases.
- (3)
- The increase of beam height results in the decrease of positive and negative shear lag effect. During the horizontal loading of tube structures due to the flexibility of beams in flange and web panels they bend under horizontal loads which results in unequal distribution of axial forces in columns of the panel. Therefore, if the beam is higher, the deformation under horizontal loads is smaller and thus the shear lag effect decreases. The storey where the transformation from the positive to the negative shear lag occurs is not conditioned by the beam height.
- (4)
- The increase in the building layout dimension on which the horizontal load acts (flange panel) results in the increase of positive and negative shear lag effect. As the flange panel widens, the cumulative deformations of flexible beams increase. The transformation from the positive to the negative shear lag is conditioned by the layout dimensions ratio in tall tube structural systems. As the flange panel on which the horizontal load acts widens, the transformation from the positive to the negative shear lag happens on progressively higher storeys of the structure.
- (5)
- The positive and negative shear lag effects are more significant for the continuous horizontal load profile with a constant value than for the actual variable wind load profile.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vlašić, A.; Puž, G.; Skokandić, D. University Manual for Tall Buildings; University of Zagreb, Faculty of Civil Engineering: Zagreb, Croatia, 2018. [Google Scholar]
- Shi, Q.; Zhang, F. Simplified calculation of shear lag effect for high-rise diagrid tube structures. J. Build. Eng. 2019, 22, 486–495. [Google Scholar] [CrossRef]
- Ghasemi, H.A. Optimal design of high-rise building bundled tube systems. Adv. Sci. Technol. Res. J. 2016, 10, 96–102. [Google Scholar] [CrossRef][Green Version]
- Zhang, Z.; Li, B. Effects of the shear lag on longitudinal strain and flexural stiffness of flanged RC structural walls. Eng. Struct. 2018, 156, 130–144. [Google Scholar] [CrossRef]
- Singh, B. Negative shear lag in framed-tube buildings. J. Struct. Eng. 1995, 120, 3105–3121. [Google Scholar] [CrossRef]
- Leonard, J. Investigation of Shear Lag Effect in High-rise Buildings with Diagrid System. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 21 May 2007. [Google Scholar]
- Lee, S.C.; Yoo, C.H.; Yoon, D.Y. Analysis of shear lag anomaly in box girders. J. Struct. Eng. 2002, 128, 1379–1386. [Google Scholar] [CrossRef]
- Chang, T.S.; Yun, D. Shear lag effect in box girder with varying depth. J. Struct. Eng. 1989, 114, 2280–2292. [Google Scholar] [CrossRef]
- Machacek, J.; Studnička, J.; Kristek, V. Coupled instability and negative shear lag phenomenon in box girders. Thin-Walled Struct. 1994, 20, 73–82. [Google Scholar] [CrossRef]
- Shushkevvich, K.W. Negative Shear Lag Explained. J. Struct. Eng. 1991, 117, 3543–3545. [Google Scholar] [CrossRef]
- Luo, Q.; Wu, Y.; Li, Q.; Tang, J.; Liu, G. A finite segment model for shear lag analysis. Eng. Struct. 2004, 26, 2113–2124. [Google Scholar] [CrossRef]
- Kwan, A.K.H. Simple method for approximate analysis of framed tube structures. J. Struct. Eng. 1994, 120, 1221–1239. [Google Scholar] [CrossRef]
- Haji-Kazemi, H.; Company, M. Exact method of analysis of shear lag in framed tube structures. Struct. Des. Tall Build. 2002, 11, 375–388. [Google Scholar] [CrossRef]
- Connor, J.J. Simple model for design of framed-tube structure. J. Struct. Eng. 1992, 117, 3623–3644. [Google Scholar] [CrossRef]
- Guan, H.; Loo, Y.-C.; Lee, K.-K. Simplified analysis of shear-lag in framed-tube structures with multiple internal tubes. Comput. Mech. 2000, 26, 447–458. [Google Scholar] [CrossRef][Green Version]
- Lee, K.-K.; Lee, L.-H.; Lee, E.-J. Prediction of shear-lag effects in framed-tube structures with internal tube(s). Struct. Des. Tall Build. 2002, 11, 73–92. [Google Scholar] [CrossRef]
- Lee, K.-K.; Loo, Y.-C.; Guan, H. Simple analysis of framed-tube structures with multiple internal tubes. J. Struct. Eng. 2001, 127, 450–460. [Google Scholar] [CrossRef]
- Samat, R.A.; Chua, F.T.; Mustakim, N.A.H.M.; Saad, S.; Abu Bakar, S. Lateral displacement and shear lag effect of combination of diagrid-frame. E3S Web Conf. 2018, 34, 01009. [Google Scholar] [CrossRef]
- Nouri, F.; Ashtari, P. Investigation of the shear lag phenomenon and structural behavior of framed-tube and braced-tube tall structures. In Proceedings of the International Conference on Civil Engineering Architecture & Urban Sustainable Development, Tabriz, East Azarbaijan, Iran, 11–12 December 2013. [Google Scholar]
- Mazinani, I.; Jumaat, M.Z.; Ismail, Z.; Chao, O.Z. Comparison of shear lag in structural steel building with framed tube and braced tube. Struct. Eng. Mech. 2014, 49, 297–309. [Google Scholar] [CrossRef]
- Gaur, H.; Goliya, R.K. Mitigating shear lag in tall buildings. Int. J. Adv. Struct. Eng. 2015, 7, 269–279. [Google Scholar] [CrossRef]
- Liu, Y.; Kopp, G.A.; Chen, S.-F. Effects of plan dimensions on gust wind loads for high-rise buildings. J. Wind. Eng. Ind. Aerodyn. 2019, 194, 103980. [Google Scholar] [CrossRef]
- Dat, B.T.; Traykov, A.; Traykova, M. Shear-lag effect and its effect on the design of high-rise buildings. E3S Web Conf. 2018, 33, 02001. [Google Scholar] [CrossRef]
- Zahiri-Hashemi, R.; Kheyroddin, A.; Farhadi, B. Effective number of mega-bracing, in order to minimize shear lag. Struct. Eng. Mech. 2013, 48, 173–193. [Google Scholar] [CrossRef]
- Pejovic, J.; Stepinac, M.; Serdar, N.; Jevric, M. Improvement of Eurocode 8 Seismic Design Envelope for Bending Moments in RC Walls of High-rise Buildings. J. Earthq. Eng. 2020. [Google Scholar] [CrossRef]
- EN 1991-1-4 “Eurocode 1: Actions on Structures—Part 1-4: General Actions: Wind Actions”. Available online: https://www.phd.eng.br/wp-content/uploads/2015/12/en.1991.1.4.2005.pdf (accessed on 4 June 2004).
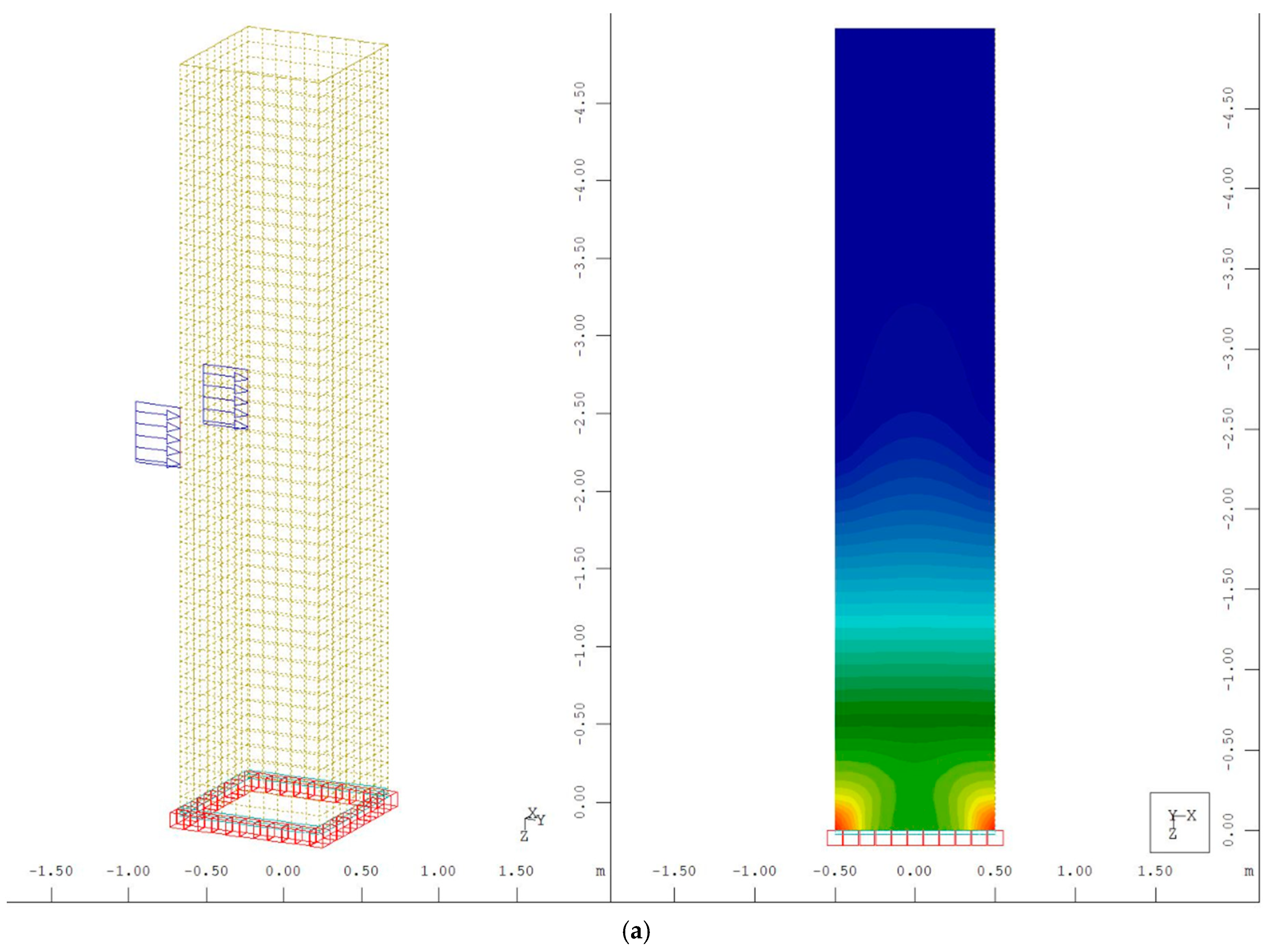
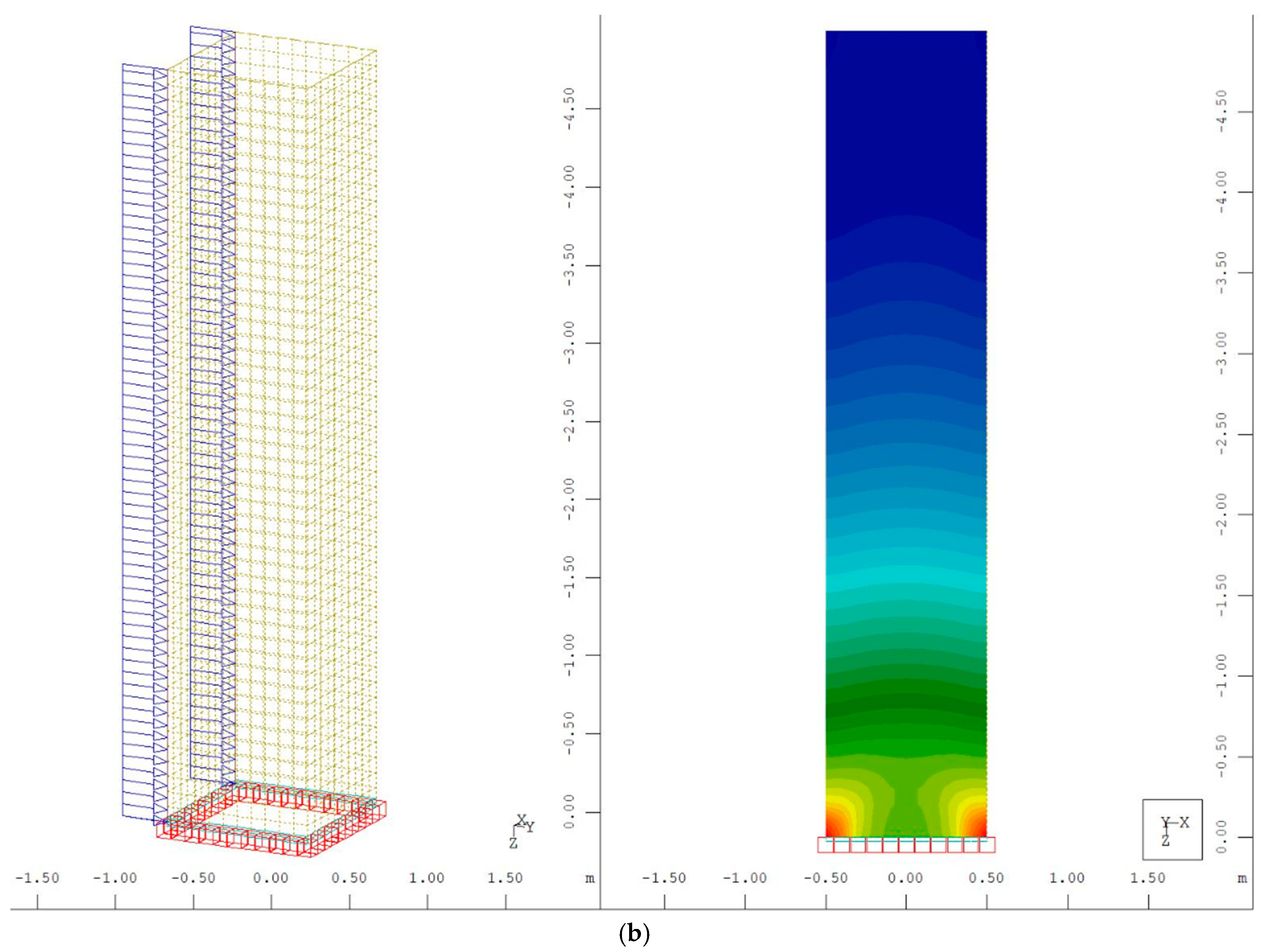
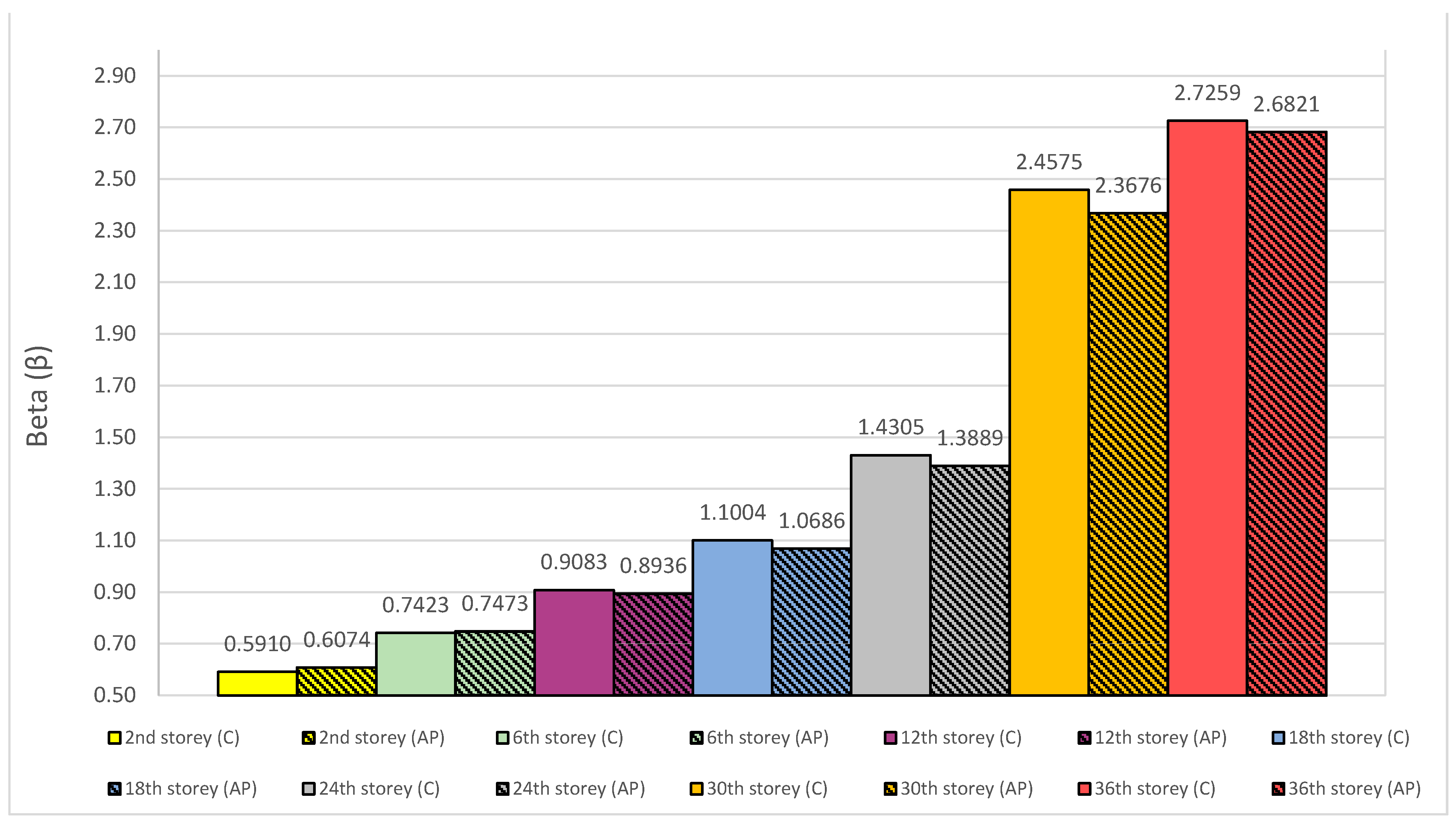
| Building | Material Used | H1/H | A/B (Squared Shape) | A/B (Rectangular Shape) | s/c |
|---|---|---|---|---|---|
| 1. The Plaza on Dewitt (Chicago) | Concrete | 2.8/120.4 = 0.0233 | - | 38/24 = 1.58 | 1.7/0.5 = 3.4 |
| 2. World Trade Center (New York) | Steel | 3.8/417 = 0.0091 | 63.4/63.4 = 1.00 | - | 1.1/0.6 = 1.83 |
| 3. Aon Center (Chicago) | Steel | 3.86/346 = 0.0112 | 59.1/59.1 = 1.00 | - | 3.0/1.0 = 3.0 |
| 4. Hancock Whitney Center (New Orleans) | Concrete/Steel | 4.15/212 = 0.0196 | - | 58.0/40.0 = 1.45 | 1.8/1.0 = 1.8 |
| 5. The Urban Hive (Seoul) | Concrete | 3.50/60 = 0.0583 | 24.0/24.0 = 1.00 | - | 1.6/0.5 = 3.2 |
| 6. Hopewell Centre (Hong Kong) | Concrete | 3.40/222 = 0.0153 | 1.00 (circular) | - | 6.0/3.0 = 2.0 |
| 7. Maya Akar business center 1 (Istanbul) | Concrete | 3.25/110 = 0.0296 | - | 31.75/24.75 = 1.28 | 3.5/1.0 = 3.5 |
| 8. Maya Akar business center 2 (Istanbul) | Concrete | 3.25/60 = 0.0542 | - | 33.50/29.45 = 1.14 | 3.5/1.0 = 3.5 |
| THE AVERAGE VALUE | - | 3.50/126 = 0.0276 | 1.00 | 1.36 | 2.75/1 = 2.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hafner, I.; Vlašić, A.; Kišiček, T.; Renić, T. Parametric Analysis of the Shear Lag Effect in Tube Structural Systems of Tall Buildings. Appl. Sci. 2021, 11, 278. https://doi.org/10.3390/app11010278
Hafner I, Vlašić A, Kišiček T, Renić T. Parametric Analysis of the Shear Lag Effect in Tube Structural Systems of Tall Buildings. Applied Sciences. 2021; 11(1):278. https://doi.org/10.3390/app11010278
Chicago/Turabian StyleHafner, Ivan, Anđelko Vlašić, Tomislav Kišiček, and Tvrtko Renić. 2021. "Parametric Analysis of the Shear Lag Effect in Tube Structural Systems of Tall Buildings" Applied Sciences 11, no. 1: 278. https://doi.org/10.3390/app11010278
APA StyleHafner, I., Vlašić, A., Kišiček, T., & Renić, T. (2021). Parametric Analysis of the Shear Lag Effect in Tube Structural Systems of Tall Buildings. Applied Sciences, 11(1), 278. https://doi.org/10.3390/app11010278






