Abstract
The increase in Power Electronic (PE) converters due to the increase in offshore wind energy deployment have given rise to technical challenges (e.g., due to unprecedented fast dynamic phenomena) related to voltage and frequency stability in the power system. In the Offshore Wind Farms (OWFs), the currently available current injection-based voltage control for PE converters are not suitable for voltage control in PE dominated systems due to the absence of continuous voltage control and ineffectiveness during islanding. Moreover, in such power systems, the conventional controllers are not suitable for frequency control due to the absence of dynamic frequency control. The paper presents the Direct Voltage Control (DVC) strategy in a real-time environment to mitigate challenges related to voltage and frequency stability during islanding of OWFs. The control strategy is implemented in the average Electro-magnetic Transient (EMT) model of Type-4 Wind Generator (WG) in RSCAD® Version 5.011.1. It is compared with the benchmark model of the control strategy in DIgSILENT PowerFactoryTM 2019 SP2 (×64) in EMT platform. The comparison based on short-term voltage stability and reactive current injection reveals that both the models provide similar results, confirming the validation of the RSCAD model. Moreover, the detailed representation of the converters in the RSCAD model provides a better depiction of the real-world operation.
1. Introduction
To combat climate change, the production of greenhouse gas emissions must be reduced to significant levels and shift to the use of Renewable Energy Sources (RES) must be accomplished. In numbers, the European Union’s (EU) Nationally Determined Contribution (NDC) under the Paris Agreement is to reduce greenhouse gas emissions by at least 40% by 2030 when compared to 1990 [1].
RES are connected to the power system through Power Electronic (PE) converters. However, PE converters do not possess inherent inertial response characteristics. Until now, the integration of RES to the power system has not created major problems since the stability of the system is maintained by the synchronous machines in power plants. Traditionally, the inertia for the power system is provided by these synchronous machines connected to the network. However, an increase in RES in the future causes an increase in PE converter based generation units. Simultaneously, the synchronous machines in conventional power plants need to be disconnected from the network. This makes the power systems weak due to low short circuit power and low system inertia. Therefore, the consequence of disconnecting the synchronous generators leads to the requirement of the PE converter based generation units to take up the role of governing the stability of the power system.
The major contributing source among the available RES is wind energy. Specifically, offshore wind energy is predicted to be the most significant source of energy among the North Sea countries by 2040 [2]. As a result, the deployment of offshore wind energy technology is expected to grow further. With the increase in integration of offshore wind energy, the inherent characteristics of offshore wind energy conversion systems will affect the nature of the power system. The vulnerable wind speed conditions due to the uncertain behaviour of wind could lead to variations in the supply and demand, and therefore, fluctuations in voltages and frequency are bound to occur. Moreover, as the power systems become weak due to the decommissioning of synchronous generators in conventional power plants that use non-renewable sources, the integration of offshore wind power plants to such weak power systems pose various research challenges on the power system stability.
One of the challenges is related to voltage stability. The continuous variation in offshore wind speed causes a constant change in the active power output of the offshore wind power plant. This could lead to an increase in the reactive power output and consequently, the voltage at the point of common coupling (PCC). The conventional current control methods using Proportional Integral (PI) controllers in the modern Wind Generators (WGs) are capable of providing voltage control by injecting reactive currents when connected to a strong network (SCR = SC/P; where SCR is the Short Circuit Ratio, SC is the Short Circuit power of the network and P is the active power generation. If SCR = 100 to 250, it is a strong grid. If SCR = 5 to 25, it is a weak grid). However, these controllers are not suitable for operation in highly PE converter dominated grids as the connected network is weak and is not capable of absorbing the injected currents. Furthermore, during the scenario of islanding, voltage control by the conventional current controllers is ineffective due to the absence of continuous voltage control, and the deviation in voltage is not high enough to activate an effective voltage reduction mechanism. There are challenges in terms of frequency stability as well since the conventional current controllers in the WGs are not equipped to provide frequency control of the network during islanding.
The drawback of these control strategies with respect to parallel operation of converters is that they require an already existing reference voltage. There are control strategies that create the reference voltage and are termed as voltage control strategies. One among the voltage control strategies is the V/F (voltage/frequency) control that is utilized for operation in the islanded mode. The drawback with V/F control is that it is not equipped for the parallel operation of various voltage forming converter units [3]. Therefore, there need to be new control strategies in the WGs that can create the reference voltage and work in parallel operation. Such control strategies are an emerging area of research and studies are being performed in this regard. Few among the new control strategies are mentioned as follows:
- Virtual Synchronous Machines (VSM): The PE converter control is modelled with the characteristics of a synchronous machine in terms of inertia and voltage support by correspondingly deriving the equivalent equations [4,5,6].
- Modified Droop Control: This strategy is common for standalone grids, where the parallel operation of voltage forming units is developed recently using the f/P (frequency/active power) and V/Q (voltage/reactive power) droop controls similar to the control in synchronous generators [7]. Few authors have named these droop control concepts as Virtual Synchronous Machines Without Inertia (VSCM0H) [8].
- Direct Voltage Control (DVC): DVC is a representation of the conventional current control approach towards a voltage control. DVC allows for the direct control of the AC converter voltage which in turn varies the current injected by the converter [9,10]. This approach provides continuous voltage control both in steady-state and dynamic scenarios.
- Extended Current Control: The control is similar to the conventional current control with an additional inertia control in the outer control loop by using a synthetic inertia controller that gives a behaviour similar to that of a synchronous machine [11,12].
The major issue with conventional control is the wind up of the integrator that causes the voltage to rise. This happens because the reference value of current remains non-zero and the measured current following islanding nearly falls to zero. In the Direct Voltage Control (DVC) implemented in Reference [9], the integrator term is avoided, and the proportional term is moved to the output end. This mitigates the above mentioned challenges related to voltage and frequency control by providing continuous voltage support without a dead band, and by providing dynamic frequency control during steady state and dynamic conditions of the network. Studies performed by I. Erlich et al. and A. Korai et al. in References [9,10] show appealing results of the implemented DVC for highly PE dominated systems. The simulations are tested for different grids based on real-world data and provide promising outcomes with effective voltage and frequency control. Hence, with such proven results and available models, the DVC strategy was chosen to be incorporated for this work.
Traditionally, the transmission of power from Offshore Wind Farm (OWF) to the offshore converter station uses a combination of 33 kV and 145 kV High Voltage Alternating Current (HVAC) cables. The OWFs are connected to an Alternating Current (AC) offshore platform using 33 kV HVAC cables. The platform holds a power transformer that is used to step-up voltage from 33 kV to 145 kV, and power is transferred from the AC platform to the offshore converter station using 145 kV HVAC cables [13]. However, the upcoming projects are expected to have a higher voltage level of 66 kV for transmission to allow twice the amount of power transferred compared to 33 kV. Therefore, this would only require 66 kV HVAC cables to directly connect OWFs to offshore converter station, avoiding the use of an AC collector platform [14].
This paper implements the DVC from Reference [9] in a digital twin representation of a 66 kV HVAC OWF network in RSCAD, and the performance of DVC is tested for highly severe dynamic conditions in the network. Such a model is unique and goes beyond the previous works performed in this direction [15]. The implementation of DVC in RSCAD depicts the real-world applicability of the control and the utilization of 66 kV HVAC offshore network is in line with the upcoming trend in offshore wind power transmission. Moreover, this model is the first important milestone in research for moving towards 2 GW models of offshore networks. Finally, the paper also compares and validates the RSCAD model against a similar digital twin representation of a 66 kV HVAC network in DIgSILENT PowerFactory with the benchmark DVC model, under similar dynamic conditions.
The sections of the paper are arranged as follows. The layout of the digital twin model in RSCAD is presented in Section 2. In Section 3, the implementation of DVC in the offshore network in RSCAD is detailed. Section 4 presents the analysis of the dynamic performance of the network in RSCAD. The digital twin representation of the model in PowerFactory is examined in Section 5. The comparison of the RSCAD and PowerFactory models is discussed in Section 6. Section 7 concludes the paper.
2. Overview of the Digital Twin Model in RSCAD
A 66 kV offshore network, as shown in Figure 1 is developed in RSCAD. The network consists of the following components:
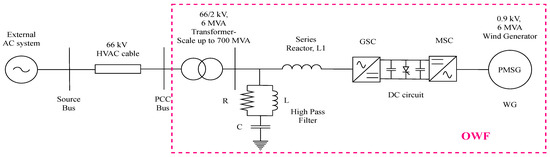
Figure 1.
Single line diagram of the 66 kV High Voltage Alternating Current (HVAC) offshore test network in RSCAD.
- An aggregated representation of ∼700 MW installed capacity OWF is modelled with the following elements:
- –
- Wind Generation System
- –
- High Pass filter (HPF) with series reactor
- –
- OWF transformer
- HVAC cables
- External AC system
2.1. Aggregated OWF
The ∼700 MW offshore wind power is represented by a single OWF consisting of 116 numbers of Type-4 WGs, each rated 6 MW connected in parallel. The aggregated model consists of PE components which require high switching frequency for operation, and hence has to be modelled for smaller time steps. For this purpose, the aggregated OWF consisting of the PE converters are modelled in a small time step environment which has a time step in the range of 1400–3750 ns in RSCAD [16]. The standard aggregated model contains the Permanent Magnet Synchronous Generator (PMSG), Machine Side Converter (MSC), Direct Current (DC) capacitors, chopper circuit, Grid Side Converter (GSC) and OWF transformer. An additional HPF with a series reactor is modelled at the output of the GSC, as illustrated in Figure 1 to mitigate harmonics content.
2.1.1. Wind Generation System
The wind generation system consists of PMSG, MSC, DC circuit and GSC. The EMT model of Type-4 WG with detailed modelling of MSC, DC circuit and GSC represented by three-level VSCs are utilized for this work. The basic models available in IEPG Section of Delft University of Technology, developed as a part of the MIGRATE project [17] is considered for this work. The control for GSC developed in Reference [18] is modified and implemented in this paper. This is explained in detail in Section 3.1.
2.1.2. High Pass Filter (HPF) with Series Reactor
The switching operation of PE converters leads to generation of harmonics. Thereby, to mitigate these harmonics, filters are provided at the output of the GSC. There are various types of filters available for this application. The common ones are the LCL filter, L filter and high pass filter [19]. In RSCAD, there is a HPF block readily available in the small time step library, as shown in Figure 2 [16]. After the HPF parameters are calculated and set, then it would only be required to tune the inductance of the series reactor to limit the flow of current and thereby stabilizing the voltage. Hence, it was decided to go with HPF.
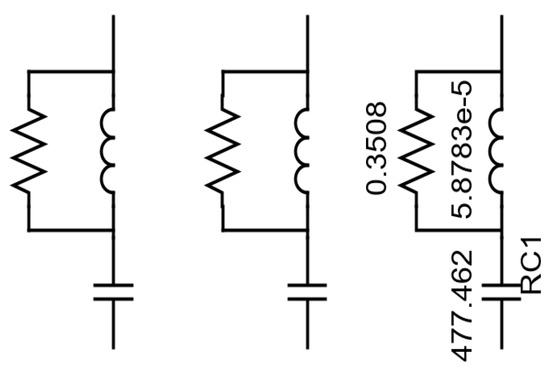
Figure 2.
High Pass Filter in RSCAD.
The base impedance on the low voltage side of transformer is calculated in ohms as in Equation (1).
The HPF should have a high impedance value at the nominal frequency (50 Hz) so that it works as an open circuit. Therefore, a higher value of 10 times base impedance is chosen. The impedance of the capacitor at 50 Hz is computed by the following equation.
Hence, the value of capacitance at 50 Hz in Farad is calculated by using Equation (3),
The next step is to calculate the inductance ’L’. The inductance must be selected so that during the switching or modulating frequency (950 Hz in this case), the impedance of the inductor and capacitor cancel each other. The switching and higher frequencies can be passed to the ground and thereby purely sinusoidal signals will be transferred to the PCC. The impedance of the inductor, resistor and capacitor must be equal at the switching frequency in order to pass the high frequencies to the ground. Therefore, to calculate inductance, it is considered as a series LC circuit. The resonant frequency of the LC circuit is given by Equation (4).
Hence, the inductance value can be calculated as per the following equation.
Upon deriving the inductance, the resistance is selected to match the impedance of the parallel inductor at the modulating frequency.
The series reactor is used for limiting the current to the AC network. The impedance value of the reactor is selected based on sensitivity analysis. A value of 0.9 mH is chosen to achieve a voltage of 1 p.u. at the PCC.
2.1.3. OWF Transformer
The GSC is connected in series to a three-phase offshore 66/2 kV, 6 MVA transformer with leakage reactance of 10%, through a series reactor and a shunt HPF as seen in Figure 1. The three-phase transformer is represented using three single-phase transformers rated 2 MVA in wye-delta connection. In RSCAD, the scaling up of power from 6 MW to the required value (∼700 MW in this case) is done by increasing the number of parallel WGs connected. This is done at the OWF transformer.
2.2. HVAC Cables
The HVAC cables transfer power from the OWF transformer to the external AC system. The HVAC cables are rated at 66 kV. When compared to 33 kV cables, 66 kV cables allow twice the amount of power to be transferred for the same area of cross-section and require lower array cabling [14].
RSCAD allows cables to be modelled as Frequency Dependent Phase, Bergeron and Pi models [16]. The Frequency Dependent Phase and the Bergeron are travelling wave models. Pi model representation of cable is chosen for this research in RSCAD. To ease the goal of comparing the performance of models in two EMT softwares, which is explained later in this section, a Pi cable model was chosen.
2.3. External AC System
The external AC system represents the infinite grid connection and is modelled as an AC voltage source. The infinite grid is similar to the representation of a synchronous generator with high inertia constant. For a strong grid, typical values of inertia constant of 5 MW/MVA depicting a synchronous generator is chosen from Reference [20]. The commonly represented damping constant is the frequency-dependent load damping constant. However, the damping constant is zero in this case as no loads and a lossless machine is considered. Alternatively, for short circuit calculations, the reference parameters given in Reference [21] can be chosen for representing an infinite grid. The parameters include short circuit power of 30 GVA and X/R of 10, where X/R = the amount of reactance X divided by the amount of resistance R. The AC source voltage is rated at 66 kV.
3. Control Structures
The control strategies are implemented for the MSC, DC chopper and GSC of the Type-4 WG. The conventional current control architecture is utilized in MSC control. The major area of interest for this paper is the control strategy of GSC. The DVC implemented in Reference [9] for a 33 kV network is implemented in the GSC for this work.
3.1. Implementation of DVC in RSCAD
The control strategy depicted in Reference [9] is achieved in RSCAD software. The control was implemented in RSCAD in Reference [18] for a 33 kV HVAC transmission network, but the final goal of achieving reactive current injection during severe dynamic conditions was lacking. The primary reason was due to the avoidance of the current limiter block that is explained later in this section. However, the block is implemented successfully in this work, and the results are illustrated. Since RSCAD allows modelling of the secondary side of the transformer as required for one WG, the control loop parameters of GSC remain the same as 33 kV for a 66 kV offshore network and are based on the benchmark values provided in Reference [22]. The parameters used for DVC is provided in Appendix A.
3.1.1. Reactive Power Control
From the control structure developed, as shown in Figure 3 and inspired by Reference [9], it can be seen that, unlike in conventional current control, the reactive current is not directly utilized for voltage control. The converter voltage is directly controlled here, and this allows the current to modify on its own according to varying network conditions. This strategy is similar to the voltage control in conventional synchronous generators. The reactive control loop consists of an outer loop based on a slow VAR controller that tracks the changes in set points required by the system-wide demand. The inner loop consists of a fast-acting controller, as the name suggests, that responds towards crucial changes in voltage where quick action is required [9].
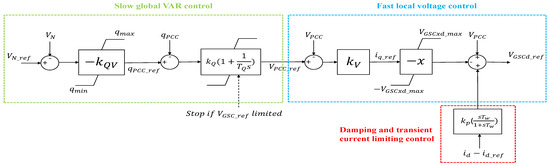
Figure 3.
Reactive power control loop.
Slow global VAR control: It is the upper-level controller and can be modelled as a power factor, reactive power or voltage controller. The reference values can be directly sent as inputs to the PI controller if the controller is made to use for reactive power or power factor control. The voltage controller is used here, and this requires reactive power reference () to be determined from a predefined voltage versus reactive power droop characteristic. A voltage value for which the injection of reactive power is zero is obtained from this characteristic. The obtained reactive power reference output is provided as input to the PI controller having a small proportional gain () and ample time constant () in order to avoid transformer tap changes and not very fast in order to avoid unwanted controller interactions. The automatic adjustment of reactive power in relation to varying voltage using the proportional gain, () is significant. There is no dead band present in order to ensure continuous voltage control. The proportional gain that represents the droop can be obtained from the following relation,
where is the difference in reference and measured voltages, is the difference in reference and measured reactive powers at the PCC.
In theory, the proportional gain can be varied with changes in power flow. But this is not practically feasible and hence it is recommended to set the reactive power reference based on load flow calculation in the network and corresponding optimum power flow (OPF) calculations. The values could be updated at regular intervals. can be determined from as,
where is desired voltage and is the voltage at which no reactive power injection is required. The reactive power limits ( and ) are the continuous values in steady state and can be computed from the P-Q diagram of the converter operation. The time constant is chosen in the range of 5–30 s wherein a value in the higher range tends to stabilize whereas a value in the lower range can cause interactions with other controllers.
The slow global VAR controller must be made inactive once the converter current limit is reached and also during cases of large voltage sags or swells by providing a signal to deactivate the controller. A scenario that could lead to the case mentioned above is a three-phase short circuit event. The output from the upper-level controller must be constant because of the chosen high integration time constant or must be limited by a blocking signal [9].
Fast local voltage control: The voltage reference output () received from the slow global VAR controller is provided as input to the fast local controller. This controller must be able to provide prompt support for grid voltage during the time of faults. The response of the controller in terms of voltage support must depend on local inputs sensed at the PCC () and not on quantities that need to be measured at remote places using a communication mechanism. A proportional gain () is used for this purpose. The proportional gain can be obtained from the following relation [9],
where is the difference in reference and measured reactive currents at the PCC.
The primary control action is provided by the feed-forward term, x, which is the reactance of the PE converter (GSC). The voltage output obtained on multiplying the current () with x is the set point voltage of GSC in steady state. The reactive power control loop parameters are provided in Table A1.
3.1.2. Active Power Control
The active power control is developed with the DC voltage, direct frequency control and Voltage Dependent Active Power Reduction (VDAPR) control, as shown in Figure 4 inspired from Reference [9]. The control of active power is provided using the q-axis component of GSC voltage as per the Equation (10). Theoretically, since the DC capacitor provides the active power control, the DC energy barrier should be made higher which is to be done by increasing the capacitor size and DC voltage when in comparison with the conventional PI based current control [9]. However, considering the practical aspect, such an increase in capacitance is not incorporated for this work and the DC voltage is not increased and is set at 4 kV. Another significant modification that was done is providing the minimum limit, , for the voltage measurement. A small value needs to be set for this parameter in RSCAD software or else an error causing division by zero would be bound to occur during the start of the simulation.
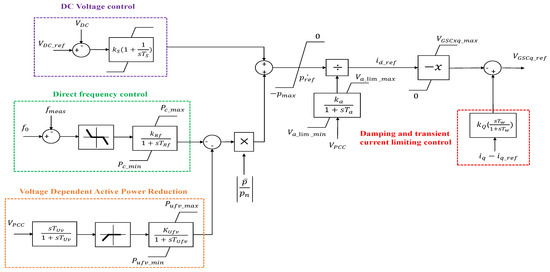
Figure 4.
Active power control loop.
The active power is calculated as follows:
where is the voltage at PCC, is the active current in the AC side of GSC and is the reactive component of voltage in the AC side of GSC.
The direct frequency control provides control in case of under frequency and over frequency. The control is modelled to be activated when the frequency is above 50.2 Hz or below 49.8 Hz. The VDAPR control is provided to control the power injection capacity of the GSC. Since power cannot be injected to the network by the GSC during the time of faults, the VDAPR allows in reducing the set point of reference power and thereby refining the dynamic stability of the network. The active power control loop parameters are provided in Table A2.
3.1.3. Current Limitation
The current limitation is an important block that protects the PE components from damage due to over current. A new maximum current () value is computed whenever the maximum current () of the PE converter is exceeded. The current limitation is incorporated in GSC based on Equations (11) and (12). The upper and lower limits for and are calculated based on the grid impedance (shown as Priority in Figure 5) and the new maximum currents ( and ) are computed. Once the reference limits are computed, the converter voltage limits are calculated by Equation (13) or by Equations (14) and (15) [9].
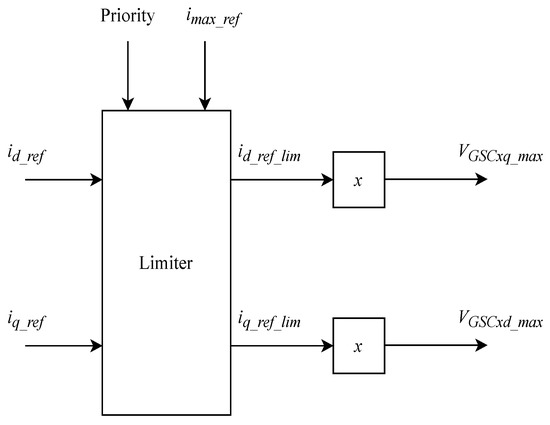
Figure 5.
Current limitation algorithm in Grid Side Converter (GSC).
If
else
As long as the reference current is not limited,
else
The current limitation parameter for DVC is provided in Table A3.
3.1.4. Voltage Limitation
The AC voltage () of the GSC is generally limited by the DC () voltage value. The factor that brings the relationship between the AC and DC voltages is the modulation index. The modulation index (m) is computed, as shown in Equation (16). The maximum value of the modulation index is set around to 1, and GSC voltage must be limited at that point to avoid non-saturation of the GSC.
4. Analysis of the Dynamic Performance of 66 kV Test System
After the 66 kV system is modelled, it has to be tested for operation in steady-state and dynamic conditions. The performance related to short-term voltage stability (fault occurring for a span of 6–10 cycles accounting for 120–200 ms) and reactive power injection by the DVC during the most severe dynamic situation in the network has to be analyzed. A three-phase short circuit in the middle of the HVAC cable is chosen to test the same.
4.1. Three-Phase Line to Ground Fault
A three-phase line to ground fault is applied at 0.5 s with a fault clearing time of 140 ms. The voltage and frequency responses are plotted for a shorter period (0.3 s to 1.3 s) to have a clearer view of the signals during the occurrence of an event. In the pre-fault condition, the voltage is stabilized at nearly 1.04 p.u., as seen in Figure 6. The frequency at the PCC computed by the Phase Locked Loop (PLL) is set to 50 Hz, and is shown in Figure 7. The OWF is generating nearly rated active power, that is, active current of nearly 1 p.u. is provided by the GSC, as depicted by the green line in Figure 8. There is no reactive current or reactive power injection by the GSC during this time, as seen from the purple line in Figure 8.
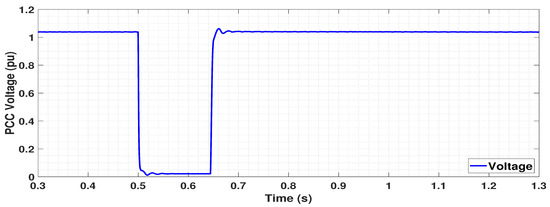
Figure 6.
Voltage at Point of Common Coupling (PCC) following a three phase fault in the middle of the cable.
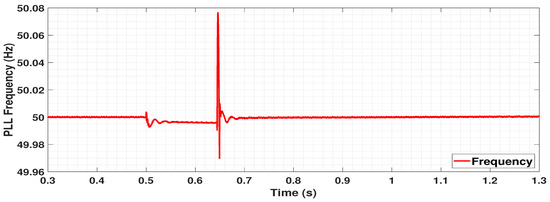
Figure 7.
Frequency response synthesised by Phase Locked Loop (PLL) following a three phase fault in the middle of the cable.
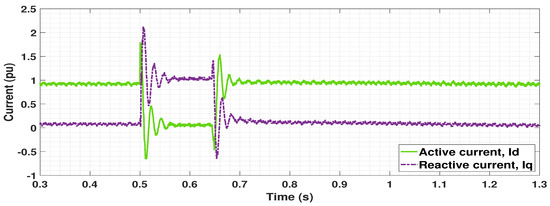
Figure 8.
Active and reactive currents flowing to the network following a three phase fault in the middle of the cable.
During the time of the fault, the voltage drops at PCC as expected for a three-phase line to ground fault. There is no significant drop in frequency since there are no loads connected to the OWF. Hence the frequency control does not get activated since deviation remains within 49.8 Hz and 50.2 Hz. DVC allows reactive current and hence reactive power to be injected by GSC during the time of fault to support the voltage, as shown in Figure 8. The corresponding behaviour is a major requirement as per the grid codes during dynamic conditions, as mentioned in Reference [23]. At the same time, the active current and thus active power is limited, and hence there is no generation from the OWF (Figure 8). As the active power output from GSC reduces, the voltage across DC link increases in order to maintain the power balance. The chopper gets activated when DC voltage goes beyond a particular limit in order to protect the DC link from overvoltage. After the fault is cleared, the DVC allows for quick recovery, the voltage and powers return to the pre-fault values.
The spike in voltage, frequency and currents after the fault is released at 0.64 s is due to the fast dynamics of DVC. Another important observation is the transients in the currents during the time of fault at 0.5 s in Figure 8. These are due to the dynamic effects that arise due to the exclusion of an integrator [9]. It can be controlled by proper tuning of washout filters.
4.1.1. Parameter Selection for Washout Filters
The damping during the transient process is ensured by the washout filters in the reactive power and active power control loops as seen in Figure 3 and Figure 4 respectively. Parameter sensitivity analysis needs to be performed for the washout filters to ensure fast damping of transients. The output of the washout filter for various proportional gains for a step response is depicted in Figure 9. The proportional gain represents values to which the output of the washout filter changes when there is a change in the input. The time constant represents the rate of this change. It can be seen that the output of the washout filter changes proportionally to the gain value specified and comes back to the initial value after a specific time, depending on the time constant mentioned.
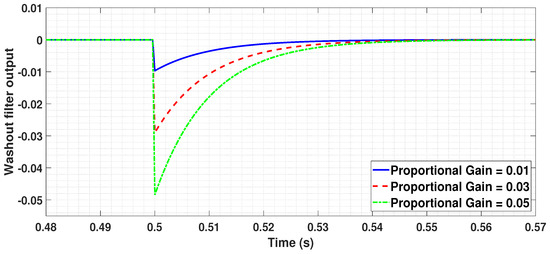
Figure 9.
Output of a washout filter for different proportional gains for a step response.
Effect of this property of washout filter is observed in the active and reactive currents at the PCC for a similar three-phase fault as performed in the previous section. Measurements are recorded between 0.45 s to 0.65 s in Figure 10 and Figure 11 for active and reactive currents, respectively to analyze the behaviour of transients. The proportional gain is set as 0.01, 0.03 and 0.05 for comparison, keeping the time constant = 0.01 s for all the three cases. It is observed that faster damping can be achieved for higher proportional gains. It makes sense as the system would try to damp the transients to the maximum possible value in order to have minimum fluctuations and also to limit interactions with other controllers during this period. Thereby, it is worthy to conclude that choosing the right parameters for the washout filter is one among the key factors in this control approach.
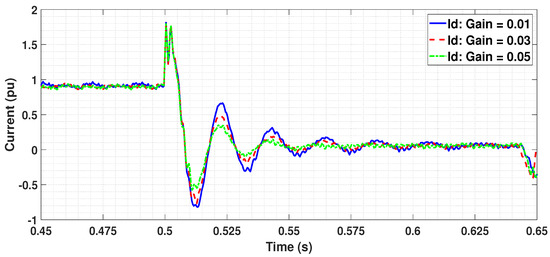
Figure 10.
Current in d axis following a three phase fault for proportional gains 0.01, 0.03 and 0.05.
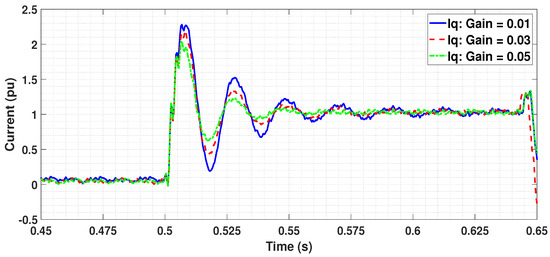
Figure 11.
Current in q axis following a three phase fault for proportional gains 0.01, 0.03 and 0.05.
5. Overview of the Digital Twin Model in PowerFactory
The 66 kV offshore network is modelled in PowerFactory as shown in Figure 12. The network consists of the following components:
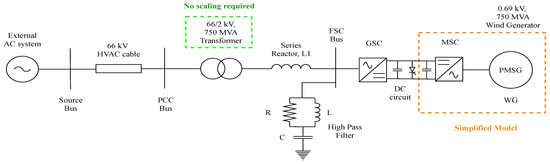
Figure 12.
Single line diagram of the 66 kV HVAC offshore test network in PowerFactory.
- A simplified model of Full Scale Converter (FSC) based Type-4 WG system consisting of the following elements:
- –
- DC circuit
- –
- GSC
- HPF with series reactor
- OWF transformer
- HVAC cables
- External AC system
5.1. Simplified FSC Based WG System
The wind turbine and MSC are simplified since they do not contribute to the dynamics of the network. GSC is modelled in detail. A constant injection of active current is proposed from the MSC to the DC side [9]. Hence it is modelled as a DC current source. The WG unit is represented as a static generator model with 750 MVA nominal apparent power. It is made to operate with constant reactive power (Q) control in order to achieve the active and reactive power set points same as in RSCAD model. The active power flow is set to ∼700 MW, similar to the RSCAD model.
5.1.1. DC Circuit
The DC circuit is detailed, and the voltage across the capacitor is set to 4 kV, same as the RSCAD model. The chopper activation control is provided when the DC voltage crosses a minimum set value.
5.1.2. GSC
Unlike the RSCAD model, a two-level GSC is utilized in this model. The PWM is not used in this model, and the GSC is modelled as a controlled voltage source. This is one among the major difference with the RSCAD model.
5.2. HPF with Series Reactor
The shunt filter available in the PowerFactory drawing toolbar is chosen. The values for R, L and C are chosen the same as mentioned in Section 2.1.2. A common impedance element available in the drawing tool is chosen for the series reactor and is connected at the output of GSC, as shown in Figure 12. The inductance value chosen is the same as the RSCAD model to have an equal impedance for both the models.
5.3. OWF Transformer
A two winding transformer available in the equipment library folder of DIgSILENT library is used. The transformer is rated 66/2 kV, 750 MVA with a wye-delta configuration to block zero sequence currents. The leakage inductance and resistance of the transformer are set the same as the RSCAD model.
5.4. HVAC Cables
The cables are rated at 66 kV same as the RSCAD model. The cable is modelled from the “Cables” section available in the equipment library in DIgSILENT library. The type of model is chosen to be the Pi model. Pi model is utilized as it is easier to input the cable parameters in terms of RLC in both RSCAD and PowerFactory.
5.5. External AC System
The external AC system in PowerFactory also represents an infinite grid. Similar to the model in RSCAD in Section 2.3, the infinite grid is modelled as an AC voltage source rated 66 kV.
5.6. Control Structures
As mentioned in Section 5.1, the wind turbine and MSC models utilized are simplified and is made to inject constant active current to the DC circuit. Hence, the control of MSC and wind turbine is not required to be modelled. However, control structures are detailed for the DC circuit and the GSC. The chopper is made to activate beyond a particular voltage limit and the benchmark model of DVC from Reference [22] is utilized here for the GSC.
6. Comparison of Models in RSCAD and PowerFactory
The major differences between the 66 kV HVAC network built in RSCAD and PowerFactory are illustrated in Table 1.

Table 1.
Differences in models in RSCAD and PowerFactory.
Representation of GSC: One of the differences in both models is the usage of average model representation of VSC with PWM in RSCAD for the GSC, whereas a controlled voltage source model is utilized in the PowerFactory model.
Scaling of power: Another significant difference between the two models is that the components connected to the secondary side of the transformer are modelled for one WG of 6 MW in RSCAD whereas it is directly modelled for ∼700 MW in PowerFactory. The scaling of power to ∼700 MW in RSCAD is done at the 66/2 kV OWF transformer, as mentioned in Section 2.1.3. This helps in modelling and analysis in the real world in terms of single WG.
However, it must be noted that these differences do not affect the performance of the control operation, and both the models have equal impedances that makes the comparison significant.
6.1. Selection of Time Step in RSCAD and PowerFactory
Before the start of the simulation, a specific time step value suitable for both the RSCAD and PowerFactory models need to be set. For RSCAD software, the ratio of large time step to small time step needs to higher than 12 if NovaCor processor is used. Since the small time step is chosen to be 2500 ns for the RSCAD model, as mentioned in Section 2.1, a value of 50 s is chosen for the large time step. The PowerFactory model is also initialized with 50 s time step.
6.2. Event Comparison in RSCAD and PowerFactory
The 66 kV offshore network model in RSCAD and PowerFactory are compared for a three-phase line to ground fault in the middle of the cable. A fault is applied at 0.5 s with a clearing time of 140 ms. The resulting voltage and current waveforms are as shown in Figure 13, Figure 14 and Figure 15 respectively. As can be observed in Figure 13, the voltage measured at PCC drops and the generation is stopped during the fault period. The voltage profile is the same in RSCAD and PowerFactory models during the pre-fault, fault and post fault conditions as can be observed. The drop in voltage in both the graphs is the same due to equal impedance in both the models.
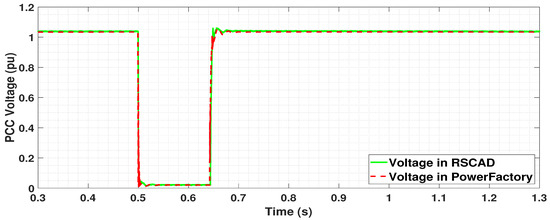
Figure 13.
Voltage measured at PCC for a three phase fault in the middle of the cable in RSCAD and PowerFactory.
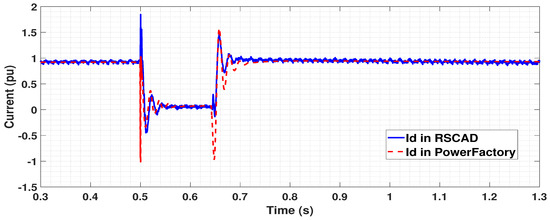
Figure 14.
Active currents flowing to the network for a three phase fault in the middle of the cable.
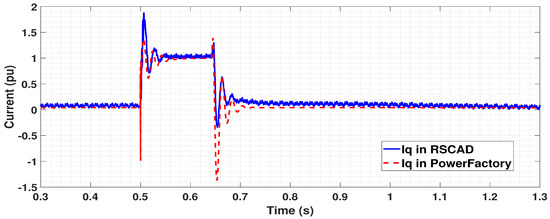
Figure 15.
Reactive currents flowing to the network for a three phase fault in the middle of the cable.
Due to the unavoidable modelling differences in the software packages, currents are measured at PCC bus for the RSCAD model and at FSC bus for the PowerFactory model. However, this does not affect the magnitude as the currents are measured in per unit. The currents in both the models have a similar profile, as summarized for the d-axis in Figure 14 and q-axis in Figure 15. The active and reactive currents generated by the WG have the same set points in both the models during the pre-fault condition, confirming that the power flow in both the models is similar. As the parameters for DVC is same for both the models, reactive power injection in RSCAD model during the time of fault is achieved similar to the PowerFactory model. The transients occurring during the time of fault at 0.5 s can be damped by controlling the parameters of the washout filters, as seen in Section 4.1.1.
Spike in the profiles at the time of fault clearance at 0.64 s is due to fast dynamics of PLL in both software packages. It is observed that the currents in RSCAD model have slight transients throughout the simulation. This is due to the detailed model representation of GSC in RSCAD when compared to a simplified representation in PowerFactory. Therefore, it can be concluded that the RSCAD model with the implemented DVC provides similar results as the benchmark PowerFactory model. Moreover, the results from RSCAD model are more detailed and hence can be used as a base model for reference as it provides a better representation of the real-world operation.
7. Conclusions
In this paper, the performance of DVC when implemented in an EMT average model of Type-4 WG connected to a 66 kV equivalent HVAC system in RSCAD is presented. The test is performed for the most severe disturbance, that is, the three-phase line to ground fault. The three-phase line to ground fault is implemented in the middle of the 66 kV HVAC cable. On viewing the voltage profile at the PCC following the fault, it is observed that DVC provides stable operation in terms of short-term voltage stability. This is due to the fast control action of the local voltage control in the reactive power loop of the DVC to support the PCC voltage during the time of the fault. In terms of reactive current injection, the DVC provides active current priority during steady state conditions and reactive current priority during the time of the fault, which is an important requirement by most of the grid codes. The effect of damping during the time of fault is controlled by the washout filters in the active and reactive power control loops. A parameter sensitivity analysis is performed for the washout filters to assess the effectiveness of damping. The performance of the implemented DVC in a average model of Type-4 WG in RSCAD for a 66 kV HVAC network is then compared with the benchmark DVC for a simplified Type-4 WG model in PowerFactory for a similar 66 kV HVAC network. The comparison is made in terms of short-term voltage stability and reactive current injection following a three-phase line to ground fault in the network. A three-phase line to ground fault in the middle of the HVAC cable is simulated in both the models in EMT platform. The voltage, active and reactive current profiles are compared and found to have good correspondence following the three-phase line to ground fault. This shows the validation of the DVC implemented in the average model of the Type-4 WG for a 66 kV HVAC offshore network in RSCAD. Moreover, it is observed that the model developed in RSCAD has slight transients in the active and reactive currents throughout the simulation. This is due to the detailed model representation of GSC in RSCAD when compared to the simplified model in PowerFactory. These results show that the RSCAD model provides a better detailed representation of the real-world operation of the implemented DVC and can be used as a reference model. The way DVC is modelled to provide voltage support during the time of fault in 66 kV HVAC network are in line with the results from previous studies, in which DVC is implemented for a 33 kV HVAC network as explained in Reference [9]. As an extension of this research, the DVC can be implemented for single-phase faults by developing a negative sequence control loop. The study can be extended for Type-3 WGs which consist of the Double Fed Induction Generator (DFIG) and selective fault analysis can be performed. Due to the increasing demand for offshore wind energy, the expansion to create large scale offshore networks (greater than or equal to 2 GW) with implemented DVC also needs to be investigated as future work.
Author Contributions
Conceptualization, S.G., A.P. and J.R.T.; formal analysis, S.G., A.P. and J.R.T.; investigation, S.G., A.P. and J.R.T.; methodology, S.G., A.P. and J.R.T.; resources, S.G., A.P. and J.R.T.; software, S.G., A.P. and J.R.T.; supervision, J.R.T., A.P., P.P. and M.v.d.M.; validation, S.G., A.P. and J.R.T.; visualization, S.G., A.P. and J.R.T.; writing—original draft, S.G., A.P. and J.R.T.; writing—review & editing, S.G., A.P., J.R.T., P.P. and M.v.d.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Acknowledgments
This research was fully funded by Delft University of Technology. The authors thank the experts and technical support staff of RTDS Technologies Inc. and DIgSILENT GmbH for the insightful discussions during the execution of this research.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A

Table A1.
Parameters of reactive power control loop in DVC.
Table A1.
Parameters of reactive power control loop in DVC.
| Parameters | Description | Unit | Value |
|---|---|---|---|
| Static gain for slow global reactive power control | p.u. | 6.6 | |
| Maximum/minimum reactive power | p.u. | 0.31 | |
| Slow global reactive power control proportional gain | p.u. | 0.002 | |
| Slow global reactive power control integral time constant | s | 15 | |
| Fast local voltage control proportional gain | p.u. | 0.2 | |
| x | Converter reactance | p.u. | 0.1 |
| Washout filter proportional gain | p.u. | 0.05 | |
| Washout filter time constant | s | 0.01 | |
| Maximum q-axis converter control voltage |

Table A2.
Parameters of active power control loop in DVC.
Table A2.
Parameters of active power control loop in DVC.
| Parameters | Description | Unit | Value |
|---|---|---|---|
| DC voltage control proportional gain | p.u. | 1 | |
| DC voltage control integral time constant | p.u. | 0.1 | |
| Proportional gain for direct frequency control | p.u. | 1 | |
| First order delay for direct frequency control | s | 0.2 | |
| Washout time constant for the voltage dependent active power reduction | s | 60 | |
| Proportional gain for voltage dependent active power reduction | p.u. | 2 | |
| First order delay for the voltage dependent active power reduction | s | 0.005 | |
| x | Converter reactance | p.u. | 0.1 |
| Washout filter proportional gain | p.u. | 0.05 | |
| Washout filter time constant | s | 0.01 | |
| Voltage measurement delay | s | 5 | |
| Deadband for direct frequency control | Hz | 0.2 | |
| Deadband for voltage dependent active power reduction | p.u. | 0.1 | |
| Maximum d-axis converter control voltage |

Table A3.
Parameters of current limitation in DVC.
Table A3.
Parameters of current limitation in DVC.
| Parameters | Description | Unit | Value |
|---|---|---|---|
| Gain for current limitation | p.u. | 1.2 |
References
- UNFCCC. Adoption of the Paris agreement. COP. In Twenty-First Session of Conference of the Parties, Paris, France, 30 November–11 December 2015; UNFCCC: Rio de Janeiro, Brazil, 2015; Volume 30. [Google Scholar]
- Ecofys. Translate COP21: 2045 Outlook and Implications for Offshore Wind in the North Seas; Technical Report; Ecofys: Utrecht, The Netherlands, 2017. [Google Scholar]
- Weise, B.; Korai, A.; Constantin, A. Comparison of Selected Grid-Forming Converter Control Strategies for Use in Power Electronic Dominated Power Systems. In Proceedings of the 18th Wind Integration Workshop, Dublin, Ireland, 16–18 October 2019; pp. 16–18. [Google Scholar]
- Markovic, U.; Chu, Z.; Aristidou, P.; Hug, G. LQR-Based Adaptive Virtual Synchronous Machine for Power Systems with High Inverter Penetration. IEEE Trans. Sustain. Energy 2018, 10, 1501–1512. [Google Scholar] [CrossRef]
- Duckwitz, D.; Welck, F.; Glöckler, C. Operational Behavior of the Virtual Synchronous Machine. In Proceedings of the Energiewende in der Stromversorgung—Systemstabilität und Systemsicherheit—12. ETG/GMA-Tagung “Netzregelung und Systemführung”, Berlin, Germany, 26–27 September 2017. [Google Scholar]
- Lu, L.; Cutululis, N.A. Virtual synchronous machine control for wind turbines: A review. J. Phys. Conf. Ser. 2019, 1356, 012028. [Google Scholar] [CrossRef]
- Bouzid, A.E.M.; Sicard, P.; Yamane, A.; Paquin, J.N. Simulation of droop control strategy for parallel inverters in autonomous AC microgrids. In Proceedings of the 2016 8th International Conference on Modelling, Identification and Control (ICMIC), Algiers, Algeria, 15–17 November 2016; pp. 701–706. [Google Scholar]
- Yu, M.; Roscoe, A.J.; Booth, C.D.; Dysko, A.; Ierna, R.; Zhu, J.; Urdal, H. Use of an inertia-less Virtual Synchronous Machine within future power networks with high penetrations of converters. In Proceedings of the 2016 Power Systems Computation Conference (PSCC), Genoa, Italy, 20–24 June 2016; pp. 1–7. [Google Scholar]
- Korai, A.W. Dynamic Performance of Electrical Power Systems with High Penetration of Power Electronic Converters: Analysis and New Control Methods for Mitigation of Instability Threats and Restoration. Ph.D. Thesis, Universität Duisburg-Essen, Duisburg, Germany, 2019. [Google Scholar] [CrossRef]
- Erlich, I.; Korai, A.; Neumann, T.; Koochack Zadeh, M.; Vogt, S.; Buchhagen, C.; Rauscher, C.; Menze, A.; Jung, J. New Control of Wind Turbines Ensuring Stable and Secure Operation Following Islanding of Wind Farms. IEEE Trans. Energy Convers. 2017, 32, 1263–1271. [Google Scholar] [CrossRef]
- Duckwitz, D. Derivation of Requirements and Comparison of Inertia Emulation Methods for Converter-based Power PlantsPower System Inertia. Ph.D. Thesis, Universität Kassel, Kassel, Germany, 2019. [Google Scholar] [CrossRef]
- Liu, X.; Lindemann, A. Control of VSC-HVDC Connected Offshore Windfarms for Providing Synthetic Inertia. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 6, 1407–1417. [Google Scholar] [CrossRef]
- Abdelwahed, M.A.; El-Saadany, E.F. Power Sharing Control Strategy of Multiterminal VSC-HVDC Transmission Systems Utilizing Adaptive Voltage Droop. IEEE Trans. Sustain. Energy 2016, 8, 605–615. [Google Scholar] [CrossRef]
- DNV.GL. 66 kV Systems for Offshore Wind Farms; Technical Brochure; DNV.GL: Arnhem, The Netherlands, 2015. [Google Scholar]
- Lozada Ayala, P. Dynamic System Performance Analysis of a Novel Grid Connection Topology for Offshore Wind Farms Using MMC-HVDC Transmission. 2018. Available online: https://repository.tudelft.nl/islandora/object/uuid%3Abfd0ac94-fc5b-46e4-a049-742c5249138a (accessed on 27 December 2020).
- RTDS Technologies Inc. RSCAD Modules. Available online: https://knowledge.rtds.com/hc/en-us/articles/360037537653-RSCAD-Modules (accessed on 27 December 2020).
- The MIGRATE Project, A EU-Funded Project Under the Framework of European Union’s HORIZON 2020. 2020. Available online: https://www.h2020-migrate.eu/#:~:text=The%20MIGRATE%20Project&text=MIGRATE%20stands%20for%20Massive%20InteGRATion,especially%20in%20future%20faced%20with. (accessed on 27 December 2020).
- Sethi, S. Real-Time Implementation for Gird Forming Control of Type-4 Wind Turbine to Mitigate Voltage and Frequency Instabilities in High Renewable Penetration. Master’s Thesis, NTNU, Trondheim, Norway, 2019. [Google Scholar]
- Beres, R.N.; Wang, X.; Liserre, M.; Blaabjerg, F.; Bak, C.L. A Review of Passive Power Filters for Three-Phase Grid-Connected Voltage-Source Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 54–69. [Google Scholar] [CrossRef]
- Kothari, D.P.; Nagrath, I. Modern Power System Analysis; Tata McGraw-Hill Education: New Delhi, India, 2003. [Google Scholar]
- Guide for the Development of Models for HVDC Converters in a HVDC Grid. Technical Brochure, CIGRE Working Group B4.57. 2014. Available online: https://e-cigre.org/publication/604-guide-for-the-development-of-models-for-hvdc-converters-in-a-hvdc-grid (accessed on 27 December 2020).
- Erlich, I.; Korai, A. Description, Modelling and Simulation of a Benchmark System for Converter Dominated Grids (Part I). 2018. Available online: https://www.digsilent.de/en/faq-reader-powerfactory/do-you-have-an-example-of-a-fault-tolerant-power-system-with-98-share-of-renewables.html (accessed on 27 December 2020).
- Mohseni, M.; Islam, S.M. Review of international grid codes for wind power integration: Diversity, technology and a case for global standard. Renew. Sustain. Energy Rev. 2012, 16, 3876–3890. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).