Conceptual Design of Composite Bridge Sandwich Structure
Abstract
1. Introduction
2. Methods and Materials
2.1. Material Constraints
2.2. Instability Constraint
2.3. Structural Design (Limit State Design)
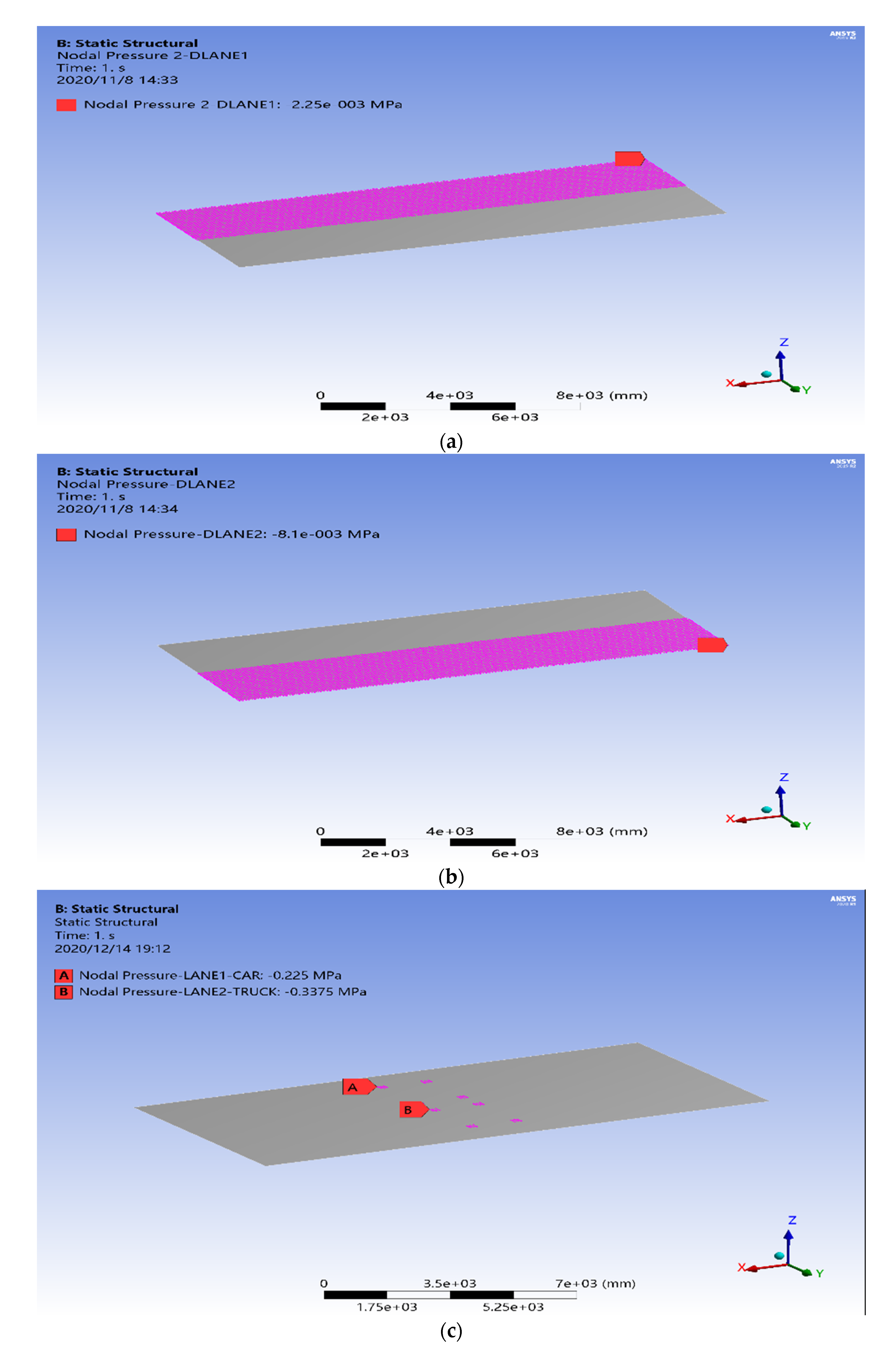
2.4. Finite Element Model of the Bridge Deck
2.5. Materials
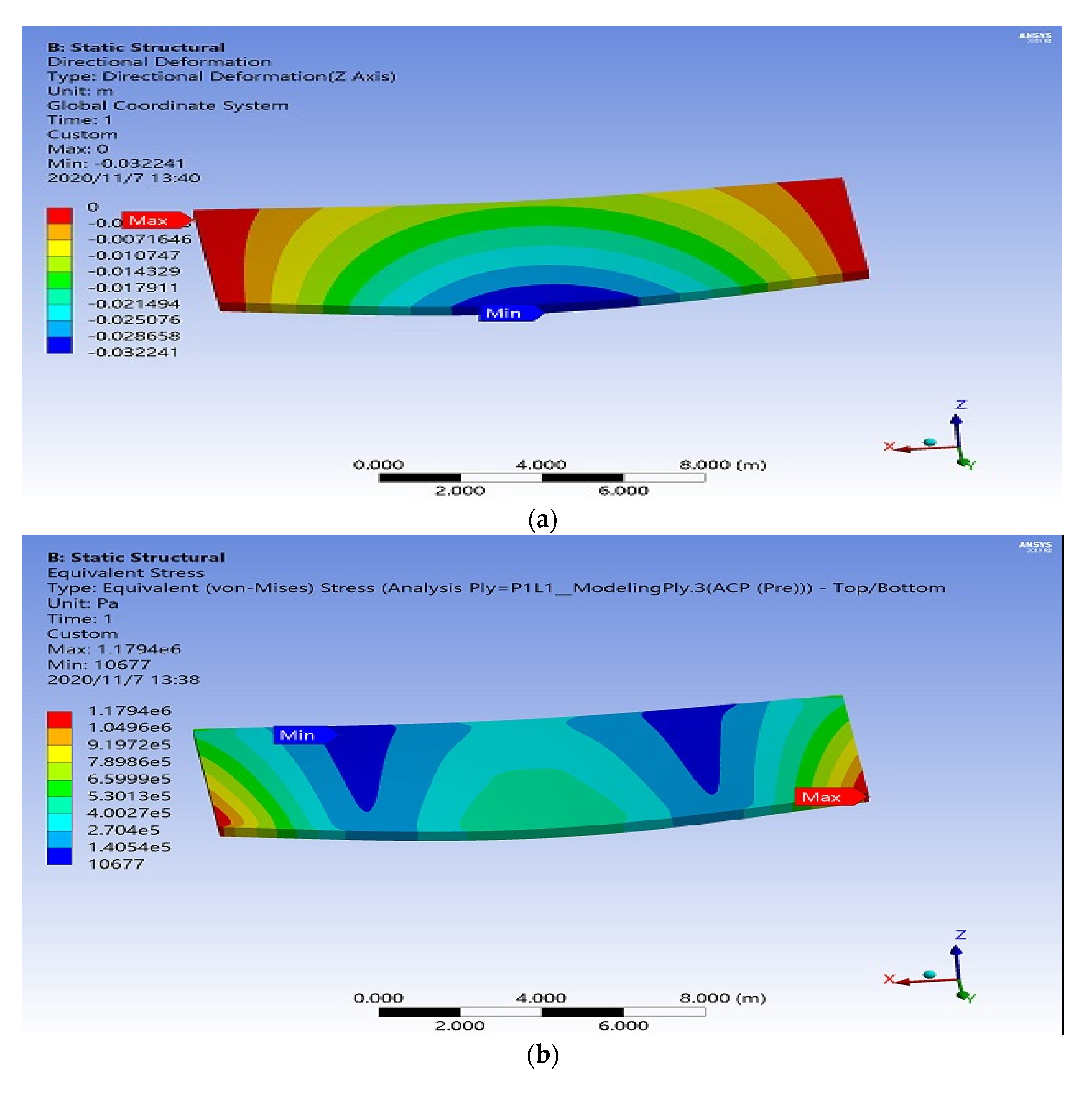
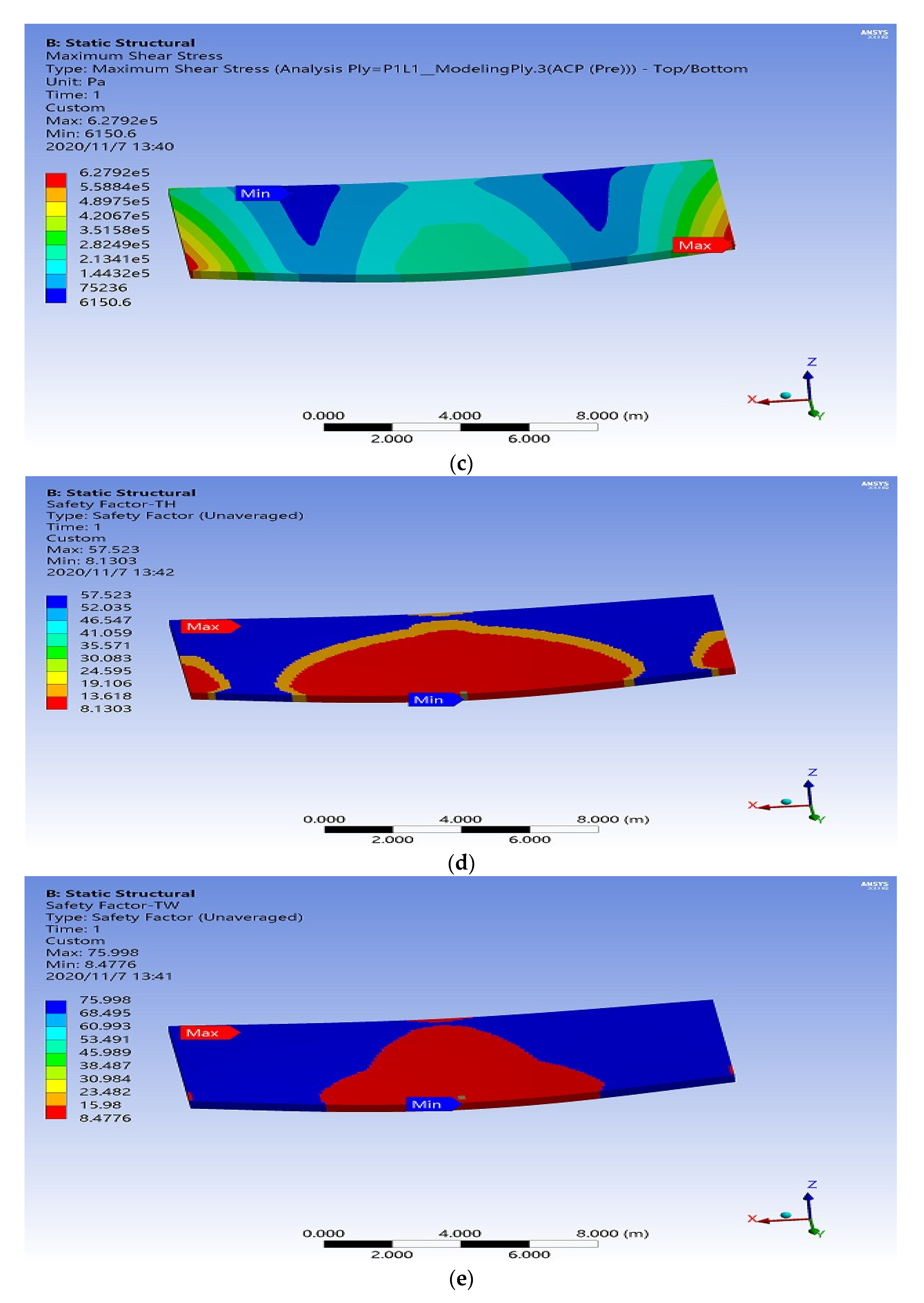
3. Results and Discussion
3.1. Lay-up [45/−45]
3.2. Lay-Up [0/90]
3.3. Best Bridge Configuration
4. Graphical Evaluation and Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, T.; Cho, J.-U. A study on damage and penetration behaviour of carbon fiber reinforced plastic sandwich at various impacts. Int. J. Precis. Eng. Manuf. 2015, 16, 1845–1850. [Google Scholar] [CrossRef]
- Fotsing, E.R.; Leclerc, C.; Sola, M.; Ross, A.; Ruiz, E. Mechanical properties of composite sandwich structures with core or face sheet discontinuities. Compos. Part B Eng. 2016, 88, 229–239. [Google Scholar] [CrossRef]
- Yan, L.; Kasal, B.; Huang, L. A review of recent research on the use of cellulosic fibres, their fibre fabric reinforced cementitious, geo-polymer and polymer composites in civil engineering. Compos. Part B Eng. 2016, 92, 94–132. [Google Scholar] [CrossRef]
- Javaid, U.; Khan, Z.M.; Khan, M.B.; Bassyouni, M.; Abdel-Hamid, S.M.-S.; Abdel-Aziz, M.H.; ul Hasan, S.W. Fabrication and thermo-mechanical characterization of glass fiber/vinyl ester wind turbine rotor blade. Compos. Part B Eng. 2016, 91, 257–266. [Google Scholar] [CrossRef]
- Jayaseelan, D.D.; Xin, Y.; Vandeperre, L.; Brown, P.; Lee, W.E. Development of multi-layered thermal protection system (TPS) for aerospace applications. Compos. Part B Eng. 2015, 79, 392–405. [Google Scholar] [CrossRef]
- Wu, H.-C.; Yan, A. Durability simulation of FRP bridge decks subject to weathering. Compos. Part B Eng. 2013, 51, 162–168. [Google Scholar] [CrossRef]
- Wang, C.; Shankar, K.; Morozov, E.V. Global design and analysis of deep sea FRP composite risers under combined environmental loads. Adv. Compos. Mater. 2017, 26, 79–98. [Google Scholar] [CrossRef]
- Imran, M.; Shi, D.; Tong, L.; Muhammad, H. Design optimization of composite submerged cylindrical pressure hull using genetic algorithm and finite element analysis. Materials 2019, 190, 145. [Google Scholar] [CrossRef]
- ASTM. Standard Terminology of Structural Sandwich Constructions; ASTM International: West Conshohocken, PA, USA, 1999. [Google Scholar]
- Yang, G.; Shi, Z.; Mo, N.; Zhao, L. Research on active magnetic bearing applied in Chinese modular high-temperature gas-cooled reactor. Prog. Nucl. Energy 2014, 77, 352–360. [Google Scholar] [CrossRef]
- Abrate, S.; Castanié, B.; Yapa, D.S.R. Dynamic Failure of Composite and Sandwich Structures; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-94-007-5329-7. [Google Scholar]
- Waqas, M.H.; Shi, D.; Imran, M.; Khan, S.Z.; Tong, L.; Ahad, F.; Zaidi, A.A.; Iqbal, J.; Ahmed, W. Conceptual Design of Composite Sandwich Structure Submarine Radome. Materials 2019, 12, 1966. [Google Scholar] [CrossRef]
- Ferdous, W.; Manalo, A.; Aravinthan, T.; Fam, A. Flexural and shear behaviour of layered sandwich beams. Constr. Build. Mater. 2018, 173, 429–442. [Google Scholar] [CrossRef]
- Tomlinson, D.; Fam, A. Flexural behavior of precast concrete sandwich wall panels with basalt FRP and steel reinforcement. PCI J. 2015. [Google Scholar] [CrossRef]
- CoDyre, L.; Mak, K.; Fam, A. Flexural and axial behaviour of sandwich panels with bio-based flax fibre-reinforced polymer skins and various foam core densities. J. Sandw. Struct. Mater. 2018, 20, 595–616. [Google Scholar] [CrossRef]
- Keller, T. Recent all-composite and hybrid fibre-reinforced polymer bridges and buildings. Prog. Struct. Eng. Mater. 2001, 3, 132–140. [Google Scholar] [CrossRef]
- Zureick, A. Fiber Reinforced Polymeric Bridge Decks. Struct. Eng. Rev. 1995, 7, 257–266. [Google Scholar]
- Kim, Y.J. State of the practice of FRP composites in highway bridges. Eng. Struct. 2019, 179, 1–8. [Google Scholar] [CrossRef]
- Robinson, M.J.; Kosmatka, J.B. Lightweight fiber-reinforced polymer composite deck panels for extreme applications. J. Compos. Constr. 2008, 12, 344–354. [Google Scholar] [CrossRef]
- Keller, T.; Rothe, J.; de Castro, J.; Osei-Antwi, M. GFRP-balsa sandwich bridge deck concept, design and experimental validation. J. Compos. Constr. 2013, 18, 04013043. [Google Scholar] [CrossRef]
- Nair, A.; Cai, C.S.; Kong, X.; Hou, S. Bridge Retrofitting Using FRP-Wrapped Balsa Wood Deck: Experimental Study and Field Evaluation. J. Aerosp. Eng. 2019, 32, 04019065. [Google Scholar] [CrossRef]
- Kulpa, M.; Siwowski, T. Stiffness and strength evaluation of a novel FRP sandwich panel for bridge redecking. Compos. Part B 2019, 167, 207–220. [Google Scholar] [CrossRef]
- Li, Z.; He, M.; Tao, D.; Li, M. Experimental buckling performance of scrimber composite columns under axial compression. Compos. Part B Eng. 2015, 86, 203–213. [Google Scholar] [CrossRef]
- Gilfillan, R.; Gilbert, S.; Patrick, G. The improved performance of home-grown timber glulam beams using fibre reinforcement. J. Inst. Wood Sci. 2001, 15, 307–317. [Google Scholar]
- Buell, T.W.; Saadatmanesh, H. Strengthening timber bridge beams using carbon fiber. J. Struct. Eng. 2005, 131, 173–187. [Google Scholar] [CrossRef]
- Bascule FRP Composite Footbridge FIRECO, Client: Vaerste AS and Fredrikstad Commune, Design: Griff kommunikasjon. Available online: http://.fireco.no/wp-content/uploads/2019/03/Gangbru-Vesterelven.pdf (accessed on 15 February 2020).
- Osei-Antwi, M.; de Castro, J.; Vassilopoulos, A.P.; Keller, T. Structural limits of FRP-balsa sandwich decks in bridge construction. Compos. Part B 2014, 63, 77–84. [Google Scholar] [CrossRef]
- Orifici, A.C.; Herszberg, I.; Thomson, R.S. Review of methodologies for composite material modelling incorporating failure. Compos. Struct. 2008, 86, 194–210. [Google Scholar] [CrossRef]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using Abaqus, 1st ed.; CRC Press Taylor nd Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Lopez, R.H.; Miguel, L.F.F.; Belo, I.M.; Cursi, J.E.S. Advantages of employing a full characterization method over FORM in the reliability analysis of laminated composite plates. Compos. Struct. 2014, 107, 635–642. [Google Scholar] [CrossRef]
- Kaw, A.K. Mechanics of Composite Materials, 2nd ed.; Mechanical and Aerospace Engineering Series; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- The European Union. Eurocode: BS EN 1990:2002+A1:2005 Basics of Structural Design; The European Union: Brussels, Belgium, 2005. [Google Scholar]
- Empfehlung, B. Tragende Kuststoffbauteile im Bauwesen—Entwurf, Bemessung und Konstruktion; Bau-Überwachungsverein: Berlin, Germany, 2010. [Google Scholar]
- Clarke, J.L. Structural Design of Polymer Composites—Eurocomp Design Code and Handbook; E & FN Spon: London, UK, 1996. [Google Scholar]
- European Standard. Eurocode 2-Part 2. Design of Concrete Structures: Concrete Bridges-Design and Detailing Rules; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
- Thai, H.-T.; Choi, D.-H. A simple first-order shear deformation theory for laminated composite plates. Compos. Struct. 2013, 106, 754–763. [Google Scholar] [CrossRef]
- Radu Chiriac and Mihai Vrabie. The First Order Shear Deformation Theory for Coposite Plates. Intersections 2016, 13, 37–47. [Google Scholar]
- ANSYS. Engineering Data; Composite Materials Library; ANSYS: Canonsburg, PA, USA, 2017. [Google Scholar]
- Fang, H.; Sun, H.; Liu, W.; Wang, L.; Bai, Y.; Hui, D. Mechanical performance of innovative GFRP-bamboo-wood sandwich beams: Experimental and modelling investigation. Compos. Part B Eng. 2015, 79, 182–196. [Google Scholar] [CrossRef]
- De Osei-Antwi, M. Structural Performance of Complex Core Systems for FRP-balsa Composite Sandwich Bridge Decks; École Polytechnique Fédérale De Lausanne: Lausanne, Switzerland, 2014. [Google Scholar]
- Green, D.E.; Winandy, J.E.; Kretschmann, D.E. Mechanical Properties of Wood. Wood Handbook: Wood as an Engineering Material; Forest Products Laboratory: Madison, WI, USA, 1999. [Google Scholar]
- Lei, Y.; Zhang, J.; Chen, Z.; Song, X.; Huang, Z.; Xiao, J. Mechanical properties of mulberry branch reconstituted square lumber. BioResources 2017, 12, 5838–5850. [Google Scholar] [CrossRef][Green Version]
- Eric, M. The Wood Database. Available online: https://www.wood-database.com/ (accessed on 18 May 2019).
- Shanmugasundaram, N.; Rajendran, I. Characterization of raw and alkali-treated mulberry fibers as potential reinforcement in polymer composites. J. Reinf. Plast. Compos. 2016, 35, 601–614. [Google Scholar] [CrossRef]
- European Standard. Eurocode 5-Part 1. Design of Timber Structures: General Common Rules and Rules for Building; European Committee for Standardization: Brussels, Belgium, 2005. [Google Scholar]
| Mechanical Properties | Glass/Epoxy | Carbon/Epoxy |
|---|---|---|
| Elastic Modulus | ||
| (MPa) | 45,000 | 121,000 |
| (MPa) | 10,000 | 8600 |
| (MPa) | 10,000 | 8600 |
| Shear Modulus | ||
| (MPa) | 5000 | 4700 |
| (MPa) | 5000 | 4700 |
| (MPa) | 3846.2 | 3100 |
| Density ( | 2000 | 1490 |
| Poisson Ratio | ||
| 0.3 | 0.27 | |
| 0.3 | 0.27 | |
| 0.4 | 0.40 | |
| Tensile Strength | ||
| (MPa) | 1100 | 2231 |
| (MPa) | 35 | 29 |
| (MPa) | 35 | 29 |
| Mechanical Properties | Paulownia Wood | Bamboo | Balsa Wood |
|---|---|---|---|
| Elastic Modulus | |||
| (MPa) | 4320 | 10,000 | 200 |
| (MPa) | 1470 | 2500 | 4320 |
| (MPa) | 1470 | 2500 | 200 |
| Shear Modulus | |||
| (MPa) | 294 | 275 | 354 |
| (MPa) | 209 | 275 | 309 |
| (MPa) | 294 | 275 | 64 |
| Density ( | 280 | 742 | 250 |
| Poisson Ratio | |||
| 0.23 | 0.31 | 0.23 | |
| 0.23 | 0.31 | 0.49 | |
| 0.23 | 0.31 | 0.66 | |
| Tensile Strength(MPa) | 49.10 | 128.53 | 23.50 |
| Component and Action | Factor | |
|---|---|---|
| ULS | SLS | |
| FRP laminates, traffic load a | 2.64 | 1.50 |
| FRP laminates, permanent load a | 2.88 | 1.50 |
| Balsa/timber b | 1.50 | 1.60 |
| Core | Material | Laminate Lay-Up Inner and Outer Skin | Inner Skin Thickness (mm) | Outer Skin Thickness (mm) | Core Thickness (mm) | Total Thickness (mm) | Deform- ation mm | Eq. Stress (MPa) | Safety Factor (MS) | Tsai-Wu | Tsai-Hill | Core Factor | Max. Shear Stress (MPa) | Mass kg |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Bamboo ULS | CFRP | 20 | 20 | 400 | 440 | −0.032 | 5.40 | 4.84 | 4.75 | 4.36 | 53.8 | 2.83 | 43,280 | |
| 20 | 20 | 400 | 440 | −0.025 | 2.25 | 9.92 | 9.94 | 9.92 | 35.9 | 1.17 | 43,280 | |||
| Bamboo ULS | GFRP | 22 | 22 | 440 | 484 | −0.028 | 4.46 | 7.77 | 7.21 | 7.01 | 77.5 | 2.31 | 50,266 | |
| 22 | 22 | 440 | 484 | −0.026 | 3.07 | 7.94 | 7.92 | 7.94 | 56.2 | 1.59 | 50,266 | |||
| Bamboo SLS | CFRP | 22 | 22 | 440 | 484 | −0.024 | 4.52 | 11.26 | 11.05 | 10.14 | 56.59 | 2.34 | 50,266 | |
| 20 | 20 | 400 | 440 | −0.025 | 2.25 | 19.07 | 19.10 | 19.07 | 33.72 | 1.17 | 43,280 | |||
| Bamboo SLS | GFRP | 22 | 22 | 440 | 484 | −0.028 | 4.46 | 14.99 | 13.91 | 13.49 | 72.69 | 2.31 | 50,266 | |
| 22 | 22 | 440 | 484 | −0.026 | 3.07 | 15.32 | 15.27 | 15.31 | 52.72 | 1.59 | 50,266 | |||
| Paulownia ULS | CFRP | 20 | 20 | 400 | 440 | −0.049 | 3.75 | 2.95 | 3.04 | 2.95 | 23.43 | 1.94 | 20,560 | |
| 20 | 20 | 400 | 440 | −0.032 | 1.17 | 8.17 | 8.47 | 8.13 | 24.28 | 0.62 | 20,560 | |||
| Paulownia ULS | GFRP | 24 | 24 | 480 | 528 | −0.035 | 2.66 | 6.099 | 6.22 | 5.18 | 40.39 | 1.38 | 27,648 | |
| 24 | 24 | 480 | 528 | −0.030 | 1.51 | 7.07 | 7.07 | 7.08 | 34.73 | 0.79 | 27,648 | |||
| Paulownia SLS | CFRP | 22 | 22 | 440 | 484 | −0.038 | 3.09 | 6.88 | 7.10 | 6.34 | 25.08 | 1.6 | 22,616 | |
| 22 | 22 | 440 | 484 | −0.024 | 0.97 | 19.05 | 19.87 | 18.93 | 25.39 | 0.52 | 22,616 | |||
| Paulownia SLS | GFRP | 24 | 24 | 480 | 528 | −0.035 | 2.66 | 11.74 | 11.96 | 9.97 | 37.81 | 1.38 | 2,7648 | |
| 24 | 24 | 480 | 528 | −0.030 | 1.5 | 13.64 | 13.64 | 13.64 | 35..52 | 0.79 | 2,7648 | |||
| Balsa ULS | CFRP | 28 | 28 | 560 | 616 | −0.039 | 0.61 | 3.44 | 3.68 | 3.18 | 22.91 | 3.47 | 2,6768 | |
| 24 | 24 | 480 | 528 | −0.029 | 0.36 | 9.51 | 11.12 | 9.46 | 30.79 | 0.21 | 22,944 | |||
| Balsa ULS | GFRP | 28 | 28 | 560 | 616 | −0.048 | 0.6 | 4.28 | 4.72 | 3.67 | 26.40 | 0.35 | 26,768 | |
| 28 | 28 | 560 | 616 | −0.034 | 0.38 | 7.37 | 7.38 | 7.37 | 33.69 | 0.22 | 26,768 | |||
| Balsa SLS | CFRP | 28 | 28 | 560 | 616 | −0.039 | 0.61 | 6.61 | 7.08 | 6.11 | 22.64 | 0.34 | 26,768 | |
| 24 | 24 | 480 | 528 | −0.029 | 0.36 | 18.26 | 21.37 | 18.16 | 30.44 | 0.21 | 22,944 | |||
| Balsa SLS | GFRP | 28 | 28 | 560 | 616 | −0.048 | 0.61 | 8.25 | 9.08 | 7.07 | 26.09 | 0.35 | 26,768 | |
| 28 | 28 | 560 | 616 | −0.034 | 0.38 | 14.21 | 14.24 | 14.21 | 33.29 | 0.22 | 26,768 |
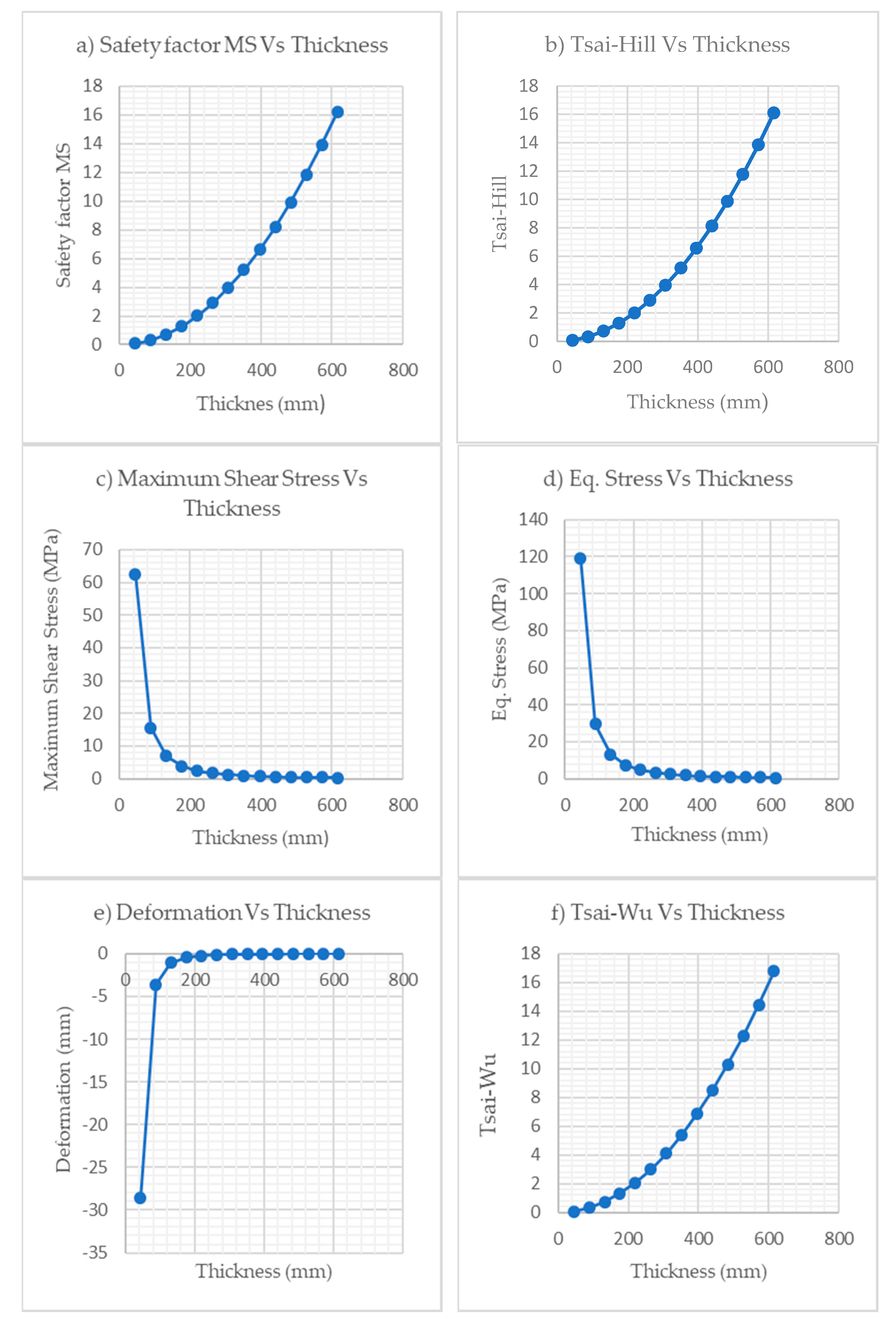
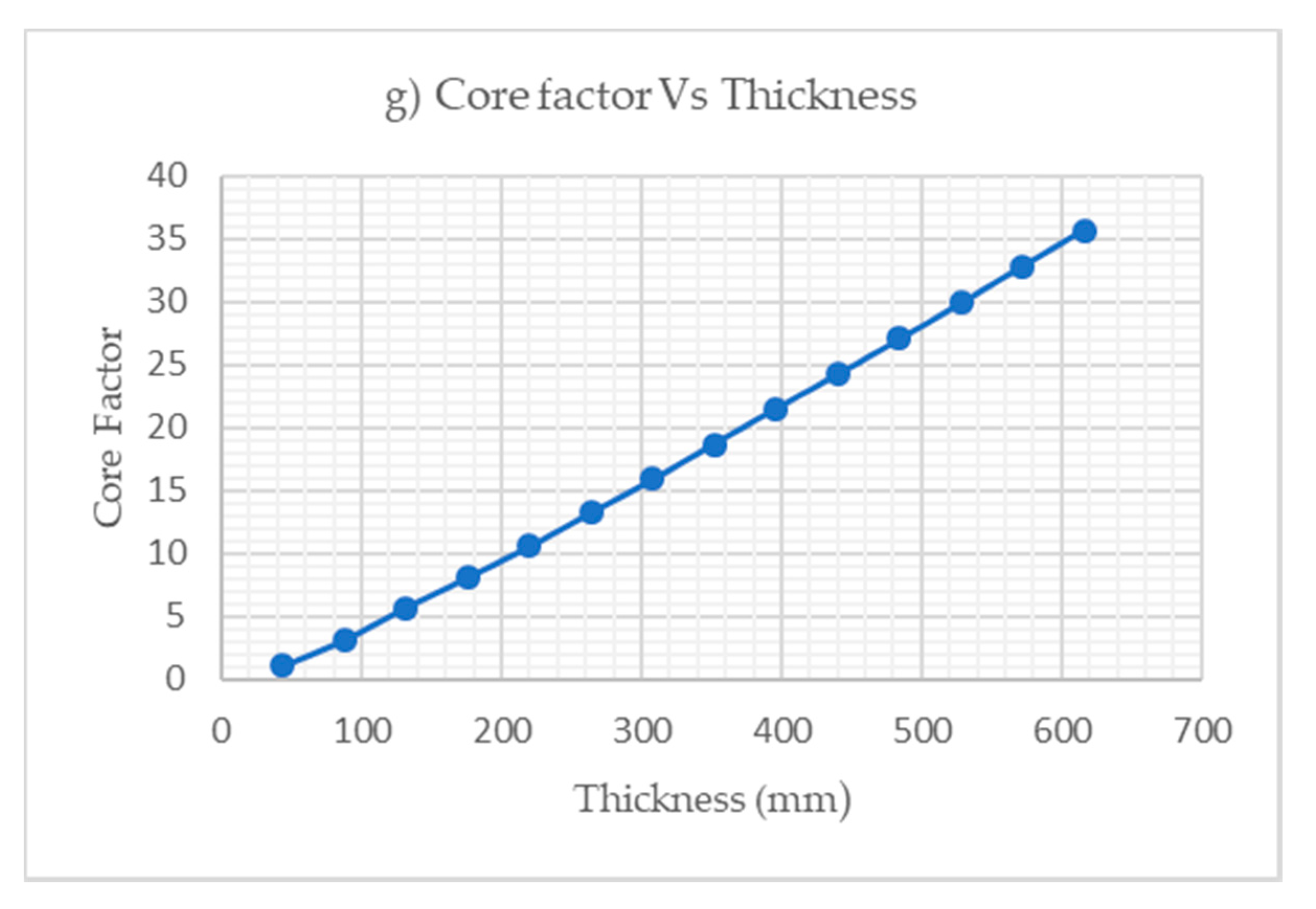
| Ply1 | Ply2 | Core | Ply1 | Ply2 | Safety Factor MS | Max. Shear Stress (MPa) | Eq. Stress (MPa) | Directional Deformation | Core Factor | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 40 | 1 | 1 | 0.08 | 0.07 | 62.49 | 118.97 | −28.61 | 0.08 | 1.07 |
| 2 | 2 | 80 | 2 | 2 | 0.32 | 0.31 | 15.66 | 29.66 | −3.59 | 0.33 | 3.07 |
| 3 | 3 | 120 | 3 | 3 | 0.72 | 0.72 | 6.91 | 13.05 | −1.07 | 0.74 | 5.64 |
| 4 | 4 | 160 | 4 | 4 | 1.29 | 1.28 | 3.89 | 7.34 | −0.45 | 1.33 | 8.07 |
| 5 | 5 | 200 | 5 | 5 | 2.02 | 2.00 | 2.48 | 4.69 | −0.23 | 2.08 | 10.61 |
| 6 | 6 | 240 | 6 | 6 | 2.91 | 2.89 | 1.72 | 3.25 | −0.13 | 3.01 | 13.24 |
| 7 | 7 | 280 | 7 | 7 | 3.97 | 3.95 | 1.27 | 2.39 | −0.088 | 4.11 | 15.94 |
| 8 | 8 | 320 | 8 | 8 | 5.20 | 5.17 | 0.97 | 1.83 | −0.060 | 5.39 | 18.69 |
| 9 | 9 | 360 | 9 | 9 | 6.60 | 6.56 | 0.77 | 1.45 | −0.043 | 6.84 | 21.47 |
| 10 | 10 | 400 | 10 | 10 | 8.17 | 8.13 | 0.62 | 1.18 | −0.032 | 8.47 | 24.28 |
| 11 | 11 | 440 | 11 | 11 | 9.92 | 9.86 | 0.52 | 0.98 | −0.024 | 10.28 | 27.12 |
| 12 | 12 | 480 | 12 | 12 | 11.84 | 11.77 | 0.44 | 0.83 | −0.019 | 12.27 | 29.96 |
| 13 | 13 | 520 | 13 | 13 | 13.93 | 13.85 | 0.37 | 0.71 | −0.015 | 14.43 | 32.82 |
| 14 | 14 | 560 | 14 | 14 | 16.20 | 16.10 | 0.32 | 0.61 | −0.012 | 16.78 | 35.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Waqas, H.M.; Shi, D.; Tong, L.; Imran, M.; Khan, S.Z.; Ahmed, W.; Qureshi, S.R. Conceptual Design of Composite Bridge Sandwich Structure. Appl. Sci. 2021, 11, 214. https://doi.org/10.3390/app11010214
Waqas HM, Shi D, Tong L, Imran M, Khan SZ, Ahmed W, Qureshi SR. Conceptual Design of Composite Bridge Sandwich Structure. Applied Sciences. 2021; 11(1):214. https://doi.org/10.3390/app11010214
Chicago/Turabian StyleWaqas, Hafiz Muhammad, Dongyan Shi, Lili Tong, Muhammad Imran, Sohaib Z. Khan, Waqas Ahmed, and Shafiq R. Qureshi. 2021. "Conceptual Design of Composite Bridge Sandwich Structure" Applied Sciences 11, no. 1: 214. https://doi.org/10.3390/app11010214
APA StyleWaqas, H. M., Shi, D., Tong, L., Imran, M., Khan, S. Z., Ahmed, W., & Qureshi, S. R. (2021). Conceptual Design of Composite Bridge Sandwich Structure. Applied Sciences, 11(1), 214. https://doi.org/10.3390/app11010214






