Abstract
We investigate the spectral degree of freedom of OAM-carrying localized waves and its influence on their transverse intensity distribution. In particular, we focus our attention on exponentially decaying spectra, which are very tightly connected to fundamental X-waves; we then show how it is possible to structure their transverse intensity distribution, thus creating a radial structure similar to that of Bessel beams.
1. Introduction
Since the invention of the laser in the 1960s by Maiman [1], optical beams have been the subject of extensive studies, mainly because of their versatility and potential for ground-breaking applications in the field of atomic and optical physics, such as material processing [2], imaging and spectroscopy [3,4], optical communications [5,6] and fundamental research [7,8], to name a few. Recently, moreover, optical beams have been employed as an efficient means to encode and transmit classical information [9,10], as a viable solution to realize high-dimensional quantum information and communication protocols [11], and for error-free quantum communication [12,13]. The key of success of optical beams in such contexts is mostly due to the possibility to structure, almost at will, their various degrees of freedom, a feature that allows great versatility. Achieving full control on degrees of freedom, such as polarization, orbital angular momentum (OAM), and spatial modes, understanding their interplay and exploiting them for various applications is the vibrant subject of current research in the field [14].
Recently, much effort has been made to understand how structured light can be generalized to optical pulses as well. For example, Abourrady and co-workers have investigated the possibility of suitably structuring the dispersion relation of optical pulses, in order to suitably represent, and structure, monochromatic and polychromatic light fields [15,16]. On a seemingly different ground, nondiffracting pulses, i.e., solutions of Maxwell’s equations that are affected by neither dispersion nor diffraction during propagation, also offer many possibilities in terms of bringing structured light fields to the polychromatic domain [17]. Their most well-known representative is the X-wave. First introduced in acoustics [18,19], they have, in fact, provided many interesting results in several different areas of physics, such as nonlinear optics [20], condensed matter [21], quantum optics [22,23,24], integrated optics [25,26] and optical communications [27]. Recently, moreover, X-waves carrying OAM have been studied theoretically, and an interesting interplay between their temporal dynamics and OAM characteristic has been reported [10,28,29].
Due to their intrinsic resilience to external perturbations, nondiffracting pulses, and X-waves in particular, represent a very interesting platform for free-space classical and quantum communication. However, X-waves are typically only characterized by a single index, i.e., their OAM, and therefore do not possess a characteristic radial structure, such as Laguerre–Gaussian beams, that would give them the possibility to be used for high-dimensional quantum information and communication protocols. Since X-waves are essentially polychromatic superpositions of Bessel beams, one possible way to overcome this problem would be to directly generalize the results concerning Bessel beams with two indices [30] to the domain of optical pulses. In doing so, however, one would have to deal with superposition of X-waves, rather than single X-waves, as Bessel beams with two indices exist only as superposition of Bessel beams.
Alternatively, one could investigate the possibility to exploit the peculiar structure of nondiffracting beams, i.e., their spatio-temporal correlation, to induce a radial structure into them, by simply shaping their frequency spectrum. This is the approach we will follow in this work. In particular, we aim at introducing a new degree of freedom, which we call spectral index, which indices, as we will show, a radial structure into X-waves similar of that of Laguerre–Gaussian beams. Here, we focus our attention on so-called fundamental X-waves, which posses exponentially decaying spectra, and investigate how their spectral properties can shape their transverse structure
This work is organized as follows: in Section 2, we first present a brief review of scalar localized pulses, and, in particular, fundamental X-waves and their spectrum. Then, we show how changing their spectral order results in the appearance of a transverse spatial structure, similar to that of Laguerre–Gaussian beams. Section 3 is then dedicated to the analysis and discussion of these results. Materials and methods used for this work are briefly discussed in Section 4, and, finally, conclusions are drawn in Section 5.
2. Results
2.1. Localized Waves
We start our analysis by considering a scalar, monochromatic solution of the Helmholtz equation
where is the wave number in a vacuum. In a cylindrical reference frame , the solution can be given in terms of Bessel beams:
where , , is the Bessel function of the first kind, m is the OAM index, and is the Bessel cone angle, which is the beam’s characteristic parameter [31]. Notice that is a propagation invariant, as the dependence is contained only in the plane-wave term , and thus the intensity distribution of a Bessel beam does not change during propagation, i.e., . With this solution at hand, we can construct an exact solution of the wave equation:
as a polychromatic superposition of monochromatic solution in the following way:
where is an arbitrary spectral function. If is constructed from Bessel beams, then the and dependence of each spectral component will be of the kind , which is the distinctive characteristic of localized waves [17]. For nondiffracting pulses, in fact, regardless of the explicit form of , it can be demonstrated that they are propagation-invariant with respect to both propagation direction and time, or, alternatively, with respect to the co-moving propagation direction [17].
In this work, we concentrate our attention on one spectral function in particular, namely the generalized exponentially decaying spectrum:
(where defines the order of the spectrum, accounts for the width of the spectrum, and is the Heaviside step function [32]), which gives rise to the so-called fundamental X-waves,. The form of the exponentially decaying spectrum for various values of the spectral index n is depicted in Figure 1.
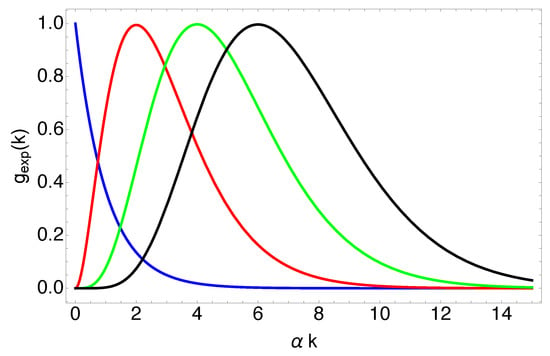
Figure 1.
Exponentially decaying spectrum of fundamental X-waves, as given by Equation (5), for different values of the parameter n, namely (blue), (red), (green), and (black). As can be seen, as n grows, the spectrum shifts its maximum towards higher frequencies. For this plot, k is measured in units of .
2.2. Fundamental X Waves with OAM
Let us consider the exponentially decaying spectrum given by Equation (5), and remember that is a constant representing the spectral order. The X-waves constructed with this spectrum are often called fundamental X-waves, and represent the most common type of localized waves normally studied.
First, let us notice that as Figure 1 suggests, as n increases, the spectrum acquires a bell-like shape, which shifts to higher frequencies with increasing n. In particular, we observe that as n grows, the maximum shifts linearly with n towards higher frequencies, and the full width half maximum (FWHM) of the spectrum changes according to:
where is the Lambert W-function [32]. Notice that grows quite slowly with n, and, in a first approximation, it remains roughly constant. Moreover, it asymptotically tends to a constant value for . In addition, for very big values of n, the exponentially decaying spectrum can be approximated by a Gaussian spectrum (centered around the maximum of ), and thus fundamental X-waves with very high n values can be easily described in terms of Bessel-X pulses [33,34].
To find the explicit expression of the electric field of a fundamental X-wave, we substitute Equation (5) into Equation (4) and use the relation 6.621.1 of reference [35], to obtain:
where , , , and is the Gauss hypergreometric function [32]. An example of the transverse structure of fundamental X-waves for several values of the spectral index n is given in Figure 2. The longitudinal structure of fundamental X-waves as a function of the spectral index n is instead given in Figure 3. As appears clear from these figures, as n increases, a richer spatial structure in appears in the paraxial region of the X-wave (i.e., close to the center of the wave).
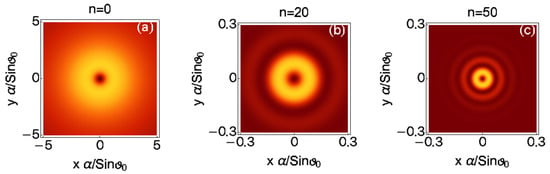
Figure 2.
Normalized intensity distribution of fundamental X-waves carrying units of orbital angular momentum (OAM) in the plane , for different values of the spectral index n, namely (a), (b), and (c). As can be seen, as n grows, several rings start to appear in the paraxial region of the pulse, i.e., near its center. For these plots, the and axes are dimensionless, i.e., they are measured in units of .
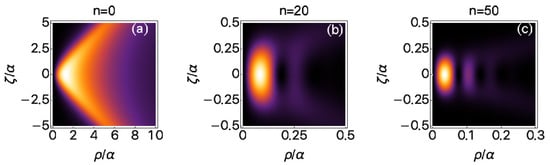
Figure 3.
Normalized longitudinal intensity distribution of fundamental X-waves carrying units of OAM, for different values of the spectral index n, namely (a), (b), and (c). As can be seen, as n grows, the initially X-shaped function breaks down into two wings (symmetric with respect to the plane . Here, only the positive wing is shown, for simplicity), leaving a region of zero intensity around , corresponding to the transverse doughnut structure seen in Figure 2. Moreover, the onset of different rings in the transverse structure of the fundamental X-wave is mimicked by the appearance of several secondary structures in the radial direction, which corresponds to the rings in the transverse structure, as seen in Figure 2. For these plots, the and axes are dimensionless, i.e., and are expressed in units of .
In particular, from Figure 2 it seems that the pulses acquire a radial structure very similar to that of LG beams or, equivalently, Bessel beams. This result can be directly compared to previous ones concerning assigning a second index to monochromatic Bessel beams [30]. However, while in the case of Bessel beams with two indices, the second index, and therefore an LG-like radial structure, was realized by constructing suitable superpositions of Bessel beams with different transverse wave vectors [30], in this case, the additional radial structure is due to the form of the spectrum. In a sense, one could say that by suitably superimposing Bessel beams of different frequencies, it is possible to induce a radial structure to them. To some extent, this is another manifestation of the spatio-temporal correlation typical of localized waves. [17].
To better understand the connection between spectral order and radial structure of fundamental X-waves, we used the algorithm described in Section 4 (Methods) to calculate the number of rings acquired by the fundamental X-waves as a function of the spectral index n, which is depicted in Figure 4.
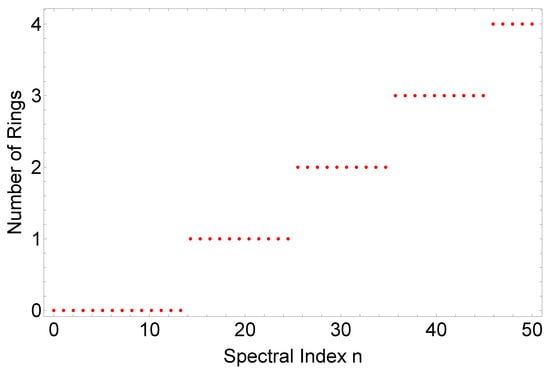
Figure 4.
Plot of the number of visible rings for different values of the spectral index n (red dots). To calculate the number of rings, we have adopted the algorithm described in Section 4 (Methods). Notice that since we consider only paraxial pulses, we have limited our analysis to only the paraxial region of the pulse, i.e., the region close to its center. For this plot, and have been assumed.
As can be seen, the number of rings grows linearly by one unit each time n increases by 10 units, starting from . For values , there are no extra rings appearing in the transverse intensity structure of the X-wave (the OAM ring does not count towards the total number of extra rings, and therefore the zero number of rings corresponding to means, in reality, that only the OAM ring is present). The functional relation between the number of extra rings and the spectral index n can be then written in a compact way by introducing the function:
where is the Heaviside step function and is an integer used to truncate the sum to the desired maximum value of n. For example, a value of will allow to only consider the appearance of ring structures up to . Defined in this way, the function then returns the number of rings possesses by the X-wave for a specific value (or interval of values) of n, essentially represented by p.
3. Discussion
In the previous section, we have reported on the appearance of an extra ring structure on fundamental X-waves as a function of the spectral index parameter n. To understand the origin of these rings, and to get more insight on the possibility to control their onset, we can look at the structure of the X-wave in the limit of large n values, i.e., when . In this limit, in fact, it is well-known that the exponentially decaying spectrum can be well-approximated with a Gaussian spectrum centered at the average frequency of the original spectrum [33,34]. For large n, in fact, as can be seen from Figure 5, we have that:
where and . In this limit, the fundamental X-wave can be de-facto considered to be a Bessel-X pulse. Besides establishing a concrete connection between fundamental X-waves and Bessel-X pulses, corroborating the results of reference [34], the result above also sheds some light on the origin of the radial structure emerging on the transverse intensity distribution of fundamental X-waves. The radial structure of Bessel-X pulses, in fact, is a Gaussian-modulated Bessel function, which, in principle, possesses infinite rings (as does the Bessel function). However, the Gaussian damping of the intensity distribution quenches most of them (and therefore allows them to be square integrable, i.e., carry infinite energy) [33]. For fundamental X-waves, this means that as n grows, the radial structure that appears is nothing but a part of the complete ring structure of a Bessel function, suitably damped by the exponentially decaying radial behavior of the hypergeometric function. For , therefore, the ring structure given by Equation (8) will reproduce the complete ring structure of the Bessel function .
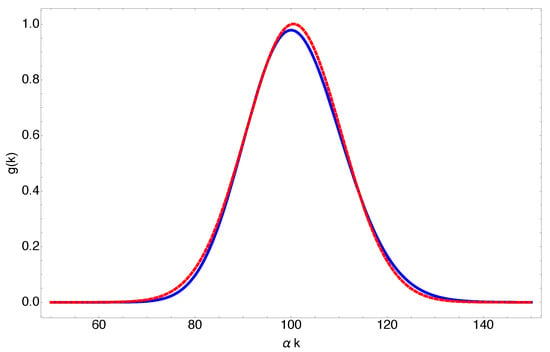
Figure 5.
Comparison between exponentially decaying spectrum with large n (blue, solid line) and Gaussian spectrum (dashed, red line), for the case of . As can be seen, the spectrum of fundamental X-waves with a large n can be very well approximated with that of Bessel-X pulses. For this plot, k is measured in units of , which means that and .
To understand this even further, let us consider the limiting value of the transverse structure of the fundamental X-waves for large values of n. We have in fact that for , since the spectrum of the fundamental X-wave must tend to the Gaussian spectrum of Bessel-X pulses, the hypergeometric radial structure of fundamental X-waves needs to tend to the Bessel function typical of Bessel-X pulses [33], i.e.,
where is a suitable function of the co-moving coordinate , such that , which represents the beam waist parameter of the Bessel-X pulse. Within this limit, it is not difficult to see, by comparing the radial structure of the two functions above (see Figure 6), that they share the same radial structure, i.e., the position of the zeros (and therefore that of the corresponding rings) is the same.
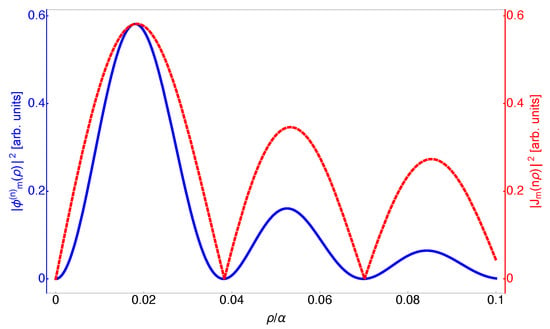
Figure 6.
Comparison between the radial structure of a fundamental X-wave with (blue, solid line) with that of the corresponding limiting form, i.e., a Bessel-X pulse with the same OAM value (red, dashed line), in the plane . Notice that the scaling of the Bessel function is , which scales the distributions of zeros of the Bessel function to match that of the hypergeometric function . The higher-order zeros cannot be easily visualized, due to the rapidly decaying behavior of the hypergeometric function for large n. For this plot, is measured in units of for the X-wave, and has been assumed for the Bessel beam.
4. Materials and Methods
Number of Rings of Localized Waves
To understand how the algorithm we used to extract information about the number of rings possessed by a localized wave and generated by its spectral index n works, let us consider the case of a fundamental X-wave with as an example of how we can calculate the number of rings appearing in the transverse cross-section of the X-wave according to its spectral index.
First, we calculate the radial derivative of the localized wave, which, in the case of fundamental X-waves, is given by:
The zeros of the above equation, which we indicate with , represent the position, as a function of the spectral index, of the ℓ-th maximum of . We can extract information about the number of rings for a given value of n directly from the zeros of the above equation if we first notice the following things:
- Not all the zeros of Equation (11) will contribute to the final number of rings. In fact, this depends on how fast the intensity distribution decays radially. If decays too quickly, only the zeros of Equation (11) that find themselves in a small region close to the center of the wave will participate in determining its radial structure.
Figure 7 depicts how the search algorithm works. For a given value of n (in our example ), we count the number of jumps (between 0 and ) of the phase of (panel (a)). This number now represents the total number of the rings’ intensity distribution . For the example in Figure 7, the number of zeros is 3. When we plot the intensity distribution for , however, we notice that the third ring is barely visible (i.e., its intensity is very small compared to that of the other two rings). This is a consequence of the rapidly radially decaying behavior of the hypergeometric function. To correctly count the number of actually appearing rings (i.e., those that have enough intensity to be non-neglectable), we compare the intensity of all the maxima of for a given value of n, fit the relative intensity of the various rings with an exponentially decaying function, and neglect all rings whose intensity falls under 1% of the intensity of the primary OAM ring.
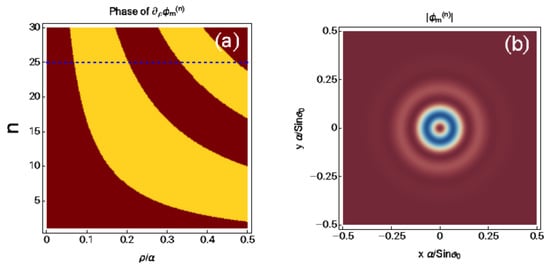
Figure 7.
Example of application of the algorithm for retrieving the number of rings of a fundamental X-wave, given a specific value of n. For this specific example, we used . Panel (a) depicts the phase of the radial derivative . The red areas correspond to regions where , while the yellow areas correspond to regions where . Once a value of n is chosen (blue, dashed line, representing in this case), by counting the number of times red regions cross the line of the constant n (blue, dashed line in panel (a)), we can retrieve the number of rings possessed by in a given radial interval, which in this case is . As can be seen, while in panel (a) we count three full crossing of the blue line with red areas, we also see, in panel (b), that the transverse correspondent transverse distribution of intensity possesses three rings, which amounts to one ring because of the units of OAM carried by the pulse, plus two extra rings deriving from the spectral structure of the pulse itself.
With this method, from Figure 7 we see that the number of rings corresponding to should actually be 3, but the exponential fitting of the intensity decay of the X-wave reveals that the third ring does not have a high enough intensity to be considered as fully developed yet. For this reason, therefore, we conclude that corresponds to two rings: the primary ring (corresponding to the OAM value ) and an extra one generated by the spectral structure of the X-wave itself.
5. Conclusions
In this work, we have studied the effect of the spectral index n on the transverse structure of fundamental X-waves, and we have discussed its origin and its link with Bessel-X pulses. We have shown that due to their innate spatio-temporal correlation, structuring the spectrum of such pulses results in the appearance of several rings in their intensity distribution, with a structure similar to those of Bessel beams, or, in the paraxial regime, Laguerre–Gaussian beams, with fixed OAM and a varying p index. Furthermore, we have shown how the number of rings increases in suitable steps of the spectral index, as shown in Equation (8). We have then finally discussed the origin of this radial structure in detail, and concluded that extra rings appear in the transverse structure of fundamental X-waves as n increases, as a progressive step into adapting their transverse shape to that of Bessel-X pulses, which constitute the natural limit of fundamental X-waves for large n values. Nevertheless, we have shown how it is possible, even with relatively low values of n, to introduce an extra degree of freedom into fundamental X-waves that could be used to tailor their transverse (and longitudinal) structure.
The recent technological advances in spectral shaping [36], realization of long-range Bessel beams [37], and the control of the spatiotemporal structure of electromagnetic waves [15,16] envisions the possibility to achieve great control over the spectral structure of Bessel-X pulses, and, possibly, to realize fundamental X-waves with different values of the spectral index n, thus being able to exploit this extra degree of freedom encoded in their spectral structure. With this at hand, OAM-carrying X-waves could be used for a number of different applications, ranging from communication (where they could be coupled with OAM-carrying waves in optical fibers to realize long-range diffraction-resilient communication systems [38]), sensing (where the spectral index could be used as a means to tune the central frequency of the X-wave spectrum to a specific compound/specimen that needs to be detected), and material processing (where the different field configurations obtained by controlling the spectrum of the X-wave could result in different geometries and possibilities for, e.g., laser drilling, and quantum information). For the latter, controlling the onset of an additional radial structure on fundamental X-waves by controlling their spectrum could provide an interesting alternative, or a complementary resource, to LG beams for the realization of high-dimensional quantum information protocols [39]. To this aim, an agile combination of X-waves or a combination with LG modes can improve the performance as well [40]. The compatibility of these newly introduced spectral indices with the protocols of classical and quantum information encoding is, however, left to a future work.
Our results on fundamental X-waves corroborate and generalize those given in references [33,34]. In these works, in fact, the ring structure of so-called Bessel-X pulses (i.e., X-waves with a Gaussian spectrum) is discussed in detail and understood as a direct consequence of the fact that the spectral bandwidth of Bessel-X pulses is narrow compared to their carrier frequency. It is well-known that Bessel-X pulses have very similar properties to fundamental X-waves (as, in many ways, they constitute their experimentally realizable counterpart). The results obtained in our work on the role of the spectral index in the radial structure of X-waves, therefore, corroborates this statement, and finds, at the same time, confirmation for the predictions of references [33,34]. However, those works differ significantly from ours in two important aspects: first, no contribution of OAM was taken into account (as only Bessel-X pulses of order were considered). Second, the analysis presented in both references [33] and [34] only deal with scalar, rather than vector, waves. By including the influence of the OAM on the ring structure of fundamental X-waves, and investigating in detail vector, rather than scalar, fields, our work extends and generalizes the one reported in references [33,34].
Author Contributions
Conceptualization, M.O.; methodology and software, S.A.; validation, S.A., and M.O.; formal analysis, S.A.; investigation, S.A.; writing—original draft preparation, S.A. and M.O.; writing—review and editing, S.A. and M.O.; visualization, S.A. and M.O.; supervision, M.O.; project administration, M.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Academy of Finland Flagship Programme, Photonics Research and Innovation (PREIN), decision 320165.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
The data presented in this study are contained in the article itself. The Mathematica files used in this article are available upon request to the correspondent author.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| OAM | Orbital Angular Momentum |
| FWHM | Full Width at Half Maximum |
| LG | Laguerre–Gaussian |
References
- Maiman, T.H. Stimulated Optical Radiation in Ruby. Nature 1960, 187, 493–494. [Google Scholar] [CrossRef]
- Meier, M.; Romano, V.; Feurer, T. Material processing with pulsed radially and azimuthally polarized laser radiation. Appl. Phys. A 2007, 86, 329–334. [Google Scholar] [CrossRef]
- Sick, B.; Hecht, B.; Novotny, L. Orientational Imaging of Single Molecules by Annular Illumination. Phys. Rev. Lett. 2000, 85, 4482–4485. [Google Scholar] [CrossRef]
- Huse, N.; Schoenle, A.; Hell, S.W. Z-polarized confocal microscopy. J. Biomed. Opt. 2001, 6, 273–276. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Forbes, A.; Nape, I. Quantum mechanics with patterns of light: Progress in high dimensional and multidimensional entanglement with structured light. AVS Quantum Sci. 2019, 1, 011701. [Google Scholar] [CrossRef]
- Weiner, A. Ultrafast Optics, 1st ed.; Wiley Series in Pure and Applied Optics; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kärtner, F.X. Few-Cycle Laser Pulse Generation and Its Applications, 1st ed.; Topics in Applied Physics 95; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photon. 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Ornigotti, M.; Conti, C.; Szameit, A. Effect of Orbital Angular Momentum on Nondiffracting Ultrashort Optical Pulses. Phys. Rev. Lett. 2015, 115, 100401. [Google Scholar] [CrossRef]
- Erhard, M.; Fickler, R.; Krenn, M.; Zeilinger, A. Twisted photons: New quantum perspectives in high dimensions. Light. Sci. Appl. 2018, 7, 17146. [Google Scholar] [CrossRef] [PubMed]
- Cerf, N.J.; Bourennane, M.; Karlsson, A.; Gisin, N. Security of Quantum Key Distribution Using d-Level Systems. Phys. Rev. Lett. 2002, 88, 127902. [Google Scholar] [CrossRef] [PubMed]
- Ecker, S.; Bouchard, F.; Bulla, L.; Brandt, F.; Kohout, O.; Steinlechner, F.; Fickler, R.; Malik, M.; Guryanova, Y.; Huber, M.; et al. Overcoming Noise in Entanglement Distribution. Phys. Rev. X 2019, 9, 041042. [Google Scholar] [CrossRef]
- Rubinsztein-Dunlop, H.; Forbes, A.; Berry, M.V.; Dennis, M.R.; Andrews, D.L.; Mansuripur, M.; Denz, C.; Alpmann, C.; Banzer, P.; Bauer, T.; et al. Roadmap on structured light. J. Opt. 2016, 19, 013001. [Google Scholar] [CrossRef]
- Bhaduri, B.; Yessenov, M.; Abouraddy, A.F. Space-time wave packets that travel in optical materials at the speed of light in vacuum. Optica 2019, 6, 139–146. [Google Scholar] [CrossRef]
- Kondakci, H.E.; Abouraddy, A.F. Optical space-time wave packets having arbitrary group velocities in free space. Nat. Commun. 2019, 10, 929. [Google Scholar] [CrossRef] [PubMed]
- Hernandez-Figueroa, H.E.; Michel Zamboni-Rached, E.R. Localized Waves, 1st ed.; Wiley Series in Microwave and Optical Engineering; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Lu, J.; Greenleaf, J.F. Nondiffracting X waves-exact solutions to free-space scalar wave equation and their finite aperture realizations. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1992, 39, 19–31. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Greenleaf, J.F. Experimental verification of nondiffracting X waves. IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 1992, 39, 441–446. [Google Scholar] [CrossRef]
- Valiulis, G.; Kilius, J.; Jedrkiewicz, O.; Bramati, A.; Minardi, S.; Conti, C.; Trillo, S.; Piskarskas, A.; Di Trapani, P. Space-time nonlinear compression and three-dimensional complex trapping in normal dispersion. In Proceedings of the Technical Digest, Summaries of papers presented at the Quantum Electronics and Laser Science Conference, Postconference Technical Digest (IEEE Cat. No.01CH37172), Baltimore, MD, USA, 11 May 2001; p. QPD10. [Google Scholar]
- Conti, C.; Trillo, S. Nonspreading Wave Packets in Three Dimensions Formed by an Ultracold Bose Gas in an Optical Lattice. Phys. Rev. Lett. 2004, 92, 120404. [Google Scholar] [CrossRef]
- Ciattoni, A.; Conti, C. Quantum electromagnetic X waves. J. Opt. Soc. Am. B 2007, 24, 2195–2198. [Google Scholar] [CrossRef]
- Ornigotti, M.; Villari, L.D.M.; Szameit, A.; Conti, C. Squeezing of X waves with orbital angular momentum. Phys. Rev. A 2017, 95, 011802. [Google Scholar] [CrossRef]
- Ornigotti, M.; Conti, C.; Szameit, A. Quantum X waves with orbital angular momentum in nonlinear dispersive media. J. Opt. 2018, 20, 065201. [Google Scholar] [CrossRef]
- Lahini, Y.; Frumker, E.; Silberberg, Y.; Droulias, S.; Hizanidis, K.; Morandotti, R.; Christodoulides, D.N. Discrete X-Wave Formation in Nonlinear Waveguide Arrays. Phys. Rev. Lett. 2007, 98, 023901. [Google Scholar] [CrossRef]
- Heinrich, M.; Szameit, A.; Dreisow, F.; Keil, R.; Minardi, S.; Pertsch, T.; Nolte, S.; Tünnermann, A.; Lederer, F. Observation of Three-Dimensional Discrete-Continuous X Waves in Photonic Lattices. Phys. Rev. Lett. 2009, 103, 113903. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.Y.; He, S. Optical X wave communications. Opt. Commun. 1999, 161, 187–192. [Google Scholar] [CrossRef]
- Ornigotti, M.; Conti, C.; Szameit, A. Universal form of the carrier frequency of scalar and vector paraxial X waves with orbital angular momentum and arbitrary frequency spectrum. Phys. Rev. A 2015, 92, 043801. [Google Scholar] [CrossRef]
- Ornigotti, M.; Conti, C.; Szameit, A. Cylindrically polarized nondiffracting optical pulses. J. Opt. 2016, 18, 075605. [Google Scholar] [CrossRef]
- Ornigotti, M.; Aiello, A. Generalized Bessel beams with two indices. Opt. Lett. 2014, 39, 5618–5621. [Google Scholar] [CrossRef] [PubMed]
- Durnin, J.; Miceli, J.J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499–1501. [Google Scholar] [CrossRef]
- Olver, F.W.J.; Lozier, D.W.; Boisvert, R.F.; Clark, C.W. NIST Handbook of Mathematical Functions, 1st ed.; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Porras, M.A.; Valiulis, G.; Trapani, P.D. Unified description of Bessel X waves with cone dispersion and tilted pulses. Phys. Rev. E 2003, 68, 016613. [Google Scholar] [CrossRef]
- Saari, P.; Sonajalg, H. Pulsed bessel beams. Laser Phys. 1997, 7, 32. [Google Scholar]
- Gradshteyn, I.; Ryzhik, I. Table of Integrals, Series, and Products, 7th ed.; Academic Press: Cambridge, MA, USA, 2007. [Google Scholar]
- Schébelin, C.; Azaña, J.; de Chatellus, H.G. Programmable broadband optical field spectral shaping with megahertz resolution using a simple frequency shifting loop. Nat. Commun. 2019, 10, 4654. [Google Scholar] [CrossRef]
- Vetter, C.; Steinkopf, R.; Bergner, K.; Ornigotti, M.; Nolte, S.; Gross, H.; Szameit, A. Realization of Free-Space Long-Distance Self-Healing Bessel Beams. Laser Photonics Rev. 2019, 13, 1900103. [Google Scholar] [CrossRef]
- Ruano, P.N.; Robson, C.W.; Ornigotti, M. Localized waves carrying orbital angular momentum in optical fibers. arXiv 2020, arXiv:2012.03609. [Google Scholar]
- Hiekkamäki, M.; Prabhakar, S.; Fickler, R. Near-perfect measuring of full-field transverse-spatial modes of light. Opt. Express 2019, 27, 31456–31464. [Google Scholar] [CrossRef] [PubMed]
- Andrews, D.L.; Babiker, M. The Angular Momentum of Light; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).