Effects of Tension–Compression Asymmetry on Bending of Steels
Abstract
1. Introduction
2. Analytical Method
- The plane section remains planar during pure bending;
- The sheet thickness is assumed to be constant during the process;
- The bending strain is proportional to its distance from the neutral surface.
2.1. Equivalent Stress and Strain
2.2. Plastic Deformation
2.3. Yield Function
2.4. Springback Prediction
2.4.1. Elastic Unloading
2.4.2. Nonlinear Unloading
3. Case Studies of Pure Bending and Springback
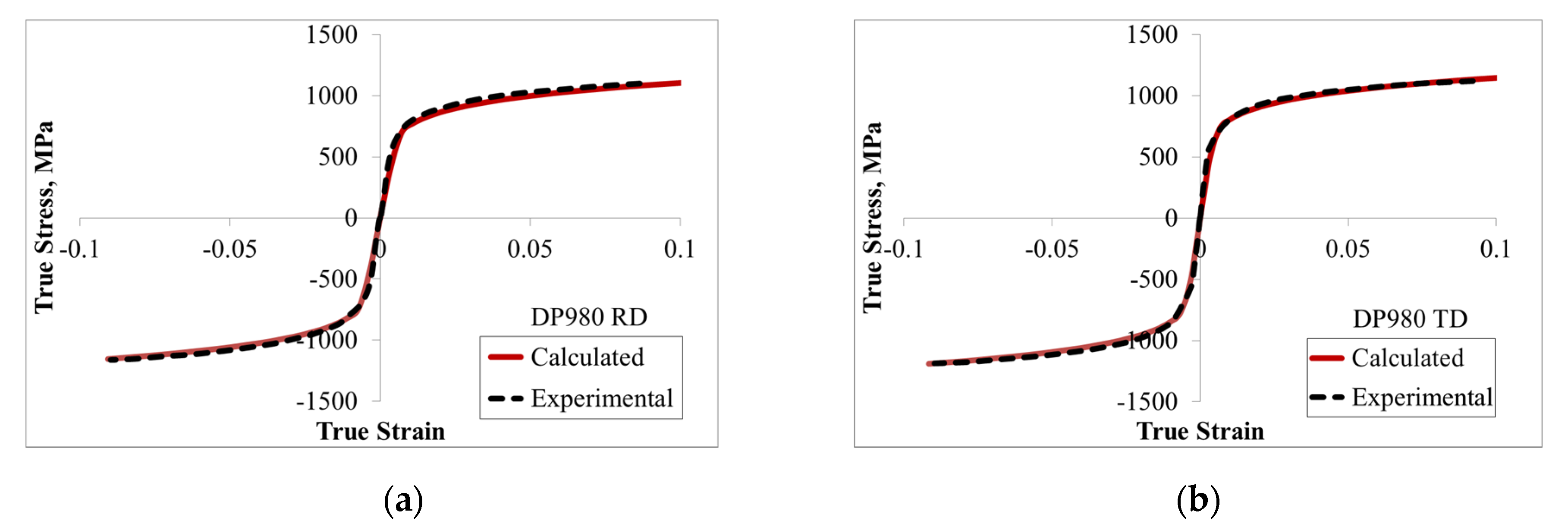
3.1. Pure Bending of DP980
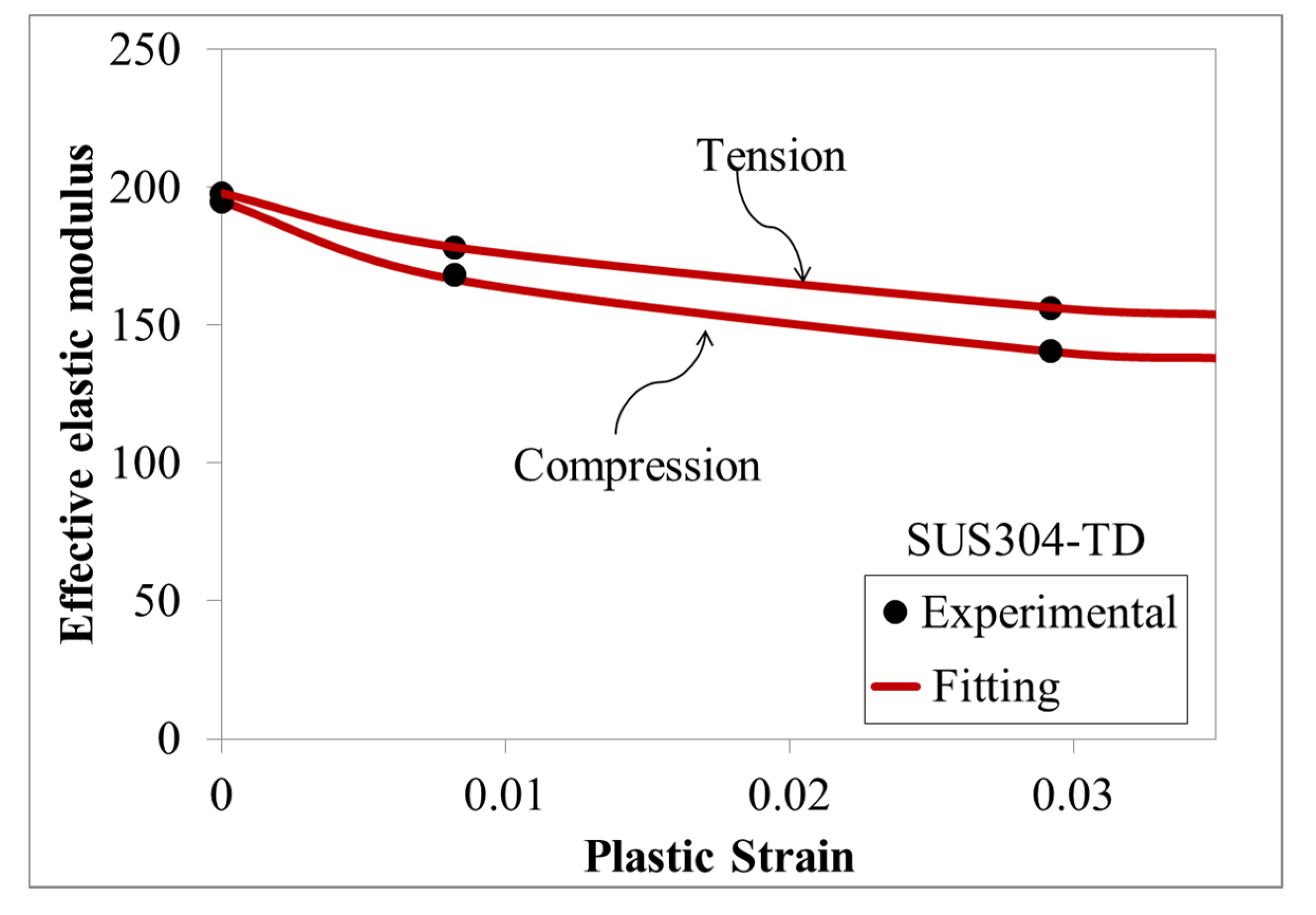
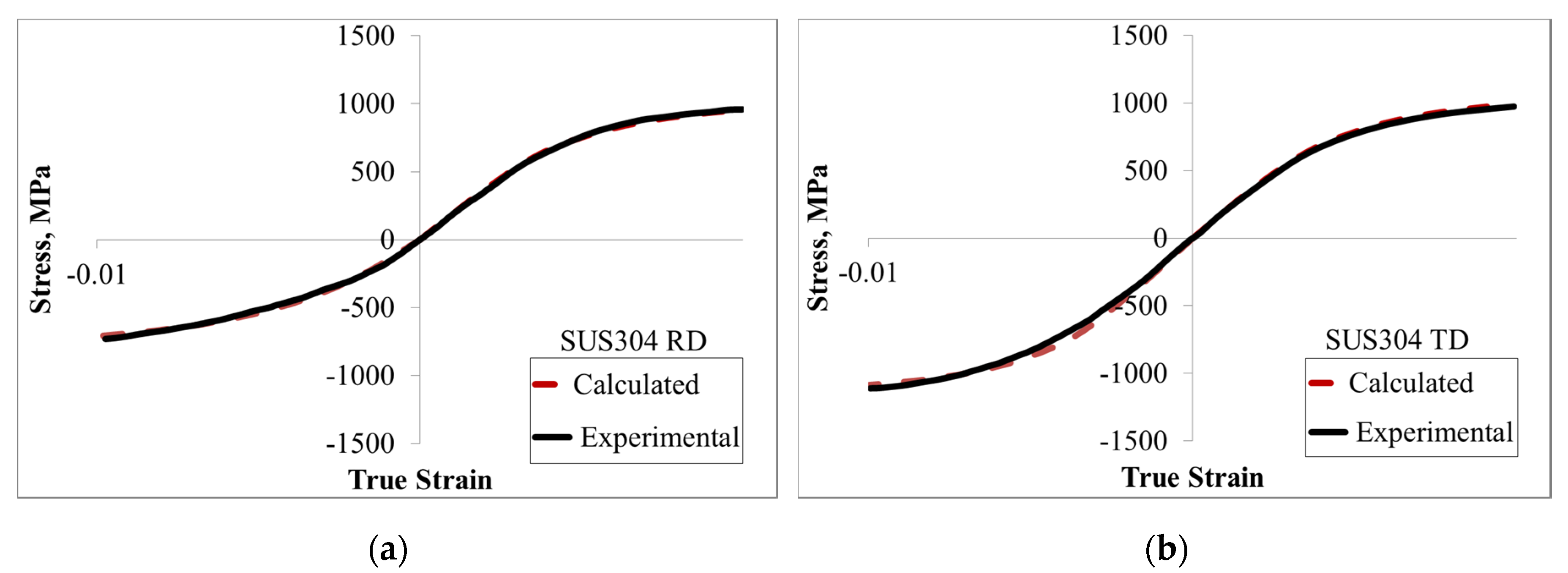
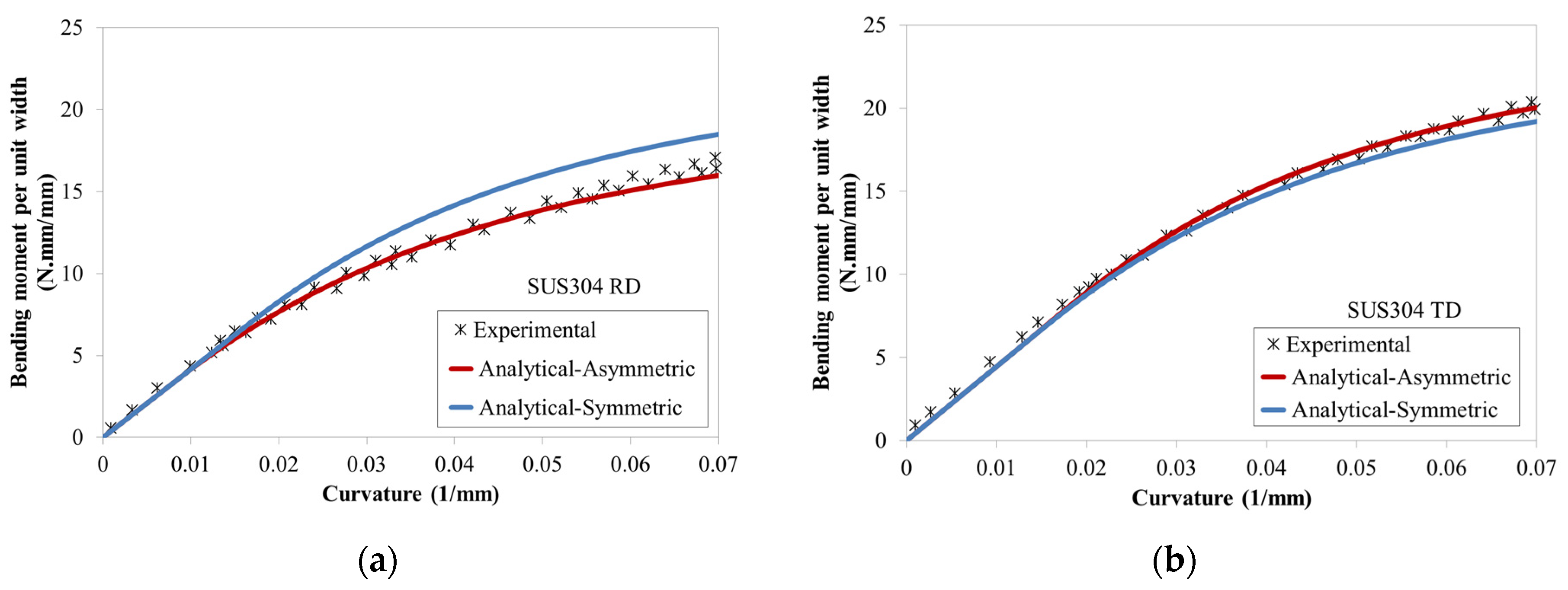
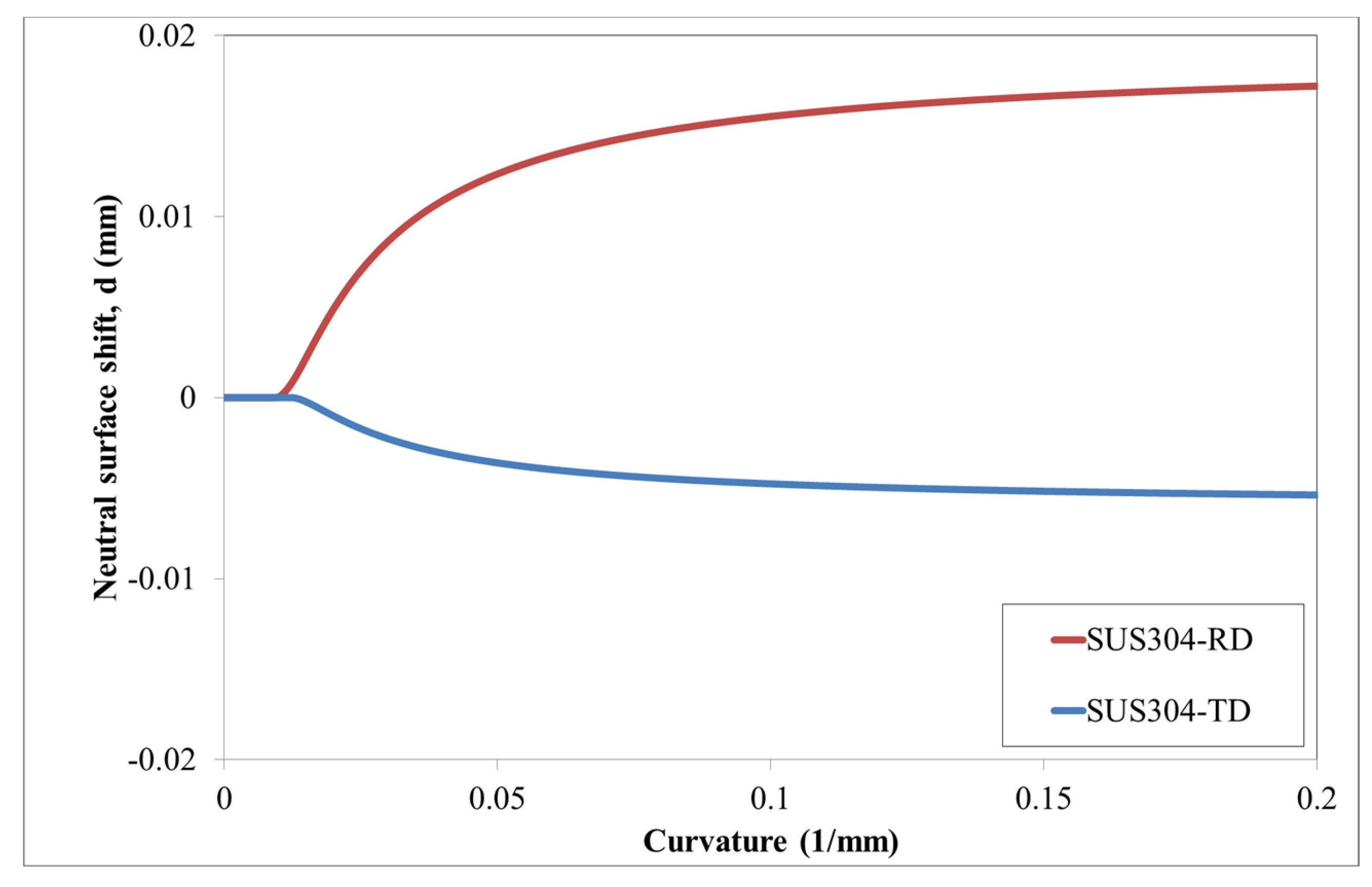
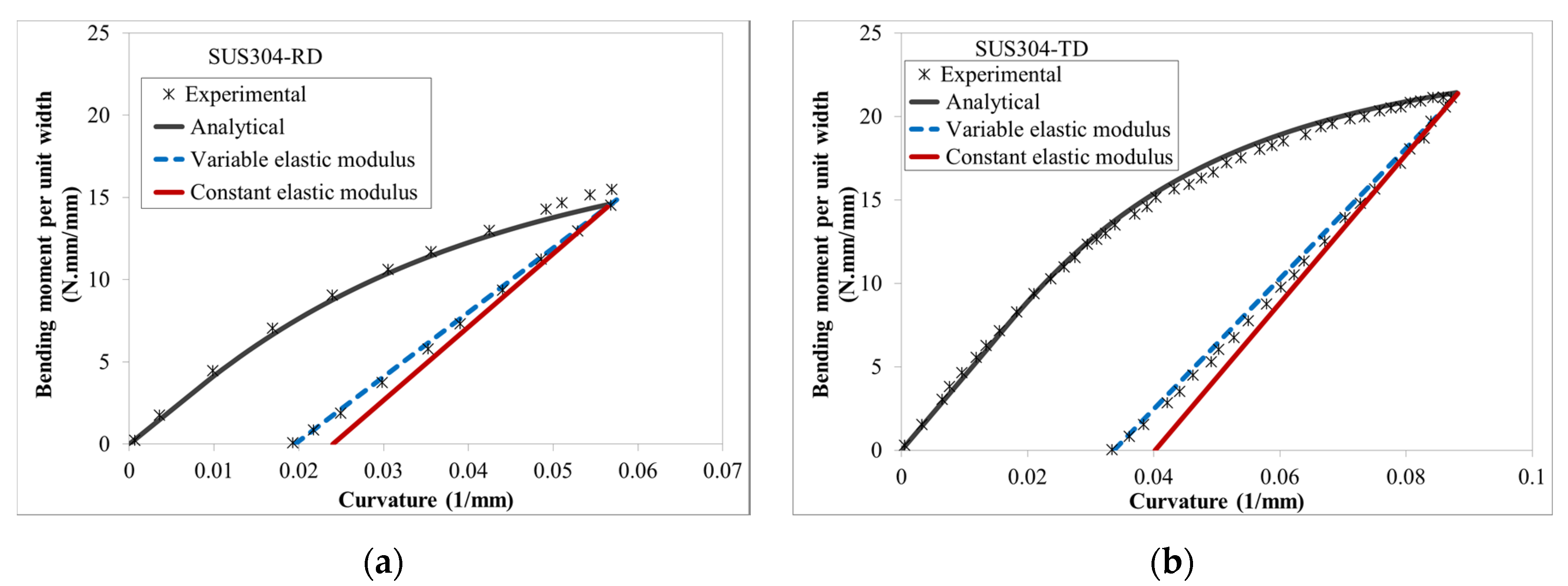
3.2. Pure Bending and Springback of Stainless Steel 304
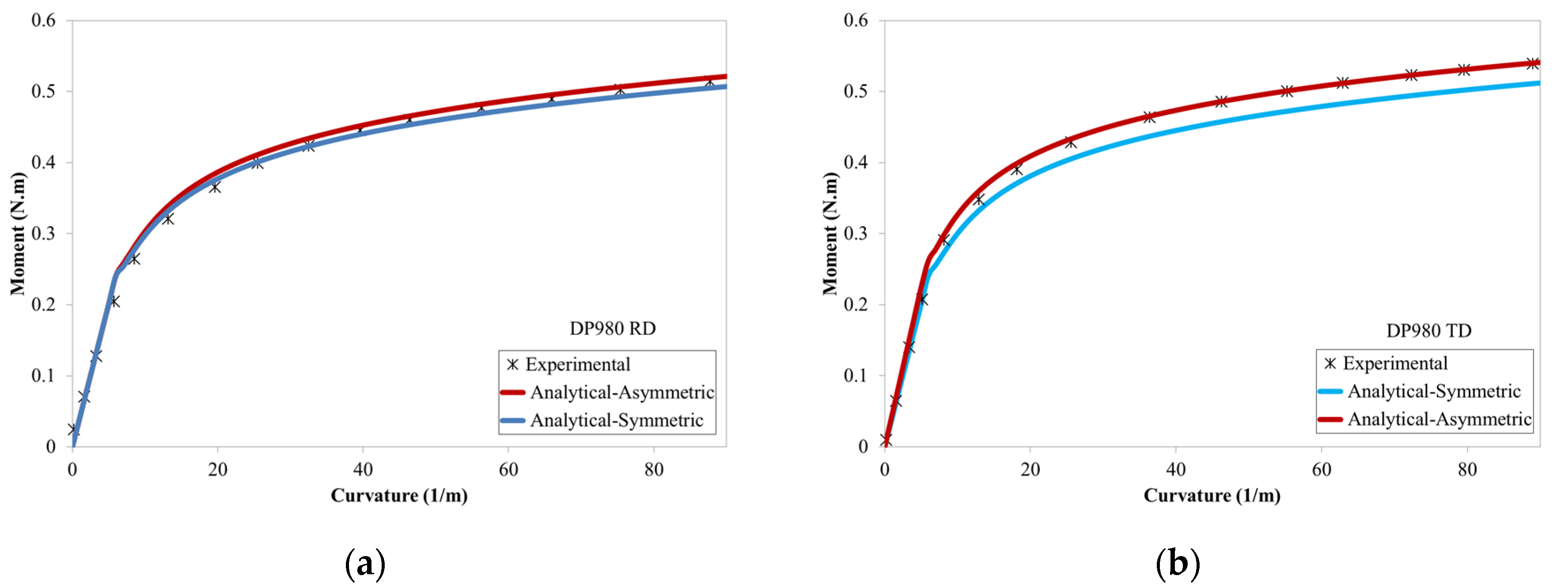
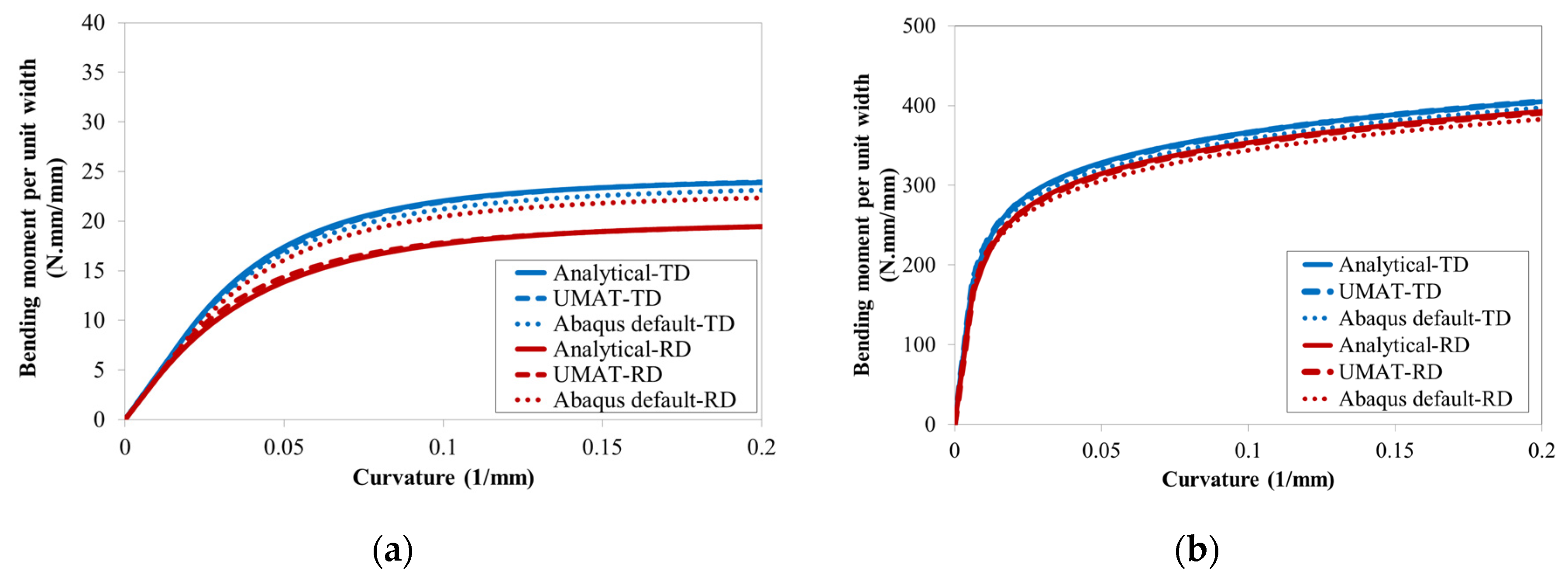
3.3. Numerical Study of Pure Bending of DP980 and SUS304
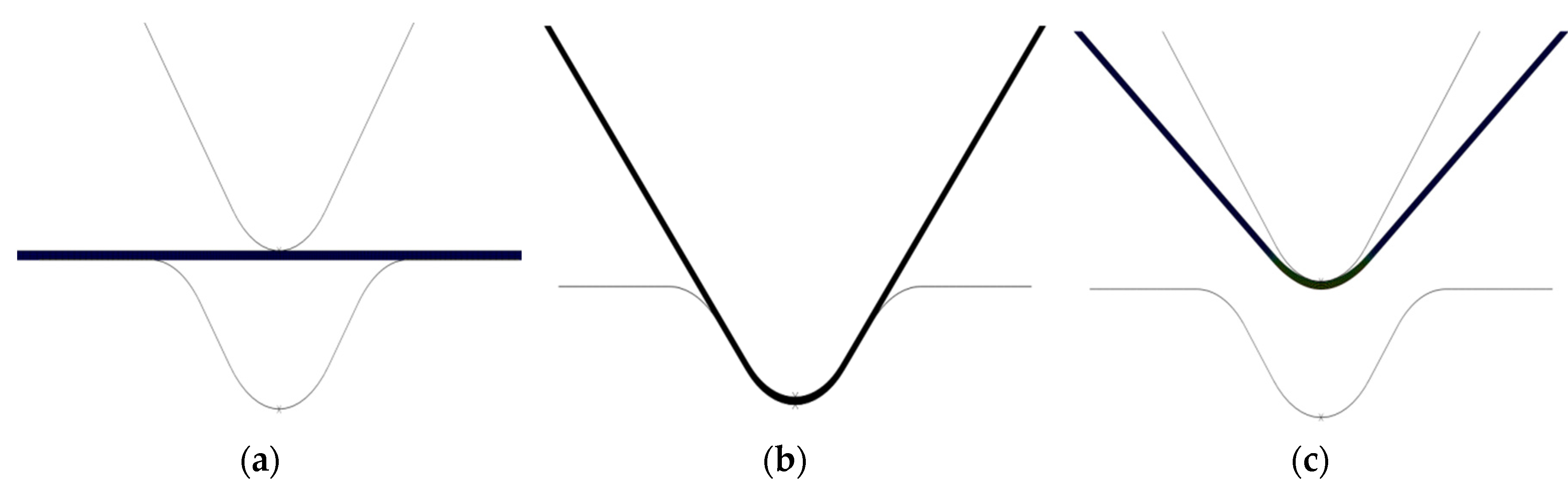
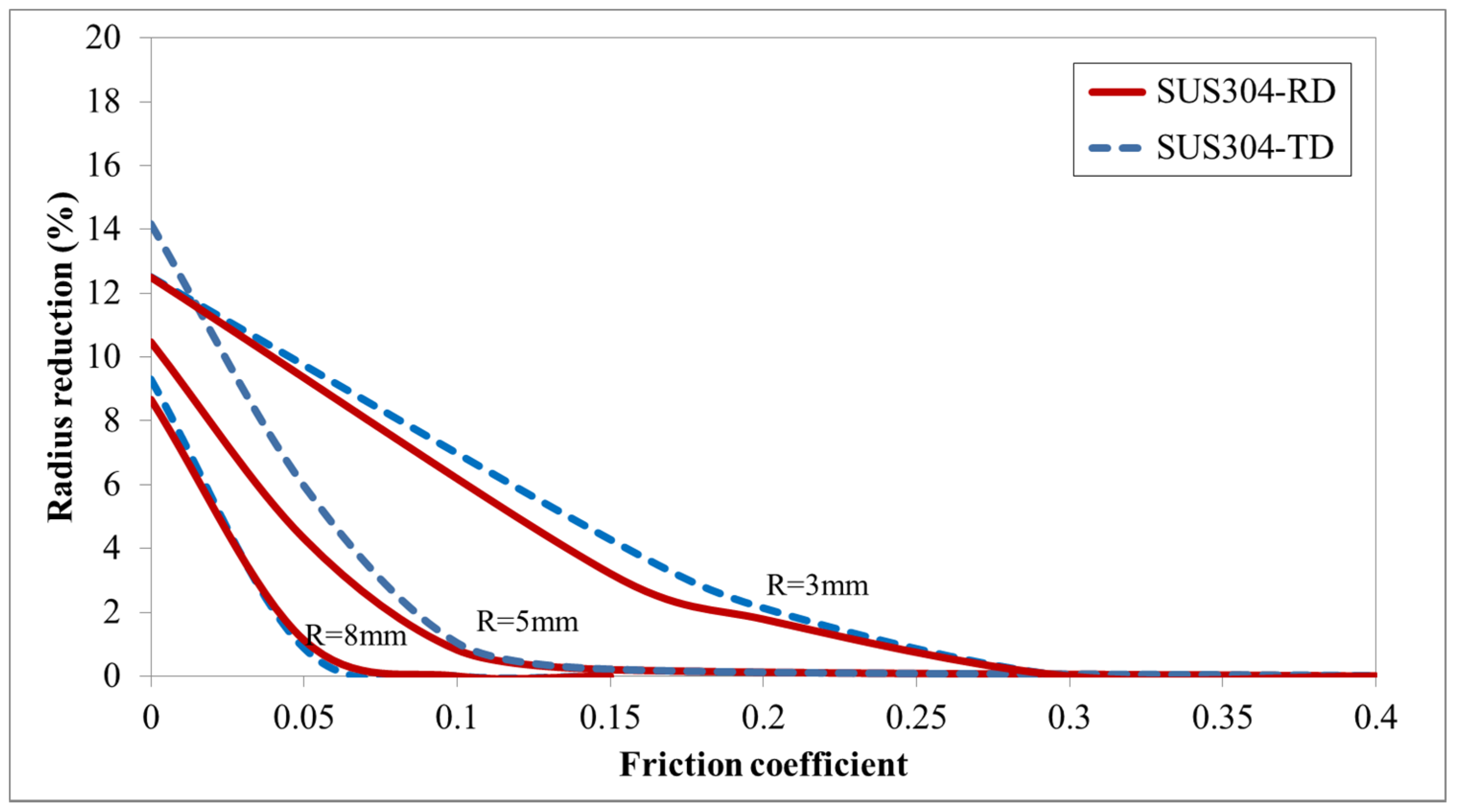
3.4. Numerical Study of SUS304 under V-Bending
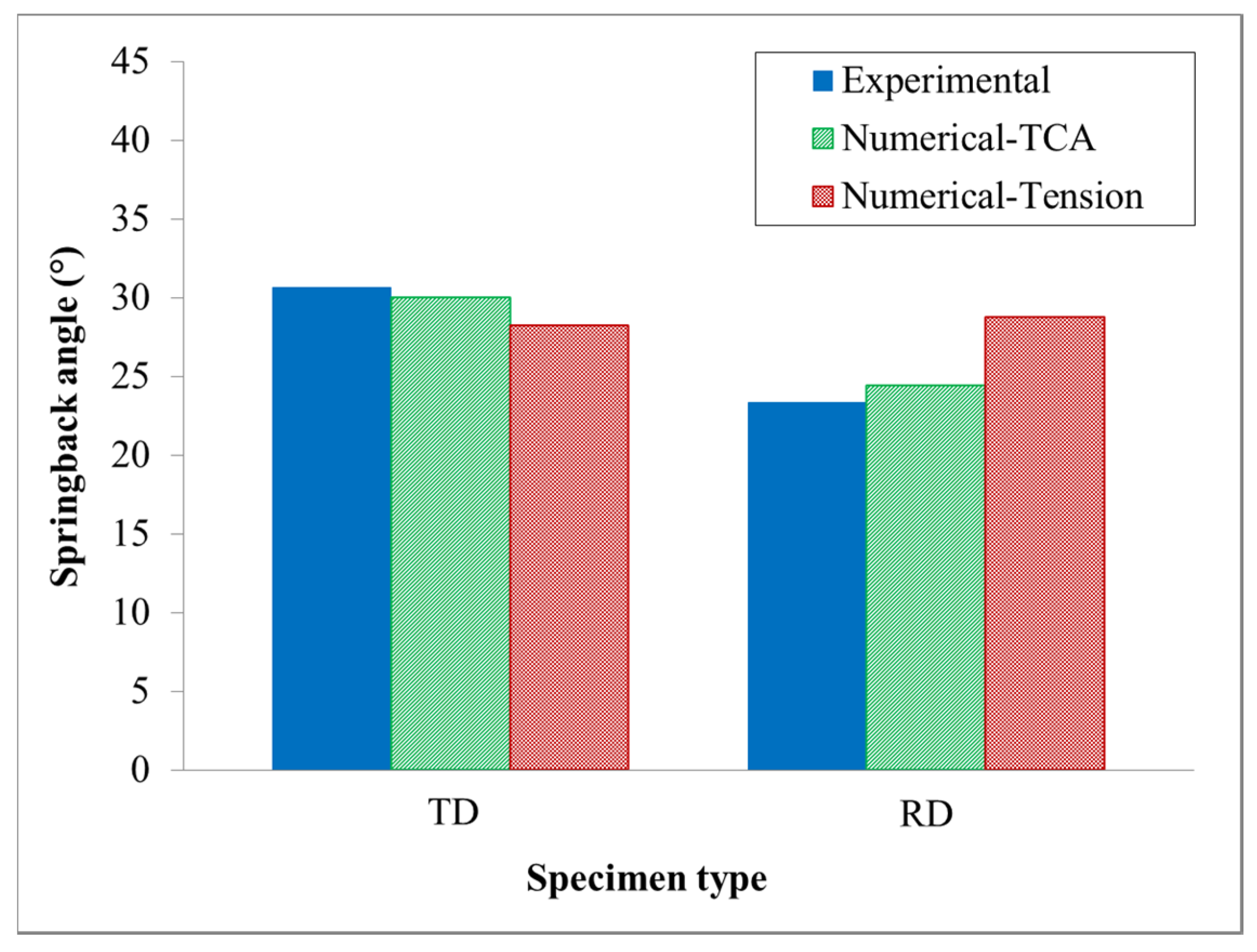
3.5. The Modified Analytical Method for Springback Prediction of SUS304 under V-Bending
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wagoner, R.H.; Lim, H.; Lee, M.-G. Advanced issues in springback. Int. J. Plast. 2013, 45, 3–20. [Google Scholar] [CrossRef]
- Lou, X.; Li, M.; Boger, R.; Agnew, S.; Wagoner, R. Hardening evolution of AZ31B Mg sheet. Int. J. Plast. 2007, 23, 44–86. [Google Scholar] [CrossRef]
- Kalish, D.; Cohen, M. Anisotropy of properties in martensite as developed by thermomechanical treatments. ASM Trans. Q. 1969, 62, 353–361. [Google Scholar]
- Lee, M.-G.; Wagoner, R.; Lee, J.; Chung, K.; Kim, H. Constitutive modeling for anisotropic/asymmetric hardening behavior of magnesium alloy sheets. Int. J. Plast. 2008, 24, 545–582. [Google Scholar] [CrossRef]
- Kuwabara, T.; Kumano, Y.; Ziegelheim, J.; Kurosaki, I. Tension–compression asymmetry of phosphor bronze for electronic parts and its effect on bending behavior. Int. J. Plast. 2009, 25, 1759–1776. [Google Scholar] [CrossRef]
- Kuwabara, T.; Saito, R.; Hirano, T.; Oohashi, N. Tension-compression asymmetry of SUS304 stainless sheet for electronic parts and its effects on bending and springback behavior. Tetsu Hagane-J. Iron Steel Inst. Jpn. 2009, 95, 732–739. [Google Scholar] [CrossRef]
- Maeda, T.; Noma, N.; Kuwabara, T.; Barlat, F.; Korkolis, Y.P. Measurement of the strength differential effect of DP980 steel sheet and experimental validation using pure bending test. J. Mater. Process. Technol. 2018, 256, 247–253. [Google Scholar] [CrossRef]
- Lee, M.-G.; Kim, D.; Kim, C.; Wenner, M.; Wagoner, R.; Chung, K. A practical two-surface plasticity model and its application to spring-back prediction. Int. J. Plast. 2007, 23, 1189–1212. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S.-J.; Lee, Y.-S.; Lee, J.-Y.; Kim, D.; Lee, M.-G. Distortional hardening concept for modeling anisotropic/asymmetric plastic behavior of AZ31B magnesium alloy sheets. Int. J. Plast. 2017, 94, 74–97. [Google Scholar] [CrossRef]
- Muhammad, W.; Mohammadi, M.; Kang, J.; Mishra, R.K.; Inal, K. An elasto-plastic constitutive model for evolving asymmetric/anisotropic hardening behavior of AZ31B and ZEK100 magnesium alloy sheets considering monotonic and reverse loading paths. Int. J. Plast. 2015, 70, 30–59. [Google Scholar] [CrossRef]
- Park, N.; Stoughton, T.B.; Yoon, J.W. A criterion for general description of anisotropic hardening considering strength differential effect with non-associated flow rule. Int. J. Plast. 2019, 121, 76–100. [Google Scholar] [CrossRef]
- Hosford, W. A generalized isotropic yield criterion. J. Appl. Mech. 1972, 39, 607–609. [Google Scholar] [CrossRef]
- Cazacu, O.; Barlat, F. A criterion for description of anisotropy and yield differential effects in pressure-insensitive metals. Int. J. Plast. 2004, 20, 2027–2045. [Google Scholar] [CrossRef]
- Drucker, D.C. Relation of experiments to mathematical theories of plasticity. J. Appl. Mech.-Trans. ASME 1949, 16, 349–357. [Google Scholar]
- Yoon, J.W.; Lou, Y.; Yoon, J.; Glazoff, M.V. Asymmetric yield function based on the stress invariants for pressure sensitive metals. Int. J. Plast. 2014, 56, 184–202. [Google Scholar] [CrossRef]
- Lee, M.; Kim, J.; Chung, K.; Kim, S.; Wagoner, R.; Kim, H. Analytical springback model for lightweight hexagonal close-packed sheet metal. Int. J. Plast. 2009, 25, 399–419. [Google Scholar] [CrossRef]
- Kim, J.H.; Lee, M.-G.; Kim, S.-J.; Chung, K.; Wagoner, R.H. Reverse effect of tensile force on sidewall curl for materials with tensile/compressive strength difference. Met. Mater. Int. 2009, 15, 353. [Google Scholar] [CrossRef]
- Mehrabi, H.; Yang, C. A theoretical study on pure bending of hexagonal close-packed metal sheet. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2018; p. 170012. [Google Scholar]
- Nguyen, N.-T.; Seo, O.S.; Lee, C.A.; Lee, M.-G.; Kim, J.-H.; Kim, H.Y. Mechanical behavior of AZ31B Mg alloy sheets under monotonic and cyclic loadings at room and moderately elevated temperatures. Materials 2014, 7, 1271–1295. [Google Scholar] [CrossRef]
- Kim, H.; Kim, C.; Barlat, F.; Pavlina, E.; Lee, M.-G. Nonlinear elastic behaviors of low and high strength steels in unloading and reloading. Mater. Sci. Eng. A 2013, 562, 161–171. [Google Scholar] [CrossRef]
- Sun, L.; Wagoner, R. Complex unloading behavior: Nature of the deformation and its consistent constitutive representation. Int. J. Plast. 2011, 27, 1126–1144. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Lee, M.-G.; Barlat, F.; Bae, G. Piecewise linear approximation of nonlinear unloading-reloading behaviors using a multi-surface approach. Int. J. Plast. 2017, 93, 112–136. [Google Scholar] [CrossRef]
- Yoshida, F.; Hamasaki, H.; Uemori, T. Modeling of anisotropic hardening of sheet metals including description of the Bauschinger effect. Int. J. Plast. 2015, 75, 170–188. [Google Scholar] [CrossRef]
- Pavlina, E.J.; Lee, M.-G.; Barlat, F. Observations on the nonlinear unloading behavior of advanced high strength steels. Metall. Mater. Trans. A 2015, 46, 18–22. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T.; Fujiwara, K. Elastic–plastic behavior of steel sheets under in-plane cyclic tension–compression at large strain. Int. J. Plast. 2002, 18, 633–659. [Google Scholar] [CrossRef]
- Ortiz, M.; Pinsky, P. Global Analysis Methods for the Solution of Elastoplastic and Viscoplastic Dynamic Problems; Dept. of Civil Engineering, University of California: Berkley, CA, USA, 1981. [Google Scholar]
- Matuszak, A. Factors influencing friction in steel sheet forming. J. Mater. Process. Technol. 2000, 106, 250–253. [Google Scholar] [CrossRef]
- Trzepieciński, T.; Bazan, A.; Lemu, H. Frictional characteristics of steel sheets used in automotive industry. Int. J. Automot. Technol. 2015, 16, 849–863. [Google Scholar] [CrossRef]
- Ramezani, M.; Ripin, Z.M.; Ahmad, R. Modelling of kinetic friction in V-bending of ultra-high-strength steel sheets. Int. J. Adv. Manuf. Technol. 2010, 46, 101–110. [Google Scholar] [CrossRef]





| Material | Loading Direction | Tensile Yield Point, σt | Compressive Yield Point, σc | c | ||
|---|---|---|---|---|---|---|
| DP980 | RD | 675 | 710 | −0.196 | 1 | −1.052 |
| TD | 706 | 738 | −0.172 | 1 | −1.045 | |
| SUS304 | RD | 335 | 260 | 0.942 | 1 | −0.776 |
| TD | 360 | 390 | −0.310 | 1 | −1.083 |
| Material | EaT (GPa) | EaC (GPa) | ξT | ξC |
|---|---|---|---|---|
| SUS304 | 148 | 133.8 | 60.76 | 75.74 |
| Loading Direction | Tensile Young’s Modulus, E (GPa) | Tensile Yield Point, σt | Compressive Yield Point, σc | K (MPa) | ε0 | n |
|---|---|---|---|---|---|---|
| RD | 186,000 | 675 | 710 | 1530 | 0.0001 | 0.139 |
| TD | 208,000 | 706 | 738 | 1563 | 0.0002 | 0.133 |
| Loading Direction | Tensile Young’s Modulus, E (GPa) | Tensile Yield Point, σt | Compressive Yield Point, σc | B (MPa) | C |
|---|---|---|---|---|---|
| RD | 185 | 335 | 260 | 680 | 300 |
| TD | 198 | 360 | 390 | 690 | 300 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mehrabi, H.; Yang, R.; Wang, B. Effects of Tension–Compression Asymmetry on Bending of Steels. Appl. Sci. 2020, 10, 3339. https://doi.org/10.3390/app10093339
Mehrabi H, Yang R, Wang B. Effects of Tension–Compression Asymmetry on Bending of Steels. Applied Sciences. 2020; 10(9):3339. https://doi.org/10.3390/app10093339
Chicago/Turabian StyleMehrabi, Hamed, Richard (Chunhui) Yang, and Baolin Wang. 2020. "Effects of Tension–Compression Asymmetry on Bending of Steels" Applied Sciences 10, no. 9: 3339. https://doi.org/10.3390/app10093339
APA StyleMehrabi, H., Yang, R., & Wang, B. (2020). Effects of Tension–Compression Asymmetry on Bending of Steels. Applied Sciences, 10(9), 3339. https://doi.org/10.3390/app10093339



_Yang.png)


