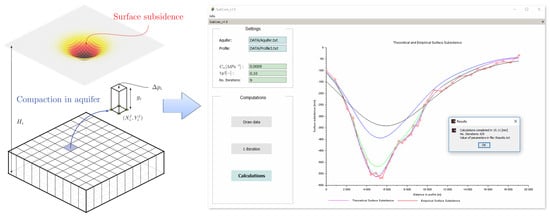
Software for Estimation of Stochastic Model Parameters for a Compacting Reservoir
Abstract
1. Introduction
- verify the efficacy of a parameter estimation method based on a stochastic model;
- implement an algorithm in open-source software;
- model subsidence due to dewatering in an underground coal mine.
2. Compaction and Subsidence Model
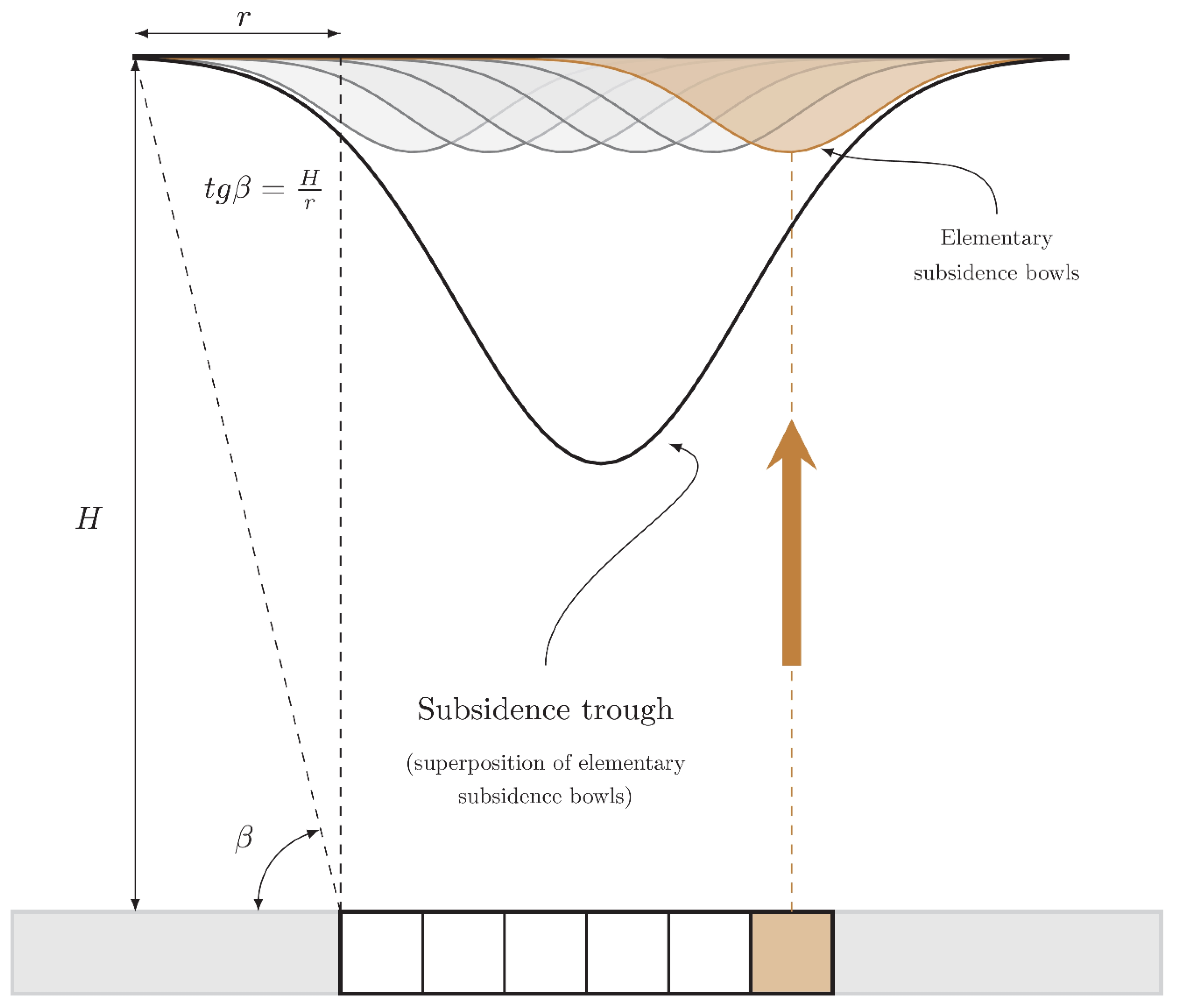
2.1. Principles of a Model Based on the Influence Function
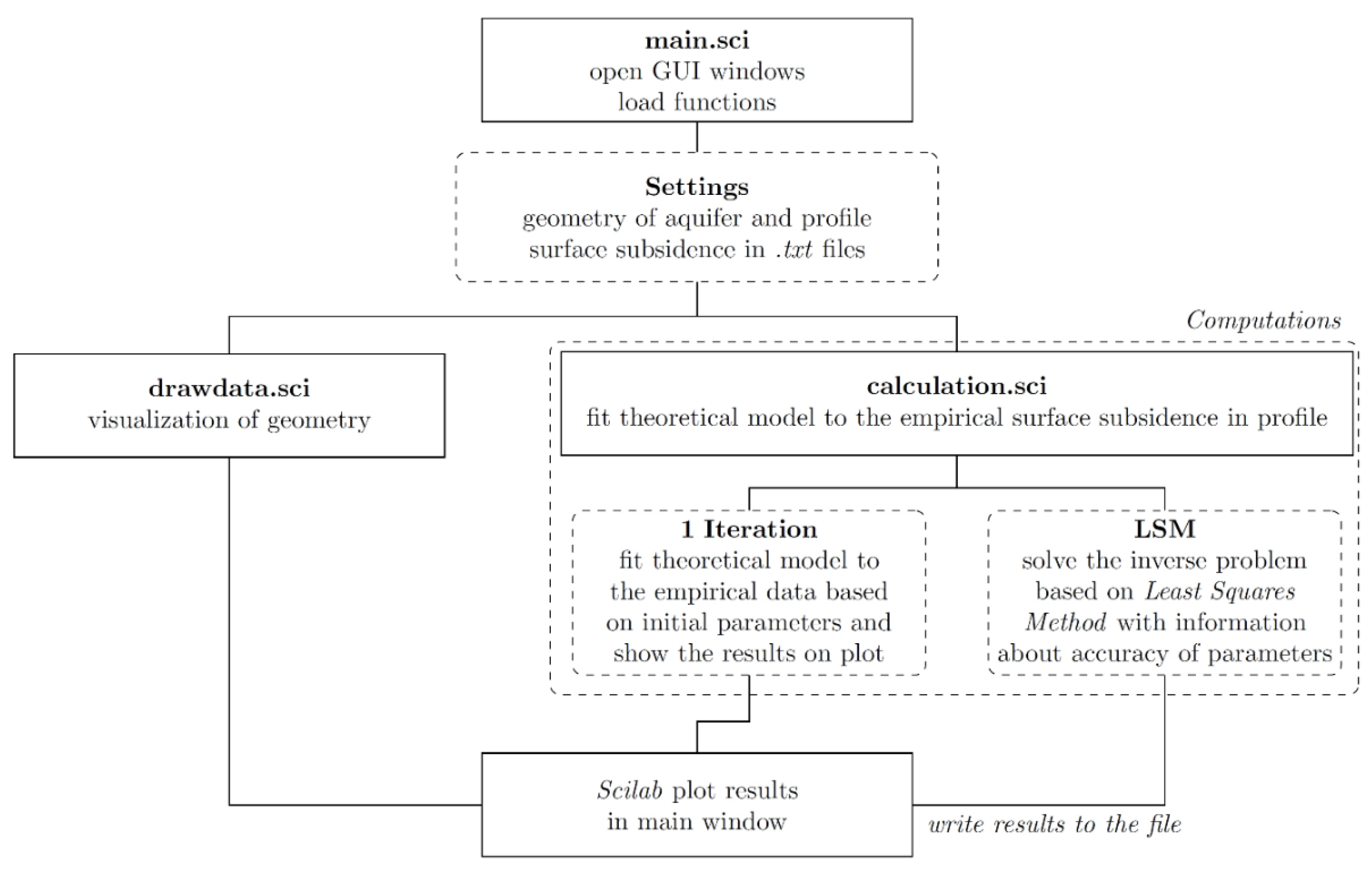
2.2. Program Framework
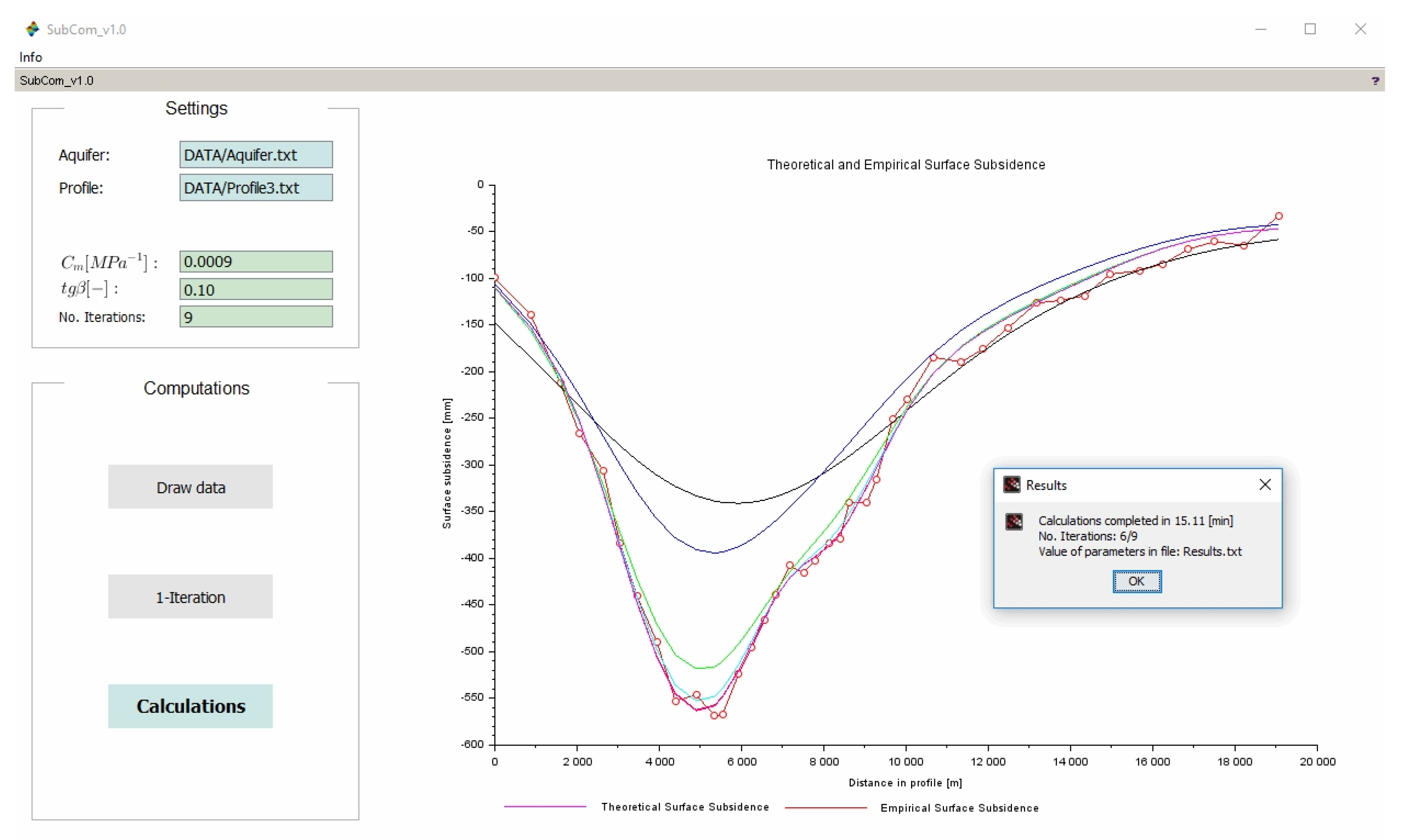
2.3. Calculations for Testing Data
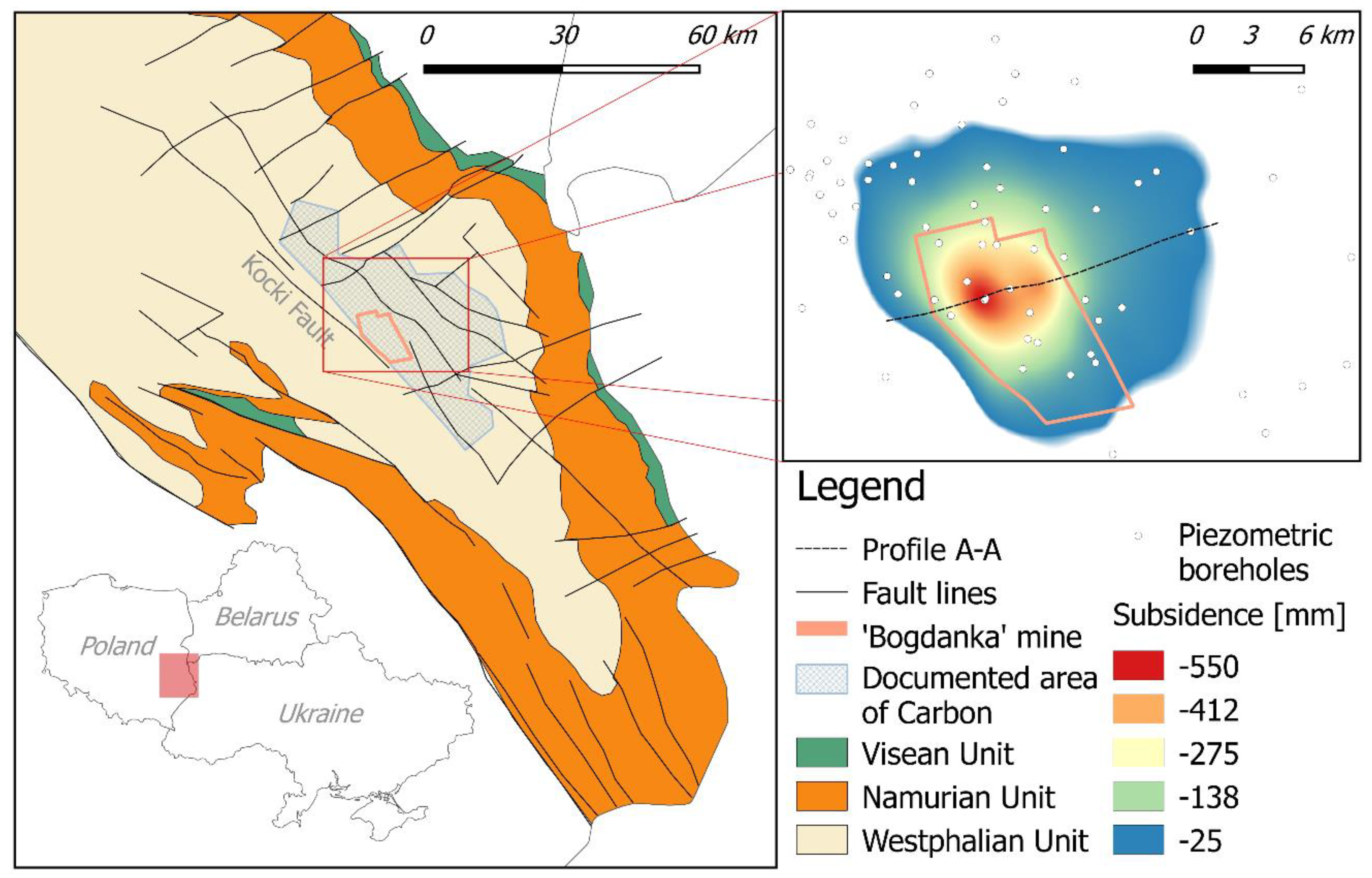
3. Study Area
3.1. Geological Background
3.2. Subsidence Due To Fluid Withdrawal
4. Results
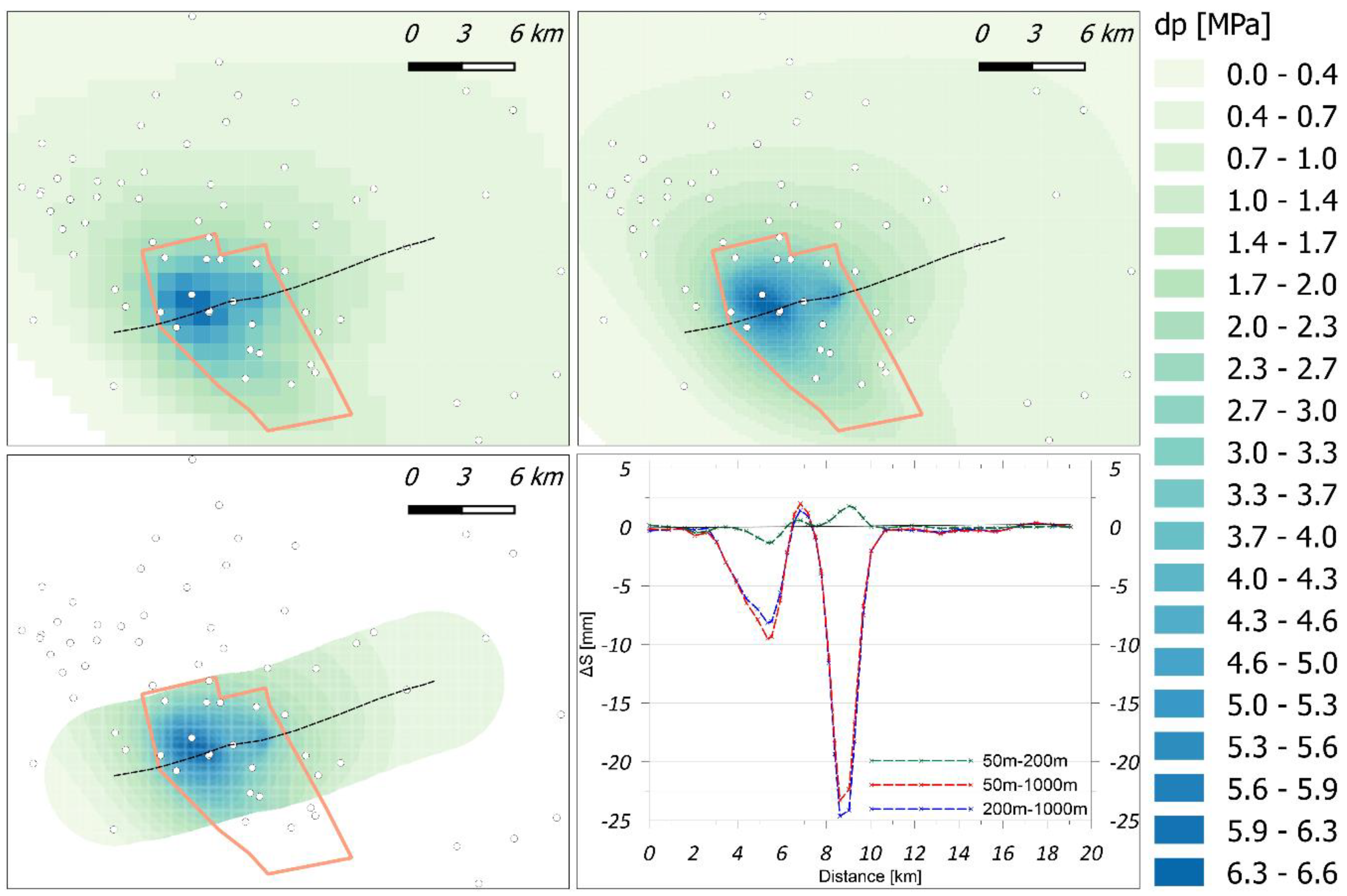
4.1. Dimension Testing Of Aquifer Elements
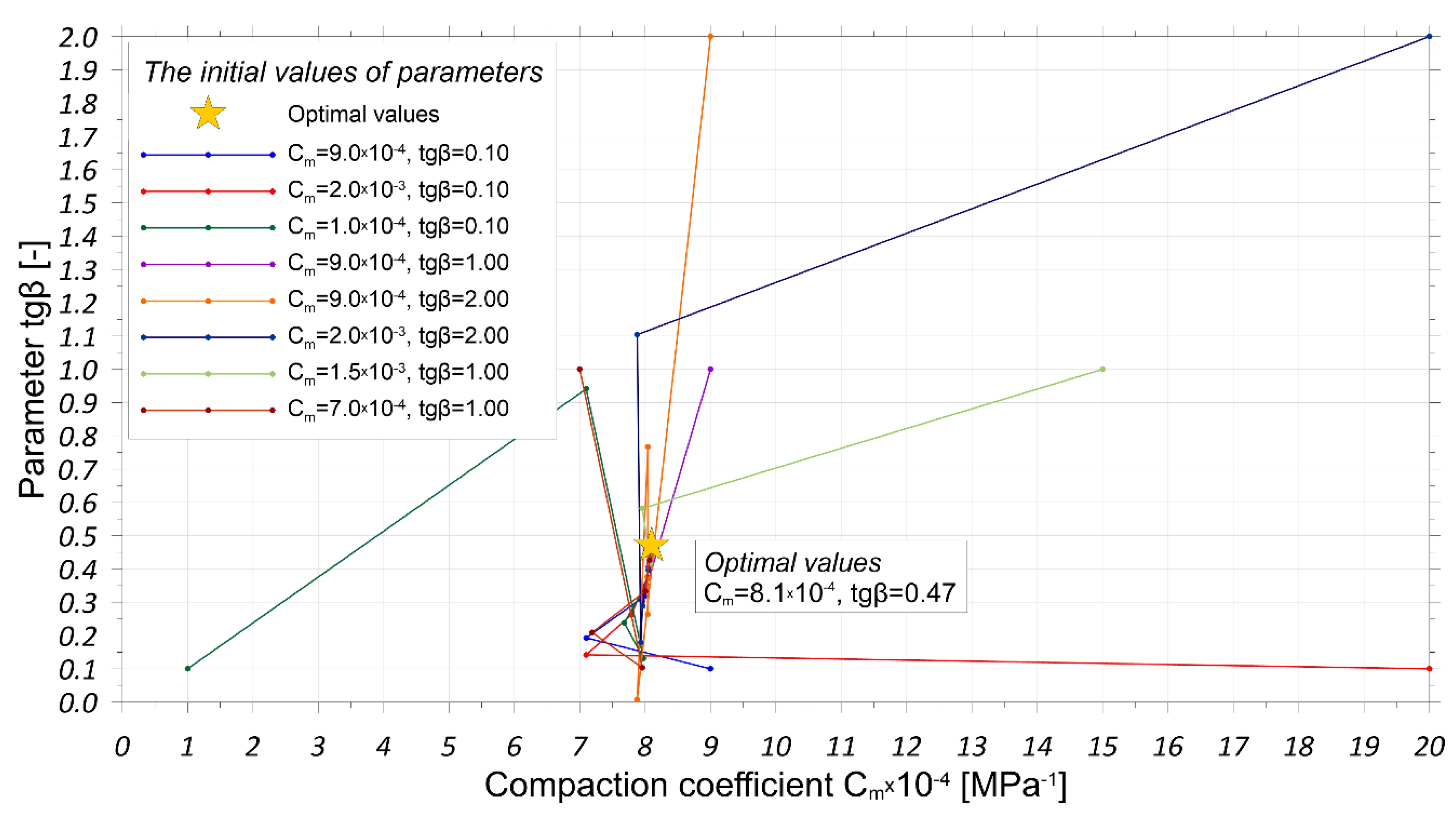
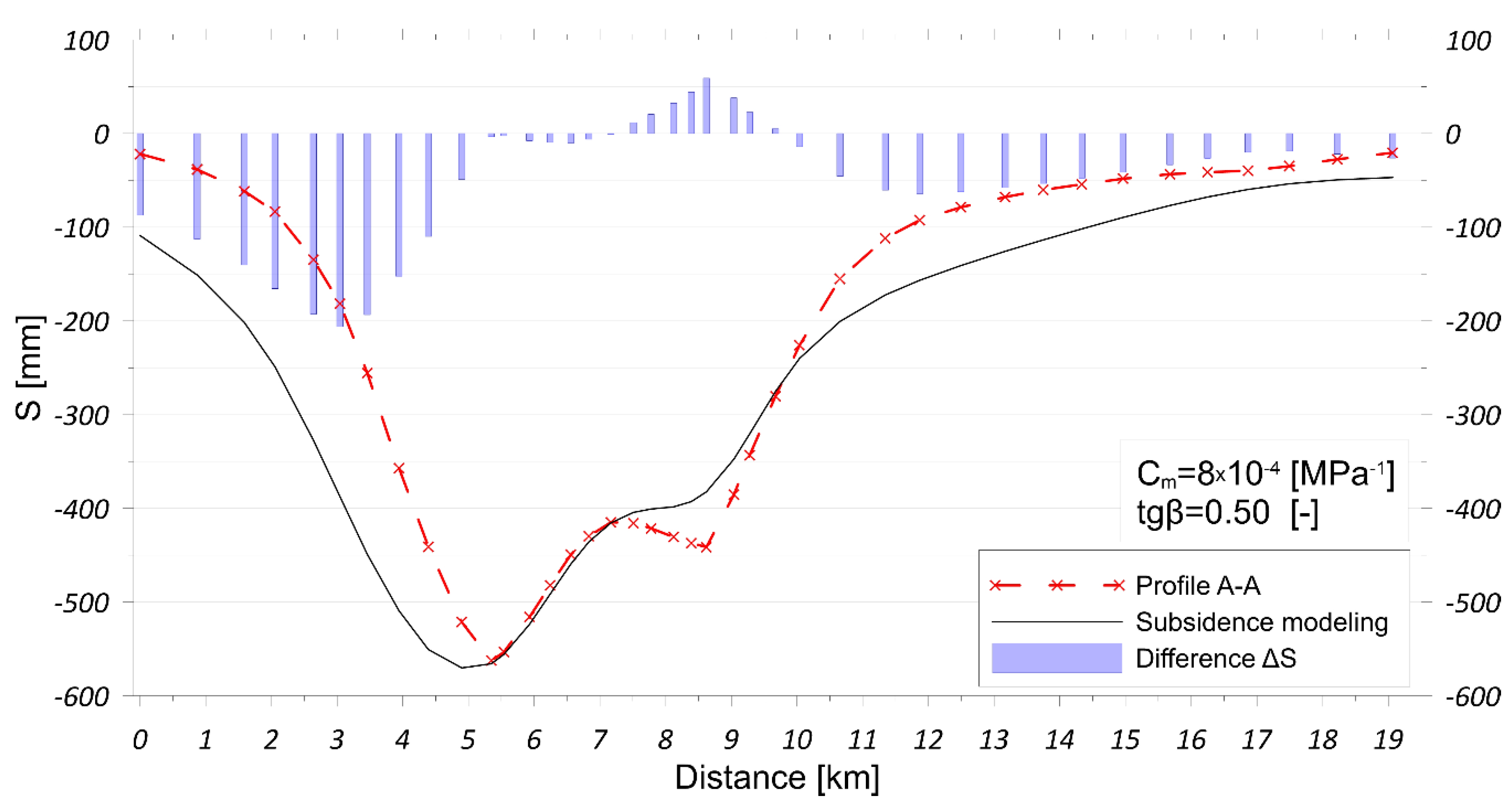
4.2. Estimation Results of Compaction Coefficient Cm and tgβ
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Ketelaar, V.B.H.G. Satellite Radar Interferometry; Remote Sensing and Digital Image Processing 14; Springer: Dordrecht, The Netherlands, 2009; pp. 113–166. [Google Scholar]
- Osmanoğlu, B.; Dixon, T.H.; Wdowinski, S.; Cabral-Cano, E.; Jiang, Y. Mexico City subsidence observed with persistent scatterer InSAR. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 1–12. [Google Scholar] [CrossRef]
- Castellazzi, P.; Garfias, J.; Martel, R.; Brouard, C.; Rivera, A. InSAR to support sustainable urbanization over compacting aquifers: The case of Toluca Valley, Mexico. Int. J. Appl. Earth Obs. Geoinf. 2017, 63, 33–44. [Google Scholar] [CrossRef]
- Teatini, P.; Tosi, L.; Strozzi, T.; Carbognin, L.; Wegmuller, U.; Rizzetto, F. Mapping regional land displacements in the Venice coastland by an integrated monitoring system. Remote. Sens. Environ. 2005, 98, 403–413. [Google Scholar] [CrossRef]
- Borowski, W. The development of the subsidence basin in the Central Coal District LZW. Prace Naukowe Politechniki Lubelskiej 1987, 171, 85–105. [Google Scholar]
- Piestrzyński, A. Monografia KGHM Polska Miedz SA; KGHM CUPRUM Sp. z o.o. CBR: Lubin, Poland, 2008. [Google Scholar]
- Witkowski, W.T. Modeling of Land Subsidence Due to Hydrological Changes with Artificial Intelligence Tools. Ph.D. Thesis, AGH University of Science and Technology, Kraków, Poland, 2017. [Google Scholar]
- Galloway, D.; Burbey, T.J. Review: Regional land subsidence accompanying groundwater extraction. Hydrogeol. J. 2011, 19, 1459–1486. [Google Scholar] [CrossRef]
- Muntendam-Bos, A.G.; Fokker, P.A. Unraveling reservoir compaction parameters through the inversion of surface subsidence observations. Comput. Geosci. 2008, 13, 43–55. [Google Scholar] [CrossRef]
- Fokker, P.A.; Van Thienen-Visser, K. Inversion of double-difference measurements from optical leveling for the Groningen gas field. Int. J. Appl. Earth Obs. Geoinf. 2016, 49, 1–9. [Google Scholar] [CrossRef]
- Zoccarato, C.; Ferronato, M.; Teatini, P. Formation compaction vs land subsidence to constrain rock compressibility of hydrocarbon reservoirs. Géoméch. Energy Environ. 2018, 13, 14–24. [Google Scholar] [CrossRef]
- Witkowski, W.T. Artificial intelligence in modelling of surface subsidence due to water withdrawal in underground mining. In Proceedings of the 15th International Multidisciplinary Scientific GeoConference-SGEM; SGEM2015 Conference Proceedings, Albena, Bulgaria, 18–24 June 2015; pp. 503–510. [Google Scholar]
- Hejmanowski, R. Zur Vorausberechnung Förderbedingter Bodensenkungen Über Erdöl-und Erdgaslagerstätten. Ph.D. Thesis, Technische Universität Clausthal, Clausthal, Germany, 1993. [Google Scholar]
- Sroka, A.; Hejmanowski, R. Subsidence prediction caused by the oil and gas development. In Proceedings of the 3rd IAG Symposium on Geodesy for Geotechnical and Structural Engineering and 12th FIG Symposium on Deformation Measurements, Baden, Germany, 22–24 May 2006. [Google Scholar]
- Hejmanowski, R.; Malinowska, A. Evaluation of reliability of subsidence prediction based on spatial statistical analysis. Int. J. Rock Mech. Min. Sci. 2009, 46, 432–438. [Google Scholar] [CrossRef]
- Malinowska, A. A fuzzy inference-based approach for building damage risk assessment on mining terrains. Eng. Struct. 2011, 33, 163–170. [Google Scholar] [CrossRef]
- Terzaghi, K. Settlement and Consolidation of Clay; McGraw Hill: New York, NY, USA, 1925; pp. 874–878. [Google Scholar]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Poland, J.F. Guidebook to Studies of Land Subsidence Due to Ground-Water Withdrawal; UNESCO: Paris, France, 1984. [Google Scholar]
- Brown, K.; Trott, S. Groundwater Flow Models in Open Pit Mining: Can We Do Better? Mine Water Environ. 2014, 33, 187–190. [Google Scholar] [CrossRef]
- Fokker, P.A.; Orlić, B. Semi-Analytic Modelling of Subsidence. Math. Geol. 2006, 38, 565–589. [Google Scholar] [CrossRef]
- Knothe, S. A profile equation for a definitely shaped subsidence through. Arch. Min. Sci. 1953, 1, 22–38. [Google Scholar]
- MSEC. Methods of Subsidence Prediction; Unpublished report by Mine Subsidence Engineering Consultants; MSEC: Chatswood, Australia, 2008. [Google Scholar]
- Diaz-Fernandez, M.E.; Álvarez-Fernández, M.I.; Álvarez-Vigil, A.E. Computation of influence functions for automatic mining subsidence prediction. Comput. Geosci. 2009, 14, 83–103. [Google Scholar] [CrossRef]
- Sroka, A.; Schöber, F. Studie zur Analyse und Vorhersage der Bodensenkungen und des Kompaktionsverhaltens des Erdgasfeldes Groningen/Emsmündung; Abschlussbericht: Clausthal-Zellerfeld, Germany, 1990. [Google Scholar]
- Hoffmann, J.; Galloway, D.; Zebker, H.A. Inverse modeling of interbed storage parameters using land subsidence observations, Antelope Valley, California. Water Resour. Res. 2003, 39. [Google Scholar] [CrossRef]
- Zhang, M.; Burbey, T.J. Inverse modelling using PS-InSAR data for improved land subsidence simulation in Las Vegas Valley, Nevada. Hydrol. Process. 2016, 30, 4494–4516. [Google Scholar] [CrossRef]
- McGovern, S.; Kollet, S.; Bürger, C.M.; Schwede, R.L.; Podlaha, O.G. Novel basin modelling concept for simulating deformation from mechanical compaction using level sets. Comput. Geosci. 2017, 148, 835–848. [Google Scholar] [CrossRef]
- Feng, X.-T.; Hudson, J.A. Specifying the information required for rock mechanics modelling and rock engineering design. Int. J. Rock Mech. Min. Sci. 2010, 47, 179–194. [Google Scholar] [CrossRef]
- Geertsma, J. Land Subsidence Above Compacting Oil and Gas Reservoirs. J. Pet. Technol. 1973, 25, 734–744. [Google Scholar] [CrossRef]
- Fokker, P.A.; Osinga, S. On the Use of Influence Functions for Subsidence Evaluation. In Proceedings of the 52nd U.S. Rock Mechanics/Geomechanics Symposium, Seattle, WA, USA, 17–20 June 2018. [Google Scholar]
- Knothe, S. Prediction of Influence Mining Exploitation; Śląsk: Katowice, Poland, 1984. [Google Scholar]
- Hebblewhite, B.; Waddington, A.A.; Wood, J.H. Regional horizontal surface displacements due to mining beneath severe surface topography. In Proceedings of the 19th International Conference on Ground Control in Mining, Morgantown, WV, USA, 8–10 August 2000. [Google Scholar]
- Ren, G.; Li, G.; Kulessa, M. Application of a Generalised Influence Function Method for Subsidence Prediction in Multi-seam Longwall Extraction. Geotech. Geol. Eng. 2014, 32, 1123–1131. [Google Scholar] [CrossRef]
- Ren, G.; Buckeridge, J.; Li, J. Estimating Land Subsidence Induced by Groundwater Extraction in Unconfined Aquifers Using an Influence Function Method. J. Water Resour. Plan. Manag. 2015, 141, 04014084. [Google Scholar] [CrossRef]
- Kraemer, S. Analytic Element Ground Water Modeling as a Research Program (1980 to 2006). Ground Water 2007, 45, 402–408. [Google Scholar] [CrossRef] [PubMed]
- Hejmanowski, R. Modeling of time dependent subsidence for coal and ore deposits. Int. J. Coal Sci. Technol. 2015, 2, 287–292. [Google Scholar] [CrossRef]
- Kwinta, A.; Gradka, R. Analysis of the damage influence range generated by underground mining. Int. J. Rock Mech. Min. Sci. 2020, 128, 104263. [Google Scholar] [CrossRef]
- Samsonov, S.; Van Der Kooij, M.; Tiampo, K. A simultaneous inversion for deformation rates and topographic errors of DInSAR data utilizing linear least square inversion technique. Comput. Geosci. 2011, 37, 1083–1091. [Google Scholar] [CrossRef]
- Maciuk, K. GPS-only, GLONASS-only and combined GPS+GLONASS absolute positioning under different sky view conditions. Tehnički Vjesnik 2018, 25, 933–939. [Google Scholar]
- Malinowska, A.; Hejmanowski, R.; Dai, H. Ground movements modeling applying adjusted influence function. Int. J. Min. Sci. Technol. 2020, 30, 243–249. [Google Scholar] [CrossRef]
- Dey, S.; Singh, A.K.; Prasad, D.K.; McDonald-Maier, K.D. SoCodeCNN: Program Source Code for Visual CNN Classification Using Computer Vision Methodology. IEEE Access 2019, 7, 157158–157172. [Google Scholar] [CrossRef]
- Wilk, Z. Hydrogeologia Polskich Złóż Kopalin i Problemy Wodne Górnictwa—Tom 1; Uczelniane Wydawnictwa Naukowo-Dydaktyczne AGH: Kraków, Poland, 2003. [Google Scholar]
- Paczyński, B.; Sadurski, A. Polish Regional Hydrogeology: Volume II—Mineral, Curative and Thermal Waters as Well as Mining Waters; Państwowy Instytut Geologiczny: Warszawa, Poland, 2007. [Google Scholar]
- Hejmanowski, R.; Sopata, P.; Stoch, T.; Wójcik, A.; Witkowski, W.T. Impact of coal rock mass drainage on surface subsidence. Przeglad Górniczy 2013, 69, 38–43. [Google Scholar]
- Doornhof, D.; Kristiansen, T.G.; Nagel, N.B.; Pattillo, P.D.; Sayers, C. Compaction and Subsidence. Oilfield Rev. 2006, 18, 50–68. [Google Scholar]
- Sroka, A.; Tajduś, K. Calculating land subsidence in the exploitation of oil and gas. Wiertnictwo Nafta Gaz 2009, 26, 327–335. [Google Scholar]
- Austad, T.; Strand, S.; Madland, M.V.; Puntervold, T.; Korsnes, R.I. Seawater in Chalk: An EOR and Compaction Fluid. SPE Reserv. Evaluation Eng. 2008, 11, 648–654. [Google Scholar] [CrossRef]
| Type of Data | Symbol | Description | Data visualization |
|---|---|---|---|
| Profile | Id, X, Y, S | Information about surface subsidence on the profile | 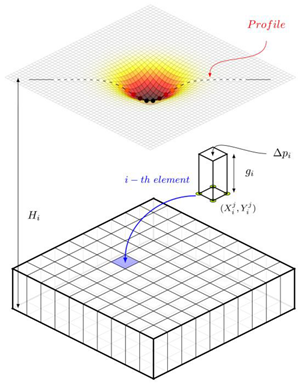 |
| Aquifer | The geometry of a single aquifer element in the same coordinate system as the profile | ||
| Hi | Depth | ||
| Mi | The thickness of a single aquifer element | ||
| Δpi | Pressure decrease in the aquifer, determined for the bottom of the aquifer element |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witkowski, W.T.; Hejmanowski, R. Software for Estimation of Stochastic Model Parameters for a Compacting Reservoir. Appl. Sci. 2020, 10, 3287. https://doi.org/10.3390/app10093287
Witkowski WT, Hejmanowski R. Software for Estimation of Stochastic Model Parameters for a Compacting Reservoir. Applied Sciences. 2020; 10(9):3287. https://doi.org/10.3390/app10093287
Chicago/Turabian StyleWitkowski, Wojciech T., and Ryszard Hejmanowski. 2020. "Software for Estimation of Stochastic Model Parameters for a Compacting Reservoir" Applied Sciences 10, no. 9: 3287. https://doi.org/10.3390/app10093287
APA StyleWitkowski, W. T., & Hejmanowski, R. (2020). Software for Estimation of Stochastic Model Parameters for a Compacting Reservoir. Applied Sciences, 10(9), 3287. https://doi.org/10.3390/app10093287