Linking Singular Spectrum Analysis and Machine Learning for Monthly Rainfall Forecasting
Abstract
1. Introduction
- Linking SSA with machine learning techniques (i.e., LS-SVR and RF) to construct hybrid models (SSA-LSSVR and SSA-RF) for monthly rainfall forecasting in two reservoir watersheds of Taiwan where the hybrid models have not been applied before.
- Comparison between the hybrid models (i.e., SSA-LSSVR and SSA-RF) and the standard models (i.e., LS-SVR and RF) to validate the efficiency of the data preprocessing technique.
2. Study Sites and Data Collection
3. Methodologies
3.1. Least-Squares Support Vector Machine
3.2. Random Forest
3.3. Singular Spectrum Analysis
3.4. Coupling SSA with Machine Learning (LS-SVR and RF)
- Initially, the time series of rainfall data was decomposed into several principal components (PCs) using SSA.
- The relevant principal components are calculated on the basis of the trend or period of each series, and a new series for each variable is constituted by adding up the primary components to be defined. The new series was used to construct model input.
- LS-SVR and RF models are applied to every component of the reconstruction so that the architecture of LS-SVR and RF is different for each component of the reconstruction.
- Finally, LS-SVR and RF models are fed with the new series to forecast the future rainfalls for 1-, 2-, and 3- month lead-time. This is the principal idea of coupling SSA with machine learning techniques (LS-SVR and RF), as illustrated in Figure 2.
3.5. Forecast Verification
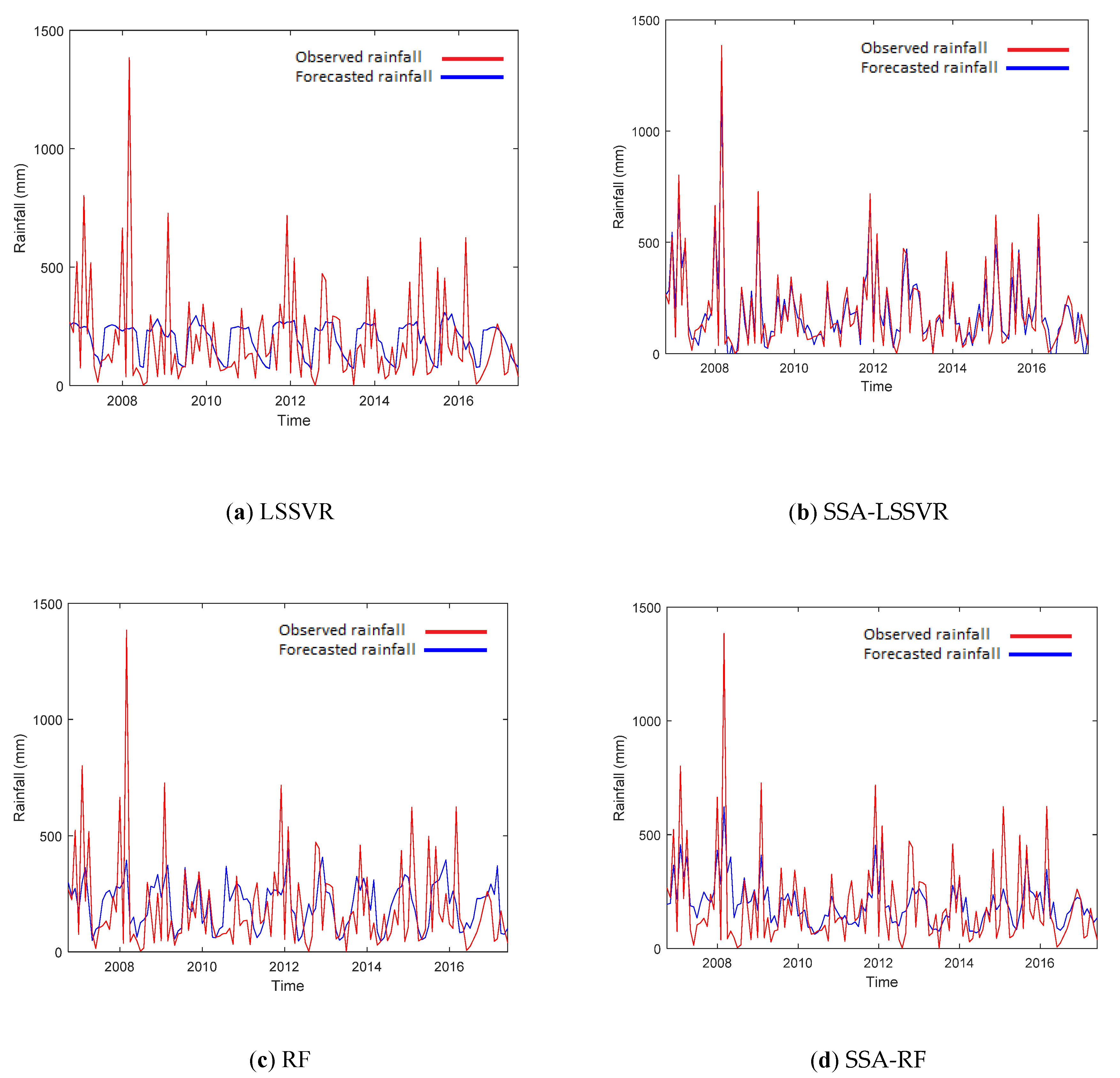
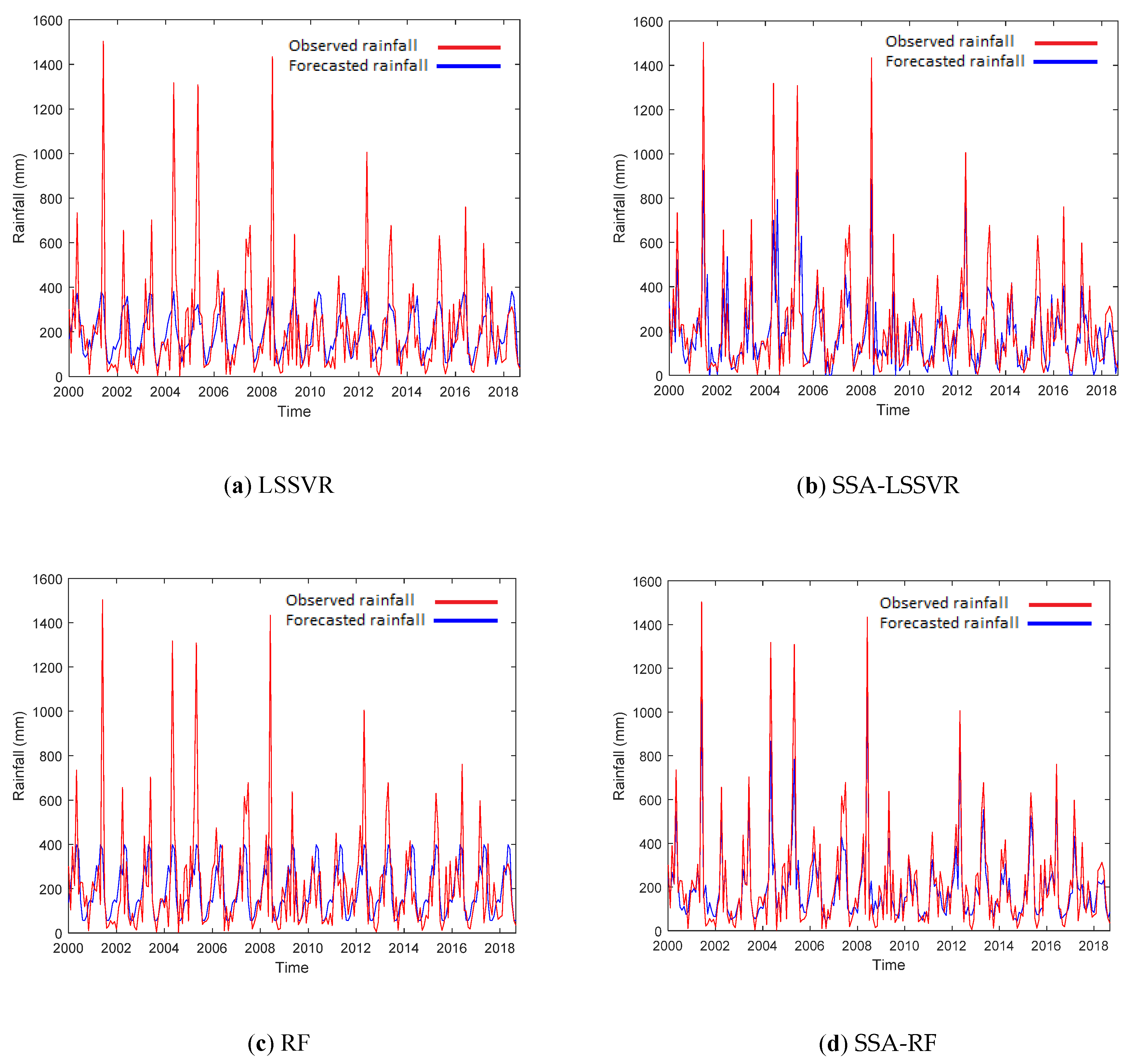
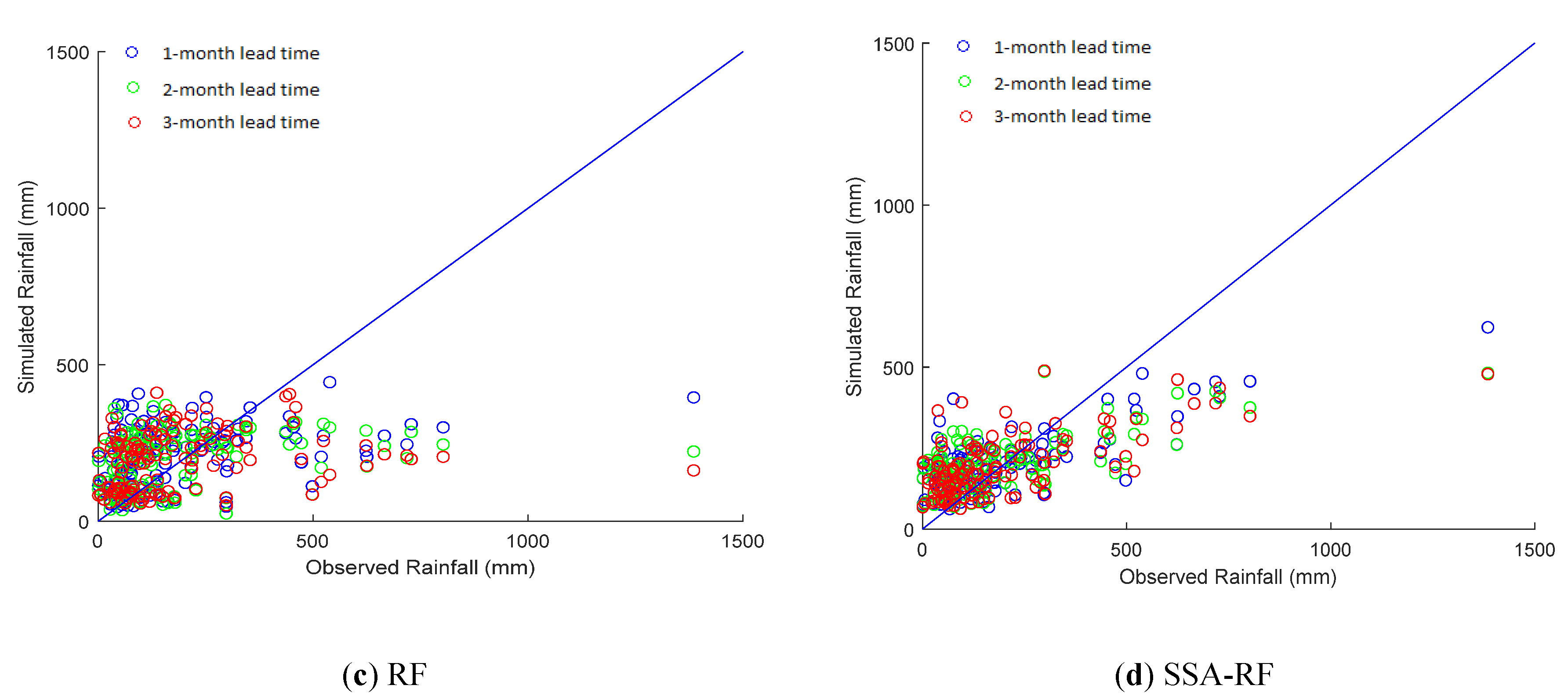
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| SSA | Singular Spectrum Analysis |
| LS-SVR | Lease Square Support Vector Regressions |
| SSA-LSSVR | Hybrid model which couples SSA with LS-SVR |
| RF | Random Forest |
| SSA-RF | Hybrid model which couples SSA with RF |
References
- Garbrecht, J.; Zhang, X.; Schneider, J.; Steiner, J. Utility of Seasonal Climate Forecasts in Management of Winter-Wheat Grazing. Appl. Eng. Agric. 2010, 26, 855–866. [Google Scholar]
- Wu, J.; Liu, M.; Jin, L. A Hybrid Support Vector Regression Approach for Rainfall Forecasting using Particle Swarm Optimization and Projection Pursuit Technology. Int. J. Comput. Intell. Appl. 2010, 9, 87–104. [Google Scholar]
- Altunkaynak, A.; Nigussie, T.A. Prediction of Daily Rainfall by a Hybrid Wavelet-Season-Neuro Technique. J. Hydrol. 2015, 529, 287–301. [Google Scholar]
- Prasad, R.; Deo, R.C.; Li, Y.; Maraseni, T. Input Selection and Performance Optimization of ANN-Based Streamflow Forecasts in the Drought-Prone Murray Darling Basin Region using IIS and MODWT Algorithm. Atmos. Res. 2017, 197, 42–63. [Google Scholar]
- Sumi, S.M.; Zaman, M.F.; Hirose, H. A Rainfall Forecasting Method using Machine Learning Models and its Application to the Fukuoka City Case. International J. Appl. Math. Comput. Sci. 2012, 22, 841–854. [Google Scholar]
- Tennant, W.J.; Hewitson, B.C. Intra-Seasonal Rainfall Characteristics and Their Importance to the Seasonal Prediction Problem. Int. J. Climatol. A J. Royal Meteorol. Soc. 2002, 22, 1033–1048. [Google Scholar]
- Frías, M.D.; Iturbide, M.; Manzanas, R.; Bedia, J.; Fernández, J.; Herrera, S.; Cofiño, A.S.; Gutiérrez, J.M. An R Package to Visualize and Communicate Uncertainty in Seasonal Climate Prediction. Environ. Model. Softw. 2018, 99, 101–110. [Google Scholar]
- Bhakar, S.; Singh, R.V.; Chhajed, N.; Bansal, A.K. Stochastic Modeling of Monthly Rainfall at Kota Region. ARPN J. Eng. Appl. Sci. 2006, 1, 36–44. [Google Scholar]
- Carlson, R.F.; MacCormick, A.; Watts, D.G. Application of Linear Random Models to Four Annual Streamflow Series. Water Resour. Res. 1970, 6, 1070–1078. [Google Scholar]
- Graham, A.; Mishra, E.P. Time Series Analysis Model to Forecast Rainfall for Allahabad Region. J. Pharmacogn. Phytochem. 2017, 6, 1418–1421. [Google Scholar]
- Tadesse, K.B.; Dinka, M.O. Application of SARIMA Model to Forecasting Monthly Flows in Waterval River, South Africa. J. Water Land Dev. 2017, 35, 229–236. [Google Scholar] [CrossRef]
- Abd Allah, A. Time Series Analysis of Nyala Rainfall using ARIMA Method. J. Eng. Comput. Sci. (JECS) 2019, 17, 5–11. [Google Scholar]
- Seneviratna, D.; Rathnayaka, R. Rainfall Data Forecasting by SARIMA and BPNN Model. IOSR J. Math 2017, 6, 57–63. [Google Scholar]
- Nourani, V.; Alami, M.T.; Aminfar, M.H. A Combined Neural-Wavelet Model for Prediction of Ligvanchai Watershed Precipitation. Eng. Appl. Artif. Intell. 2009, 22, 466–472. [Google Scholar] [CrossRef]
- Delleur, J.W.; Kavvas, M.L. Stochastic models for monthly rainfall forecasting and synthetic generation. J. Appl. Meteorol. 1978, 17, 1528–1536. [Google Scholar] [CrossRef]
- Unnikrishnan, P.; Jothiprakash, V. Daily Rainfall Forecasting for one year in a Single Run using Singular Spectrum Analysis. J. Hydrol. 2018, 561, 609–621. [Google Scholar] [CrossRef]
- Nayak, D.R.; Mahapatra, A.; Mishra, P. A Survey on Rainfall Prediction using Artificial Neural Network. Int. J. Comput. Appl. 2013, 72, 16. [Google Scholar]
- Abbot, J.; Marohasy, J. The Potential Benefits of Using Artificial Intelligence for Monthly Rainfall Forecasting for the Bowen Basin, Queensland, Australia. Water Resour. Manag. VII 2013, 171, 287. [Google Scholar]
- Mitchell, R.; Michalski, J.; Carbonell, T. An Artificial Intelligence Approach; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Wu, C.; Chau, K.-W. Prediction of Rainfall Time Series using Modular Soft Computing Methods. Eng. Appl. Artif. Intell. 2013, 26, 997–1007. [Google Scholar] [CrossRef]
- Mehr, A.D.; Nourani, V.; Khosrowshahi, V.K.; Ghorbani, M. A hybrid Support Vector Regression–Firefly Model for Monthly Rainfall Forecasting. Int. J. Environ. Sci. Technol. 2019, 16, 335–346. [Google Scholar] [CrossRef]
- Abarghouei, H.B.; Hosseini, S.Z. Using Exogenous Variables to Improve Precipitation Predictions of ANNs in Arid and Hyper-Arid Climates. Arab. J. Geosci. 2016, 9, 663. [Google Scholar] [CrossRef]
- Aksoy, H.; Dahamsheh, A. Artificial Neural Network Models for Forecasting Monthly Precipitation in Jordan. Stoch. Environ. Res. Risk Assess. 2009, 23, 917–931. [Google Scholar] [CrossRef]
- Fahimi, F.; Yaseen, Z.M.; El-shafie, A. Application of Soft Computing Based Hybrid Models in Hydrological Variables Modeling: A Comprehensive Review. Theor. Appl. Climatol. 2017, 128, 875–903. [Google Scholar] [CrossRef]
- Bushara, N.O.; Abraham, A. Using Adaptive Neuro-Fuzzy Inference System (ANFIS) to Improve the Long-term Rainfall Forecasting. J. Netw. Innov. Comput. 2015, 3, 146–158. [Google Scholar]
- Solgi, A.; Nourani, V.; Pourhaghi, A. Forecasting Daily Precipitation using Hybrid Model of Wavelet-Artificial Neural Network and Comparison with Adaptive Neurofuzzy Inference System (Case Study: Verayneh Station, Nahavand). Adv. Civil Eng. 2014, 2014. [Google Scholar] [CrossRef]
- Kisi, O.; Shiri, J. Precipitation Forecasting using Wavelet-Genetic Programming and Wavelet-Neuro-Fuzzy Conjunction Models. Water Resour. Manag. 2011, 25, 3135–3152. [Google Scholar] [CrossRef]
- Kim, T.W.; Valdés, J.B. Nonlinear Model for Drought Forecasting Based on a Conjunction of Wavelet Transforms and Neural Networks. J. Hydrol. Eng. 2003, 319–328. [Google Scholar]
- Van Gestel, T.; Suykens, J.A.; Baesens, B.; Viaene, S.; Vanthienen, J.; Dedene, G.; De Moor, B.; Vandewalle, J. Benchmarking Least Squares Support Vector Machine Classifiers. Mach. Learn. 2004, 54, 5–32. [Google Scholar] [CrossRef]
- Samsudin, R.; Shabri, A.; Saad, P. A comparison of Time Series Forecasting using Support Vector Machine and Artificial Neural Network Model. J. Appl. Sci. 2010, 10, 950–958. [Google Scholar] [CrossRef]
- Dutta, S.; Bandopadhyay, S.; Ganguli, R.; Misra, D. Machine Learning Algorithms and their Application to Ore Reserve Estimation of Sparse and Imprecise Data. J. Intell. Learn. Syst. Appl. 2010, 2, 86. [Google Scholar] [CrossRef][Green Version]
- Bhagwat, P.P.; Maity, R. Hydroclimatic Streamflow Prediction using least Square-Support Vector Regression. ISH J. Hydraul. Eng. 2013, 19, 320–328. [Google Scholar] [CrossRef]
- Goyal, M.K.; Bharti, B.; Quilty, J.; Adamowski, J.; Pandey, A. Modeling of Daily Pan Evaporation in Sub Tropical Climates Using ANN, LS-SVR, Fuzzy Logic, and ANFIS. Expert Syst. Appl. 2014, 41, 5267–5276. [Google Scholar] [CrossRef]
- Hwang, S.H.; Ham, D.H.; Kim, J.H. Forecasting Performance of LS-SVM for Nonlinear Hydrological Time Series. KSCE J. Civil Eng. 2012, 16, 870–882. [Google Scholar] [CrossRef]
- Kisi, O. Least Squares Support Vector Machine for Modeling Daily Reference Evapotranspiration. Irrig. Sci. 2013, 31, 611–619. [Google Scholar] [CrossRef]
- Mellit, A.; Pavan, A.M.; Benghanem, M. Least Squares Support Vector Machine for Short-Term Prediction of Meteorological Time Series. Theor. Appl. Climatol. 2013, 111, 297–307. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Liong, S.-Y.; Pasha, M. Rainfall and Runoff Forecasting with SSA–SVM Approach. J. Hydroinform. 2001, 3, 141–152. [Google Scholar] [CrossRef]
- Pandhiani, S.M.; Shabri, A.B. Time Series Forecasting using Wavelet-Least Squares Support Vector Machines and Wavelet Regression Models for Monthly Stream Flow Data. Open J. Stat. 2013, 3, 183. [Google Scholar] [CrossRef]
- Pham, Q.B.; Yang, T.-C.; Kuo, C.-M.; Tseng, H.-W.; Yu, P.-S. Combing Random Forest and Least Square Support Vector Regression for Improving Extreme Rainfall Downscaling. Water 2019, 11, 451. [Google Scholar] [CrossRef]
- Okkan, U. Performance of Least Squares Support Vector Machine for Monthly Reservoir Inflow Prediction. Fresenius Environ. Bull. 2012, 21, 611–620. [Google Scholar]
- Bhagwat, P.P.; Maity, R. Multistep-Ahead River Flow Prediction using LS-SVR at Daily Scale. J. Water Resour. Prot. 2012, 4, 528. [Google Scholar] [CrossRef]
- Maity, R.; Bhagwat, P.P.; Bhatnagar, A. Potential of Support Vector Regression for Prediction of Monthly Streamflow using Endogenous Property. Hydrol. Process. An Int. J. 2010, 24, 917–923. [Google Scholar] [CrossRef]
- Chan, J.C.-W.; Paelinckx, D. Evaluation of Random Forest and Adaboost Tree-Based Ensemble Classification and Spectral Band Selection for Ecotope Mapping using Airborne Hyperspectral Imagery. Remote Sens. Environ. 2008, 112, 2999–3011. [Google Scholar] [CrossRef]
- Stumpf, A.; Kerle, N. Object-Oriented Mapping of Landslides using Random Forests. Remote Sens. Environ. 2011, 115, 2564–2577. [Google Scholar] [CrossRef]
- Vincenzi, S.; Zucchetta, M.; Franzoi, P.; Pellizzato, M.; Pranovi, F.; De Leo, G.A.; Torricelli, P. Application of a Random Forest algorithm to Predict Spatial Distribution of the Potential Yield of Ruditapes Philippinarum in the Venice lagoon, Italy. Ecol. Model. 2011, 222, 1471–1478. [Google Scholar] [CrossRef]
- Pour, S.H.; Shahid, S.; Chung, E.-S. A Hybrid Model for Statistical Downscaling of Daily Rainfall. Procedia Eng. 2016, 154, 1424–1430. [Google Scholar] [CrossRef]
- Verikas, A.; Gelzinis, A.; Bacauskiene, M. Mining Data with Random Forests: A Survey and Results of New Tests. Pattern Recognit. 2011, 44, 330–349. [Google Scholar] [CrossRef]
- Meyer, D.; Leisch, F.; Hornik, K. The Support Vector Machine Under Test. Neurocomputing 2003, 55, 169–186. [Google Scholar] [CrossRef]
- Wang, Z.; Lai, C.; Chen, X.; Yang, B.; Zhao, S.; Bai, X. Flood Hazard Risk Assessment Model Based on Random Forest. J. Hydrol. 2015, 527, 1130–1141. [Google Scholar] [CrossRef]
- Chen, J.; Li, M.; Wang, W. Statistical Uncertainty Estimation using Random Forests and its Application to Drought Forecast. Math. Probl. Eng. 2012, 2012, 915053. [Google Scholar] [CrossRef]
- Firth, L.; Hazelton, M.L.; Campbell, E.P. Predicting the Onset of Australian Winter Rainfall by Nonlinear Classification. J. Clim. 2005, 18, 772–781. [Google Scholar] [CrossRef]
- Nguyen, T.-T. An L1-Regression Random Forests Method for Forecasting of Hoa Binh Reservoir's Incoming Flow. Proceedings of 2015 Seventh International Conference on Knowledge and Systems Engineering (KSE), Ho Chi Minh City, Vietnam, 8–10 October 2015; pp. 360–364. [Google Scholar]
- Monira, S.S.; Faisal, Z.M.; Hirose, H. Comparison of Artificially Intelligent Methods in Short Term Rainfall Forecast. Proceedings of 2010 13th International Conference on Computer and Information Technology (ICCIT), Dhaka, Bangladesh, 23–25 December 2010; pp. 39–44. [Google Scholar]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial Prediction Models for Shallow Landslide Hazards: a Comparative Assessment of the Efficacy of Support Vector Machines, Artificial Neural Networks, Kernel Logistic Regression, and Logistic Model Tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Karthikeyan, L.; Kumar, D.N. Predictability of Nonstationary Time Series using Wavelet and EMD based ARMA Models. J. Hydrol. 2013, 502, 103–119. [Google Scholar] [CrossRef]
- Figueiredo, M.B.; de Almeida, A.; Ribeiro, B. Wavelet Decomposition and Singular Spectrum Analysis for Electrical Signal Denoising. Proceedings of 2011 IEEE International Conference on Systems, Man, and Cybernetics, Anchorage, AL, USA, 2011, 9–12 October; pp. 3329–3334.
- Vatuard, R.; Yiou, P.; Ghil, M. Singular Spectrum Analysis: A Toolkit for Short, Noisy and Chaotic Series. Phys. D 1992, 58, 126. [Google Scholar]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Hu, T.; Wu, F.; Zhang, X. Rainfall–Runoff Modeling using Principal Component Analysis and Neural Network. Hydrol. Res. 2007, 38, 235–248. [Google Scholar] [CrossRef]
- Ghodsi, M.; Hassani, H.; Sanei, S.; Hicks, Y. The use of Noise Information for Detection of Temporomandibular Disorder. Biomed. Signal Process. Control 2009, 4, 79–85. [Google Scholar] [CrossRef]
- Hassani, H.; Webster, A.; Silva, E.S.; Heravi, S. Forecasting US Tourist Arrivals using Optimal Singular Spectrum Analysis. Tour. Manag. 2015, 46, 322–335. [Google Scholar] [CrossRef]
- Marques, C.; Ferreira, J.; Rocha, A.; Castanheira, J.; Melo-Gonçalves, P.; Vaz, N.; Dias, J. Singular Spectrum Analysis and Forecasting of Hydrological Time series. Phys. Chem. Earth Parts A/B/C 2006, 31, 1172–1179. [Google Scholar] [CrossRef]
- Alexandrov, T.; Golyandina, N. Automatic Trend Extraction and Forecasting for a Family of Time Series. In Proceedings of the Int. Symp. on Forecasting, International Institute of Forecasters, Santander, Spain, 11–14 June 2006. [Google Scholar]
- Unnikrishnan, P.; Jothiprakash, V. Extraction of Nonlinear Rainfall Trends using Singular Spectrum Analysis. J. Hydrol. Eng. 2015, 20, 05015007. [Google Scholar] [CrossRef]
- Rodrigues, P.C.; De Carvalho, M. Spectral Modeling of Time Series with Missing Data. Appl. Math. Model. 2013, 37, 4676–4684. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Sakai, K.; Dimitrova, Z.I. SSA, PCA, TDPSC, ACFA: Useful Combination of Methods for Analysis of Short and Nonstationary Time Series. Chaos, Solitons & Fractals 2008, 37, 187–202. [Google Scholar]
- Wu, C.; Chau, K.; Li, Y. Methods to Improve Neural Network Performance in Daily Flows Prediction. J. Hydrol. 2009, 372, 80–93. [Google Scholar] [CrossRef]
- Lisi, F.; Nicolis, O.; Sandri, M. Combining Singular-Spectrum Analysis and Neural Networks for Time Series Forecasting. Neural Process. Lett. 1995, 2, 6–10. [Google Scholar] [CrossRef][Green Version]
- Zubaidi, S.L.; Dooley, J.; Alkhaddar, R.M.; Abdellatif, M.; Al-Bugharbee, H.; Ortega-Martorell, S. A Novel Approach for Predicting Monthly Water Demand by Combining Singular Spectrum Analysis with Neural Networks. J. Hydrol. 2018, 561, 136–145. [Google Scholar] [CrossRef]
- Alexandrov, T. A Method of Trend Extraction Using Singular Spectrum Analysis. arXiv 2008, arXiv:0804.3367. [Google Scholar]
- Adhikari, K.R.; Tan, Y.-C.; Lai, J.-S.; Chen, Z.-S.; Lin, Y.-J. Climate Change Impacts and Responses: A Case of Shihmen Reservoir in Taiwan. Proceedings of oral presentation at the 2nd Int’l conference “Climate Change: Impacts and Responses, Brisbane, Australia, 8–10 July 2010. [Google Scholar]
- Guo, G.; Li, S.Z.; Chan, K.L. Support Vector Machines for Face Recognition. Image Vis. Comput. 2001, 19, 631–638. [Google Scholar] [CrossRef]
- Cao, L.-J.; Tay, F.E.H. Support Vector Machine with Adaptive Parameters in Financial Time Series Forecasting. IEEE Trans. Neural Netw. 2003, 14, 1506–1518. [Google Scholar] [CrossRef]
- Gryllias, K.C.; Antoniadis, I.A. A Support Vector Machine Approach Based on Physical Model Training for Rolling Element Bearing Fault Detection in Industrial Environments. Eng. Appl. Artif. Intell. 2012, 25, 326–344. [Google Scholar] [CrossRef]
- Suykens, J.A.; Vandewalle, J. Least Squares Support Vector Machine Classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Byun, H.; Lee, S.-W. Applications of Support Vector Machines for Pattern Recognition: A survey. In International Workshop on Support Vector Machines; Springer: Berlin/Heidelberg, Germany, 2002; pp. 213–236. [Google Scholar]
- Kasiri, K.; Kazemi, K.; Dehghani, M.J.; Helfroush, M.S. Atlas-Based Segmentation of Brain MR Images using Least Square Support Vector Machines. Proceedings of 2010 2nd International Conference on Image Processing Theory, Tools and Applications, Paris, France, 7–10 July 2010; pp. 306–310. [Google Scholar]
- Niwas, S.I.; Palanisamy, P.; Zhang, W.; Isa, N.A.M.; Chibbar, R. Log-Gabor Wavelets Based Breast Carcinoma Classification using Least Square Support Vector Machine. Proceedings of 2011 IEEE International Conference on Imaging Systems and Techniques, Batu Ferringhi, Malaysia, 17–18 May 2011; pp. 219–223. [Google Scholar]
- Ismail, S.; Shabri, A.; Samsudin, R. A Hybrid Model of Self-Organizing Maps (SOM) and Least Square Support Vector Machine (LSSVM) for Time-Series Forecasting. Expert Syst. Appl. 2011, 38, 10574–10578. [Google Scholar] [CrossRef]
- Wang, X.-L.; Wang, M.-W. Short-Term Wind Speed Forecasting Based on Wavelet Decomposition and Least Square Support Vector Machine. Power Syst. Technol. 2010, 1. [Google Scholar]
- AK, S.J.; PL, V.J. Least Squares Support Vector Machines; World scientific: Singapore, 2002. [Google Scholar]
- Kisi, O. Pan Evaporation Modeling using Least Square Support Vector Machine, Multivariate Adaptive Regression Splines and M5 Model Tree. J. Hydrol. 2015, 528, 312–320. [Google Scholar] [CrossRef]
- Suykens, J.A.; De Brabanter, J.; Lukas, L.; Vandewalle, J. Weighted Least Squares Support Vector Machines: Robustness and Sparse Approximation. Neurocomputing 2002, 48, 85–105. [Google Scholar] [CrossRef]
- Wang, J.; Li, L.; Niu, D.; Tan, Z. An Annual Load Forecasting Model Based on Support Vector Regression with Differential Evolution Algorithm. Appl. Energy 2012, 94, 65–70. [Google Scholar] [CrossRef]
- Zhang, X.; Qiu, D.; Chen, F. Support Vector Machine with Parameter Optimization by a Novel Hybrid Method and its Application to Fault Diagnosis. Neurocomputing 2015, 149, 641–651. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Breiman, L. Manual–Setting Up, using, and Understanding Random Forests, v4. 2003. Available online: ftp://ftp.stat.berkeley.edu/pub/users/breiman/Using_random_forests_v4.0.pdf11 (accessed on 5 May 2020).
- Liaw, A.; Wiener, M. Classification and Regression by Random Forest. R News 2002, 2, 18–22. [Google Scholar]
- Broomhead, D.S.; King, G.P. Extracting Qualitative Dynamics from Experimental Data. Phys. D Nonlinear Phenom. 1986, 20, 217–236. [Google Scholar] [CrossRef]
- Golyandina, N.; Nekrutkin, V.; Zhigljavsky, A.A. Analysis of Time Series Structure: SSA and Related Techniques; Chapman and Hall/CRC: Boca Raton, FL, USA, 2001. [Google Scholar]
- Chau, K.; Wu, C. A Hybrid Model Coupled with Singular Spectrum Analysis for Daily Rainfall Prediction. J. Hydroinform. 2010, 12, 458–473. [Google Scholar] [CrossRef]
- Hassani, H.; Zhigljavsky, A. Singular Spectrum Analysis: Methodology and Application to Economics Data. J. Syst. Sci. Complex. 2009, 22, 372–394. [Google Scholar] [CrossRef]
- Breiman, L. Manual on Setting up, using, and Understanding Random Forests v3. 1; Statistics Department University of California: Berkeley, CA, USA, 2002; p. 58. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Haytham, A.; Salem, G.; Gabor, M. Urban Water Flow and Water Level Prediction Based on Deep Learning. In Proceedings of the European Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases (ECML PKDD), Skopje, Macedonia, 18–22 September 2017. [Google Scholar]
- Nourani, V.; Davanlou Tajbakhsh, A.; Molajou, A.; Gokcekus, H. Hybrid Wavelet-M5 Model tree for Rainfall-Runoff Modeling. J. Hydrol. Eng. 2019, 24, 04019012. [Google Scholar] [CrossRef]
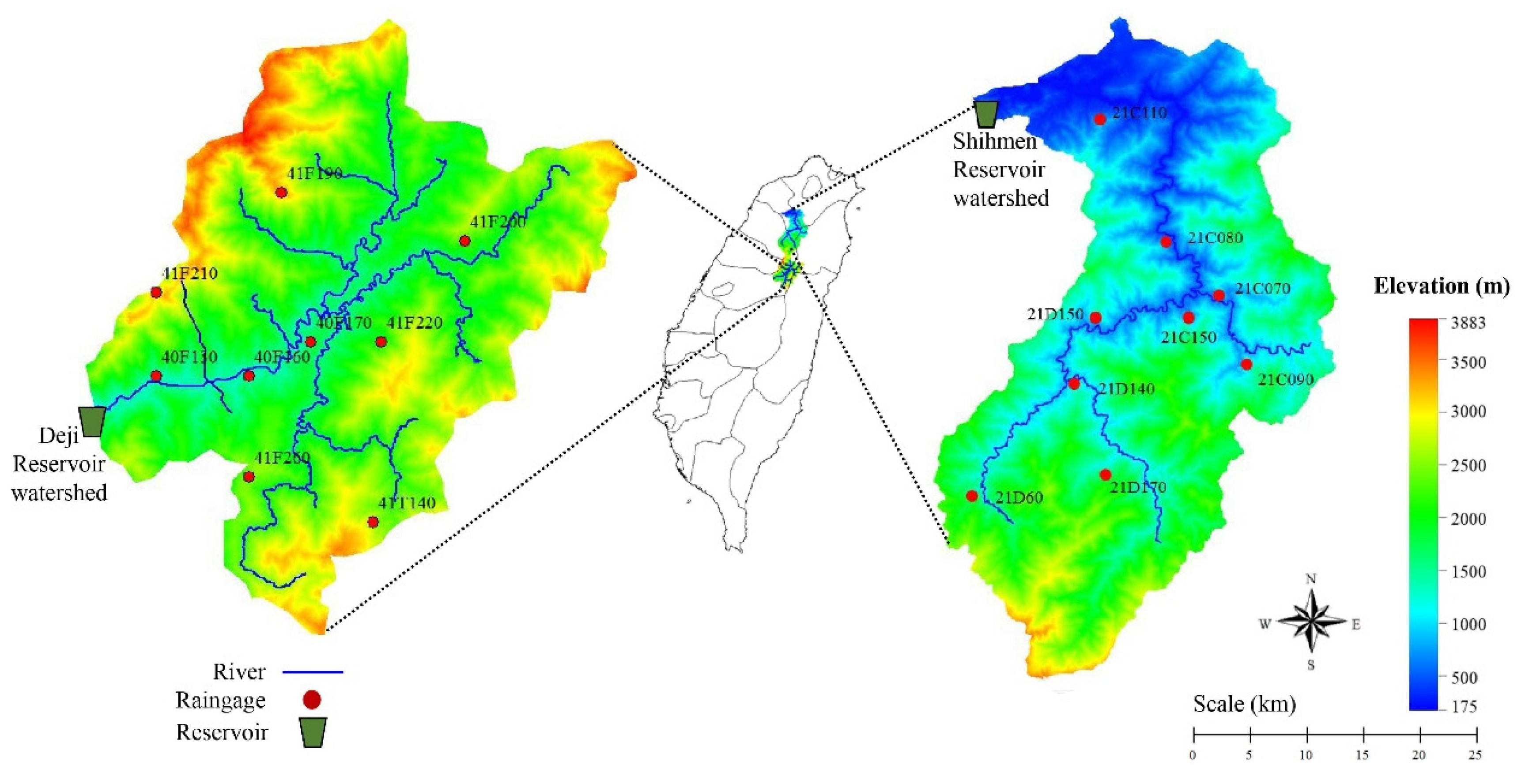



| Station Name | Station Code | Location | Elevation (m) | |
|---|---|---|---|---|
| Longitude (˚E) | Latitude (˚N) | |||
| Deji | 40F13 | 121.19 | 24.26 | 1513 |
| Lishan | 40F16 | 121.24 | 24.26 | 1858 |
| Sungmao | 40F17 | 121.27 | 24.28 | 1457 |
| Chihchiayangtashan | 41F19 | 121.26 | 24.36 | 3000 |
| Pingyenshan | 41F20 | 121.36 | 24.33 | 2800 |
| Chiayangshan | 41F21 | 121.19 | 24.31 | 2700 |
| Taoshan | 41F22 | 121.31 | 24.28 | 2350 |
| Sungfeng | 41F26 | 121.24 | 24.21 | 2596 |
| Hohuanyakou | 41T14 | 121.31 | 24.19 | 2600 |
| Hohuanshan | C0F95 | 121.27 | 24.14 | 3370 |
| Lishan | C0F86 | 121.26 | 24.26 | 1980 |
| Tayuling | C0T97 | 121.32 | 24.19 | 2565 |
| Station Name | Station Code | Location | Elevation (m) | |
|---|---|---|---|---|
| Longitude (˚E) | Latitude (˚N) | |||
| Shihmen | 21C050 | 121.23 | 24.81 | 255 |
| Baling | 21C070 | 121.39 | 24.69 | 1220 |
| Kaoyi | 21C080 | 121.35 | 24.71 | 620 |
| Kalaho | 21C090 | 121.39 | 24.64 | 1260 |
| Changhsing | 21C110 | 121.30 | 24.80 | 350 |
| Sankuang | 21C150 | 121.36 | 24.67 | 630 |
| Hsiuluan | 21D140 | 121.28 | 24.62 | 840 |
| Yufeng | 21D150 | 121.29 | 24.66 | 780 |
| Hsinpaishih | 21D160 | 121.25 | 24.59 | 1620 |
| Chen-His-Pao | 21D170 | 121.30 | 24.58 | 630 |
| Watershed | Mean (mm) | Standard Deviation (mm) | Skewness | Kurtosis |
|---|---|---|---|---|
| Deji | 193.71 | 184.80 | 1.91 | 5.15 |
| Shihmen | 200.35 | 208.09 | 2.56 | 9.29 |
| Watershed | Model | RMSE | NSE | ||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | ||
| Deji | LSSVR | 193.58 | 192.31 | 199.45 | 0.05 | 0.07 | 0.01 |
| SSA-LSSVR | 75.29 | 79.48 | 91.09 | 0.86 | 0.84 | 0.80 | |
| RF | 195.88 | 198.34 | 196.28 | 0.04 | 0.03 | 0.03 | |
| SSA-RF | 121.76 | 137.77 | 154.83 | 0.63 | 0.53 | 0.39 | |
| Shihmen | LS-SVR | 195.55 | 197.77 | 197.88 | 0.30 | 0.27 | 0.28 |
| SSA-LSSVR | 132.81 | 120.91 | 115.71 | 0.67 | 0.73 | 0.75 | |
| RF | 227.14 | 221.93 | 223.21 | 0.06 | 0.08 | 0.08 | |
| SSA-RF | 98.75 | 108.88 | 119.10 | 0.82 | 0.78 | 0.74 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bojang, P.O.; Yang, T.-C.; Pham, Q.B.; Yu, P.-S. Linking Singular Spectrum Analysis and Machine Learning for Monthly Rainfall Forecasting. Appl. Sci. 2020, 10, 3224. https://doi.org/10.3390/app10093224
Bojang PO, Yang T-C, Pham QB, Yu P-S. Linking Singular Spectrum Analysis and Machine Learning for Monthly Rainfall Forecasting. Applied Sciences. 2020; 10(9):3224. https://doi.org/10.3390/app10093224
Chicago/Turabian StyleBojang, Pa Ousman, Tao-Chang Yang, Quoc Bao Pham, and Pao-Shan Yu. 2020. "Linking Singular Spectrum Analysis and Machine Learning for Monthly Rainfall Forecasting" Applied Sciences 10, no. 9: 3224. https://doi.org/10.3390/app10093224
APA StyleBojang, P. O., Yang, T.-C., Pham, Q. B., & Yu, P.-S. (2020). Linking Singular Spectrum Analysis and Machine Learning for Monthly Rainfall Forecasting. Applied Sciences, 10(9), 3224. https://doi.org/10.3390/app10093224





