Selecting a Proper Microsphere to Combine Optical Trapping with Microsphere-Assisted Microscopy
Abstract
1. Introduction
2. The Selection of Microsphere Types
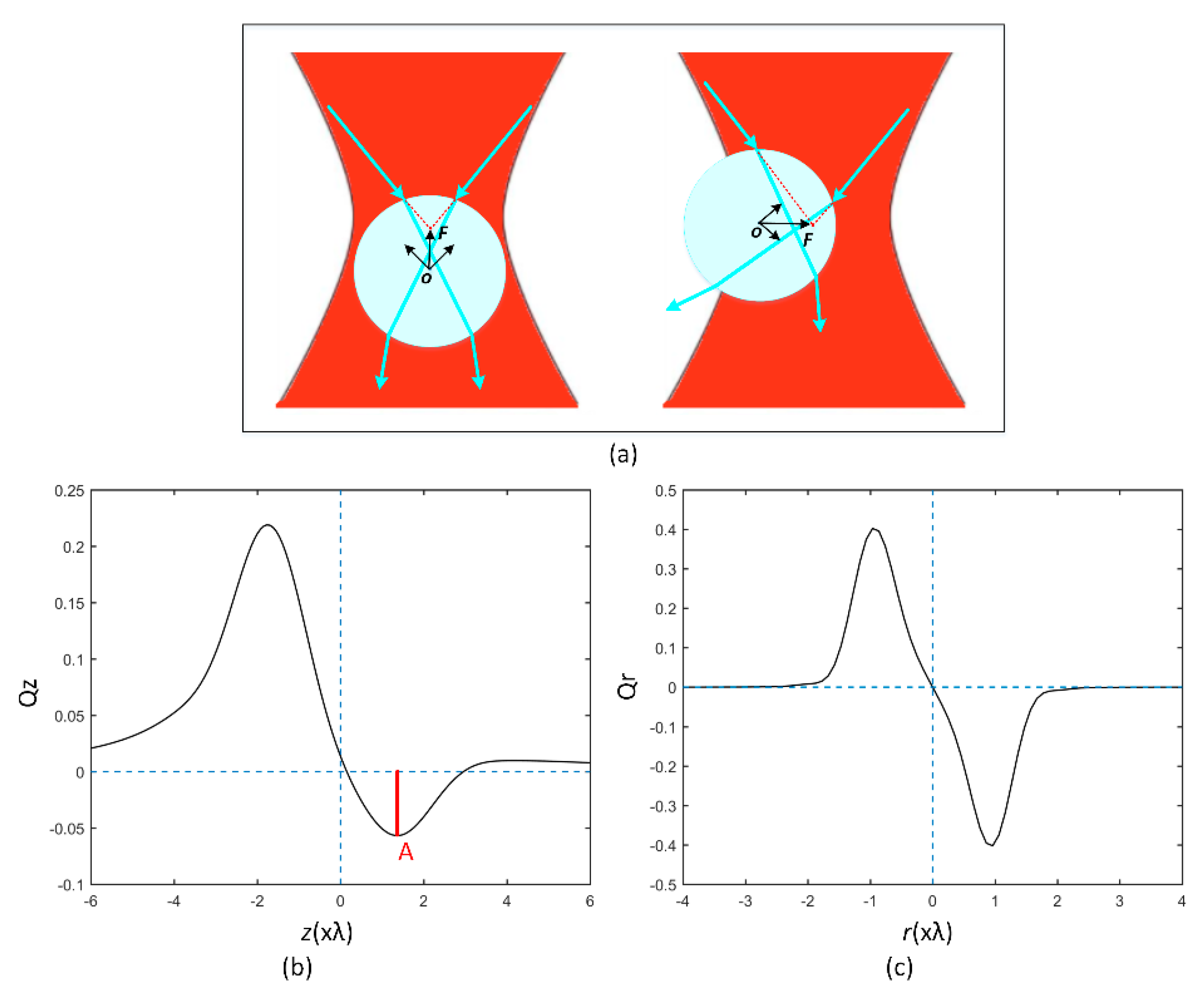
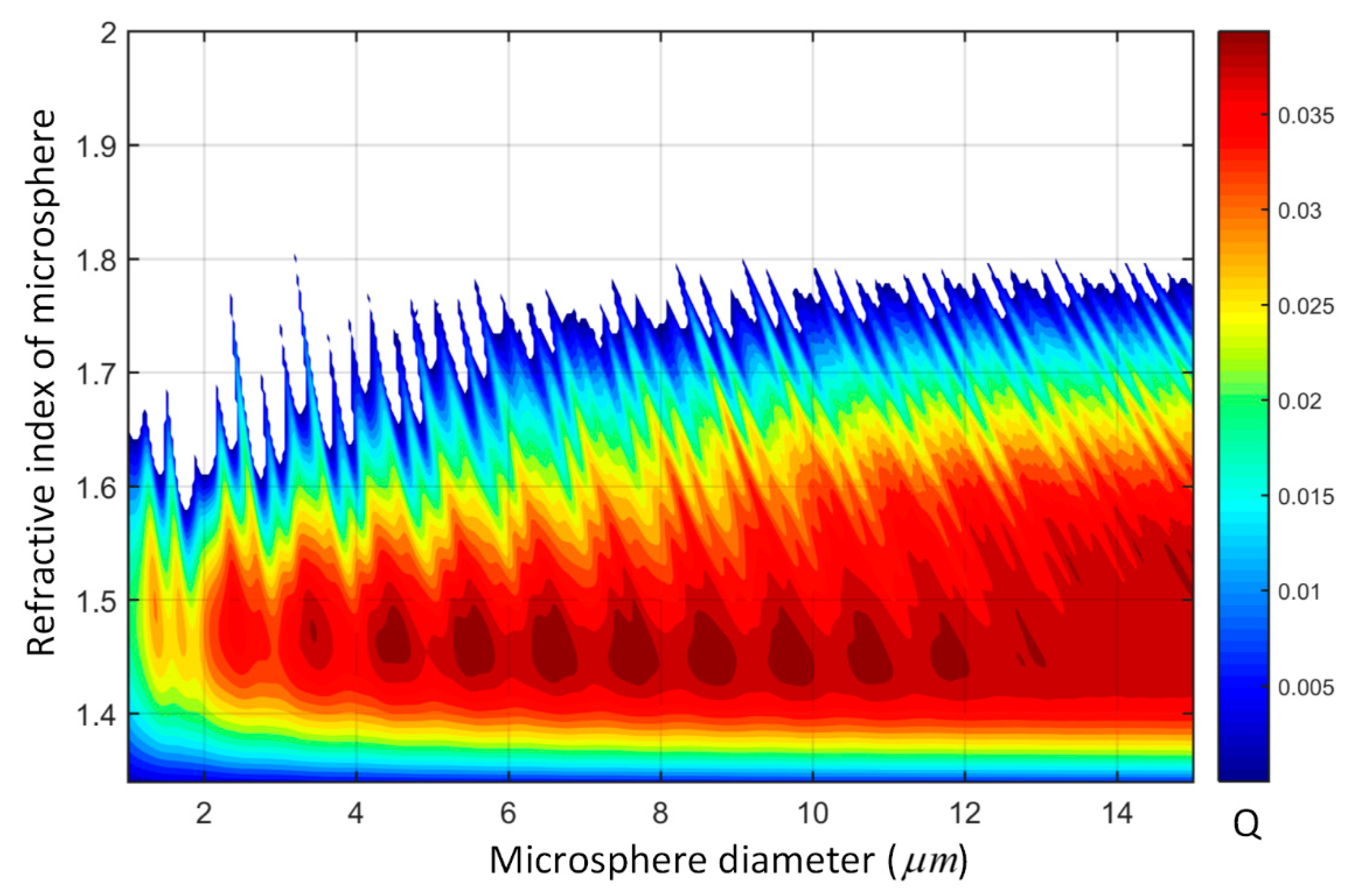
2.1. Optical Trapping Simulations
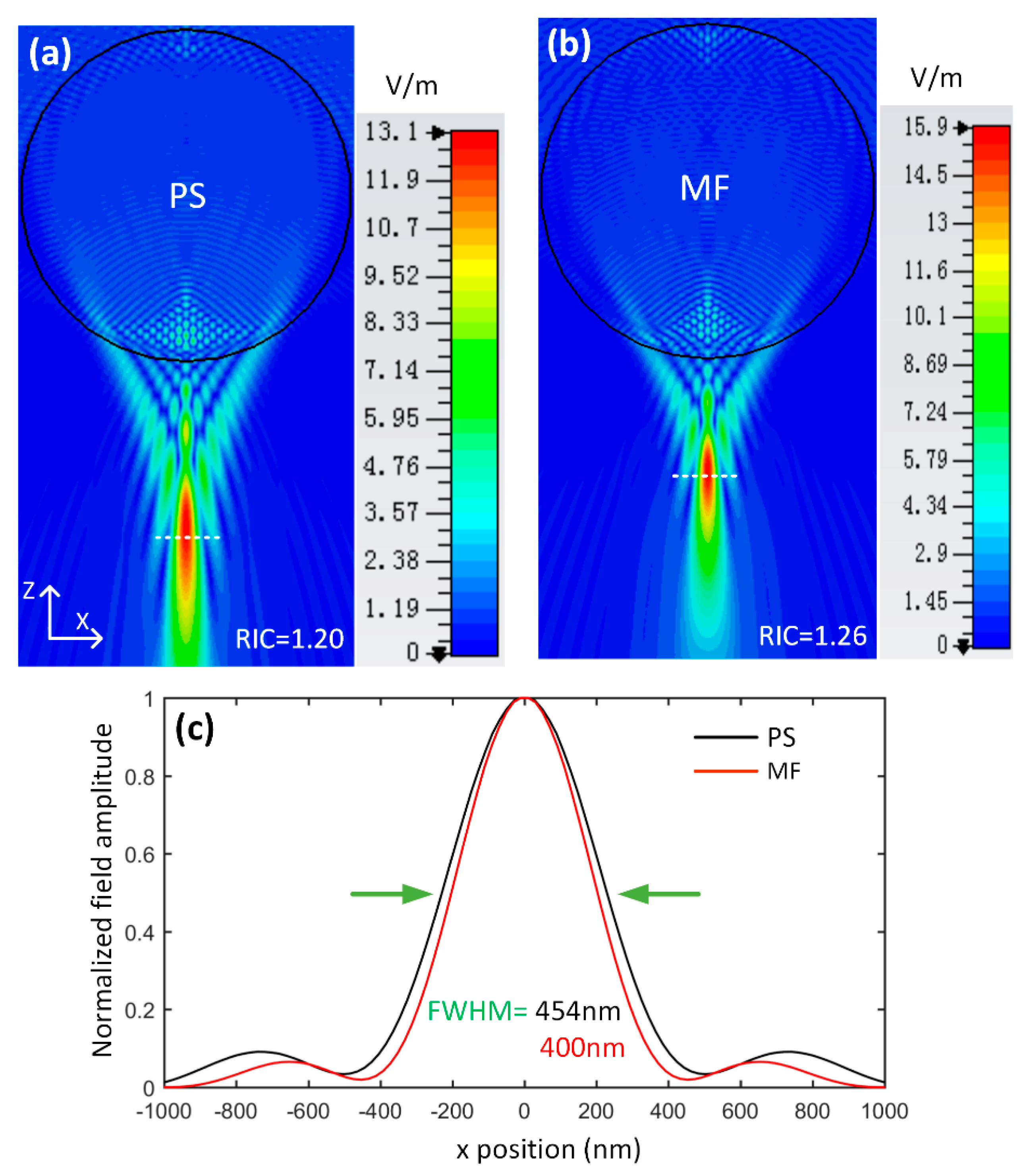
2.2. The Super-Resolution Imaging Ability of Index-Different Microspheres
3. Experiments and Analysis
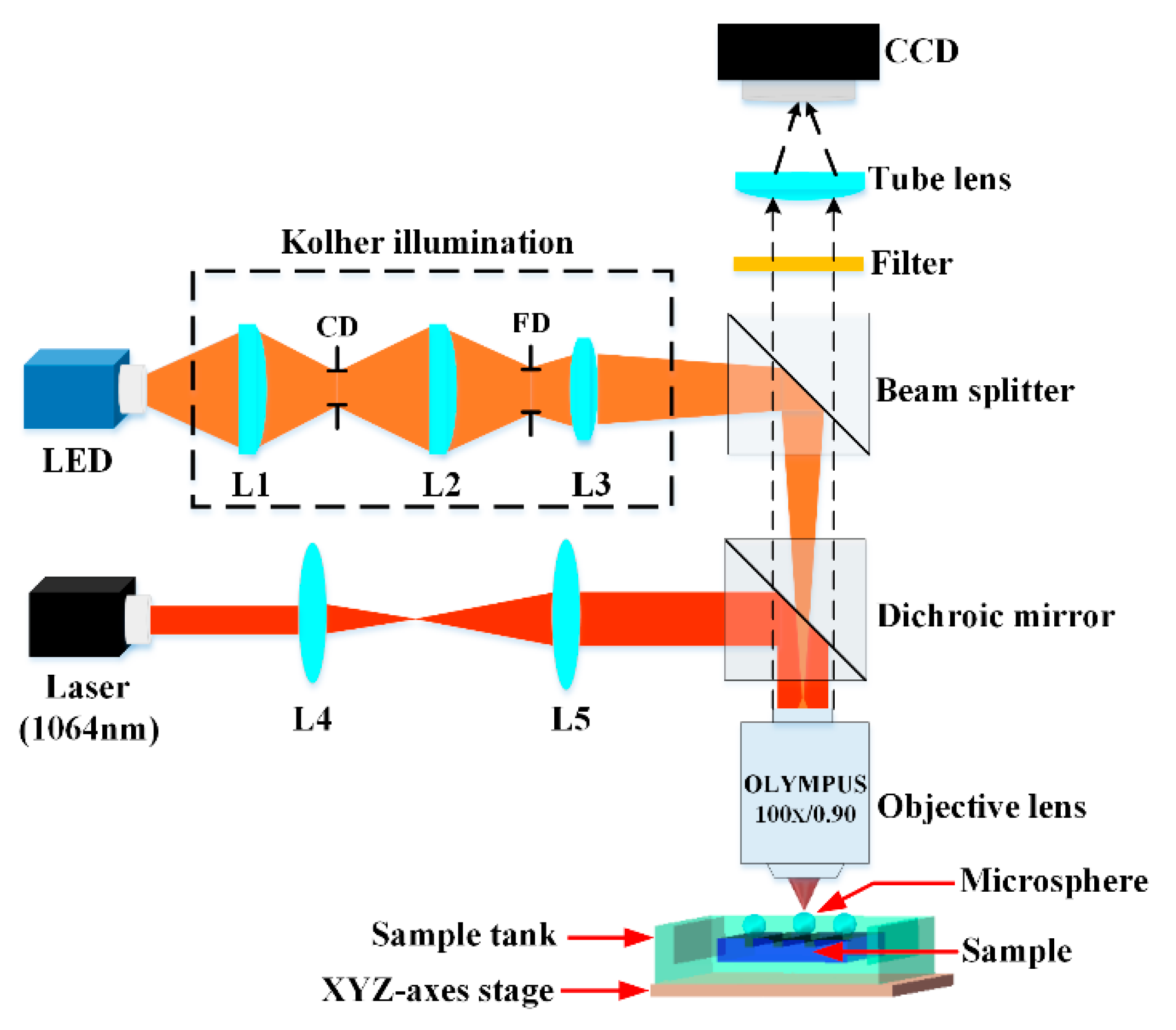
3.1. Experiment Setup
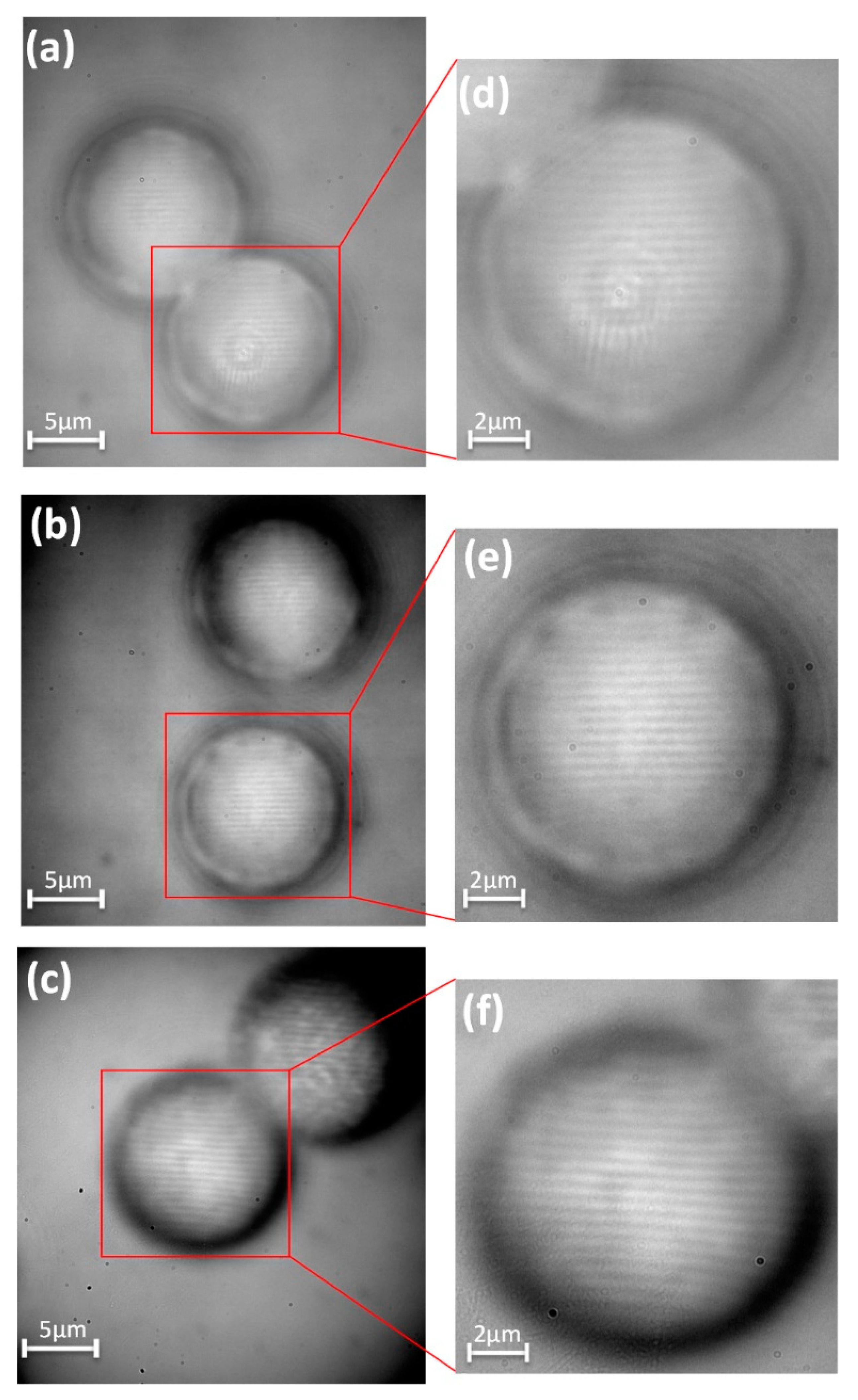
3.2. Results and Analysis
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Inouye, Y.; Kawata, S. Near-field scanning optical microscope with a metallic probe tip. Opt. Lett. 1994, 19, 159–161. [Google Scholar] [CrossRef]
- Rogers, E.T.F.; Lindberg, J.; Roy, T.; Savo, S.; Chad, J.E.; Dennis, M.R.; Zheludev, N.I. A super-oscillatory lens optical microscope for subwavelength imaging. Nat. Mater. 2012, 11, 432–435. [Google Scholar] [CrossRef]
- Terris, B.D.; Mamin, H.J.; Rugar, D.; Studenmund, W.R.; Kino, G.S. Near-field optical data storage using a solid immersion lens. Appl. Phys. Lett. 1994, 65, 388–390. [Google Scholar] [CrossRef]
- Betzig, E.; Patterson, G.H.; Sougrat, R.; Lindwasser, O.W.; Olenych, S.; Bonifacino, J.S.; Davidson, M.W.; Lippincott-Schwartz, J.; Hess, H.F. Imaging intracellular fluorescent proteins at nanometer resolution. Science 2006, 313, 1642. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, Z.; Minin, O.V.; Minin, I.V. Deep Subwavelength-Scale Light Focusing and Confinement in Nanohole-Structured Mesoscale Dielectric Spheres. Nanomaterials 2019, 9, 186. [Google Scholar] [CrossRef]
- Wang, Z.; Guo, W.; Li, L.; Luk’yanchuk, B.; Khan, A.; Liu, Z.; Chen, Z.; Hong, M. Optical virtual imaging at 50 nm lateral resolution with a white-light nanoscope. Nat. Commun. 2011, 2, 218. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, Y.; Deng, Q.; Zhao, L.; Hu, S. Contrast enhancement of microsphere-assisted super-resolution imaging in dark-field microscopy. Appl. Phys. Express 2017, 10, 082501. [Google Scholar] [CrossRef]
- Kassamakov, I.; Lecler, S.; Nolvi, A.; Leong-Hoï, A.; Montgomery, P.; Hæggström, E. 3d super-resolution optical profiling using microsphere enhanced mirau interferometry. Sci. Rep. 2017, 7, 3683. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Li, L.; Ben-Aryeh, Y.; Wang, Z.; Guo, W. Overcoming the diffraction limit induced by microsphere optical nanoscopy. J. Opt. 2013, 15, 125710. [Google Scholar] [CrossRef]
- Li, J.; Liu, W.; Li, T.; Rozen, I.; Zhao, J.; Bahari, B.; Kante, B.; Wang, J. Swimming microrobot optical nanoscopy. Nano Lett. 2016, 16, 6604–6609. [Google Scholar] [CrossRef] [PubMed]
- Darafsheh, A.; Walsh, G.F.; Dal Negro, L.; Astratov, V.N. Optical super-resolution by high-index liquid-immersed microspheres. Appl. Phys. Lett. 2012, 101, 141128. [Google Scholar] [CrossRef]
- Darafsheh, A. Influence of the background medium on imaging performance of microsphere-assisted super-resolution microscopy. Opt. Lett. 2017, 42, 735–738. [Google Scholar] [CrossRef] [PubMed]
- Minin, I.V.; Minin, O.V.; Geints, Y.E. Localized EM and photonic jets from non-spherical and non-symmetrical dielectric mesoscale objects: Brief review. Ann. Der Phys. 2015, 527, 491–497. [Google Scholar] [CrossRef]
- Pacheco-Peña, V.; Beruete, M.; Minin, I.V.; Minin, O.V. Terajets produced by dielectric cuboids. Appl. Phys. Lett. 2014, 105, 084102. [Google Scholar] [CrossRef]
- Chen, L.; Zhou, Y.; Li, Y.; Hong, M. Microsphere enhanced optical imaging and patterning: From physics to applications. Appl. Phys. Rev. 2019, 6, 021304. [Google Scholar] [CrossRef]
- Wang, Z.; Luk’yanchuk, B. Super-resolution imaging and microscopy by dielectric particle-lenses. In Label-Free Super-Resolution Microscopy; Astratov, V., Ed.; Springer International Publishing: Cham, Switzerland, 2019; pp. 371–406. [Google Scholar]
- Ben-Aryeh, Y. Increase of resolution by use of microspheres related to complex snell’s law. J. Opt. Soc. Am. A 2016, 33, 2284–2288. [Google Scholar] [CrossRef]
- Krivitsky, L.A.; Wang, J.J.; Wang, Z.; Luk’yanchuk, B. Locomotion of microspheres for super-resolution imaging. Sci. Rep. 2013, 3, 3501. [Google Scholar] [CrossRef]
- Wang, F.; Liu, L.; Yu, H.; Wen, Y.; Yu, P.; Liu, Z.; Wang, Y.; Li, W.J. Scanning superlens microscopy for non-invasive large field-of-view visible light nanoscale imaging. Nat. Commun. 2016, 7, 13748. [Google Scholar] [CrossRef]
- Darafsheh, A.; Guardiola, C.; Palovcak, A.; Finlay, J.C.; Cárabe, A. Optical super-resolution imaging by high-index microspheres embedded in elastomers. Opt. Lett. 2015, 40, 5–8. [Google Scholar] [CrossRef]
- Lianwei, C.; Yan, Z.; Mengxue, W.; Minghui, H. Remote-mode microsphere nano-imaging: New boundaries for optical microscopes. Opto Electron. Adv. 2018, 1, 170001. [Google Scholar]
- Ashkin, A.; Dziedzic, J.M.; Bjorkholm, J.E.; Chu, S. Observation of a single-beam gradient force optical trap for dielectric particles. Opt. Lett. 1986, 11, 288–290. [Google Scholar] [CrossRef]
- Bouloumis, T.D.; Nic Chormaic, S. From Far-Field to Near-Field Micro- and Nanoparticle Optical Trapping. Appl. Sci. 2020, 10, 1375. [Google Scholar] [CrossRef]
- Minin, I.V.; Minin, O.V.; Cao, Y.; Liu, Z.; Geints, Y.E.; Karabchevsky, A. Optical vacuum cleaner by optomechanical manipulation of nanoparticles using nanostructured mesoscale dielectric cuboid. Sci. Rep. 2019, 9, 12748. [Google Scholar] [CrossRef] [PubMed]
- McLeod, E.; Arnold, C.B. Subwavelength direct-write nanopatterning using optically trapped microspheres. Nat. Nanotechnol. 2008, 3, 413–417. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, M.; Kurosawa, T.; Hane, K. Micro-objective manipulated with optical tweezers. Appl. Phys. Lett. 1997, 70, 785–787. [Google Scholar] [CrossRef]
- Michihata, M.; Kim, J.; Takahashi, S.; Takamasu, K.; Mizutani, Y.; Takaya, Y. Surface imaging technique by an optically trapped microsphere in air condition. Nanomanufacturing Metrol. 2018, 1, 32–38. [Google Scholar] [CrossRef]
- Bezryadina, A.; Li, J.; Zhao, J.; Kothambawala, A.; Ponsetto, J.; Huang, E.; Wang, J.; Liu, Z. Localized plasmonic structured illumination microscopy with an optically trapped microlens. Nanoscale 2017, 9, 14907–14912. [Google Scholar] [CrossRef]
- Yang, H.; Trouillon, R.l.; Huszka, G.; Gijs, M.A.M. Super-resolution imaging of a dielectric microsphere is governed by the waist of its photonic nanojet. Nano Lett. 2016, 16, 4862–4870. [Google Scholar] [CrossRef]
- Yang, H.; Moullan, N.; Auwerx, J.; Gijs, M.A.M. Super-resolution biological microscopy using virtual imaging by a microsphere nanoscope. Small 2014, 10, 1712–1718. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.S.; Paniagua-Domínguez, R.n.; Minin, I.; Minin, O.; Wang, Z. Refractive index less than two: Photonic nanojets yesterday, today and tomorrow [invited]. Opt. Mater. Express 2017, 7, 1820–1847. [Google Scholar] [CrossRef]
- Nieminen, T.A.; Loke, V.L.Y.; Stilgoe, A.B.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. T-matrix method for modelling optical tweezers. J. Mod. Opt. 2011, 58, 528–544. [Google Scholar] [CrossRef]
- Nieminen, T.A.; Loke, V.L.Y.; Stilgoe, A.B.; Knöner, G.; Brańczyk, A.M.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Optical tweezers computational toolbox. J. Opt. A: Pure Appl. Opt. 2007, 9, S196–S203. [Google Scholar] [CrossRef]
- Sun, B.; Grier, D.G. The effect of mie resonances on trapping in optical tweezers: Comment. Opt. Express 2009, 17, 2658–2660. [Google Scholar] [CrossRef] [PubMed]
- Van der Horst, A.; van Oostrum, P.D.J.; Moroz, A.; van Blaaderen, A.; Dogterom, M. High trapping forces for high-refractive index particles trapped in dynamic arrays of counterpropagating optical tweezers. Appl. Opt. 2008, 47, 3196–3202. [Google Scholar] [CrossRef]
- Perrin, S.; Li, H.; Leong-Hoi, A.; Lecler, S.; Montgomery, P. Illumination conditions in microsphere-assisted microscopy. J. Microsc. 2019, 274, 69–75. [Google Scholar] [CrossRef]
- Li, L.; Guo, W.; Yan, Y.; Lee, S.; Wang, T. Label-free super-resolution imaging of adenoviruses by submerged microsphere optical nanoscopy. Light: Sci. Appl. 2013, 2, e104. [Google Scholar] [CrossRef]
- Hou, B.; Zhang, L. Liquid microdroplet as an optical component to achieve imaging of 100 nm nanostructures on a far-field microscope. J. Opt. 2018, 20, 055606. [Google Scholar] [CrossRef]

| Microsphere | Optical Trapping | Super-Resolution Ability |
|---|---|---|
| SiO2 | √ | x |
| PS | √ | √ |
| Melamine formaldehyde (MF) | √ | √ |
| Barium titanate glass (BTG) | x | √ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Hu, S.; Tang, Y.; Xie, Z.; Liu, J.; He, Y. Selecting a Proper Microsphere to Combine Optical Trapping with Microsphere-Assisted Microscopy. Appl. Sci. 2020, 10, 3127. https://doi.org/10.3390/app10093127
Liu X, Hu S, Tang Y, Xie Z, Liu J, He Y. Selecting a Proper Microsphere to Combine Optical Trapping with Microsphere-Assisted Microscopy. Applied Sciences. 2020; 10(9):3127. https://doi.org/10.3390/app10093127
Chicago/Turabian StyleLiu, Xi, Song Hu, Yan Tang, Zhongye Xie, Junbo Liu, and Yu He. 2020. "Selecting a Proper Microsphere to Combine Optical Trapping with Microsphere-Assisted Microscopy" Applied Sciences 10, no. 9: 3127. https://doi.org/10.3390/app10093127
APA StyleLiu, X., Hu, S., Tang, Y., Xie, Z., Liu, J., & He, Y. (2020). Selecting a Proper Microsphere to Combine Optical Trapping with Microsphere-Assisted Microscopy. Applied Sciences, 10(9), 3127. https://doi.org/10.3390/app10093127




