Electronic Emulator of Biological Tissue as an Electrical Load during Electroporation
Abstract
Featured Application
Abstract
1. Introduction
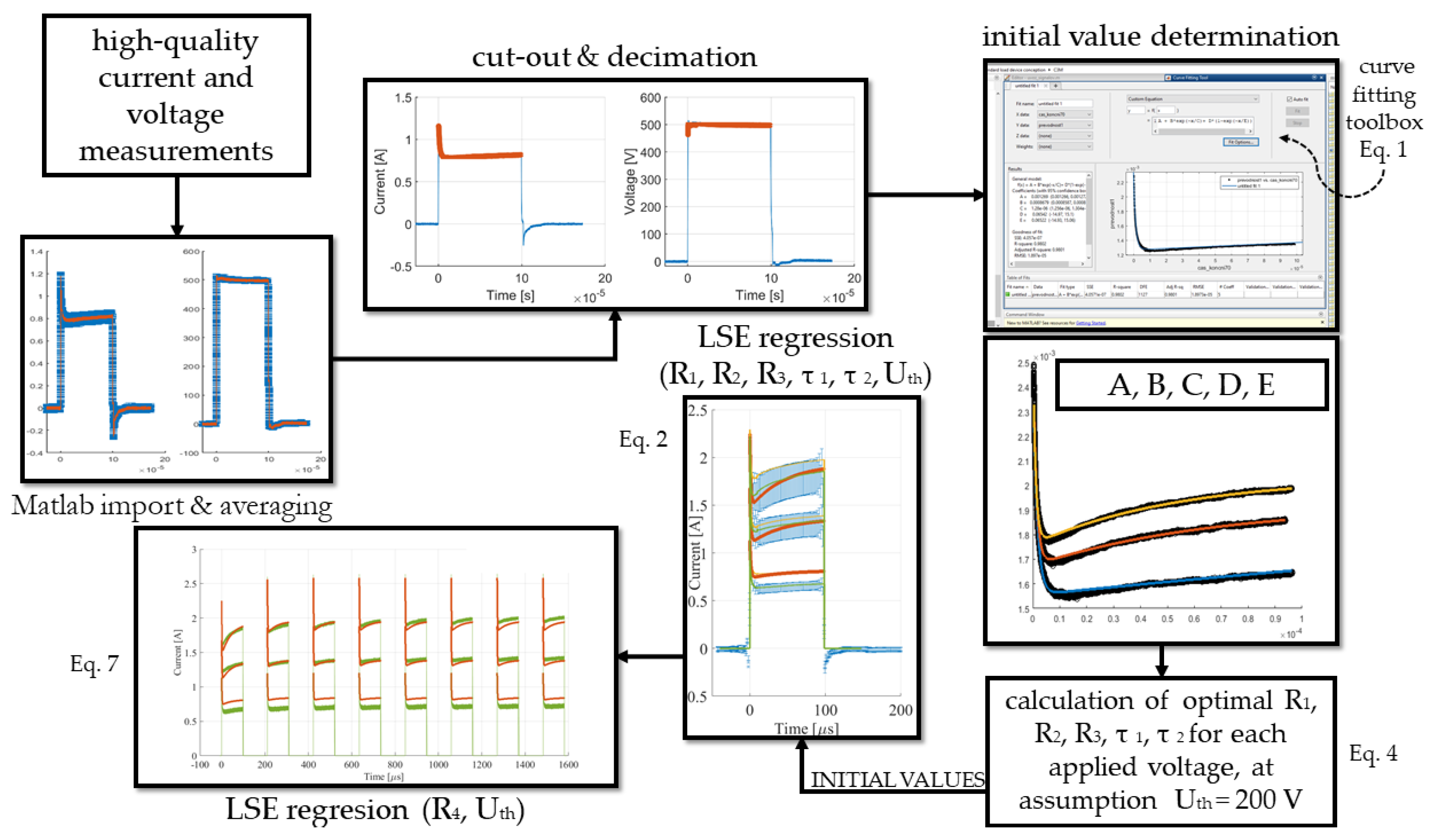
2. Methods and Materials
2.1. Mathematical Model
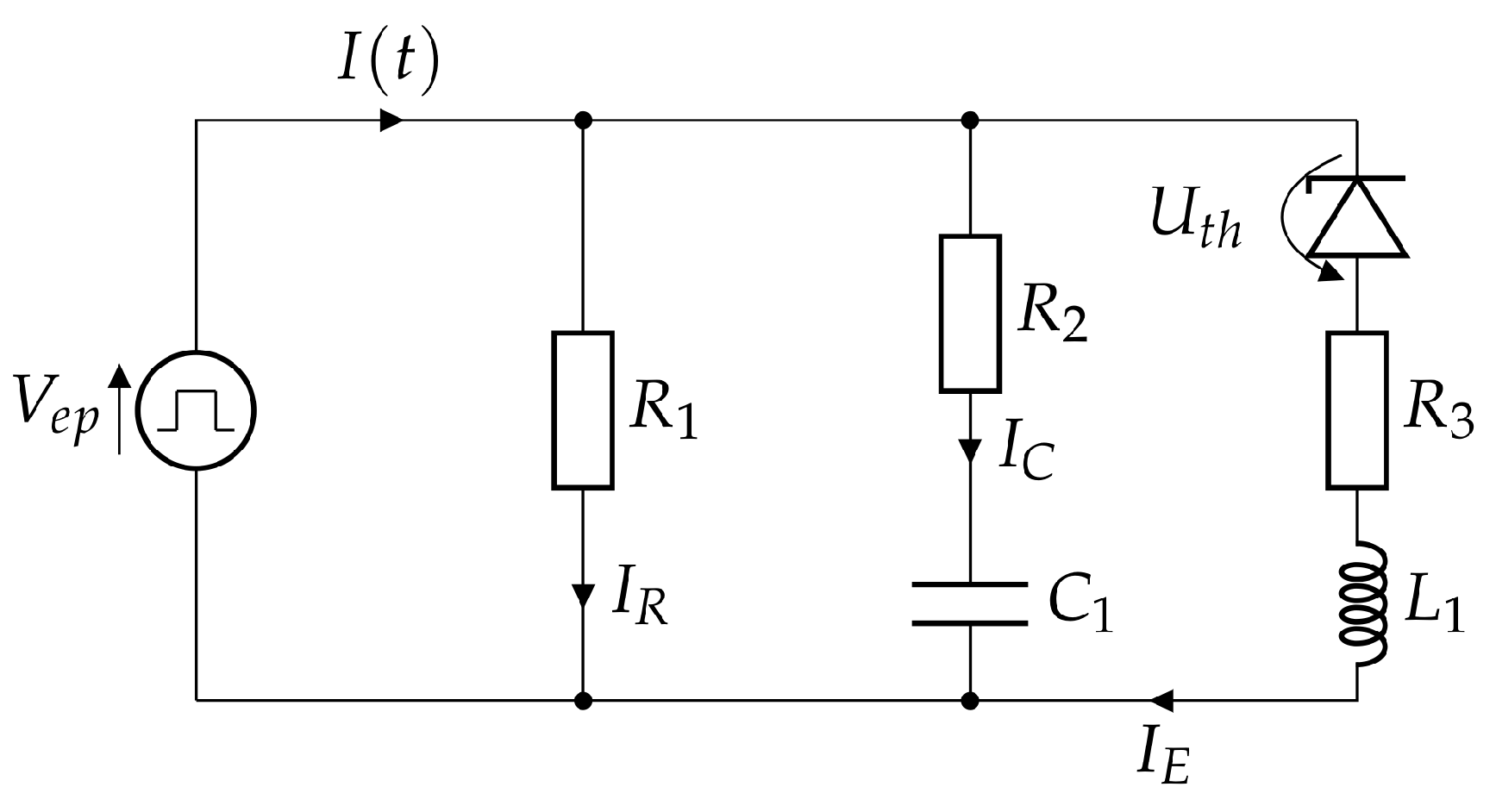
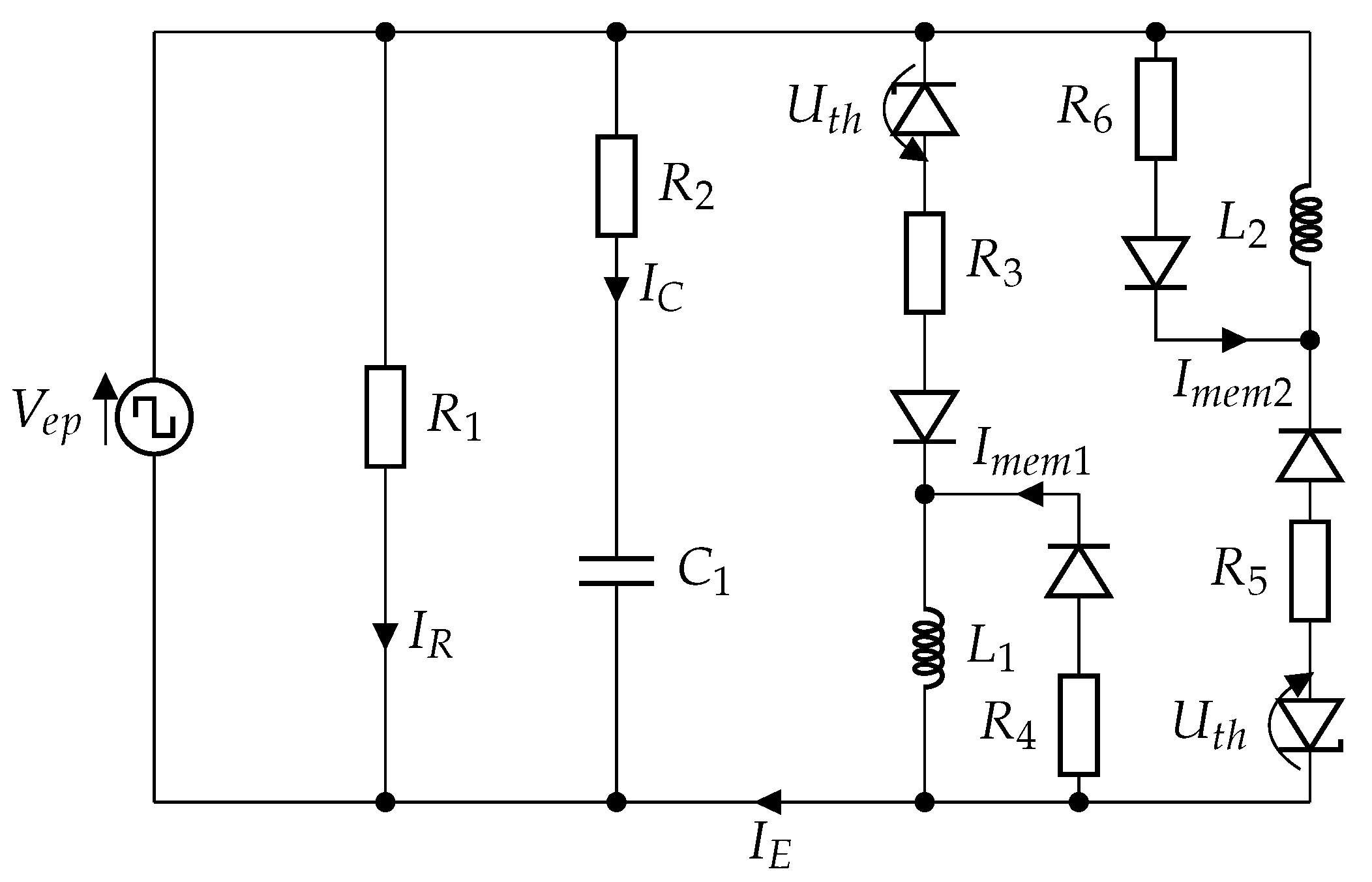
2.2. Circuit Model
2.2.1. Single Monopolar Pulse Model
2.2.2. Multiple Monopolar Pulse Model
2.3. Electronic Load Emulator
3. Results
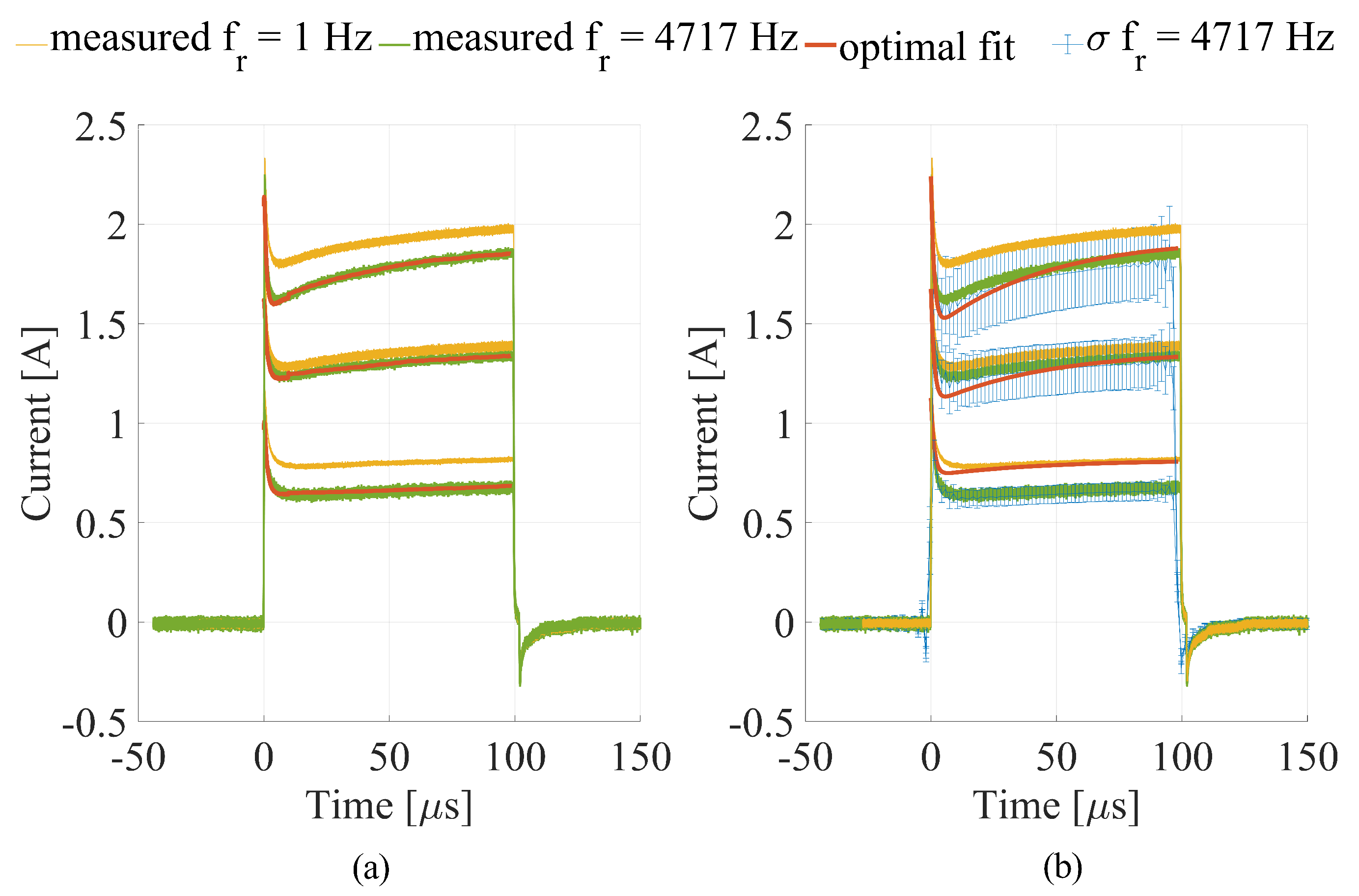
3.1. Numerical Calculations
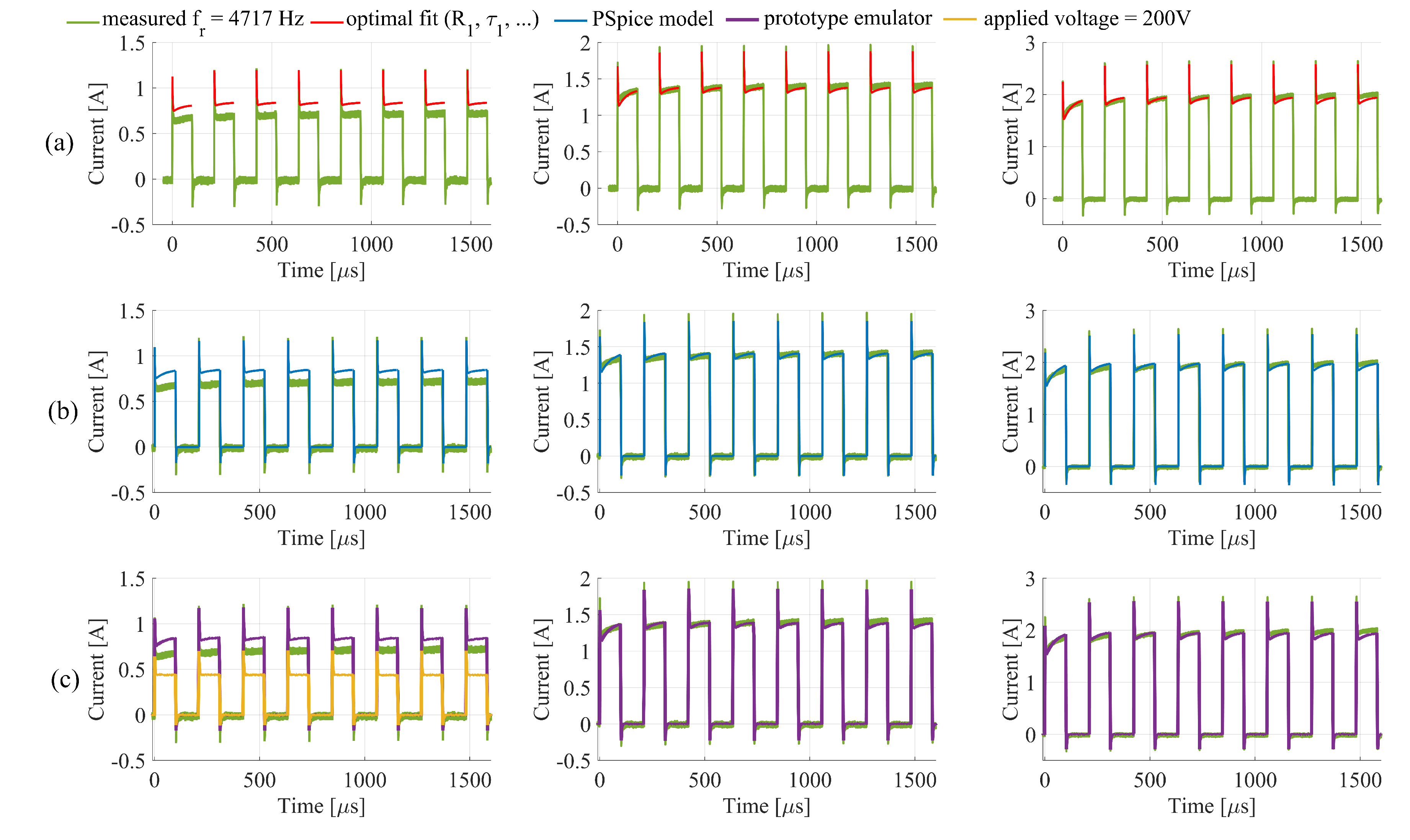
3.2. PSpice Model and Electronic Emulator
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ECT | Electrochemotherapy |
| PEF | Pulsed electric fields |
| LSE | Least square error |
| RMSE | Root mean square error |
References
- Yarmush, M.L.; Golberg, A.; Serša, G.; Kotnik, T.; Miklavčič, D. Electroporation-based technologies for medicine: Principles, applications, and challenges. Annu. Rev. Biomed. Eng. 2014, 16, 295–320. [Google Scholar] [CrossRef]
- Miklavčič, D. Network for development of electroporation-based technologies and treatments: COST TD1104. J. Membr. Biol. 2012, 245, 591–598. [Google Scholar] [CrossRef]
- Kotnik, T.; Rems, L.; Munir, T.; Miklavčič, D. Membrane electroporation and electropermeabilization: Mechanisms and models. Annu. Rev. Biophys. 2019, 48, 63–91. [Google Scholar] [CrossRef] [PubMed]
- Miklavčič, D.; Davalos, R.V. Electrochemotherapy (ECT) and irreversible electroporation (IRE)-advanced techniques for treating deep-seated tumors based on electroporation. Biomed. Eng. Online 2015, 14, I1. [Google Scholar] [CrossRef] [PubMed]
- Mir, L.M.; Orlowski, S.; Belehradek, J.; Paoletti, C. Electrochemotherapy potentiation of antitumour effect of bleomycin by local electric pulses. Eur. J. Cancer Clin. Oncol. 1991, 27, 68–72. [Google Scholar] [CrossRef]
- Serša, G.; Miklavčič, D.; Čemažar, M.; Rudolf, Z.; Pucihar, G.; Snoj, M. Electrochemotherapy in treatment of tumours. Eur. J. Surg. Oncol. 2008, 34, 232–240. [Google Scholar] [CrossRef]
- Mali, B.; Jarm, T.; Snoj, M.; Serša, G.; Miklavčič, D. Antitumor effectiveness of electrochemotherapy: A systematic review and meta-analysis. Eur. J. Surg. Oncol. 2013, 39, 4–16. [Google Scholar] [CrossRef]
- Mir, L.M.; Gehl, J.; Serša, G.; Collins, C.G.; Garbay, J.-R.; Billard, V.; Geertsen, P.F.; Rudolf, Z.; O’Sullivan, G.C.; Marty, M. Standard operating procedures of the electrochemotherapy: Instructions for the use of bleomycin or cisplatin administered either systemically or locally and electric pulses delivered by the CliniporatorTM by means of invassive or non-invasive electrodes. Eur. J. Cancer Suppl. 2006, 4, 14–25. [Google Scholar] [CrossRef]
- Gehl, J.; Sersa, G.; Matthiessen, L.W.; Muir, T.; Soden, D.; Occhini, A.; Quaglino, P.; Curatolo, P.; Campana, L.G.; Kunte, C.; et al. Updated standard operating procedures for electrochemotherapy of cutaneous tumours and skin metastases. Acta Oncol. 2018, 57, 874–882. [Google Scholar] [CrossRef] [PubMed]
- Reberšek, M.; Miklavčič, D.; Bertacchini, C.; Sack, M. Cell membrane electroporation-Part 3: The equipment. IEEE Elect. Insul. Mag. 2014, 30, 8–18. [Google Scholar] [CrossRef]
- Pirc, E.; Reberšek, M.; Miklavčič, D. 12 Dosimetry in Electroporation-Based Technologies and Treatments. In Dosimetry in Bioelectromagnetics; Markov, M., Ed.; CRC Press: Boca Raton, FL, USA, 2017; pp. 233–268. [Google Scholar]
- Puc, M.; Reberšek, S.; Miklavčič, D. Requirements for a clinical electrochemotherapy device—Electroporator. Radiol. Oncol. 1997, 31, 368–373. [Google Scholar]
- Ivorra, A. Tissue Electroporation as a Bioelectric Phenomenon: Basic Concepts. In Irreversible Electroporation; Rubinsky, B., Ed.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 23–61. [Google Scholar]
- Canatella, P.J.; Black, M.M.; Bonnichsen, D.M.; McKenna, C.; Prausnitz, M.R. Tissue Electroporation: Quantification and Analysis of Heterogeneous Transport in Multicellular Environments. Biophys. J. 2004, 86, 3260–3268. [Google Scholar] [CrossRef]
- Powell, K.T.; Morgenthaler, A.W.; Weaver, J.C. Tissue electroporation. Observation of reversible electrical breakdown in viable frog skin. Biophys. J. 1989, 56, 1163–1171. [Google Scholar] [CrossRef]
- Sel, D.; Cukjati, D.; Batiuskaite, D.; Slivnik, T.; Mir, L.M.; Miklavčič, D. Sequential finite element model of tissue electropermeabilization. IEEE Trans. Biomed. Eng. 2005, 52, 816–827. [Google Scholar] [CrossRef] [PubMed]
- Ivorra, A.; Al-Sakere, B.; Rubinsky, B.; Mir, L.M. In vivo electrical conductivity measurements during and after tumor electroporation: Conductivity changes reflect the treatment outcome. Phys. Med. Biol. 2008, 54, 5949–5963. [Google Scholar] [CrossRef] [PubMed]
- Neal, R.E., II; Garcia, P.A.; Robertson, J.L.; Davalos, R.V. Experimental Characterization and Numerical Modeling of Tissue Electrical Conductivity during Pulsed Electric Fields for Irreversible Electroporation Treatment Planning. IEEE Trans. Biomed. Eng. 2012, 59, 1076–1085. [Google Scholar] [CrossRef] [PubMed]
- Langus, J.; Kranjc, M.; Kos, B.; Šuštar, T.; Miklavčič, D. Dynamic finite-element model for efficient modelling of electric currents in electroporated tissue. Sci. Rep. 2016, 6, 26409. [Google Scholar] [CrossRef]
- Pintar, M.; Langus, J.; Edhemović, I.; Brecelj, E.; Kranjc, M.; Sersa, G.; Šuštar, T.; Rodič, T.; Miklavčič, D.; Kotnik, T.; et al. Time-Dependent Finite Element Analysis of In Vivo Electrochemotherapy Treatment. Technol. Cancer Res. Treat. 2018, 17, 1–9. [Google Scholar] [CrossRef]
- Cukjati, D.; Batiuskaite, D.; André, F.; Miklavčič, D.; Mir, L.M. Real time electroporation control for accurate and safe in vivo non-viral gene therapy. Bioelectrochemistry 2007, 70, 501–507. [Google Scholar] [CrossRef]
- Puc, M.; Corović, S.; Flisar, K.; Petkovsek, M.; Nastran, J.; Miklavčič, D. Techniques of signal generation required for electropermeabilization. Survey of electropermeabilization devices. Bioelectrochemistry 2004, 64, 113–124. [Google Scholar] [CrossRef]
- Reberšek, M.; Miklavčič, D. Concepts of Electroporation Pulse Generation and Overview of Electric Pulse Generators for Cell and Tissue Electroporation. In Advanced Electroporation Techniques in Biology and Medicine; Pakhomov, A.G., Miklavčič, D., Markov, M.S., Eds.; CRC Press: Boca Raton, FL, USA, 2010; Chapter 16; pp. 323–339. [Google Scholar]
- Chicaybam, L.; Barcelos, C.; Peixoto, B.; Carneiro, M.; Limia, C.G.; Redondo, P.; Lira, C.; Paraguassú-Braga, F.; De Vasconcelos, Z.F.M.; Barros, L.; et al. An Efficient Electroporation Protocol for the Genetic Modification of Mammalian Cells. Front. Bioeng. Biotechnol. 2017, 4, 99. [Google Scholar] [CrossRef] [PubMed]
- Iversen, N.; Birkenes, B.; Torsdalen, K.; Djurovic, S. Electroporation by nucleofector is the best nonviral transfection technique in human endothelial and smooth muscle cells. Genet. Vaccines Ther. 2005, 3, 2. [Google Scholar] [CrossRef]
- Arslan-Yildiz, A.; El Assal, R.; Chen, P.; Guven, S.; Inci, F.; Demirci, U. Towards artificial tissue models: Past, present, and future of 3D bioprinting. Biofabrication 2016, 8, 014103. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Liu, H.; Bhonsle, S.P.; Wang, Z.; Davalos, R.V.; Yao, C. Ablation outcome of irreversible electroporation on potato monitored by impedance spectrum under multi-electrode system. Biomed. Eng. Online 2018, 17, 126. [Google Scholar] [CrossRef] [PubMed]
- Ruarus, A.H.; Vroomen, L.G.; Puijk, R.S.; Scheffer, H.J.; Faes, T.J.C.; Meijerink, M.R. Conductivity Rise During Irreversible Electroporation: True Permeabilization or Heat? Cardiovasc. Intervent Radiol. 2018, 41, 1257–1266. [Google Scholar] [CrossRef]
- Kranjc, M.; Bajd, F.; Serša, I.; Miklavčič, D. Magnetic resonance electrical impedance tomography for measuring electrical conductivity during electroporation. Physiol. Meas. 2014, 35, 985–996. [Google Scholar] [CrossRef]
- Ivorra, A.; Rubinsky, B. In Vivo Electrical Impedance Measurements during and after Electroporation of Rat Liver. Bioelectrochemistry 2017, 70, 287–295. [Google Scholar] [CrossRef]
- Pavlin, M.; Miklavčič, D. Theoretical and experimental analysis of conductivity, ion diffusion and molecular transport during cell electroporation-relation between short-lived and long-lived pores. Bioelectrochemistry 2008, 74, 38–46. [Google Scholar] [CrossRef]
- Lacković, I.; Magjarević, R.; Miklavčič, D. Three-dimensional Finite-element Analysis of Joule Heating in Electrochemotherapy and in vivo Gene Electrotransfer. IEEE Trans. Dielectr. Electr. Insul. 2009, 16, 1338–1347. [Google Scholar] [CrossRef]
- Stern, J.V.; Gowrishankar, T.R.; Smith, K.C.; Weaver, J.C. Broad pore lifetime distributions: A fundamental concept for cell electroporation. arXiv 2017, arXiv:1708.076133v1. [Google Scholar]
- Merla, C.; Pakhomov, A.G.; Semenov, I.; Vernier, P.T. Frequency spectrum of induced transmembrane potential and permeabilization efficacy of bipolar electric pulses. Biochim. Biophys. Acta (BBA)-Biomembr. 2017, 1859, 1282–1290. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.K.; Chopra, Y.C.; Bajwa, J.S.; Sohi, B.S.; Tiwari, R.K. A reliable microprocessor-based defibrillator analyzer. IEEE. Trans. Instrum. Meas. 1982, IM-31, 28–31. [Google Scholar] [CrossRef]




| Voltage [V] | [nF] | [mH] | [V] | |||
|---|---|---|---|---|---|---|
| 500 | 787.5 | 1.152 | 0.176 | 1.1 | 609,400 | 200 |
| 750 | 621.1 | 1.626 | 3.192 | 0.77 | 182.5 | 200 |
| 1000 | 639.9 | 1.401 | 2.393 | 0.65 | 106.9 | 200 |
| [nF] | [mH] | [V] | ||||
|---|---|---|---|---|---|---|
| 682.4 | 1.287 | 1.287 | - | 0.998 | 57.5 | 400 |
| 682.4 | 1.287 | 1.287 | 171.1 | 0.998 | 57.5 | 366.7 |
| [nF] | [mH] | [V] | ||||
|---|---|---|---|---|---|---|
| 680 | 1.2 | 1.2 | 175 | 1 | 57.5 | 360 |
| SET VOLTAGE, REP. F | ||||
|---|---|---|---|---|
| [mA] | [mA] | [mA] | [mA] | |
| 500 V, 1 Hz | 38.5 | 40.3 | 38 | 101.1 |
| 500 V, 4717 Hz | 46.3 | 125.8 | 132.1 | 101.4 |
| 750 V, 1 Hz | 115.1 | 111.6 | 106.2 | 72.6 |
| 750 V, 4717 Hz | 124.7 | 41.4 | 40.7 | 471.4 |
| 1000 V, 1 Hz | 116.1 | 192.7 | 189.5 | 131.6 |
| 1000 V, 4714 Hz | 177 | 55.7 | 58.1 | 705.7 |
| Total RMSE | 108.87 | 356.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirc, E.; Balosetti, B.; Miklavčič, D.; Reberšek, M. Electronic Emulator of Biological Tissue as an Electrical Load during Electroporation. Appl. Sci. 2020, 10, 3103. https://doi.org/10.3390/app10093103
Pirc E, Balosetti B, Miklavčič D, Reberšek M. Electronic Emulator of Biological Tissue as an Electrical Load during Electroporation. Applied Sciences. 2020; 10(9):3103. https://doi.org/10.3390/app10093103
Chicago/Turabian StylePirc, Eva, Bertrand Balosetti, Damijan Miklavčič, and Matej Reberšek. 2020. "Electronic Emulator of Biological Tissue as an Electrical Load during Electroporation" Applied Sciences 10, no. 9: 3103. https://doi.org/10.3390/app10093103
APA StylePirc, E., Balosetti, B., Miklavčič, D., & Reberšek, M. (2020). Electronic Emulator of Biological Tissue as an Electrical Load during Electroporation. Applied Sciences, 10(9), 3103. https://doi.org/10.3390/app10093103





