Abstract
Conscious and functional use of online social spaces can support the elderly with mind cognitive impairment (MCI) in their daily routine, not only for systematic monitoring, but to achieve effective targeted engagement. In this sense, although social involvement can be obtained when elder’s experiences, interests, and goals are shared and accepted by the community, an important subsistence for aging depends on the compelling information, users’ co-operation, and resource reliability. Unfortunately, applications aimed at optimizing the information content and the reliability of online users are still missing. Within the SystEm of Nudge theory-based ICT applications for OldeR citizens (SENIOR) project, an advanced social platform will be created in which the elderly with MCI will be involved in “optimized” social communities, where suggestions for general well-being will be recognized as useful by users and shared by care providers. We report the results of our study addressing this issue from a theoretical perspective: we propose a computational problem and a heuristic solution where “expert users” can engage and support the elderly by suggesting available services and facilities for their conditions. The numerical experiments on synthetic data are of interest when considering large communities, which is the most natural situation for online social spaces.
1. Introduction
Mind cognitive impairment (MCI) is rapidly becoming one of the most common clinical manifestations affecting the elderly. It is characterized by deterioration of memory and cognitive function that is beyond what is expected based on age and educational level. MCI does not interfere significantly with individuals’ daily activities. It can act as a transitional level of evolving dementia with a range of conversion of 10–15% per year [1]. Therefore, it is crucial to protect older people against MCI.
The SystEm of Nudge theory-based ICT applications for OldeR citizens (SENIOR) project (a project supported by the Cariplo Foundation according to well-being and social cohesion planned intervention strategies) will create an advanced nudge-based [2,3] social platform, collecting and integrating significant physiological and behavioral data to interact with elderly people and to provide personalized suggestions about preventive measures, social participation, and overall wellness. The challenge of SENIOR will be to move many elderly with MCI at a first stage towards a conscious and functional use of new technologies by exploiting the advantages of being connected, not only to be clinically monitored, but to remain in contact with an expert audience of users.
Proper handling of procedures and data is therefore fundamental to convert available information into useful formulation. We address this issue from a theoretical perspective: we propose a computational problem that aims to leverage user-user and user-item relationships for identifying heterogeneous communities of users and items (we also use the term “resource” as a synonym for “item”) where “expert users” (or “experts”) can engage and support elderly by suggesting available services and facilities for their conditions and social well-being (hospitals, care providers, leisure services, cultural activities). In our model, “experts” will be a sort of intermediary (“facilitators”) who, thanks to their experience and ability to meet the elderly’s needs (acquaintances, patients with similar history, care providers, parents), will be able to encourage social participation under therapeutic plans and objectives. In other terms, solving the proposed computational problem will allow SENIOR’s engine to offer heterogeneous communities where the elderly can find optimized target “spaces of interest” for their wellness. Importantly, this “social space” will be exploited by SENIOR’s future technological component: a recommender system able to strengthen and influence elderly engagement and participation in the identified communities.
Our intent, in this paper, is to introduce the “social space identification" problem, a computational optimization problem for target communities identification, and to provide heuristic-based solutions for the considered formulation. The paper is organized as follows. In Section 2, we review the related literature. We summarize the theoretical concepts in Section 3. In Section 4, we discuss the GA-based approach to seek approximate solutions for the proposed problem. We extend the applied framework to distributed environments in Section 5. In Section 6, we discusses numerical results using synthetic data, and in Section 7, we conclude the paper by discussing future developments of our research.
2. Related Work
Online education plays a fundamental role in the prevention and conscious participation of patients in the care process. In particular, some online social networks have been emphasized as a useful tool that acts as social support for the elderly, capable of shielding, in some circumstances, from psychological stress and encouraging participation and engagement [4,5,6,7,8,9].
Some of these platforms, such as PatientsLikeMe (http://www.patientslikeme.com), CureTogether (http://www.curetogether.com), or MedHelp (http://www.medhelp.org), have provided users self-management of personal activities for their own diseases. For example, in [10], an auto-tracking system called “Empower”was designed to allow the self-management of patients and their treating physicians. In this case, specialists can provide recommendations and monitor patient’s daily progress. Similarly, HealthNet (HN) [11] allows users to access suggestions on both doctors and health facilities that best fit the patient’s clinical profile. The main component of HN is a recommender system that is able to suggest similar profiled patients and indicate health services for a specific condition.
Moreover, understanding (or even inducing) the formation of social ties within online health networks, their structure, and functions, as well as the associated mechanisms linking these to health services, can be extremely relevant for several reasons. For example,
- To reduce information overload [12,13,14];
- To provide trust-based communications [15,16,17];
- To handle complex relationships among the networks’ elements [18];
- To allocate limited resources properly [19,20].
In this regard, one of the most convincing ideas for promoting the creation of suitable health social spaces has been the application of recommender systems (RS). Unfortunately, these mechanisms have not yet been widely used in the medical context (and in health informatics). Above all, in these fields, they still lack the fulfillment of the above issues simultaneously. To some extent, current solutions are limited to conferring direct benefits either to health professionals or patients, rather than inducing both optimized and reliable information content spaces for targeted allocation of health services. Wiesner and Pfeifer [21] distinguished two different scenarios. On the one hand, healthcare professionals are the beneficiaries of the recommendations to find, for example, additional information for specific case studies, guidelines, or research articles. On the other hand, the beneficiaries are the patients. In the latter case, RS focuses on delivering high quality, evidence-based, health-related content to end-user patients, for example suggesting clinical examinations [22], lifestyle changes [23,24], or improving patient safety [25]. Similarly, they are also used to indicate to the patient a better understanding of his/her personal health status, to retrieve semantically-related content, or to suggest web sites concerning specific diseases [26,27].
To the best of our knowledge, no framework exists that specifies how health-related recommender systems can guide the network creation process and, in particular, can generate networks that comply with the requirements argued previously. It is our opinion that promising new research in this direction can be conducted by applying computational methods to the study of heterogeneous information networks more widely [18,28,29,30,31,32]. In this context, graph theory and optimization techniques could provide future recommendation systems with the ability to influence and effectively support user communication in online health spaces. For example, in the literature, some algorithms designed for this purpose, i.e., to identify specific subgraph communities such as cliques or k-clubs, can be found in [33,34,35,36]. It is worth noting that the optimization of targeting social spaces for potential recommender systems, and therefore the theoretical identification of these communities, may lead to combinatorial optimization issues, which, in turn, bring the identification of intrinsically complex (intractable) problems [37]. Anyway, even in these circumstances, common approaches exist for applying specific heuristics or designing particular (machine) learning techniques that offer approximate, but efficient solutions [38,39,40,41,42].
3. The “Social Space Identification” Problem
In some circumstances, friendship is not the only factor that allows us to build reliable suggestions for a recommendation system. Instead, for users, sharing information about available facilities and services, being involved in common goals, or even sharing their own history and experience with other users should be the key issues to consider when providing adequate recommendations. With this perspective, SENIOR’s social engine will be formulated as a computational problem aimed at optimizing heterogeneous groups of people and resources by exploiting the involvement and the skills of “expert users”, i.e., care providers, specialized personal, acquaintances, patients with similar experiences.
Without loss of generality, we can consider the case of a “clinic oriented engagement”. Suppose users are recently diagnosed (RD) patients who want to be involved in managing their diseases through the experience of other users (e.g., being followed up for similar diseases), say “expert patients” (EX). In this situation, new users may be interested in acquiring information about, e.g., follow-up treatments, specialized hospitals, and doctors; in general terms, they should be interested in knowing as much as possible about the caregivers (here, we will also use the term health service provider or its acronym HSP) and the services they offer. In this case, the platform should motivate new patients to socialize with experts who have already been followed up, for example, in the same health centers or by other specific caregivers. It is more likely that, under these circumstances, EX patients can share reliable and convincing suggestions.
Importantly, the identification of potential users and resources would, therefore, allow properly providing the recommendation system with effective information, which, in turn, would allow inducing the targeted communication within the chosen group.
3.1. Problem Formulation
Modeling the situation described in the previous section naturally leads to the problem of identifying (large and dense) communities of users and items. In our case, the role of expert users is fundamental to apply the method properly. We could represent EX patients through “entities”, which act as “bridges” between new patients and HSPs: their role is to connect RD patients and HSPs, indirectly. In such a situation, the interest becomes that of identifying a large (and dense) community in which RD users can be at most at a distance of two from HSPs, being connected through the “experts” who can offer their support.
The problem can, therefore, be formulated as follows. Within a given network, identify the largest community in which users are connected (through paths of length two) to items through available specific users. This model leads to the theoretical concept of two-clubs (i.e., graphs with particular properties). For the sake of clarity, before defining the problem computationally, we recall some important definitions in the context of graph theory.
3.2. Main Notation and Definitions
Graphs are abstract models of complex relationships commonly established in current networks. Formally, a graph is a collection of the network’s entities (i.e., vertices, V) and interactions among them (edges, E). Given a graph G, we use the corresponding adjacency matrix A, which indicates whether two vertices of G are connected by an edge, i.e., , if . We also use the notation to denote the sub-matrix of A indexed by the rows and columns . Moreover, we denote by the subgraph of G induced by the subset of vertices .
A path in G is a finite (or infinite) sequence of edges that joins a sequence of distinct vertices. The distance, , between two distinct vertices u and v is the number of edges in the shortest path connecting them. The diameter of is defined as , i.e., the maximum distance between any two vertices in V. Finally, we denote by the neighborhood of a vertex v. The following definitions are fundamental for our objectives:
Definition 1.
Two-clubs are subgraphs where all the vertices are at a distance at most two. Importantly, given a graph , a two-club in G is a subgraph , with , whose diameter is at most equal to two.
Let G be a graph, its set of vertices, and T, X, and R the set of RD patients, EX patients, and HSP centers, respectively. Consider a labeling function that assigns to each vertex in V a (type of) service in S. Notice that a service can be required by new users (e.g., v requires information about ), already prescribed for some expert (e.g., v was followed up with ) or available in some center (i.e., health service is available in v).
Definition 2.
A vertex , for which there exists, in , at least one pair , where , will be named a “feasible vertex”. Moreover, we call the set of “feasible vertices”, , a “feasible set” and the pair, , a feasible pair.
In our example, feasible vertices are experts “equipped” with pairs consisting of a new patient t with the available caregiver r. In other terms, when a new (target) patient requires information, our interest will be to supply with his/her “own” heterogeneous community of users/items , with , consisting of the largest number of feasible pairs. More formally, we seek a maximum size two-club for (i.e., included), which has the further property of providing, the largest number of (feasible) pairs whose vertices t and r are connected with at least one simple path passing through some , such that , i.e., the information about service , requested by , is available with (the caregiver) r. This information can be obtained consulting x.
For any “target”, the identification of the largest size two-club (with the largest number of feasible pairs) offers multiple sources of alternative information (each node of a two-club community being reachable through paths of size two). In other words, “targets” can acquire greater awareness in reaching available resources by exploiting different paths and through different “experts”. For example, in our case, recent patients (i.e., target users) can collect information on alternative providers (HSP) from the same expert, as well as information on the same center from different available experts. With the above concepts, we can formulate the optimization problem in the following general terms.
Problem 1.
Input: (1) A graph , with , where T is the set of RD patients, X is the set of EX patients, and R is the set of HSP centers. (2) A set of service S and a labeling h, such that , i.e., h labels expert patients, recent patients, and services. (3) The target patient . Output: A set , such that and is a two-club having both maximum size and the largest number of feasible pairs.
4. Approximate Solutions
Problem 1 is a computational variant of the max s-club problem, whose complexity is NP-hard for [39]. Similarly, this result also applies to Problem 1.
In order to find approximate solutions at a reasonable cost (time), in this paper, we designed a genetic-based heuristic by defining specific operators that allow obtaining fast solutions.
4.1. Chromosome Representation
Let be an input graph and , with a given feasible solution for Problem 1. Consider a binary vector c such that if , and if . In this way, we assume that c is used to represent a (chromosome) solution obtained through the evolution of randomly initialized binary vectors (starting population) of dimension . In other terms, we represent with binary vectors a population of chromosomes that state the vertices to be included within the corresponding identified community (two-club). With a slight abuse of notation, we indicate with the subgraph of G induced by c and with and the corresponding sets of vertices and edges, respectively, i.e., .
4.2. Fitness Function
Genetic algorithms (GAs) promote system adaptation in such a way that candidate chromosomes (in our case, being able to represent graphs with a diameter value no larger than two) “evolve” through standard elitism. The evaluation of a chromosome is then obtained by applying a fitness function [43]. Here, we give a general formulation for the fitness we apply in the following paragraphs.
where the value of will be functionally related either to (1) the health services and vertex-type distributions around the neighborhoods of vertices in or (2) the number of feasible pairs in the neighborhoods of vertices in . Therefore, the objective of Equation (1) is to promote differently (depending on the role of (i.e., either Case 1 or 2)) large sized sub-networks for correct diameter values (i.e., by weighting with the number of vertices, , of , i.e., ). More in detail, will be evaluated as follows.
4.2.1. Case 1
In this case, is functionally related to the health service and vertex-type distributions around the neighborhoods of vertices in . In particular,
- From one side, Equation (1) promotes chromosomes that identify, around feasible vertices, different (types of) services operated by HSPs and different (types of) services required by targets, i.e., we promote uniform distributions of the supply and demand of services.
- From the other side, we promote chromosomes that identify, around feasible vertices, the participation of different types of entities (here, we focus on two types of entities only: HSPs and target users, respectively), i.e., we promote uniform user-/resource-type distributions around feasible .
Notice that the above objectives are reflected, in turn, by the entropy of the corresponding distributions, i.e., a “distribution of entities”, say , obtained by counting the different types of entities in for each , and a “distribution of services” (supplied or demanded by entities), say , obtained by counting the different types of services in , for each (These estimations are clearly biased due to the “relationships” between neighborhoods. In fact, here, we are assuming the independence between the distributions of vertices in different neighborhoods.).
As the entropy (respectively, ) reaches the maximum if all the outcomes are equally likely, in this case fitness (1), it should promote those chromosomes that represent uniform service-/entity-type distributions around EX patients. Hence, following the above arguments, we set .
4.2.2. Case 2
In this case, is functionally related to the number of feasible pairs around the neighborhoods of vertices in . Given a chromosome c and the set of induced vertices , we sample, for each feasible vertex , a set (of observations) . In this way, we have a fast computational estimation, , by counting the number of all feasible pairs within the observed samples. Finally, for this case, we set .
4.3. Mutation
The objective of mutation is to encourage system adaptation. The following three genetic operators are applied (with equal probability).
- Mutation Operator 1:Let c be a chromosome observed during some step of the evolution process. Assume that, at such a step of evolution, , the current hypothesis conjectured by c, is not feasible for Problem 1. Moreover, let be the subgraph induced by . In order to provide the system’s compliance to get feasible solutions, to obtain feasible two-clubs sparingly, we randomly sampled the vertices , and for each , we checked whether the minimum length between and v was . If this test was negative, then was flipped to zero, thus orienting the system towards the feasibility.
- Mutation Operator 2:Through this operator, we aimed to increment the size of a feasible solution. Let and be defined as above. We randomly sampled from , and then, we checked if the shortest distance of from was . If this test was negative, then was flipped to one.
- Mutation Operator 3:In this case, a standard mutation procedure was applied: bits were randomly switched either “on” or “off”.
4.4. Cross-Over
The following cross-over operators were designed.
- Logical AND/OR cross-over: New offspring was generated by applying AND/OR logic operations on parent chromosomes.
- Standard cross-over: This operation is typical and is often used in standard applications of genetic algorithms. Parent chromosomes are reported and mixed in new descendants.
5. Distributed Learning
The large number of data observed in online social interactions and the intrinsic complexity of the proposed problem make it difficult to solve the optimization target computationally. The effective distribution of the learning task is therefore desirable.
The idea of “distributed learning” in GAs has been explored with many motivations [44]. Most of these approaches share the concept of evolving independent (genetic) populations in parallel. Similarly, our goal in this paper is task-motivated: we framed the optimization Problem 1 into independent, local smaller optimization tasks, while returning (local) solutions that could be associated with specific subgraphs.
A Genetic Cascade Model
Distributed learning was conceived following the process in Figure 1. Large scale optimization was divided into smaller problems, where different populations evolved over different (computational) “sites” independently. Each “site” was locally “trained” with the GA described in Section 4, using only a part of the input instances.
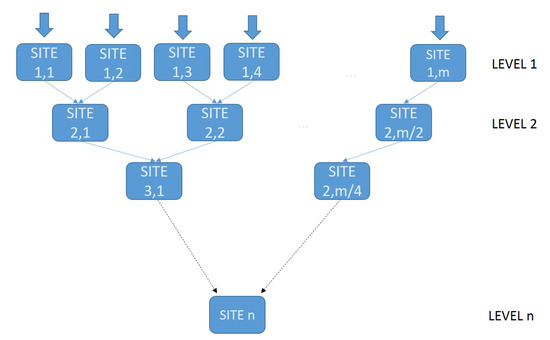
Figure 1.
Distributed process. Different populations evolve over different (computational) “sites” independently. Each “site” is locally trained with the GA, and the best chromosomes from the pair of “ascendents” initialize the lower level site population.
Without loss of generality, we can assume that the sets of expert patients, X, recent patients T, and health providers R form an indexed collection of elements , whose values (to simplify the notation, here we use as a shortcut for ) also index the rows and columns of the graph adjacency matrix of . Moreover, let us assume that the computational load is distributed on a first sequence of different units (say, sites of Level 1) in such a way that each unit of this sequence (say, site i of Level 1, ) executes the GA, only on a part of the available users and items data in B. In particular, we distribute to only a sub-sequence of k input elements , where is either a user or an item in B. For example, site in Figure 2 works on the sequence consisting of the first five elements . Similarly, the second site employs the successive elements .
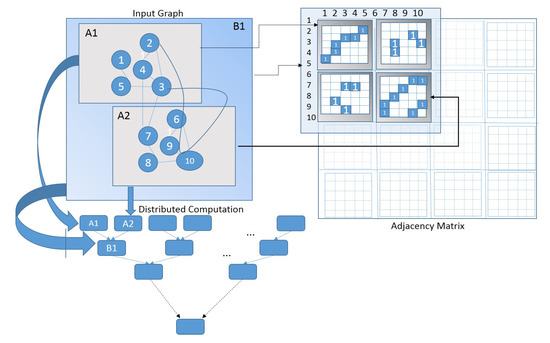
Figure 2.
Local solution: Site is trained with the first five elements to return the solution for . Similarly, uses the successive elements for . The best chromosomes from and initialize ’s population, which, in turn, is trained to provide feasible solutions for .
Using this load distribution, each (first level) site processes its own solution for the graph adjacency (sub)matrix whose rows and columns are associated, respectively, with the corresponding sequence of k(input data) elements .
Given two (subsequent) first-level sites and , their input workload and , and the respective GAs solutions obtained in and , we can insert the best chromosomes (from and , respectively) within the population of a new processing unit (say, site , of Level 2). In this way, the new chromosome population in is properly initialized to return the local solution for the corresponding input subgraph. Indeed, by extending the chromosome representation reported in Section 4.1, we can train the GA employed in on the set of elements , thus providing feasible solutions for the extended set of input instances, which, in turn, represent a larger local solution whose graph adjacency matrix is:
Figure 2 displays the situation when ’s population (initialized by the best chromosomes from its ascendents and ) is trained to provide solutions for .
Finally, by extending the process to the lower level site, we complete the evolution of all input data. The best solution provided by the last site identifies, in this way, the community (i.e., the two-club) on the whole input network.
6. Numerical Experiments
The numerical experiments mainly aimed at evaluating the ability of the GA-based approach to obtain correct solutions in a reasonable time. In order to promote large sized sub-networks, we applied the two cases of fitness introduced in Section 4.2. In particular, we applied Case 1 (distribution-based) for a standard GA evolution (reported as “centralized” in the following discussion) and Case 2 (feasible pairs estimation) for the distributed learning.
6.1. Centralized Learning
As we could not compare the solution of the GAs with the problem’s optimal solution (NP-hardness), we evaluated the possibility of identifying communities where the services operated by health centers and the services required by users were best distributed around feasible vertices. As discussed in Section 4.2, we encouraged, on the one hand, the offer of a large number of services versus a differentiated request for services and, on the other, the participation of different types of entities around feasible users (uniform distributions).
The procedures were coded in R using the “GA” package [45]. The experiments used synthetic data by sampling Erdos–Renyi (ER) random graphs, , for different numbers of vertices, , and edge probability [46]. The results are reported in Table 1. The following observations emerged from the results.

Table 1.
Performances: Models (Erdos–Renyi); average input diameter (AvInD); average diameter (AvOutD); output nodes (OutN); user (T1) and system Time (T2) in seconds; average entropy of (HTS); average entropy of (HVS); target included, average number (TI); Avnumber of feasible vertices (%) w.r.t. the number of vertices in the final solution (FeasA).
- All models except identified two-clubs correctly.
- We considered the average value of the entropy for the health service and vertex-type distributions around expert patients. It is worth emphasizing that the system returned solutions whose entropy could not be associated with distributions having the whole probability mass centered on any specific value. Notice that, since only RD patients and HSP could be found around EX users, then we had . Similarly, as we had , i.e., five types of services were considered in our experiments, then was such that .
- Moreover, notice that, at least of the output nodes were identified as feasible. Larger values are reported for large input networks, e.g., or . This was a compelling property, for example, in the case of large communities.
- System time seemed reasonable (T2 s) for the applied instances.
6.2. Distributed Learning
In this case, fitness promoted the identification of large networks by weighting the chromosomes with the estimation of the number of feasible pairs (Case 2 fitness) observed in the corresponding chromosome representation. We coded the procedures with the “Multiprocessing” Python package, working on local concurrency with four cores (i.e., the cascade model used four starting sites). The R and Python interfaces were managed by the rpy2 (https://rpy2.readthedocs.io/en/version_2.8.x) utility. Experiments were executed on Apple OSX 10.12.6, system type MacBook Pro Retina, processor Intel(R), Core(TM) i5-6360U 2.00 GHz, 3.100 GHz, 2 core(s), 4 logical processors; installed physical memory (RAM) 8.00 GB. Results are given in Table 2 and Table 3. In particular, we compared the results with “centralized” (not distributed) executions. The following attributes were used.

Table 2.
Models (Erdos–Renyi), input diameter (InpDiam), output diameter (OutDiam), output nodes (OutN), output feasible pairs (OutP). The standard deviation is shown in brackets.

Table 3.
Models (Erdos–Renyi), best fitness (Fit), iteration (Iter), CPU Av. time., the ratio between input and output vertices. The standard deviation is shown in brackets.
- Input/Output diameters: the input graph diameter and output graph diameter proposed by the best chromosome solutions.
- Output vertices: the number of final vertices obtained in the chromosome solution.
- Fitness value: as described in Section 4.
- Ratio between the number of input vertices and the number of vertices within the two-club represented by the chromosome solution.
- Average CPU user time: for a single processing unit, i.e., standard GA evolution, this quantity corresponded to the (GA) execution time; when applying distributed learning, the whole execution time was averaged over the number of (framework) levels.
- Early stopping: the number of consecutive generations without improvement of the fitness value; the GA execution was stopped after the “early stopping”.
- Max number of generations: the maximum number of iterations before the GA search was halted.
- Final generation number: the iteration number associated with the final solution. Notice that, in our case (i.e., distributed evolution), this number corresponded to the iterations of the lowest site.
The following observations can be given.
- All models, except , returned correct two-clubs. This was an interesting result when large input graphs (e.g., more than 1000 vertices in our table) were considered.
- Similarly to previous experiments, as we could not confront the problem’s optimal solution, to evaluate the solution proposed by the genetic algorithm qualitatively, we report the ratio between the number of vertices of the input and the output graphs. Notice that the approximability of the problem was very hard to obtain (not approximable within a factor , for each [47]). Considering our results, in particular the ratio in Table 3, we concluded that the most interesting solutions were those for which the larger the input graph (number of vertices), the lower the difference between the ratio and the unit.
- Although the size of the identified communities did not seem to differ, the (average) number of iterations of the last level site (distributed execution) was much lower than the iterations reported by the standard, centralized evolution. This was also evident from the decrease in the average execution time per level, reported by the distributed process. Since GAs use the same parameters for the standard and the distributed evolution, this behavior could be traced back to the initialization that each lower level site received from the higher levels.
- The computational cost seemed to depend on both the edge numbers (i.e., high expected connectivity of random models ) and the number of input vertices. As the fitness computational complexity was related to the diameter computation, this assertion could be justified considering the diameter computational cost, which is known to be bounded by .
7. Conclusions
The challenge set by the SENIOR project is to involve the elderly, with mind cognitive impairment, in target communities where the shared information and the available resources can be exploited as best as possible by users and caregivers. The SENIOR social engine will be designed as a specific recommender system able to leverage on-line information to influence elderly participation and to promote resources for their well-being. As recognized above, to the best of our knowledge, no framework exists that specifies how health-related recommender systems can promote this “network creation process”. In this regard, the expected value of the proposed ideas is to promote the creation of online “health spaces” by enhancing trust-based communication between patients and “experts” for suitable resource allocation. In this model, the “experts” not only play an essential role for patients in the real world, but represent mediation nodes for suggesting “items” (i.e., resources) accurately. The recommender system should, therefore, influence the development of the social network with appropriate suggestions.
In conclusion, we can characterize the contributions of this article as follows.
- We formulated a computational optimization problem for the future suggestions of the SENIOR recommender system.
- Algorithmic solutions were proposed as well, based on evolutionary heuristics, both for centralized and parallel processing environments.
Further extension of our research will be addressed as follows.
- As reported in recent studies, using additional user and item relationships could improve the recommendation quality [48,49]. In this perspective, the optimization objective formulated in Equation (1) will be further constrained by taking into account relationships between target users. These relationships could be interpretable as either “friendships between target users” or “targets sharing similar experiences”. The feasible solutions (i.e., two-clubs) optimized with such a type of connection would allow the future recommendation system to induce even more compelling communication among users, perhaps looking for similar reliable resources.Furthermore, edges among “experts ” (within the identified two-clubs) could be used as an endorsement, thus allowing target users to evaluate new different experiences or the consistency of the information of other expert users. Such links could also induce more effective communication between experts to facilitate final patient support. Similarly, a constrained optimization accounting for “resource to resource” relationships, within the identified community, could offer the user equivalent available resources.
- In Section 4.2, we presented a general fitness formulation for two different evaluations of a free parameter (). A more context-based formulation able to manage real needs will certainly provide more effective results in this sense. As an example, we can consider the first reported case (Number 1), where is related to the health service and vertex-type distributions. In this situation, a linear combination of entropies is used to optimize (and balance) an induced two-club community. Direct comparisons (e.g., using cross-entropy evaluations) of user requirement distribution vs. service distribution could be similarly evaluated for future numerical experiments.
- Finally, we assumed so far that each provider could supply one service only. In fact, this was “coded” by the labeling function h discussed in Section 3.2. It is straightforward to extend this labeling to multiple services for a more realistic implementation.
Author Contributions
Conceptualization, I.Z., A.T., S.M., and D.M.; formal analysis, I.Z.; funding acquisition, I.Z. and G.C.; methodology, G.C.; project administration, G.C.; resources, G.M. and G.P.; software, I.Z.; writing, original draft, S.M.; writing, review and editing, I.Z., A.T., S.M., D.M., G.M., G.P., and G.C. All authors read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This research is part of the SENIOR project SystEm of Nudge theory-based ICT applications for OldeR citizens–supported by Cariplo Foundation.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Petersen, R.C.; Smith, G.E.; Waring, S.C.; Ivnik, R.J.; Tangalos, E.G.; Kokmen, E. Mild cognitive impairment: Clinical characterization and outcome. Arch. Neurol. 1999, 56, 303–308. [Google Scholar] [CrossRef]
- Arno, A.; Thomas, S. The efficacy of nudge theory strategies in influencing adult dietary behaviour: A systematic review and meta-analysis. BMC Public Health 2016, 16, 676. [Google Scholar] [CrossRef]
- Richard, H.; Thaler, C.R.S. Nudge: Improving Decisions about Health, Wealth, and Happiness; Yale University Press: New Haven, CT, USA, 2008. [Google Scholar]
- Olsson, T.; Samuelsson, U.; Viscovi, D. Resources and repertoires: Elderly online practices. Eur. J. Commun. 2019, 34, 38–56. [Google Scholar] [CrossRef]
- Chen, L.; Alston, M.; Guo, W. The influence of social support on loneliness and depression among older elderly people in China: Coping styles as mediators. J. Community Psychol. 2019, 47, 1235–1245. [Google Scholar] [CrossRef]
- Haritou, M.; Anastasiou, A.; Kouris, I.; Villalonga, S.G.; Gancedo, I.O.; Koutsouris, D. Go-myLife: A context-aware social networking platform adapted to the needs of elderly users. In Proceedings of the 6th International Conference on PErvasive Technologies Related to Assistive Environments, Island of Rhodes, Greece, 29–31 May 2013; pp. 1–5. [Google Scholar]
- Harley, D.; Howland, K.; Harris, E.; Redlich, C. Online communities for older users: What can we learn from local community interactions to create social sites that work for older people. In Proceedings of the 28th International BCS Human Computer Interaction Conference (HCI 2014), Southport, UK, 9–12 September 2014; pp. 42–51. [Google Scholar]
- Pensas, H.; Kivimäki, T.; Vainio, A.M.; Konakas, S.; Costicoglou, S.; Kölndorfer, P.; Summanen, K.; Moisio, H.; Vanhala, J. Building a client-server social network application for elders and safety net. In Proceedings of the International Conference on Making Sense of Converging Media, Tampere, Finland, 1–4 October 2013; pp. 310–312. [Google Scholar]
- Dangon, J.M.; Mendoza, A. A Conceptual Framework to Evaluate Usability in Mobile Aged Care Applications: A health care initiative. In Proceedings of the International Conference on Information Resources Management: Managing IT in a Consumerized IT World, Natal, Brazil, 22–24 May 2013. [Google Scholar]
- Mantwill, S.; Fiordelli, M.; Ludolph, R.; Schulz, P.J. EMPOWER-support of patient empowerment by an intelligent self-management pathway for patients: Study protocol. BMC Med. Inform. Decis. Mak. 2015, 15, 18. [Google Scholar] [CrossRef]
- Narducci, F.; Lops, P.; Semeraro, G. Power to the patients: The HealthNetsocial network. Inf. Syst. 2017, 71, 111–122. [Google Scholar] [CrossRef]
- Lee, A.R.; Son, S.M.; Kim, K.K. Information and communication technology overload and social networking service fatigue: A stress perspective. Comput. Hum. Behav. 2016, 55, 51–61. [Google Scholar] [CrossRef]
- Zhang, S.; Zhao, L.; Lu, Y.; Yang, J. Do you get tired of socializing? An empirical explanation of discontinuous usage behaviour in social network services. Inf. Manag. 2016, 53, 904–914. [Google Scholar] [CrossRef]
- Bawden, D.; Robinson, L. Information Overload: An Overview; Clarendon Press: Oxford, UK, 2020. [Google Scholar]
- Urena, R.; Kou, G.; Dong, Y.; Chiclana, F.; Herrera-Viedma, E. A review on trust propagation and opinion dynamics in social networks and group decision making frameworks. Inf. Sci. 2019, 478, 461–475. [Google Scholar] [CrossRef]
- Golbeck, J. Generating predictive movie recommendations from trust in social networks. In Proceedings of the International Conference on Trust Management, Pisa, Italy, 16–19 May 2006; pp. 93–104. [Google Scholar]
- Robinson, Y.H.; Julie, E.G. MTPKM: Multipart trust based public key management technique to reduce security vulnerability in mobile ad-hoc networks. Wirel. Pers. Commun. 2019, 109, 739–760. [Google Scholar] [CrossRef]
- Interdonato, R.; Atzmueller, M.; Gaito, S.; Kanawati, R.; Largeron, C.; Sala, A. Feature-rich networks: Going beyond complex network topologies. Appl. Netw. Sci. 2019, 4, 4. [Google Scholar] [CrossRef]
- Christakis, N.A. Social networks and collateral health effects. BMJ 2004, 329, 184. [Google Scholar] [CrossRef]
- Valente, T.W. Network interventions. Science 2012, 337, 49–53. [Google Scholar] [CrossRef]
- Wiesner, M.; Pfeifer, D. Health recommender systems: Concepts, requirements, technical basics and challenges. Int. J. Environ. Res. Public Health 2014, 11, 2580–2607. [Google Scholar] [CrossRef]
- Pattaraintakorn, P.; Zaverucha, G.M.; Cercone, N. Web based health recommender system using rough sets, survival analysis and rule-based expert systems. In Proceedings of the International Workshop on Rough Sets, Fuzzy Sets, Data Mining, and Granular-Soft Computing, Toronto, ON, Canada, 14–16 May 2007; pp. 491–499. [Google Scholar]
- Liang, Y. Recommender system for developing new preferences and goals. In Proceedings of the 13th ACM Conference on Recommender Systems, Copenhagen, Denmark, 16–20 September 2019; pp. 611–615. [Google Scholar]
- Vairale, V.S.; Shukla, S. Recommendation Framework for Diet and Exercise Based on Clinical Data: A Systematic Review. In Data Science and Big Data Analytics; Springer: Berlin/Heidelberg, Germany, 2019; pp. 333–346. [Google Scholar]
- Roitman, H.; Messika, Y.; Tsimerman, Y.; Maman, Y. Increasing patient safety using explanation-driven personalized content recommendation. In Proceedings of the 1st ACM International Health Informatics Symposium, Arlington, VA, USA, 11–12 November 2010; pp. 430–434. [Google Scholar]
- Wiesner, M.; Pfeifer, D. Adapting recommender systems to the requirements of personal health record systems. In Proceedings of the 1st ACM International Health Informatics Symposium, Arlington, VA, USA, 11–12 November 2010; pp. 410–414. [Google Scholar]
- Morrell, T.G.; Kerschberg, L. Personal health explorer: A semantic health recommendation system. In Proceedings of the 2012 IEEE 28th International Conference on Data Engineering Workshops, Arlington, VA, USA, 1–5 April 2012; pp. 55–59. [Google Scholar]
- Shi, C.; Zhang, Z.; Ji, Y.; Wang, W.; Philip, S.Y.; Shi, Z. SemRec: A personalized semantic recommendation method based on weighted heterogeneous information networks. World Wide Web 2019, 22, 153–184. [Google Scholar] [CrossRef]
- Wang, C.; He, X.; Zhou, A. HEEL: Exploratory entity linking for heterogeneous information networks. Knowl. Inf. Syst. 2020, 62, 485–506. [Google Scholar]
- Hu, J.; Cheng, R.; Chang, K.C.C.; Sankar, A.; Fang, Y.; Lam, B.Y. Discovering maximal motif cliques in large heterogeneous information networks. In Proceedings of the 2019 IEEE 35th International Conference on Data Engineering (ICDE), Macao, China, 8–12 April 2019; pp. 746–757. [Google Scholar]
- Shi, C.; Li, Y.; Zhang, J.; Sun, Y.; Philip, S.Y. A survey of heterogeneous information network analysis. IEEE Trans. Knowl. Data Eng. 2016, 29, 17–37. [Google Scholar] [CrossRef]
- Sun, Y.; Han, J. Mining heterogeneous information networks: Principles and methodologies. Synth. Lect. Data Min. Knowl. Discov. 2012, 3, 1–159. [Google Scholar] [CrossRef]
- Galbrun, E.; Gionis, A.; Tatti, N. Top-k overlapping densest subgraphs. Data Min. Knowl. Discov. 2016, 30, 1134–1165. [Google Scholar] [CrossRef]
- Dondi, R.; Hermelin, D. Computing the k Densest Subgraphs of a Graph. arXiv 2020, arXiv:cs.DS/2002.07695. [Google Scholar]
- Chalupa, D. Partitioning networks into cliques: A randomized heuristic approach. Inf. Sci. Technol. Bull. Acm Slovak. 2020, 6, 1–8. [Google Scholar]
- Dondi, R.; Mauri, G.; Sikora, F.; Italo, Z. Covering a graph with clubs. J. Graph Algorithms Appl. 2019, 23. [Google Scholar] [CrossRef]
- Cormen, T.H.; Leiserson, C.E.; Rivest, R.L.; Stein, C. Introduction to Algorithms, 3rd ed.; MIT Press: Cambridge, MA, USA, 2009. [Google Scholar]
- Dondi, R.; Mauri, G.; Zoppis, I. Orthology correction for gene tree reconstruction: Theoretical and experimental results. Procedia Comput. Sci. 2017, 108, 1115–1124. [Google Scholar] [CrossRef]
- Bourjolly, J.; Laporte, G.; Pesant, G. An exact algorithm for the maximum k-club problem in an undirected graph. Eur. J. Oper. Res. 2002, 138, 21–28. [Google Scholar] [CrossRef]
- Dondi, R.; Mauri, G.; Zoppis, I. On the tractability of finding disjoint clubs in a network. Theor. Comput. Sci. 2019, 777, 243–251. [Google Scholar] [CrossRef]
- Perozzi, B.; Al-Rfou, R.; Skiena, S. Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD International Conference On Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014; pp. 701–710. [Google Scholar]
- Castelli, M.; Dondi, R.; Mauri, G.; Zoppis, I. Comparing incomplete sequences via longest common subsequence. Theor. Comput. Sci. 2019, 796, 272–285. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms; Pearson Education: Bengaluru, India, 2006. [Google Scholar]
- Gong, Y.J.; Chen, W.N.; Zhan, Z.H.; Zhang, J.; Li, Y.; Zhang, Q.; Li, J.J. Distributed evolutionary algorithms and their models: A survey of the state-of-the-art. Appl. Soft Comput. 2015, 34, 286–300. [Google Scholar] [CrossRef]
- Scrucca, L. GA: A Package for Genetic Algorithms in R. J. Stat. Softw. 2013, 53, 1–37. [Google Scholar] [CrossRef]
- Bollobas, B. Random Graphs; Cambridge University Press: Cambridge, MA, USA, 2001. [Google Scholar]
- Asahiro, Y.; Miyano, E.; Samizo, K. Approximating Maximum Diameter-Bounded Subgraphs. In Proceedings of the LATIN 2010: Theoretical Informatics, 9th Latin American Symposium, Oaxaca, Mexico, 19–23 April 2010; pp. 615–626. [Google Scholar]
- Ma, H.; Zhou, D.; Liu, C.; Lyu, M.R.; King, I. Recommender systems with social regularization. In Proceedings of the Fourth ACM International Conference on Web Search and Data Mining, Hong Kong, China, 9–12 February 2011; pp. 287–296. [Google Scholar]
- Zhang, Y.; Chen, W.; Yin, Z. Collaborative filtering with social regularization for TV program recommendation. Knowl.-Based Syst. 2013, 54, 310–317. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).