Finite-Time Fault-Tolerant Control for a Robot Manipulator Based on Synchronous Terminal Sliding Mode Control

Abstract

In this paper, two finite-time active fault-tolerant controllers for a robot manipulator, which combine a synchronous terminal sliding mode control with an extended state observer, are proposed. First, an extended state observer is adopted to estimate the lumped uncertainties, disturbances, and faults. The estimation information is used to compensate the controller designed in the following step. We present an active fault-tolerant control with finite-time synchronous terminal sliding mode control, largely based on a novel finite-time synchronization error and coupling position error. We also present an active fault-tolerant control that does not use a coupling position error. By using synchronization control, the position error at each joint can simultaneously approach toward zero and toward equality, which may reduce the picking phenomenon associated with the active fault-tolerant controller strategy. Finally, simulation and experimental results for a three degree-of-freedom robot manipulator verify the effectiveness of the two proposed active fault-tolerant controllers.

1. Introduction

In robot manipulator systems, the occurrence of faults or failures in the actuators or sensors may lead to degraded robot system performance, system breakdown, and economic loss. In response to the requirements of enhanced reliability and safety, fault-tolerant control (FTC) has attracted the attention of researchers over the past few decades. FTC strategies can be divided into two main types [1]: passive FTC (PFTC) [2,3], and active FTC (AFTC) [4,5,6].

In PFTC, the ability to tolerate abnormal operation in the presence of faults/failures in components mainly depends on the robustness of the controller, which can use sliding mode control (SMC) [7,8] or adaptive control [9,10]. For example, in SMC, faults are considered to be external disturbances. To guarantee the stability of a system, knowledge of the bounded values of the faults is required in the SMC design. However, when the bounded value of a fault has a high magnitude, oscillation can occur during normal operation of a system due to the problem of high gain control. Therefore, the ability of PFTC to deal with high magnitude faults is limited. Unlike PFTC, AFTC uses the fault information from the fault estimation process to compensate the conventional controller. Fault estimation (FE) is a powerful technique that includes fault detection, fault isolation, and fault identification within a step. The accuracy of the FE highly affects the performance of AFTC, so many estimation techniques have been developed to improve FE accuracy, such as sliding mode fault estimation [11,12], the extended state observer technique [6,13], and the learning observer technique [4]. The combination of FE and a conventional controller not only helps AFTC handle faults with a high magnitude, but also overcomes the high gain control issue associated with PFTC. Most work on developing AFTC focuses on improving the FE accuracy [14,15] or increasing performance of the controller [5,16]. Those AFTC approaches have led to acceptable performance, but the slow response issue still exists, causing the picking phenomenon after a fault occurs. This strongly affects the performance of AFTC. Therefore, in this paper, using the concept of synchronization control, reduction of the picking phenomenon is addressed to increase the performance of AFTC.

Synchronization control is known as an effective controller for close-loop chain mechanism systems, such as parallel robot manipulators [17], cable-driver parallel manipulators [18,19], dual-drive gantry mechanisms [20], and cooperation robot manipulators [21]. Due to the constraints of the close-loop chain and the existence of position errors at the actuators during motion of the system, tensor internal forces may occur. This type of force is considered to be an internal uncertainty that can degrade the performance of a conventional controller. Using a synchronization controller, the position errors can simultaneously be equal and tend to zero, reducing the effect of the internal force. Therefore, the synchronization control technique can improve performance of a close-loop chain system. In an open-chain system, such as a serial robot manipulator, this kind of internal force may not exist, so the synchronization technique is not effective. However, the position errors at each joint still simultaneously approach zero when using synchronization control. In this paper, we use the synchronization technique in a fault-tolerant controller to reduce the effect of the picking phenomenon associated with the AFTC strategy (AFTCs). When a fault occurs at an actuator, a controller using the synchronization technique can make the position error at each joint equal, so the controller can quickly respond to a fault before the controller has the feedback information from the fault estimation process. Therefore, the picking phenomenon can be reduced.

In this paper, two finite-time active fault-tolerant controls for robot manipulators are proposed. Both use a synchronization technique based on the synchronous terminal sliding mode control (S-TSMC) and the extended state observer. First, to estimate lumped uncertainties, disturbances, and faults, an extended state observer (ESO) [22] is adopted. An ESO is a simple technique for estimating faults in which simply adjusting the observer parameters leads to simple application in real systems. Next, an AFTC using the synchronization technique based on terminal sliding mode control (TSMC) [23] with a novel synchronization error and coupling position error (AFTC S-TSMC1) is proposed. The novel synchronization error can approach zero in a finite time compared to the conventional coupling position error in [24]. In addition, the novel synchronization error has an advantage over the conventional error [25], because it is more closely related to other joints. Compared with existing finite-time synchronization controls, such as [26], the novel synchronization error does not lead to a singularity when the desired trajectory crosses zero. This improves the range of the robot manipulator over that in [26]. Some authors (such as in [27,28]) use graphic theory and prescribe performance control in the synchronization control. However, the conventional prescribed performance term can become a singularity during operation, and graphic theory may not be suitable for a single robot manipulator controller. The second proposed AFTC based on the synchronization technique (AFTC S-TSMC2), but without the coupling position error, is designed to improve the synchronization of the synchronous terminal sliding mode control. With the combination of ESO and the synchronization technique, the two proposed AFTC S-TSMCs can avoid the drawbacks of the PFTC strategy, and their fast response leads to a robot system that can deal with high-magnitude faults while reducing the picking phenomenon. Finally, both simulated and experimental results from the two proposed AFTCs verify the effectiveness of the two novel synchronous terminal sliding mode controllers. The contributions of this paper are summarized as follows:

(1)Two active fault-tolerant control algorithms for robot manipulators, based on novel finite-time synchronous terminal sliding mode controllers and an extended state observer, are proposed. The novel finite-time synchronization technique has the ability to make both the joint position error and the synchronization error simultaneously approach to zero. Due to these internal constraints of the synchronization control, the proposed controller can make the system quickly respond to the faults in a forward way before its feedback response after a fault estimation. Therefore, the proposed controller can reduce the occurrence of the picking phenomenon due to the slow feedback response of AFTC strategy.

(2) The novel synchronization error leads to better synchronization because it uses more information from other joints than the conventional synchronization error in [25], which has the information from only one neighbor joint.

(3) The novel coupling error can make the position error approach zero in a finite-time while the conventional coupling error in [24] cannot guarantee the finite-time convergence.

(4) Two proposed AFTCs can avoid the singularity in both the desired trajectory and the control action, while the control algorithms in [26,27,28] cannot guarantee avoiding the singularity. This ability allows increase in the workspace of the robot.

(5) Experimental results show the effectiveness of the proposed AFTC in reducing both the picking phenomenon and in handling faults of high magnitude.

The rest of this paper is organized as follows. In Section 2, the dynamic model of a robot manipulator and associated faults are presented. Fault estimation based on the extended state observer is discussed in Section 3. In Section 4, a novel synchronization error, coupling position error, and the finite-time active fault-tolerant control using a synchronous fast terminal sliding mode control are proposed. Simulation results and discussion about the effect of synchronization parameters are given in Section 5. In Section 6, the experimental results are shown to verify the effectiveness of the proposed AFTC. Finally, conclusions are given in Section 7.

2. Dynamic Model of a Robot Manipulator and Fault

The dynamics of an n-degree-of-freedom (DOF) robot manipulator are defined as:

$$\mathbf{M}(q)\ddot{q}+\mathbf{C}(q,\dot{q})\dot{q}+\mathbf{G}(q)+{\mathbf{F}}_f(\dot{q})=\tau$$

(1)

where $\ddot{q},\dot{q},q\in {\Re }^n$ are the vectors for joint acceleration, velocity, and position, respectively. $\mathbf{M}(q)\in {\Re }^{n\times n}$, $\mathbf{C}(q,\dot{q})\in {\Re }^{n\times n}$, and $\mathbf{G}(q)\in {\Re }^n$ represent the inertia matrix, the centripetal and Coriolis matrix, and the vector of gravitation force, respectively. ${\mathbf{F}}_f(\dot{q})\in {\Re }^n$ is the vector of friction term which includes a viscous friction and a dynamic friction, and $\tau \in {\Re }^n$ is the vector of torque at the joints.

In practice, the dynamic model of a robot is not known exactly, so Equation (1) can be written as:

$$(\mathbf{M}(q)+\Delta M(q))\ddot{q}+(\mathbf{C}(q,\dot{q})+\Delta C(q,\dot{q}))\dot{q}+(\mathbf{G}(q)+\Delta G(q))+({\mathbf{F}}_f(\dot{q})+\Delta F_f(\dot{q}))+\delta =\tau$$

(2)

where $\Delta M,\Delta C,\Delta G$, and $\Delta F$ are unknown dynamic uncertainties, and $\delta$ is an unknown external disturbance. $\mathbf{M}(q),\hspace{0.17em}\mathbf{C}(q,\dot{q}),\hspace{0.17em}\mathbf{G}(q)\hspace{0.17em}\mathrm{and}\hspace{0.17em}\mathbf{F}(\dot{q})$ are estimates of $\mathbf{M}(q),\mathbf{C}(q,\dot{q}),\mathbf{G}(q)\hspace{0.17em}\mathrm{and}\hspace{0.17em}\mathbf{F}(\dot{q})$. Thus, Equation (2) can be rewritten as:

$$\mathbf{M}(q)\ddot{q}+\mathbf{C}(q,\dot{q})\dot{q}+\mathbf{G}(q)+{\mathbf{F}}_f(\dot{q})+\mathsf{\psi }(q,\dot{q},\ddot{q},t)=\tau$$

(3)

where $\mathsf{\psi }(q,\dot{q},\ddot{q},t)=\Delta M\ddot{q}+\Delta C\dot{q}+\Delta G+\Delta F+\delta$.

In general, actuator faults can be divided into two types: bias faults and gain faults. In a robot manipulator, these are known as loss-of-effectiveness and lock-in-place faults. In practice, both kinds of actuator faults commonly occur. Therefore, the total torque including both kinds of actuator faults can be comprehensively described as:

$${\tau }^t=(I-\mathsf{\rho }(t))\tau +\mathbf{f}(t)\hspace{1em}(t>t_f)$$

(4)

where $\mathbf{f}(t)=diag(f_i)\in {\Re }^n$ denotes a bounded signal. $\mathsf{\rho }(t)=diag({\rho }_i(t))\in {\Re }^{n\times n}$, $0\le {\rho }_i(t)<1$ $(i=1,2,\dots ,n)$, which is unknown, denotes the remaining control rate. $I\in {\Re }^{n\times n}$ is the identity matrix, and $t_f$ is the time of occurrence of each fault.

Substituting Equation (4) into Equation (3), the dynamics model of an n-degree-of-freedom robot manipulator with actuator faults can be written as:

$$\mathbf{M}(q)\ddot{q}+\mathbf{C}(q,\dot{q})\dot{q}+\mathbf{G}(q)+{\mathbf{F}}_f(\dot{q})+\mathsf{\psi }(q,\dot{q},\ddot{q},t)=(I-\mathsf{\rho }(t))\tau +\mathbf{f}(t)$$

(5)

3. Fault Estimation Using an Extended State Observer

In this section, an extended state observer of uncertainties/disturbances and faults/failures is presented.

The dynamic model of the robot manipulator of Equation (5) can be rewritten in state space as:

$$\ddot{q}={\mathbf{M}}^{-1}(q)(\tau -\mathbf{H}(q,\dot{q}))-{\mathbf{M}}^{-1}(q)\mathsf{\zeta }(q,\dot{q},\ddot{q},\tau ,t)$$

(6)

where $\mathbf{H}(q,\dot{q})=\mathbf{C}(q,\dot{q})q+\mathbf{G}(q)+{\mathbf{F}}_f(\dot{q})$. $\mathsf{\zeta }(q,\dot{q},\ddot{q},\tau ,t)=\mathsf{\rho }(t)\tau +\mathsf{\psi }(q,\dot{q},\ddot{q},t)-\mathbf{f}(t)$ represents uncertainties/disturbances and faults/failures.

In the state space, the dynamic model of Equation (6) becomes:

$$\{\begin{array}{l}{\dot{x}}_1=x_2\\ {\dot{x}}_2=f(x_1,x_2,\tau )+\varphi (x_2,x_2,\tau ,t)\end{array}$$

(7)

where $x_1=q\in {\Re }^n$, $x_2=\dot{q}\in {\Re }^n$, $f(x_1,x_2,\tau )={\mathbf{M}}^{-1}(q)(\tau -\mathbf{H}(q,\dot{q}))$, and $\varphi (x_1,x_2,\tau ,t)=-{\mathbf{M}}^{-1}(q)\mathsf{\zeta }(q,\dot{q},\ddot{q},\tau ,t)$.

An extended state observer [22] is given as:

$$\{\begin{array}{l}{\dot{\widehat{x}}}_1={\widehat{x}}_2+\frac{{\alpha }_1}{\epsilon }(x_1-{\widehat{x}}_1)\\ {\dot{\widehat{x}}}_2=\widehat{f}(x_1,{\widehat{x}}_2,\tau )+\frac{{\alpha }_2}{{\epsilon }^2}(x_1-{\widehat{x}}_1)+\widehat{\varphi }\\ \dot{\widehat{\varphi }}=\frac{{\alpha }_3}{{\epsilon }^3}(x_1-{\widehat{x}}_1)\end{array}$$

(8)

where ${\widehat{x}}_1,{\widehat{x}}_2,\widehat{f}$, and $\widehat{\varphi }$ are estimates of $x_1,x_2,f$, and $\varphi$, respectively,${\alpha }_1,{\alpha }_2$, and ${\alpha }_3$ are positive constants, polynomial $s^3+{\alpha }_1{s}^2+{\alpha }_{2}s+{\alpha }_3$ is Hurwitz, and $0<\epsilon <1$.

The stability of system Equation (7) with observer Equation (8) is shown in [6] with the conditions $0<\epsilon <1$ and $\left|\dot{\varphi }\right|\le L$. The observer error convergence is given as:

$$\Vert \tilde{e}\Vert \le \frac{2\epsilon L\Vert PB\Vert }{{\lambda }_{\min }(Q)}$$

(9)

where $A=\left[\begin{array}{ccc}-{\alpha }_1& 1& 0\\ -{\alpha }_2& 0& 1\\ -{\alpha }_3& 0& 0\end{array}\right]\hspace{1em}and\hspace{1em}B=\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]$, and there is a symmetric positive definite matrix Q satisfying the Lyapunov equation:

$$A^{T}P+PA=-Q$$

(10)

4. Finite-Time Fault-Tolerant Control Using Synchronous Terminal Sliding Mode Control

In this section, two finite-time fault-tolerant controls based on a synchronous terminal sliding mode control are proposed.

Some definition will be useful in the rest of the paper.

Definition 1.

We define$\lceil x{\rfloor }^{\Lambda }=\left[\right|x_1{|}^{{\lambda }_1}sign(x_1),|x_2{|}^{{\lambda }_2}sign(x_2),\dots |x_n{|}^{{\lambda }_n}sign(x_n){]}^T\in {\Re }^n$, where${\lambda }_i(i=1,2,\dots ,n)>0$and$\Lambda =diag({\lambda }_i)$. $x={[x_1,x_2,\dots ,x_n]}^T\in {\Re }^n$and$y={[y_1,y_2,\dots ,y_n]}^T\in {\Re }^n$.

Definition 2.

We define$x\cdot y={\left[x_1{y}_1,x_2{y}_2,\dots ,x_n{y}_n\right]}^T\in {\Re }^n$.

Definition 3.

The time derivative of$\lceil x{\rfloor }^{\Lambda }$is$\frac{d}{dt}\lceil x{\rfloor }^{\Lambda }=\Lambda |x{|}^{\Lambda -1}·\dot{x}=\left[\lambda \right|x_1{|}^{\lambda -1}{\dot{x}}_1,\lambda |x_2{|}^{\lambda -1}{\dot{x}}_2,\dots ,\lambda |x_n{|}^{\lambda -1}{\dot{x}}_n{]}^T$, and$x^{\Lambda -I}=\left[x_1^{{\lambda }_1-1},x_2^{{\lambda }_2-1},\dots ,x_n^{{\lambda }_n-1}\right]\in {\Re }^n$, where$I=diag(1)\in {\Re }^{n\times n}$.

The novel synchronization error is defined as:

$$\begin{array}{l}{\epsilon }_1=(1+{\psi }_1{\psi }_n)e_1-{\psi }_1{e}_2-{\psi }_1{e}_n\\ {\epsilon }_2=(1+{\psi }_2{\psi }_1)e_2-{\psi }_2{e}_3-{\psi }_2{e}_1\\ ⋮\\ {\epsilon }_n=(1+{\psi }_n{\psi }_{n-1})e_n-{\psi }_n{e}_2-{\psi }_n{e}_1\end{array}$$

(11)

where $e_i(i=1,2,\dots ,n)$ is the error at each joint, and ${\psi }_i(i=1,2,\dots ,n)$ is the corresponding positive gain. In matrix form,

$$\epsilon =Te$$

(12)

where $\epsilon ={[{\epsilon }_1,{\epsilon }_2,\dots ,{\epsilon }_n]}^T\in {\Re }^n$, $e={[e_1,e_2,\dots ,e_n]}^T\in {\Re }^n$, $T\in {\Re }^{n\times n}$, and

$$T=\left[\begin{array}{ccccc}(1+{\psi }_1{\psi }_n)& -{\psi }_1& 0& \cdots & -{\psi }_1\\ -{\psi }_2& (1+{\psi }_2{\psi }_1)& -{\psi }_2& \cdots & 0\\ 0& -{\psi }_3& (1+{\psi }_3{\psi }_2)& \cdots & 0\\ ⋮& & & & \\ -{\psi }_n& -{\psi }_n& 0& \cdots & (1+{\psi }_n{\psi }_{n-1})\end{array}\right]$$

(13)

4.1. The Proposed Active Fault-Tolerant Control with Synchronous Terminal Sliding Mode Control 1 (AFTC S-TSMC1)

The novel finite-time coupling position error is defined as:

$$E=\alpha e+\beta \int \lceil \epsilon {\rfloor }^{\Lambda }dt$$

(14)

where $E={\left[E_1,E_2,\dots ,E_n\right]}^T\in {\Re }^n$, $\alpha =diag({\alpha }_i)\in {\Re }^{n\times n}$, and $\beta =diag({\beta }_i)\in {\Re }^{n\times n}$ are coupling parameters and positive $\Lambda =diag({\lambda }_i)\hspace{0.17em}0<{\lambda }_i<1$.

The synchronous terminal sliding surface is defined as:

$$S=\dot{E}+\Gamma \lceil E{\rfloor }^{\Lambda }$$

(15)

where $S={\left[S_1,S_2,\dots ,S_n\right]}^T\in {\Re }^n$, $\dot{E}={\left[{\dot{E}}_1,{\dot{E}}_2,\dots ,{\dot{E}}_n\right]}^T\in {\Re }^n$, $\Gamma =diag({\gamma }_i)\in {\Re }^{n\times n}$, and ${\gamma }_i>0$.

The proposed finite-time active fault-tolerant control is given as:

$$\tau ={\tau }_{eq}+{\tau }_0+{\tau }_{ob}$$

(16)

where ${\tau }_{eq}=\mathbf{M}(q)\left({\ddot{q}}_d+{\alpha }^{-1}\beta \Lambda {\left|\epsilon \right|}^{\Lambda -I}\cdot \dot{\epsilon }+{\alpha }^{-1}\Gamma \Lambda {\left|{\rm E}\right|}^{\Lambda -I}\cdot \dot{{\rm E}}\right)+\mathbf{H}(q,\dot{q})$, ${\tau }_0=\mathbf{M}(q)K_{1}sign(S)$, ${\tau }_{ob}=-\mathbf{M}(q)\widehat{\varphi }$, where $K_1=diag(k_{1i})\in {\Re }^{n\times n}$.

Theorem 1.

The system described in Equation (5), using the controller specified in Equation (16) guarantees that$e\to 0$ as finite-time.

Proof of Theorem 1.

The Lyapunov function can be selected as:

$$V=\frac{1}{2}{S}^{T}S$$

(17)

The time derivative of V in Equation (17) is:

$$\begin{array}{ll}\dot{V}& =S^T\dot{S}\\ & =S^T\left(\ddot{E}+\Gamma \Lambda {\left|{\rm E}\right|}^{\Lambda -1}\cdot \dot{{\rm E}}\right)\\ & =S^T\left(\alpha \left({\ddot{q}}_d-\ddot{q}\right)+\beta \Lambda {\left|\epsilon \right|}^{\Lambda -I}\cdot \dot{\epsilon }+\Gamma \Lambda {\left|{\rm E}\right|}^{\Lambda -1}\cdot \dot{{\rm E}}\right)\\ & =S^T\left(\begin{array}{l}\alpha \left(\begin{array}{l}{\ddot{q}}_d-{\mathbf{M}}^{-1}(q)\left(\tau -\mathbf{H}(q,\dot{q})\right)\\ +{\mathbf{M}}^{-1}(q)\mathsf{\zeta }(q,\dot{q},\tau ,t)\end{array}\right)+\beta \lambda {\left|\epsilon \right|}^{\Lambda -I}\cdot \dot{\epsilon }\\ +\Gamma \Lambda {\left|{\rm E}\right|}^{\Lambda -I}\cdot \dot{{\rm E}}\end{array}\right)\end{array}$$

(18)

Substituting Equation (16) into Equation (18):

$$\begin{array}{ll}\dot{V}& =-S^T\left(K_{1}sign(S)\right)\\ & \le -{\sigma }_1{V}^{\frac{1}{2}}<0\end{array}$$

(19)

where ${\sigma }_1={\lambda }_{\min }(K_1)$. When $S=0$ converges, then $E=0$ and $\dot{E}=0$, and we have:

$$\begin{array}{l}{\dot{e}}_i=-\frac{{\beta }_i}{{\alpha }_i}\lceil {\epsilon }_i{\rfloor }^{\lambda }\\ =\frac{{\beta }_i}{{\alpha }_i}{\left|(1+{\psi }_i{\psi }_{i-1})e_i-{\psi }_i{e}_{i-1}-{\psi }_i{e}_{i+1}\right|}^{\lambda }sign\left(\begin{array}{l}(1+{\psi }_i{\psi }_{i-1})e_i\\ -{\psi }_i{e}_{i-1}-{\psi }_i{e}_{i+1}\end{array}\right)\end{array}$$

(20)

The system in Equation (20) has equilibrium points at $e_i=0\hspace{0.17em}(i=1,2,\dots ,n;\hspace{0.17em}n+1=1)$. According to the definition of terminal attractors [29], we have:

$$\left|\frac{\partial {\dot{e}}_i}{\partial e_j}\right|=\frac{{\beta }_i}{{\alpha }_i}\lambda {\left|(1+{\psi }_i{\psi }_{i-1})e_i-{\psi }_i{e}_{i-1}-{\psi }_i{e}_{i+1}\right|}^{\lambda -1}\left|\frac{\partial {\epsilon }_i}{\partial e_j}\right|=\infty$$

(21)

where $j=(i-1,i,i+1)\hspace{0.17em}(i=1,2,\dots ,n)$. □

From Equation (5), we have $e_i\hspace{0.17em}\to 0(i=1,2,\dots ,n;\hspace{0.17em})$ at a finite-time. Therefore, Theorem 1 is proven.

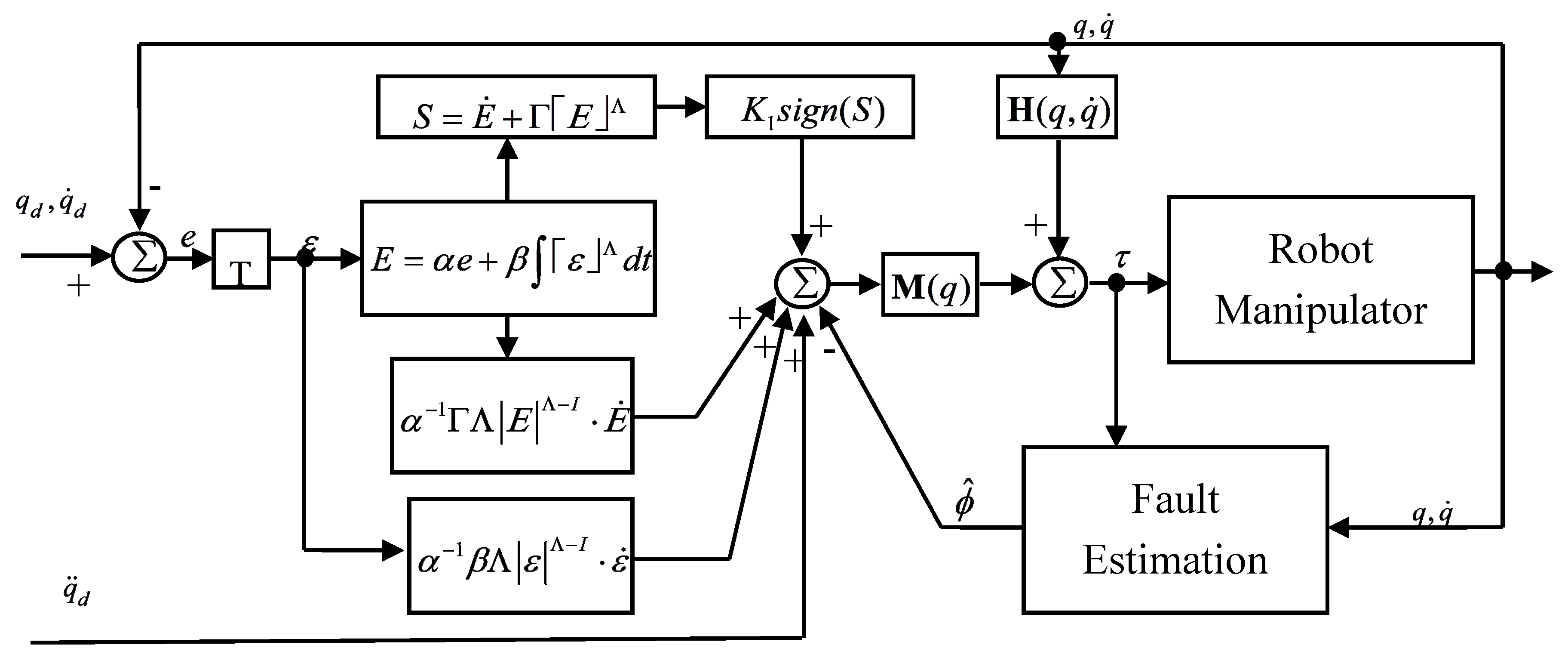
In Figure 1, the block diagram of the proposed controller AFTC-S-TSMC1 is presented. The block T in the diagram is synchronization matrix in Equation (13). The block of Fault Estimation uses the extended state observer in Equation (8). The fault estimation results were used to compensate with a novel finite-time synchronous terminal sliding mode controller 1.

Remark 1.

Time convergence from initial state to zero:

$$t=t_r+t_{s_i}+t_{e_i}$$

(22)

Time convergence$S\to 0$:

$$t_r\le \frac{2}{{\sigma }_1}\left(\ln \left({\sigma }_1{V}_0^{\frac{1}{2}}+{\sigma }_2\right)-\ln {\sigma }_2\right)$$

(23)

Time convergence$E\to 0$:

$$t_{s_i}(1)=\frac{1}{c_i(1-{\lambda }_i)}\left(\ln \left({\gamma }_i+{\sigma }_2{E}_i^{1-{\lambda }_i}(0)\right)-\ln {\gamma }_1\right)$$

(24)

Time convergence$e_i\to 0$:

$$t_{e_i}=\frac{{\alpha }_i}{{\beta }_i(1-{\lambda }_i)}{\left(a{x}_i(0)+b{x}_{i-1}(0)+c{x}_{i+1}(0)\right)}^{1-{\lambda }_i}$$

(25)

where$a=1+{\psi }_i{\psi }_{i-1},b=-{\psi }_i$and$c=-{\psi }_i$.

4.2. The Proposed Active Fault-Tolerant Control with Synchronous Terminal Sliding Mode Control 2 (AFTC S-TSMC2)

The novel synchronous terminal sliding surface:

$$\begin{array}{ll}S& =\dot{e}+\pi \lceil \epsilon {\rfloor }^{\Lambda }\\ & =\dot{e}+\pi \lceil Te{\rfloor }^{\Lambda }\end{array}$$

(26)

where $c=diag(c_i)\in {\Re }^{n\times n}$ is the positive matrix gain.

The proposed active fault-tolerant control with synchronous terminal sliding mode 2 (AFTC S-FTSMC2) is given as:

$$\tau ={\tau }_{eq}+{\tau }_0+{\tau }_{ob}$$

(27)

where ${\tau }_{eq}=\mathbf{M}(q)({\ddot{q}}_d+\pi \Lambda {\left|\epsilon \right|}^{\Lambda -I}\cdot \dot{\epsilon })+\mathbf{H}(q,\dot{q})$, ${\tau }_o=\mathbf{M}(q)K_{1}sign(S)$, ${\tau }_{ob}=-\mathbf{M}(q)\widehat{\varphi }$ and where $K_1=diag(k_{1i})\in {\Re }^{n\times n}$.

Theorem 2.

The system described in Equation (5), using the controller specified in Equation (27) guarantees that$e\to 0$as finite-time.

Proof of Theorem 2.

The Lyapunov function can be selected as:=

$$V=\frac{1}{2}{S}^{T}S$$

(28)

The time derivative of V in Equation (28) is:

$$\begin{array}{ll}\dot{V}& =S^T\dot{S}\\ & =S^T\left(\ddot{e}+\Lambda \pi {\left|\epsilon \right|}^{\Lambda -I}\cdot \dot{\epsilon }\right)\\ & =S^T\left({\ddot{q}}_d-\ddot{q}+\Lambda \pi {\left|\epsilon \right|}^{\Lambda -I}\cdot \dot{\epsilon }\right)\\ & =S^T\left(\begin{array}{l}{\ddot{q}}_d-{\mathbf{M}}^{-1}(q)\left(\tau -\mathbf{H}(q,\dot{q})\right)\\ +{\mathbf{M}}^{-1}(q)\mathsf{\zeta }(q,\dot{q},\tau ,t)+\Lambda \pi {\left|\epsilon \right|}^{\Lambda -I}\cdot \dot{\epsilon }\end{array}\right)\end{array}$$

(29)

Substituting Equation (27) into Equation (29) we have:

$$\dot{V}=-S^T{K}_{1}sign(S)\le -{\sigma }_1{V}^{\frac{1}{2}}\le 0$$

(30)

where ${\sigma }_1={\lambda }_{\min }(K_1)$. When the sliding mode achieves, the system become as Equation (20) and shown as above. Therefore, Theorem 2 is proven. □

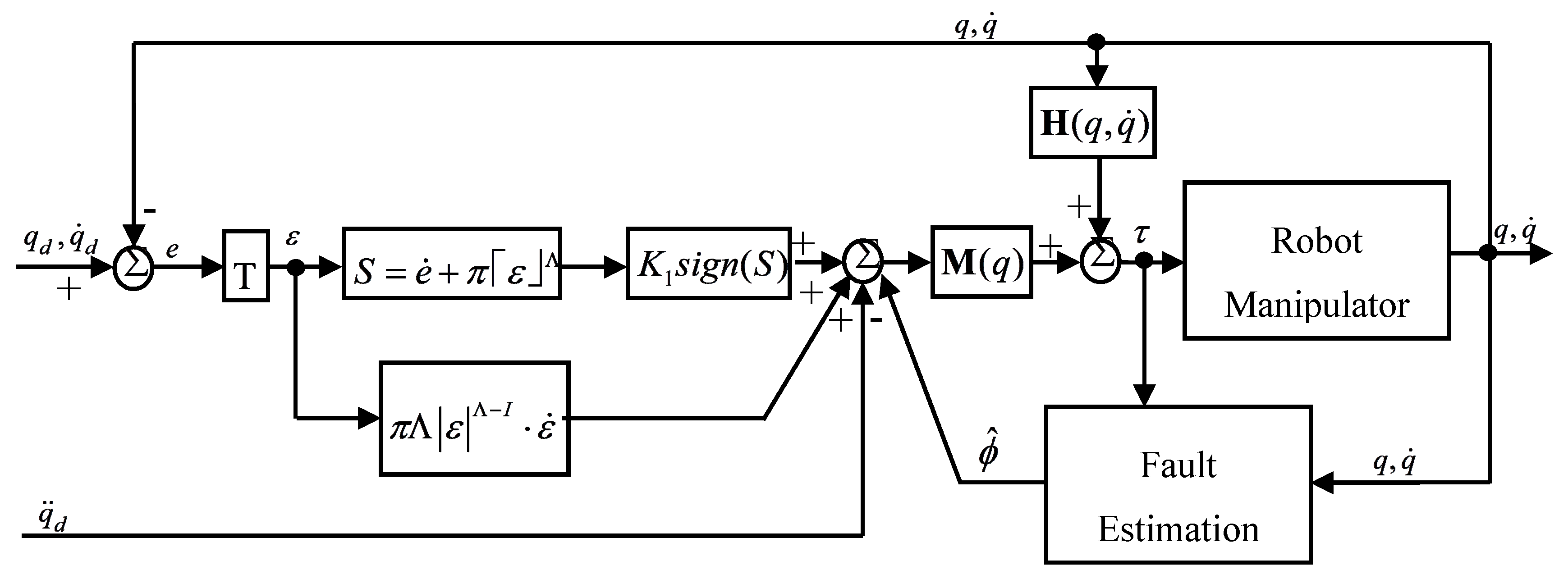
In Figure 2, the block diagram of the proposed controller AFTC-S-TSMC2 was shown. The block T is the synchronization matrix in Equation (13). The block of Fault Estimation uses the same extended state observer in Equation (8) to estimate the lumped uncertainties, disturbances and faults. Compared with the first proposed controller, the second proposed controller has less computation, and the ability to converge in a finite-time.

Remark 2.

A singularity may occur at${\left|\epsilon \right|}^{\Lambda -I}\mathrm{and}\hspace{0.17em}{\left|E\right|}^{\Lambda -I}$in Equation (17) and Equation (27) as$S$approaches zero. By using saturation function$sat(x^{\Lambda -I},u_s),x=\left|\epsilon \right|\hspace{0.17em}\mathrm{and}\hspace{0.17em}\left|E\right|$where$u_s>0$, the singularity can be avoided and the system retains finite-time stability [23].

Remark 3.

The time convergence can be shown as:

$$t=t_r+t_{e_i}$$

(31)

where $t_r$is as shown in Equation (23), and $t_{e_i}$ is as shown in Equation (25).

5. Simulation Results

In this section, the simulation results for a conventional terminal sliding mode control combined with an extended state observer([23]+ESO) and the two proposed AFTCs on a 3-DOF robot manipulator are shown and discussed. The mechanical model of the 3-DOF robot manipulator was built on the SolidWorks (Dassault Systems, Waltham, MA, USA) with the geometry parameters from the catalog of the SAMSUNG FARA-AT2 (Samsung, Namdong-gu, Incheon, Korea). Then, a robot manipulator model was exported to Matlab (MathWorks, Natick, MA, USA) simulation environment by Simmechanics toolbox. It can be seen in Figure 3, and the parameters of the robot manipulator are shown in

Table 1. Parameters of 3-DOF robot manipulator in Matlab simulation.

Links	Length (m)	Weight (kg)	Center of Mass (m)	Inertia (kg.m2)
Link 1	0.15	56.5	[−98.3 × 10−3−2.9 × 10−8−85.4 × 10−3]	[Ixx=0.39 Iyy=0.59 Izz=0.56]
Link 2	0.255	35.6	[−5.5 × 10−30.001 × 10−3−156.9 × 10−3]	[Ixx=0.76 Iyy=0.44 Izz=0.39
Link 3	0.41	58.9	[54.6 × 10−3−0.01 × 10−3 80.5 × 10−3]	[Ixx=0.22 Iyy=1.2 Izz=1.2]

.

For this trajectory tracking simulation, the desired trajectories at each joint are given as:

$$\{\begin{array}{l}{q}_{1d}=0.5\cos (t/2)-0.5\\ q_{2d}=0.3\cos (t)-0.3\\ q_{3d}=0.2\cos (t)-0.2\end{array}$$

(32)

where ${\dot{q}}_d$ and ${\ddot{q}}_d$ are the first order and second order derivatives of the desired position, respectively.

The friction at each joint was assumed to be:

$$\{\begin{array}{l}{F}_{1f}=0.2sgn({\dot{q}}_1)+0.3{\dot{q}}_1\\ F_{2f}=0.2sgn({\dot{q}}_2)+0.3{\dot{q}}_2\\ F_{3f}=0.2sgn({\dot{q}}_3)+0.3{\dot{q}}_3\end{array}$$

(33)

The total torque function at each joint was assumed to be:

$$\{\begin{array}{l}{\tau }_1^t={\tau }_1\\ {\tau }_2^t=(1-{\rho }_2(t)){\tau }_2+f_2(t)\hspace{1em}t>5\\ {\tau }_3^t={\tau }_3\end{array}$$

(34)

where ${\rho }_2(t)=0.4\sin (\pi t)$ and $f_2(t)=-80\sin (\pi t/2)$.

The related parameters for the ESO were chosen to be ${\alpha }_1=8,{\alpha }_2=28,{\alpha }_3=7$, and $\epsilon =0.01$. The controller ([23]+ESO) is given as:

$${\tau }_{[23]+ESO}={\tau }_0+{\tau }_{smc}+{\tau }_{ob}$$

(35)

where ${\tau }_{eq}=\mathbf{M}(q)({\ddot{q}}_d+c\Lambda {\left|e\right|}^{\Lambda -I}\cdot \dot{e})+\mathbf{H}(q,\dot{q})$, ${\tau }_o=\mathbf{M}(q)K_{1}sign(S)$ and ${\tau }_{ob}=-\mathbf{M}(q)\widehat{\varphi }$, where $K_1=diag(k_{1i})\in {\Re }^{n\times n}$. The sliding mode surface was selected as:

$$S=\dot{e}+c\lceil e{\rfloor }^{\Lambda }$$

(36)

The parameters for the [23]+ESO were chosen as $c=diag(7;7;7),K_1=diag(80;80;110)$, $u_s=20$, and $\Lambda =diag(0.58;0.58;0.58)$. The parameters for the AFTC S-TSMC1were chosen as ${\psi }_1={\psi }_2={\psi }_3=2$, $\alpha =diag(1;1;1)$, $\beta =diag(0.5;0.5;0.5)$, $\Lambda =diag(0.6;0.6;0.6)$, $u_s=20,$ $\Gamma =diag(7;7;7)$ and $K_1=diag(80;80;110)$. The parameters for theAFTCS-TSMC2were chosen as ${\psi }_1={\psi }_2={\psi }_3=2$, $\Lambda =diag(0.6;0.6;0.6)$, $c=diag(7;7;7)$, $u_s=20$ and $K_1=diag(80;80;110)$.

To avoid a singularity, the terms containing power $\Lambda -I$ in Equations (16),(27) and (35) are replaced with the saturation function.

$$sat(u_f,u_s)=\{\begin{array}{c}{u}_s\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{0.17em}{u}_f\ge u_s\\ u_f\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{0.17em}{u}_f<u_s\end{array}$$

(37)

where $u_s=20$ is a positive constant, and $u_f=\Lambda {\left|x\right|}^{\Lambda -I}\cdot \dot{x}$ with $x=e,\epsilon$ and E.

To avoid chattering, the signum function in Equations (16), (27) and (35) are replaced with the saturation function.

$$sat(s)=\{\begin{array}{ll}sgn(s)& if\left|s\right|\ge \lambda \\ \frac{s}{\lambda }& if\left|s\right|<\lambda \end{array}$$

(38)

where $\lambda =1.7$.

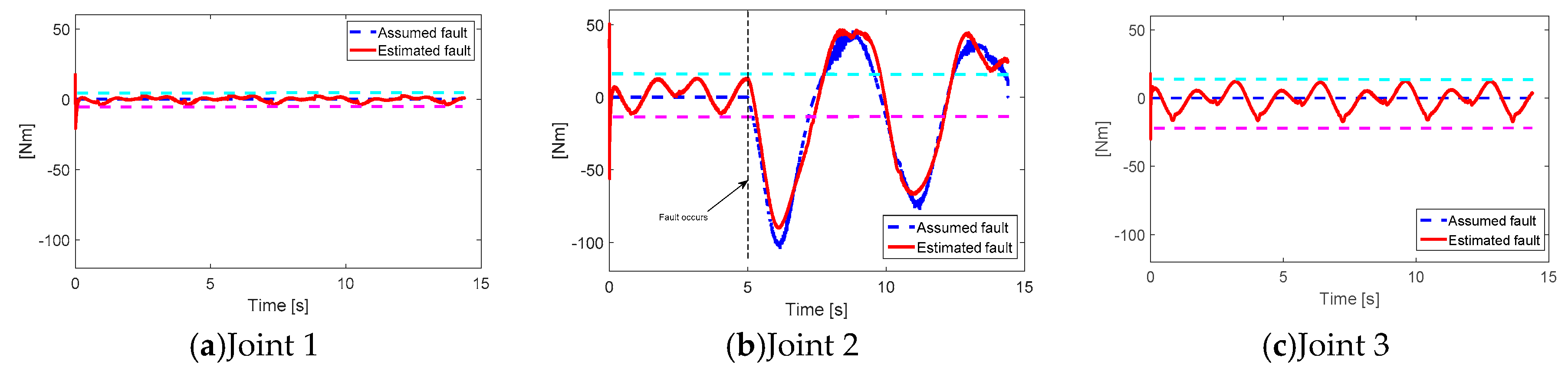
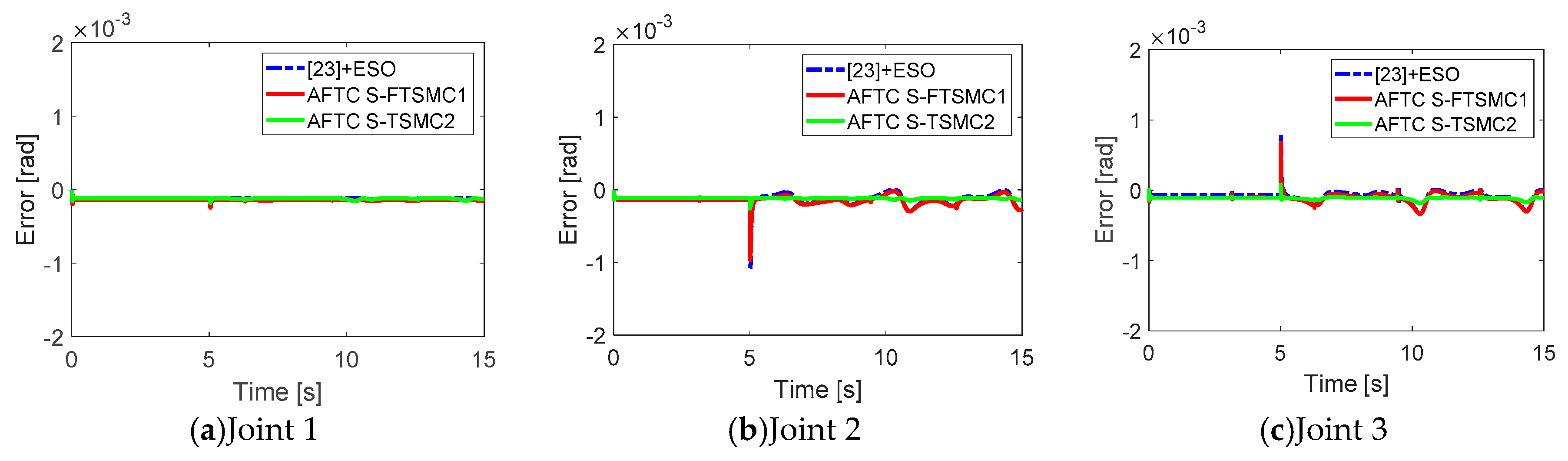
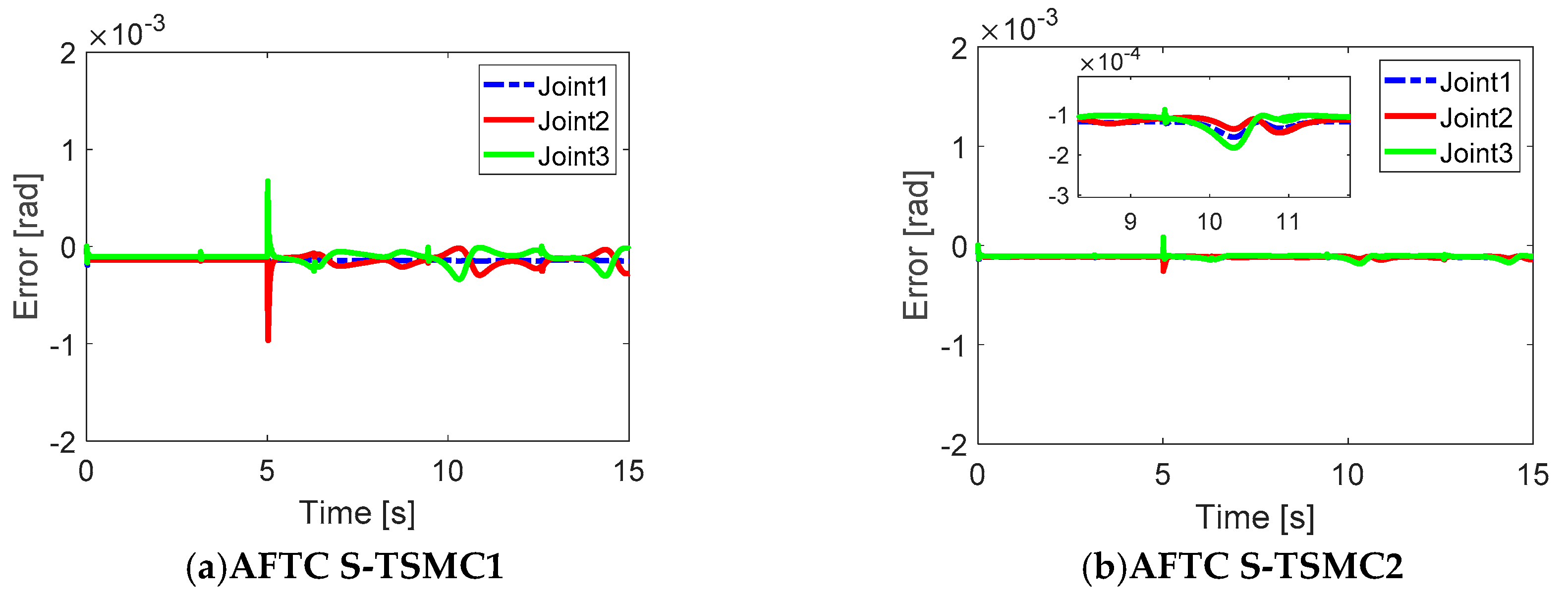
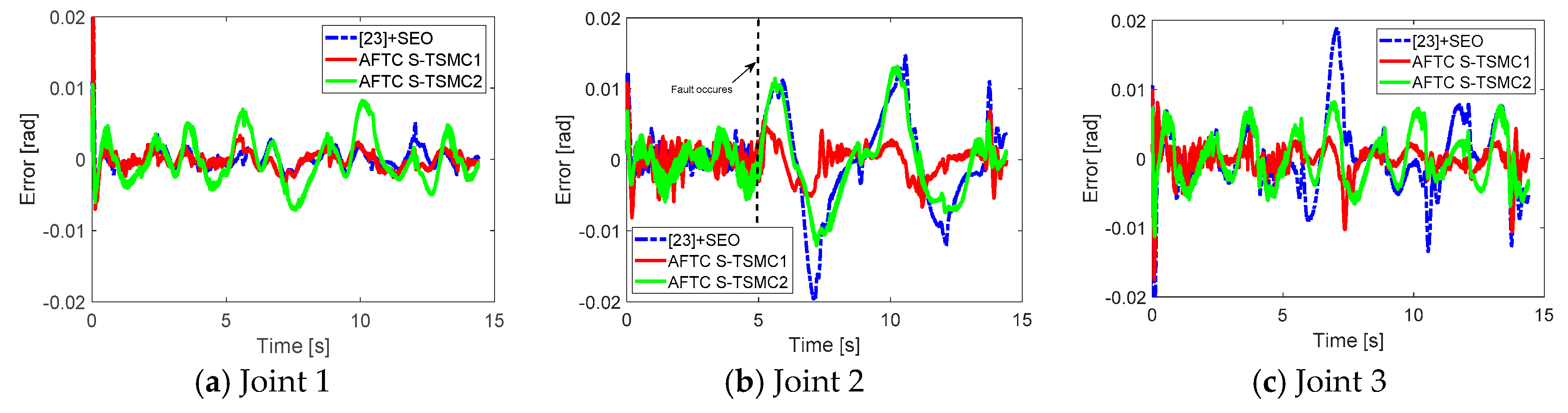
Fault estimation using the extended state observer is presented in Figure 4. The estimation error with a high fault value at joint 2 is acceptable. The error trajectory tracking results are shown in Figure 5. In general, all three controllers have an accuracy of within ${10}^{-3}$ rad, indicating that the AFTC strategy can tolerate faults, and shows acceptable performance. Now, the three controllers are discussed in more detail. It can be seen from Figure 5 that before five seconds, the errors associated with the three controllers are similar. As mentioned in Section 1, in the normal operation mode of the serial robot manipulator, there is no internal force during motion, so the synchronization technique has no effect in this case. After five seconds, it can be seen that the AFTC S-TSMC2 shows a smaller picking value than the other controller. In addition, the error characteristics seen with the AFTC S-TSMC2 are different from those seen with the other controller. This is because this controller has the ability to make the error at each joint simultaneously approach the zero of the synchronization control. However, in Figure 6, the synchronizations of AFTC S-TSMC1 and AFTC S-TSMC2 are significantly different, causing the picking value of AFTC S-TSMC2 to be smaller than the other two controllers. In controller (17), AFTC S-TSMC1 uses the coupling position error for sliding mode control. It can be seen that synchronization only occurs after the coupling position error approaches zero. Therefore, this method does not show the synchronization effect during fault compensation in fault-tolerant control. Unlike AFTC S-TSMC1, AFTC S-TSMC2 can achieve synchronization after reaching the sliding mode phase. Hence, the synchronization of the error position in AFTC S-TSMC2 is effective in fault-tolerant control. From these results and the above analysis, it can be said that the ability to reduce the picking value of AFTC S-TSMC2 is greater than AFTC S-TSMC1, due to the effective synchronization in AFTC S-TSMC2.

6. Experimental Results

In this section, implementations of the two proposed active fault-tolerant controls with a synchronous terminal sliding mode control and AFTC with a conventional terminal sliding mode control([23]+ESO) are described.

6.1. Experimental Setup

The experimental setup is shown in Figure 7 and uses a 3-DOF FARA-AT2 robot manipulator. This robot manipulator has 6-DOF, but for these experiments, joints 4, 5, and 6 were blocked. The 3-DOF FARA-AT2 robot had a CSMP series motor at each joint. The CSMP-02BB driver (Samsung, Namdong-gu, Incheon, Korea) was used for joints 1 and 2, while the CSMP-01BB driver was used for joint 3. The gear box at each joint was 120:1,120:1, and 100:1 at joints 1, 2, and 3, respectively. The encoder at each joint was a 2048 line count incremental encoder. The controller was run on Labview-FPGA, NI-PXI-8110 and NI-PXI-7842R PXI cards (National Instruments, Austin, TX, USA) with the frequency control set at 500Hz. The NI-PXI-8110 was run on a Windows operating system.

The desired trajectory at each joint is given as:

$$q_{id}(t)=\frac{\pi }{6}\sin (\frac{\pi t}{1600})(i=1,2,3)$$

(39)

The related parameters were chosen to be ${\alpha }_1=8,{\alpha }_2=28,{\alpha }_3=7$ and $\epsilon =0.01$. The [23]+ESO is given as:

$${\tau }_{[23]+ESO}={\tau }_0+{\tau }_{smc}+{\tau }_{ob}$$

(40)

where ${\tau }_{eq}=\mathbf{M}(q)({\ddot{q}}_d+c\Lambda {\left|e\right|}^{\Lambda -I}\cdot \dot{e})+\mathbf{H}(q,\dot{q})$, ${\tau }_o=\mathbf{M}(q)K_{1}sign(S)$ and ${\tau }_{ob}=-\mathbf{M}(q)\widehat{\varphi }$, where $K_1=diag(k_{1i})\in {\Re }^{n\times n}$. The sliding mode surface was selected as:

$$S=\dot{e}+c\lceil e{\rfloor }^{\Lambda }$$

(41)

The parameters for the [23]+ESO were chosen as $c=diag(7;7;7),K_1=diag(80;80;110)$, $u_s=10$ and $\Lambda =diag(0.5;0.5;0.5)$. The parameters for AFTC S-TSMC1 were chosen as ${\psi }_1={\psi }_2={\psi }_3=2$, $\alpha =diag(1;1;1)$, $\beta =diag(0.5;0.5;0.5)$, $\Lambda =diag(0.5;0.5;0.5)$, $u_s=3$, $\Gamma =diag(7;7;7)$ and $K_1=diag(80;80;110)$. The parameters for AFTC S-TSMC2 were chosen as ${\psi }_1={\psi }_2={\psi }_3=2$, $\Lambda =diag(0.5;0.5;0.5)$, $c=diag(7;7;7)$, $u_s=3$ and $K_1=diag(80;80;110)$.

To avoid a singularity, the terms containing power $\Lambda -I$ in Equations (16), (27) and (35) are replaced with the saturation function.

$$sat(u_f,u_s)=\{\begin{array}{c}{u}_s\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{0.17em}{u}_f\ge u_s\\ u_f\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{0.17em}{u}_f<u_s\end{array}$$

(42)

where $u_s$ is a positive constant, and $u_f=\Lambda {\left|x\right|}^{\Lambda -I}\cdot \dot{x}$ with $x=e,\epsilon$ and E.

To avoid chattering, the signum functions in Equations (16), (27) and (35) are replaced with the saturation function.

$$sat(s)=\{\begin{array}{ll}sgn(s)& if\left|s\right|\ge \lambda \\ \frac{s}{\lambda }& if\left|s\right|<\lambda \end{array}$$

(43)

where $\lambda =1.7$.

6.2. Experimental Results

The fault estimation results are shown in Figure 8.To reduce the high-frequency chattering and noises of fault estimation of $\widehat{\varphi }$ in Equation (8) before it is used in the AFTC scheme, a simple low-pass filter was adopted as:

$${\widehat{\varphi }}_k^{filted}=(1-\upsilon ){\widehat{\varphi }}_{k-1}^{filted}+\upsilon {\widehat{\varphi }}_k$$

(44)

where ${\widehat{\varphi }}_k^{filted}$ and ${\widehat{\varphi }}_k$ are the output and input, respectively, of the low-pass filter at the $k^{th}$ step.

The low-pass filter allowed the signal from the fault estimation (FE) to become smoother and was suitably applied to the AFTC schemes. However, the fault estimation also increased the time delay of the feedback to the controller. To ensure that the smoothness and time delay were acceptable, $\upsilon =0.05$ was selected. Unlike in the simulation, the real system included large uncertainties, so upper and lower thresholds were used to detect faults. In Figure 9, the error tracking trajectory is presented. These results show that before five seconds, the error values at each joint were similar. However, after five seconds, due to the effects of synchronization control, the errors at each joint were different. Unlike in the simulation results, these experimental results show that AFTC S-TSMC1 is more effective than AFTC S-TSMC2. In a real system with large uncertainties and noise, the coupling position error in AFTC S-TSMC1 with the integral term may affect how uncertainties are handled. In general, both proposed AFTCs can reduce the picking phenomenon, but the effect of each controller is different, and depends on its knowledge of the system.

7. Conclusions

In this paper, two finite-time active fault-tolerant controllers for a robot manipulator which combine a novel synchronous terminal sliding mode control with an extended state observer were proposed. The proposed controller can make the system quickly respond to the faults in a forward way before its feedback response after a fault estimation. This characteristic of two proposed controllers can reduce the occurrence of a picking phenomenon, due to the slow response of an active fault-tolerant control strategy. In addition, a novel synchronization error, coupling position error, and synchronous terminal sliding surface show better features such as better synchronization, avoiding the singularities when the trajectories cross zero, increasing the workspace of a robot, and finite-time convergence of the position errors. However, it should be noted that the effectiveness of the synchronization techniques depends on their knowledge of the system. The proposed active fault-tolerant control with synchronous terminal sliding mode control 2 performs better in a well-known system, while the proposed active fault-tolerant control with synchronous terminal sliding mode control 1is more effective when the system has large uncertainties and noises. In the future work, the optimal tuning synchronization parameters will be studied with methods such as the genetic algorithm and neural network technique, to improve the effectiveness of synchronization technique in a fault-tolerant control.