Numerical Simulation for Fractional-Order Bloch Equation Arising in Nuclear Magnetic Resonance by Using the Jacobi Polynomials
Abstract
1. Introduction
2. Preliminaries
3. Construction of Algorithm
4. Convergence Analysis
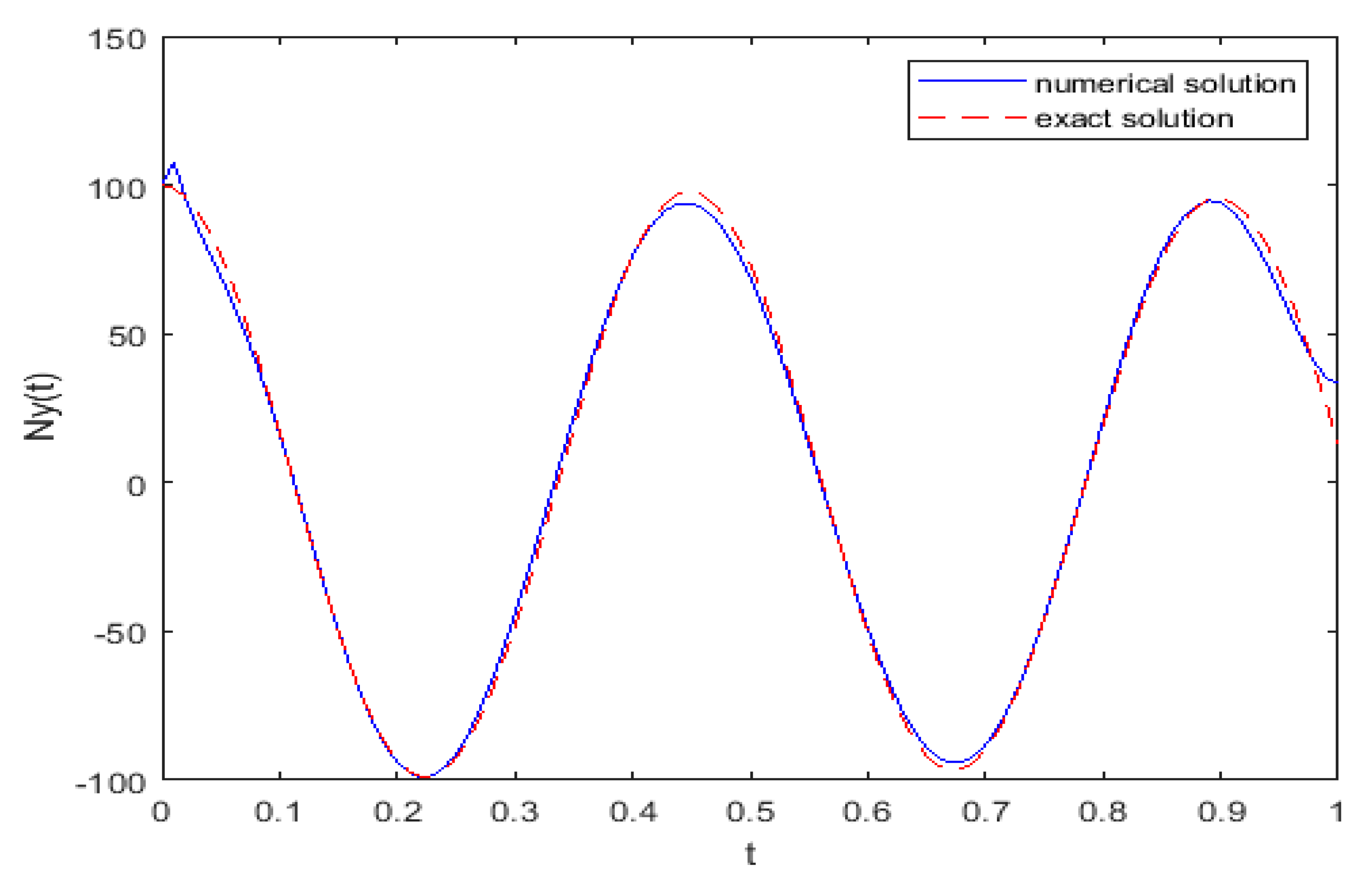
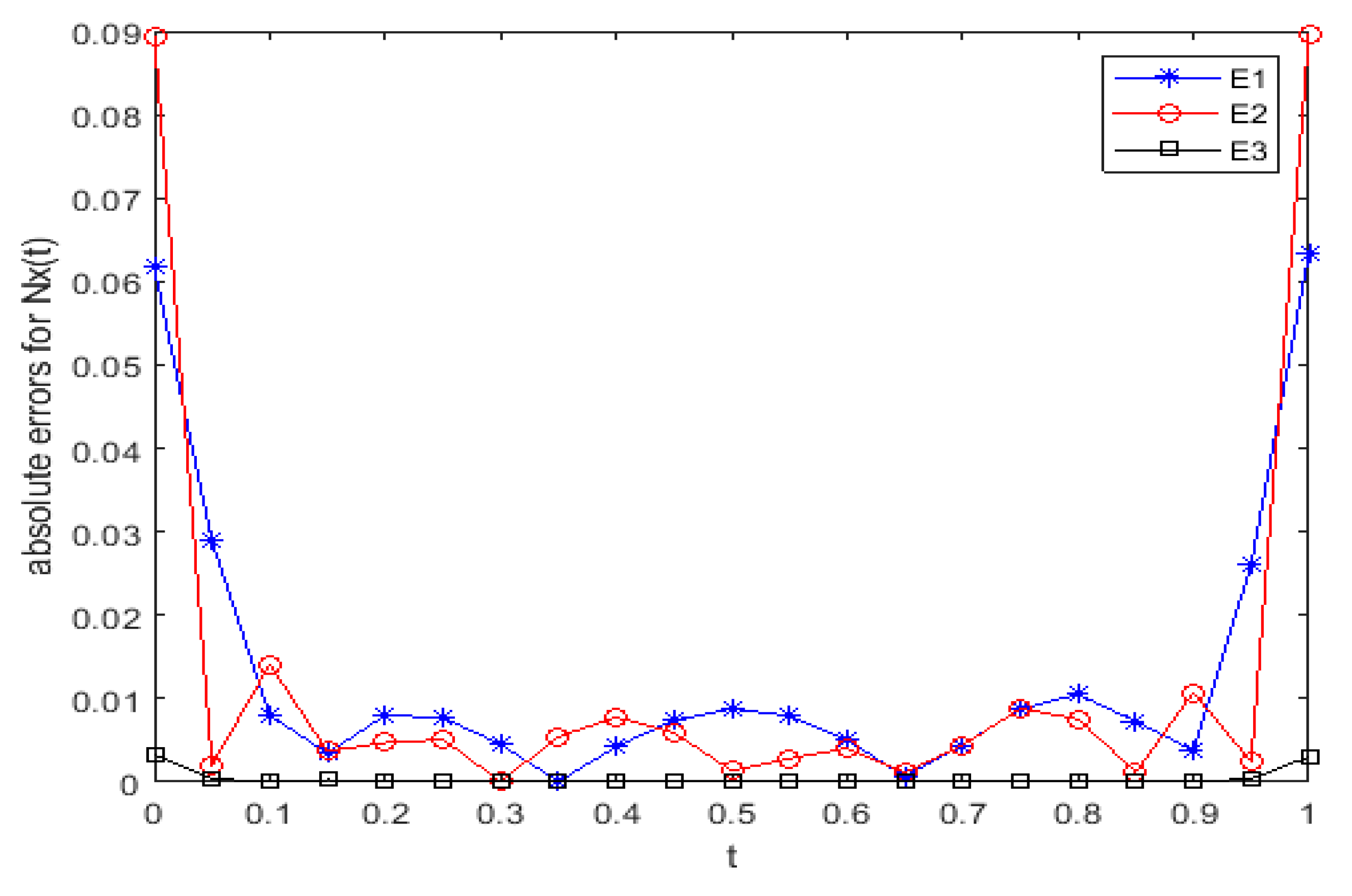
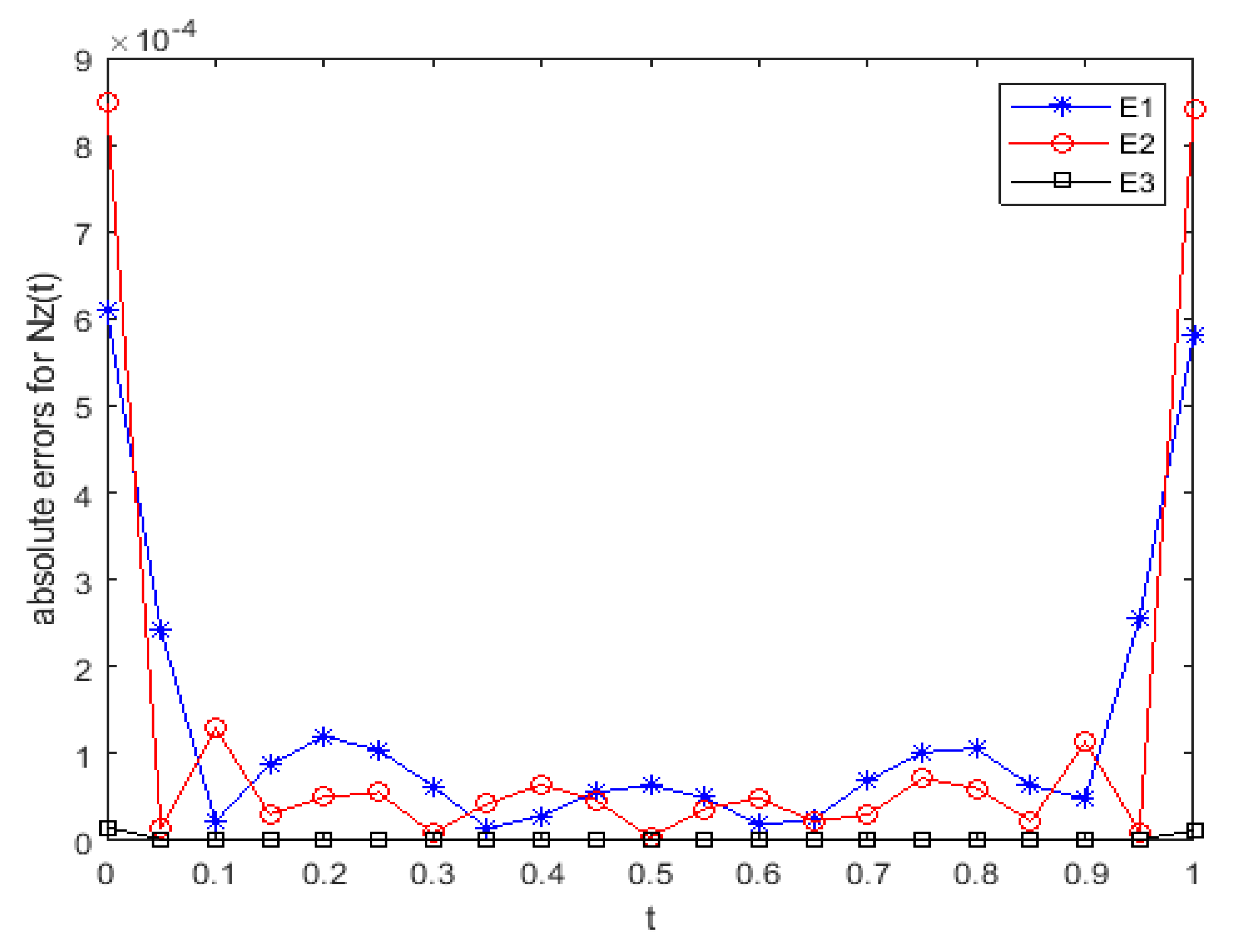
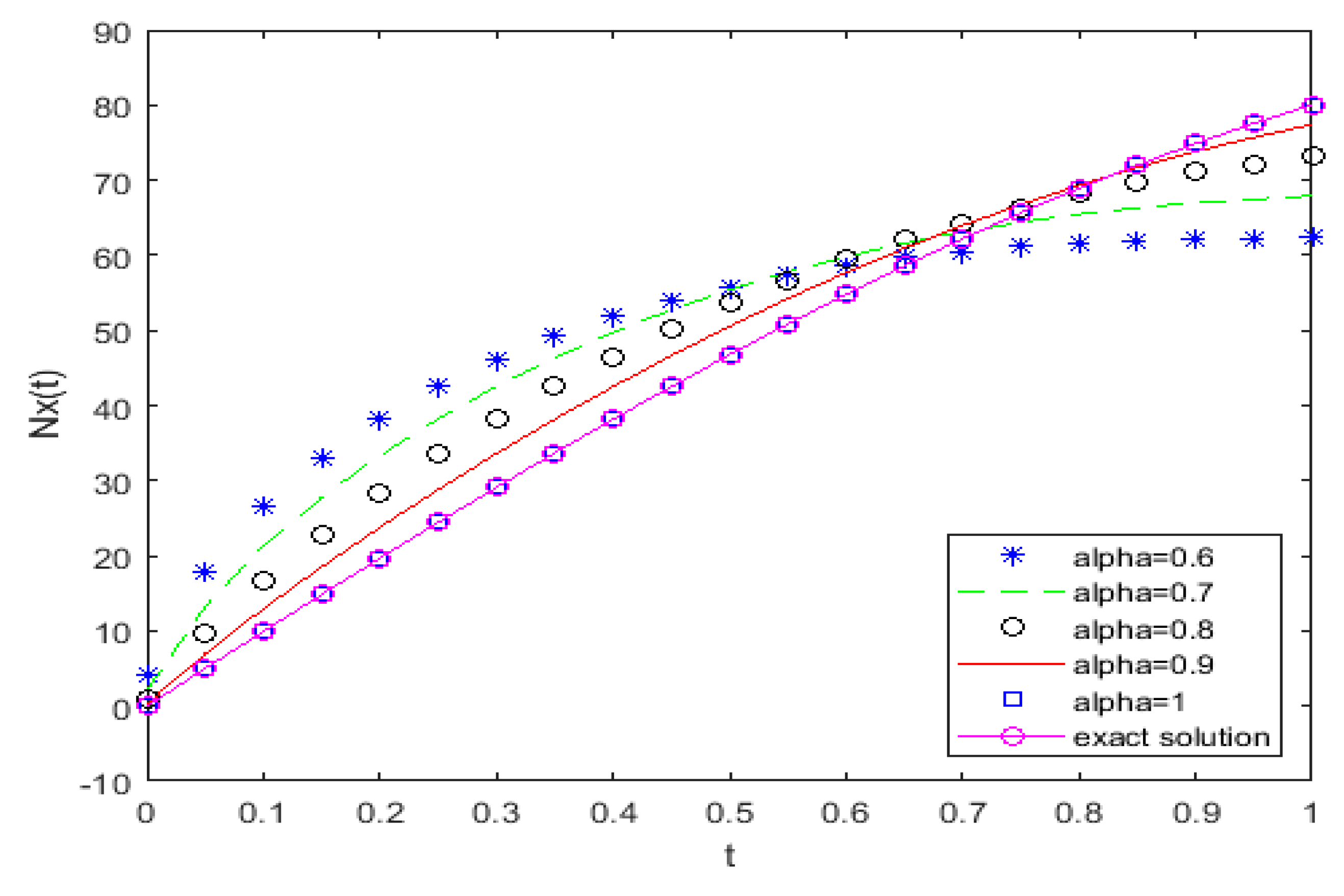
5. Numerical Results and Discussion
6. Conclusions and Future Scope
Author Contributions
Funding
Conflicts of Interest
References
- Bagley, R.L.; Torvik, P.J. A theoretical basis for the application of fractional calculus to viscoelasticity. J. Rheol. 1983, 27, 201–210. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Shah, F.A.; Abass, R. An application of the Gegenbauer wavelet method for the numerical solution of the fractional Bagley-Torvik equation. Russ. J. Math. Phys. 2019, 26, 77–93. [Google Scholar] [CrossRef]
- Bagley, R.L.; Torvik, P.J. Fractional calculus in the transient analysis of viscoelasticity damped structures. AIAA J. 1985, 23, 918–925. [Google Scholar] [CrossRef]
- Robinson, A.D. The use of control systems analysis in neurophysiology of eye movements. Annu. Rev. Neurosci. 1981, 4, 462–503. [Google Scholar] [CrossRef] [PubMed]
- Singh, H. A new stable algorithm for fractional Navier-Stokes equation in polar coordinate. Int. J. Appl. Comput. Math. 2017, 3, 3705–3722. [Google Scholar] [CrossRef]
- Bohannan, G.W. Analog fractional order controller in temperature and motor control applications. J. Vib. Control 2008, 14, 1487–1498. [Google Scholar] [CrossRef]
- Panda, R.; Dash, M. Fractional generalized splines and signal processing. Signal Process 2006, 86, 2340–2350. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Li, X. Numerical solution of fractional partial differential equations using cubic B-spline wavelet collocation method. Adv. Comput. Math. Appl. 2012, 1, 159–164. [Google Scholar]
- Daftardar-Gejji, V.; Bhalekar, S. Solving fractional diffusion-wave equations using a new iterative method. Fract. Calc. Appl. Anal. 2008, 11, 193–202. [Google Scholar]
- Awojoyogber, O.B. Analytical solution of the time dependent Bloch NMR, flow equations: A translational mechanical analysis. Phys. A Stat. Mech. Appl. 2004, 339, 437–460. [Google Scholar] [CrossRef]
- Murase, K.; Tanki, N. Numerial solution to the time dependent Bloch equations revisited. Magn. Reson. Imaging 2011, 29, 126–131. [Google Scholar] [CrossRef] [PubMed]
- Leyte, J.C. Some solutions of the Bloch equations. Chem. Phys. Lett. 1990, 165, 231–240. [Google Scholar] [CrossRef]
- Yan, H.; Chen, B.; Gore, J.C. Approximate solutions of the Bloch equations for selective excitation. J. Magn. Reson. 1987, 75, 83–95. [Google Scholar] [CrossRef]
- Hoult, D.I. The solution of the Bloch equation in presence of varying B 1 field—An approach to selective pulse analysis. J. Magn. Reson. 1979, 35, 69–86. [Google Scholar] [CrossRef]
- Xu, Z.; Chan, A.K. A Near-Resonance solution to the Bloch equations and its application to RF pulse design. J. Magn. Reson. 1999, 138, 225–231. [Google Scholar] [CrossRef]
- Magin, R.; Feng, X.; Baleanu, D. Solving the fractional order Bloch Equation. Concepts Magn. Reson. Part A 2009, 34, 16–23. [Google Scholar] [CrossRef]
- Kumar, S.; Faraz, N.; Sayevand, K. A fractional model of Bloch equation in NMR and its analytic approximate solution. Walailak J. Sci. Technol. 2014, 11, 273–285. [Google Scholar]
- Singh, H. A New Numerical Algorithm for Fractional Model of Bloch equation in nuclear magnetic resonance. Alex. Eng. J. 2016, 55, 2863–2869. [Google Scholar] [CrossRef]
- Singh, H. Operational matrix approach for approximate solution of fractional model of Bloch equation. J. King Saud Univ. Sci. 2017, 29, 235–240. [Google Scholar] [CrossRef]
- Petráš, L. Modeling and numerical analysis of fractional-order Bloch equations. Comput. Math. Appl. 2011, 61, 341–356. [Google Scholar] [CrossRef]
- Ahmadian, A.; Chan, C.S.; Salahshour, S.; Vaitheeswaran, V. FTFBE: A numerical approximation for fuzzy time-fractional Bloch equation. In Proceedings of the International conference on fuzzy systems (FUZZ-IEEE), World Congress on Computational Intelligence, Beijing, China, 6–11 July 2014; pp. 418–423. [Google Scholar]
- Wu, J.L. A wavelet operational method for solving fractional partial differential equations numerically. Appl. Math. Comput. 2009, 214, 31–40. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.M.; Kumar, D. A reliable numerical algorithm for the fractional vibration equation. Chaos Solitons Fractals 2017, 103, 131–138. [Google Scholar] [CrossRef]
- Tohidi, E.; Bhrawy, A.H.; Erfani, K. A collocation method based on Bernoulli operational matrix for numerical solution of generalized pantograph equation. Appl. Math. Model. 2013, 37, 4283–4294. [Google Scholar] [CrossRef]
- Kazem, S.; Abbasbandy, S.; Kumar, S. Fractional order Legendre functions for solving fractional-order differential equations. Appl. Math. Model. 2013, 37, 5498–5510. [Google Scholar] [CrossRef]
- Singh, C.S.; Singh, H.; Singh, V.K.; Singh, O.P. Fractional order operational matrix methods for fractional singular integro-differential equation. Appl. Math. Model. 2016, 40, 10705–10718. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.M. Jacobi collocation method for the approximate solution of some fractional-order Riccati differential equations with variable coefficients. Phys. A Stat. Mech. Appl. 2019, 523, 1130–1149. [Google Scholar] [CrossRef]
- Singh, C.S.; Singh, H.; Singh, S.; Kumar, D. An efficient computational method for solving system of nonlinear generalized Abel integral equations arising in astrophysics. Phys. A Stat. Mech. Appl. 2019, 525, 1440–1448. [Google Scholar] [CrossRef]
- Singh, H.; Pandey, R.K.; Baleanu, D. Stable numerical approach for fractional delay differential equations. Few-Body Syst. 2017, 58, 156. [Google Scholar] [CrossRef]
- Srivastava, H.M. Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J. 2020, 60, 73–116. [Google Scholar]
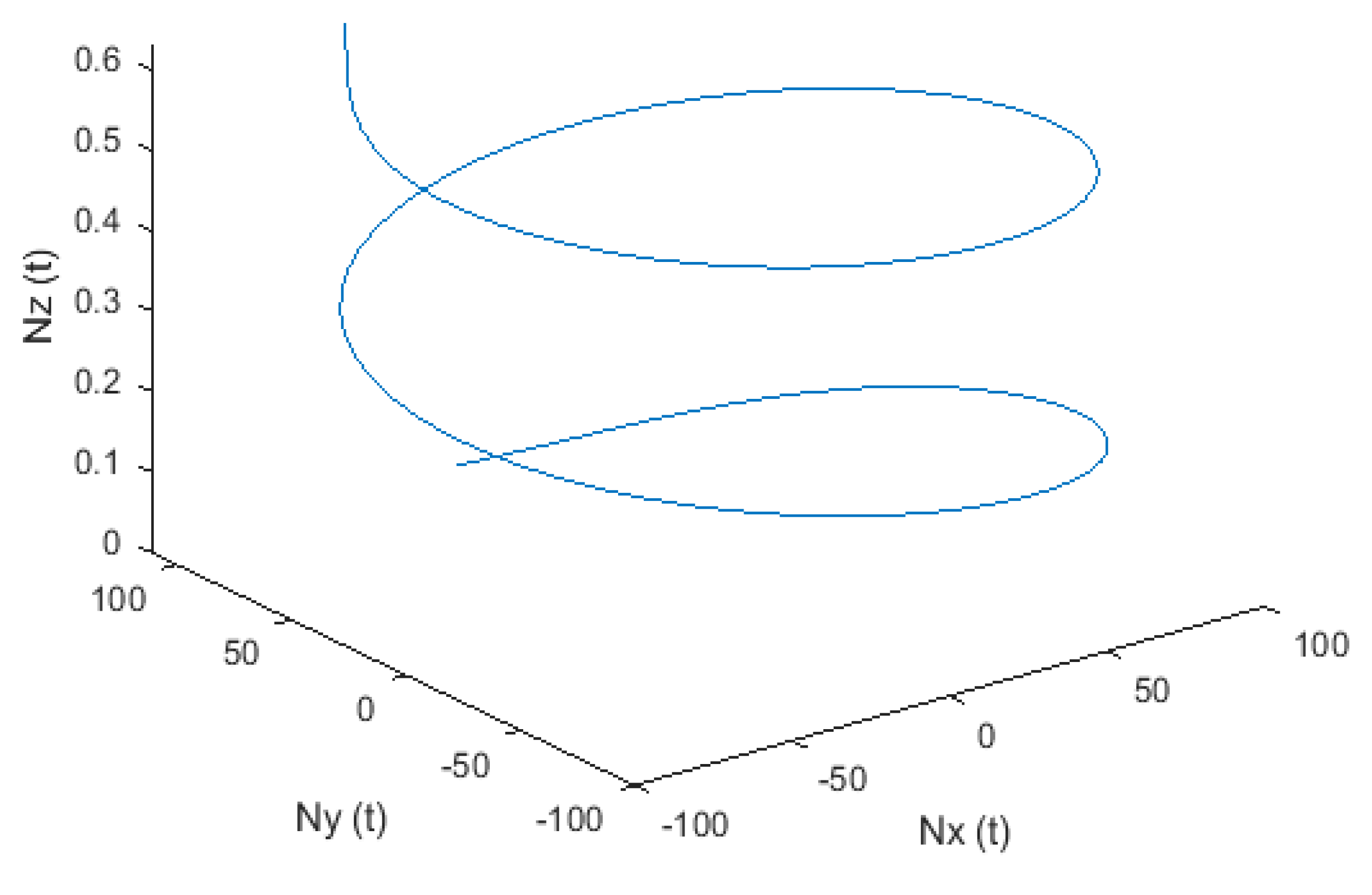
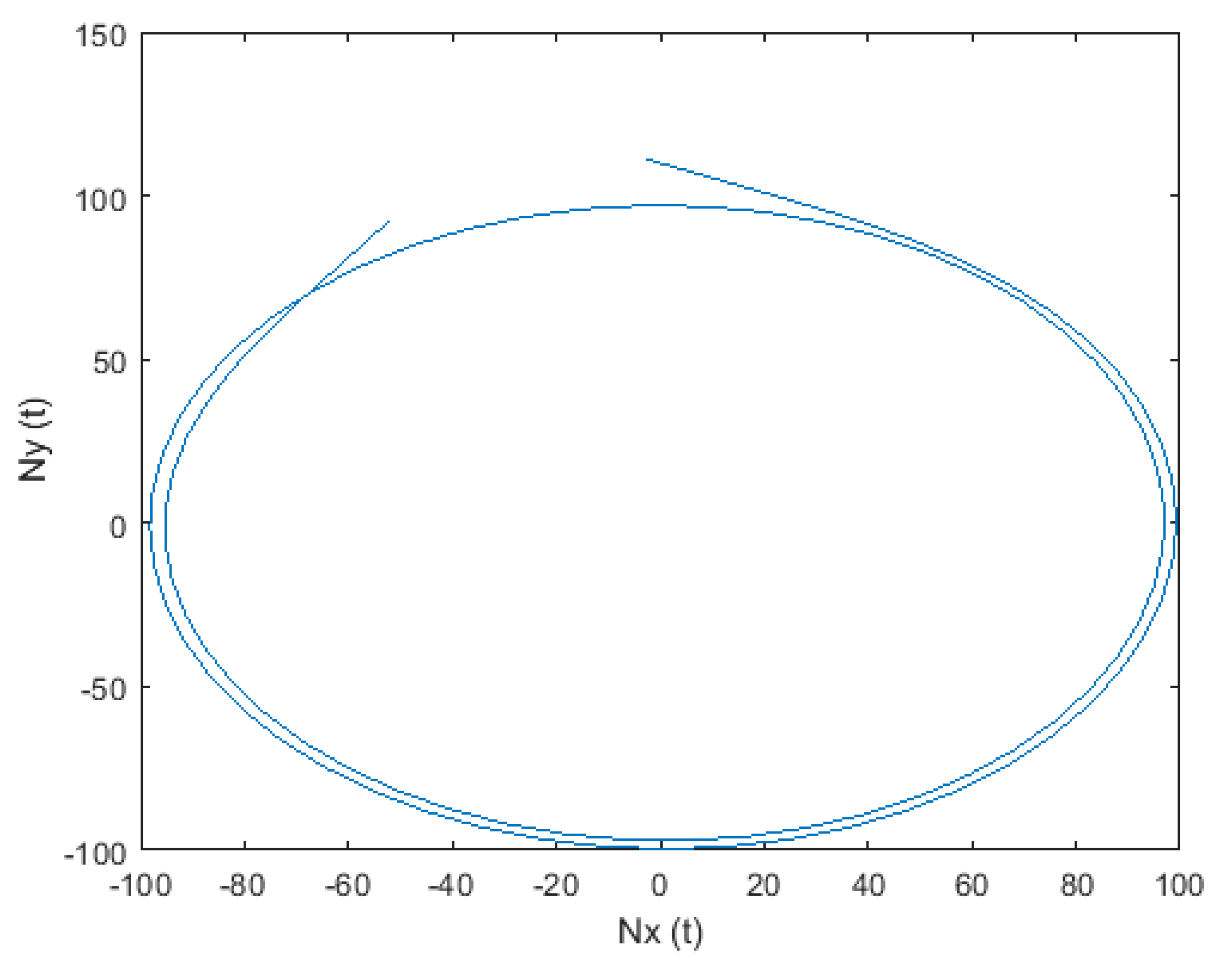

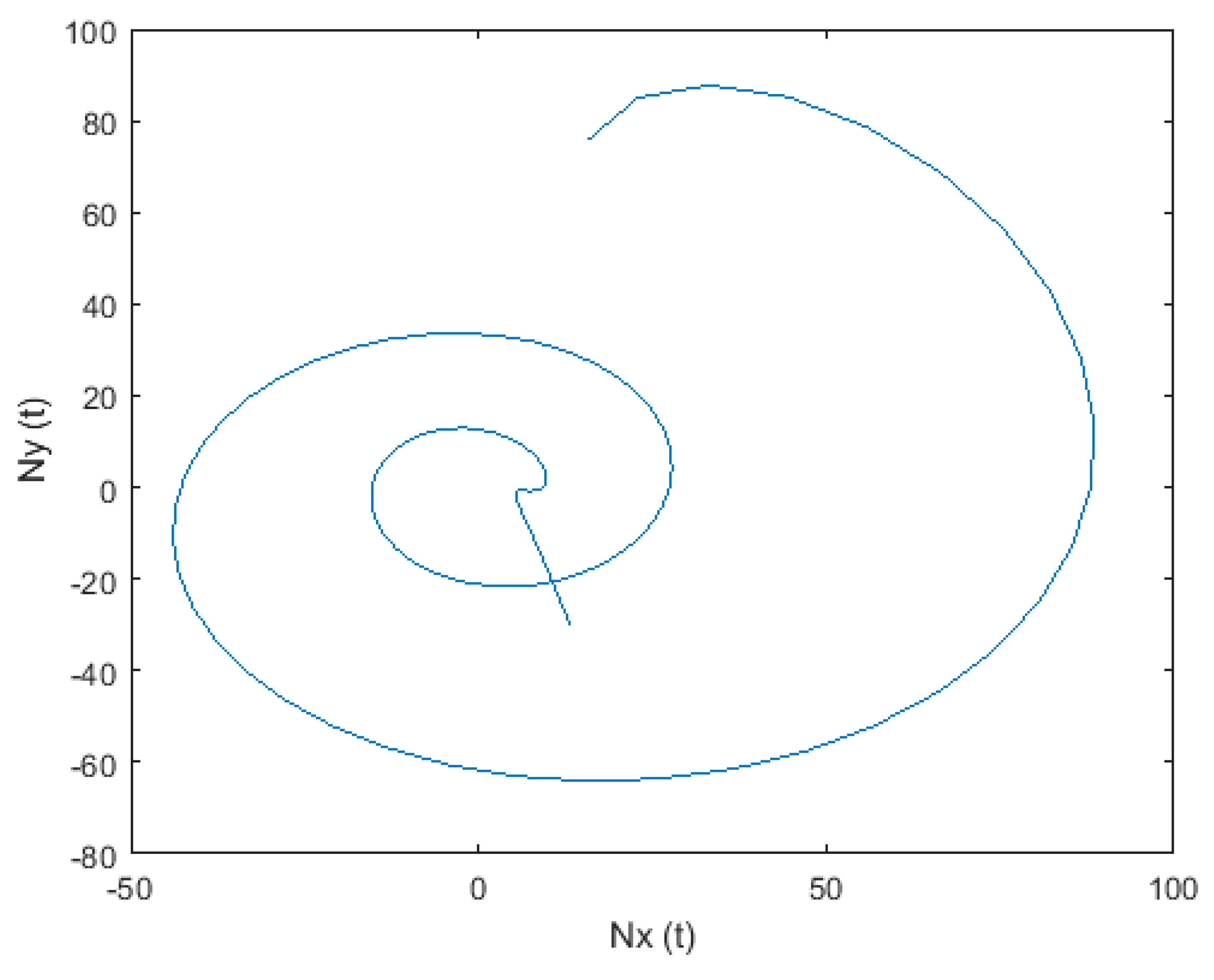
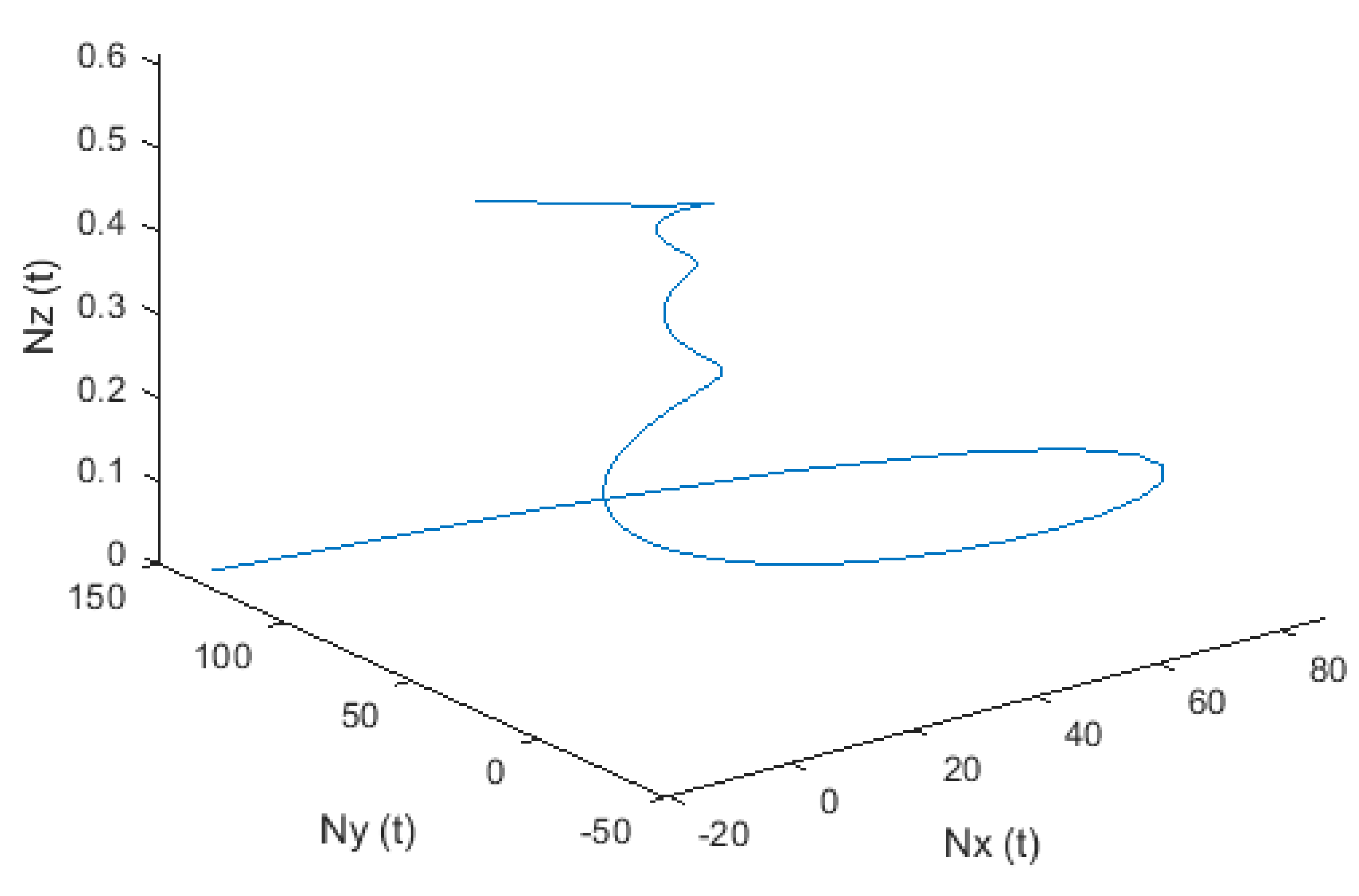
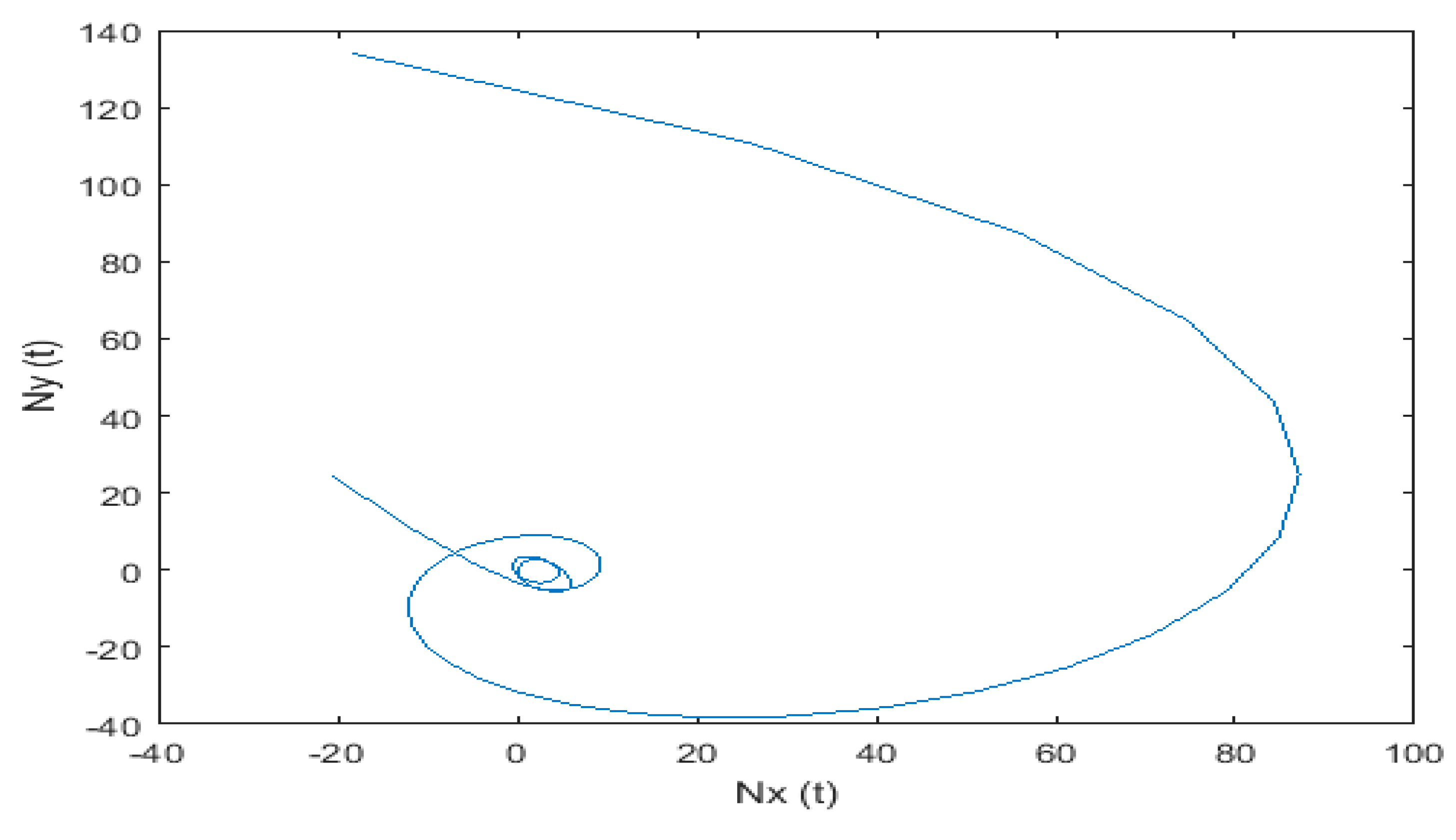
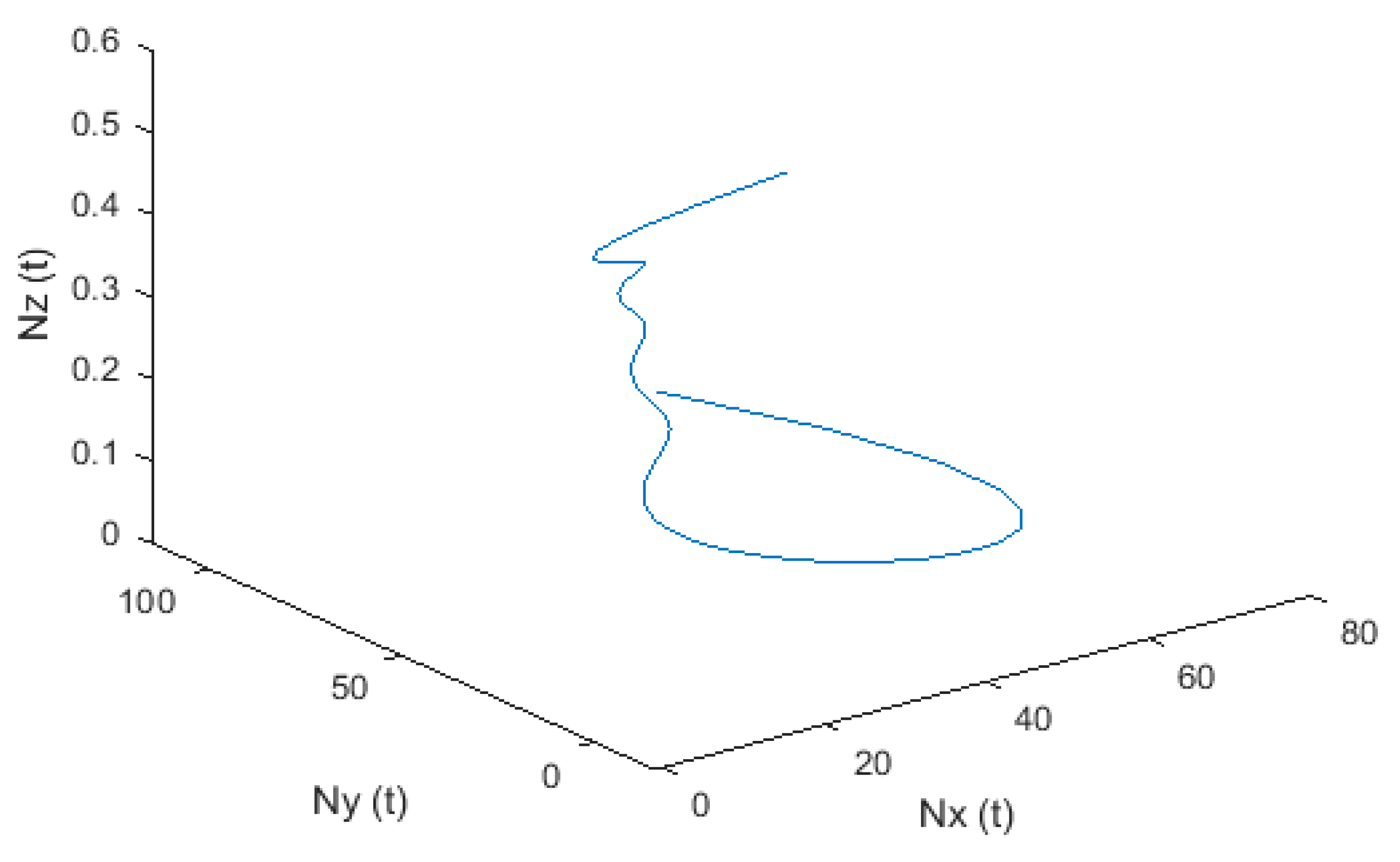

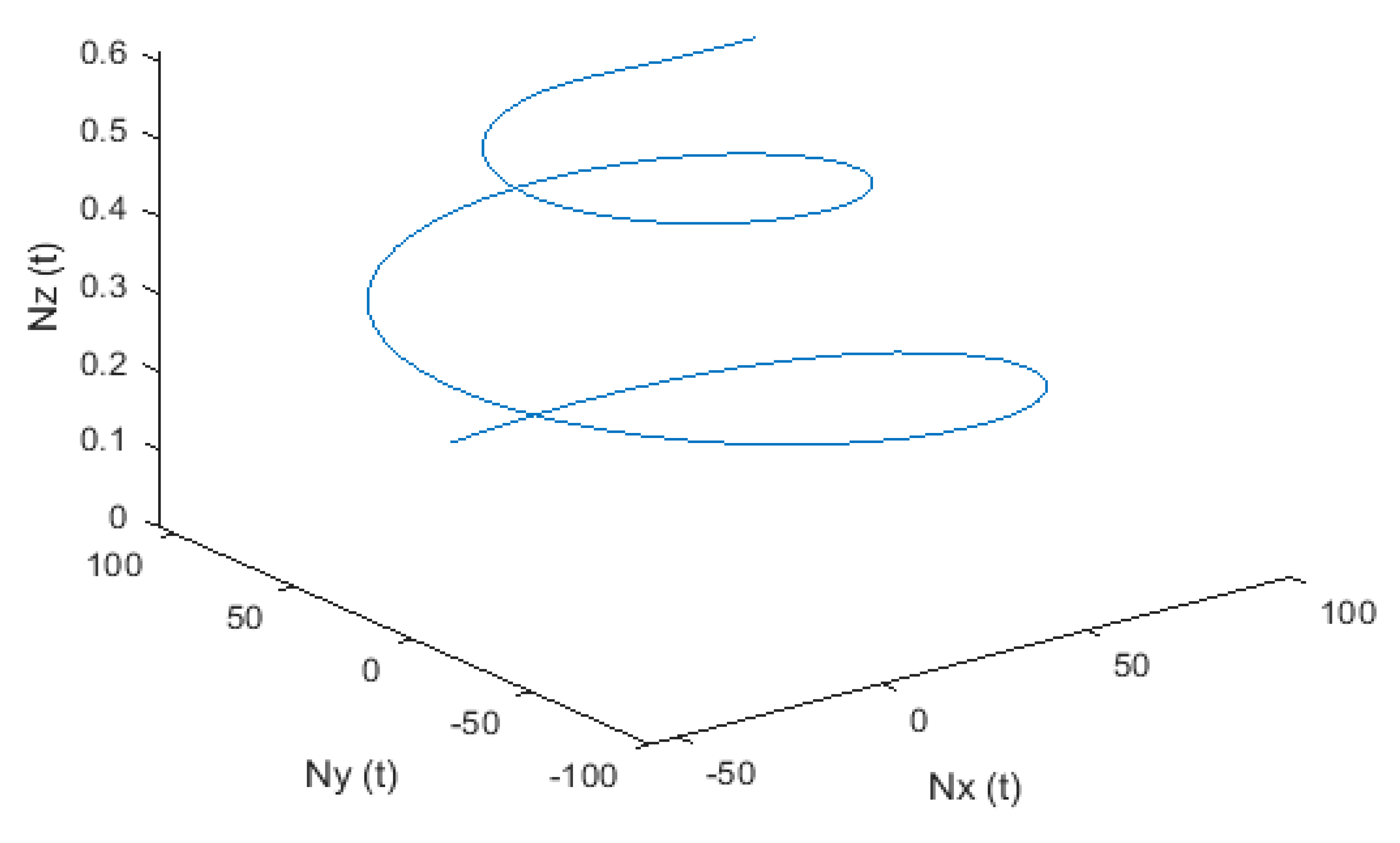
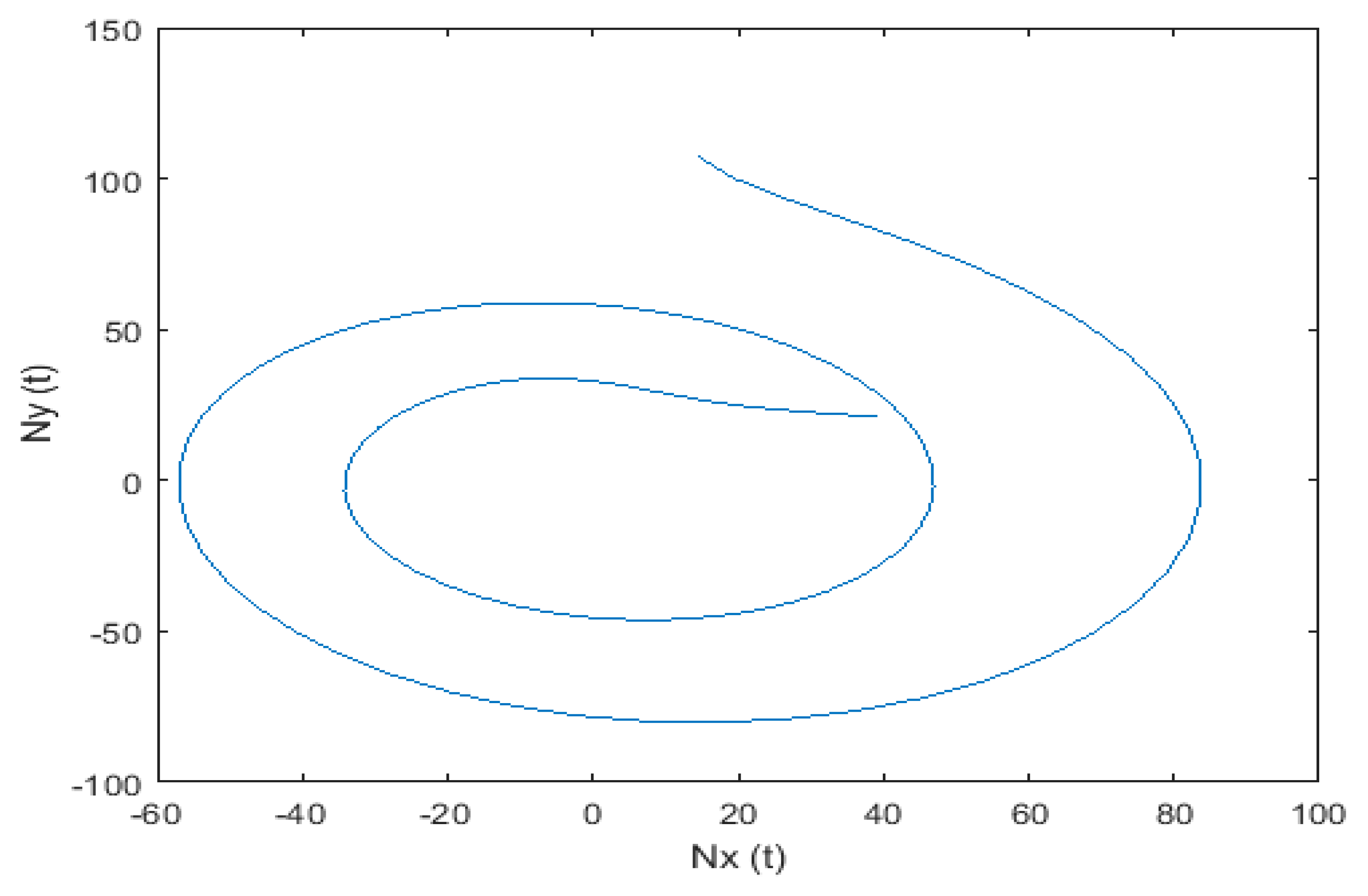
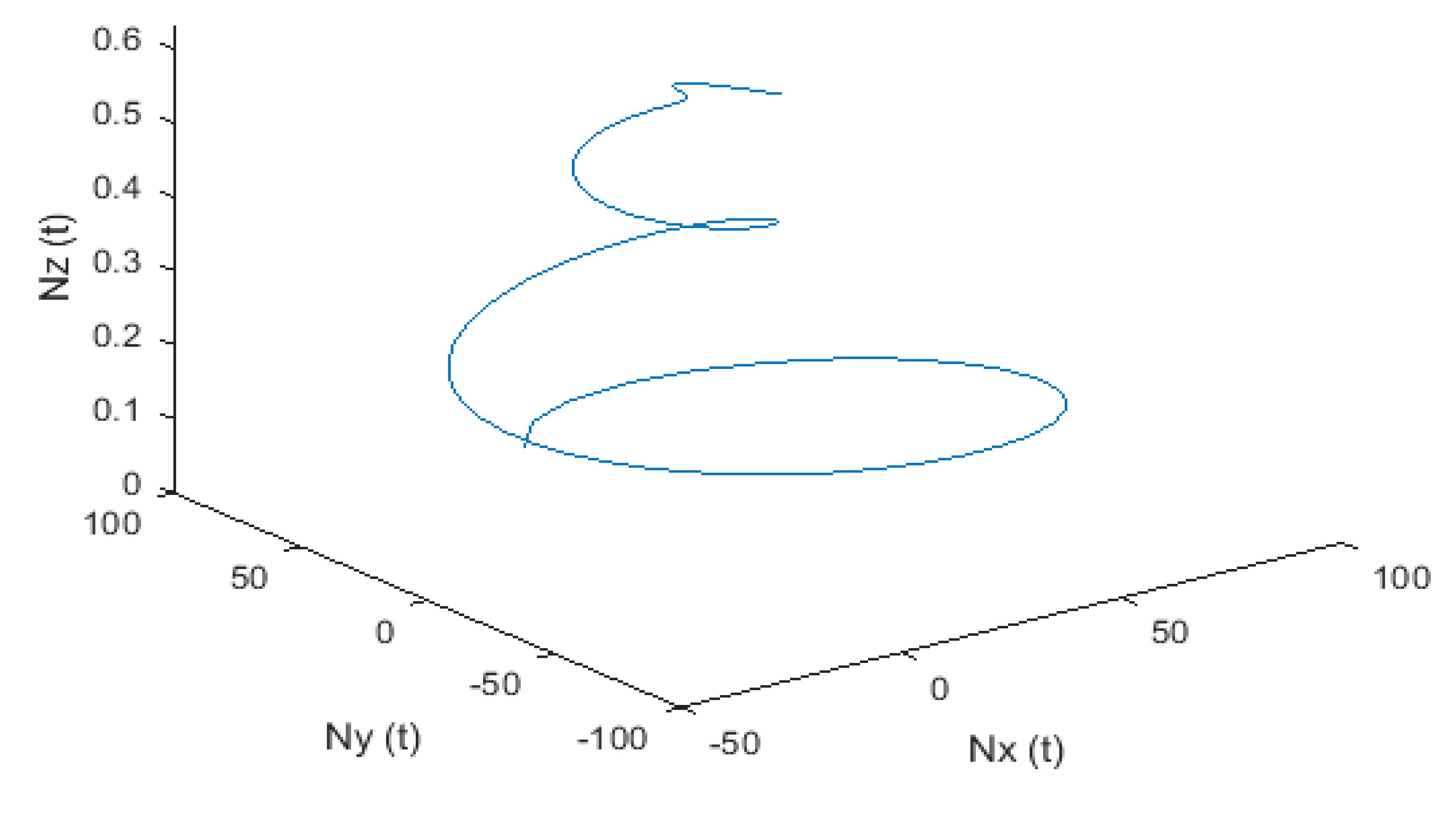
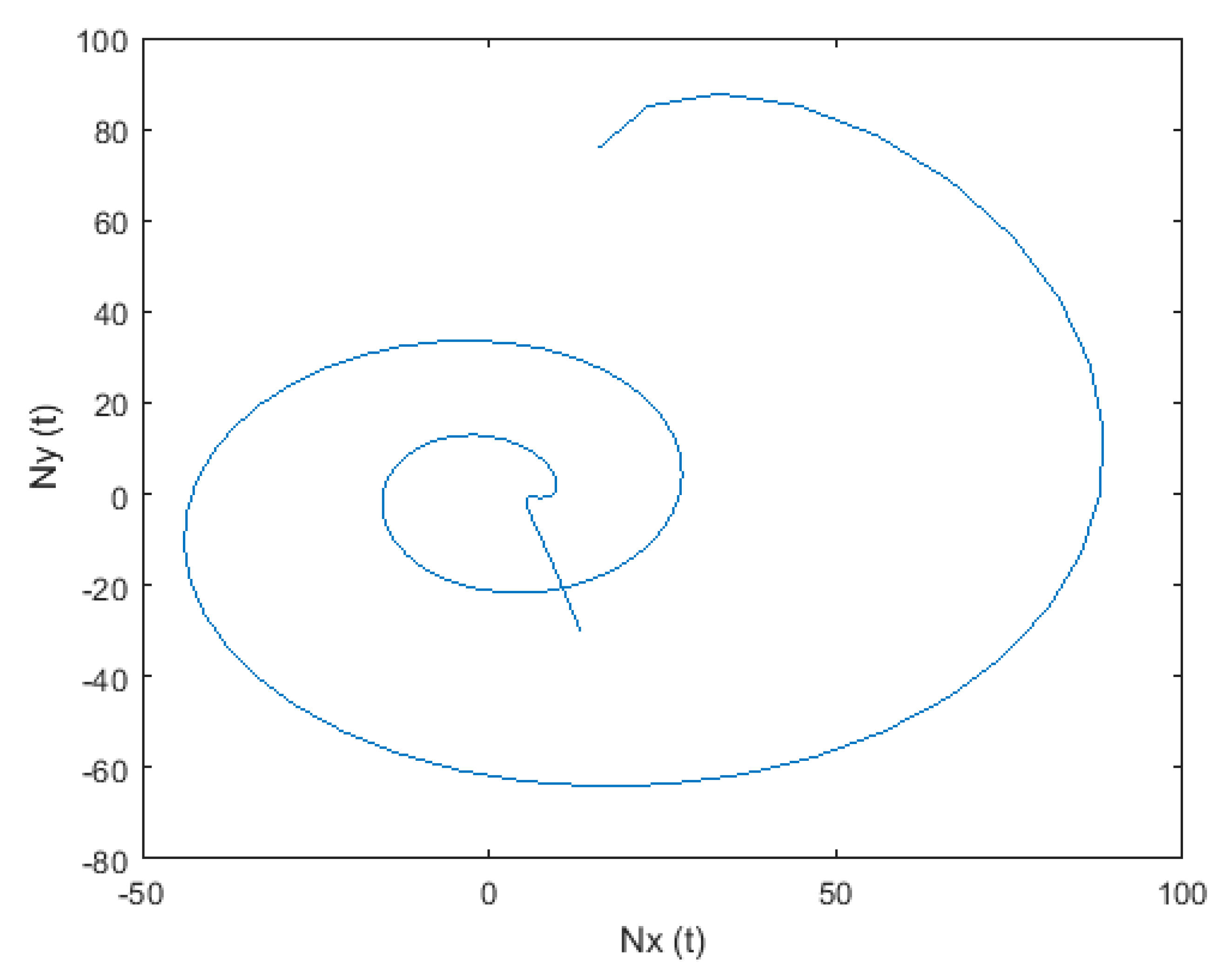

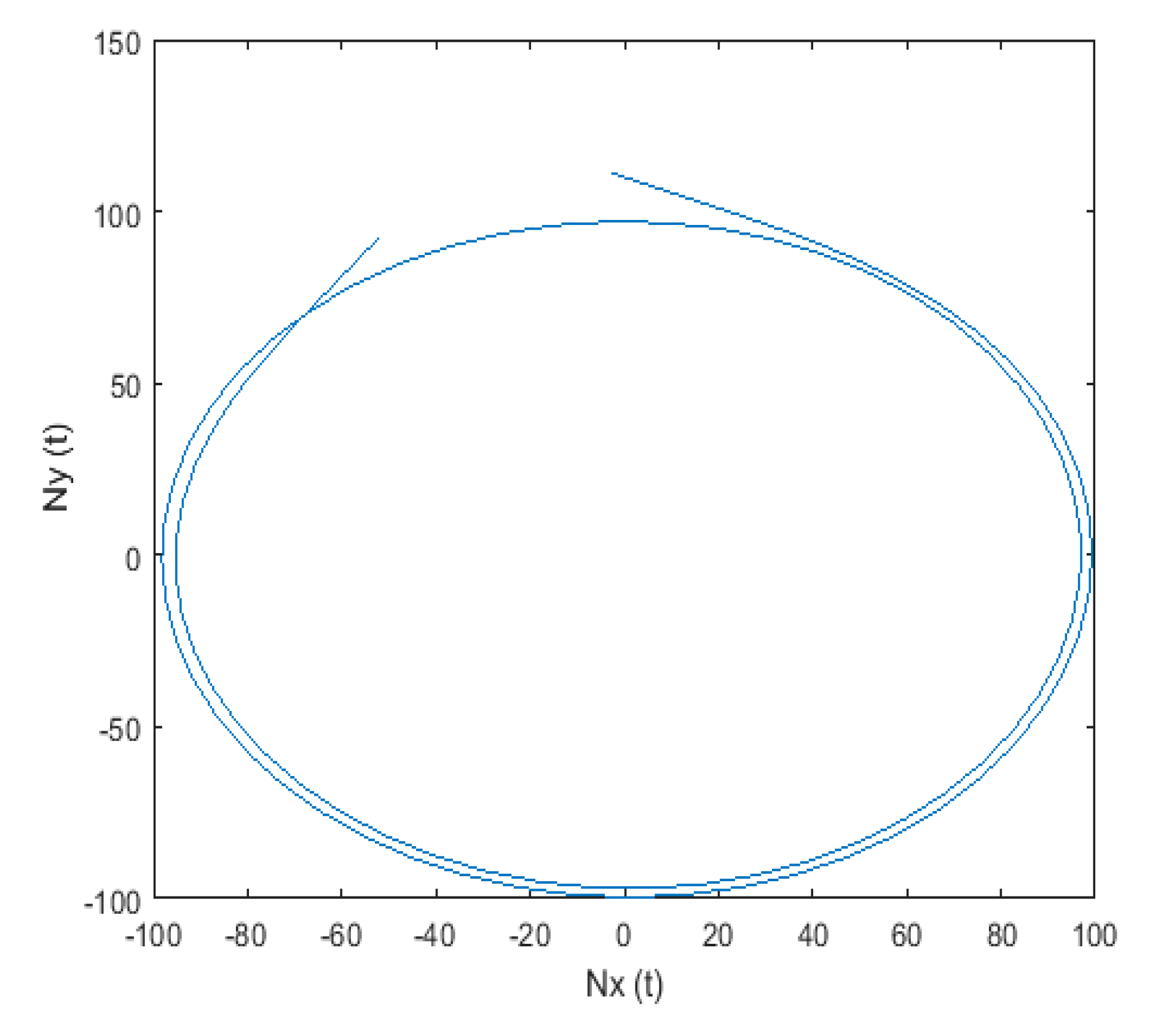
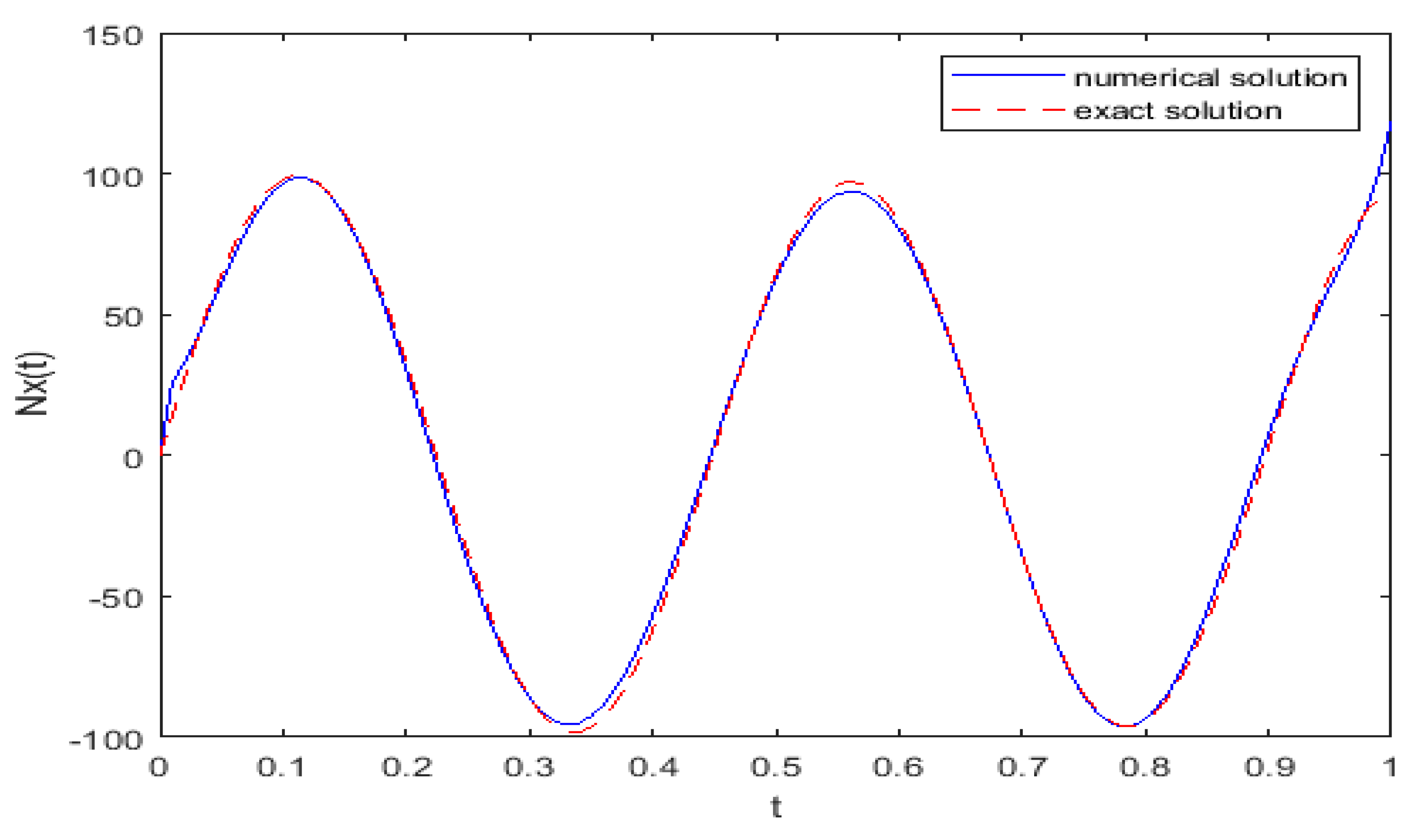

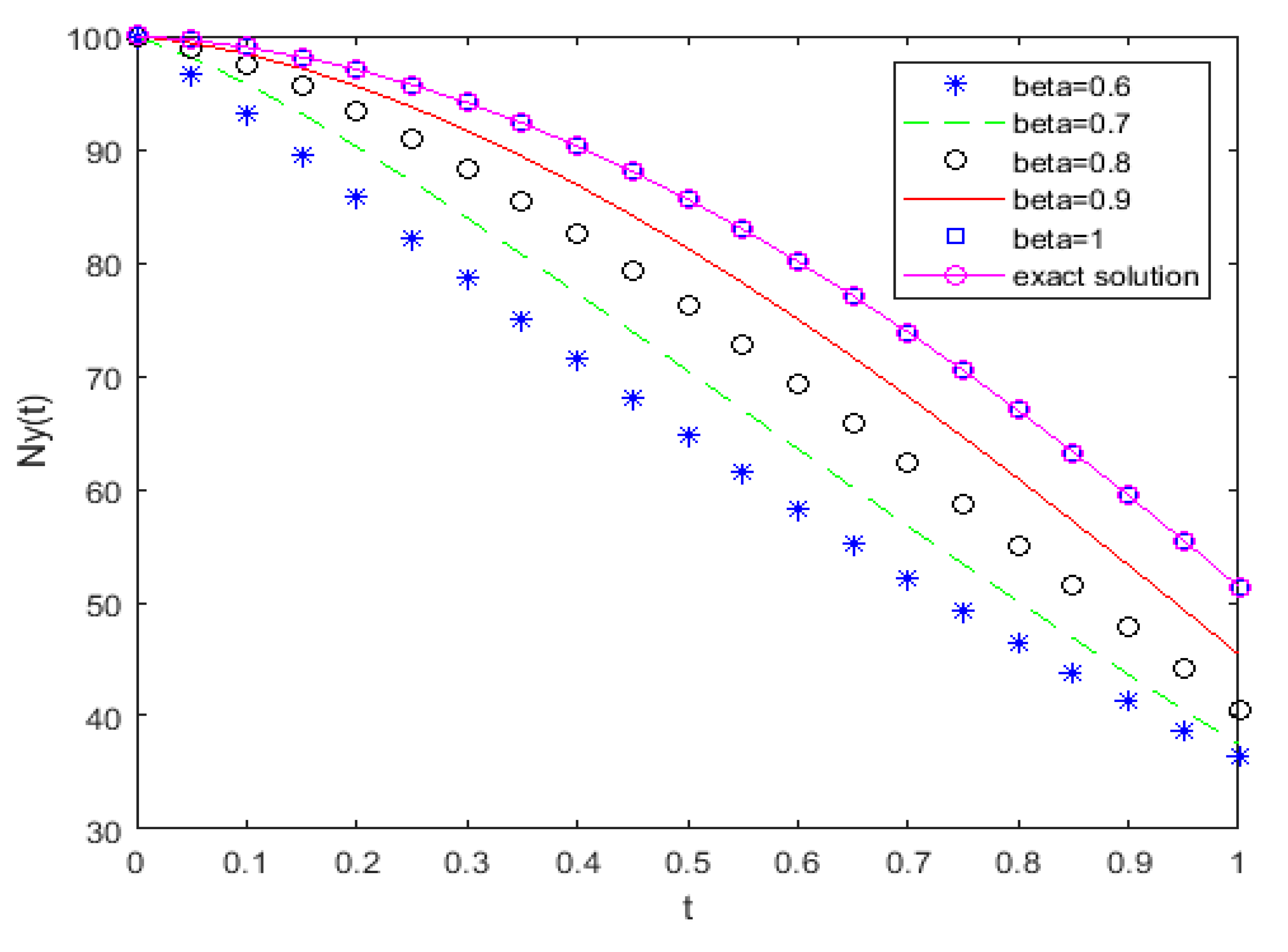
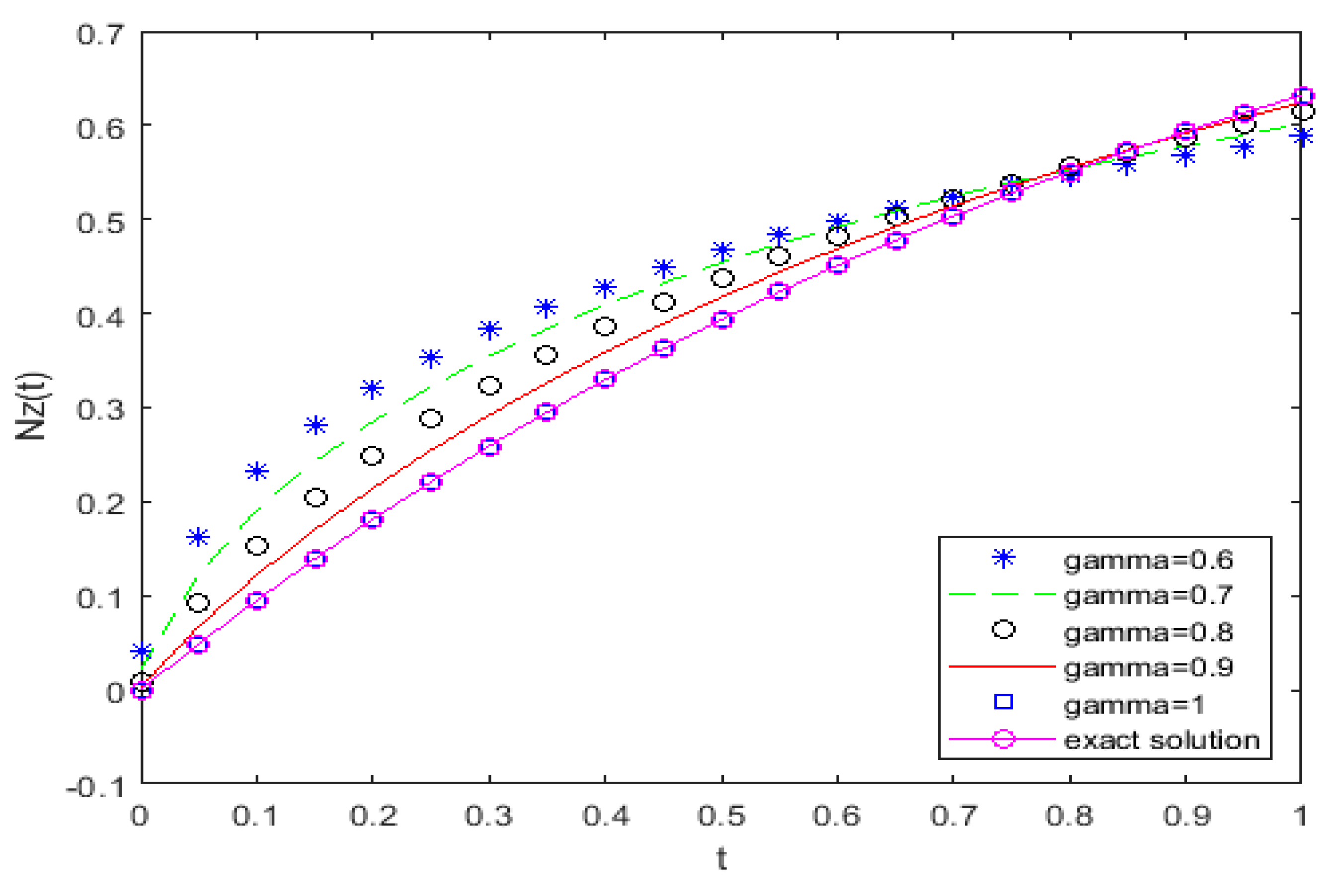
| 2.0349 × 10−4 | 4.2101 × 10−8 | |
| 5.7209 × 10−6 | 9.2050 × 10−10 | |
| 1.9648 × 10−4 | 6.2953 × 10−10 | |
| 5.5559 × 10−6 | 6.2953 × 10−10 | |
| 1.7733 × 10−6 | 5.7426 × 10−10 | |
| 5.0010 × 10−8 | 6.8075 × 10−12 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singh, H.; Srivastava, H.M. Numerical Simulation for Fractional-Order Bloch Equation Arising in Nuclear Magnetic Resonance by Using the Jacobi Polynomials. Appl. Sci. 2020, 10, 2850. https://doi.org/10.3390/app10082850
Singh H, Srivastava HM. Numerical Simulation for Fractional-Order Bloch Equation Arising in Nuclear Magnetic Resonance by Using the Jacobi Polynomials. Applied Sciences. 2020; 10(8):2850. https://doi.org/10.3390/app10082850
Chicago/Turabian StyleSingh, Harendra, and H. M. Srivastava. 2020. "Numerical Simulation for Fractional-Order Bloch Equation Arising in Nuclear Magnetic Resonance by Using the Jacobi Polynomials" Applied Sciences 10, no. 8: 2850. https://doi.org/10.3390/app10082850
APA StyleSingh, H., & Srivastava, H. M. (2020). Numerical Simulation for Fractional-Order Bloch Equation Arising in Nuclear Magnetic Resonance by Using the Jacobi Polynomials. Applied Sciences, 10(8), 2850. https://doi.org/10.3390/app10082850






