Grating Metamaterials Based on CdTe/CdMgTe Quantum Wells as Terahertz Detectors for High Magnetic Field Applications
Abstract
1. Introduction
2. Samples and Experiment
2.1. Wafers’ Description and Characterization
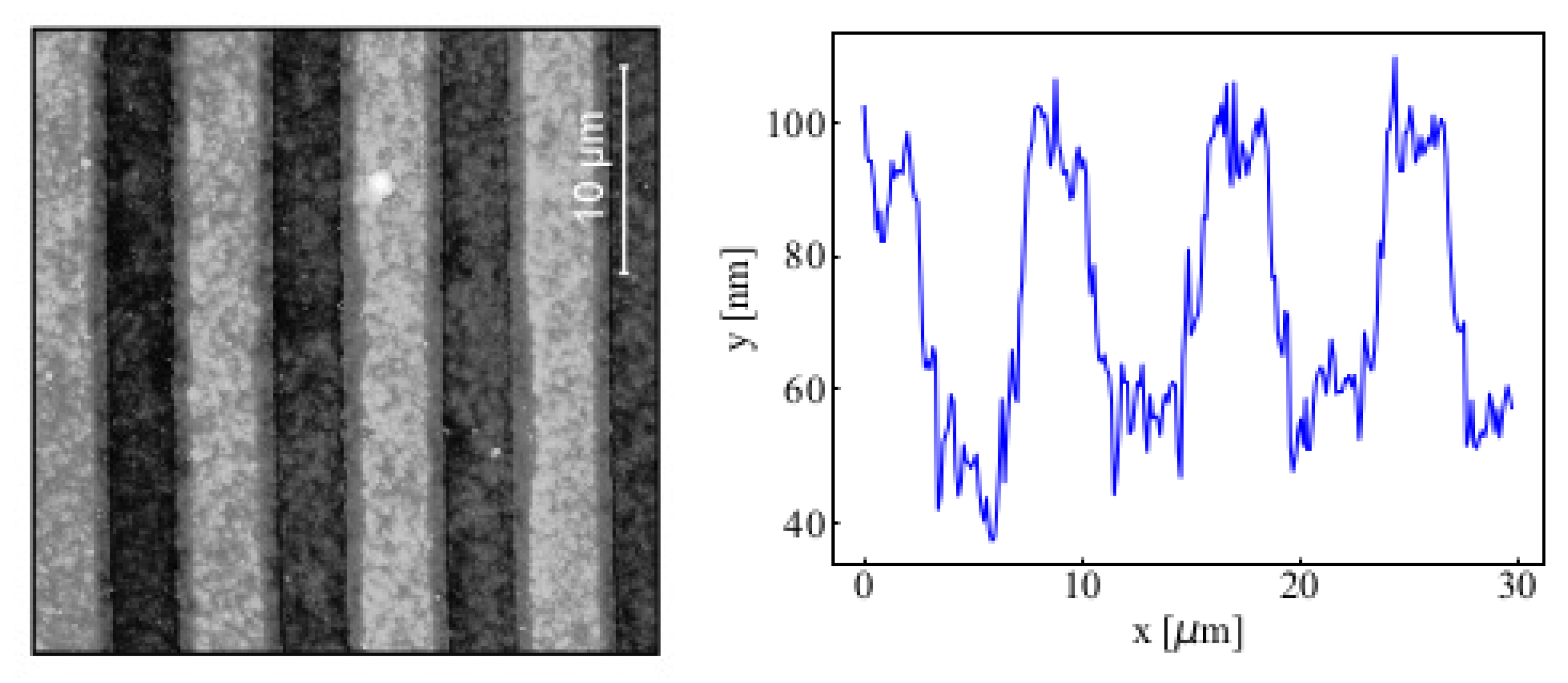
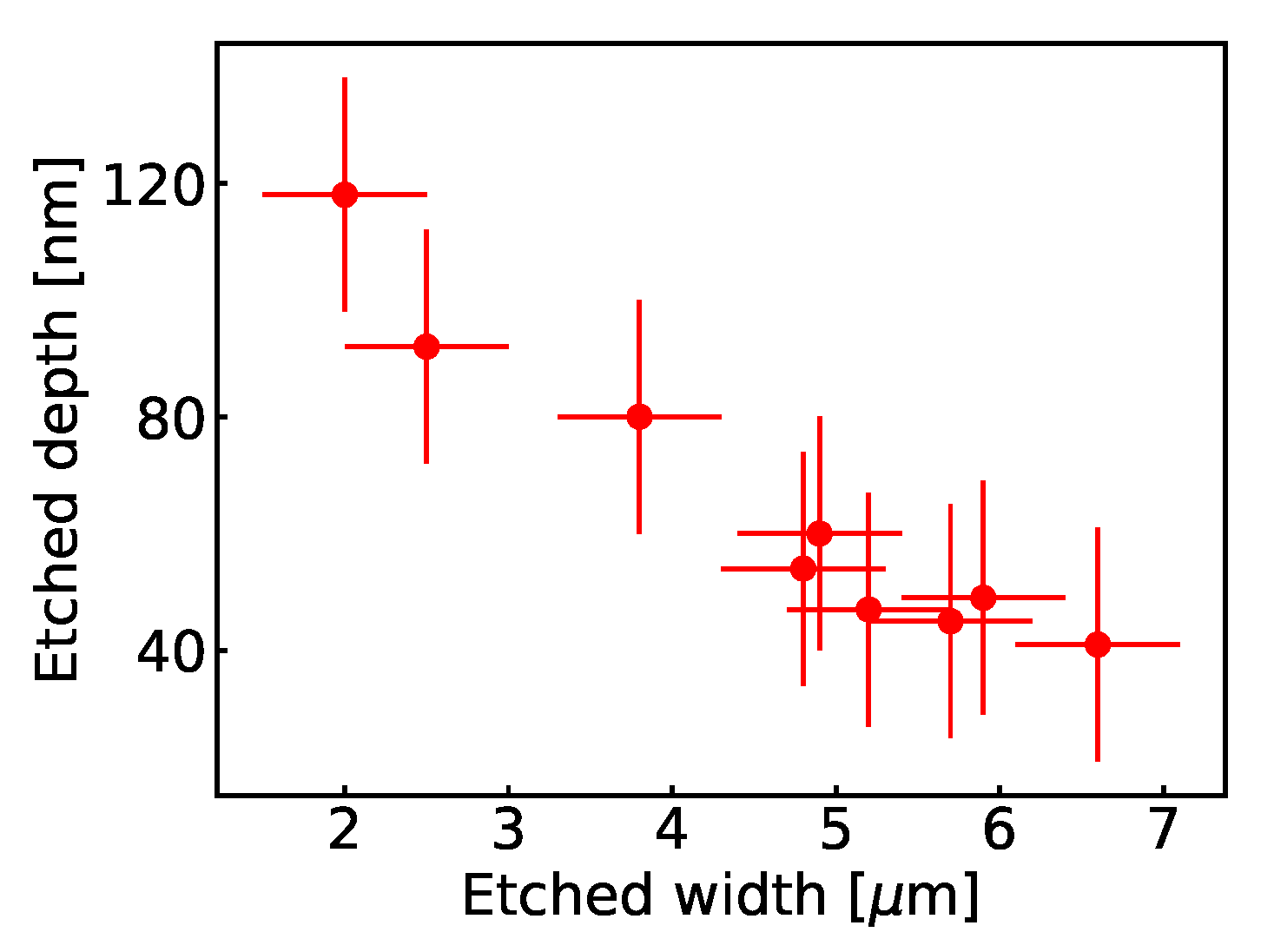
2.2. Etching
3. Results
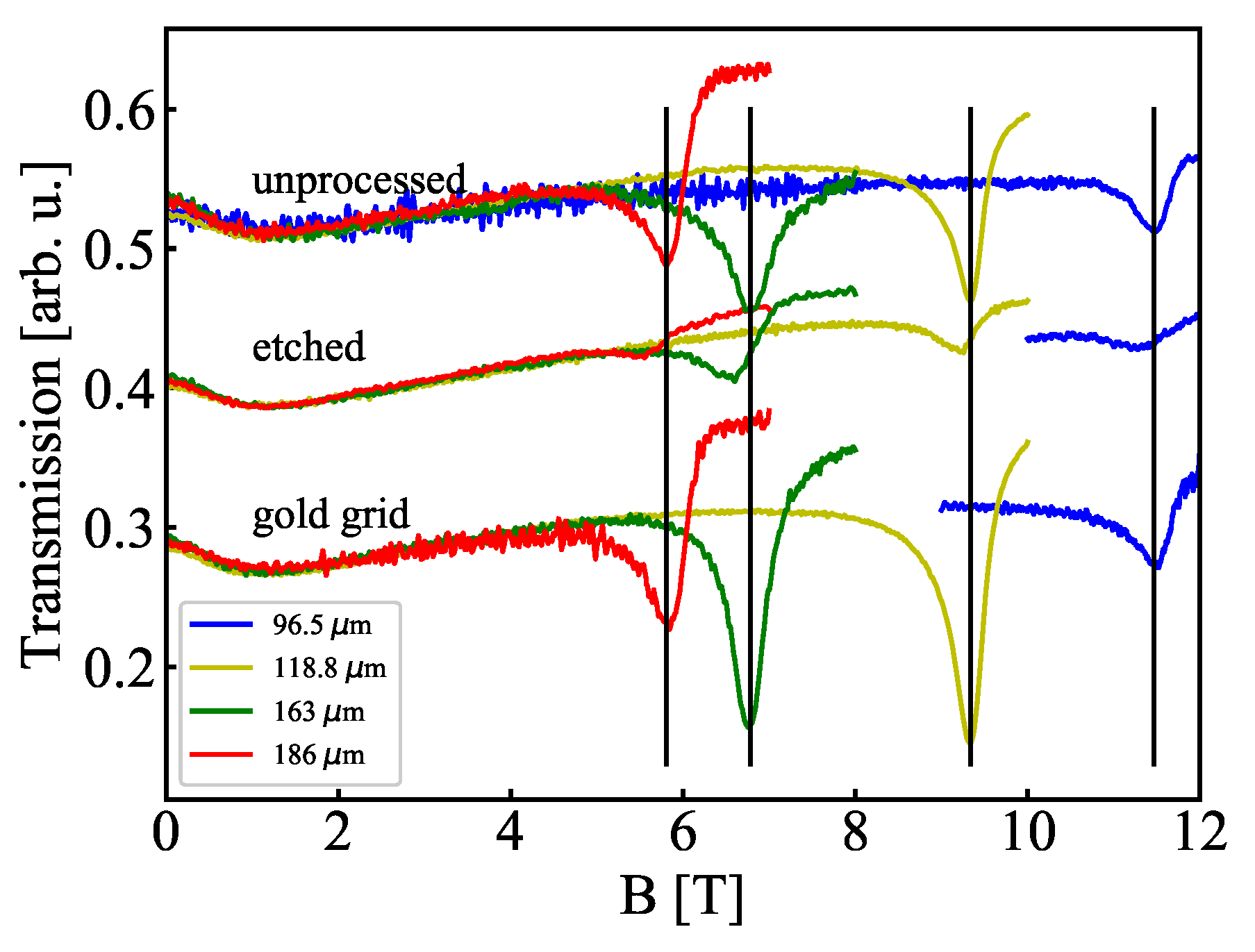
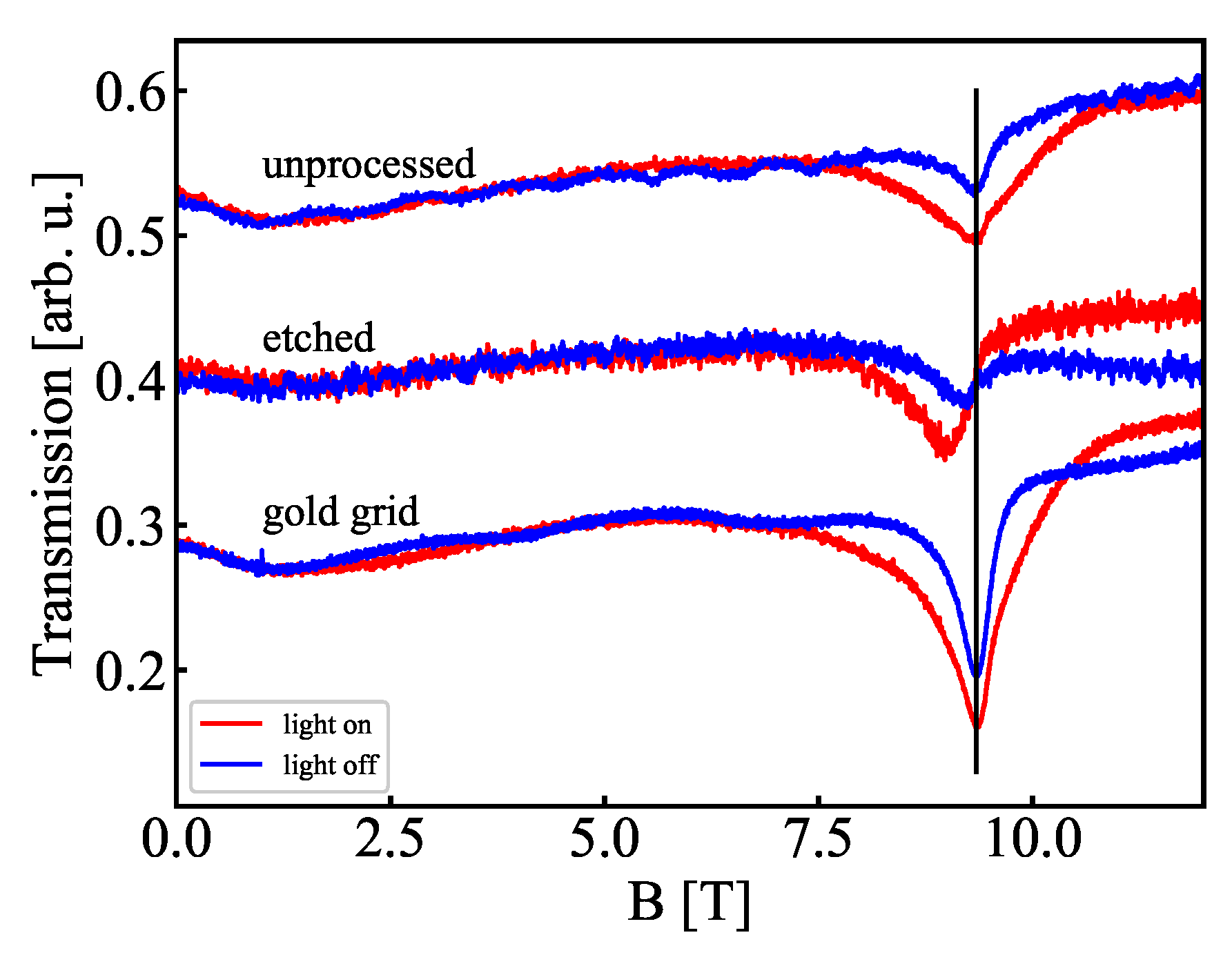
3.1. Comparison of Etched and Au Gratings
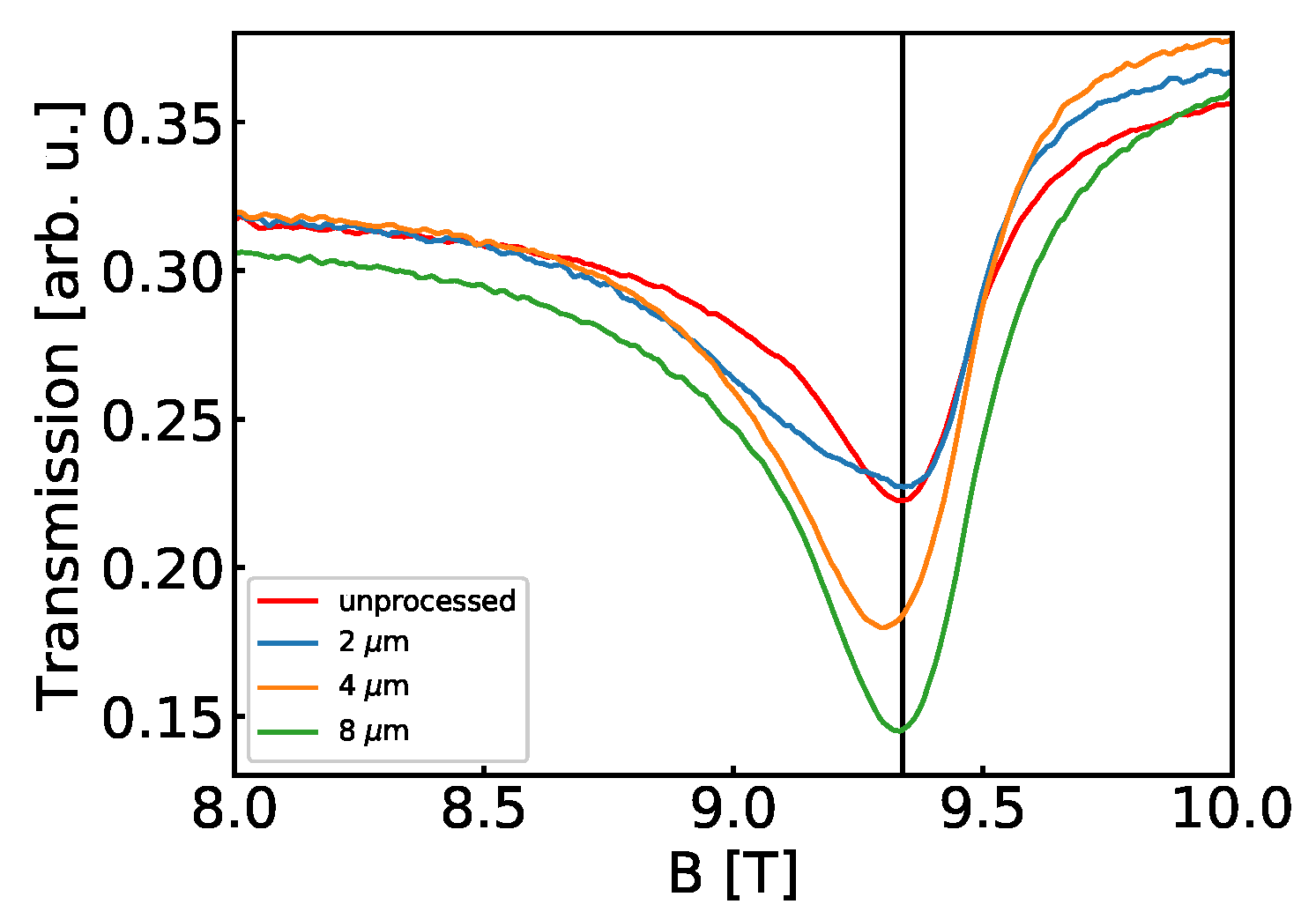
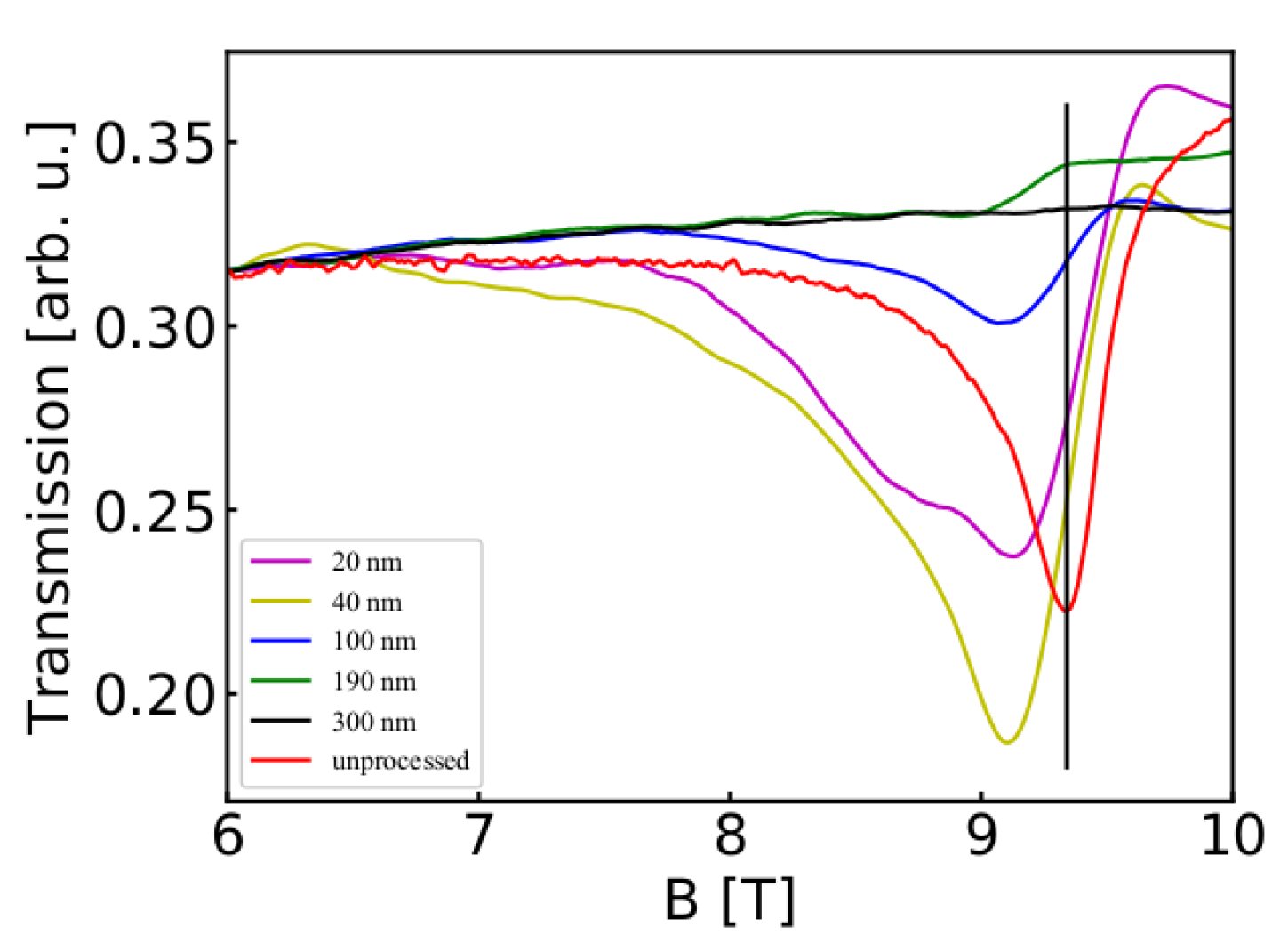
3.2. Dependence on the Grooves’ Depth
3.3. Influence of Illumination with the White Light
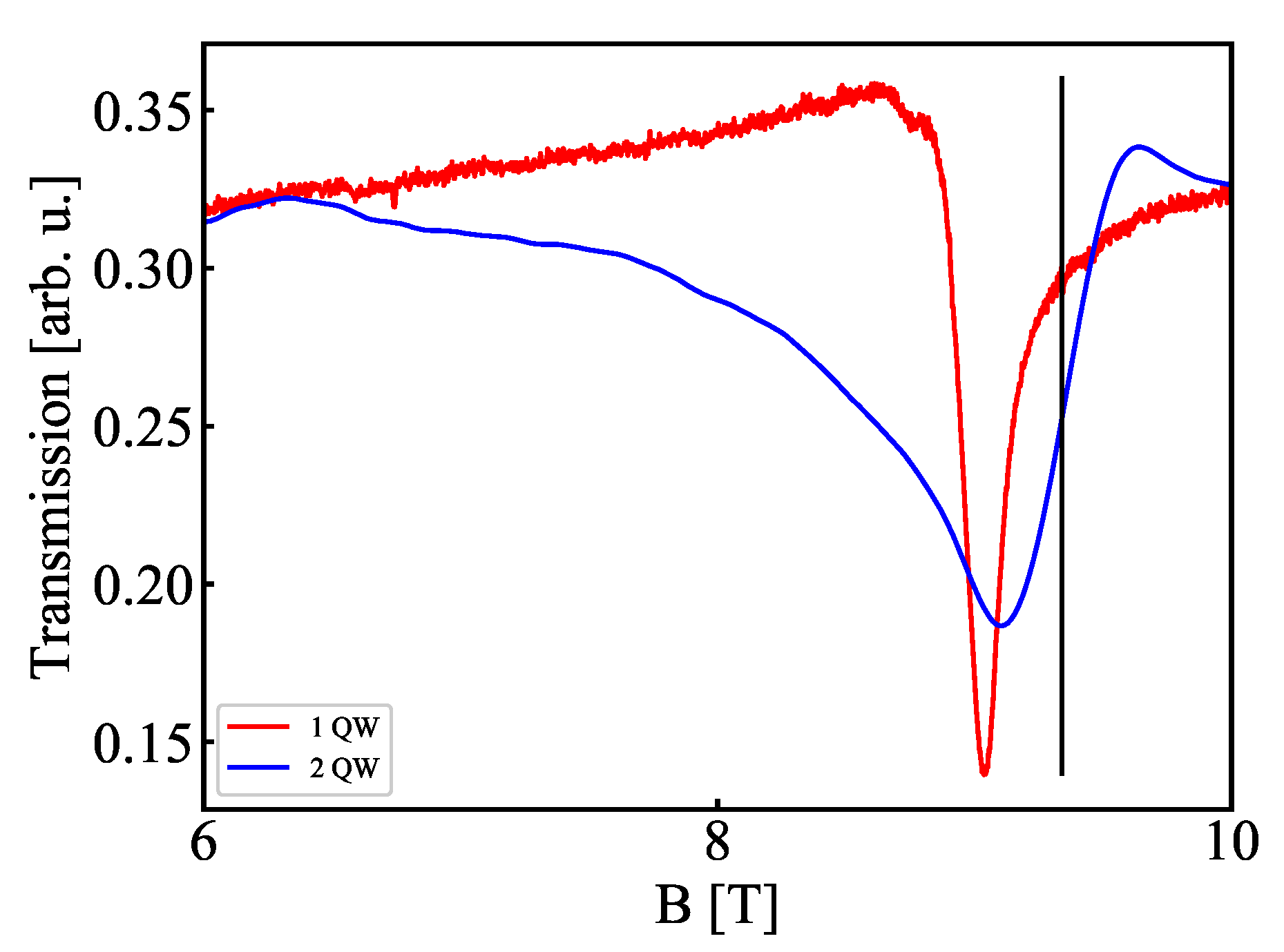
4. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| 2DEG | two-dimensional electron gas |
| AFM | atomic force microscope |
| CR | cyclotron resonance |
| EBL | electron beam lithography |
| MP | magnetoplasmon |
| PMMA | polymethyl methacrylate |
| SEM | scanning electron microscope |
| SPSL | short period superlattice |
| QW | quantum well |
Appendix A
References
- Dyakonov, M.; Shur, M.S. Shallow water analogy for a ballistic field effect transistor: New mechanism of plasma wave generation by dc current. Phys. Rev. Lett. 1993, 71, 2465–2468. [Google Scholar] [CrossRef]
- Dyakonov, M.; Shur, M.S. Detection, mixing, and frequency multiplication of terahertz radiation by two-dimensional electronic fluid. IEEE Trans. Electron Devices 1996, 43, 380–387. [Google Scholar] [CrossRef]
- Knap, W.; Teppe, F.; Meziani, Y.; Dyakonova, N.; Łusakowski, J.; Boeuf, F.; Skotnicki, T.; Maude, D.; Rumyantsev, S.; Shur, M.S. Plasma wave detection of sub-terahertz and terahertz radiation by silicon field-effect transistors. Appl. Phys. Lett. 2004, 85, 675–677. [Google Scholar] [CrossRef]
- Ikamas, K.; Cibiraite, D.; Lisauskas, A.; Bauer, M.; Krozer, V.; Roskos, H.G. Broadband terahertz power detectors based on 90-nm silicon CMOS transistors with flat responsivity up to 2.2 THz. IEEE Electron Device Lett. 2018, 39, 1413–1416. [Google Scholar] [CrossRef]
- Muravev, V.A.; Gusikhin, P.A.; Zarezin, A.M.; Andreev, I.V.; Gubarev, S.I.; Kukushkin, I.V. Two-dimensional plasmon induced by metal proximity. Phys. Rev. B 2019, 99, 241406. [Google Scholar] [CrossRef]
- Shchepetilnikov, A.V.; Kaysin, B.D.; Gusikhin, P.A.; Muravev, V.M.; Tsydynzhapov, G.E.; Nefyodov, Y.A.; Dremin, A.A.; Kukushkin, I.V. Optimization of the frequency response of a novel GaAs plasmonic terahertz detector. Opt. Quantum Electron. 2019, 51, 1–8. [Google Scholar] [CrossRef]
- Bandurin, D.A.; Svintsov, D.; Gayuchenko, I.; Shuigang, G.X.; Principi, A.; Moskotin, M.; Tretyakov, I.; Yagodkin, D.; Zhukov, S.; Taniguchi, T.; et al. Resonant terahertz detection using graphene plasmons. Nat. Commun. 2018, 9, 5392. [Google Scholar] [CrossRef]
- Knap, W.; Dur, D.; Raymond, A.; Meny, C.; Leotin, J.; Huant, S.; Etienne, B. A far-infrared spectrometer based on cyclotron resonance emission sources. Rev. Sci. Instr. 1992, 63, 3293–3297. [Google Scholar] [CrossRef]
- Knap, W.; Łusakowski, J.; Parenty, T.; Bollaert, S.; Cappy, A.; Popov, V.V.; Shur, M.S. Terahertz emission by plasma waves in 60 nm gate high electron mobility transistors. Appl. Phys. Lett. 2004, 84, 2331–2333. [Google Scholar] [CrossRef]
- Knap, W.; Łusakowski, J.; Karpierz, K.; Orsal, B.; Robert, J.-L. Improved performance of magnetically tunable GaAs and InP far-infrared detectors. J. Appl. Phys. 1992, 72, 680–683. [Google Scholar] [CrossRef]
- Yavorskiy, D.; Karpierz, K.; Grynberg, M.; Knap, W.; Łusakowski, J. Indium antimonide detector for spectral characterization of terahertz sources. J. Appl. Phys. 2018, 123, 064502. [Google Scholar] [CrossRef]
- Białek, M.; Witowski, A.M.; Orlita, M.; Potemski, M.; Czapkiewicz, M.; Wróbel, J.; Umansky, V.; Grynberg, M.; Łusakowski, J. Plasmonic terahertz detectors based on a high-electron mobility GaAs/AlGaAs heterostructure. J. Appl. Phys. 2014, 115, 214503. [Google Scholar] [CrossRef]
- Grynberg, M.; Huant, S.; Martinez, G.; Kossut, J.; Wojtowicz, T.; Karczewski, G.; Shi, J.-M.; Peeters, F.M.; Devreese, J.T. Magneto-polaron effect on shallow indium donors in CdTe. Phys. Rev. B 1996, 54, 1467–1470. [Google Scholar] [CrossRef] [PubMed]
- Höschl, P.; Polívka, P.; Prosser, V.; Skárivxaxnkovxax, M.; Vidra, M. Cadmium Telluride nuclear radiation detectors. Jpn. J. Appl. Phys. 1977, 16, 279–281. [Google Scholar] [CrossRef]
- Dornhaus, R.; Nimtz, G. The properties and applications of the Hg1−xCdxTe alloy systems. In Narrow—Gap Smiconductors; Höhler, G., Ed.; Springer: Berlin/Heidelberg, Germany, 1985. [Google Scholar]
- Duplantier, B.; Rivasseae, V.; Fuchs, J.N. (Eds.) Dirac Matter; Progress in Mathematical Physics; Springer International Publishing: Cham, Switzerland, 2017; Volume 71. [Google Scholar]
- Shen, S.-Q. Topological Insulators, 2nd ed.; Springer Series in Solid-State Sciences; Keimer, K., Merlin, R., Queisser, H.-J., von Klitzing, K., Eds.; Springer Nature Singapore Pte Ltd.: Singapore, 2017; Volume 187. [Google Scholar]
- Zawadzki, W. Semirelativity in semiconductors: A review. J. Phys. Condens. Matter 2017, 29, 373004. [Google Scholar] [CrossRef]
- Gałązka, R.R.; Wojtowicz, T. CdTe-based semimagnetic semiconductors. In CdTe and Related Compounds; Physics, Defects, Hetero- and Nano-Structures, Crystal Growth, Surfaces and Applications, Part I; Triboulet, R., Siffert, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2010; pp. 133–168. [Google Scholar]
- Kobak, J.; Smoleński, T.; Goryca, M.; Papaj, M.; Gietka, K.; Bogucki, A.; Koperski, M.; Rousset, J.-G.; Suffczyński, J.; Janik, E.; et al. Designing quantum dots for solotronics. Nat. Commun. 2014, 5, 3191. [Google Scholar] [CrossRef]
- Piot, B.A.; Kunc, J.; Potemski, M.; Maude, D.K.; Betthausen, C.; Vogl, A.; Weiss, D.; Karczewski, G.; Wojtowicz, T. Fractional quantum Hall effect in CdTe. Phys. Rev. B 2010, 82, 081307. [Google Scholar] [CrossRef]
- Furdyna, J.K.; Lee, S.; Dobrowolska, M.; Wojtowicz, T.; Liu, X. Band-Offset Engineering in Magnetic/Non-Magnetic Semiconductor Quantum Structures. In Introduction to the Physics of Diluted Magnetic Semiconductors; Springer Series in Materials Science; Kossut, J., Gaj, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 103–160. [Google Scholar]
- Grigelionis, I.; Białek, M.; Grynberg, M.; Czapkiewicz, M.; Kolkovskiy, V.; Wiater, M.; Wojciechowski, T.; Wróbel, J.; Wojtowicz, T.; Diakonova, N.; et al. Terahertz magneto-spectroscopy of a point contact based on CdTe/CdMgTe quantum well. J. Nanophotonics 2015, 9, 093082. [Google Scholar] [CrossRef]
- Grigelionis, I.; Nogajewski, K.; Karczewski, G.; Wojtowicz, T.; Czapkiewicz, M.; Wróbel, J.; Boukari, H.; Mariette, H.; Łusakowski, J. Magnetoplasmons in high electron mobility CdTe/CdMgTe quantum wells. Phys. Rev. B 2015, 91, 075424. [Google Scholar] [CrossRef]
- Imanaka, Y.; Takamasu, T.; Kido, G.; Karczewski, G.; Wojtowicz, T.; Kossut, J. Cyclotron resonance in high mobility CdTe/CdMgTe 2D electron system in the integer quantum Hall regime. Phys. B Condens. Matter 1998, 457, 256–258. [Google Scholar] [CrossRef]
- Karczewski, G.; Wojtowicz, T.; Wang, Y.; Wu, X.; Peeters, F. Electron effective mass and resonant polaron effect in CdTe/CdMgTe quantum wells. Phys. Status Solidi B 2002, 229, 597–600. [Google Scholar] [CrossRef]
- Białek, M.; Czapkiewicz, M.; Wróbel, J.; Umansky, V.; Łusakowski, J. Plasmon dispersions in high electron mobility terahertz detectors. Appl. Phys. Lett. 2014, 104, 263514. [Google Scholar] [CrossRef]
- Białek, M.; Łusakowski, J.; Czapkiewicz, M.; Wróbel, J.; Umansky, V. Photoresponse of a two-dimensional electron gas at the second harmonic of the cyclotron resonance. Phys. Rev. B 2015, 91, 045437. [Google Scholar] [CrossRef]
- Nogajewski, K.; Łusakowski, J.; Knap, W.; Popov, V.V.; Teppe, F.; Rumyantsev, S.L.; Shur, M.S. Localized and collective magnetoplasmon excitations in AlGaN/GaN-based grating-gate terahertz modulators. Appl. Phys. Lett. 2011, 99, 213501. [Google Scholar] [CrossRef]
- Łusakowski, J. Plasmon—Terahertz photon interaction in high-electron-mobility heterostructures. Semicond. Sci. Technol. 2016, 32, 013004. [Google Scholar] [CrossRef]
- Kushvaha, M.S. Plasmons and magnetoplasmons in semiconductor heterostructures. Surf. Sci. Rep. 2001, 41, 1–416. [Google Scholar] [CrossRef]
- Bobko, E.; Płoch, D.; Wiater, M.; Wojtowicz, T.; Wróbel, J. Fabrication of CdMgTe/Cd(Mn)Te nanostructures with the application of high-resolution electron-beam lithography. Opto-Electron. Rev. 2017, 25, 65–68. [Google Scholar] [CrossRef]
- Szczytko, J.; Stolarek, M.; Piętka, B.; Łusakowski, J.; Barańska, A.; Papis, E.; Wawro, A.; Adomavisius, R.; Krotkus, A.; Pałka, N.; et al. Terahertz properties of metallic layers and grids. In Proceedings of the 19th International Conference on Microwaves, Radar and Wireless Communications—MIKON 2012, Warsaw, Poland, 21–23 May 2012; pp. 271–275. [Google Scholar]
- Von Ortenberg, M. Substrate effects on the cyclotron resonance in surface layers of Silicon. Solid State Commun. 1975, 17, 1335–1338. [Google Scholar] [CrossRef]
- Narozhyny, B.N.; Levchenko, A. Coulomb drag. Rev. Mod. Phys. 2016, 88, 025003. [Google Scholar] [CrossRef]
- Mikhailov, S.A. Plasma instability and amplification of electromagnetic waves in low-dimensional electron system. Phys. Rev. B 1998, 58, 1517–1532. [Google Scholar] [CrossRef]
- Mikhailov, S.A. Microwave-induced magnetotransport phenomena in two-dimensional electron systems: Importance of electrodynamic effects. Phys. Rev. B 2004, 70, 165311. [Google Scholar] [CrossRef]
- Eguiluz, A.; Lee, T.K.; Quinn, J.J.; Chiu, K.W. Interface excitations in metal-insulator-semiconductor structures. Phys. Rev. B 1975, 11, 4989–4993. [Google Scholar] [CrossRef]
- Chaplik, A.V. Possible crystalization of charge carriers in low-dimensional inversion layers. Sov. Phys. JETP 1972, 35, 395–398. [Google Scholar]
- Popov, V.V. Plasmon Excitation and Plasmonic Detection of Terahertz Radiation in the Grating-Gate Field-Effect-Transistor Structures. J. Infrared Mill. Terahz. Wave 2011, 32, 1178–1191. [Google Scholar] [CrossRef]
- Zabolotnykh, A.A.; Volkov, V.A. Interaction of gated and ungated plasmons in two-dimensiona electron systems. Phys. Rev. B 2019, 99, 165304. [Google Scholar] [CrossRef]
- Bylinkin, A.; Totova, E.; Mikheev, V.; Zhukova, E.; Zhukov, S.; Belyanchikov, M.; Kashchenko, M.; Miakonkikh, A.; Svintsov, D. Tight-binding terahertz plasmon in chemical-vapor-deposited graphene. Phys. Rev. Appl. 2019, 11, 054017. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yavorskiy, D.; Szoła, M.; Karpierz, K.; Bożek, R.; Rudniewski, R.; Karczewski, G.; Wojtowicz, T.; Wróbel, J.; Łusakowski, J. Grating Metamaterials Based on CdTe/CdMgTe Quantum Wells as Terahertz Detectors for High Magnetic Field Applications. Appl. Sci. 2020, 10, 2807. https://doi.org/10.3390/app10082807
Yavorskiy D, Szoła M, Karpierz K, Bożek R, Rudniewski R, Karczewski G, Wojtowicz T, Wróbel J, Łusakowski J. Grating Metamaterials Based on CdTe/CdMgTe Quantum Wells as Terahertz Detectors for High Magnetic Field Applications. Applied Sciences. 2020; 10(8):2807. https://doi.org/10.3390/app10082807
Chicago/Turabian StyleYavorskiy, Dmitriy, Maria Szoła, Krzysztof Karpierz, Rafał Bożek, Rafał Rudniewski, Grzegorz Karczewski, Tomasz Wojtowicz, Jerzy Wróbel, and Jerzy Łusakowski. 2020. "Grating Metamaterials Based on CdTe/CdMgTe Quantum Wells as Terahertz Detectors for High Magnetic Field Applications" Applied Sciences 10, no. 8: 2807. https://doi.org/10.3390/app10082807
APA StyleYavorskiy, D., Szoła, M., Karpierz, K., Bożek, R., Rudniewski, R., Karczewski, G., Wojtowicz, T., Wróbel, J., & Łusakowski, J. (2020). Grating Metamaterials Based on CdTe/CdMgTe Quantum Wells as Terahertz Detectors for High Magnetic Field Applications. Applied Sciences, 10(8), 2807. https://doi.org/10.3390/app10082807




