A Deep Bed Filtration Model of Two-Component Suspension in Dual-Zone Porous Medium
Abstract
1. Introduction
2. Mathematical Model of Two-Component Suspension Filtration
3. Numerical Algorithm of Solving the Problem
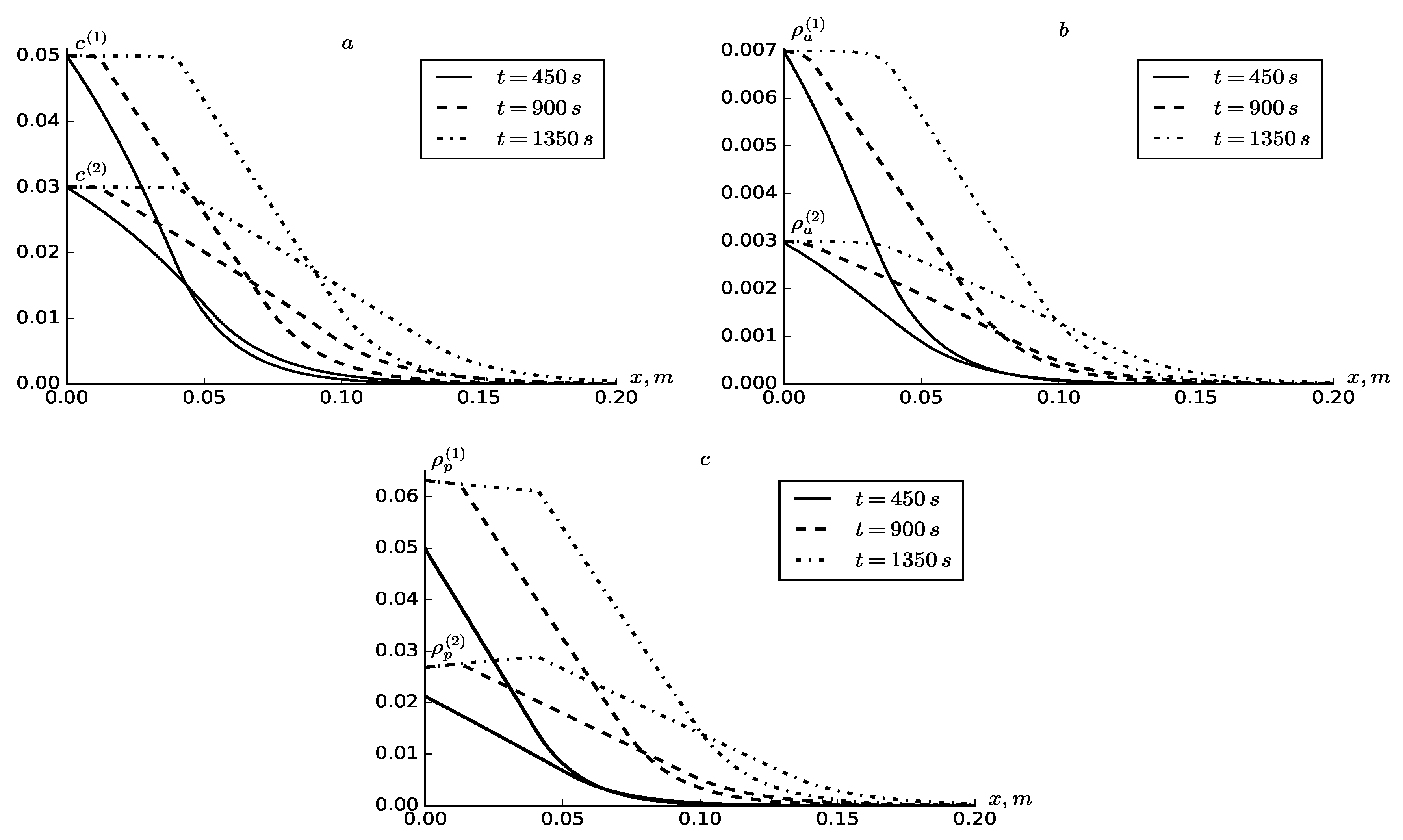
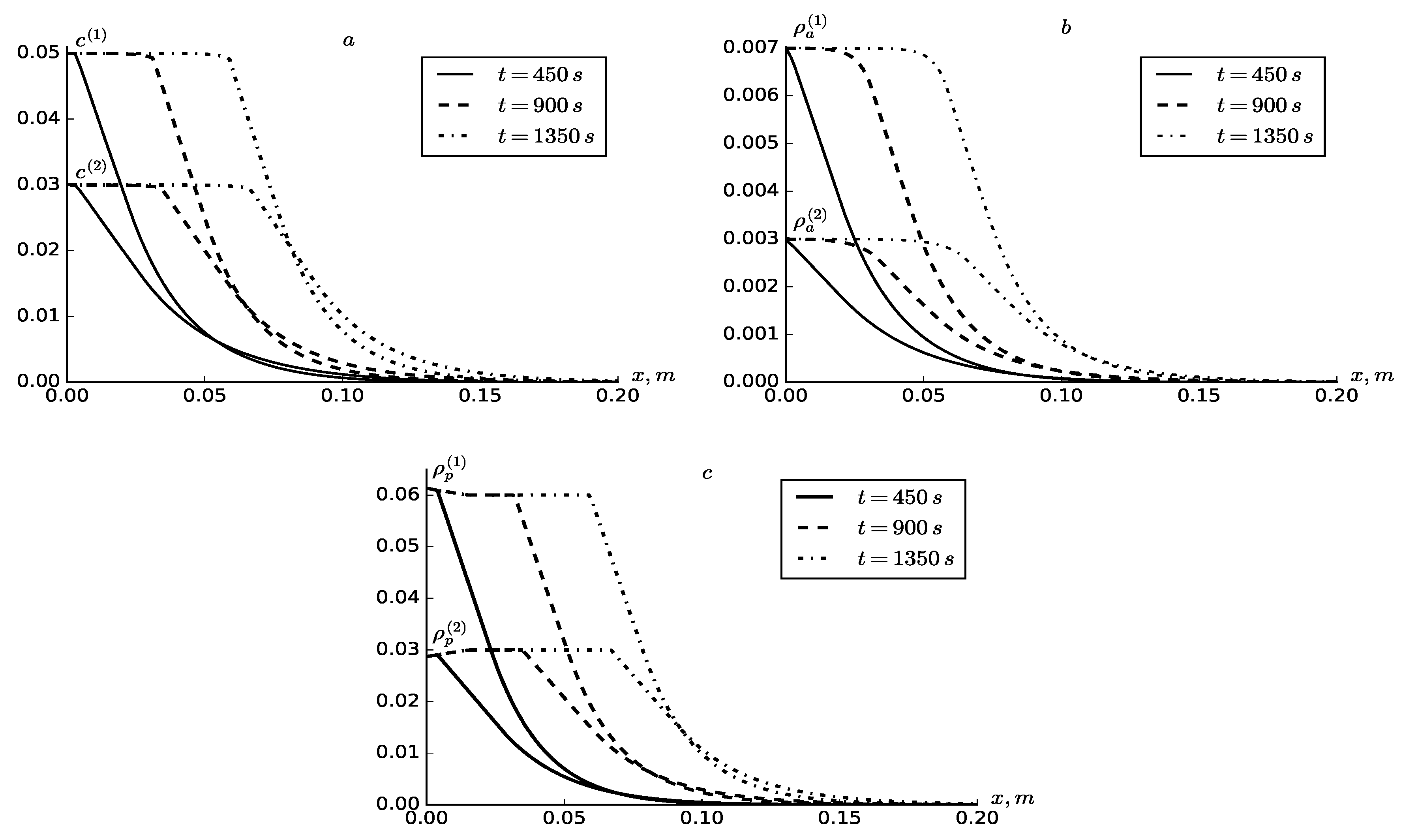
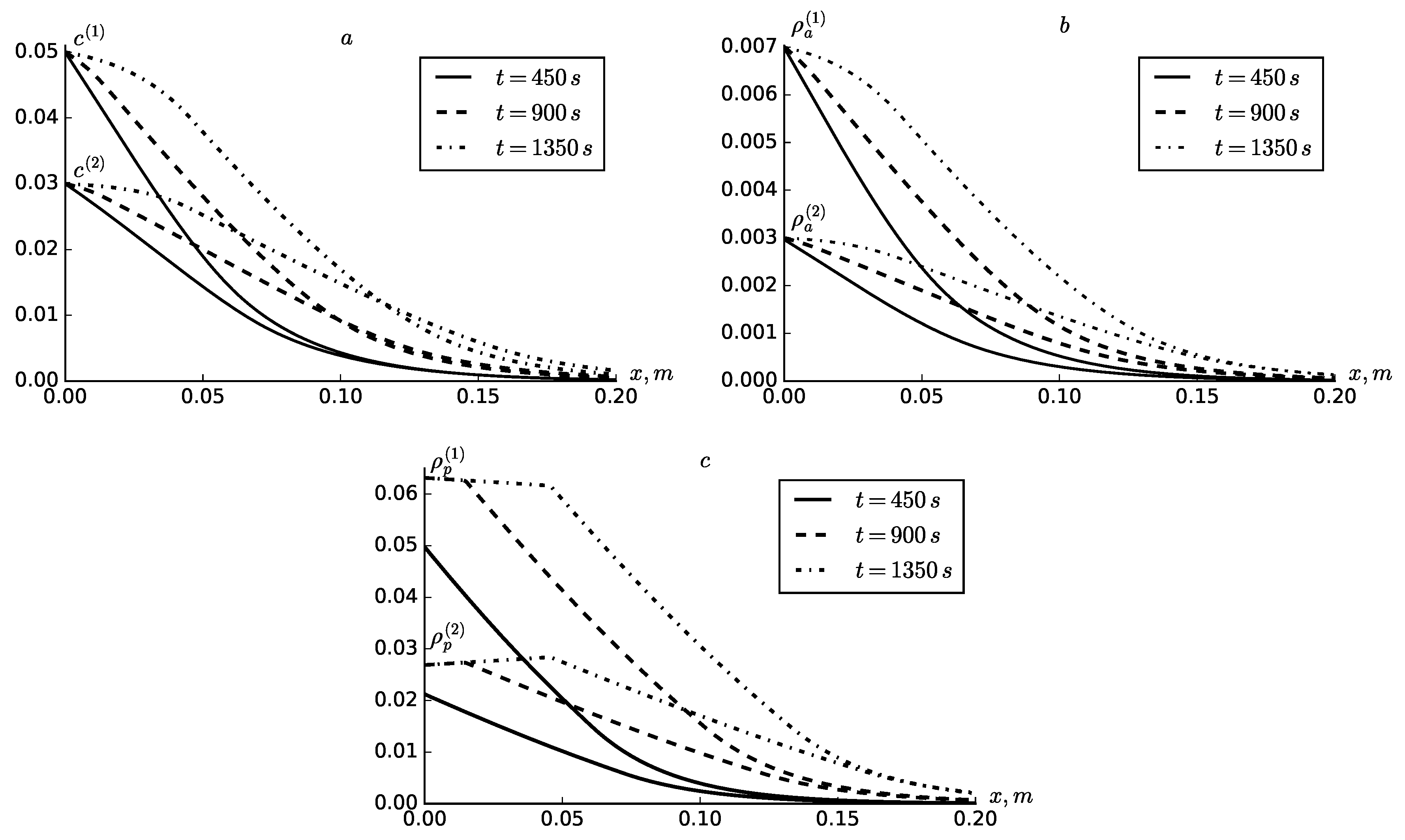
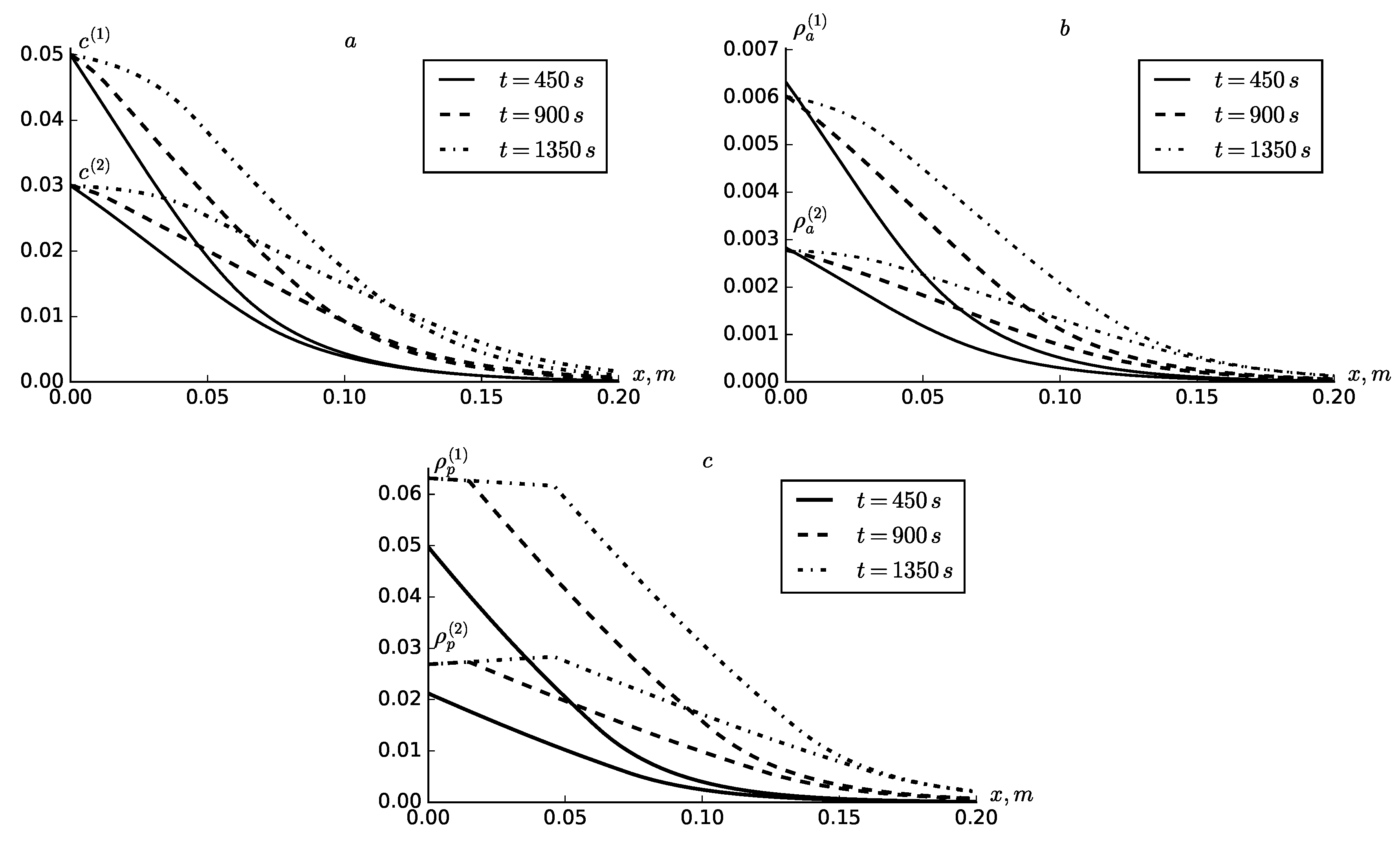
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Droste, R.L.; Gehr, R.L. Theory and Practice of Water and Wastewater Treatment, 2nd ed.; Wiley: New York, NY, USA, 2019. [Google Scholar]
- Bedrikovetsky, P. Mathematical Theory of Oil and Gas Recovery; Springer: Dordrecht, The Netherlands, 1993. [Google Scholar]
- Bradford, S.; Torkzaban, S. Colloid transport and retention in unsaturated porous media: A review of interface-, collector-, and pore-scale processes and models. Vadose Zone J. 2008, 7, 667–681. [Google Scholar] [CrossRef]
- Tien, C. Principles of Filtration; Elsevier: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Tien, C. Introduction to Cake Filtration; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Sacramento, R.N.; Yang, Y.; You, Z.; Waldmann, A.; Martins, A.L.; Vaz, A.S.L.; Zitha, P.L.J.; Bedrikovetsky, P. Deep bed and cake filtration of two-size particle suspension in porous media. J. Pet. Sci. Eng. 2015, 126, 201–210. [Google Scholar] [CrossRef]
- Gitis, V.; Rubinstein, I.; Livshits, M.; Ziskind, G. Deep-bed filtration model with multistage deposition kinetics. Chem. Eng. J. 2010, 163, 78–85. [Google Scholar] [CrossRef]
- Todd, A.C.; Somerville, J.E.; Scott, G. The Application of Depth of Formation Damage Measurements in Predicting Water Injectivity Decline. In Proceedings of the SPE Formation Damage Control Symposium, Bakersfield, CA, USA, 13–14 February 1984; pp. 233–244. [Google Scholar] [CrossRef]
- Sharma, M.M.; Yortsos, Y.C. Transport of Particulate Suspensions in Porous Media: Model Formulation. AIChE J. 1987, 33, 1636–1643. [Google Scholar] [CrossRef]
- Sharma, M.M.; Yortsos, Y.C. A network model for deep bed filtration processes. AIChE J. 1987, 33, 1644–1653. [Google Scholar] [CrossRef]
- Rege, S.D.; Fogler, H.S. A Network Model for Deep Bed Filtration of Solid Particles and Emulsion Drops. AIChE J. 1988, 34, 1761–1772. [Google Scholar] [CrossRef]
- Yang, H.; Balhoff, M.T. Pore-Network Modeling of Particle Retention in Porous Media. AIChE J. 2017, 63, 3118–3131. [Google Scholar] [CrossRef]
- Payatakes, A.C.; Tien, C.; Turian, R.M. A new model for granular porous media. I model formulation. AIChE J. 1973, 19, 58–76. [Google Scholar] [CrossRef]
- Mackie, R.I.; Homer, R.M.W.; Jarvis, R.J. Dynamic modelling of deep bed filtration. AIChE J. 1987, 133, 1761–1775. [Google Scholar] [CrossRef]
- Rajagopalan, R.; Tien, C. Trajectory analysis of deep-bed filtration with sphere-in-cell porous media model. AIChE J. 1976, 22, 523–533. [Google Scholar] [CrossRef]
- Herzig, J.P.; Leclerc, D.M.; Goff, P. Flow of suspensions through porous media—Application to deep filtration. Ind. Eng. Chem. 1970, 62, 8–35. [Google Scholar] [CrossRef]
- Ives, K.J. Theory of filtration. In Special Lecture No.7, Proceedings of the International Water Supply Association, Eight Congress, Vienna, Austria, 1–5 September 1969; IWA Publishing: London, UK, 1969; Volume 1, pp. K3–K28. [Google Scholar]
- Khuzhaerov, B.K. Model of colmatage-suffosion filtration of disperse systems in a porous medium. J. Eng. Phys. Thermophys. 2000, 73, 668–673. [Google Scholar] [CrossRef]
- Kavanagh, J.M.; Teresa, T.I.; Carrasco, C.; Riad, M.; Birch, G. Particle capture models: Comparison with experimental data. ANZIAM J. 2011, 53, C249–C265. [Google Scholar] [CrossRef]
- Ahfir, N.D.; Wang, H.Q.; Benamar, A.; Alem, A.; Massei, N.; Dupont, J.P. Transport and deposition of suspended particles in saturated porous media: Hydrodynamic effect. Hydrogeol. J. 2007, 15, 659–668. [Google Scholar] [CrossRef]
- Ahfir, N.D.; Benamar, A.; Alem, A.; Wang, H.Q. Influence of internal structure and medium length on transport and deposition of suspended particles: A laboratory study. Transp. Porous Media 2007, 76, 289–307. [Google Scholar] [CrossRef]
- Chrysikopoulos, C.V.; Vasiliki, S.I. Effect of gravity on colloid transport through water-saturated columns packed with glass beads: Modeling and experiments. Environ. Sci. Technol. 2014, 48, 6805–6813. [Google Scholar] [CrossRef]
- Katzourakis, V.E.; Chrysikopoulos, C.V. Mathematical modeling of colloid and virus cotransport in porous media: Application to experimental data. Adv. Water Resour. 2014, 68, 62–73. [Google Scholar] [CrossRef]
- Bai, B.; Xu, T.; Guo, Z. An experimental and theoretical study of the seepage migration of suspended particles with different sizes. Hydrogeol. J. 2016, 24, 2063–2078. [Google Scholar] [CrossRef]
- Bedrikovetsky, P. Upscaling of stochastic micro model for suspension transport in porous media. Transp. Porous Med. 2008, 75, 335–369. [Google Scholar] [CrossRef]
- Jegatheesan, V.; Vigneswaran, S. Deep Bed Filtration: Mathematical Models and Observations. Crit. Rev. Environ. Sci. Technol. 2005, 35, 515–569. [Google Scholar] [CrossRef]
- Mackie, R.I.; Bai, R. Suspended particle size distribution and the performance of deep bed filters. Water Res. 1992, 26, 1571–1575. [Google Scholar] [CrossRef]
- Ben Aim, R.; Vigneswaran, S.H.; Jegatheesan, V. Influence of particle size and size distribution in granular bed filtration and dynamic microfiltration. Water Sci. Technol. 1997, 36, 207–215. [Google Scholar] [CrossRef]
- Chang, J.S.; Vigneswaran, S.; Kandasamy, J.K.; Tsai, L.J. Effect of pore size and particle size distribution on granular bed filtration and microfiltration. Sep. Sci. Technol. 2008, 43, 1771–1784. [Google Scholar] [CrossRef]
- Ahfir, N.D.; Hammadi, A.; Alem, A.; Wang, H.Q.; Le Bras, G.; Ouahbi, T. Porous media grain size distribution and hydrodynamic forces effects on transport and deposition of suspended particles. J. Environ. Sci. 2016, 53, 161–172. [Google Scholar] [CrossRef]
- Zhang, P.; Bai, B.; Jiang, S.; Wang, P.; Li, H. Transport and deposition of suspended particles in saturated porous media: Effect of hydrodynamic forces and pore structure. Water Sci. Technol. Water Supply 2016, 16, 951–960. [Google Scholar] [CrossRef]
- Bai, B.; Long, F.; Rao, D.; Xu, T. The effect of temperature on the seepage transport of suspended particles in a porous medium. Hydrol. Process. 2016, 31, 382–393. [Google Scholar] [CrossRef]
- Cui, X.; Fan, Y.; Wang, H.; Huang, S. Experimental investigation of suspended particles transport in porous medium under variable temperatures January. Hydrol. Process. 2019, 33, 1117–1126. [Google Scholar] [CrossRef]
- Venitsianov, E.V.; Rubinstein, R.N. Dynamics of Sorption from Liquid Media; Nauka: Moscow, Russia, 1983. (In Russian) [Google Scholar]
- Venitsianov, E.V.; Senyavin, M.M. Mathematical description of filtration clarification of suspensions. Theor. Found. Chem. Technol. 1976, 10, 584–591. (In Russian) [Google Scholar]
- Khuzhayorov, B.; Fayziev, B. A model of suspension filtration in porous media with multistage accumulation kinetics. Int. J. Adv. Res. Sci. Eng. Technol. 2017, 4, 4643–4648. [Google Scholar]
- Khuzhayorov, B.K.; Makhmudov, Z.M.; Fayziev, B. A suspension filtration problem in porous media with “charging” and dynamic factors. Rep. Acad. Sci. Uzb. 2012, 2, 34–38. [Google Scholar]
- Elimelech, M.; Gregory, J.; Jia, X.; Williams, R.A. Particle Deposition and Aggregation: Measurement, Modelling, and Simulation; Colloid and Surface Engineering Series; Butterworth-Heinemann: Oxford, UK, 1998. [Google Scholar]
- Tien, C.; Ramarao, B.V. Granular Filtration of Aerosols and Hydrosols, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Hammadi, A.; Ahfir, N.D.; Alem, A.; Wang, H. Effects of particle size non-uniformity on transport and retention in saturated porous media. Transp. Porous Media 2017, 118, 1–14. [Google Scholar] [CrossRef]
- Makhmudov, Z.M.; Saidullaev, U.Z.; Khuzhayorov, B.K. Mathematical model of deep-bed filtration of a two-component suspension through a porous medium. Fluid Dyn. 2017, 52, 299–308. [Google Scholar] [CrossRef]
- Khuzhaerov, B. A model of multicomponent grouting and suffosion filtration. J. Eng. Phys. Thermophys. 1994, 66, 373–379. [Google Scholar] [CrossRef]
- Golubev, V.I.; Mikhailov, D.N. Modeling the dynamics of filtration of a two-particle suspension through a porous medium. Work. MIPT 2011, 3, 143–147. [Google Scholar]
- Kuzmina, L.; Osipov, Y.; Galaguz, Y. A model of two-velocity particles transport in a porous medium. Int. J. Non-Linear Mech. 2017, 93, 1–6. [Google Scholar] [CrossRef]
- Ma, E.; Ouahbi, T.; Wang, H.; Ahfir, N.D.; Alem, A.; Hammadi, A. Modeling of retention and re-entrainment of mono- and poly-disperse particles: Effects of hydrodynamics, particle size and interplay of different-sized particles retention. Sci. Total Environ. 2017, 596–597, 222–229. [Google Scholar] [CrossRef]
- Ma, E.; Ouahbi, T.; Wang, H.; Ahfir, N.D.; Alem, A.; Hammadi, A. Modeling of the transport and deposition of polydispersed particles: Effects of hydrodynamics and spatiotemporal evolution of the deposition rate. Environ. Pollut. 2017, 237, 1011–1022. [Google Scholar] [CrossRef]
- Thomas, J.W. Numerical Partial Differential Equations: Finite Difference Methods; Springer: New York, NY, USA, 1995. [Google Scholar]
- Samarskii, A.A. The Theory of Difference Schemes; CRC Press: New York, NY, USA, 2001. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khuzhayorov, B.; Fayziev, B.; Ibragimov, G.; Md Arifin, N. A Deep Bed Filtration Model of Two-Component Suspension in Dual-Zone Porous Medium. Appl. Sci. 2020, 10, 2793. https://doi.org/10.3390/app10082793
Khuzhayorov B, Fayziev B, Ibragimov G, Md Arifin N. A Deep Bed Filtration Model of Two-Component Suspension in Dual-Zone Porous Medium. Applied Sciences. 2020; 10(8):2793. https://doi.org/10.3390/app10082793
Chicago/Turabian StyleKhuzhayorov, Bakhtiyor, Bekzodjon Fayziev, Gafurjan Ibragimov, and Norihan Md Arifin. 2020. "A Deep Bed Filtration Model of Two-Component Suspension in Dual-Zone Porous Medium" Applied Sciences 10, no. 8: 2793. https://doi.org/10.3390/app10082793
APA StyleKhuzhayorov, B., Fayziev, B., Ibragimov, G., & Md Arifin, N. (2020). A Deep Bed Filtration Model of Two-Component Suspension in Dual-Zone Porous Medium. Applied Sciences, 10(8), 2793. https://doi.org/10.3390/app10082793




