Numerical and Experimental Analysis of Torsion Springs Using NURBS Curves
Abstract
:1. Introduction
2. Torsion-Spring Design
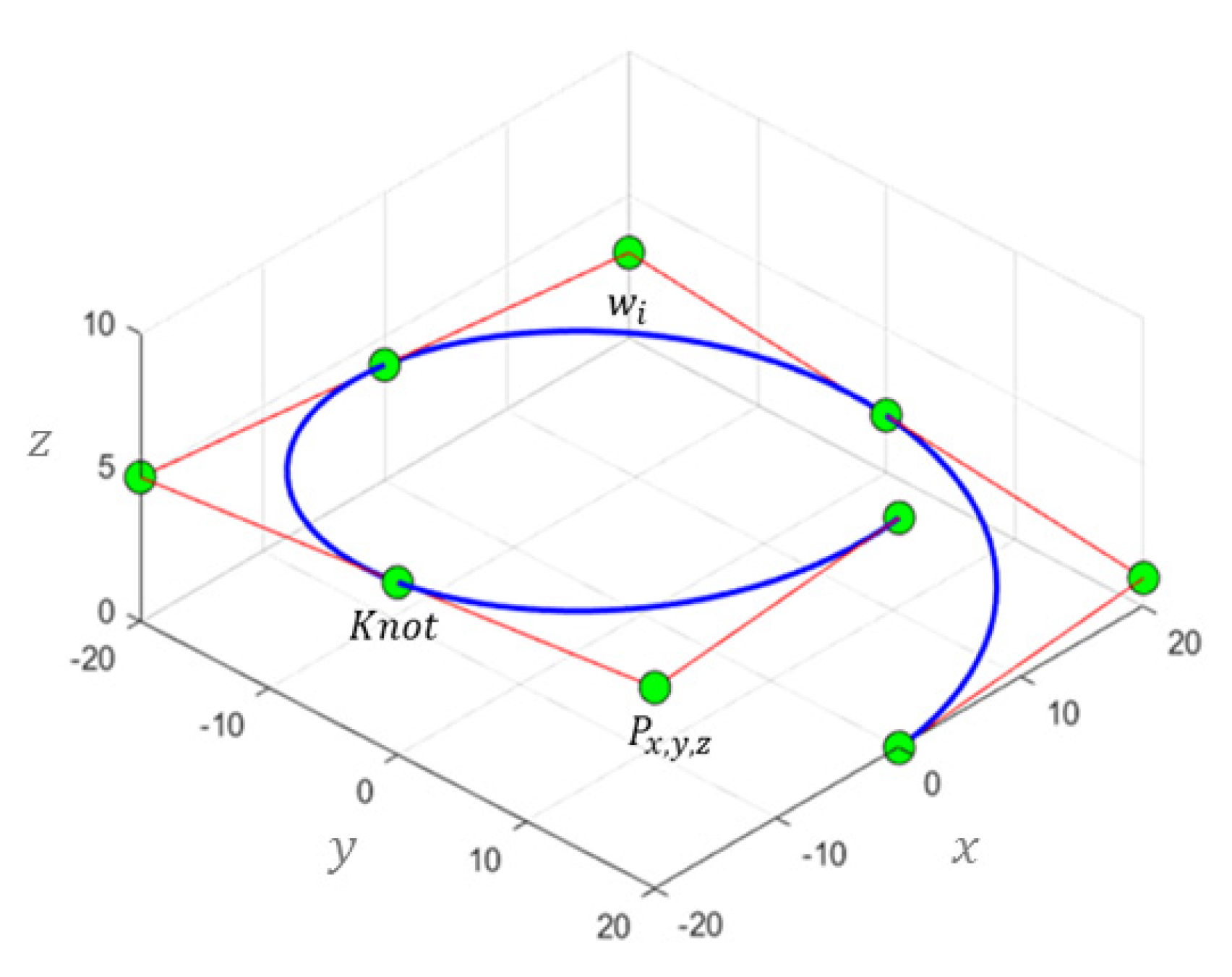
2.1. NURBS Curve
2.2. Expression of Torsion Spring Through NURBS Curves
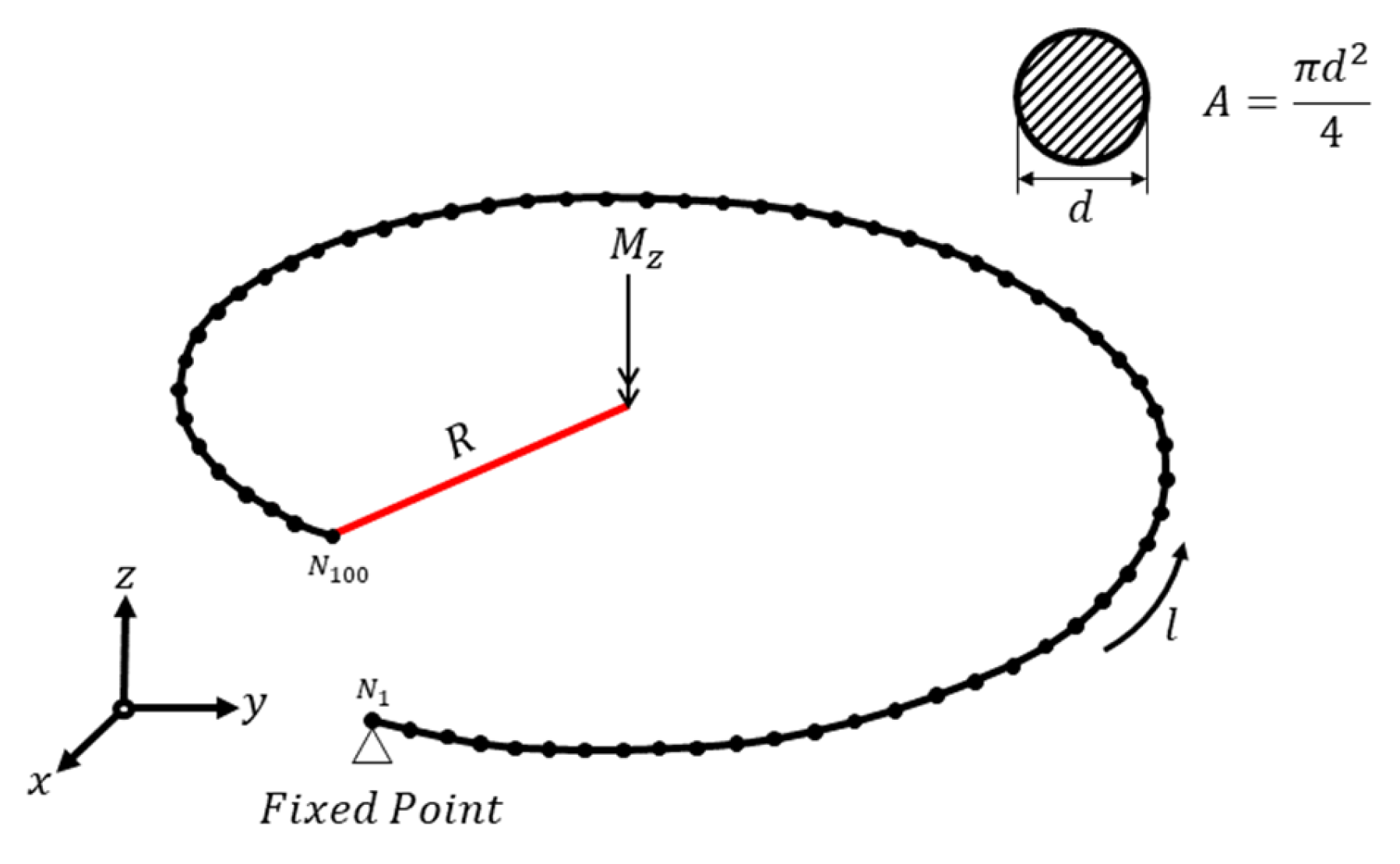
3. Torsion-Spring Displacement Analysis
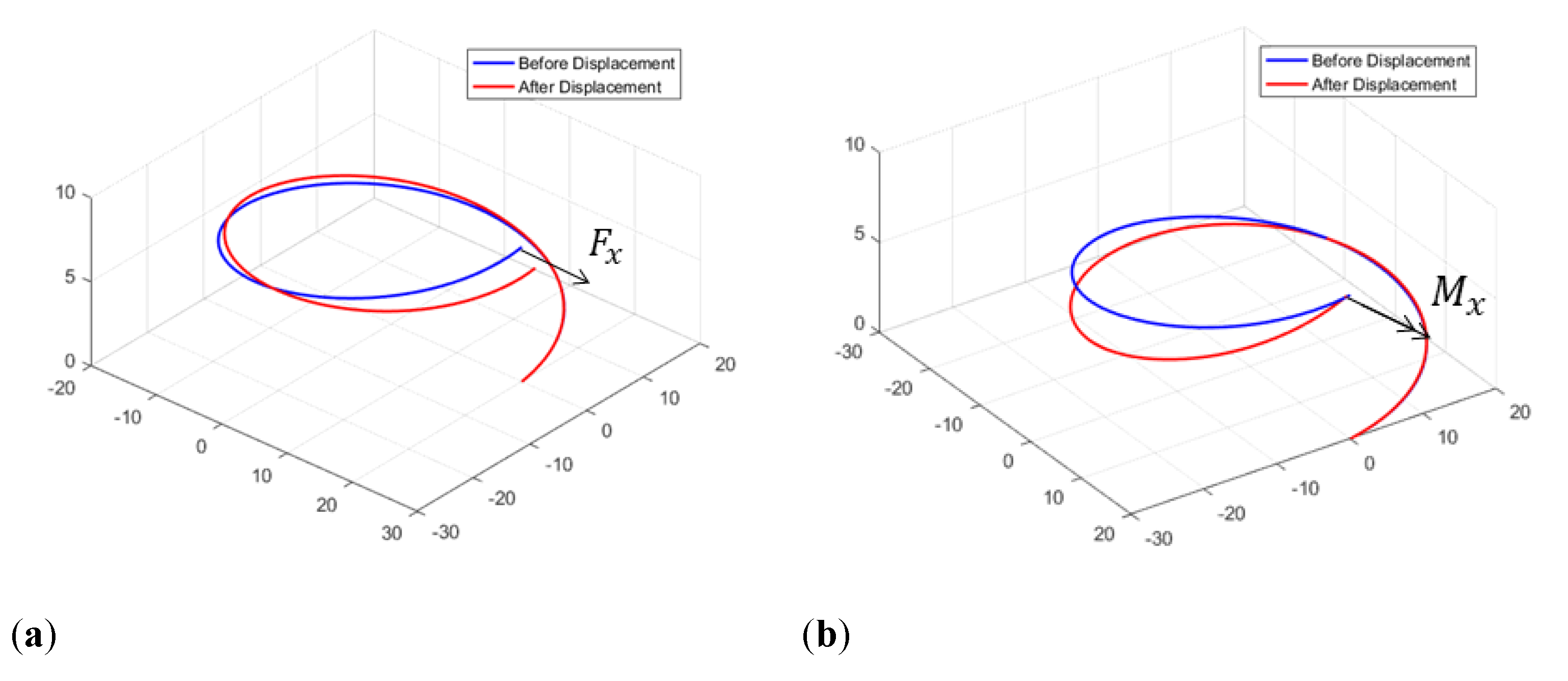
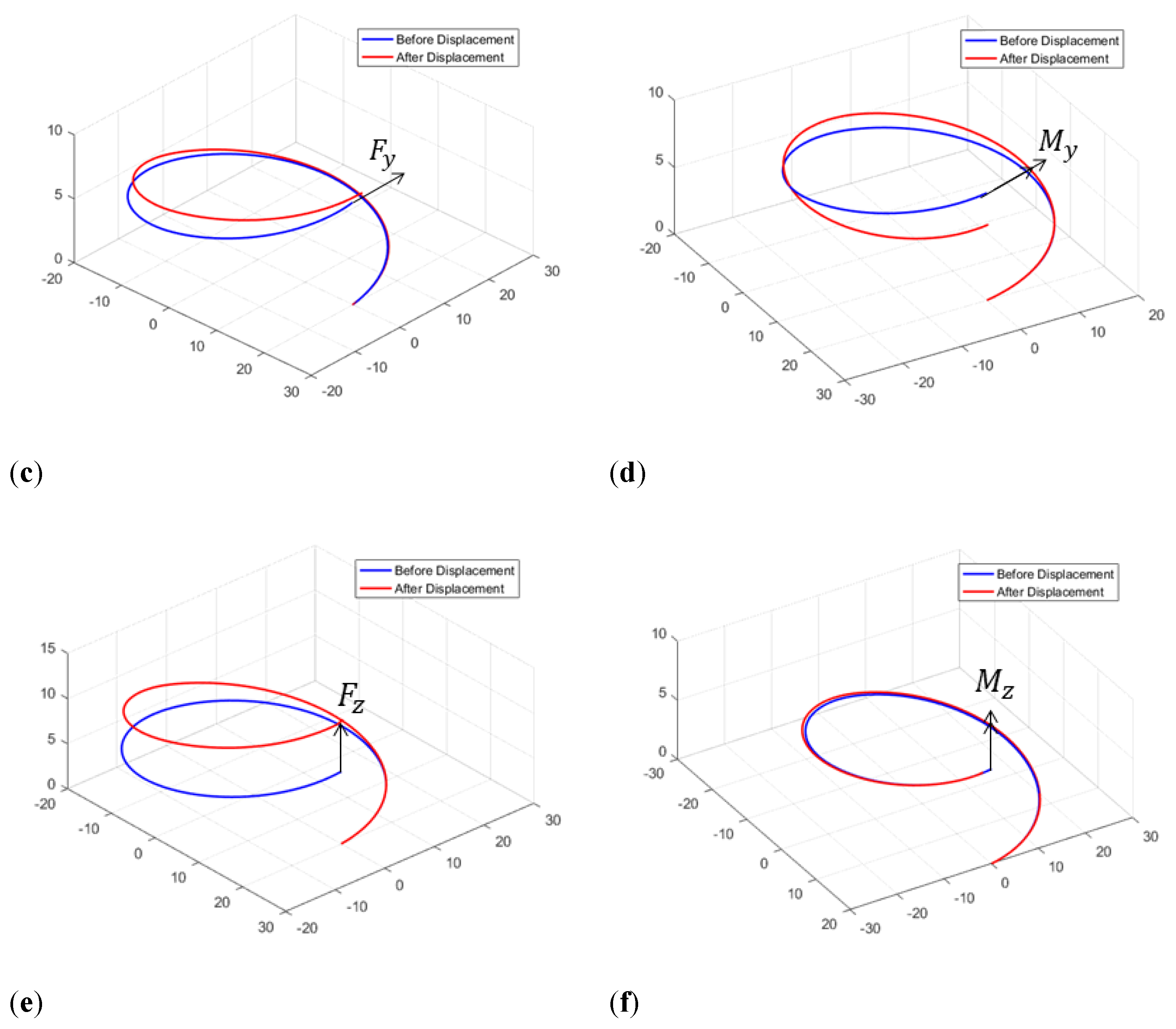
3.1. Torsion-Spring Displacement Analysis
3.2. Experiment-Equipment Setup
4. Results and Discussion
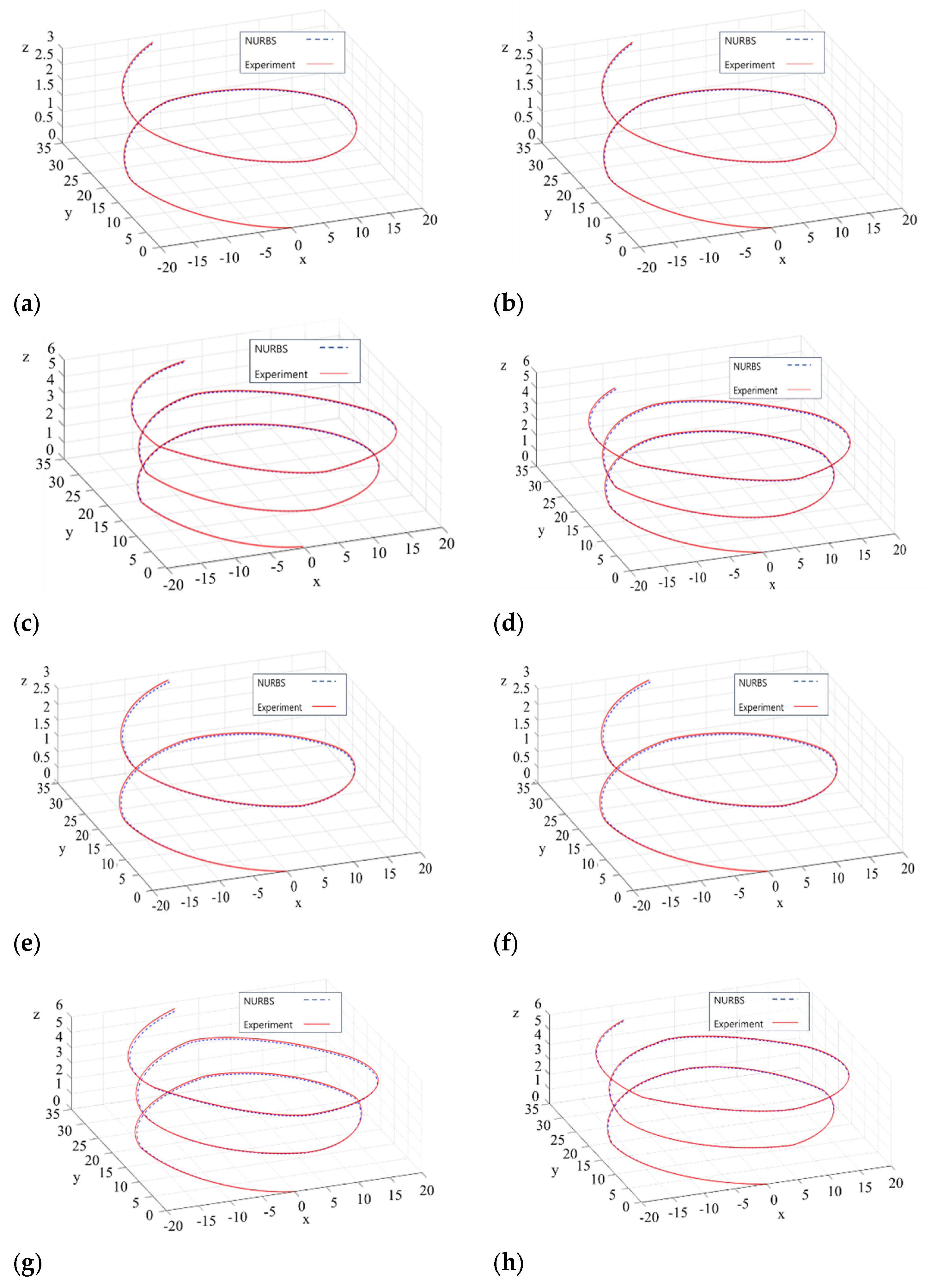
4.1. Experiment-Data Analysis
4.2. Comparative Analysis of Analytical Results and Experiment Values
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Yuldirim, V. Exact determination of the global tip deflection of both close-coiled and open-coiled cylindrical helical compression spring having arbitrary doubly-symmetric cross-section. Int. J. Mech. Sci. 2016, 115–116, 280–298. [Google Scholar] [CrossRef]
- Wahl, A.M.; Bisshopp, K.E. Mechanical Springs (Second Edition). J. Appl. Mech. 1964, 31, 159–160. [Google Scholar] [CrossRef]
- Pollanen, I.; Martikka, H. Opimal re-design of helical spring using fuzzy design and FEM. Adv. Eng. Softw. 2010, 41, 410–414. [Google Scholar] [CrossRef]
- Chaudhury, A.N.; Datta, D. Analysis of prismatic springs of non-circular coil shape and non-prismatic springs of circular coil shape by analytical and finite element methods. J. Comput. Des. Eng. 2017, 4, 178–191. [Google Scholar] [CrossRef]
- Gzal, M.; Groper, M.; Gendelman, O. Analytical, experimental and finite element analysis of elliptical cross-section helical spring with small helix angle under static load. Int. J. Mech. Sci. 2017, 130, 476–486. [Google Scholar] [CrossRef]
- Chassie, G.; Becker, L.; Cleghorn, W. On the buckling of helical springs under combined compression and torsion. Int. J. Mech. Sci. 1997, 39, 697–704. [Google Scholar] [CrossRef]
- Gao, J.; Luo, Z.; Xiao, M.; Gao, L.; Li, P. A NURBS-based Multi-Material Interpolation (N-MMI) for isogeometric topology optimization of structures. Appl. Math. Model. 2020, 81, 818–843. [Google Scholar] [CrossRef]
- Alderson, T.; Samavati, F. Multiscale NURBS curves on the sphere and ellipsoid. Comput. Graph. 2019, 82, 243–249. [Google Scholar] [CrossRef]
- Timoshenko, S.P. Mechanics of Materials; Chaoman & Hall: London, UK, 1911. [Google Scholar]
- Piegl, L.; Tiller, W.; Piegl, L. The NURBS Book; Springer: Heidelberg, Germany, 1997. [Google Scholar]
- Ferreira, A.J.M. MATLAB Codes for Finite Element Analysis: Solid Mechanics and its Applications; Springer: Heidelberg, Germany, 2008; Volume 157. [Google Scholar]
- Shimoseki, M.; Hamano, T.; Inaizumi, T. FEM for Springs; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Zhao, X.-Y.; Zhu, C. Injectivity of NURBS curves. J. Comput. Appl. Math. 2016, 302, 129–138. [Google Scholar] [CrossRef]
- Zhang, B.; Li, C.; Wang, T.; Wang, Z.; Ma, H. Design and experimental study of zero-compensation steering gear load simulator with double torsion springs. Meas. 2019, 148, 106930. [Google Scholar] [CrossRef]
- Kilic, M.; Yazicioglu, Y.; Kurtulus, D.F. Synthesis of a torsional spring mechanism with mechanically adjustable stiffness using wrapping cams. Mech. Mach. Theory 2012, 57, 27–39. [Google Scholar] [CrossRef]





| Parameters | Unit | Dimension |
|---|---|---|
| Spring cross-section diameter () | mm | 3 |
| Spring radius () | mm | 20 |
| Spring length () | mm | 125.6 |
| Moment in the z-axis direction () | N m | 1000 |
| Elastic modulus | GPa | 206 |
| Type | (mm) | (mm) | |
|---|---|---|---|
| 1 | 2.6 | 32.6 | 1.5 |
| 2 | 2.6 | 32.6 | 2.5 |
| 3 | 2.8 | 32.8 | 1.5 |
| 4 | 2.8 | 32.8 | 2.5 |
| 5 | 3.0 | 33.0 | 1.5 |
| 6 | 2.0 | 33.0 | 2.5 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.S.; Song, Y.J.; Jeon, E.S. Numerical and Experimental Analysis of Torsion Springs Using NURBS Curves. Appl. Sci. 2020, 10, 2629. https://doi.org/10.3390/app10072629
Kim YS, Song YJ, Jeon ES. Numerical and Experimental Analysis of Torsion Springs Using NURBS Curves. Applied Sciences. 2020; 10(7):2629. https://doi.org/10.3390/app10072629
Chicago/Turabian StyleKim, Young Shin, Yu Jun Song, and Euy Sik Jeon. 2020. "Numerical and Experimental Analysis of Torsion Springs Using NURBS Curves" Applied Sciences 10, no. 7: 2629. https://doi.org/10.3390/app10072629
APA StyleKim, Y. S., Song, Y. J., & Jeon, E. S. (2020). Numerical and Experimental Analysis of Torsion Springs Using NURBS Curves. Applied Sciences, 10(7), 2629. https://doi.org/10.3390/app10072629





