A New Analytical Approach for Nonlinear Global Buckling of Spiral Corrugated FG-CNTRC Cylindrical Shells Subjected to Radial Loads
Abstract
1. Introduction
2. Equivalent Model of Spiral Corrugated FG-CNTRC Cylindrical Shells
3. Governing Equations
4. Approximate Solution and Galerkin Procedure
5. Numerical Investigations and Remarks
6. Conclusions
- (1)
- The corrugated FG-CNTRC cylindrical shells are homogenized by equivalent non-corrugated FG-CNTRC cylindrical shells.
- (2)
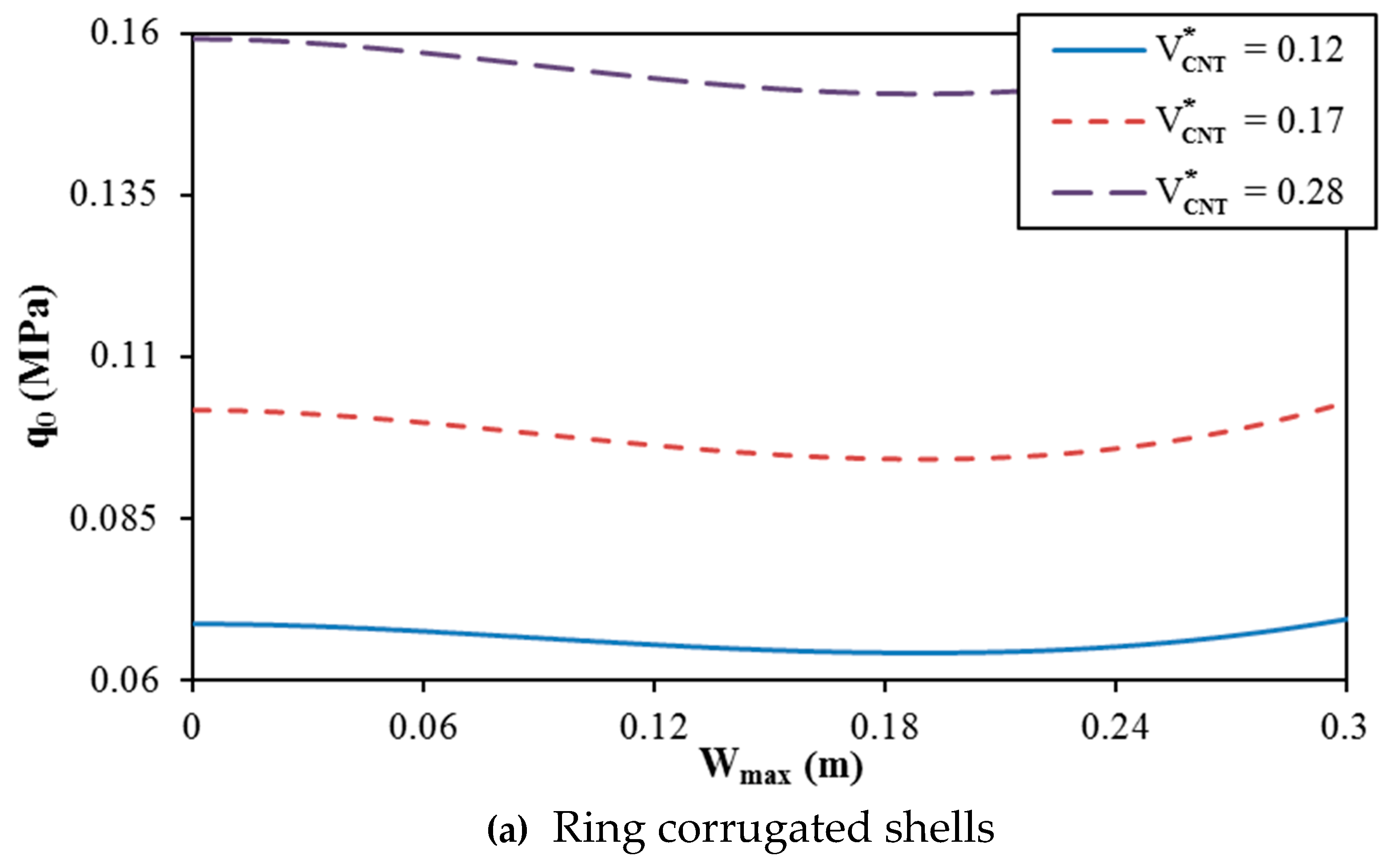
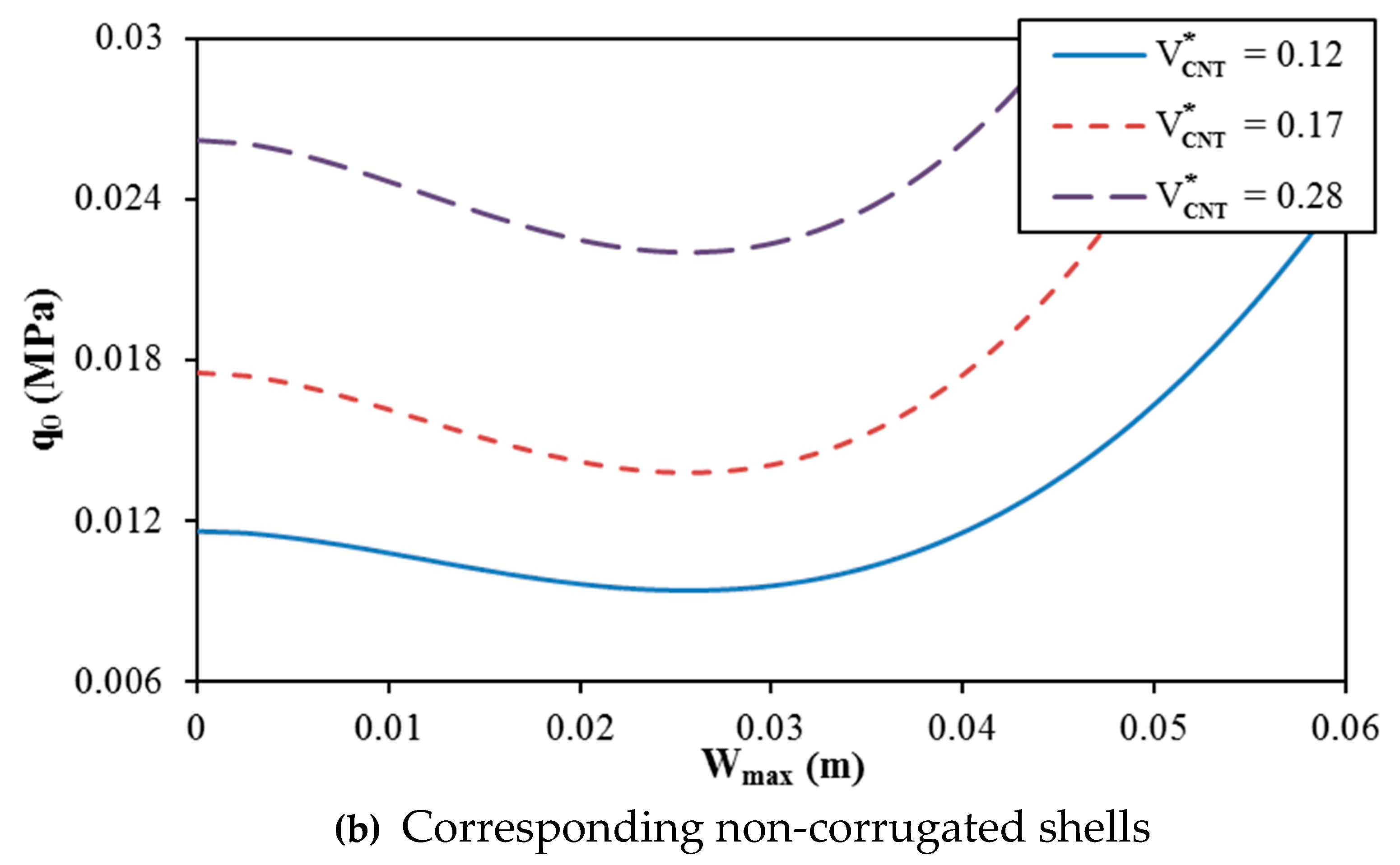
- The critical buckling load of a corrugated FG-CNTRC cylindrical shell is must larger than that of a non-corrugated FG-CNTRC cylindrical shell.
- (3)
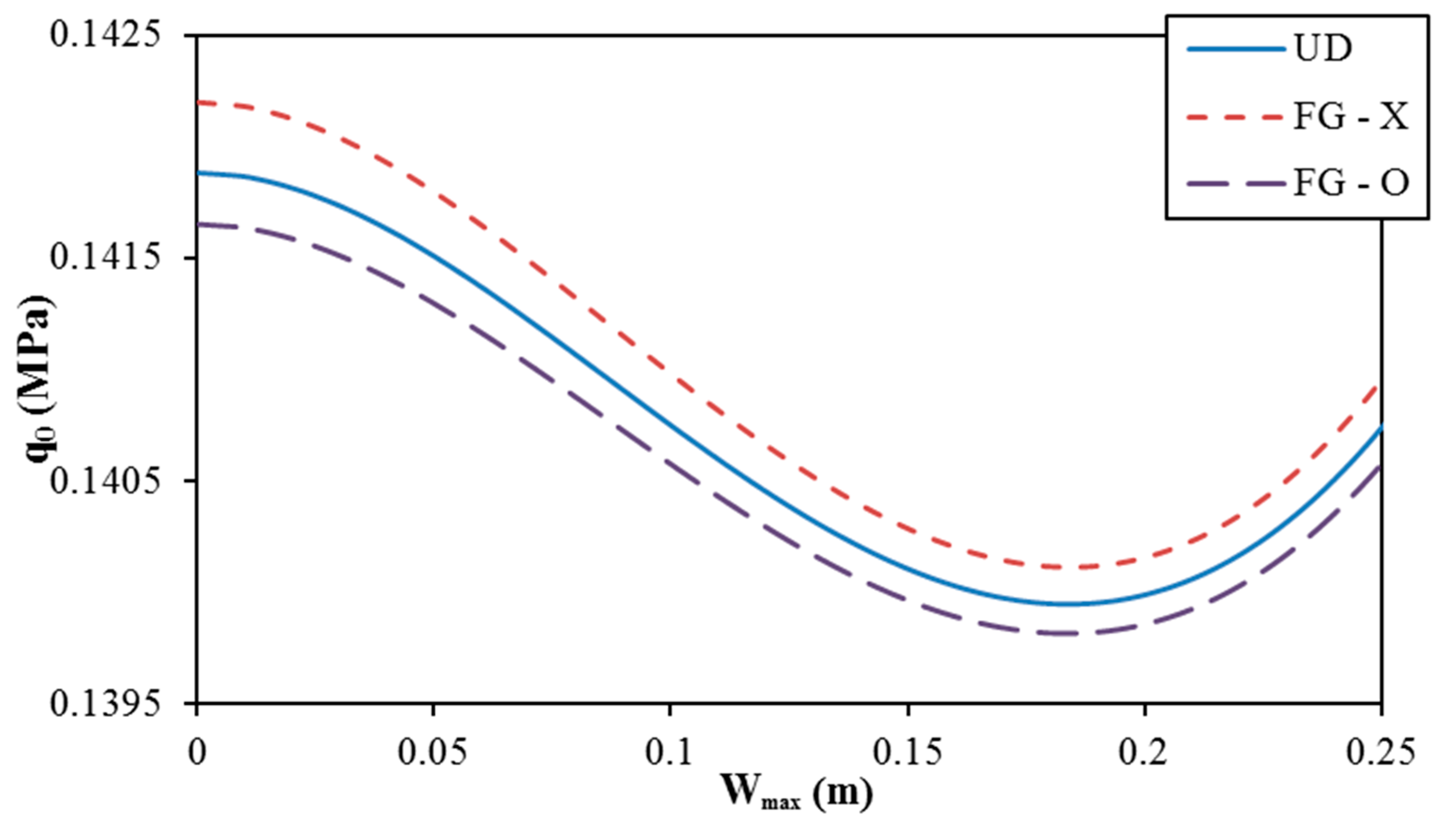
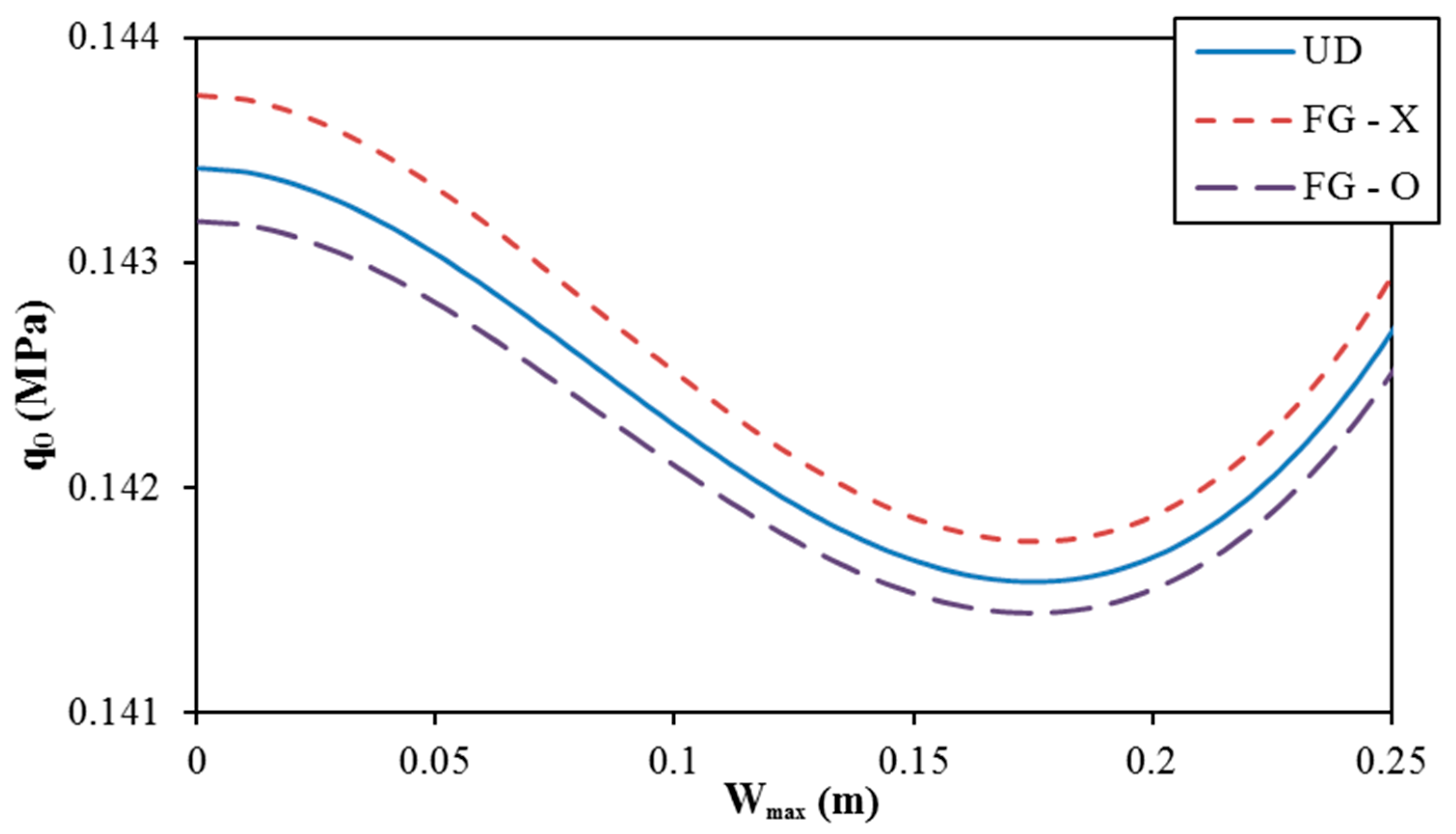
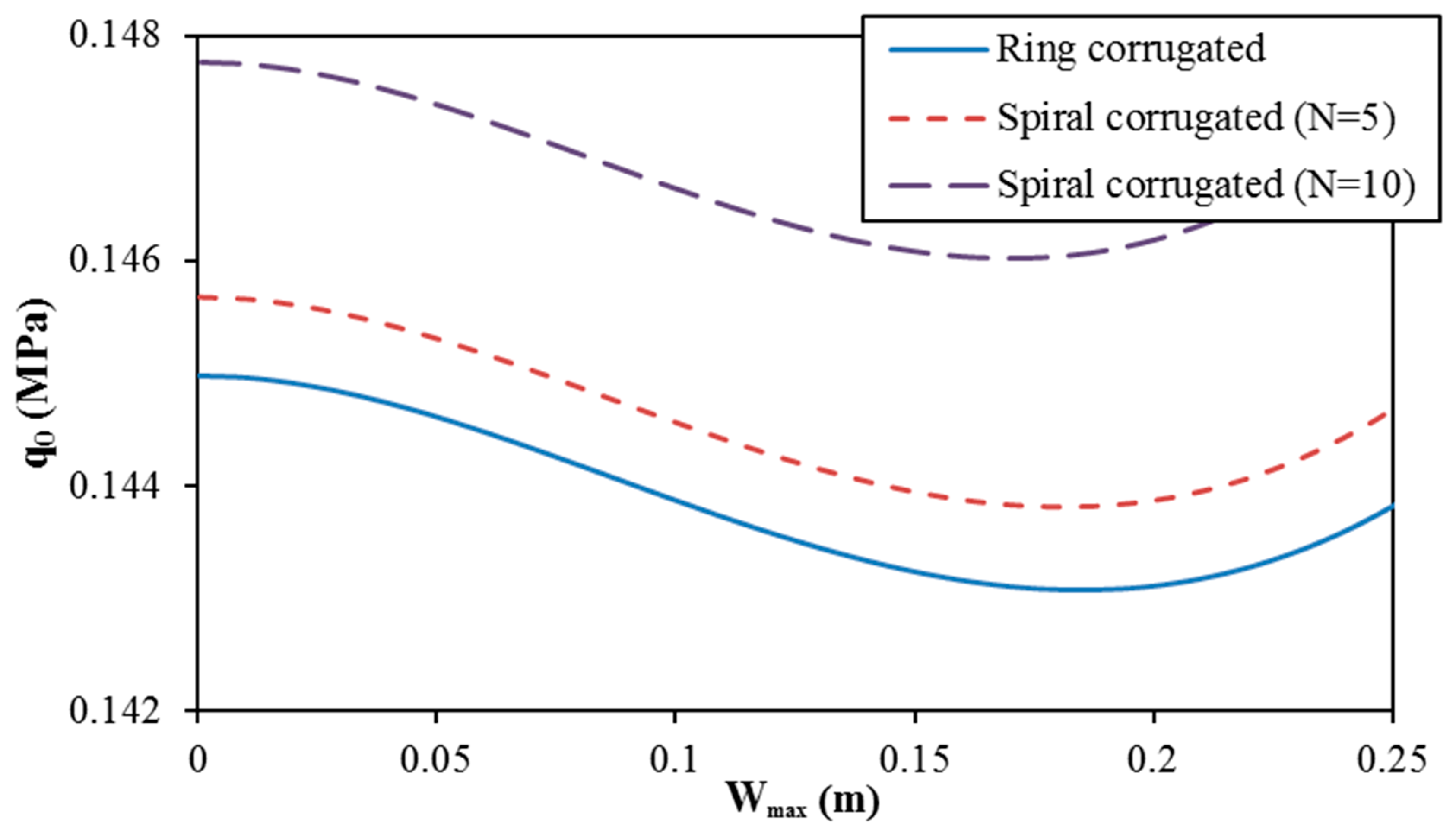
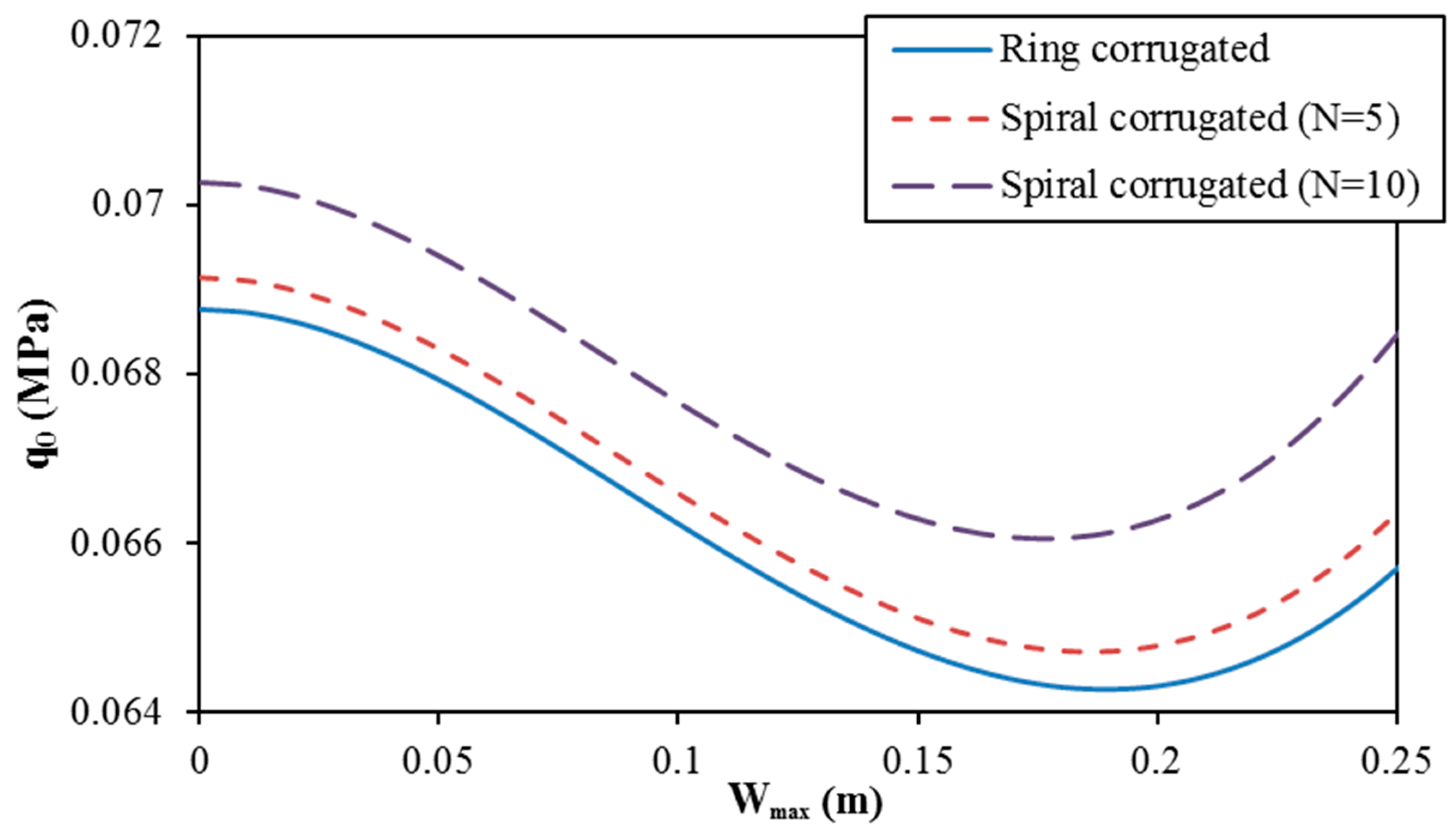
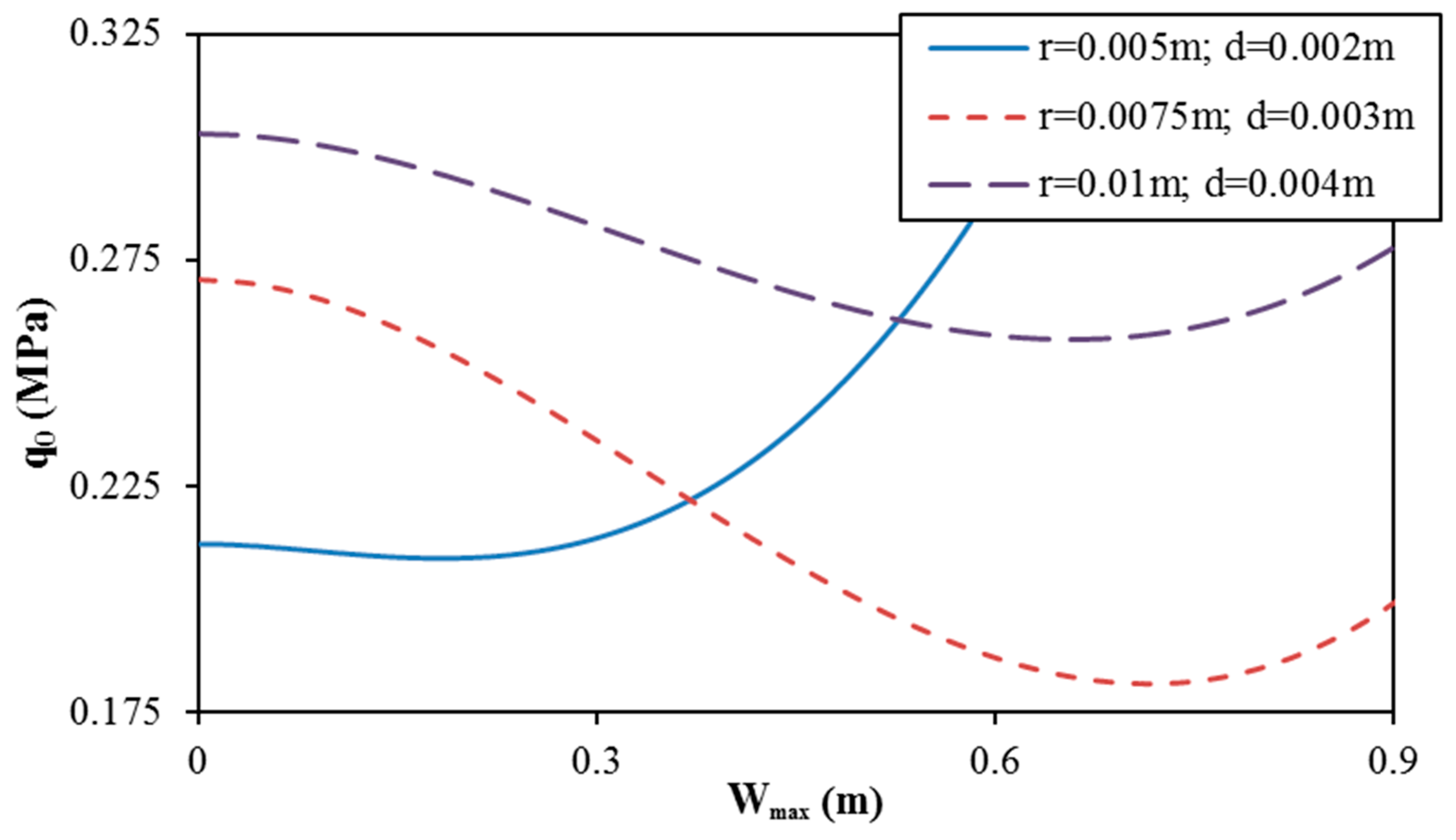
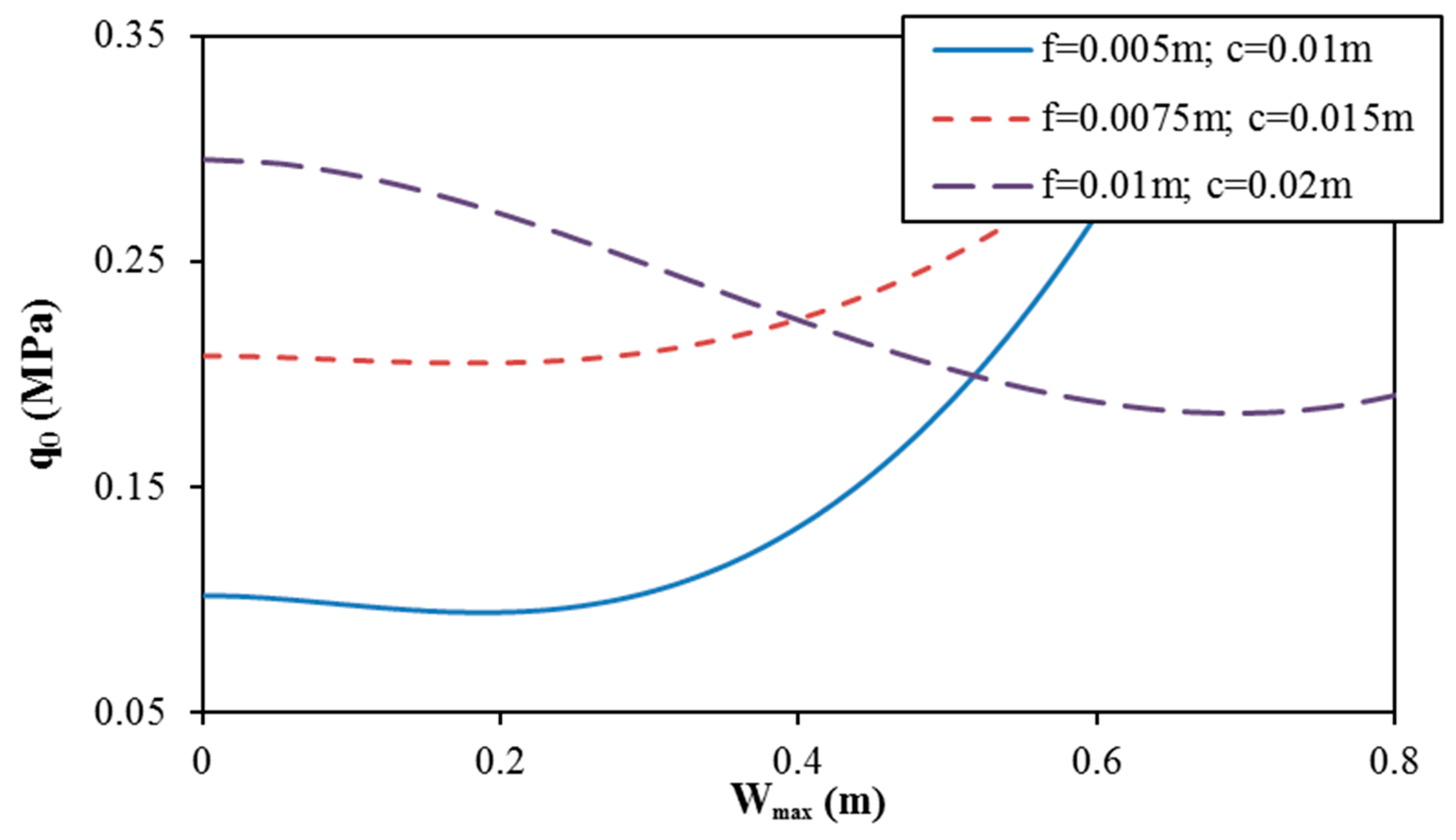
- Geometrical properties of two types of corrugations and material parameters of FG-CNTRC shells significantly influence the linear and nonlinear buckling responses of shells.
Author Contributions
Funding
Conflicts of Interest
References
- Shen, H.S. Postbuckling analysis of axially-loaded functionally graded cylindrical shells in thermal environments. Compos. Sci. Technol. 2002, 62, 977–987. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling analysis of pressure-loaded functionally graded cylindrical shells in thermal environments. Eng. Struct. 2003, 25, 487–497. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Postbuckling of pressure-loaded piezolaminated cylindrical shells with temperature dependent properties. Int. J. Struct. Stab. Dyn. 2007, 7, 1–22. [Google Scholar] [CrossRef]
- Huang, H.; Han, Q. Buckling of imperfect functionally graded cylindrical shells under axial compression. Eur. J. Mech. A Solids 2008, 27, 1026–1036. [Google Scholar] [CrossRef]
- Huang, H.; Han, Q. Nonlinear elastic buckling and postbuckling of axially compressed functionally graded cylindrical shells. Int. J. Mech. Sci. 2009, 51, 500–507. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Schnak, E. The stability of functionally graded cylindrical shells under linearly increasing dynamic torsional loading. Eng. Struct. 2004, 26, 1321–1331. [Google Scholar] [CrossRef]
- Sofiyev, A.H. Buckling analysis of FGM circular shells under combined loads and resting on the Pasternak type elastic foundation. Mech. Res. Commun. 2010, 37, 539–544. [Google Scholar] [CrossRef]
- Sofiyev, A.H. The buckling of FGM truncated conical shells subjected to combined axial tension and hydrostatic pressure. Compos. Struct. 2010, 92, 488–498. [Google Scholar] [CrossRef]
- Sofiyev, A.H. The buckling of FGM truncated conical shells subjected to axial compressive load and resting on Winkler–Pasternak foundations. Int. J. Press. Vessel. Pip. 2010, 87, 753–761. [Google Scholar] [CrossRef]
- Sofiyev, A.H. On the vibration and stability of clamped FGM conical shells under external loads. J. Compos. Mater. 2011, 45, 771–788. [Google Scholar] [CrossRef]
- Heydarpour, Y.; Malekzadeh, P.; Dimitri, R.; Tornabene, F. Thermoelastic Analysis of Functionally Graded Cylindrical Panels with Piezoelectric Layers. Appl. Sci. 2020, 10, 1397. [Google Scholar] [CrossRef]
- Bagherizadeh, E.; Kiani, Y.; Eslami, M.R. Mechanical buckling of functionally graded material cylindrical shells surrounded by Pasternak elastic foundation. Compos. Struct. 2011, 93, 3063–3071. [Google Scholar] [CrossRef]
- Allahkarami, F.; Tohidi, H.; Dimitri, R.; Tornabene, F. Dynamic Stability of Bi-Directional Functionally Graded Porous Cylindrical Shells Embedded in an Elastic Foundation. Appl. Sci. 2020, 10, 1345. [Google Scholar] [CrossRef]
- Hakula, H.; Laaksonen, M. Frequency Response Analysis of Perforated Shells with Uncertain Materials and Damage. Appl. Sci. 2019, 9, 5299. [Google Scholar] [CrossRef]
- Nam, V.H.; Phuong, N.T.; Minh, K.V.; Hieu, P.T. Nonlinear thermo-mechanical buckling and post-buckling of multilayer FGM cylindrical shell reinforced by spiral stiffeners surrounded by elastic foundation subjected to torsional loads. Eur. J. Mech. A Solid 2018, 72, 393–406. [Google Scholar] [CrossRef]
- Nam, V.H.; Phuong, N.T.; Trung, N.T. Nonlinear buckling and postbuckling of sandwich FGM cylindrical shells reinforced by spiral stiffeners under torsion loads in thermal environment. Acta Mech. 2019, 230, 3183–3204. [Google Scholar] [CrossRef]
- Nam, V.H.; Phuong, N.T.; Doan, C.V.; Trung, N.T. Nonlinear Thermo-Mechanical Stability Analysis of Eccentrically Spiral Stiffened Sandwich Functionally Graded Cylindrical Shells Subjected to External Pressure. Int. J. Appl. Mech. 2019, 11, 1950045. [Google Scholar] [CrossRef]
- Phuong, N.T.; Nam, V.H.; Trung, N.T.; Duc, V.M.; Phong, P.V. Nonlinear Stability of Sandwich Functionally Graded Cylindrical Shells with Stiffeners Under Axial Compression in Thermal Environment. Int. J. Struct. Stab. Dyn. 2019, 19, 1950073. [Google Scholar] [CrossRef]
- Nam, V.H.; Trung, N.T.; Hoa, L.K. Buckling and postbuckling of porous cylindrical shells with functionally graded composite coating under torsion in thermal environment. Thin Walled Struct. 2019, 144, 106253. [Google Scholar] [CrossRef]
- Miller, B.; Ziemiański, L. Maximization of Eigenfrequency Gaps in a Composite Cylindrical Shell Using Genetic Algorithms and Neural Networks. Appl. Sci. 2019, 9, 2754. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part I: Axially-loaded shells. Compos. Struct. 2011, 93, 2096–2108. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling of nanotube-reinforced composite cylindrical shells in thermal environments, Part II: Pressure-loaded shells. Compos. Struct. 2011, 93, 2496–2503. [Google Scholar] [CrossRef]
- Shen, H.S. Postbuckling of nanotube-reinforced composite cylindrical panels resting on elastic foundations subjected to lateral pressure in thermal environments. Eng. Struct. 2016, 122, 174–183. [Google Scholar] [CrossRef]
- Shen, H.S.; Xiang, Y. Postbuckling of nanotube-reinforced composite cylindrical shells under combined axial and radial mechanical loads in thermal environment. Compos. Part B Eng. 2013, 52, 311–322. [Google Scholar] [CrossRef]
- Jam, J.E.; Kiani, Y. Buckling of pressurized functionally graded carbon nanotube reinforced conical shells. Compos. Struct. 2015, 125, 586–595. [Google Scholar] [CrossRef]
- Kiani, Y. Dynamics of FG-CNT reinforced composite cylindrical panel subjected to moving load. Thin Walled Struct. 2017, 111, 48–57. [Google Scholar] [CrossRef]
- Kiani, Y. Analysis of FG-CNT reinforced composite conical panel subjected to moving load using Ritz method. Thin Walled Struct. 2017, 119, 47–57. [Google Scholar] [CrossRef]
- Kiani, Y.; Dimitri, R.; Tornabene, F. Free vibration of FG-CNT reinforced composite skew cylindrical shells using the Chebyshev-Ritz formulation. Compos. Part B Eng. 2018, 147, 169–177. [Google Scholar] [CrossRef]
- Hajmohammad, M.H.; Kolahchi, R.; Zarei, M.S.; Maleki, M. Earthquake induced dynamic deflection of submerged viscoelastic cylindrical shell reinforced by agglomerated CNTs considering thermal and moisture effects. Compos. Struct. 2018, 187, 498–508. [Google Scholar] [CrossRef]
- Hajmohammad, M.H.; Farrokhian, A.; Kolahchi, R. Smart control and vibration of viscoelastic actuator-multiphase nanocomposite conical shells-sensor considering hygrothermal load based on layerwise theory. Aerosp. Sci. Technol. 2018, 78, 260–270. [Google Scholar] [CrossRef]
- Hosseini, H.; Kolahchi, R. Seismic response of functionally graded-carbon nanotubes-reinforced submerged viscoelastic cylindrical shell in hygrothermal environment. Physica E Low Dimens. Syst. Nanostruct. 2018, 102, 101–109. [Google Scholar] [CrossRef]
- Jiao, P.; Chen, Z.; Li, Y.; Ma, H.; Wu, J. Dynamic buckling analyses of functionally graded carbon nanotubes reinforced composite (FG-CNTRC) cylindrical shell under axial power-law time-varying displacement load. Compos. Struct. 2019, 220, 784–797. [Google Scholar] [CrossRef]
- Qin, Z.; Pang, X.; Safaei, B.; Chu, F. Free vibration analysis of rotating functionally graded CNT reinforced composite cylindrical shells with arbitrary boundary conditions. Compos. Struct. 2019, 220, 847–860. [Google Scholar] [CrossRef]
- Torabi, J.; Ansari, R.; Hassani, R. Numerical study on the thermal buckling analysis of CNT-reinforced composite plates with different shapes based on the higher-order shear deformation theory. Eur. J. Mech. A Solid 2019, 73, 144–160. [Google Scholar] [CrossRef]
- Vinyas, M. A higher-order free vibration analysis of carbon nanotube-reinforced magneto-electro-elastic plates using finite element methods. Compos. Part B Eng. 2019, 158, 286–301. [Google Scholar] [CrossRef]
- SafarPour, H.; Ghanbari, B.; Ghadiri, M. Buckling and free vibration analysis of high speed rotating carbon nanotube reinforced cylindrical piezoelectric shell. Appl. Math. Model. 2019, 65, 428–442. [Google Scholar] [CrossRef]
- Zhao, J.; Choe, K.; Shuai, C.; Wang, A.; Wang, Q. Free vibration analysis of functionally graded carbon nanotube reinforced composite truncated conical panels with general boundary conditions. Compos. Part B Eng. 2019, 160, 225–240. [Google Scholar] [CrossRef]
- Sofiyev, A.H.; Turkaslan, B.E.; Bayramov, R.P.; Sala, M.U. Analytical solution of stability of FG-CNTRC conical shells under external pressures. Thin Walled Struct. 2019, 144, 106338. [Google Scholar] [CrossRef]
- Ghasemi, A.R.; Mohandes, M.; Dimitri, R.; Tornabene, F. Agglomeration effects on the vibrations of CNTs/fiber/polymer/metal hybrid laminates cylindrical shell. Compos. Part B Eng. 2019, 167, 700–716. [Google Scholar] [CrossRef]
- Arefi, M.; Masoud, M.; Sara, A.A.; Rabczuk, T. FSDT electro-elastic analysis of FG-CNTRC cylindrical three-layered pressure vessels with piezoelectric face-sheets. Thin Walled Struct. 2019, 144, 106320. [Google Scholar] [CrossRef]
- Mallek, H.; Jrad, H.; Algahtani, A.; Wali, M.; Dammak, F. Geometrically non-linear analysis of FG-CNTRC shell structures with surface-bonded piezoelectric layers. Comput. Methods Appl. Mech. Eng. 2019, 347, 679–699. [Google Scholar] [CrossRef]
- Chakraborty, S.; Dey, T.; Kumar, R. Stability and vibration analysis of CNT-Reinforced functionally graded laminated composite cylindrical shell panels using semi-analytical approach. Compos. Part B Eng. 2019, 168, 1–14. [Google Scholar] [CrossRef]
- Dindarloo, H.M.; Li, L. Vibration analysis of carbon nanotubes reinforced isotropic doubly-curved nanoshells using nonlocal elasticity theory based on a new higher order shear deformation theory. Compos. Part B Eng. 2019, 175, 107170. [Google Scholar] [CrossRef]
- Khosravi, S.; Arvin, H.; Kiani, Y. Interactive thermal and inertial buckling of rotating temperature-dependent FG-CNT reinforced composite beams. Compos. Part B Eng. 2019, 175, 107178. [Google Scholar] [CrossRef]
- Zhou, T.; Song, Y. Three-dimensional nonlinear bending analysis of FG-CNTs reinforced composite plates using the element-free Galerkin method based on the S-R decomposition theorem. Compos. Struct. 2019, 207, 519–530. [Google Scholar] [CrossRef]
- Beni, N.N. Free vibration analysis of annular sector sandwich plates with FG-CNT reinforced composite face-sheets based on the Carrera’s Unified Formulation. Compos. Struct. 2019, 214, 269–292. [Google Scholar] [CrossRef]
- Fang, H.; Tan, P.; Du, X.; Li, B.; Yang, K.; Zhang, Y. Numerical and Experimental Investigation of the Effect of Traffic Load on the Mechanical Characteristics of HDPE Double-Wall Corrugated Pipe. Appl. Sci. 2020, 10, 627. [Google Scholar] [CrossRef]
- Xia, Y.; Friswell, M.I.; Flores, E.I.S. Equivalent models of corrugated panels. Int. J. Solids Struct. 2012, 49, 1453–1462. [Google Scholar] [CrossRef]
- Brush, D.D.; Almroth, B.O. Buckling of Bars, Plates and Shells; Mc. Graw-Hill: New York, NY, USA, 1975. [Google Scholar]
- Han, Y.; Elliott, J. Molecular dynamics simulations of the elastic properties of polymer/carbon nanotube composites. Comp. Mater. Sci. 2007, 39, 315–323. [Google Scholar] [CrossRef]

| UD | Shen [22] | 42.68(1,10) * | 23.40(1,8) | 18.18(1,7) | |
| Present | 42.82(1,10) | 23.45(1,8) | 18.51(1,7) | ||
| FG-X | Shen [22] | 49.48(1,10) | 25.60(1,8) | 19.91(1,7) | |
| Present | 48.65(1,10) | 25.37(1,8) | 19.78(1,7) | ||
| UD | Shen [22] | 70.06(1,10) | 38.98(1,8) | 30.81(1,7) | |
| Present | 70.28(1,10) | 39.06(1,8) | 30.85(1,7) | ||
| FG-X | Shen [22] | 82.76(1,10) | 43.83(1,8) | 34.15(1,7) | |
| Present | 81.44(1,10) | 43.47(1,8) | 33.94(1,7) | ||
| UD | Shen [22] | 84.34(1,10) | 45.11(1,8) | 35.56(1,7) | |
| Present | 84.67(1,10) | 45.22(1,8) | 35.62(1,7) | ||
| FG-X | Shen [22] | 109.42(1,10) | 55.84(1,8) | 43.24(1,7) | |
| Present | 108.68(1,10) | 56.01(1,8) | 43.44(1,7) |
| UD | FG-X | FG-O | |
|---|---|---|---|
| Round corrugated cylindrical shells = 0.12, = 0.0075 m, = 0.003 m. | |||
| Non corrugated | 0.0207(1,5) * | 0.0267(1,5) | 0.0124(1,6) |
| Ring corrugated | 0.1668(1,1) | 0.1732(1,1) | 0.1625(1,1) |
| N = 1 | 0.1673(1,1) | 0.1737(1,1) | 0.1630(1,1) |
| N = 3 | 0.1716(1,1) | 0.1782(1,1) | 0.1672(1,1) |
| N = 5 | 0.1803(1,1) | 0.1874(1,1) | 0.1756(1,1) |
| Maximal critical buckling load | 0.8079(1,3,59) ** | 0.8083(1,3,59) | 0.8076(1,3,59) |
| Trapezoidal corrugated cylindrical shells = 0.12, = 0.015 m, = 0.0075 m, | |||
| Non corrugated | 0.0116(1,6) | 0.0160(1,6) | 0.0073(1,6) |
| Ring corrugated | 0.1419(1,2) | 0.1422(1,2) | 0.1417(1,2) |
| N = 1 | 0.1419(1,2) | 0.1423(1,2) | 0.1417(1,2) |
| N = 3 | 0.1424(1,2) | 0.1428(1,2) | 0.1422(1,2) |
| N = 5 | 0.1434(1,2) | 0.1437(1,2) | 0.1432(1,2) |
| Maximal critical buckling load | 0.3544(1,3,59) | 0.3548(1,3,59) | 0.3541(1,3,58) |
| (m) | (m) | Non Corrugated | Ring Corrugated | Spiral Corrugated | |||
|---|---|---|---|---|---|---|---|
| N = 1 | N = 3 | N = 5 | |||||
| 0 | 0.005 | 0.002 | 0.0016(1,9) | 0.0072(1,2) | 0.0072(1,2) | 0.0073(1,2) | 0.0073(1,2) |
| 0.0075 | 0.003 | 0.0016(1,9) | 0.0108(1,2) | 0.0108(1.2) | 0.0109(1,2) | 0.0110(1,2) | |
| 0.01 | 0.004 | 0.0016(1,9) | 0.0176(1,2) | 0.0176(1,2) | 0.0177(1,2) | 0.0180(1,2) | |
| 0.12 | 0.005 | 0.002 | 0.0207(1,5) | 0.1450(1,2) | 0.1450(1,2) | 0.1452(1,2) | 0.1457(1,2) |
| 0.0075 | 0.003 | 0.0207(1,5) | 0.1668(1,1) | 0.1673(1,1) | 0.1716(1,1) | 0.1803(1,1) | |
| 0.01 | 0.004 | 0.0207(1,5) | 0.1913(1,1) | 0.1922(1,1) | 0.1996(1,1) | 0.2149(1,1) | |
| 0.17 | 0.005 | 0.002 | 0.0311(1,6) | 0.2119(1,2) | 0.2119(1,2) | 0.2123(1,2) | 0.2129(1,2) |
| 0.0075 | 0.003 | 0.0311(1,6) | 0.2630(1,1) | 0.2638(1,1) | 0.2707(1,1) | 0.2848(1,1) | |
| 0.01 | 0.004 | 0.0311(1,6) | 0.2900(1,1) | 0.2915(1,1) | 0.3030(1,1) | 0.3267(1,1) | |
| 0.28 | 0.005 | 0.002 | 0.0449(1,5) | 0.3410(1,2) | 0.3411(1,2) | 0.3416(1,2) | 0.3427(1,2) |
| 0.0075 | 0.003 | 0.0449(1,5) | 0.3531(1,1) | 0.3542(1,1) | 0.3630(1,1) | 0.3809(1,1) | |
| 0.01 | 0.004 | 0.0449(1,5) | 0.4286(1,1) | 0.4306(1,1) | 0.4468(1,1) | 0.4799(1,1) | |
| (m) | (m) | Non Corrugated | Ring Corrugated | Spiral Corrugated | |||
|---|---|---|---|---|---|---|---|
| N = 1 | N = 3 | N = 5 | |||||
| 0 | 0.01 | 0.005 | 0.0009(1,9) | 0.0048(1,3) | 0.0048(1,3) | 0.0048(1,3) | 0.0048(1,3) |
| 0.015 | 0.0075 | 0.0009(1,9) | 0.0072(1,2) | 0.0072(1,2) | 0.0073(1,2) | 0.0074(1,2) | |
| 0.02 | 0.01 | 0.0009(1,9) | 0.0091(1,2) | 0.0091(1,2) | 0.0092(1,2) | 0.0093(1,2) | |
| 0.12 | 0.01 | 0.005 | 0.0116(1,6) | 0.0688(1,2) | 0.0688(1,2) | 0.0689(1,2) | 0.0691(1,2) |
| 0.015 | 0.0075 | 0.0116(1,6) | 0.1419(1,2) | 0.1419(1,2) | 0.1424(1,2) | 0.1434(1,2) | |
| 0.02 | 0.01 | 0.0116(1,6) | 0.1741(1,1) | 0.1752(1,1) | 0.1837(1,1) | 0.2018(1,1) | |
| 0.17 | 0.01 | 0.005 | 0.0175(1,6) | 0.1018(1,2) | 0.1018(1,2) | 0.1020(1,2) | 0.1024(1,2) |
| 0.015 | 0.0075 | 0.0175(1,6) | 0.2074(1,2) | 0.2075(1,2) | 0.2082(1,2) | 0.2097(1,2) | |
| 0.02 | 0.01 | 0.0175(1,6) | 0.2796(1,1) | 0.2813(1,1) | 0.2953(1,1) | 0.3248(1,1) | |
| 0.28 | 0.01 | 0.005 | 0.0262(1,6) | 0.1592(1,2) | 0.1592(1,2) | 0.1595(1,2) | 0.1600(1,2) |
| 0.015 | 0.0075 | 0.0262(1,6) | 0.3337(1,2) | 0.3338(1,2) | 0.3350(1,2) | 0.3373(1,2) | |
| 0.02 | 0.01 | 0.0262(1,6) | 0.3586(1,1) | 0.3607(1,1) | 0.3778(1,1) | 0.4138(1,1) | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vu, T.H.; Vu, H.N.; Dang, T.D.; Le, N.L.; Nguyen, T.T.X.; Trung, N.-T.; Nguyen, T.P. A New Analytical Approach for Nonlinear Global Buckling of Spiral Corrugated FG-CNTRC Cylindrical Shells Subjected to Radial Loads. Appl. Sci. 2020, 10, 2600. https://doi.org/10.3390/app10072600
Vu TH, Vu HN, Dang TD, Le NL, Nguyen TTX, Trung N-T, Nguyen TP. A New Analytical Approach for Nonlinear Global Buckling of Spiral Corrugated FG-CNTRC Cylindrical Shells Subjected to Radial Loads. Applied Sciences. 2020; 10(7):2600. https://doi.org/10.3390/app10072600
Chicago/Turabian StyleVu, Tho Hung, Hoai Nam Vu, Thuy Dong Dang, Ngoc Ly Le, Thi Thanh Xuan Nguyen, Nguyen-Thoi Trung, and Thi Phuong Nguyen. 2020. "A New Analytical Approach for Nonlinear Global Buckling of Spiral Corrugated FG-CNTRC Cylindrical Shells Subjected to Radial Loads" Applied Sciences 10, no. 7: 2600. https://doi.org/10.3390/app10072600
APA StyleVu, T. H., Vu, H. N., Dang, T. D., Le, N. L., Nguyen, T. T. X., Trung, N.-T., & Nguyen, T. P. (2020). A New Analytical Approach for Nonlinear Global Buckling of Spiral Corrugated FG-CNTRC Cylindrical Shells Subjected to Radial Loads. Applied Sciences, 10(7), 2600. https://doi.org/10.3390/app10072600






