Vertical Dynamic Response Prediction of the Electromagnetic Levitation Systems
Abstract
1. Introduction
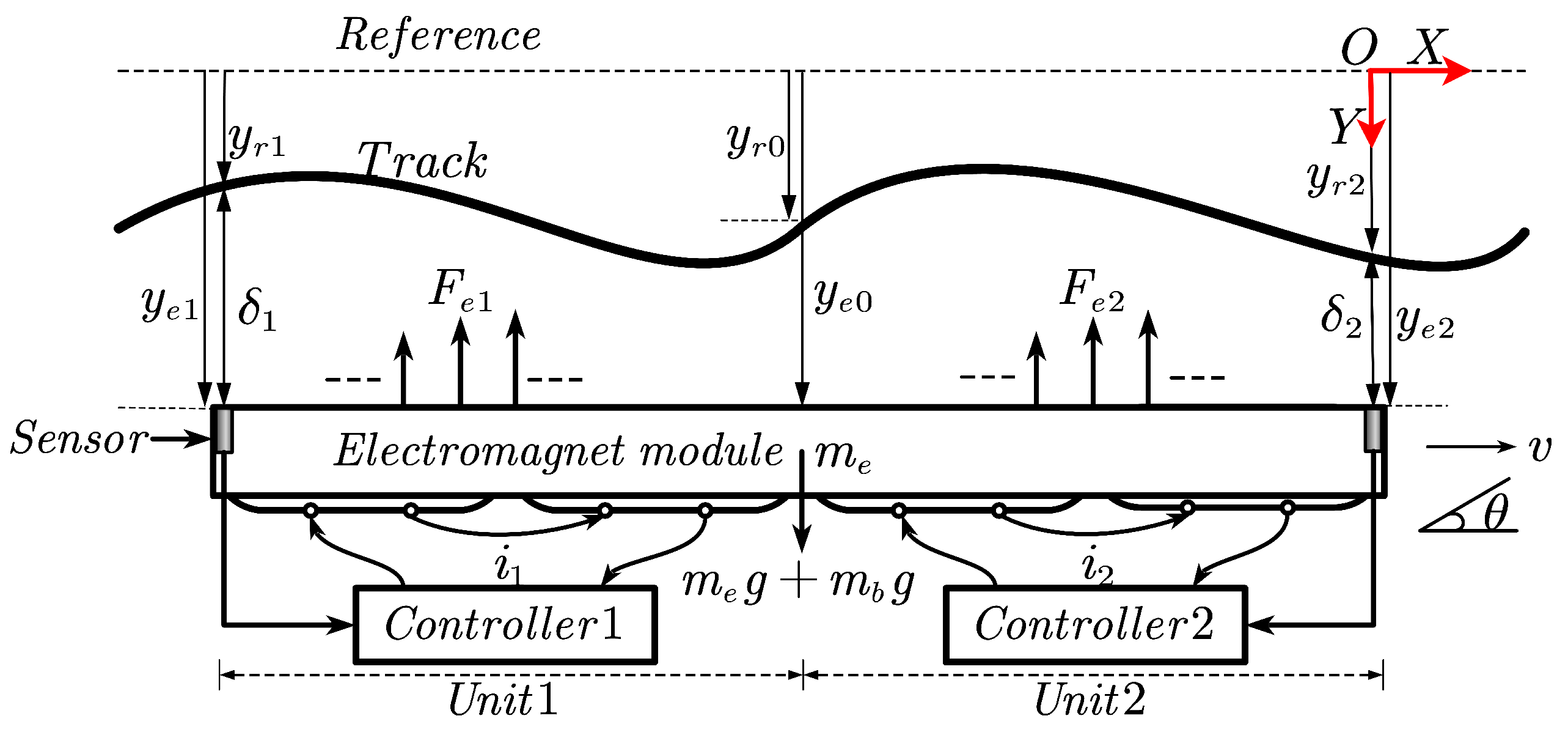
2. Vertical Dynamic Modeling of the Electromagnetic Levitation System
2.1. Modeling of the Electromagnetic Levitation System
2.2. Linear Model in the Frequency Domain
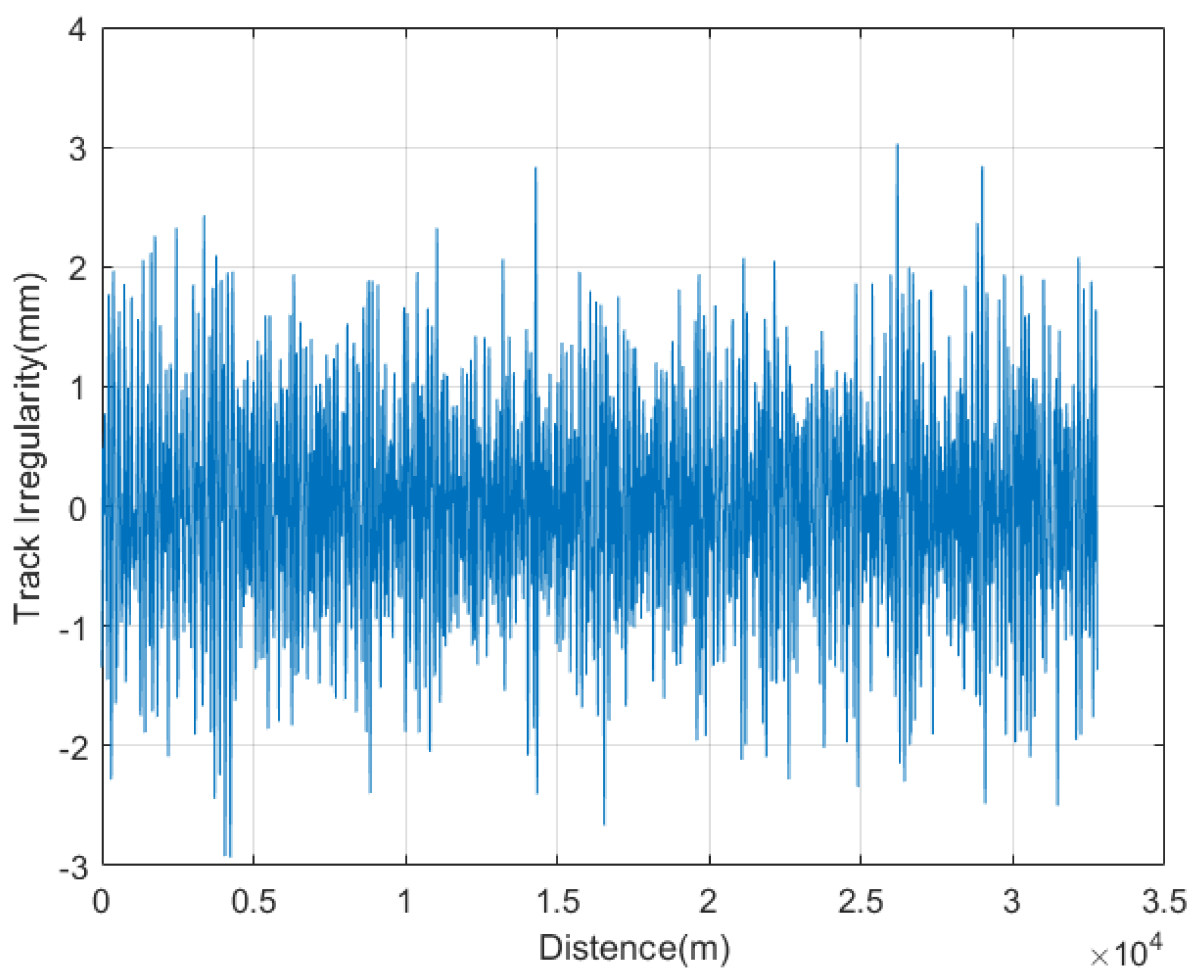
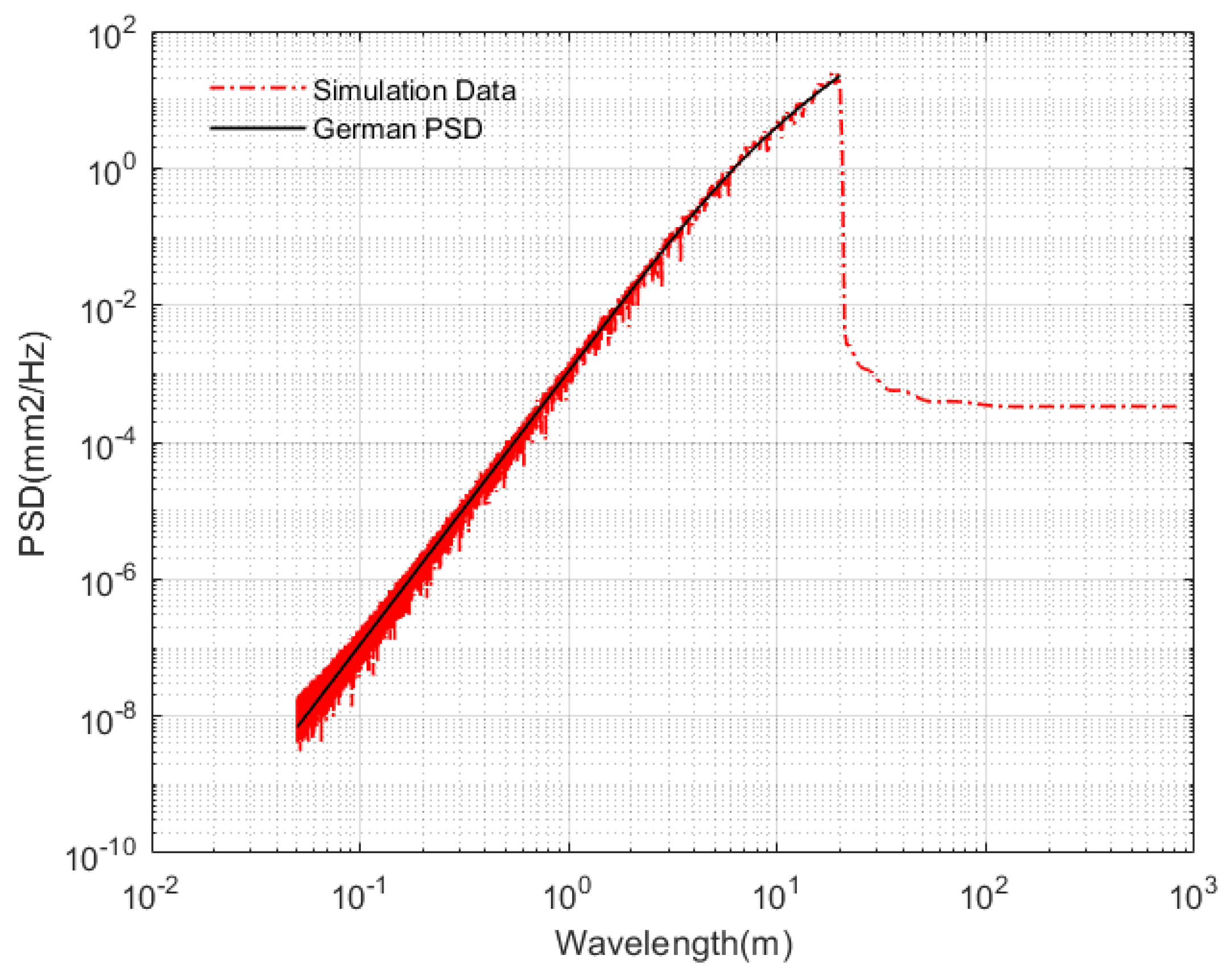
3. Vertical Dynamic Prediction under Track Irregularity
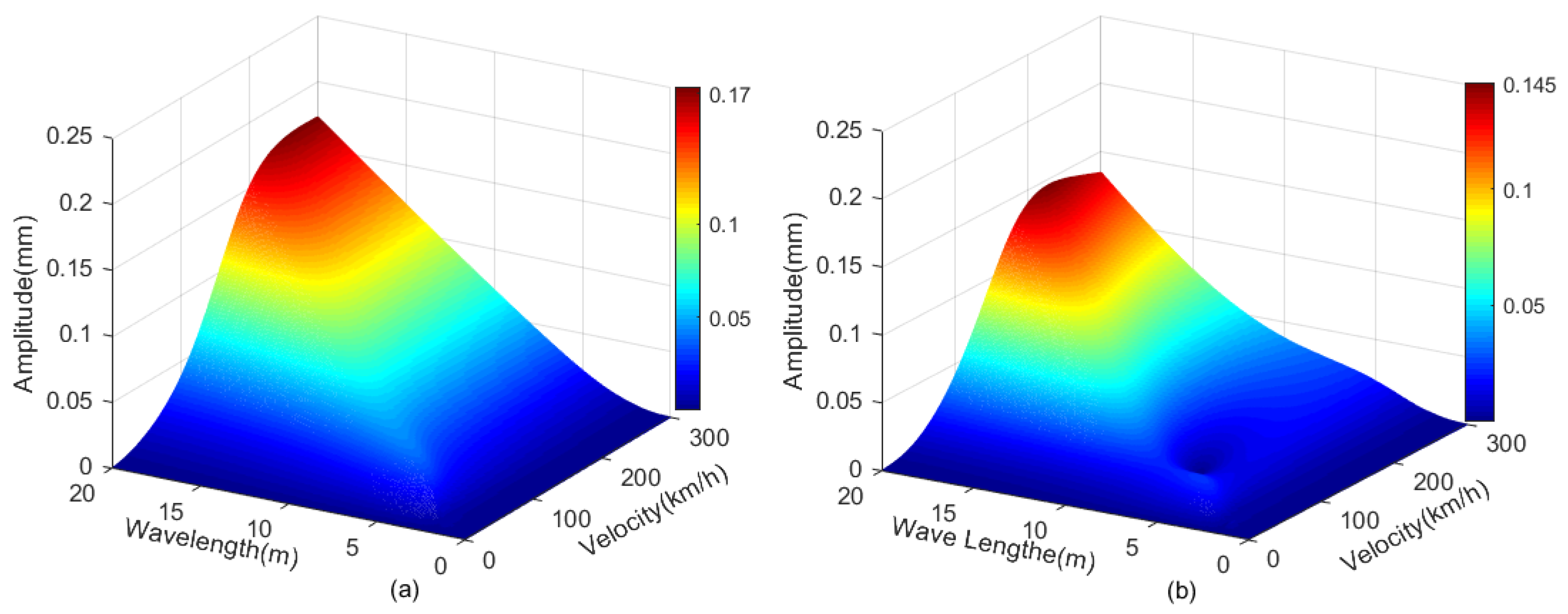
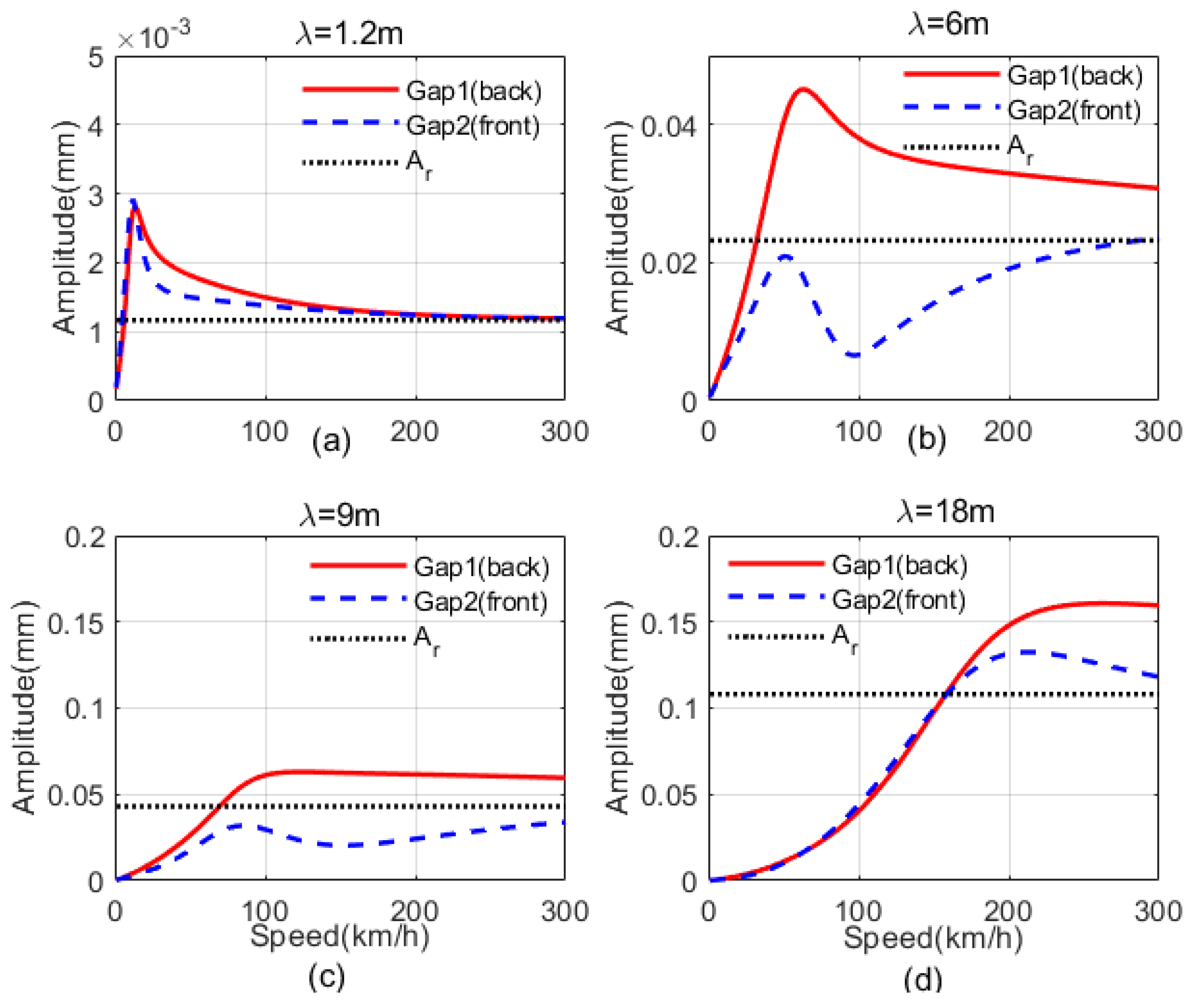
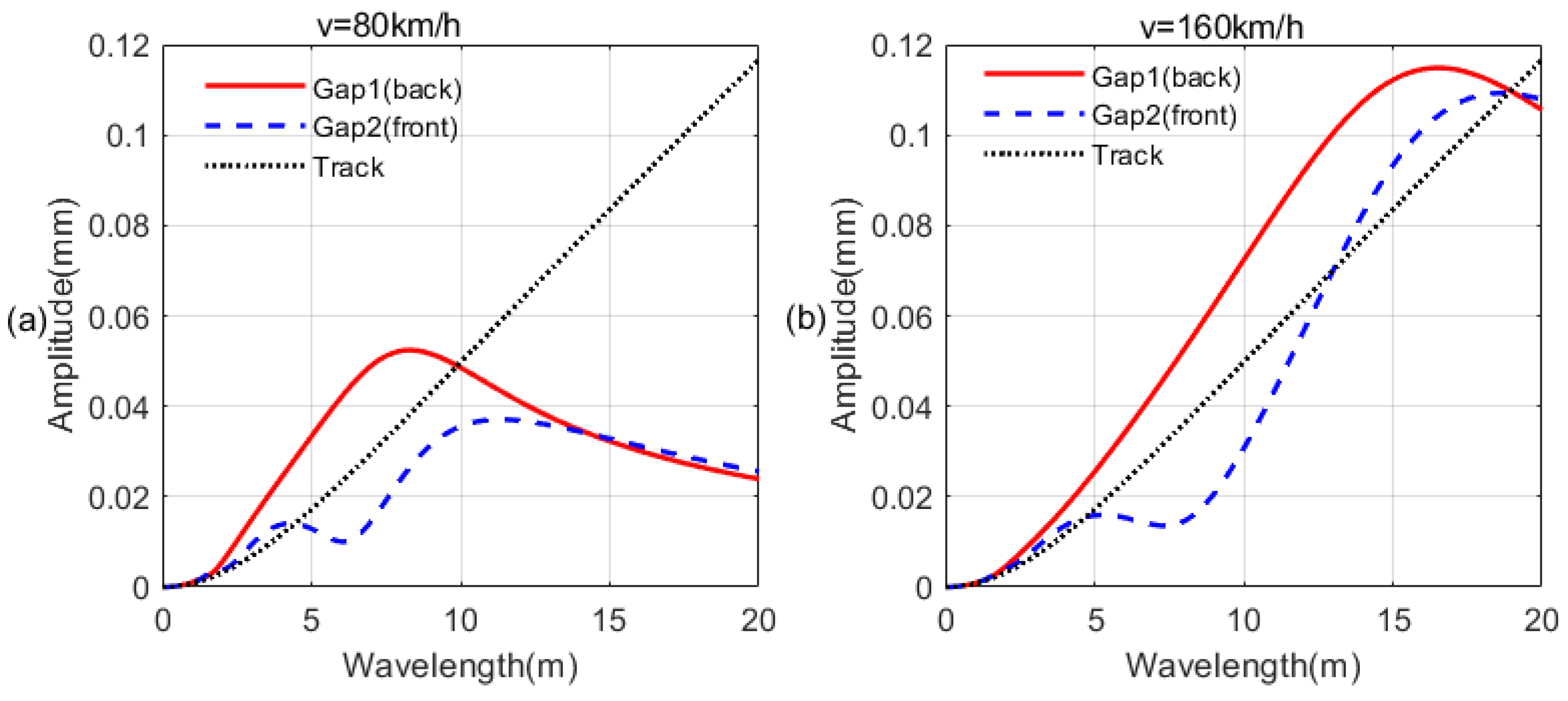
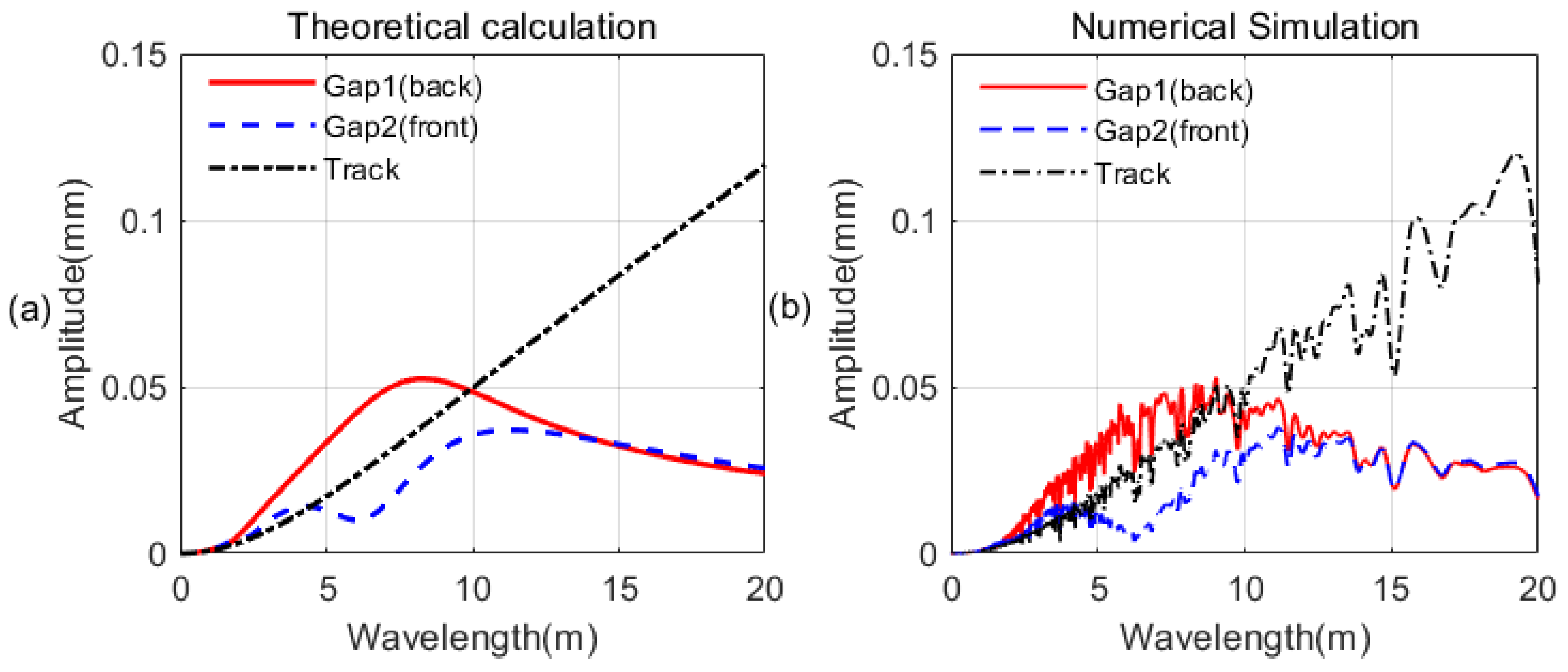
- When the speed is very low, the amplitudes of both levitation gaps are relatively small at different wavelengths, which means that the electromagnet module can strictly track the space trajectory of the track. With the increase of the speed, the amplitude spectrum values of the levitation gaps generally rise, which means that the tracking performance of the electromagnet module is reduced.
- When the wavelength is close to 0, the amplitude spectrum values of both levitation gaps are relatively small at different speeds. In this case, the electromagnet module keeps its inertial position stable and does not track the space trajectory of the track. Therefore, the amplitude of the levitation gap is equal to the amplitude of the track. However, as the amplitude of the track at small wavelengths is small, the amplitude values of the levitation gaps are relatively small. Although this means that the tracking performance of the levitation control system is very weak, it is consistent with the phenomenon that the high-frequency signal is ignored, which is expected in the levitation control system.
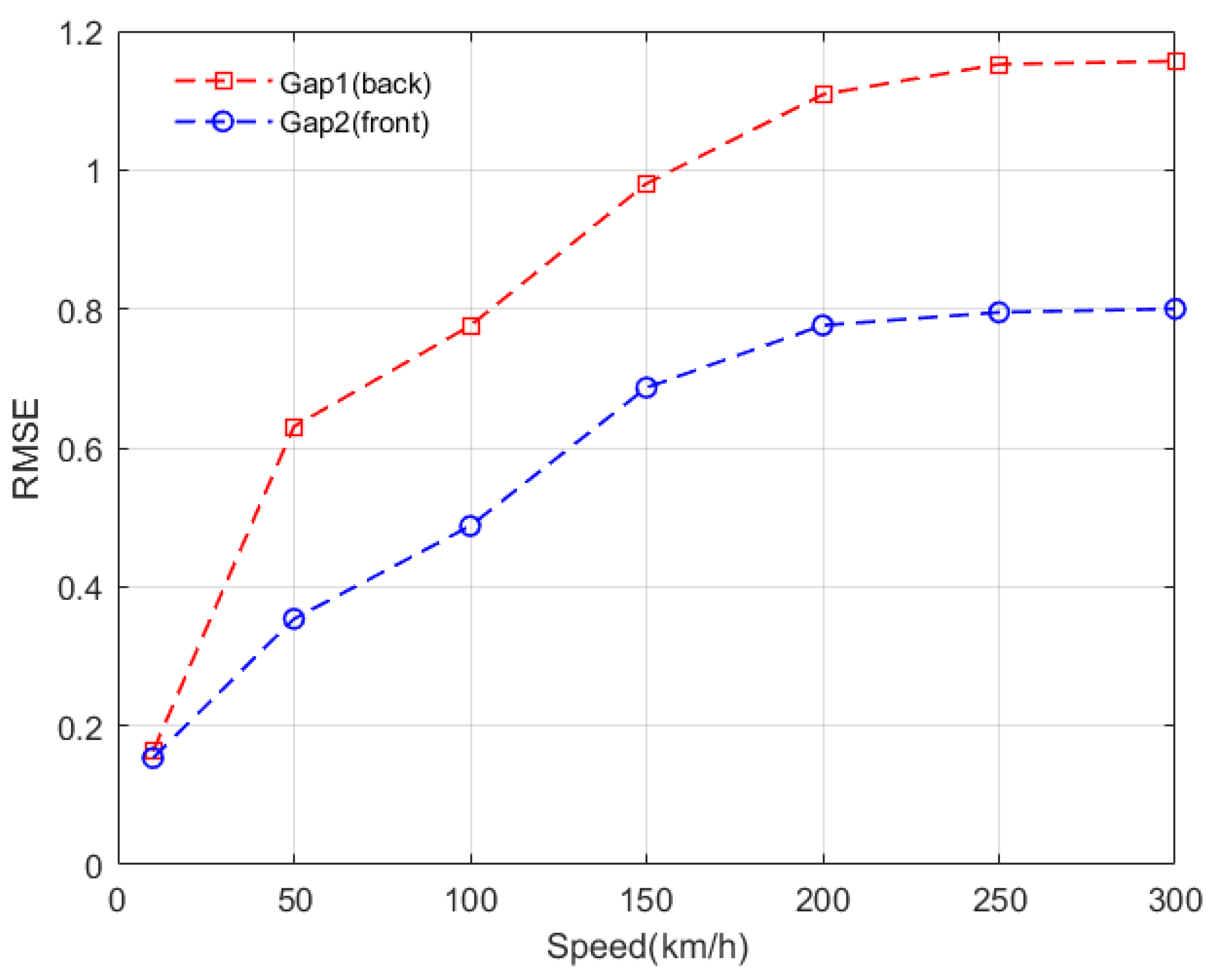
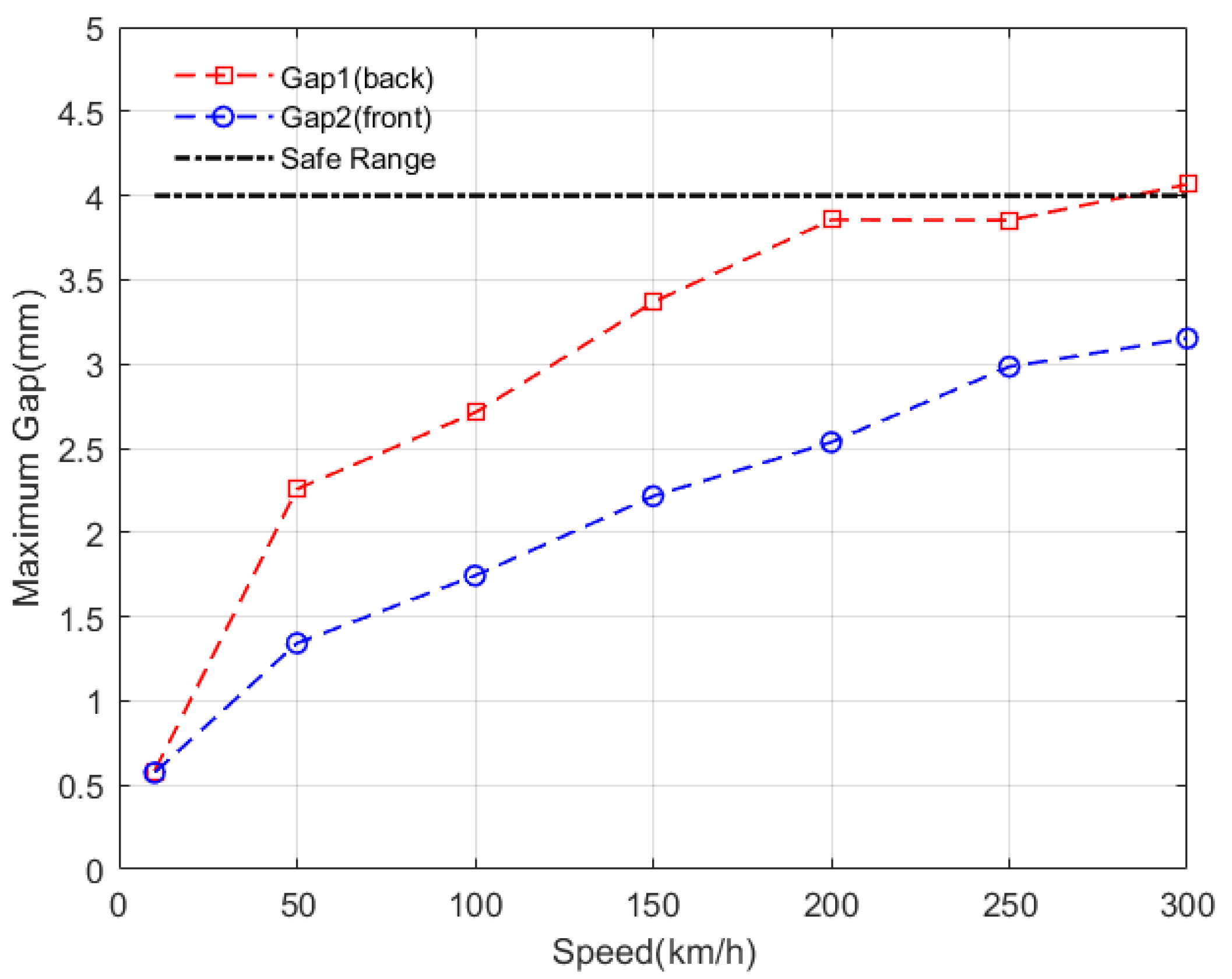
- The maximum value appears in the case of high speed and large wavelength, which is consistent with engineering experience. When the speed is very high, we need to pay special attention to the track irregularities at large wavelengths. Due to the larger amplitude of the long-wave track irregularities, the contributions of the long-wave track irregularities to the gap deviation is also large.
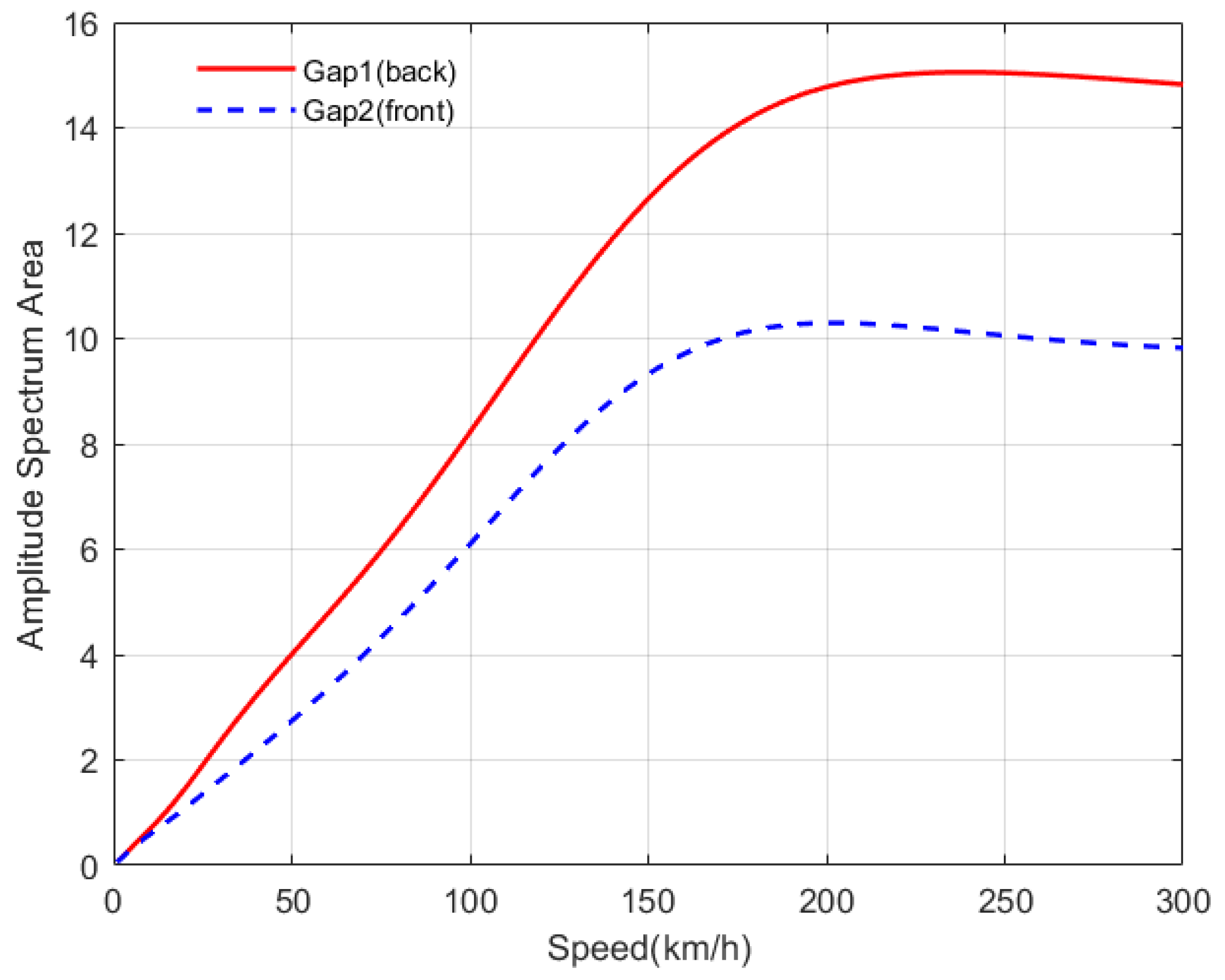
- The amplitudes of the two levitation gaps are different. Moreover, in a broad range of wavelength and speed, the amplitudes of the back gap are larger than that of the front gap. As the input amplitudes of the two levitation gaps are the same, the difference in the transfer functions is the main reason for the dynamic response difference.
3.1. Analysis of Levitation Gap Deviation
3.2. Analysis of Typical Wavelengths
3.3. Analysis of Typical Speeds
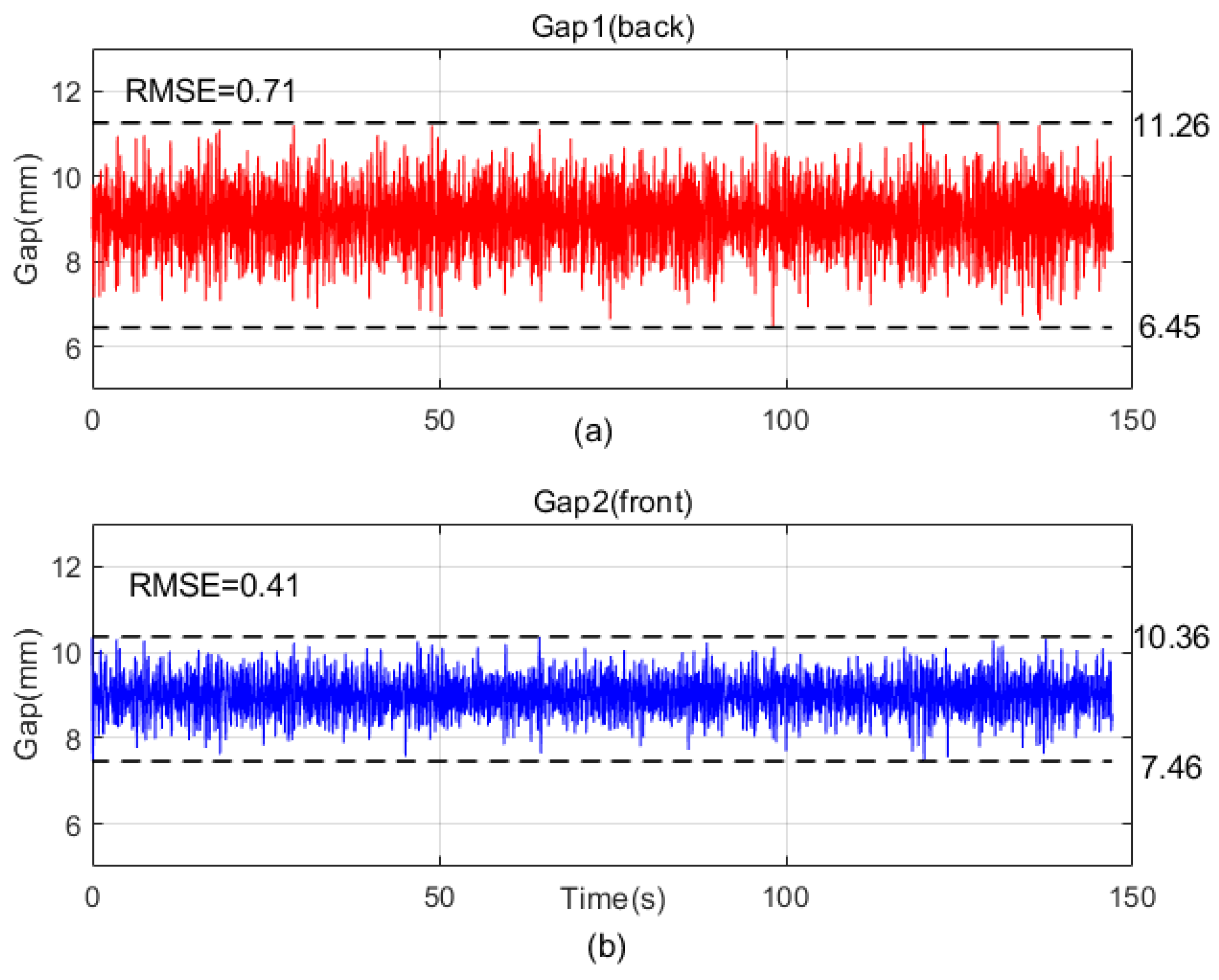
4. Numerical Simulation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lee, H.W.; Lee, J.; Kim, K.C. Review of Maglev Train Technologies. IEEE Trans. Magn. 2006, 42, 1917–1925. [Google Scholar]
- Yan, L. Progress of the Maglev Transportation in China. IEEE Trans. Appl. Supercond. 2006, 16, 1138–1141. [Google Scholar]
- Lin, G.; Sheng, X. Application and further development of Maglev transportation in China. Transp. Syst. Technol. 2018, 4, 36–43. [Google Scholar] [CrossRef]
- Zhang, G.; Li, J.; Yang, Z. Estimation of Power Spectrum Density Track Irregularities of Low-speed maglev railway lines. J. China Railw. Soc. 2011, 33, 73–78. [Google Scholar]
- Zhou, D.; Yu, P.; Li, J.; Wang, L. An adaptive vibration control method to suppress the vibration of the maglev train caused by track irregularities. J. Sound Vib. 2017, 408, 331–350. [Google Scholar] [CrossRef]
- Shu, G.; Meisinger, R.; Shen, G. Simulation of a maglev train with periodic guideway deflections. In Proceedings of the 2008 Asia Simulation Conference—7th International Conference on System Simulation and Scientific Computing, Beijing, China, 10–12 October 2008; pp. 421–425. [Google Scholar]
- Yu, P.; Li, J.; Li, J.; Wang, L. Influence of track periodical irregularities to the suspension system of low-speed maglev vehicle. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 8479–8484. [Google Scholar]
- Wang, Z.; Long, Z.; Li, X. Track Irregularity Disturbance Rejection for Maglev Train Based on Online Optimization of PnP Control Architecture. IEEE Access 2019, 7, 12610–12619. [Google Scholar] [CrossRef]
- Yau, J.D. Vibration control of maglev vehicles traveling over a flexible guideway. J. Sound Vib. 2009, 321, 184–200. [Google Scholar] [CrossRef]
- Ren, S.; Arie, R.; Klap, K. Dynamic Simulation of the Maglev Vehicle/Guideway System. J. Bridge Eng. 2009, 15, 269–278. [Google Scholar] [CrossRef]
- Shi, J.; Wei, Q.; Zhao, Y. Analysis of dynamic response of the high-speed EMS maglev vehicle/guideway coupling system with random irregularity. Vehicle Syst. Dyn. 2007, 45, 1077–1095. [Google Scholar] [CrossRef]
- Zhao, C.; Zhai, W. Maglev Vehicle/Guideway Vertical Random Response and Ride Quality. Veh. Syst. Dyn. 2002, 38, 185–210. [Google Scholar] [CrossRef]
- Lee, J.S.; Kwon, S.D.; Kim, M.Y.; Yeo, I.H. A parametric study on the dynamics of urban transit maglev vehicle running on flexible guideway bridges. J. Sound Vib. 2009, 328, 301–317. [Google Scholar] [CrossRef]
- Wang, Z.L.; Xu, Y.L.; Li, G.Q.; Yang, Y.B.; Chen, S.W.; Zhang, X.L. Modelling and validation of coupled high-speed maglev train-and-viaduct systems considering support flexibility. Vehicle Syst. Dyn. 2019, 57, 161–191. [Google Scholar] [CrossRef]
- Zhou, D.; Hansen, C.H.; Li, J. Suppression of maglev vehicle–girder self-excited vibration using a virtual tuned mass damper. J. Sound Vib. 2011, 330, 883–901. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zhou, D.; Cui, P.; Yu, P. The Active Control of Maglev Stationary Self-Excited Vibration With a Virtual Energy Harvester. IEEE Trans. Ind. Electron. 2015, 62, 2942–2951. [Google Scholar] [CrossRef]
- Min, D.J.; Kwon, S.D.; Kwark, J.W.; Kim, M.Y. Gust Wind Effects on Stability and Ride Quality of Actively Controlled Maglev Guideway Systems. Shock Vib. 2017, 2017, 1–23. [Google Scholar] [CrossRef]
- Shi, J.; Wang, Y. Dynamic response analysis of single-span guideway caused by high speed maglev train. Lat. Am. J. Solid. Stuc. 2011, 8, 213–228. [Google Scholar] [CrossRef]
- Han, H.S.; Yim, B.H.; Lee, N.J.; Kim, Y.J. Prediction of ride quality of a Maglev vehicle using a full vehicle multi-body dynamic model. Veh. Syst. Dyn. 2009, 47, 1271–1286. [Google Scholar] [CrossRef]
- Huang, J.; Zhou, X.; Shang, L.; Wu, Z.; Xu, W. Influence analysis of track irregularity on running comfort of Maglev train. Transp. Syst. Technol. 2018, 4, 129–140. [Google Scholar] [CrossRef]
- Li, Y.; Yu, P.; Zhou, D.; Li, J. Magnetic flux feedback strategy to suppress the gap fluctuation of Low speed maglev train caused by track steps. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 983–989. [Google Scholar]
- Leng, P.; Li, Y.; Zhou, D.; Li, J.; Zhou, S. Decoupling Control of Maglev Train Based on Feedback Linearization. IEEE Access 2019, 7, 130352–130362. [Google Scholar] [CrossRef]
- Zhou, D.; Yu, P.; Li, J.; Wang, L. An Approach to Reduce Vibration of the Levitation System when the Urban Maglev Train is Traveling. In Proceedings of the 2018 37th Chinese Control Conference (CCC), Wuhan, China, 25–27 July 2018; pp. 7736–7741. [Google Scholar]
- Li, Y.; Zhou, D.; Cui, P.; Yu, P.; Chen, Q.; Wang, L.; Li, J. Dynamic Performance Optimization of Electromagnetic Levitation System Considering Sensor Position. IEEE Access 2020, 8, 29446–29455. [Google Scholar] [CrossRef]
- Li, J.; Li, J.; Zhang, G. A practical robust nonlinear controller for maglev levitation system. J. Cent. South. Univ. 2013, 20, 2991–3001. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, J. Model Predictive Control of Unknown Nonlinear Dynamical Systems Based on Recurrent Neural Networks. IEEE Trans. Ind. Electron. 2012, 59, 3089–3101. [Google Scholar] [CrossRef]
- Sinha, P.K.; Pechev, A.N. Model reference adaptive control of a maglev system with stable maximum descent criterion. Automatica 1999, 35, 1457–1465. [Google Scholar] [CrossRef]
- Matsumura, F.; Namerikawa, T.; Hagiwara, K.; Fujita, M. Application of gain scheduled H∞ robust controllers to a magnetic bearing. IEEE Trans. Control Syst. Technol. 1996, 4, 484–493. [Google Scholar] [CrossRef]
- Chen, Q.; Tan, Y.; Li, J.; Oetomo, D.; Mareels, I. Model-guided data-driven decentralized control for magnetic levitation systems. IEEE Access 2018, 6, 43546–43562. [Google Scholar] [CrossRef]
- Sinha, P.K. Electromagnetic Suspension Dynamics & Control; Peter Peregrinus Ltd.: London, UK, 1987. [Google Scholar]
- Li, Y.; Chang, W. Cascade control of an EMS maglev vehicle’s levitation control system. Acta Autom. Sin. 1999, 25, 247–251. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhou, D.; Li, J. Vertical Dynamic Response Prediction of the Electromagnetic Levitation Systems. Appl. Sci. 2020, 10, 2580. https://doi.org/10.3390/app10072580
Li Y, Zhou D, Li J. Vertical Dynamic Response Prediction of the Electromagnetic Levitation Systems. Applied Sciences. 2020; 10(7):2580. https://doi.org/10.3390/app10072580
Chicago/Turabian StyleLi, Yajian, Danfeng Zhou, and Jie Li. 2020. "Vertical Dynamic Response Prediction of the Electromagnetic Levitation Systems" Applied Sciences 10, no. 7: 2580. https://doi.org/10.3390/app10072580
APA StyleLi, Y., Zhou, D., & Li, J. (2020). Vertical Dynamic Response Prediction of the Electromagnetic Levitation Systems. Applied Sciences, 10(7), 2580. https://doi.org/10.3390/app10072580





