Improved Rapid Visual Earthquake Hazard Safety Evaluation of Existing Buildings Using a Type-2 Fuzzy Logic Model
Abstract
1. Introduction
2. Review of Rapid Visual Screening Procedures
3. Type-2 Fuzzy Logic System
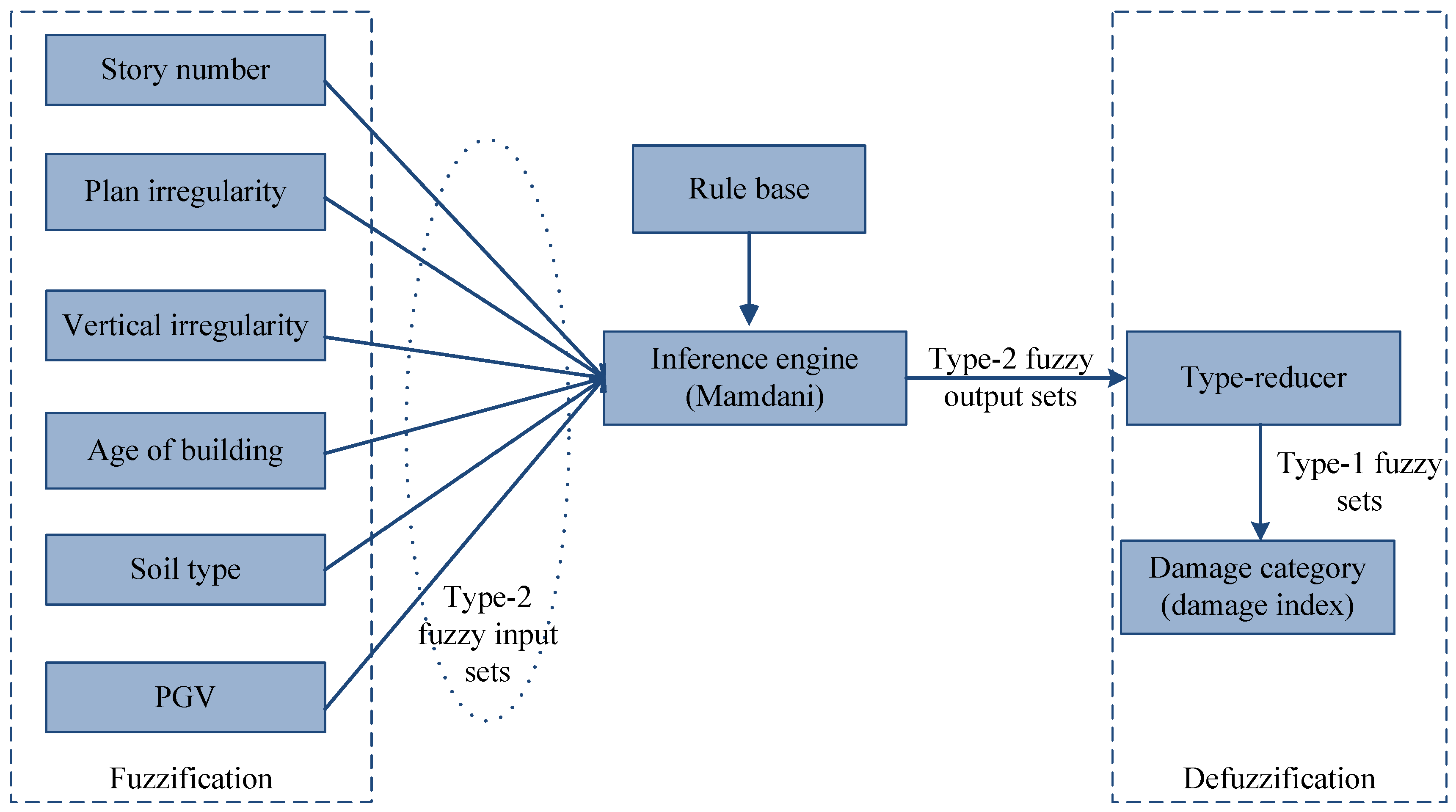
RVS Modeling Based on Interval Type-2 Fuzzy System
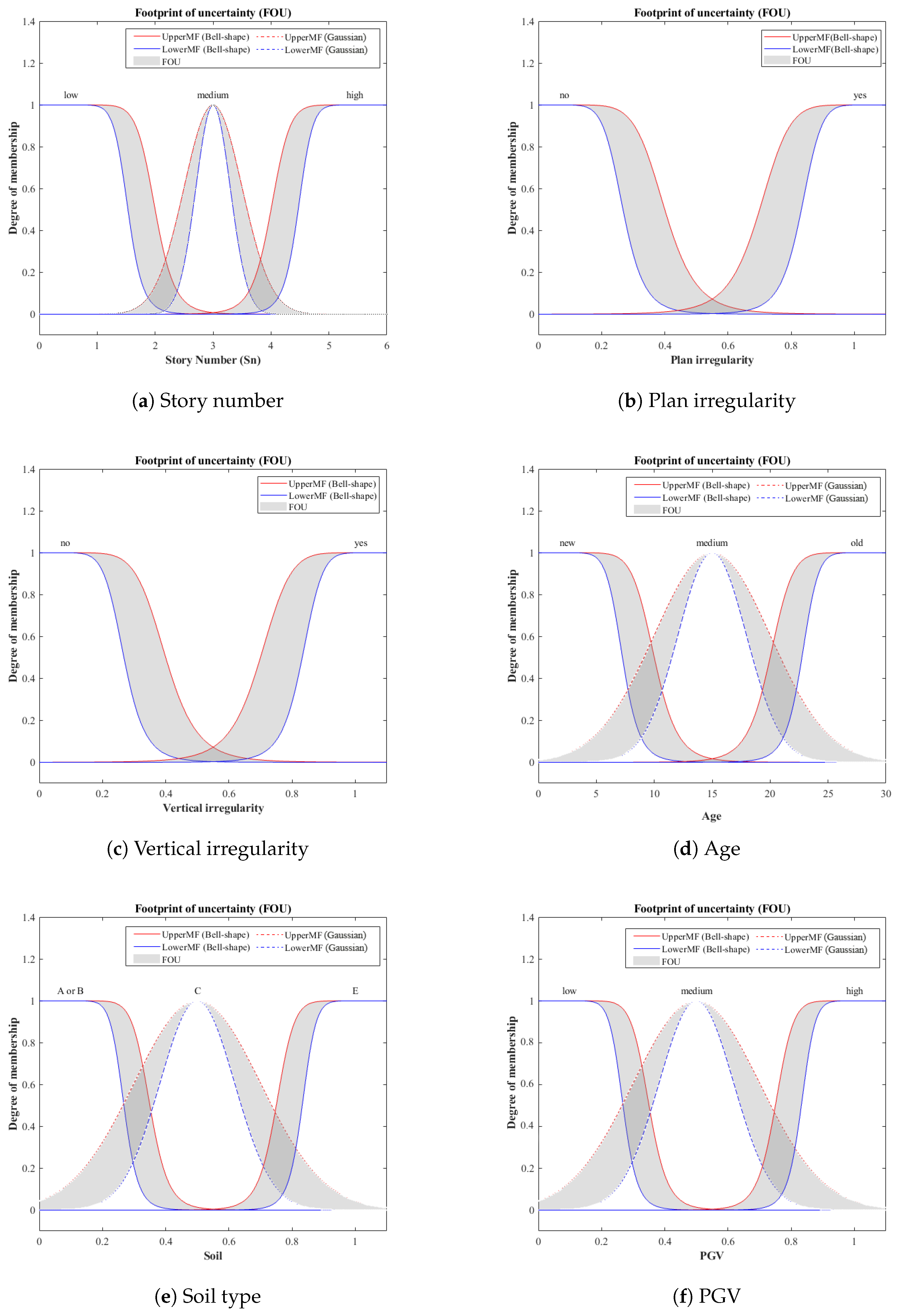
- Story number: Depending on the number of stories, one of the following classes should be selected. The classifications on this study are for mid-rise buildings as the number of stories less than 3 (Low), between 3 and 6 (Medium), and more than 6 (High) as presented in Figure 2a.
- Plan Irregularity: This parameter should be considered when any of the irregularities, for instance, buildings with re-entrant corners (L, T, U, E, + shape) and buildings with different lateral resistance in both directions, have been observed. Any asymmetrical plan and distribution of vertical elements can cause torsion to the building (Figure 2b).
- Vertical irregularity: If any of the irregularities such as steps in elevation view, inclined walls, buildings on a hill, soft story, buildings with short columns, and discontinuity in frames are identified, then this parameter should be considered (see Figure 2c).
- Age of building: This parameter is classified into three different input variable membership function as New (age <15 years), Moderate (15 < age < 30), and Old (age > 30) as presented in Figure 2d.
- Soil type: The soil type is classified into three different input variable membership function as A/B (rock and dense soil), C (stiff soil), and E (soft) as shown in Figure 2e.
- Peak Ground Velocity (PGV): The velocity is used to characterize the amplitude of seismic motion at intermediate frequencies therefore, it is useful to indicate the potential damage for structures sensitive to the field of intermediate frequencies [9,47]. In this paper, the PGV numerical values at any desired locations are based on the micro zoning studies by Sucuoglu and Yilmaz [48], which are fuzzified into three MFs as Low, Medium, and High, which are illustrated in Figure 2f.
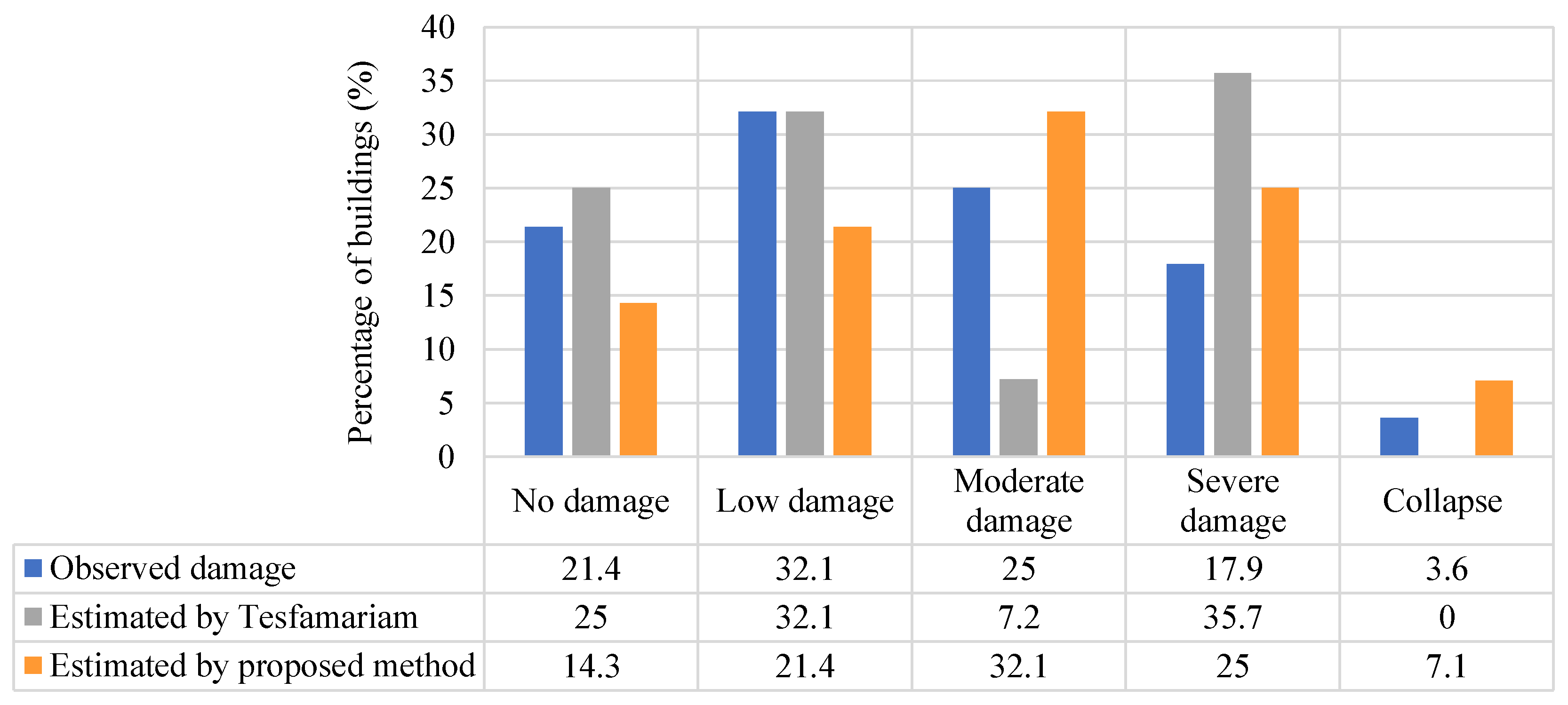
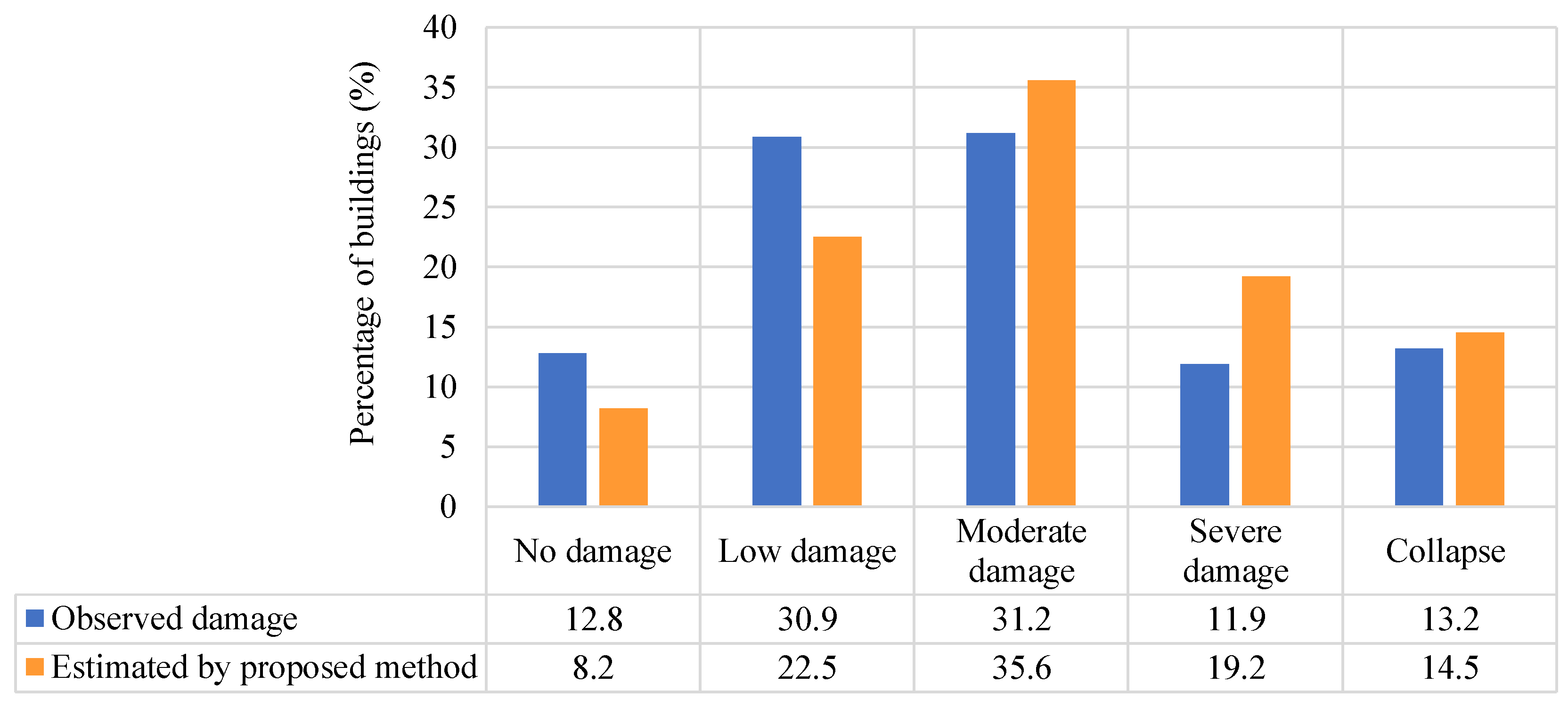
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Rad, K.G. Application of domino theory to justify and prevent accident occurance in construction sites. IOSR J. Mech. Civ. Eng. IOSR-JMCE 2013, 6, 72–76. [Google Scholar]
- Sucuoğlu, H.; Yazgan, U.; Yakut, A. A Screening Procedure for Seismic Risk Assessment in Urban Building Stocks. Earthq. Spectra 2007, 23, 441–458. [Google Scholar] [CrossRef]
- Harirchian, E.; Harirchian, A. Earthquake Hazard Safety Assessment of Buildings via Smartphone App: An Introduction to the Prototype Features- 30. Forum Bauinformatik: Von jungen Forschenden für junge Forschende: September 2018, Informatik im Bauwesen; Professur Informatik im Bauwesen; Bauhaus-Universität Weimar: Weimar, Germany, 2018; pp. 289–297. [Google Scholar] [CrossRef]
- Tesfamariam, S.; Saatcioglu, M. Seismic vulnerability assessment of reinforced concrete buildings using hierarchical fuzzy rule base modeling. Earthq. Spectra 2010, 26, 235–256. [Google Scholar] [CrossRef]
- Mendel, J.M.; John, R.B. Type-2 fuzzy sets made simple. IEEE Trans. Fuzzy Syst. 2002, 10, 117–127. [Google Scholar] [CrossRef]
- Federal Emergency Management Agency. Rapid Visual Screening of Buildings for Potential Seismic Hazards: A Handbook (FEMA P-154); Homeland Security Department, Federal Emergency Management Agency: Washington, DC, USA, 2015.
- Yadollahi, M.; Adnan, A.; Zin, R. Seismic vulnerability functional method for rapid visual screening of existing buildings. Arch. Civ. Eng. 2012, 58, 363–377. [Google Scholar] [CrossRef][Green Version]
- Rai, D.C. Review of Documents on Seismic Evaluation of Existing Buildings; Indian Institute of Technology Kanpur India: Kanpur, India, 2005. [Google Scholar]
- Ansal, A.; Özaydın, K.; Edinçliler, A.; Sağlamer, A.; Sucuoğlu, H.; Özdemir, P. Earthquake Master Plan for Istanbul; Metropolital Municipality of Istanbul, Planning and Construction Directorate; Geotechnical and Earthquake Investigation Department: Istanbul, Turkey, 2003.
- Angeletti, P.; Bellina, A.; Guagenti, E.; Moretti, A.; Petrini, V. Comparison between vulnerability assessment and damage index, some results. In Proceedings of the 9th World Conference on Earthquake Engineering, Tokyo, Japan, 2–9 August 1988; Volume 7, pp. 181–186. [Google Scholar]
- Vallejo, C.B. Rapid Visual Screening of Buildings in the City of Manila, Philippines. In 5th Civil Engineering Conference in the Asian Region and Australasian Structural Engineering Conference 2010; Engineers Australia: Sydney, Australia, 2010; pp. 513–518. [Google Scholar]
- Harirchian, E.; Lahmer, T.; Buddhiraju, S.; Mohammad, K.; Mosavi, A. Earthquake Safety Assessment of Buildings through Rapid Visual Screening. Buildings 2020, 10, 51. [Google Scholar] [CrossRef]
- Harirchian, E.; Lahmer, T. Earthquake Hazard Safety Assessment of Buildings via Smartphone App: A Comparative Study. IOP Conf. Ser. Mater. Sci. Eng. 2019, 652, 012069. [Google Scholar] [CrossRef]
- Işık, E. Investigation of an Existing RC Building with Different Rapid Assessment Methods. Bitlis Eren Univ. J. Sci. Technol. 2015, 5, 71–74. [Google Scholar] [CrossRef]
- Ketsap, A.; Hansapinyo, C.; Kronprasert, N.; Limkatanyu, S. Uncertainty and fuzzy decisions in earthquake risk evaluation of buildings. Eng. J. 2019, 23, 89–105. [Google Scholar] [CrossRef]
- Jain, S.K.; Mitra, K.; Kumar, M.; Shah, M. A proposed rapid visual screening procedure for seismic evaluation of RC-frame buildings in India. Earthq. Spectra 2010, 26, 709–729. [Google Scholar] [CrossRef]
- Ningthoujam, M.; Nanda, R.P. Rapid visual screening procedure of existing building based on statistical analysis. Int. J. Disaster Risk Reduct. 2018, 28, 720–730. [Google Scholar] [CrossRef]
- Morfidis, K.E.; Kostinakis, K.G.; Networks, A.N.; Vulnerability, S. Use Of Artificial Neural Networks in the R/C Buildings’ Seismic Vulnerabilty Assessment: The Practical Point. In Proceedings of the 7th International Conference on Computational Methods in Structural Dynamics and Earthquake Engineering, Crete, Greece, 24–26 June 2019; pp. 24–26. [Google Scholar]
- Morfidis, K.; Kostinakis, K. Approaches to the rapid seismic damage prediction of r/c buildings using artificial neural networks. Eng. Struct. 2018, 165, 120–141. [Google Scholar] [CrossRef]
- Morfidis, K.; Kostinakis, K. Seismic parameters’ combinations for the optimum prediction of the damage state of R/C buildings using neural networks. Adv. Eng. Softw. 2017, 106, 1–16. [Google Scholar] [CrossRef]
- Tesfamariam, S.; Liu, Z. Earthquake induced damage classification for reinforced concrete buildings. Struct. Saf. 2010, 32, 154–164. [Google Scholar] [CrossRef]
- Nanda, R.P.; Majhi, D.R. Review on Rapid Seismic Vulnerability Assessment for Bulk of Buildings. J. Inst. Eng. India Ser. A 2013, 94, 187–197. [Google Scholar] [CrossRef]
- Gowd, B.P.; Jayasree, K.; Hegde, M.N. Comparison of artificial neural networks and fuzzy logic approaches for crack detection in a beam like structure. Int. J. Artif. Intell. Appl. 2018, 9, 35–51. [Google Scholar]
- Irwansyah, E.; Hartati, S. Three-Stage Fuzzy Rule-Based Model for Earthquake Non-Engineered Building House Damage Hazard Determination. J. Adv. Comput. Intell. Intell. Inform. 2017, 21, 1298–1311. [Google Scholar] [CrossRef]
- Shahriar, A.; Modirzadeh, M.; Sadiq, R.; Tesfamariam, S. Seismic induced damageability evaluation of steel buildings: A Fuzzy-TOPSIS method. Earthq. Struct. 2012, 3, 695–717. [Google Scholar] [CrossRef]
- Şen, Z. Supervised fuzzy logic modeling for building earthquake hazard assessment. Expert Syst. Appl. 2011, 38, 14564–14573. [Google Scholar] [CrossRef]
- Şen, Z. Rapid visual earthquake hazard evaluation of existing buildings by fuzzy logic modeling. Expert Syst. Appl. 2010, 37, 5653–5660. [Google Scholar] [CrossRef]
- Tesfamariam, S.; Saatcioglu, M. Risk-based seismic evaluation of reinforced concrete buildings. Earthq. Spectra 2008, 24, 795–821. [Google Scholar] [CrossRef]
- Moseley, J.; Dritsos, S. Rapid assessment of seismic vulnerability using fuzzy logic. In Proceedings of the 3rd Conference on Earthquake Engineering and Engineering Seismology, Athens, Greece, 5–7 November 2008. [Google Scholar]
- Demartinos, K.; Dritsos, S. First-level pre-earthquake assessment of buildings using fuzzy logic. Earthq. Spectra 2006, 22, 865–885. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Zadeh, L.A. The concept of a linguistic variable and its application to approximate reasoning-III. Inf. Sci. 1975, 9, 43–80. [Google Scholar] [CrossRef]
- Tan, W.W.; Chua, T.W. Uncertain rule-based fuzzy logic systems: Introduction and new directions (Mendel, JM; 2001) [book review]. IEEE Comput. Intell. Mag. 2007, 2, 72–73. [Google Scholar] [CrossRef]
- Chen, Y. Study on centroid type-reduction of interval type-2 fuzzy logic systems based on noniterative algorithms. Complexity 2019. [Google Scholar] [CrossRef]
- Mendel, J.M. A comparison of three approaches for estimating (synthesizing) an interval type-2 fuzzy set model of a linguistic term for computing with words. Granul. Comput. 2016, 1, 59–69. [Google Scholar] [CrossRef]
- Hagras, H.; Wagner, C. Towards the wide spread use of type-2 fuzzy logic systems in real world applications. IEEE Comput. Intell. Mag. 2012, 7, 14–24. [Google Scholar] [CrossRef]
- Mendoza, O.; Melín, P.; Castillo, O. Interval type-2 fuzzy logic and modular neural networks for face recognition applications. Appl. Soft Comput. 2009, 9, 1377–1387. [Google Scholar] [CrossRef]
- Wu, D.; Mendel, J.M. Computing with words for hierarchical decision making applied to evaluating a weapon system. IEEE Trans. Fuzzy Syst. 2010, 18, 441–460. [Google Scholar] [CrossRef]
- Aisbett, J.; Rickard, J.T.; Morgenthaler, D.G. Type-2 fuzzy sets as functions on spaces. IEEE Trans. Fuzzy Syst. 2010, 18, 841–844. [Google Scholar] [CrossRef]
- Cheng, S.; Zadeh, L. On fuzzy mapping and control. IEEE Trans. Syst. Man Cybern. 1972, 2, 30–34. [Google Scholar] [CrossRef]
- Liu, F. An efficient centroid type-reduction strategy for general type-2 fuzzy logic system. Inf. Sci. 2008, 178, 2224–2236. [Google Scholar] [CrossRef]
- Mendel, J.M. On KM algorithms for solving type-2 fuzzy set problems. IEEE Trans. Fuzzy Syst. 2012, 21, 426–446. [Google Scholar] [CrossRef]
- Wu, D.; Mendel, J.M. Enhanced karnik–mendel algorithms. IEEE Trans. Fuzzy Syst. 2008, 17, 923–934. [Google Scholar]
- Liu, X.; Mendel, J.M.; Wu, D. Study on enhanced Karnik–Mendel algorithms: Initialization explanations and computation improvements. Inf. Sci. 2012, 184, 75–91. [Google Scholar] [CrossRef]
- Chua, T.W.; Tan, W.W. Ga optimisation of non-singleton fuzzy logic system for ecg classification. In Proceedings of the 2007 IEEE Congress on Evolutionary Computation, Singapore, 25–28 September 2007; pp. 1677–1684. [Google Scholar]
- Wu, D.; Mendel, J.M. Recommendations on designing practical interval type-2 fuzzy systems. Eng. Appl. Artif. Intell. 2019, 85, 182–193. [Google Scholar] [CrossRef]
- Allen, T.I.; Wald, D.J.; Hotovec, A.J.; Lin, K.W.; Earle, P.S.; Marano, K.D. An Atlas of ShakeMaps for Selected Global Earthquakes; Technical Report; US Geological Survey: Reston, VA, USA, 2008.
- Sucuoglu, H.; Yilmaz, T. Duzce, Turkey: A city hit by two major earthquakes in 1999 within three months. Seismol. Res. Lett. 2001, 72, 679–689. [Google Scholar] [CrossRef]
- SERU. Middle East Technical University, Ankara, Turkey. Archival Material from Düzce Database Located at Website. Available online: http://www.seru.metu.edu.tr (accessed on 31 January 2020).
- Aydan, Ö.; Ulusay, R.; Miyajima, M. The Bingöl Earthquake of May 1, 2003; Japan Society of Civil: Tokyo, Japan, 2003. [Google Scholar]
- Akkar, S.; Boore, D.M.; GüLkan, P. An evaluation of the strong ground motion recorded during the May 1, 2003 Bingöl Turkey, Earthquake. J. Earthq. Eng. 2005, 9, 173–197. [Google Scholar] [CrossRef]
- Ozcebe, G.; Ramirez, J.; Wasti, S.; Yakut, A. May 2003 Bingöl Earthquake Engineering Report; TUBITAK: Ankara, Turkey, 2003; pp. 75–100.
- Bayhan, B.; Gülkan, P. Buildings subjected to recurring earthquakes: A tale of three cities. Earthq. Spectra 2011, 27, 635–659. [Google Scholar] [CrossRef]
- Chever, L. Use of seismic assessment methods for planning vulnerability reduction of existing building stock. In Proceedings of the 15th World Conference on Earthquake Engineering—WCEE, Lisbon, Portugal, 24–28 September 2012; p. 10. [Google Scholar]
- Tesfamariam, S. Seismic Risk Assessment of Reinforced Concrete Buildings Using Fuzzy Based Techniques. Ph.D. Thesis, University of Ottawa, Ottawa, ON, Canada, 2008. [Google Scholar]
- Allali, S.A.; Abed, M.; Mebarki, A. Post-earthquake assessment of buildings damage using fuzzy logic. Eng. Struct. 2018, 166, 117–127. [Google Scholar] [CrossRef]
| Author(s) | Year | Studied Data | Purpose | Parameters | Fuzzy Inference |
|---|---|---|---|---|---|
| Ketsap et al. [15] | 2019 | Chiang Rai, Thailand | Earthquake risk evaluation of buildings by using Fuzzy risk model | Building occupancy (occupancy risk index), building vulnerability (FEMA 154 final score), Seismic hazard (PGA) | Hierarchical fuzzy rule-based |
| Irwansyah et al. [24] | 2017 | 1450 (1000 modeling, 400 tests, 50 outlined) non-engineered buildings in Aceh, Indonesia | A three-stage fuzzy rule-based model to determine the hazard rate of building on the impact of earthquake for non-engineered houses | Structural (ring balk, floor block, column, foundation), non-structural (wall crack, wall cover, floor cover, tombak layer), ground condition (PGA, slope, fault distance) | Three-Stage Fuzzy Rule-Based |
| Shahriar et al. [25] | 2012 | 43 Steel buildings in Northridge, USA | A risk-based seismic vulnerability assessment method using fuzzy-TOPSIS for damageability evaluation of steel buildings. | Structural system, vertical irregularity, plan irregularity, year of construction, construction quality, spectral acceleration | Fuzzy-TOPSIS, Mamdani |
| Şen [26] | 2011 | 747 RC buildings in Istanbul, Turkey | Proposed a fuzzy logic model as supervised hazard center classification inference methodology for rapid and rational hazard classification. | Building height, soft height ratio, cantilever extension ratio, moment of inertia, frame number, column ratio, shear wall ratio, and PGV | Supervised fuzzy rule-based, Mamdani |
| Şen [27] | 2010 | 1249 RC buildings in Istanbul, Turkey | Proposed a fuzzy logic model and software for rapid visual earthquake hazard evaluation of existing buildings. | Story number, cantilever extension, soft story, weak story, building quality, pounding effect, hill-slope effect, and PGV | Fuzzy rule-based, Mamdani |
| Tesfamariam and Saatcioglu [4] | 2010 | 28 RC buildings in Bingöl, Turkey | Proposed a risk-based seismic vulnerability assessment based on fuzzy logic for prioritizing buildings for retrofit and repair. | Soft story, weak story, and short column effect, relative strength at joints, plan irregularity, torsional irregularity, diaphragm continuity, re-entrant corners, structural walls, construction and design quality, code enforcement, damage from previous earthquake, damage due to deterioration, relative height of slabs | Hierarchical fuzzy rule-based, Mamdani |
| Tesfamariam and Saatcioglu [28] | 2008 | 93 RC (73 modeling and 20 test) buildings in Northridge, USA | Proposed a risk-based seismic vulnerability assessment based on FEMA154 and fuzzy logic for prioritizing buildings for retrofit and repair. | Structural system, plan irregularity, vertical irregularity, year of construction, construction quality, building importance and occupancy | Hierarchical fuzzy rule-based, Mamdani |
| Moseley and Dritsos [29] | 2008 | 101 and 454 buildings in Athens, Greece | Proposed a fuzzy logic rapid visual screening procedure based on Greece method to improve the screening procedures | Same as below parameters | Hierarchical fuzzy rule-based, Sugano |
| Demartinos and Dristos [30] | 2006 | 102 buildings in Athens, Greece | Fuzzy logic–based rapid visual screening procedure for categorization of buildings into five different types of possible damage with respect to the potential occurrence of a major seismic event. | Seismic hazard (ground motion, soil quality, building height), structural strength (building height, infill wall layout, soft story, short columns, design code), regularity (plan regularity, torsion possibility, height regularity, pounding possibility, plan regularity), structure’s condition (previous damage, maintenance) | Hierarchical fuzzy rule-based, Sugano |
| Rule No. | Input Variable | Output (Damage) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NS | PI | VI | Age | ST | PGV | ||||||||
| 1 | Low | and | No | and | No | and | Old | and | A/B | and | Low | Then | No damage |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 171 | Medium | and | Yes | and | No | and | Old | and | E | and | Medium | Then | Severe |
| … | … | … | … | … | … | … | … | … | … | … | … | … | … |
| 324 | High | and | Yes | and | Yes | and | New | and | E | and | High | Then | Severe |
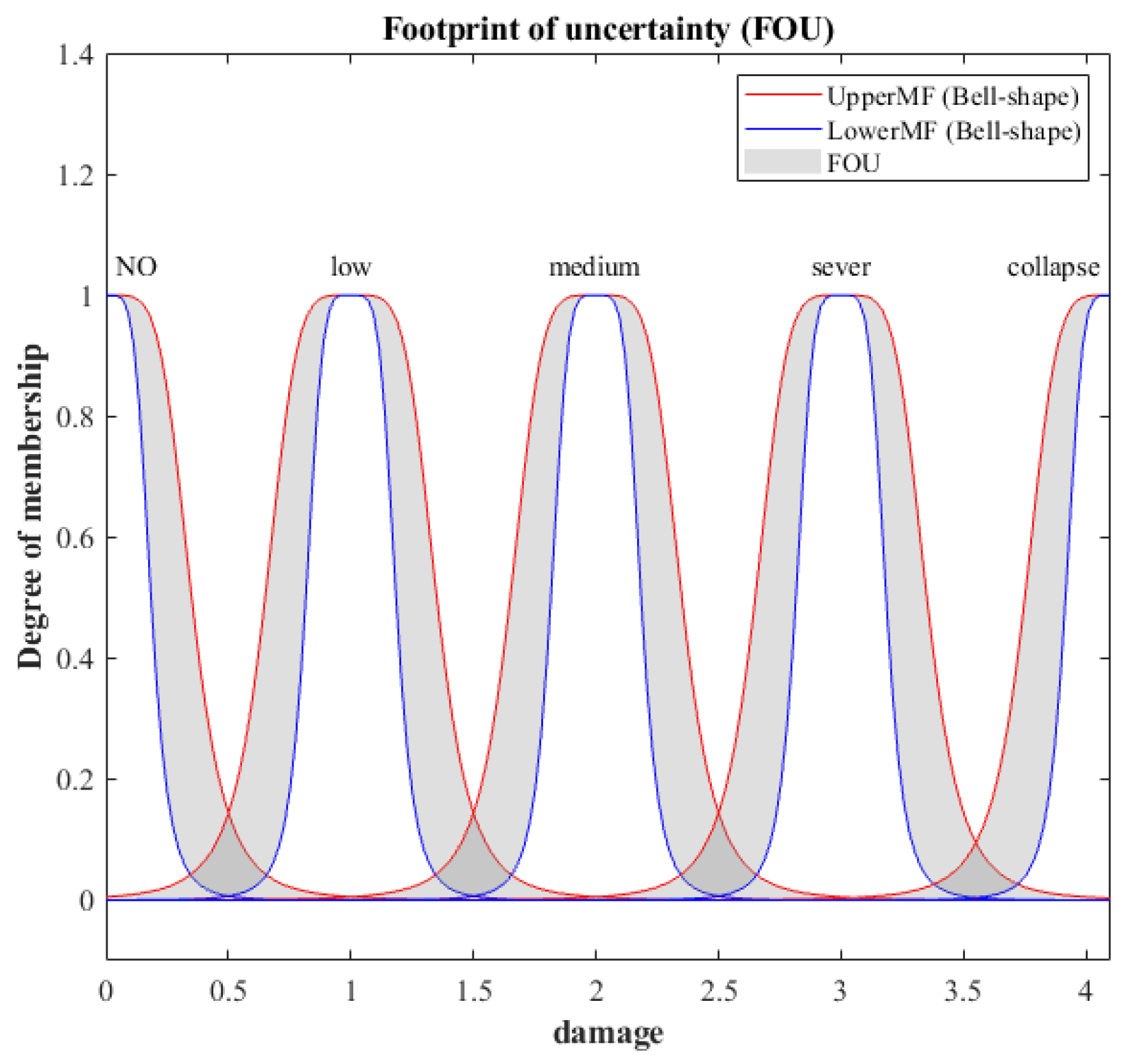
| Damage State | Description | Decision |
|---|---|---|
| No damage | No damage, small cracks | Safe |
| Low damage | Isolated non-structural damage, cracks in the interior walls or ceilings, damage in water lines, etc. | Slightly safe, might need small repair |
| Moderate damage | Significant non-structural damage and slight structural damage | Moderate safe, needs repair and retrofitting |
| Severe damage | Heavy non-structural damage and important structural damage | Slightly dangerous, need immediate repair and strengthening |
| Collapse | Collapsed buildings or condemned to demolition | Dangerous, evacuation and demolish needed |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Harirchian, E.; Lahmer, T. Improved Rapid Visual Earthquake Hazard Safety Evaluation of Existing Buildings Using a Type-2 Fuzzy Logic Model. Appl. Sci. 2020, 10, 2375. https://doi.org/10.3390/app10072375
Harirchian E, Lahmer T. Improved Rapid Visual Earthquake Hazard Safety Evaluation of Existing Buildings Using a Type-2 Fuzzy Logic Model. Applied Sciences. 2020; 10(7):2375. https://doi.org/10.3390/app10072375
Chicago/Turabian StyleHarirchian, Ehsan, and Tom Lahmer. 2020. "Improved Rapid Visual Earthquake Hazard Safety Evaluation of Existing Buildings Using a Type-2 Fuzzy Logic Model" Applied Sciences 10, no. 7: 2375. https://doi.org/10.3390/app10072375
APA StyleHarirchian, E., & Lahmer, T. (2020). Improved Rapid Visual Earthquake Hazard Safety Evaluation of Existing Buildings Using a Type-2 Fuzzy Logic Model. Applied Sciences, 10(7), 2375. https://doi.org/10.3390/app10072375






