One Computational Innovation Transition-Based Recovery Policy for Flexible Manufacturing Systems Using Petri nets

Featured Application

This paper proposes one novel transition-based control policy to solve the deadlock problem of flexible manufacturing systems. This paper contains some acronyms. For easy tracking, their corresponding meaning is present in Appendix A.

Abstract

In the third and fourth industrial revolutions, smart or artificial intelligence flexible manufacturing systems (FMS) seem to be the key machine equipment for capacity of factory production. However, deadlocks could hence appear due to resources competition between robots. Therefore, how to prevent deadlocks of FMS occurring is a very important and hot issue. Based on Petri nets (PN) theory, in existing literature almost all research adopts control places as their deadlock prevention mean. However, under this strategy the real optimal reachable markings are not achieved even if they claimed that their control policy is maximally permissive. Accordingly, in this paper, the author propose one novel transition-based control policy to solve the deadlock problem of FMS. The proposed control policy could also be viewed as deadlock recovery since it can recover all initial deadlock and quasi-deadlock markings. Furthermore, control transitions can be calculated and obtained once the proposed three-dimension matrix, called generating and comparing aiding matrix (GCAM) in this paper, is built. Finally, an iteration method is used until all deadlock markings become live ones. Experimental results reveal that our control policy seems still the best one among all existing methods in the literature regardless of whether these methods belong to places or transitions based.

1. Introduction

In the third and fourth industrial revolutions, smart or artificial intelligence flexible manufacturing systems (FMS) are much adopted for capacity of factory production. However, deadlocks could hence appear due to resources competition between robots [1]. Therefore, how to prevent FMS deadlocks occurring is a very important and hot issue. In the existing literature, automata theory [2,3], queueing theory [4,5], Petri nets theory [6], and state chart/flow [7] are all used as mathematical tools to process above deadlock problems of FMS. Among them, Petri nets (PN) have been recognized as the most powerful semantic-based tool to solve FMS’s deadlock problem. The reason is that it is well suited to represent such discrete event dynamic system (DEDS) [8] characteristics such as precedence relations, concurrence, conflict and synchronization. Especially for FMS, the complexity resulting from the inherent nonlinearity and state space dimension found in most of these systems leads to unusual difficulty in design and analysis.

Traditionally, in existing literature, two main analysis technologies are applied to develop deadlock prevention policy for FMS: system structural analysis [9,10,11,12,13,14,15,16,17,18,19,20,21,22] and reachability graph analysis [23,24,25,26,27,28,29,30,31,32,33,34]. The former one depends on some structural analysis, such as siphon control, to design proper control subnet to solve deadlock problems. Under this technology, computation is often simple but suffering from explosion problems since the number of siphons exponentially increases as the model becomes larger and more complicated.

Reachability graph analysis can be used to design the optimal or maximally permissive deadlock prevention policy. In this approach, all reachable states of PN model are needed firstly to compute reachability graph. Although this technology could be a NP-hard problem since it needs to generate the reachability graph of a PN, it is still widely used to solve the deadlock problem of FMS. Whatever, this analysis owns maximally permissive controllers.

Under the method, Uzam firstly adopts the theory of regions [23] to design one optimal (maximally permissive) deadlock prevention based on the novel concepts of deadlock zone (DZ) and deadlock-free zone (DFZ). In the following, Ghaffari et al. [24] also design one optimal (maximally permissive) deadlock prevention by giving a redefinition of the theory of regions based on forbidden marking, dangerous marking, legal marking, and the set of marking/transition-separation instances (MTSI). For enhancing computational efficiency of the above two kinds of traditional theory of regions, Huang and Pan [31], and Huang et al. [32] propose one new optimal deadlock prevention using the concept of crucial marking/transition-separation instances (CMTSI).

For reducing computing time of the theory of regions, Uzam and Zhou [35] propose a reduction technique to simplify large FMS models. Huang and Pan also adopted the reduction approach to [36] so that the computational efficiency of CMTSI can be further enhanced.

On the other hand, Pirrodi et al. [37] consider selective siphons with reachability graph to reduce redundancy problems and provide small-size controllers. The control policy solves deadlock problems of FMSs successfully. It also makes FMSs optimal. However, as indicated by [38], the process of eliminating all critical markings is time consuming, since all legal markings must be checked in each iterative step. According to the above descriptions, it is clear that determining how to obtain optimal (maximally permissive) controllers for solving the FMS deadlock problem seems an extremely time-consuming and difficult issue.

For improving above disadvantage, Chen et al. [39,40,41] proposed one novel technology called MFFP (i.e., the maximal number of forbidding first bad marking (FBM) problem) to obtain maximally permissive reachable markings with very a smaller number of controllers based on Place Invariant (PI) [17] and reachability graph analysis methods. It successfully solves the problem of the excessive consumption of time. It is so pity, when the complexity of one flexible manufacturing system increases, the computational burden raises rapidly. Besides, under our survey the MFFP could just be applied in some special net, outside S³PR (The Systems of Simple Sequential Processes with Resources) [10] the method would be failed. Therefore, in author’s previous paper [42] the author proposes one iterative deadlock prevention policy to circumvent its disadvantage of conventional MFFP. Besides, the author also proposes one computational improved deadlock concept called IMFFP [43] to enhance MFFP’s computational efficiency.

Huang et al. [44] firstly introduced the concept of transition-based deadlock prevention policy in their paper, but not the optimal method yet, due to its manual designing process and low control efficiency documented in the expansion literature [45]. Both have the same feature, which helps little in larger and more complicated system [44,45].

In the following, Chen et al. [46] developed another transition-based control policy to obtain proper supervisors and propose two different kinds of concepts to recover the deadlock problem of FMS. The first one adopts iteration approach. At each iterative step, one integer linear programming problem (ILPP) is calculated to obtain a transition-based controller until all deadlock markings are recovered. The second stage is one-time skill that can find and pick up all transition-based controllers. Although Chen et al. claim that the policy can be applied to all classes of FMS, according to [47], it suffers from the computation complexity problem, since there are too many constraints and variables in the formulated ILPPs.

Besides, Bashir et al. [48] presented an iteration procedure to design a deadlock prevention policy via control transition constraints. In their work, the structural property of Petri net models is considered for preventing the state explosion problem in reachability graph analysis. Then the controlling transitions are generated and attached to the model to raise up system activity. Nevertheless, this method is still suboptimal since it does not recover system completely.

Row and Pan [49] propose one improved concept to solve system’s deadlock problem based on [44]. This article presents an optimal transition-based recovering policy rather than existing method via control places, which just forbids undesirable deadlock states with disadvantage of reducing system liveness. The brand-new method helps accessing all reachable system states and each of them has activated-able transition, implying enough resources for providing competing process.

Dong et al. [47] also adopt the transition-based controllers to solve deadlock problem of FMS based on a vector intersection approach. Next, an iteration is used to calculate one small number of recovery controllers to recover all illegal markings.

On the other hand, many experts devote some new concept for the deadlock prevention domain of flexible manufacturing systems [50,51,52,53,54,55,56,57,58,59,60,61,62].

Rather than preventing the system from accessing to undesirable state, in this paper the author firstly presents a new method to recover all deadlock markings by attaching control transitions (CT) to deadlock system. Within reachability graph analysis, transitions connect all reachable markings, in other words, a deadlock state could be re-directed to another legal state by adding a computed CT to the system rather than forbidding the deadlock state.

In order to recover deadlock system states, the author adopted the most effective CT for the system. To build the corresponding CT, one deadlock marking and one legal marking must be determined before the main computation, which denotes start and end points of CT in several systems. After two points have being chosen, CT could be calculated out with some simple processes. Experimental results reveal that the new method proposed in this paper is as good as existing methods in the literature.

Section 2 describes the definitions of PNs and the properties of the reachability graph analysis. Section 3 and Section 4 present the proposed theory and policy. Section 5 shows examples and relative experimental data. Finally, conclusions are made in Section 6.

2. Preliminary

2.1. Petri Nets (PN)

A Petri Net model is a five tuple $N=\left(P,T,F,W,M_0\right)$, which is also a kind of directed model. $P$ and $T$ are two finite, nonempty and disjoint sets. $P$ is a set of places and $T$ is a set of transitions. $F\subseteq \left(P\times T\right)\cup \left(T\times P\right)$ implies the set of arcs of this net, which is symbolized by arrows going from places to transitions or from transitions to places denotes a flow relation in the Petri Net model. $W:\left(P\times T\right)\cup \left(T\times P\right)\to \mathbb{N}$ is a mapping that assigns a weight to an arc: $W\left(x,y\right)>0$ for each $\left(x,y\right)\in F$, where $x,y\in \left(P\cup T\right)$ and $\mathbb{N}$ is the set of non-negative integers. ${}_{}{}^{•}x=\{y\in P\cup T|\left(y,x\right)\in F\}$ is called the preset of x, and $x^{•}=\{y\in P\cup T|\left(x,y\right)\in F\}$ is called the postset of $x$. A marking $M$ is a multiset of Petri nets places, which allocates tokens to each place of a Petri net model. $M\left(p\right)$ denotes the number of tokens in place $p$. M₀ is the initial marking of N. A net is pure if $\forall \left(x,y\right)\in \left(P\times T\right)\cup \left(T\times P\right),W\left(x,y\right)>0,$ implying that $W\left(y,x\right)=0$. The incidence matrix $\left[N\right]$ of the pure net $N$ is a $\left|P\right|\times \left|T\right|$ integer matrix with $\left[N\right]\left(p,t\right)=W\left(t,p\right)-W\left(p,t\right)$.

A transition $t\in T$ is enabled at marking $M$ if $\forall p\in {}_{}{}^{•}t,M\left(p\right)\ge W\left(p,t\right)$, which is denoted as $M[t⟩$. Once an enabled transition $t$ fires, it generates a new marking $M\prime$, denoted as $M[t⟩M\prime$, where $M^{\prime }\left(p\right)=M\left(p\right)-W\left(p,t\right)+W\left(t,p\right)$. $M[⟩$ represents the set of all markings reachable from $M$ by firing any possible sequence of transitions. $M_0[⟩$ is the set of reachable markings of net $N$ with initial marking $M_0$, often denoted as $R\left(N,M_0\right)$. It can be graphically represented by a reachability graph, which can, in turn, be denoted as $G\left(N,M_0\right)$. It is a directed graph in which each node represents a marking in $R\left(N,M_0\right)$, and arcs are labeled by the fired transitions.

Let $\left(N,M_0\right)$ be a net system with $N=\left(P,T,F,W\right)$. A transition $t\in T$ is live at $M_0$ if $\forall M\in R\left(N,M_0\right),\exists M^{\prime }\in R\left(N,M_0\right),M\prime [t⟩$. $\left(N,M_0\right)$ is live if $\forall t\in T$, $t$ is live at $M_0$. It is dead at $M_0$ if $\nexists t\in T,M_0[t⟩$.

A P-vector is a column vector $I:P\to \mathbb{Z}$ indexed by $P$. P-vector $I$ is called a P-invariant (place invariant, PI for short) if $I\ne 0$ and $I^T\left[N\right]=0^T$. P-invariant $I$ is said to be a P semi flow if $I\ge 0$. Let $I$ be a PI of $\left(N,M_0\right)$ and $M$ be a reachable marking from $M_0$. Then, $I^{T}M=I^T{M}_0$.

2.2. Reachability Graph (RG) Analysis

In reachability graph (RG) analysis, all reachable markings can be divided into two main groups: legal and illegal markings. Illegal markings include deadlock and quasi-dead markings. In the above, the legal, illegal, deadlock, and quasi-dead markings can be defined as follows:

Definition 1.

The set of deadlock markings ${ℳ}_D$ = {M∈ R(N, M₀)| at M, no transition can be enabled}.

Further, the quasi-dead marking is defined as follows:

Definition 2.

The set of quasi-dead markings ${ℳ}_Q$ = {M∈R(N, M₀)| M must eventually evolve to a dead one regardless of transition firing sequences}.

The reachable markings except quasi-deadlock and deadlock markings are called legal markings. The set of legal markings ${ℳ}_L$ in conventional deadlock prevention means the maximal number of reachable markings of one system, from which the initial marking $M_0$ is reachable without leaving ${ℳ}_L$. However, in this paper, it just represents the group of legal markings outside deadlock and quasi-deadlock markings. The set of legal markings ${ℳ}_L$ can be defined as follows:

Definition 3.

${ℳ}_L=\left\{M\in R\left(N,M_0\right)\wedge M\notin \left(M_D\cup M_Q\right)\right\}$

In fact, $\left(M_D\cup M_Q\right)$ of Definition 3 means the set of illegal markings. Therefore, the set of illegal markings ${ℳ}_I$ can be defined as:

Definition 4.

${ℳ}_I=\left\{M\in R\left(N,M_0\right)\wedge M\in \left(M_D\cup M_Q\right)\right\}$

Besides,

Definition 5.

A zone consisting of all dead markings is called a dead zone, denoted by Z_D.

Definition 6.

A zone consisting of all quasi-dead markings is called a quasi-dead zone, denoted by Z_Q.

Definition 7.

A zone consisting of all quasi-dead and dead markings, i.e., Z_I = Z_D ∪ Z_Q, is called an illegal zone.

All markings except quasi-dead and dead markings are legal ones. Once a legal marking is enforced into the illegal zone, the net will eventually become deadlock.

Definition 8.

A zone consisting of all legal markings is called a legal zone, i.e., Z_L = R(N, M₀) - Z_I.

Please notice again, that in this paper, deadlock markings and legal markings are used in the proposed deadlock recovery policy. Besides, all markings will be identified in reachability graph analysis stage. Further, in the traditional deadlock prevention domain, the maximal permissive or optimal control means the maximal number of legal markings in a live system. In our recovery policy, our controllers will make all markings live including deadlock and quasi-dead markings. In other words, our designed policy recovers one deadlock system.

3. Basic Theory

Before designing CT, it is essential to spread out whole RG and determine the set of legal and deadlock markings. According to these two groups of markings, a three-dimensional matrix, called the generating and comparing aiding matrix (GCAM), is created to list all possible and effective CT. There are certainly two dimensions in GCAM, deadlock and legal markings. Note that only deadlock markings are considered in DZ, which includes deadlock and illegal markings, since trying to recover the latter will make more computational cost which is not necessary. This three-dimensional GCAM can be simplified as two-dimensional by regarding each transition as a single element. Creating GCAM helps numerating all effective CT, and the size of GCAM relies on the size of the model. The objective in this section is to find out the most effective CT in GCAM, hence, we have to compare every CT with each other. During creating GCAM, we define row as deadlock markings and column as legal markings. Note that the CTs in same row must be different, due to their same start point. Within process of comparing CTs, if a CT matches any ones in the chosen row, this CT can also connect corresponding deadlock marking to else legal marking, then the rest of this row will be skipped. After whole comparing process, we choose the most recovered CT as supervisor in this iteration and do next one, until DZ becomes empty.

3.1. Leading Transitions

In reachability graph analysis, all reachable states are needed to be identified and connected by enabled transitions. Therefore, all enabled transitions play one important role in a Petri nets model. One marking changes to another marking by firing any enabled transition.

For example, there are two different markings belonging to the same reachability graph of a Petri nets model of FMS, which is shown in Figure 1. These two markings are connected by one arc labelling transition $t$_x. Under one marking $M_i$, this model may have one or more enabled transitions including t_x. Note that the transition t_x must be enabled in $M_i$, or the arc labeled with transition t_x, which is shown in Figure 1, could not be generated within the reachability graph. When transition t_x is activated in $M_i$, the state will be fired to another marking $M_j$, which is presented as the terminal of the arc t_x in Figure 1. Therefore, in the reachability graph, $M_i$ and $M_j$ are connected with a single-direction arrow leading from $M_i$ to $M_j$. Figure 2 is a PN model of FMS and its reachable graph is shown in Figure 3.

For easy tracking, the detailed information of all markings are shown in

Table 1. The detailed information of all markings of Figure 3.

Marking No.	Information of Marking	Marking No.	Information of Marking
$M_1$	$3p_1+3p_8+p_9+p_{10}+p_{11}$	$M_{11}$	$3p_1+p_5+p_6+p_8+p_9$
$M_2$	$2p_1+p_2+3p_8+p_{10}+p_{11}$	$M_{12}$	$3p_1+p_7+2p_8+p_{10}+p_{11}$
$M_3$	$3p_1+p_5+2p_8+p_9+p_{10}$	$M_{13}$	$p_1+p_2+p_4+3p_8+p_{10}$
$M_4$	$2p_1+p_3+3p_8+p_9+p_{11}$	$M_{14}$	$p_1+p_2+p_3+p_5+2p_8$
$M_5$	$2p_1+p_2+p_5+2p_8+p_{10}$	$M_{15}$	$2p_1+p_2+p_5+p_6+p_8$
$M_6$	$3p_1+p_6+2p_8+p_9+p_{11}$	$M_{16}$	$3p_1+p_5+p_7+p_8+p_{10}$
$M_7$	$p_1+p_2+p_3+3p_8+p_{11}$	$M_{17}$	$p_1+p_3+p_4+3p_8+p_9$
$M_8$	$2p_1+p_4+3p_8+p_9+p_{10}$	$M_{18}$	$3p_1+p_6+p_7+p_8+p_{11}$
$M_9$	$2p_1+p_3+p_5+2p_8+p_9$	$M_{19}$	$p_2+p_3+p_4+3p_8$
$M_{10}$	$2p_1+p_2+p_6+2p_8+p_{11}$	$M_{20}$	$3p_1+p_5+p_6+p_7$

. Each marking in reachability graph is connected with existing transition, and each of its deadlock marking has no reachable marking. For example, in Figure 3, there are two markings, the legal marking $M_7$ and the dead marking $M_{14}$, which are linked by transition $t_5$. In other words, the legal marking M₇ through the transition t₅ is fired to the dead marking M₁₄. In this case, $i=7$, $j=14$ and $t_x=t_5$ is shown in Equation (1) as below:

$$M_7+t_5=M_{14}$$

(1)

Equation (1) can be present in Equation (2):

$$t_5=M_{14}-M_7$$

(2)

Similarly, some transition $t_c$ can also change the dead marking $M_{14}$ to the legal marking $M_7$ shown in Equation (3) as below:

$$t_c=M_7-M_{14}$$

(3)

Therefore, a generated control transition $t_c$ can lead $M_D$ to $M_L$ and the computation can be simply presented shown in Equation (4) as below:

$$t_c=M_L-M_D$$

(4)

Definition 9.

One added transition $t_c$ between one legal marking $M_L$ and one deadlock marking $M_D$ is called the leading transition if $t_c=M_L-M_D$.

3.2. Generating and Comparing Aiding Matrix (GCAM)

Huang et al. [44] control the PN model of FMS by adding control transition to recover all deadlock markings, though the control policy cannot afford too huge system and has more structural complexity. The proposed method can solve these two problems and either of the possibly occurring live-lock situations. This method compares all possible generated control transitions to find out the optimal one in each iteration until DZ becomes empty. A three-dimension matrix, also called the generating and comparing aiding matrix (GCAM), is built and helps comparing computation a lot. According to the set of legal and deadlock markings, GCAM is created, where the first dimension is deadlock markings, the second dimension is legal ones and the third dimension is $M_L-M_D$. Before building GCAM, the reachability graph analysis hence has to be done to partition the RG into legal, illegal and deadlock markings. For easy tracking, GCAM can be represented in simple model called simplified GCAM (SGCAM) in this paper. For example, the uncontrolled PN model of FMS shown in Figure 2 and Figure 3 has two deadlock markings, 15 legal markings and 11 places, then the size of its GCAM is $2\times 15\times 11$.

Table 2. Generating and comparing aiding matrix (GCAM) of Example 1.

		$M_{14}:$ $p_1+p_2+p_3+p_5+2p_8$	$M_{15}:$ $2p_1+p_2+p_5+p_6+p_8$
		$2p_1-p_2-p_3-p_5+p_8+p_9+p_{10}+p_{11}$	$p_1-p_2-p_5-p_6+2p_8+p_9+p_{10}+p_{11}$
$M_2:$	$2p_1+p_2+3p_8+p_{10}+p_{11}$	$p_1-p_3-p_5+p_8+p_{10}+p_{11}$	$-p_5-p_6+2p_8+p_{10}+p_{11}$
$M_3$:	$3p_1+p_5+2p_8+p_9+p_{10}$	$2p_1-p_2-p_3+p_9+p_{10}$	$p_1-p_2-p_6+p_8+p_9+p_{10}$
$M_4:$	$2p_1+p_3+3p_8+p_9+p_{11}$	$p_1-p_2-p_5+p_8+p_9+p_{11}$	$-p_2+p_3-p_5-p_6+2p_8+p_9+p_{11}$
$M_6:$	$3p_1+p_6+2p_8+p_9+p_{11}$	$2p_1-p_2-p_3-p_5+p_6+p_9+p_{11}$	$p_1-p_2-p_5+p_8+p_9+p_{11}$
$M_7:$	$p_1+p_2+p_3+3p_8+p_{11}$	$-p_5+p_8+p_{11}$	$-p_1+p_3-p_5-p_6+2_8+p_{11}$
$M_8:$	$2p_1+p_4+3p_8+p_9+p_{10}$	$p_1-p_2-p_3+p_4-p_5+p_8+p_9+p_{10}$	$-p_2+p_4-p_5-p_6+2p_8+p_9+p_{10}$
$M_{11}:$	$3p_1+p_5+p_6+p_8+p_9$	$2p_1-p_2-p_3+p_5-p_8+p_9$	$p_1-p_2+p_9$
$M_{12}:$	$3p_1+p_7+2p_8+p_{10}+p_{11}$	$2p_1-p_2-p_3-p_5+p_7+p_{10}+p_{11}$	$p_1-p_2-p_5-p_6+p_7+p_8+p_{10}+p_{11}$
$M_{13}:$	$p_1+p_2+p_4+3p_8+p_{10}$	$-p_3+p_4-p_5+p_8+p_{10}$	$-p_1+p_4-p_5-p_6+2p_8+p_{10}$
$M_{16}:$	$3p_1+p_5+p_7+p_8+p_{10}$	$2p_1-p_2-p_3+p_7-p_8+p_{10}$	$p_1-p_2-p_6+p_7+p_{10}$
$M_{17}:$	$p_1+p_3+p_4+3p_8+p_9$	$-p_2+p_4-p_5+p_8+p_9$	$-p_1-p_2+p_3+p_4-p_5-p_6+2p_8+p_9$
$M_{18}:$	$3p_1+p_6+p_7+p_8+p_{11}$	$2p_1-p_2-p_3-p_5+p_6+p_7-p_8+p_{11}$	$p_1-p_2-p_5+p_7+p_{11}$
$M_{19}:$	$p_2+p_3+p_4+3p_8$	$-p_1+p_4-p_5+p_8$	$-2p_1+p_3+p_4-p_5-p_6+2p_8$
$M_{20}:$	$3p_1+p_5+p_6+p_7$	$2p_1-p_2-p_3+p_6+p_7-2p_8$	$p_1-p_2+p_7-p_8$

and

Table 3. Simplified GCAM (SGCAM) of Example 1.

	${\mathit{M}}_{14}$	${\mathit{M}}_{15}$
$M_1$	$t_{14,1}$	$t_{15,1}$
$M_2$	$t_{14,2}$	$t_{15,2}$
$M_3$	$t_{14,3}$	$t_{15,3}$
$M_4$	${\mathit{t}}_{\mathbf{14},\mathbf{4}}$	$t_{15,4}$
$M_6$	$t_{14,6}$	${\mathit{t}}_{\mathbf{15},\mathbf{6}}$
$M_7$	$t_{14,7}$	$t_{15,7}$
$M_8$	$t_{14,8}$	$t_{15,8}$
$M_{11}$	$t_{14,11}$	$t_{15,11}$
$M_{12}$	$t_{14,12}$	$t_{15,12}$
$M_{13}$	$t_{14,13}$	$t_{15,13}$
$M_{16}$	$t_{14,16}$	$t_{15,16}$
$M_{17}$	$t_{14,17}$	$t_{15,17}$
$M_{18}$	$t_{14,18}$	$t_{15,18}$
$M_{19}$	$t_{14,19}$	$t_{15,19}$
$M_{20}$	$t_{14,20}$	$t_{15,20}$

show its GCAM and SGCAM, respectively. Please notice that only the deadlock markings are adopted to build up the first dimension of GCAM rather than all illegal ones, because only deadlock ones need to be recovered and other illegal ones in DZ still have enough liveness. All control transitions in GCAM are compared with each other, and the computation complexity depends on the scale of the size of reachability graph and GCAM, precisely, about ${\left(M_D\times M_L\right)}^2$ times comparing would be executed in computation of an iteration.

4. Algorithm

The proposed deadlock control policy is presented in this section, which aims to raise up system liveness by recovering all undesired deadlock situations. Aforementioned techniques are summed up to designed effective supervisors. PN model in Figure 2 and its reachability graph shown in Figure 3 help demonstrating proposed method as following.

Definition 10.

Let function $R\left(t_c\right)$ denote the recovering efficiency of $t_c$, which is used to recognize the most effective control transition in GCAM. The values of $R\left(t_c\right)$ are possible zero or positive integer, and initially reset as zero before comparing comparison from $t_c$ to others. The value of $R\left(t_c\right)$ increases by one when a deadlock is identified being solved by $t_c$. After whole computation of $t_c$, the value of $R\left(t_c\right)$ indicates the number of deadlocks recovered by $t_c$.

Algorithm 1: GCAM-based Recovery Control Transition Designing

Input: One PN model of a FMS with deadlock and quasi-deadlock markings.  Output: One optimal controlled FMS with control transitions 1. Illustrate reachability graph with all reachable markings. 2. Identify the set of legal markings ${ℳ}_L$ and the set of deadlock markings ${ℳ}_D$. 3. Build GCAM and SGCAM including all possible control transitions. 4. Comparing computation.  while $(M_D\ne \varnothing )$ do   for $(i,j\in \mathbb{N}\mathrm{and}{t}_{i,j}\in \mathrm{GCAM})$ do    $R\left(t_{i,j}\right)\leftarrow 0$    for $(k\in \mathbb{N},M_k\in M_D)$ do     for $(l\in \mathbb{N},M_l\in M_L)$ do      if $(t_{i,j}=t_{k,l})$ then      $R\left(t_{i,j}\right)\leftarrow R\left(t_{i,j}\right)+1$       $k\leftarrow k+1$       let l be 1 /*reset the value of k and l to skip the rest of column Mk and start the next column. */       end if     end for    end for    end for    Add the control transition tc with the maximal $R\left(t_c\right)$ to the PN model.   if $(M_D\ne \varnothing )$ then    Do reachability graph analysis and build GCAM for next loop.   end if  end while 5. Output completely recovered system with $M_D=\varnothing$ and all markings reachable.

Algorithm 1 based on reachability graph analysis accordingly illustrates its maximally reachable graph at first. Notice that reachability graph will be calculated at each iteration, due to the LZ and DZ changes after attaching generated supervisors to system. Under provided control policy, generally, LZ extends and DZ reduces after every iteration. The presented approach aims to recover all existing deadlock markings, the set of legal and deadlock markings, are therefore, recognized in the reachability graph at the beginning within each loop.

After attaching new control transition (usually the most effective one) to PN model, a brand new reachability graph is illustrated due to its updated model. Although repeating analysis to generate reachability graph makes more computation heavy, the following process of designing supervisors is much more timesaving and systematic than other methods, such as MFFP (ILPP) [40], which is a kind of NP-hard problem.

Finally, please notice that building GCAM and SGCAM is extremely essential for the main comparing computation process. Viewing the entire recovery possibility of the whole system is clearer than generating a leading transition before each comparing process.

5. Experimental Results

This section will demonstrate our proposed deadlock recovery policy which is proposed in Section 4 through two classic S³PR [10] (the system of simple sequential process with resources) examples. Besides, for easy checking, the two examples used INA [63] and PN-Tools [64] to run their reachability graph, respectively.

Definition 11.

An S³PR [10] is defined as the union of a set of nets N_i sharing common places, called resource idle places (i.e., called resource places in this paper) P_Ri, such that $N_i=\left(P_i\cup \left\{p_i^0\right\}\cup P_{Ri},T_i,F_i\right)$, where (1) P_i ≠ ∅, p_i⁰ ∉ P_i (2) $N_i^{\prime }$ is a strongly connected state machine where $N_i^{\prime }=\left(P_i\cup \left\{p_i^0\right\},T_i,F_i^{\prime }\right)$ is the resultant net after P_Ri is removed from N_i; (3) every circuit of $N_i^{\prime }$ contains the place $p_i^0$ and (4) any two $N_i^{\prime }$ are composable when they share a set of common resource idle places. In the above definition, $p_i^0$ is called the process idle place and P_i the set of operation places. The $N_i^{\prime }$ shall be called a process net. An S³PR has an important characteristic that only one shared resource is allowed at each operation state, i.e., a place in P_i is marked. The resource used in a state is released when the system moves to the next state.

5.1. Examples

Example 1.

Firstly, please refer to Figure 2, there are two idle places, six operation places and three resource places, which are denoted as $P^0=\left\{p_1,p_8\right\}$, $P_A=\left\{p_2,p_3,p_4,p_5,p_6,p_7\right\}$ and $P_R=\left\{p_9,p_{10},p_{11}\right\}$. Since there are two prebuilt process competing resources in this example, deadlock states hence occur. Further, according to reachability graph analysis, the system’s reachability graph consists of 20 reachable states in total, shown in Figure 3, including fifteen legal and five illegal markings (three quasi-dead markings, i.e., M₅, M₉ and, M₁₀, and two deadlock markings, i.e., M₁₄ and M₁₅). Please notice that under our proposed transition-based recovery control policy, only deadlock and legal markings are needed to be considered, and are adopted to build its GCAM and SGCAM matrixes. Therefore, we show both of them in Table 2 and Table 3, respectively. Furthermore, for easy tracking we show the GCAM matrix in PN places form. Based on Equation (3), each leading (control) transition can then be obtained under two deadlock markings and fifteen legal ones. For instance, $t_{14,1}$ can be built by the two markings, $\left\{M_{14},M_1\right\}$, shown in Equation (5) as follows:

$$t_{14,1}=M_1-M_{14}$$

(5)

In Equation (5), it is worthy note that the marking M₁ belongs to ${ℳ}_L$ and the marking M₁₄ belongs to ${ℳ}_D$. Further, Equation (5) can then be Equation (6) as follows:

$$t_{14,1}=M_1-M_{14}=\left[3p_1+3p_8+p_9+p_{10}+p_{11}\right]-\left[p_1+p_2+p_3+p_5+2p_8\right]$$

(6)

After the computation in Equation (6), the leading transition of $t_{14,1}$ is equal to $\left[2p_1-p_2-p_3-p_5+p_8+p_9+p_{10}+p_{11}\right]$. It is also present in Table 2 (please refer to bold face). Note that all leading transitions in GCAM can be viewed as control transitions since they can recover their corresponding (relative) dead markings simultaneously. Furthermore, it means that they can recover the same dead markings once two sets or more of markings (one legal with one dead markings) in GCAM have the same leading transition.

Accordingly, one can recognize that the two sets of markings $\left[M_{14},M_4\right]$ and $\left[M_{15},M_6\right]$ have the same leading transition since $t_{14,4}=t_{15,6}=\left[p_1-p_2-p_5+p_8+p_9+p_{11}\right]$. In other words, it means that the set of leading transition can make the two deadlock markings M₁₄ and M₁₅ live and make this system recovery. Further, this system will be optimal controlled once the control transition t_c is equal to [$p_1-p_2-p_5+p_8+p_9+p_{11}$]. Figure 4 shows that the control transition is added into the system. Further, all illegal (i.e., quasi-dead and deadlock) markings are recovered and become live as shown in Figure 5. In summary, the system has real maximal permissive states since all original 20 reachable markings are held totally.

Example 2.

Here is another classical example used to evaluate our policy and presented in Figure 6, with totally 19 places and 14 transitions. In this PN model, there are two idle places, eleven operation places and six resource places, denoted as $P^0=\left\{p_1,p_8\right\}$, $P_A=\left\{p_2-p_7,p_9-p_{13}\right\}$ and $P_R=\left\{p_{14}-p_{19}\right\}$. After reachability graph analysis, there are 282 markings identified totally, including 16 deadlock markings (M₈₉, M₁₀₇, M₁₅₄, M₁₆₂, M₁₇₀, M₁₇₄, M₁₉₈, M₂₀₂, M₂₀₅, M₂₁₁, M₂₂₇, M₂₄₉, M₂₅₆, M₂₅₇, M₂₆₁, and M₂₇₇) and 205 legal ones based on PN-tools [18]. Please note that due to the space limitation of this paper, we will not present the detailed information of CGAM, SCGAM, and all detailed process of seeking leading transitions. We just show the key information. Firstly, the properties of deadlock and legal markings in matrix form are present in

Table 4. The detailed information of all deadlock markings of Example 2.

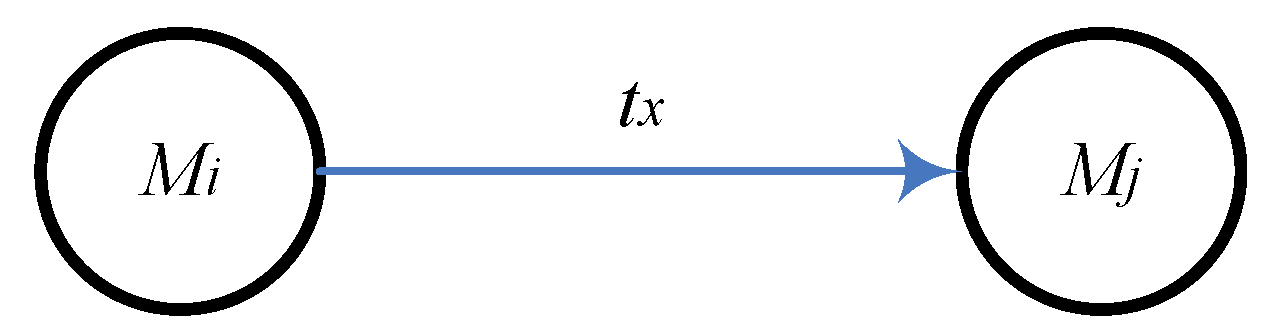
Marking No.	Information of Markings [p1~p19]	Marking No.	Information of Markings [p1~p19]
$M_{89}$	3 1 1 1 0 0 0 4 1 1 0 0 0 0 0 1 0 0 0	$M_{205}$	3 0 0 1 1 1 0 4 1 1 0 0 0 0 1 0 0 0 0
$M_{107}$	5 0 1 0 0 0 0 3 1 1 1 0 0 1 0 1 0 0 0	$M_{211}$	4 0 1 0 0 1 0 3 1 1 1 0 0 1 0 0 0 0 0
$M_{154}$	4 0 0 0 1 1 0 4 1 1 0 0 0 1 1 0 0 0 0	$M_{227}$	5 0 0 1 0 0 0 2 1 1 1 1 0 0 0 1 0 0 0
$M_{162}$	4 0 1 1 0 0 0 3 1 1 1 0 0 0 0 1 0 0 0	$M_{249}$	3 0 1 1 0 1 0 3 1 1 1 0 0 0 0 0 0 0 0
$M_{170}$	4 1 0 1 0 0 0 3 1 1 0 1 0 0 0 1 0 0 0	$M_{256}$	3 1 0 1 0 1 0 3 1 1 0 1 0 0 0 0 0 0 0
$M_{174}$	6 0 0 0 0 0 0 2 1 1 1 1 0 1 0 1 0 0 0	$M_{257}$	4 0 0 0 1 1 0 3 1 1 0 1 0 1 0 0 0 0 0
$M_{198}$	2 1 1 1 0 1 0 4 1 1 0 0 0 0 0 0 0 0 0	$M_{261}$	5 0 0 0 0 1 0 2 1 1 1 1 0 1 0 0 0 0 0
$M_{202}$	3 0 1 0 1 1 0 4 1 1 0 0 0 1 0 0 0 0 0	$M_{277}$	4 0 0 1 0 1 0 2 1 1 1 1 0 0 0 0 0 0 0

and

Table 5. The detailed information of all legal markings of Example 2.

Marking No.	Information of markings [p1~p19]																			Marking No.	Information of markings [p1~p19]
1	6	0	0	0	0	0	0	6	0	0	0	0	0	1	1	1	1	1	1	120	3	0	1	1	0	1	0	5	1	0	0	0	0	0	0	0	1	1	0
2	5	1	0	0	0	0	0	6	0	0	0	0	0	1	1	1	1	0	1	121	3	1	1	0	0	1	0	5	0	1	0	0	0	1	0	0	0	0	1
3	6	0	0	0	0	0	0	5	1	0	0	0	0	1	1	1	1	1	0	122	4	0	0	0	0	1	1	6	0	0	0	0	0	1	1	0	1	1	0
4	5	0	1	0	0	0	0	6	0	0	0	0	0	1	0	1	1	1	1	123	4	0	0	0	1	1	0	5	0	1	0	0	0	1	1	0	0	0	1
5	5	0	0	1	0	0	0	6	0	0	0	0	0	0	1	1	1	1	1	124	4	0	1	0	0	0	1	5	0	1	0	0	0	1	0	1	0	1	0
6	5	1	0	0	0	0	0	5	1	0	0	0	0	1	1	1	1	0	0	127	3	1	0	1	0	1	0	5	0	1	0	0	0	0	1	0	0	0	1
7	6	0	0	0	0	0	0	5	0	1	0	0	0	1	1	1	0	1	1	128	4	0	0	1	0	0	1	5	0	1	0	0	0	0	1	1	0	1	0
8	4	1	1	0	0	0	0	6	0	0	0	0	0	1	0	1	1	0	1	129	4	0	0	1	0	1	0	4	1	1	0	0	0	0	1	0	0	1	0
9	5	0	0	0	1	0	0	6	0	0	0	0	0	1	1	1	1	0	1	130	4	0	0	1	0	1	0	5	0	0	1	0	0	0	1	0	1	0	1
10	5	0	1	0	0	0	0	5	1	0	0	0	0	1	0	1	1	1	0	132	5	0	0	0	0	0	1	5	0	0	0	1	0	1	0	1	1	1	0
11	4	1	0	1	0	0	0	6	0	0	0	0	0	0	1	1	1	0	1	133	5	0	0	0	0	1	0	4	0	1	1	0	0	1	1	0	0	0	1
12	5	0	0	1	0	0	0	5	1	0	0	0	0	0	1	1	1	1	0	134	5	0	0	0	0	1	0	4	1	0	0	1	0	1	0	0	1	1	0
13	5	1	0	0	0	0	0	5	0	1	0	0	0	1	1	1	0	0	1	135	4	1	0	0	0	1	0	5	0	0	0	1	0	1	0	0	1	0	1
14	6	0	0	0	0	0	0	4	1	1	0	0	0	1	1	1	0	1	0	136	5	0	0	0	0	1	0	5	0	0	0	0	1	1	1	0	1	0	1
15	6	0	0	0	0	0	0	5	0	0	1	0	0	1	1	1	1	0	1	137	5	0	0	1	0	0	0	3	1	1	0	1	0	0	0	1	0	1	0
16	4	0	1	1	0	0	0	6	0	0	0	0	0	0	0	1	1	1	1	139	5	0	0	0	1	0	0	4	0	1	0	1	0	1	0	1	0	0	1
17	4	1	1	0	0	0	0	5	1	0	0	0	0	1	0	1	1	0	0	141	5	0	0	1	0	0	0	4	0	1	0	0	1	0	1	1	0	0	1
18	5	0	0	0	0	1	0	6	0	0	0	0	0	1	1	0	1	1	1	145	3	0	1	0	1	0	1	6	0	0	0	0	0	1	0	1	1	0	0
19	5	0	0	0	1	0	0	5	1	0	0	0	0	1	1	1	1	0	0	146	3	0	1	0	1	1	0	5	1	0	0	0	0	1	0	0	1	0	0
20	5	0	1	0	0	0	0	5	0	1	0	0	0	1	0	1	0	1	1	147	3	0	0	1	1	0	1	6	0	0	0	0	0	0	1	1	1	0	0
21	4	1	0	1	0	0	0	5	1	0	0	0	0	0	1	1	1	0	0	148	3	0	0	1	1	1	0	5	1	0	0	0	0	0	1	0	1	0	0
22	5	0	0	1	0	0	0	5	0	1	0	0	0	0	1	1	0	1	1	149	3	0	1	1	0	1	0	5	0	1	0	0	0	0	0	0	0	1	1
23	5	1	0	0	0	0	0	4	1	1	0	0	0	1	1	1	0	0	0	150	3	1	1	0	0	0	1	5	0	1	0	0	0	1	0	1	0	0	0
24	6	0	0	0	0	0	0	4	1	0	1	0	0	1	1	1	1	0	0	152	3	1	0	0	0	1	1	6	0	0	0	0	0	1	1	0	1	0	0
25	6	0	0	0	0	0	0	5	0	0	0	1	0	1	0	1	1	1	1	153	4	0	0	0	1	0	1	5	0	1	0	0	0	1	1	1	0	0	0
27	4	0	1	0	1	0	0	6	0	0	0	0	0	1	0	1	1	0	1	157	3	1	0	1	0	0	1	5	0	1	0	0	0	0	1	1	0	0	0
28	4	0	0	1	1	0	0	6	0	0	0	0	0	0	1	1	1	0	1	159	4	0	0	1	0	0	1	5	0	0	1	0	0	0	1	1	1	0	0
29	4	0	1	1	0	0	0	5	1	0	0	0	0	0	0	1	1	1	0	160	4	0	0	1	0	1	0	4	1	0	1	0	0	0	1	0	1	0	0
30	4	1	1	0	0	0	0	5	0	1	0	0	0	1	0	1	0	0	1	161	4	0	0	1	0	1	0	5	0	0	0	1	0	0	0	0	1	1	1
31	4	1	0	0	0	1	0	6	0	0	0	0	0	1	1	0	1	0	1	163	4	1	0	0	0	0	1	5	0	0	0	1	0	1	0	1	1	0	0
32	5	0	0	0	0	0	1	6	0	0	0	0	0	1	1	1	1	1	0	164	5	0	0	0	0	0	1	5	0	0	0	0	1	1	1	1	1	0	0
33	5	0	0	0	0	1	0	5	1	0	0	0	0	1	1	0	1	1	0	165	5	0	0	0	0	0	1	4	0	1	1	0	0	1	1	1	0	0	0
34	5	0	0	0	1	0	0	5	0	1	0	0	0	1	1	1	0	0	1	166	5	0	0	0	0	1	0	3	1	1	1	0	0	1	1	0	0	0	0
35	5	0	1	0	0	0	0	4	1	1	0	0	0	1	0	1	0	1	0	167	5	0	0	0	0	1	0	4	0	1	0	1	0	1	0	0	0	1	1
37	4	1	0	1	0	0	0	5	0	1	0	0	0	0	1	1	0	0	1	168	4	1	0	0	0	1	0	4	1	0	0	1	0	1	0	0	1	0	0
38	5	0	0	1	0	0	0	4	1	1	0	0	0	0	1	1	0	1	0	169	5	0	0	0	0	1	0	4	1	0	0	0	1	1	1	0	1	0	0
39	5	0	0	1	0	0	0	5	0	0	1	0	0	0	1	1	1	0	1	171	5	0	0	0	1	0	0	3	1	1	0	1	0	1	0	1	0	0	0
40	6	0	0	0	0	0	0	4	0	1	1	0	0	1	1	1	0	0	1	173	5	0	0	1	0	0	0	3	1	1	0	0	1	0	1	1	0	0	0
41	6	0	0	0	0	0	0	4	1	0	0	1	0	1	0	1	1	1	0	176	3	0	1	0	0	1	1	6	0	0	0	0	0	1	0	0	1	1	0
42	5	1	0	0	0	0	0	5	0	0	0	1	0	1	0	1	1	0	1	177	3	0	1	0	1	1	0	5	0	1	0	0	0	1	0	0	0	0	1
43	6	0	0	0	0	0	0	5	0	0	0	0	1	1	1	1	1	0	1	178	3	0	0	1	0	1	1	6	0	0	0	0	0	0	1	0	1	1	0
45	4	0	1	0	0	1	0	6	0	0	0	0	0	1	0	0	1	1	1	179	3	0	0	1	1	1	0	5	0	1	0	0	0	0	1	0	0	0	1
46	4	0	1	0	1	0	0	5	1	0	0	0	0	1	0	1	1	0	0	180	3	0	1	1	0	0	1	5	0	1	0	0	0	0	0	1	0	1	0
47	4	0	0	1	0	1	0	6	0	0	0	0	0	0	1	0	1	1	1	183	4	0	0	0	0	1	1	5	0	1	0	0	0	1	1	0	0	1	0
48	4	0	0	1	1	0	0	5	1	0	0	0	0	0	1	1	1	0	0	185	4	0	0	1	0	0	1	5	0	0	0	1	0	0	0	1	1	1	0
49	4	0	1	1	0	0	0	5	0	1	0	0	0	0	0	1	0	1	1	186	4	0	0	1	0	1	0	4	0	1	1	0	0	0	1	0	0	0	1
50	4	1	1	0	0	0	0	4	1	1	0	0	0	1	0	1	0	0	0	187	4	0	0	1	0	1	0	4	1	0	0	1	0	0	0	0	1	1	0
51	4	1	0	0	0	0	1	6	0	0	0	0	0	1	1	1	1	0	0	189	4	0	0	0	1	1	0	5	0	0	0	1	0	1	0	0	1	0	1
52	4	1	0	0	0	1	0	5	1	0	0	0	0	1	1	0	1	0	0	190	4	0	0	1	0	1	0	5	0	0	0	0	1	0	1	0	1	0	1
53	5	0	0	0	0	1	0	5	0	1	0	0	0	1	1	0	0	1	1	191	5	0	0	0	0	0	1	4	0	1	0	1	0	1	0	1	0	1	0
54	5	0	0	0	1	0	0	4	1	1	0	0	0	1	1	1	0	0	0	192	5	0	0	0	0	1	0	3	1	1	0	1	0	1	0	0	0	1	0
56	4	1	0	1	0	0	0	4	1	1	0	0	0	0	1	1	0	0	0	193	4	1	0	0	0	1	0	4	0	1	0	1	0	1	0	0	0	0	1
57	5	0	0	1	0	0	0	4	1	0	1	0	0	0	1	1	1	0	0	195	5	0	0	0	0	1	0	4	0	1	0	0	1	1	1	0	0	0	1
58	5	0	0	1	0	0	0	5	0	0	0	1	0	0	0	1	1	1	1	199	2	1	1	0	0	1	1	6	0	0	0	0	0	1	0	0	1	0	0
59	6	0	0	0	0	0	0	3	1	1	1	0	0	1	1	1	0	0	0	200	3	0	0	0	1	1	1	6	0	0	0	0	0	1	1	0	1	0	0
60	6	0	0	0	0	0	0	4	0	1	0	1	0	1	0	1	0	1	1	201	3	0	1	0	1	0	1	5	0	1	0	0	0	1	0	1	0	0	0
61	5	1	0	0	0	0	0	4	1	0	0	1	0	1	0	1	1	0	0	203	2	1	0	1	0	1	1	6	0	0	0	0	0	0	1	0	1	0	0
62	6	0	0	0	0	0	0	4	1	0	0	0	1	1	1	1	1	0	0	204	3	0	0	1	1	0	1	5	0	1	0	0	0	0	1	1	0	0	0
64	3	1	1	0	0	1	0	6	0	0	0	0	0	1	0	0	1	0	1	208	3	1	0	0	0	1	1	5	0	1	0	0	0	1	1	0	0	0	0
65	4	0	0	0	1	1	0	6	0	0	0	0	0	1	1	0	1	0	1	209	4	0	0	0	0	1	1	5	0	0	1	0	0	1	1	0	1	0	0
66	4	0	1	0	0	0	1	6	0	0	0	0	0	1	0	1	1	1	0	213	4	0	0	0	1	0	1	5	0	0	0	1	0	1	0	1	1	0	0
67	4	0	1	0	0	1	0	5	1	0	0	0	0	1	0	0	1	1	0	214	4	0	0	1	0	0	1	5	0	0	0	0	1	0	1	1	1	0	0
68	4	0	1	0	1	0	0	5	0	1	0	0	0	1	0	1	0	0	1	215	4	0	0	1	0	0	1	4	0	1	1	0	0	0	1	1	0	0	0
69	3	1	0	1	0	1	0	6	0	0	0	0	0	0	1	0	1	0	1	216	4	0	0	1	0	1	0	3	1	1	1	0	0	0	1	0	0	0	0
70	4	0	0	1	0	0	1	6	0	0	0	0	0	0	1	1	1	1	0	217	4	0	0	1	0	1	0	4	0	1	0	1	0	0	0	0	0	1	1
71	4	0	0	1	0	1	0	5	1	0	0	0	0	0	1	0	1	1	0	219	4	0	0	0	1	1	0	4	1	0	0	1	0	1	0	0	1	0	0
72	4	0	0	1	1	0	0	5	0	1	0	0	0	0	1	1	0	0	1	220	4	0	0	1	0	1	0	4	1	0	0	0	1	0	1	0	1	0	0
73	4	0	1	1	0	0	0	4	1	1	0	0	0	0	0	1	0	1	0	221	4	1	0	0	0	0	1	4	0	1	0	1	0	1	0	1	0	0	0
75	4	1	0	0	0	1	0	5	0	1	0	0	0	1	1	0	0	0	1	223	5	0	0	0	0	0	1	4	0	1	0	0	1	1	1	1	0	0	0
76	5	0	0	0	0	0	1	5	0	1	0	0	0	1	1	1	0	1	0	224	4	1	0	0	0	1	0	3	1	1	0	1	0	1	0	0	0	0	0
77	5	0	0	0	0	1	0	4	1	1	0	0	0	1	1	0	0	1	0	226	5	0	0	0	0	1	0	3	1	1	0	0	1	1	1	0	0	0	0
78	5	0	0	0	0	1	0	5	0	0	1	0	0	1	1	0	1	0	1	228	2	0	1	1	0	1	1	6	0	0	0	0	0	0	0	0	1	1	0
80	5	0	0	1	0	0	0	4	0	1	1	0	0	0	1	1	0	0	1	229	3	0	1	0	0	1	1	5	0	1	0	0	0	1	0	0	0	1	0
81	5	0	0	1	0	0	0	4	1	0	0	1	0	0	0	1	1	1	0	230	3	0	0	1	0	1	1	5	0	1	0	0	0	0	1	0	0	1	0
83	5	0	0	0	1	0	0	5	0	0	0	1	0	1	0	1	1	0	1	232	4	0	0	0	0	1	1	5	0	0	0	1	0	1	0	0	1	1	0
84	5	0	0	1	0	0	0	5	0	0	0	0	1	0	1	1	1	0	1	233	4	0	0	1	0	0	1	4	0	1	0	1	0	0	0	1	0	1	0
85	6	0	0	0	0	0	0	3	1	1	0	1	0	1	0	1	0	1	0	234	4	0	0	1	0	1	0	3	1	1	0	1	0	0	0	0	0	1	0
86	5	1	0	0	0	0	0	4	0	1	0	1	0	1	0	1	0	0	1	236	4	0	0	0	1	1	0	4	0	1	0	1	0	1	0	0	0	0	1
88	6	0	0	0	0	0	0	4	0	1	0	0	1	1	1	1	0	0	1	238	4	0	0	1	0	1	0	4	0	1	0	0	1	0	1	0	0	0	1
90	3	0	1	1	0	1	0	6	0	0	0	0	0	0	0	0	1	1	1	241	2	0	1	0	1	1	1	6	0	0	0	0	0	1	0	0	1	0	0
91	3	1	1	0	0	0	1	6	0	0	0	0	0	1	0	1	1	0	0	242	2	0	0	1	1	1	1	6	0	0	0	0	0	0	1	0	1	0	0
92	3	1	1	0	0	1	0	5	1	0	0	0	0	1	0	0	1	0	0	243	2	1	1	0	0	1	1	5	0	1	0	0	0	1	0	0	0	0	0
93	4	0	0	0	1	0	1	6	0	0	0	0	0	1	1	1	1	0	0	244	3	0	0	0	1	1	1	5	0	1	0	0	0	1	1	0	0	0	0
94	4	0	0	0	1	1	0	5	1	0	0	0	0	1	1	0	1	0	0	246	2	1	0	1	0	1	1	5	0	1	0	0	0	0	1	0	0	0	0
95	4	0	1	0	0	1	0	5	0	1	0	0	0	1	0	0	0	1	1	247	3	0	0	1	0	1	1	5	0	0	1	0	0	0	1	0	1	0	0
97	3	1	0	1	0	0	1	6	0	0	0	0	0	0	1	1	1	0	0	250	3	1	0	0	0	1	1	5	0	0	0	1	0	1	0	0	1	0	0
98	3	1	0	1	0	1	0	5	1	0	0	0	0	0	1	0	1	0	0	251	4	0	0	0	0	1	1	5	0	0	0	0	1	1	1	0	1	0	0
99	4	0	0	1	0	1	0	5	0	1	0	0	0	0	1	0	0	1	1	253	4	0	0	0	1	0	1	4	0	1	0	1	0	1	0	1	0	0	0
100	4	0	0	1	1	0	0	4	1	1	0	0	0	0	1	1	0	0	0	255	4	0	0	1	0	0	1	4	0	1	0	0	1	0	1	1	0	0	0
102	4	1	0	0	0	0	1	5	0	1	0	0	0	1	1	1	0	0	0	259	4	0	0	1	0	1	0	3	1	1	0	0	1	0	1	0	0	0	0
103	4	1	0	0	0	1	0	4	1	1	0	0	0	1	1	0	0	0	0	262	2	0	1	1	0	1	1	5	0	1	0	0	0	0	0	0	0	1	0
104	5	0	0	0	0	0	1	5	0	0	1	0	0	1	1	1	1	0	0	263	3	0	0	1	0	1	1	5	0	0	0	1	0	0	0	0	1	1	0
105	5	0	0	0	0	1	0	4	1	0	1	0	0	1	1	0	1	0	0	264	4	0	0	0	0	1	1	4	0	1	0	1	0	1	0	0	0	1	0
106	5	0	0	0	0	1	0	5	0	0	0	1	0	1	0	0	1	1	1	267	2	0	1	0	1	1	1	5	0	1	0	0	0	1	0	0	0	0	0
108	5	0	0	1	0	0	0	3	1	1	1	0	0	0	1	1	0	0	0	268	2	0	0	1	1	1	1	5	0	1	0	0	0	0	1	0	0	0	0
109	5	0	0	1	0	0	0	4	0	1	0	1	0	0	0	1	0	1	1	271	3	0	0	0	1	1	1	5	0	0	0	1	0	1	0	0	1	0	0
111	5	0	0	0	1	0	0	4	1	0	0	1	0	1	0	1	1	0	0	272	3	0	0	1	0	1	1	5	0	0	0	0	1	0	1	0	1	0	0
112	5	0	0	1	0	0	0	4	1	0	0	0	1	0	1	1	1	0	0	273	3	1	0	0	0	1	1	4	0	1	0	1	0	1	0	0	0	0	0
113	5	1	0	0	0	0	0	3	1	1	0	1	0	1	0	1	0	0	0	275	4	0	0	0	0	1	1	4	0	1	0	0	1	1	1	0	0	0	0
115	6	0	0	0	0	0	0	3	1	1	0	0	1	1	1	1	0	0	0	278	3	0	0	1	0	1	1	4	0	1	0	1	0	0	0	0	0	1	0
117	3	0	1	0	1	1	0	6	0	0	0	0	0	1	0	0	1	0	1	280	3	0	0	0	1	1	1	4	0	1	0	1	0	1	0	0	0	0	0
118	3	0	0	1	1	1	0	6	0	0	0	0	0	0	1	0	1	0	1	282	3	0	0	1	0	1	1	4	0	1	0	0	1	0	1	0	0	0	0
119	3	0	1	1	0	0	1	6	0	0	0	0	0	0	0	1	1	1	0

, respectively.

In this example, we cannot merely use only one leading (control) transition to solve the system’s deadlock problem and make the system recovery due to the complexity of this system. Under this situation, therefore, we must try to identify the least number of leading (control) transitions so that they can recover maximal number of deadlock markings.

Accordingly, in the first iteration, there are 40 sets of leading transitions identified and they all can recover maximal eight same deadlock markings (i.e., M₁₀₇, M₁₇₂, M₁₇₄, M₂₁₁, M₂₂₇, M₂₄₉, M₂₆₁, and M₂₇₇), which are listed as follows (refer to

Table 6. The detailed information of all leading transition of Example 2 in first iteration.

Leading Transition ${\mathit{t}}_{\mathit{i}, \mathit{j}}$	The Number of Deadlock Markings	The Property of Leading Transition
$t_{107,4}$	8	$3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}$
$t_{107,10}$	8	$2p_8-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{107,20}$	8	$2p_8-p_9-p_{11}+p_{18}+p_{19}$
$t_{107,66}$	8	$-p_1+p_7+3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{107,124}$	8	$-p_1+p_7+2p_8-p_9-p_{11}+p_{18}$
$t_{162,16}$	8	$3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}$
$t_{162,29}$	8	$2p_8-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{162,49}$	8	$2p_8-p_9-p_{11}+p_{18}+p_{19}$
$t_{162,119}$	8	$-p_1+p_7+3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{162,180}$	8	$-p_1+p_7+2p_8-p_9-p_{11}+p_{18}$
$t_{174,25}$	8	$3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}$
$t_{174,41}$	8	$2p_8-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{174,60}$	8	$2p_8-p_9-p_{11}+p_{18}+p_{19}$
$t_{174,132}$	8	$-p_1+p_7+3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{174,191}$	8	$-p_1+p_7+2p_8-p_9-p_{11}+p_{18}$
$t_{211,45}$	8	$3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}$
$t_{211,67}$	8	$2p_8-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{211,95}$	8	$2p_8-p_9-p_{11}+p_{18}+p_{19}$
$t_{211,176}$	8	$-p_1+p_7+3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{211,229}$	8	$-p_1+p_7+2p_8-p_9-p_{11}+p_{18}$
$t_{227,58}$	8	$3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}$
$t_{227,81}$	8	$2p_8-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{227,109}$	8	$2p_8-p_9-p_{11}+p_{18}+p_{19}$
$t_{227,185}$	8	$-p_1+p_7+3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{227,233}$	8	$-p_1+p_7+2p_8-p_9-p_{11}+p_{18}$
$t_{249,90}$	8	$3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}$
$t_{249,120}$	8	$2p_8-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{249,149}$	8	$2p_8-p_9-p_{11}+p_{18}+p_{19}$
$t_{249,228}$	8	$-p_1+p_7+3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{249,262}$	8	$-p_1+p_7+2p_8-p_9-p_{11}+p_{18}$
$t_{261,106}$	8	$3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}$
$t_{261,134}$	8	$2p_8-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{261,167}$	8	$2p_8-p_9-p_{11}+p_{18}+p_{19}$
$t_{261,232}$	8	$-p_1+p_7+3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{261,264}$	8	$-p_1+p_7+2p_8-p_9-p_{11}+p_{18}$
$t_{277,161}$	8	$3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}$
$t_{277,187}$	8	$2p_8-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{277,217}$	8	$2p_8-p_9-p_{11}+p_{18}+p_{19}$
$t_{277,263}$	8	$-p_1+p_7+3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}$
$t_{277,278}$	8	$-p_1+p_7+2p_8-p_9-p_{11}+p_{18}$

):

Please notice that above all leading transitions can be viewed as the first control transition of this example. Besides, anyone of them can recover all eight deadlock markings. Under the proposed algorithm, the first one of all leading transition is chosen. Accordingly, $t_{107,4}=\left[3p_8-p_9-p_{10}-p_{11}+p_{17}+p_{18}+p_{19}\right]$ is chosen as the first control transition since it is the first one identified from CGAM. After the controller is added into this system eight deadlock markings are still left (i.e., 16 − 8 = 8). Therefore, we must run second iteration for recovering the other deadlock markings.

In second reachability graph, eight deadlock markings and 246 legal markings are identified. Therefore, the new GCAM’s size is: $8\times 246\times 19$. In the following, accordingly, 25 sets of all leading transitions are identified since they all can recover the maximal five same deadlock markings, which are listed as follows (refer to

Table 7. The detailed information of all leading transition of Example 2 in second iteration.

Leading Transition ${\mathit{t}}_{\mathit{i}, \mathit{j}}$	The Number of Deadlock Markings	The Property of Leading Transition
$t_{89,8}$	5	$p_1-p_4+2p_8-p_9-p_{10}+p_{14}+p_{17}+p_{19}$
$t_{89,17}$	5	$p_1-p_4+p_8-p_{10}+p_{14}+p_{17}$
$t_{89,30}$	5	$p_1-p_4+p_8-p_9+p_{14}+p_{19}$
$t_{89,91}$	5	$-p_4+p_7+2p_8-p_9-p_{10}+p_{14}+p_{17}$
$t_{89,150}$	5	$-p_4+p_7+p_8-p_9+p_{14}$
$t_{170,42}$	5	$p_1-p_4+2p_8-p_9-p_{10}+p_{14}+p_{17}+p_{19}$
$t_{170,61}$	5	$p_1-p_4+p_8-p_{10}+p_{14}+p_{17}$
$t_{170,86}$	5	$p_1-p_4+p_8-p_9+p_{14}+p_{19}$
$t_{170,163}$	5	$-p_4+p_7+2p_8-p_9-p_{10}+p_{14}+p_{17}$
$t_{170,221}$	5	$-p_4+p_7+p_8-p_9+p_{14}$
$t_{198,64}$	5	$p_1-p_4+2p_8-p_9-p_{10}+p_{14}+p_{17}+p_{19}$
$t_{198,92}$	5	$p_1-p_4+p_8-p_{10}+p_{14}+p_{17}$
$t_{198,121}$	5	$p_1-p_4+p_8-p_9+p_{14}+p_{19}$
$t_{198,199}$	5	$-p_4+p_7+2p_8-p_9-p_{10}+p_{14}+p_{17}$
$t_{198,243}$	5	$-p_4+p_7+p_8-p_9+p_{14}$
$t_{205,65}$	5	$p_1-p_4+2p_8-p_9-p_{10}+p_{14}+p_{17}+p_{19}$
$t_{205,94}$	5	$p_1-p_4+p_8-p_{10}+p_{14}+p_{17}$
$t_{205,123}$	5	$p_1-p_4+p_8-p_9+p_{14}+p_{19}$
$t_{205,200}$	5	$-p_4+p_7+2p_8-p_9-p_{10}+p_{14}+p_{17}$
$t_{205,244}$	5	$-p_4+p_7+p_8-p_9+p_{14}$
$t_{256,135}$	5	$p_1-p_4+2p_8-p_9-p_{10}+p_{14}+p_{17}+p_{19}$
$t_{256,168}$	5	$p_1-p_4+p_8-p_{10}+p_{14}+p_{17}$
$t_{256,193}$	5	$p_1-p_4+p_8-p_9+p_{14}+p_{19}$
$t_{256,250}$	5	$-p_4+p_7+2p_8-p_9-p_{10}+p_{14}+p_{17}$
$t_{256,273}$	5	$-p_4+p_7+p_8-p_9+p_{14}$

):

Again, under the proposed algorithm, the first leading transition is chosen. Accordingly, $t_{89,8}=\left[p_1-p_4+2p_8-p_9-p_{10}+p_{14}+p_{17}+p_{19}\right]$ is chosen as the second control transition since it is the first one identified from CGAM. After the controller is added into this system, three deadlock markings are still left (i.e., 8 − 5 = 3). Therefore, we must run third iteration for recovering the other deadlock markings.

In the third iteration, three deadlock markings and 276 legal markings are identified. Therefore, the GCAM′s scale is: $3\times 276\times 19$. Further, there are 81 sets of leading transitions identified and they all can recover final three deadlock markings. Due to the space limitation of this paper, the author just shows the first leading transition and it is [$2p_1-p_5-p_6+2p_8-p_9-p_{10}+p_{16}+p_{17}+p_{18}+p_{19}]$. Further, it is chosen as the third control transition. When the third control transition is added into the system with previous two controllers the system is deadlock free. Most importantly, the total reachable legal markings are 282. In other words, the three controllers recover the system. Figure 7 presents the controlled system of Figure 6 when the above three controllers is added into Example 2.

5.2. Comparison

In this subsection, the author will make comparison with all existing transition-based methods based on above two classical examples. Firstly, we discuss the computational efficiency in Example 1. From

Table 8. Comparisons with existing literature in Example 1.

Policy	The Number of Control Transitions	The Numberof Control Arcs	Total Number of Reachable States
Huang et al. [44]	2	16	20
Row and Pan -1 [49]	2	16	20
Row and Pan -2 [49]	2	12	20
Row et al. [62]	2	12	20
This paper	1	6	20

, the five methods, including the one proposed in this paper, all adopt control transition to recover the system. It is obvious that the four methods from the literature [44,49,62] all need two controllers to make system live and optimal. However, in this paper we just need one controller to achieve the same optimal result. Therefore, in other words, the computation efficiency of our method is the best among existing ones.

In the following, we discuss the Example 2. In existing literature, there are eight methods adopting control transition to solve the deadlock problem of Example 2. From

Table 9. Comparisons with existing literature in Example 2.

Policy	The Number of Control Transitions	The Numberof Control Arcs	Total Number of Reachable States
Huang et al. [44]	7	69	282
Row and Pan [49]	6	53	282
Row et al. [62]	5	36	282
Bashir et al. [48]	4	14	282
Chen et al.-1 [46]	3	27	282
Chen et al.-2 [46]	3	25	282
Dong et al. [47]	3	25	282
This paper	3	25	282

, one can realize that the computation efficiency of the proposed method is still best with respect to Chen et al.-2 [46] and Dong et al. [47] since we all merely need just three control transitions and 25 control arcs to make system recovered and optimal.

6. Conclusions

In existing research, the deadlock prevention policy seems to be the best technology among all strategies and is almost used to solve the FMS ’deadlock problems since it can check the deadlock situation in advance. Almost all of the research adopts places based as system controllers regardless of it they use structure methods or reachability graph analysis. However, all of them cannot make the optimal control even if they claimed that they can obtain maximally permissive controllers. Based on the above reason, in previous works [44,49,62], our teammates start to develop all kinds of control transitions deadlock prevention policies to solve the deadlock problem of flexible manufacturing systems. This research [44] is the first paper which adopted the concept of control transitions to solve the deadlock problem. The advantage of these strategies is that it can obtain more live states by adopting state equations. It is a pity that they cannot identify the optimal number of maximally permissive markings of the reachability graph of one FMS in advance although it does recover the deadlock system. In [49], the author proposed two different algorithms (i.e., “the all reachability graph viewpoint” and “the first deadlock marking viewpoint”) to obtain recovery controllers. The two algorithms can not only obtain the correct optimal number of maximal reachable states firstly, but recovers all original illegal ones and makes them alive whatever these states initially belong to deadlock or quasi-deadlock ones. Besides, the number of controllers becomes six. It is better than [44]. In [62], the developed method can identify the maximal saturated tokens of idle places of one deadlock FMS in advance and still reserves all kinds of original markings. The really maximal permissive number of markings of one system’s reachability graph can then be examined, once the saturated number of tokens in idle places is identified. Furthermore, the number of controllers is less with respect to [44,49]. Further, in this paper, the author adopts the developed CGAM to further reduce the number of controllers and relative arcs. Undoubtedly, this new policy in this research is evident better than almost existing literature. Preciously, the new policy is very simple and easy. In future work, the author will propose a new algorithm to further reduce the number of control arcs to make the real best one among existing literature.