Comparative Study of Wheel–Rail Contact Impact Force for Jointed Rail and Continuous Welded Rail on Light-Rail Transit
Abstract
1. Introduction
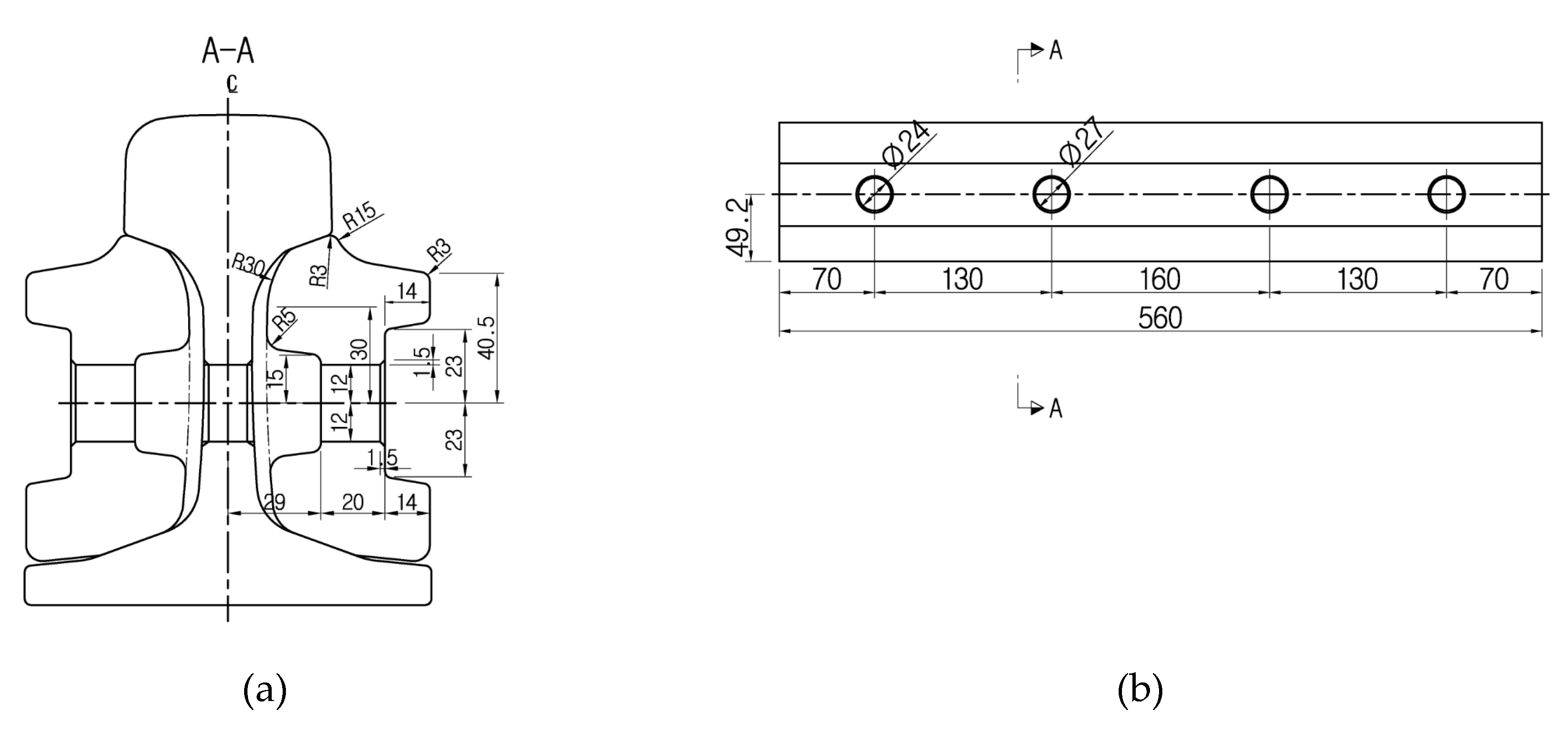
2. Field Measurement
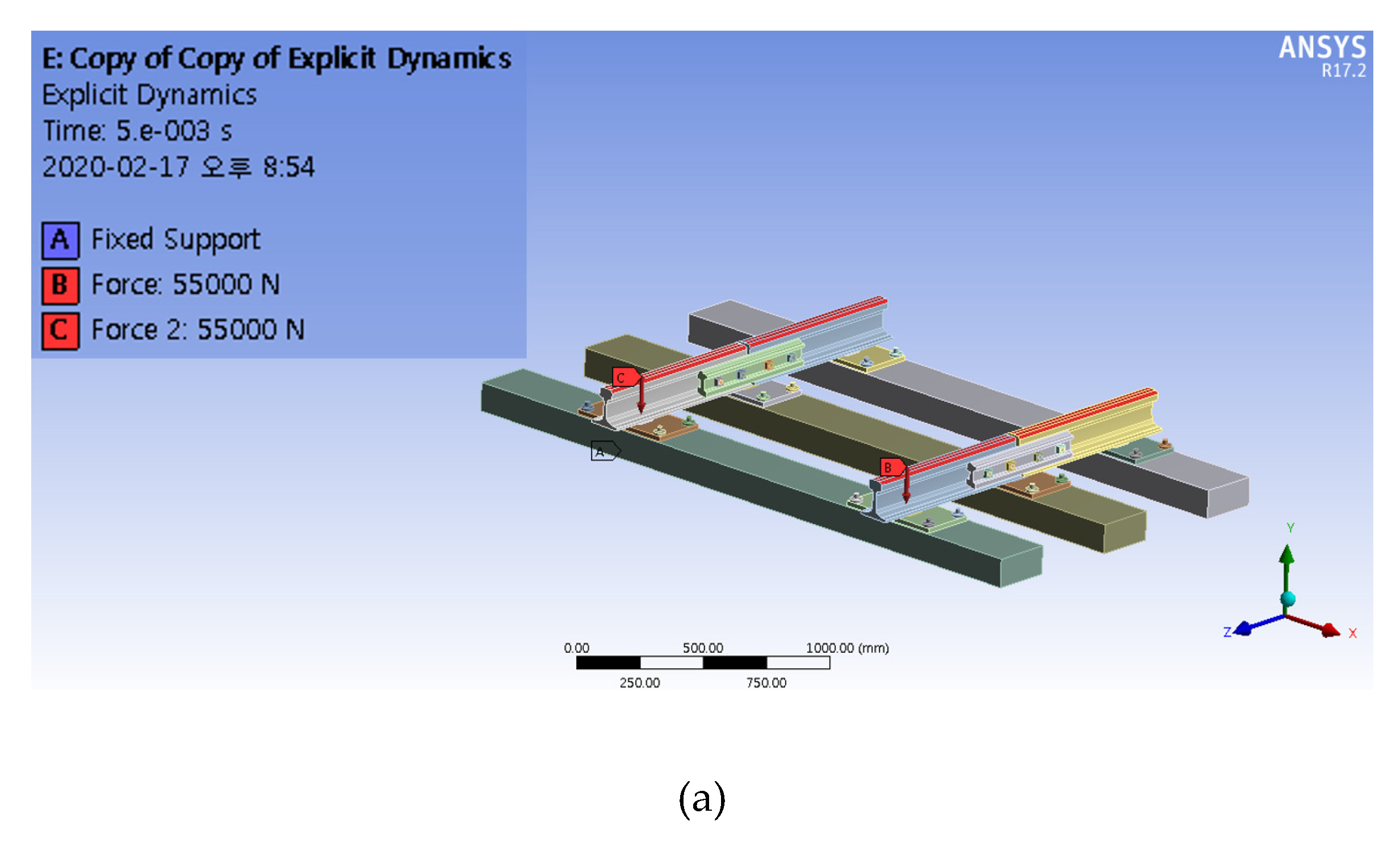
3. Finite Element Analysis
4. Results and Discussion
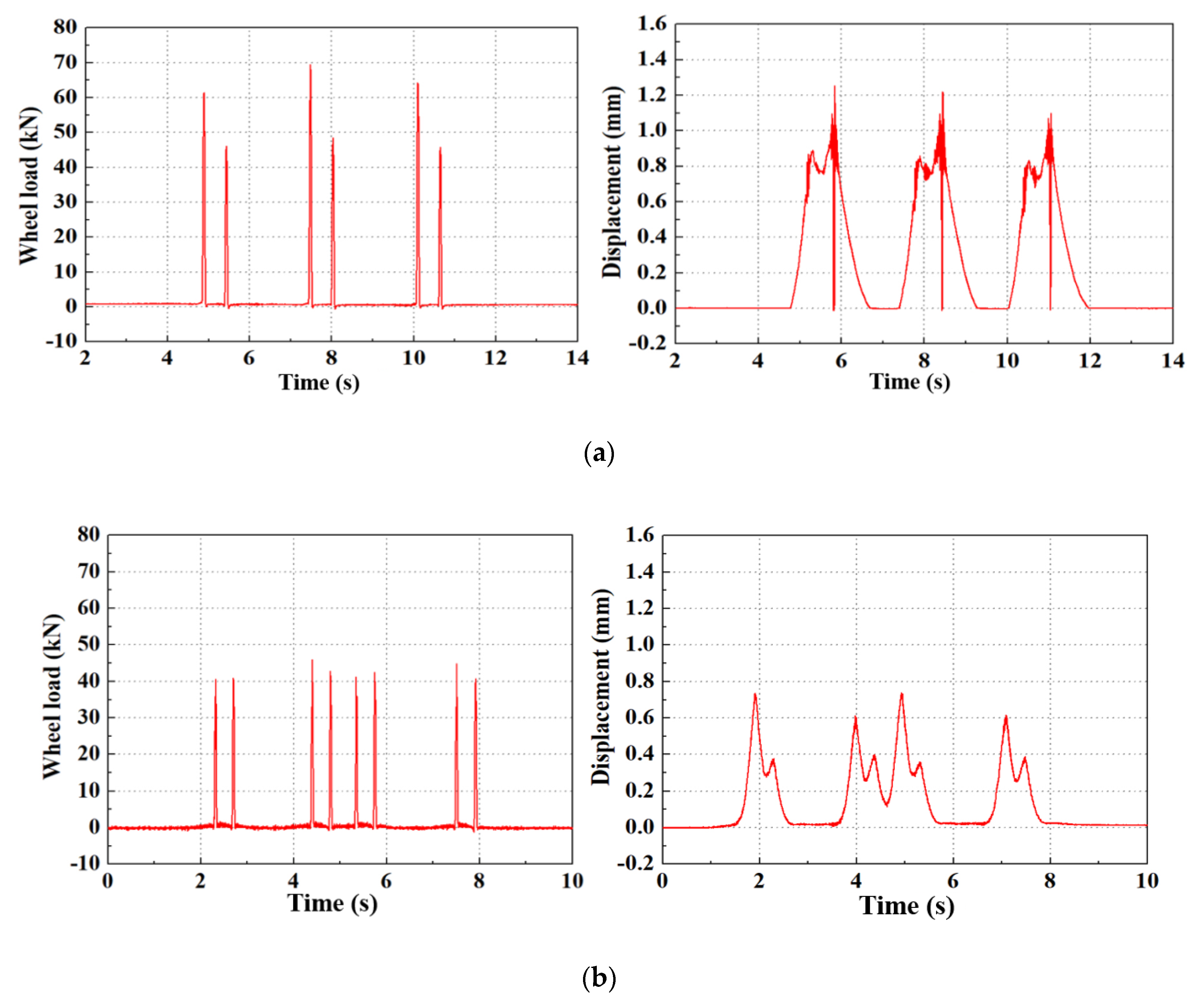
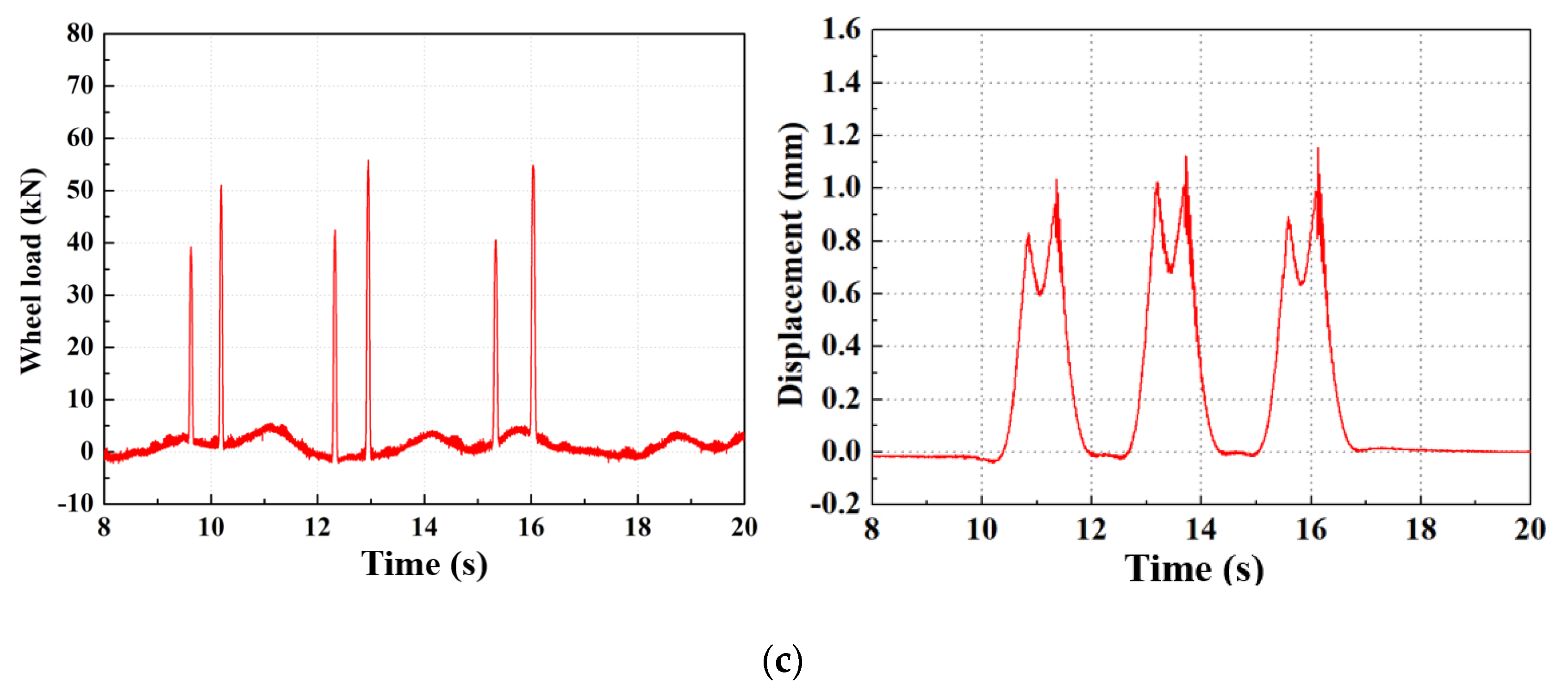
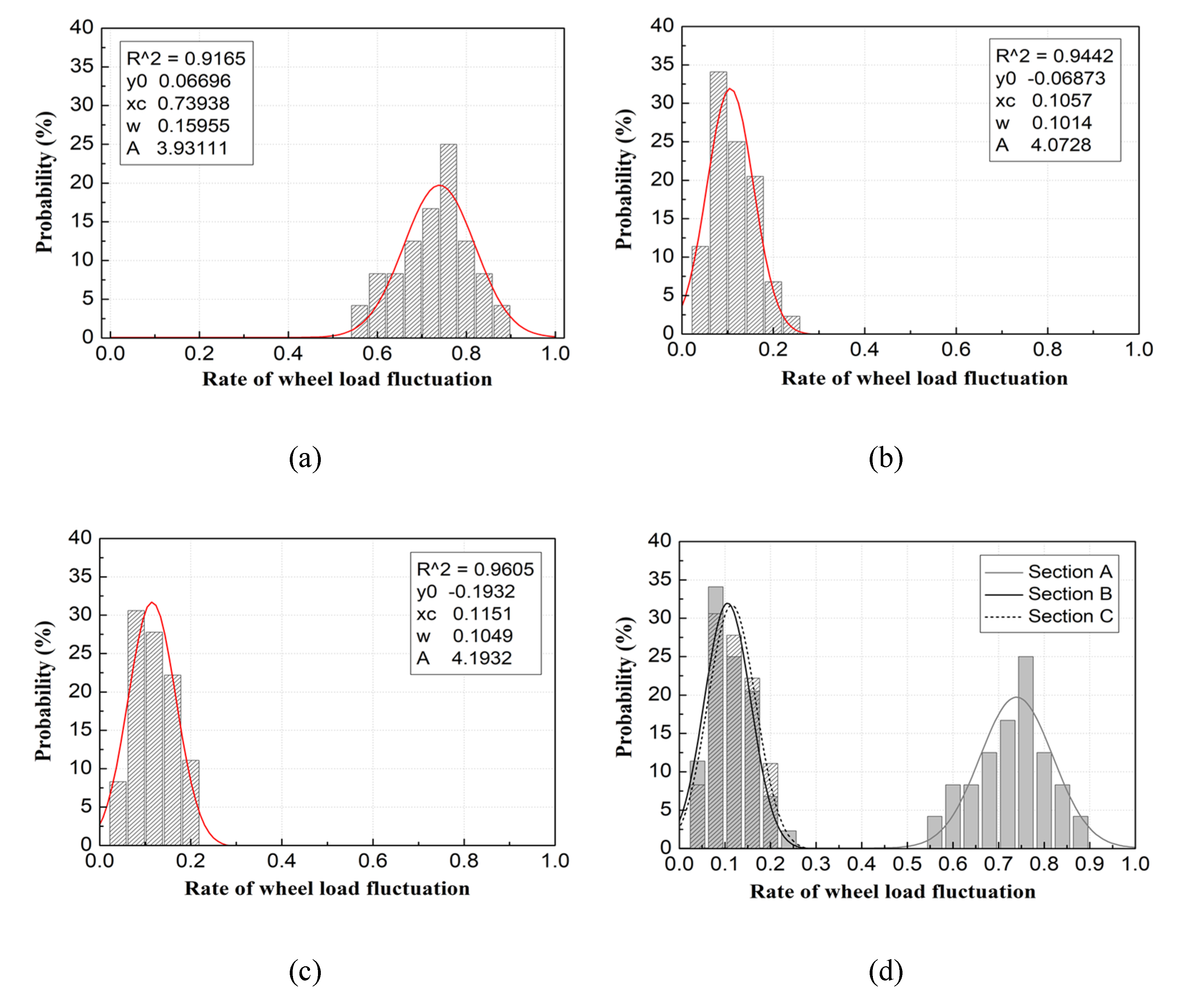
4.1. Track Impact Factor According to Measured Dynamic Wheel Load
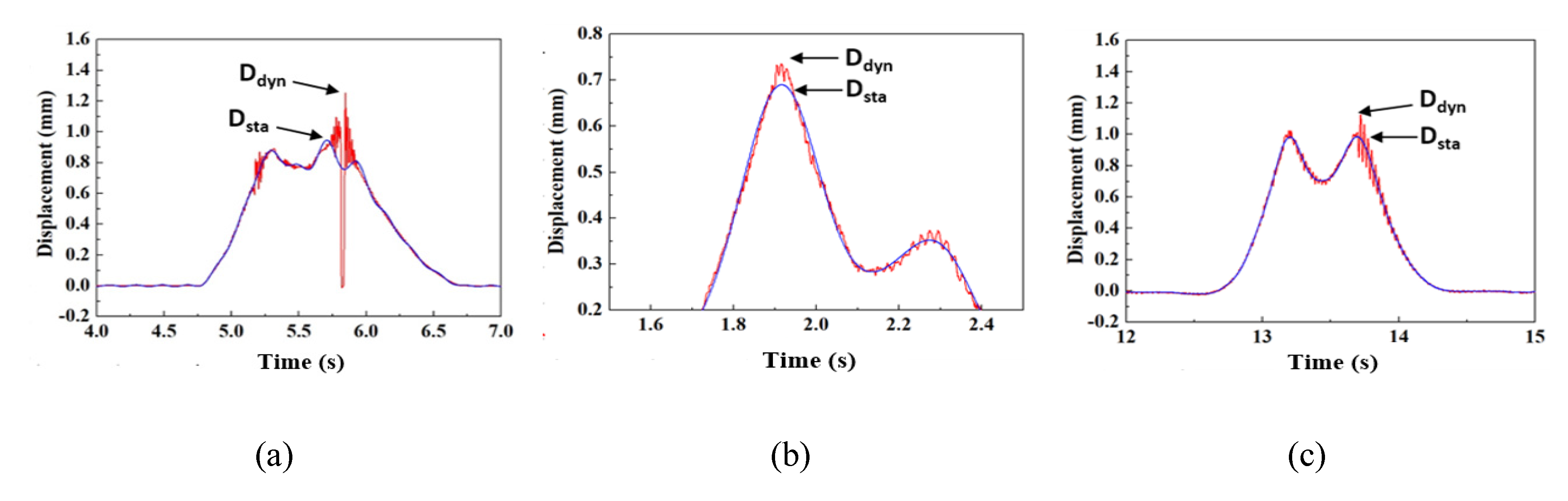
4.2. Track Impact Factor Based on the Measured Vertical Rail Displacement
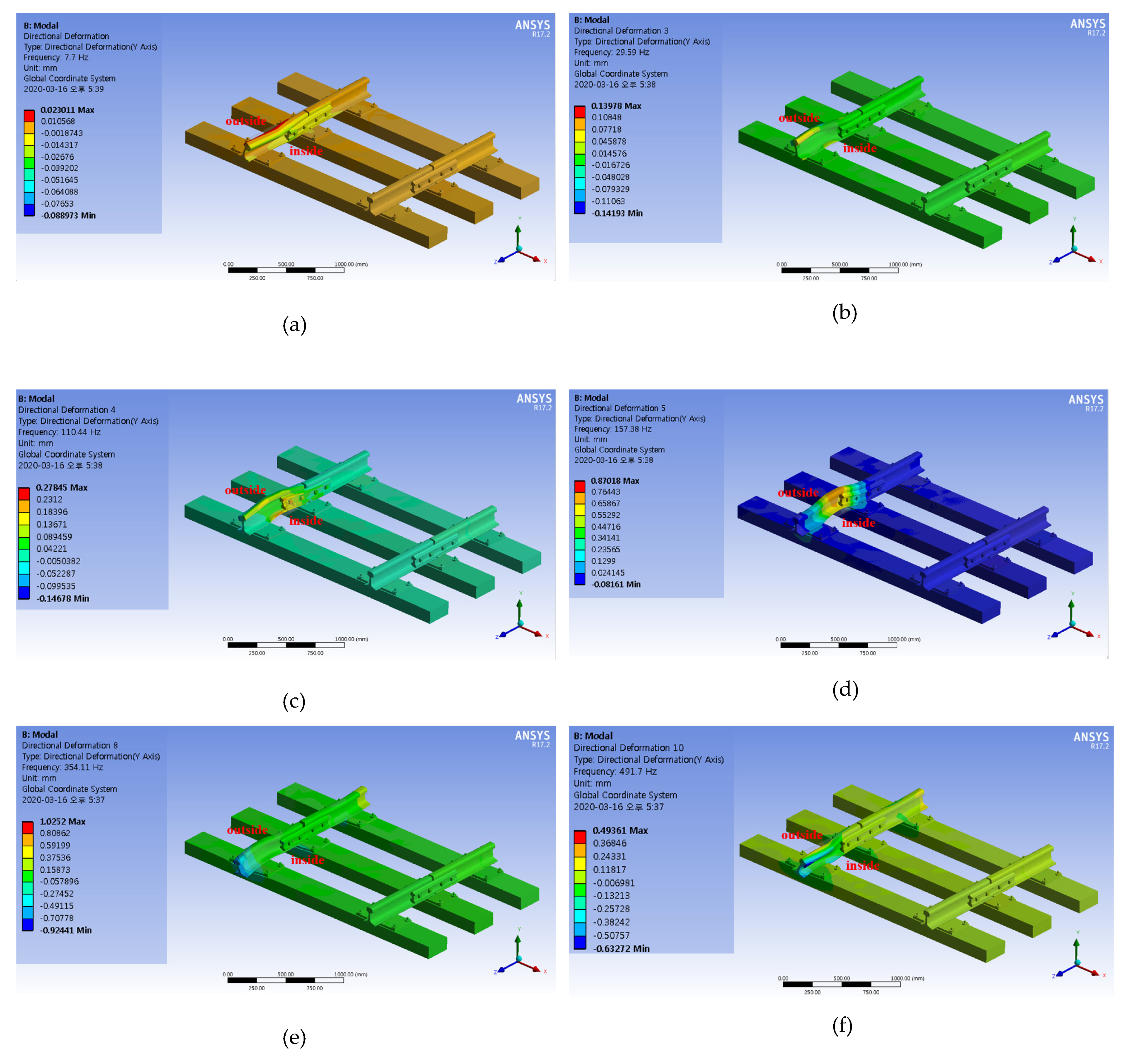
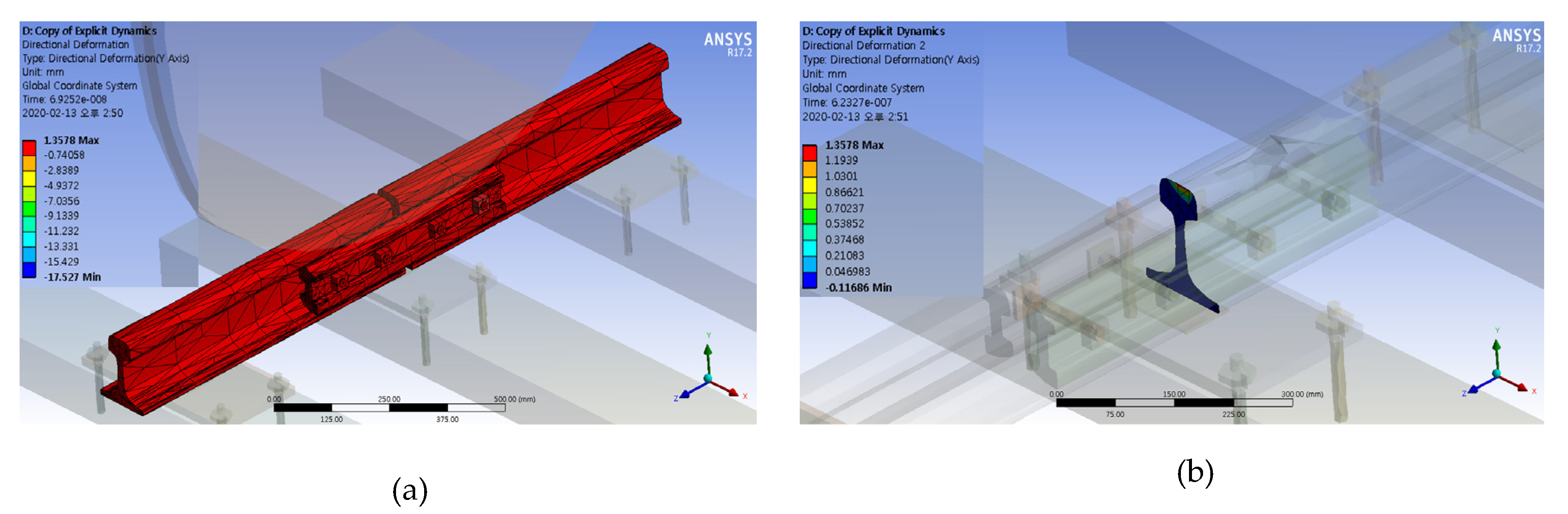
4.3. Track Impact Factor Based on the FE Analyzed Vertical Rail Displacement
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Lichtberger, B. Track Compendium; Eurail Press: Hamburg, Germany, 2010. [Google Scholar]
- Choi, J.Y. Qualitative Analysis for Dynamic Behavior of Railway Ballasted Track. Ph.D. Thesis, Technical University of Berlin, Berlin, Germany, 2014. [Google Scholar]
- Choi, J.Y. Influence of track support stiffness of ballasted track on dynamic wheel-rail forces. ASCE J. Transp. Eng. 2013, 139, 709–718. [Google Scholar] [CrossRef]
- Lim, N.H.; Choi, J.Y.; Lee, W.C. An analytical study about the reduction method of sleeper displacements in the end zone of rail expansion joint. Korean Soc. Civ. Eng. 2008, 2008, 982–985. [Google Scholar]
- Zong, N.; Wexler, D.; Dhanasekar, M. Structural and material characterization of insulated rail joints. Electron. J. Struct. Eng. 2013, 13, 75–87. [Google Scholar]
- Mandal, N.K.; Peach, B. An engineering analysis of insulated rail joints: A general perspective. Int. J. Eng. Sci. Technol. 2010, 2, 3964–3988. [Google Scholar]
- Pombo, J.C.; Ambrósio, A.C. Application of a wheel–rail contact model to railway dynamics in small radius curved tracks. Multibody Syst. Dyn. 2008, 19, 91–114. [Google Scholar] [CrossRef]
- Sugiyama, H.; Yamashita, S.; Suda, Y. Curving simulation of ultralow-floor light rail vehicles with independently rotating wheelsets. ASME 2010 Int. Mech. Eng. Congr. Expo. 2010, 11, 869–875. [Google Scholar]
- Wen, Z.; Jin, X.; Zhang, W. Contact-impact stress analysis of rail joint region using the dynamic finite element method. Wear 2005, 258, 1301–1309. [Google Scholar] [CrossRef]
- Sharma, S.K.; Kumar, A. Dynamics analysis of wheel rail contact using FEA. Procedia Eng. 2016, 144, 1119–1128. [Google Scholar] [CrossRef]
- Yang., Z.; Boogaard, A.; Wei, Z.; Liu, J.; Dollevoet, R.; Li, Z. Numerical study of wheel-rail impact contact solutions at an insulated rail joint. Int. J. Mech. Sci. 2018, 138–139, 310–322. [Google Scholar] [CrossRef]
- Choi, J.Y.; Kim, S.H. Impact evaluation of track girder bearing on yeongjong grand bridge. Appl. Sci. 2020, 10, 68. [Google Scholar] [CrossRef]
- Raymond, G.P. Design for railroad ballast and subgrade support. J. Geotech. Eng. Div. ASCE 1978, 104, 45–60. [Google Scholar]
- Selig, E.T.; Waters, J.M. Track Geotechnology and Substructure Management, 1st ed.; Technology Development and Application Committee, on behalf of the railways of Australia; Thomas Telford Services Ltd.: London, England, 1994. [Google Scholar]
- Liang, B.; Zhu, D. Dynamic analysis of the vehicle-subgrade model of a vertical coupled system. J. Sound Vib. 2001, 245, 79–92. [Google Scholar] [CrossRef]
- Kaewunruen, S.; Remennikov, A. In-Field Dynamic Testing and Measurements of Railway Tracks in Central Queensland; March-June Research Report; CRC Railway Engineering and Technologies: Queensland, Australia, 2005. [Google Scholar]
- Kaewunruen, S.; Remennikov, A. Field trials for dynamic characteristics of railway track and its components using impact excitation technique. NDT E Int. 2007, 40, 510–519. [Google Scholar] [CrossRef]
- ANSYS. Release 17.2 Documentation for ANSYS; ANSYS Inc.: Cannonsberg, PA, USA, 2008. [Google Scholar]
- With, C.; Bodare, A. Evaluation of track stiffness with a vibrator for prediction of train-induced displacement on railway embankments. Soil Dyn. Earthq. Eng. 2009, 29, 1187–1197. [Google Scholar] [CrossRef]
- Kumaran, G.; Menon, D.; Krishman Nair, K. Dynamic studies of rail track sleepers in a track structure system. J. Sound Vib. 2003, 268, 485–501. [Google Scholar] [CrossRef]
- Esveld, C. Modern Railway Track, 2nd ed.; Esveld: Zaltbommel, The Netherlands, 2002. [Google Scholar]
- KR CODE; KOREA RAIL NETWORK AUTHORITY: Daejeon, South Korea, 2012.



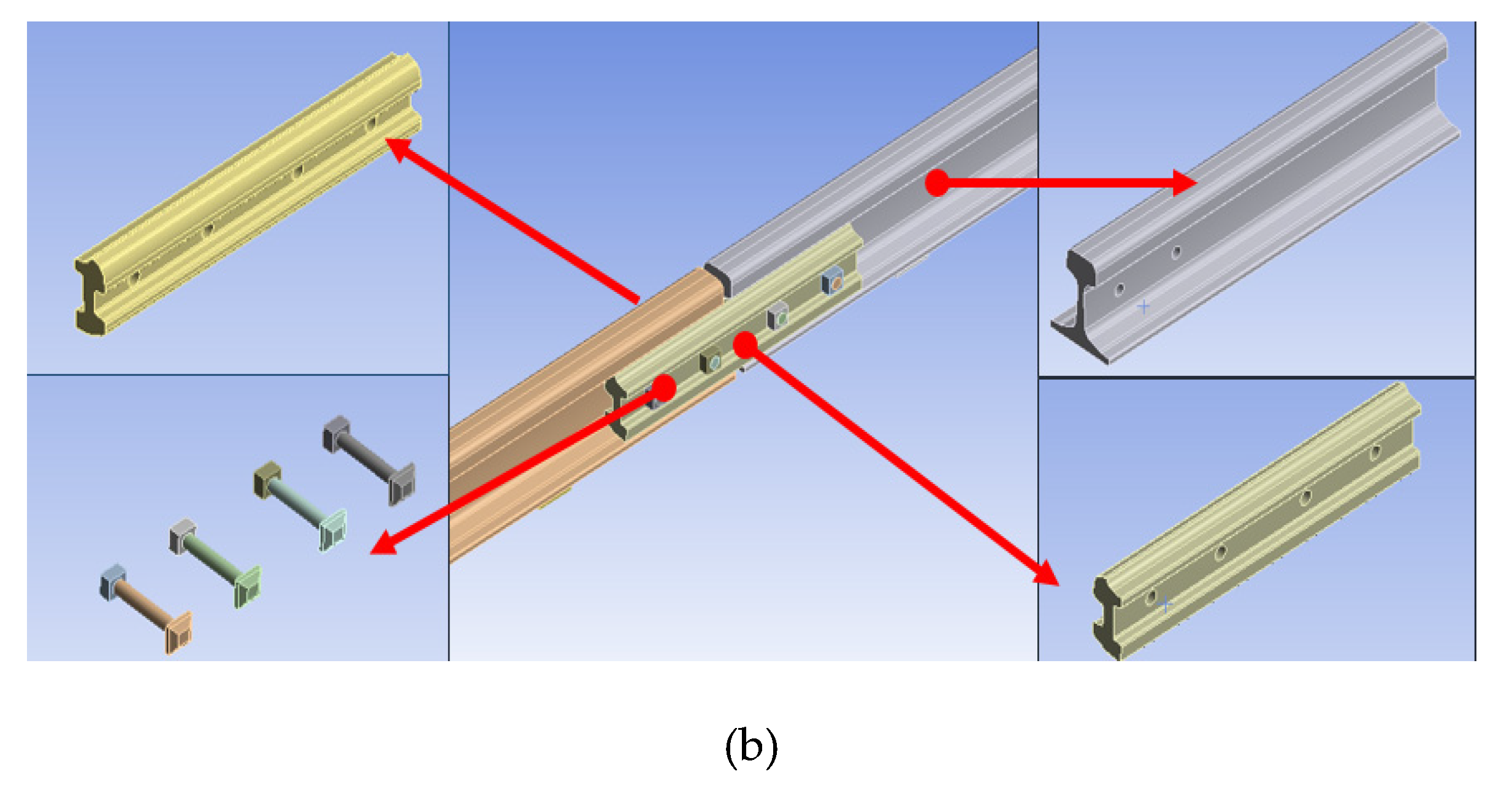
| Curvature (m) | Cant (mm) | Vd | Vo | Track Components | ||||
|---|---|---|---|---|---|---|---|---|
| Rail Type | Rail Fastener | Sleeper Type | Ballast | |||||
| Section A | 60 | 0 | 15 | 15 | 50 kg/m rail joint | E-clip | Wood | Gravel |
| Section B | 300 | 140 | 63 | 60 | 50 kg/m CWR (GPW)1) | Fast clip2) | - | - |
| Section C | 100 | 120 | 33 | 30 | 50 kg/m CWR (GPW)1) | E-clip3) | - | - |
| Properties | Rail (50 kgN) | Wooden Sleeper |
|---|---|---|
| Section area (cm2) | 64.2 | 360 |
| Elastic modulus (kN/cm2) | 21,000 | 1000 |
| Weight density (kN/cm3) | 7.85 × 10−5 | 0.75 × 10−5 |
| Poisson ratio (ʋ) | 0.30 | 0.33 |
| Test Section | Korean Design TIF | |||
|---|---|---|---|---|
| A (Rail Joint) | B (CWR) | C (CWR) | ||
| Measured TIF (2σ) | 1.899 | 1.207 | 1.220 | 1.410 V/80 |
| Measured/design value (%) | 134.68 | 85.60 | 86.52 | |
| Description | Track Impact Factor (i) | |||
|---|---|---|---|---|
| Using Dynamic Wheel Load | Ratio (%) | Using Vertical Rail Displacement | Ratio (%) | |
| Section A (rail joint) | 1.899 | (+) 57.33 | 1.326 | (+) 24.16 |
| Section B (CWR) | 1.207 | - | 1.068 | - |
| Section C (CWR) | 1.220 | (+) 1.08 | 1.141 | (+) 6.84 |
| Number of Model | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Frequency (Hz) | 7.7 | 24.55 | 29.59 | 110.44 | 157.38 | 214.70 | 263.15 | 354.11 | 369.68 | 491.70 |
| Description | Vertical Rail Displacement (mm) | Relative Error (%) | |
|---|---|---|---|
| Measurement (1) | FEA (2) | ||
| Section A | 1.326 | 1.357 | −3 |
| Section B | 1.068 | 1.145 | −7 |
| Section C | 1.141 | 1.160 | −2 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, J.-Y.; Yun, S.-W.; Chung, J.-S.; Kim, S.-H. Comparative Study of Wheel–Rail Contact Impact Force for Jointed Rail and Continuous Welded Rail on Light-Rail Transit. Appl. Sci. 2020, 10, 2299. https://doi.org/10.3390/app10072299
Choi J-Y, Yun S-W, Chung J-S, Kim S-H. Comparative Study of Wheel–Rail Contact Impact Force for Jointed Rail and Continuous Welded Rail on Light-Rail Transit. Applied Sciences. 2020; 10(7):2299. https://doi.org/10.3390/app10072299
Chicago/Turabian StyleChoi, Jung-Youl, Sang-Won Yun, Jee-Seung Chung, and Sun-Hee Kim. 2020. "Comparative Study of Wheel–Rail Contact Impact Force for Jointed Rail and Continuous Welded Rail on Light-Rail Transit" Applied Sciences 10, no. 7: 2299. https://doi.org/10.3390/app10072299
APA StyleChoi, J.-Y., Yun, S.-W., Chung, J.-S., & Kim, S.-H. (2020). Comparative Study of Wheel–Rail Contact Impact Force for Jointed Rail and Continuous Welded Rail on Light-Rail Transit. Applied Sciences, 10(7), 2299. https://doi.org/10.3390/app10072299




