Out-of-Plane Bending of Functionally Graded Thin Plates with a Circular Hole
Abstract
:1. Introduction
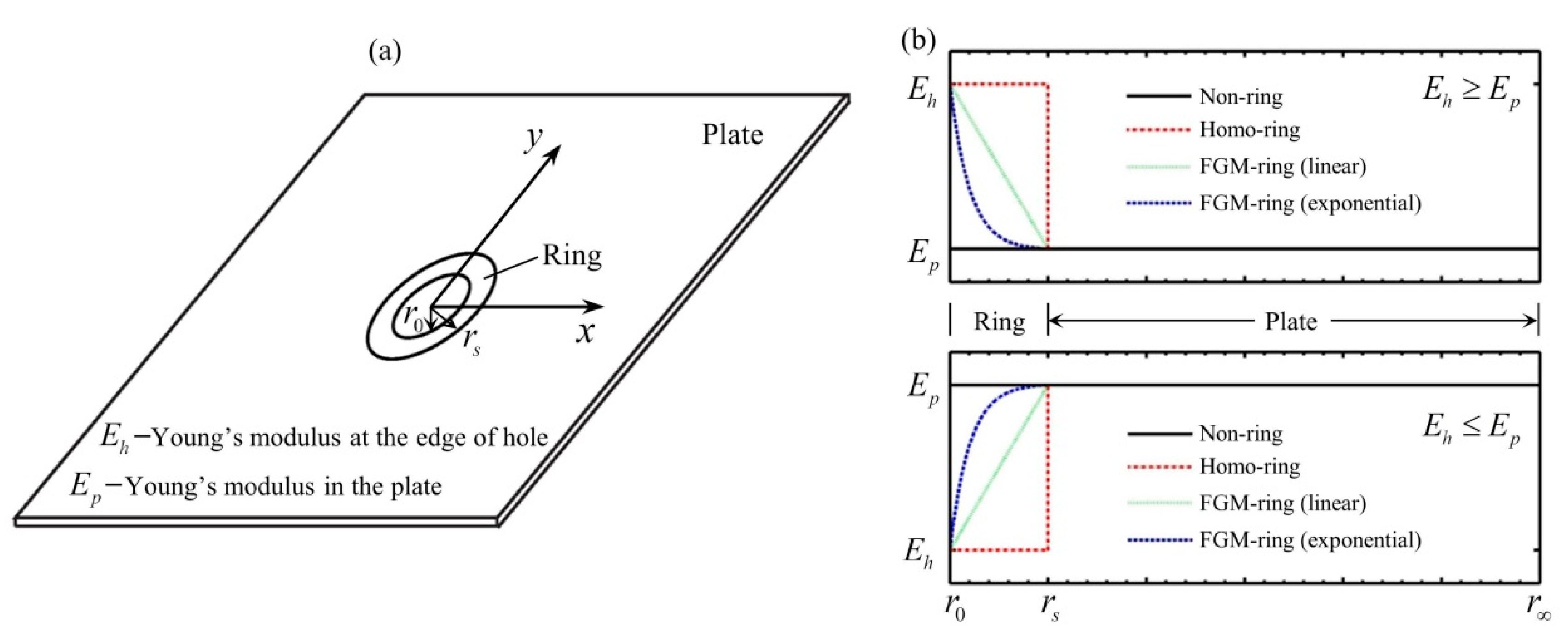
2. Problem Formulations
3. General Solutions
4. Numerical Examples
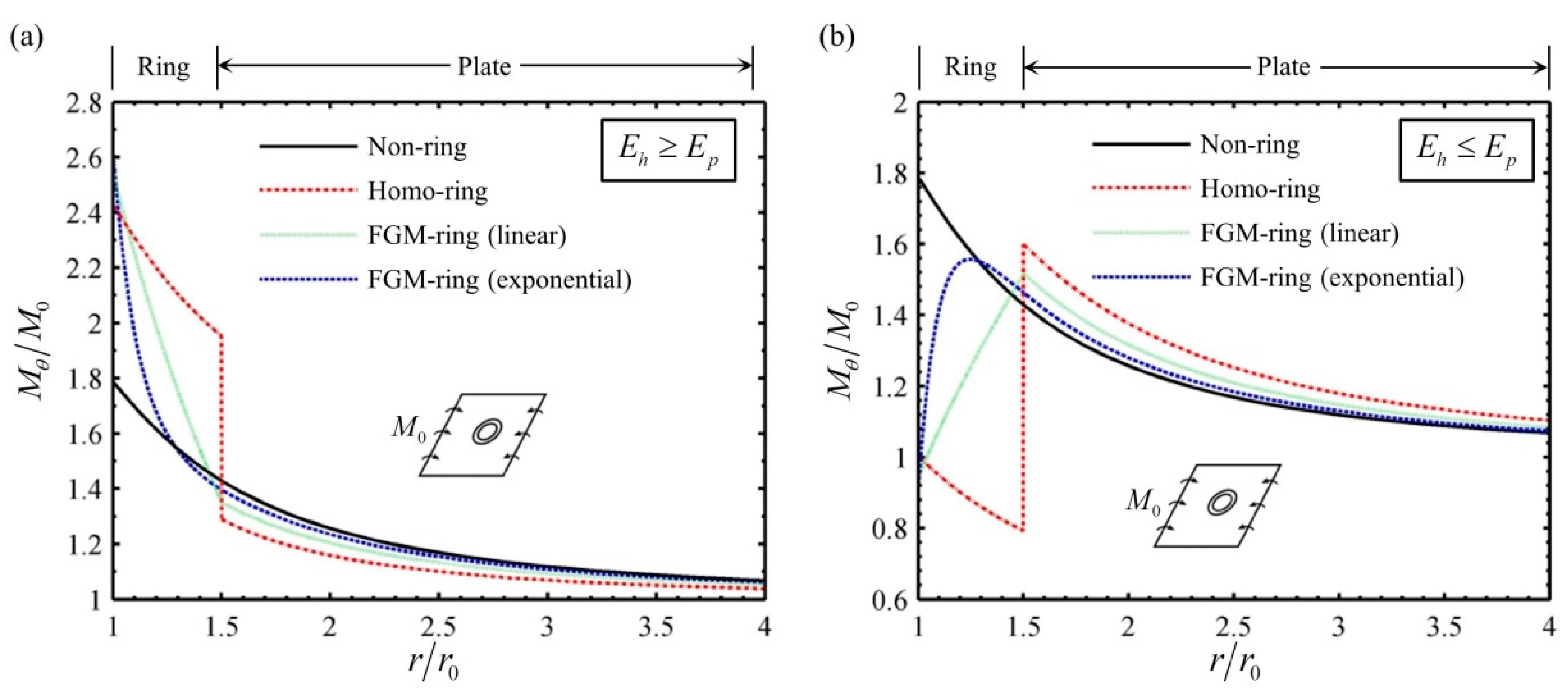
4.1. The Case for a Whole FGM Plate with a Circular Hole
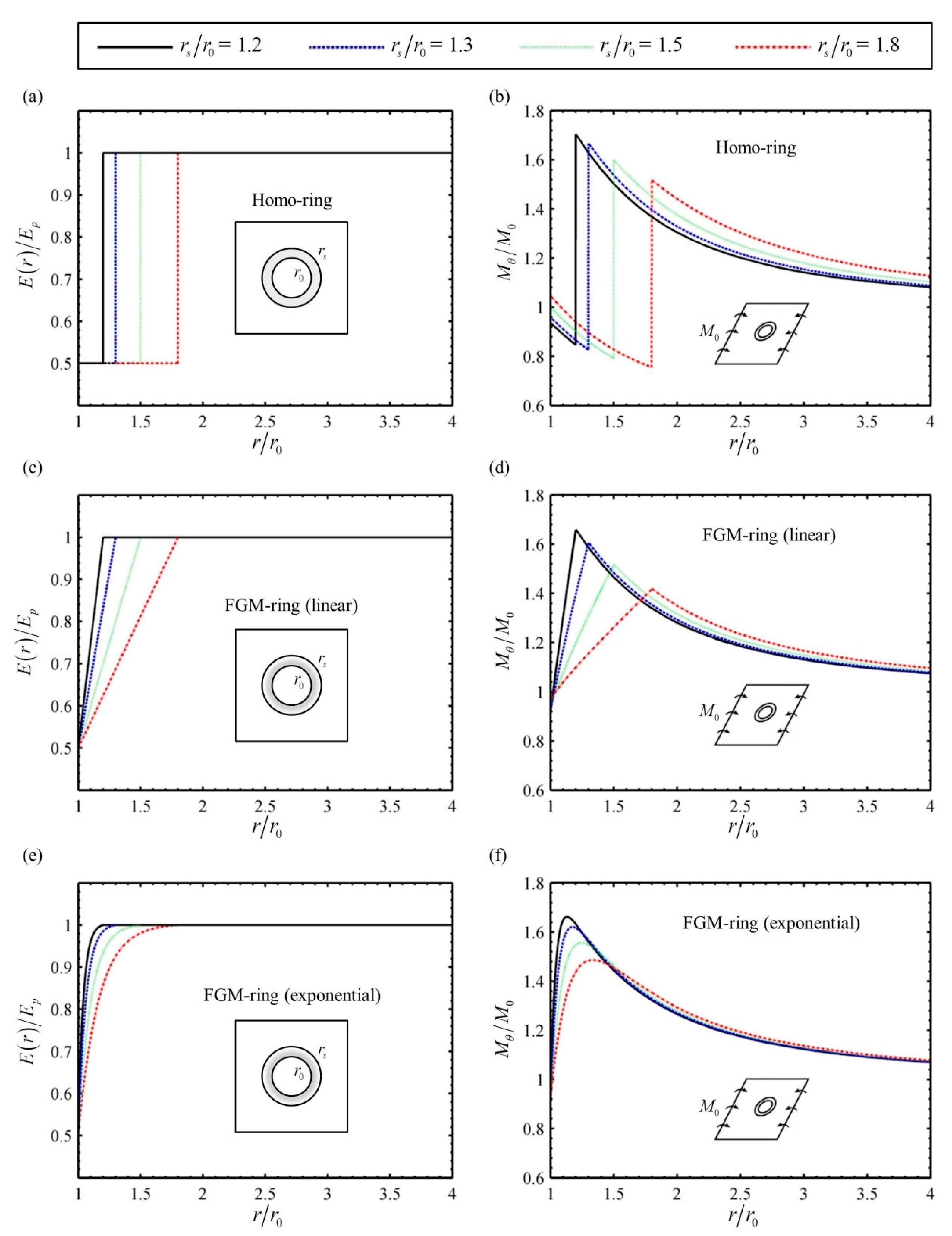
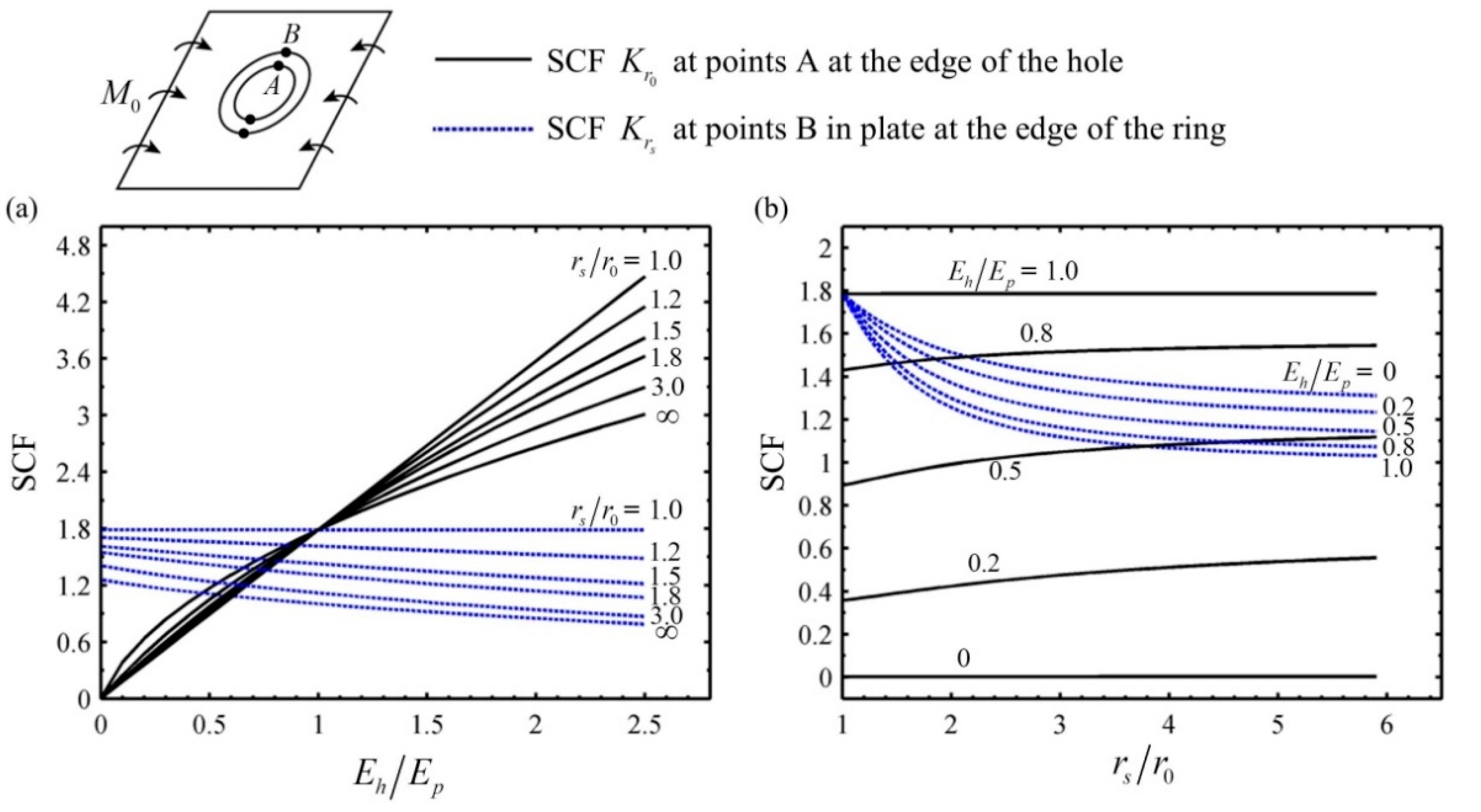
4.2. The Case for an FGM Ring Reinforced in a Homogeneous Plate
5. Conclusions
- (1)
- For the case of a whole FGM plate, it is found that the bending stress concentration, caused by the geometric discontinuity of the hole in the traditional homogeneous plate, can be well relieved or even eliminated by choosing an appropriate radially increasing Young’s modulus in the plate. The radial change of Poisson’s ratio has little effect on reducing the bending stress concentration.
- (2)
- For the case of an FGM ring reinforced in a homogeneous plate, it is found the FGM reinforcing ring with radially increasing Young’s modulus can not only relieve the bending stress concentration around the hole, but also avoid the stress concentration at the interface between the ring and the plate compared with that of the homogeneous reinforcing ring.
- (3)
- The linear and exponential FGM rings can both reduce the stress concentration near the hole, and their effects are almost equally good. The only difference of their results are the distribution shapes of the bending moments. The linear FGM ring makes the moment vary along a linear way in the ring, while the exponential FGM ring brings the moment with a similarly exponential change.
- (4)
- The increase of the width of the reinforcing ring is beneficial to relieve the bending stress concentration, but the effect will not be obvious after the width reacheds a certain value.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Norton, R.L. Machine Design: An Integrated Approach; Prentice Hall: Boston, MA, USA, 2014. [Google Scholar]
- Budynas, R.G.; Nisbett, J.K.; Shigley, J.E. Shigley’s Mechanical Engineering Design; McGraw-Hill: New York, NY, USA, 2020. [Google Scholar]
- Young, W.C.; Budynas, R.G. Roark’s Formulas for Stress and Strain; McGraw-Hill: New York, NY, USA, 2002. [Google Scholar]
- Pilkey, W.D.; Pilkey, D.F. Peterson’s Stress Concentration Factors; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar]
- Savin, G.N. Stress Concentration around Holes; Pergamon Press: New York, NY, USA, 1961. [Google Scholar]
- Lekhnitskii, S.G. Anisotropic Plates; Gordon and Breach: New York, NY, USA, 1968. [Google Scholar]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Yang, Q.; Gao, C.F. Reduction of the stress concentration around an elliptic hole by using a functionally graded layer. Acta Mech. 2016, 227, 2427–2437. [Google Scholar] [CrossRef]
- Sburlati, R.; Atashipour, S.R.; Atashipour, S.A. Reduction of the stress concentration factor in a homogeneous panel with hole by using a functionally graded layer. Compos. Part B 2014, 61, 99–109. [Google Scholar] [CrossRef]
- Goyat, V.; Verma, S.; Garg, R.K. Reduction in stress concentration around a pair of circular holes with functionally graded material layer. Acta Mech. 2018, 229, 1045–1060. [Google Scholar] [CrossRef]
- Goyat, V.; Verma, S.; Garg, R.K. Reduction of stress concentration for a rounded rectangular hole by using a functionally graded material layer. Acta Mech. 2017, 228, 3695–3707. [Google Scholar] [CrossRef]
- Udupa, G.; Rao, S.S.; Gangadharan, K.V. Functionally graded composite materials. An overview. Procedia Mater. Sci. 2014, 5, 1291–1299. [Google Scholar] [CrossRef]
- Sburlati, R. Analytical elastic solutions for pressurized hollow cylinders with internal functionally graded coatings. Compos. Struct. 2012, 94, 3592–3600. [Google Scholar] [CrossRef]
- Gupta, A.; Talha, M. Recent development in modeling and analysis of functionally graded materials and structures. Prog. Aerosp. Sci. 2015, 79, 1–14. [Google Scholar] [CrossRef]
- Huang, J.; Venkataraman, S.; Rapoff, A.J.; Haftka, R.T. Optimization of axisymmetric elastic modulus distributions around a hole for increased strength. Struct. Multidiscip. Optim. 2003, 25, 225–236. [Google Scholar] [CrossRef]
- Huang, J.; Rapoff, A.J. Optimization design of plates with holes by mimicking bones through nonaxisymmetric functionally graded material. P I Mech. Eng. L-J. Mater. 2003, 217, 23–27. [Google Scholar] [CrossRef]
- Kubair, D.V.; Bhanu-Chandar, B. Stress concentration factor due to a circular hole in functionally graded panels under uniaxial tension. Int. J. Mech. Sci. 2008, 50, 732–742. [Google Scholar] [CrossRef]
- Wang, W.; Yuan, H.; Li, X.; Shi, P. Stress concentration and damage factor due to central elliptical hole in functionally graded panels subjected to uniform tensile traction. Materials 2019, 12, 422. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, Q.; Gao, C.F.; Chen, W.T. Stress analysis of a functional graded material plate with a circular hole. Arch. Appl. Mech. 2010, 80, 895–907. [Google Scholar] [CrossRef]
- Yang, Q.; Gao, C.F.; Chen, W.T. Stress concentration in a finite functionally graded material plate. Sci. China Phys. Mech. Astron. 2012, 55, 1263–1271. [Google Scholar] [CrossRef]
- Mohammadi, M.; Dryden, J.R.; Jiang, L.Y. Stress concentration around a hole in a radially inhomogeneous plate. Int. J. Solids Struct. 2011, 48, 483–491. [Google Scholar] [CrossRef]
- Goyat, V.; Verma, S.; Garg, R.K. On the reduction of stress concentration factor in an infinite panel using different radial functionally graded materials. Int. J. Mater. Prod. Technol. 2018, 57, 109–131. [Google Scholar] [CrossRef]
- Sburlati, R. Stress concentration factor due to a functionally graded ring around a hole in an isotropic plate. Int. J. Solids Struct. 2013, 50, 3649–3658. [Google Scholar] [CrossRef] [Green Version]
- Nie, G.J.; Zhong, Z.; Batra, R.C. Material tailoring for reducing stress concentration factor at a circular hole in a functionally graded material (FGM) panel. Compos. Struct. 2018, 205, 49–57. [Google Scholar] [CrossRef]
- Kubair, D.V. Stress concentration factors and stress-gradients due to circular holes in radially functionally graded panels subjected to anti-plane shear loading. Acta Mech. 2013, 224, 2845–2862. [Google Scholar] [CrossRef]
- Kubair, D.V. Stress concentration factor in functionally graded plates with circular holes subjected to anti-plane shear loading. J. Elast. 2014, 114, 179–196. [Google Scholar] [CrossRef]
- Shi, P.P. Stress field of a radially functionally graded panel with a circular elastic inclusion under static anti-plane shear loading. J. Mech. Sci. Technol. 2015, 29, 1163–1173. [Google Scholar] [CrossRef]
- Guan, Y.; Li, Y. Stress concentration and optimized analysis of an arbitrarily shaped hole with a graded layer under anti-plane shear. Appl. Sci. Basel 2018, 8, 2619. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Chen, W.Q.; Ding, H.J. 3D elasticity solutions for equilibrium problems of transversely isotropic FGM plates with holes. Acta Mech. 2015, 226, 1571–1590. [Google Scholar] [CrossRef]
- Yang, B.; Chen, W.Q.; Ding, H.J. Equilibrium of transversely isotropic FGM plates with an elliptical hole: 3D elasticity solutions. Arch. Appl. Mech. 2016, 86, 1391–1414. [Google Scholar] [CrossRef]
- Dave, J.M.; Sharma, D.S. Stresses and moments in through-thickness functionally graded plate weakened by circular/elliptical cut-out. Int. J. Mech. Sci. 2016, 105, 146–157. [Google Scholar] [CrossRef]
- Muskhelishvili, N.I. Some Basic Problem of Mathematical Theory of Elasticity; Noordhoff: Groningen, The Netherlands, 1975. [Google Scholar]
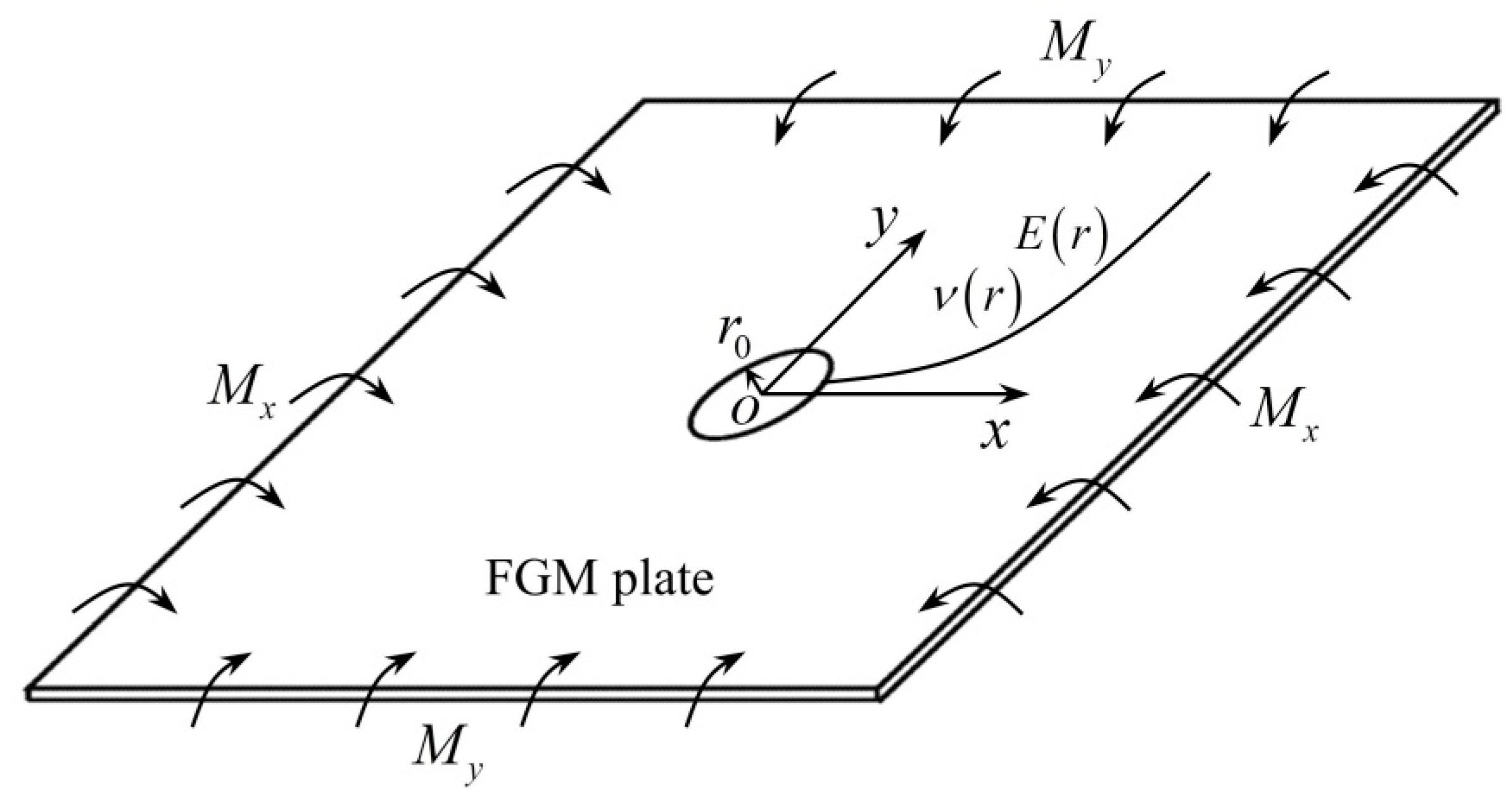
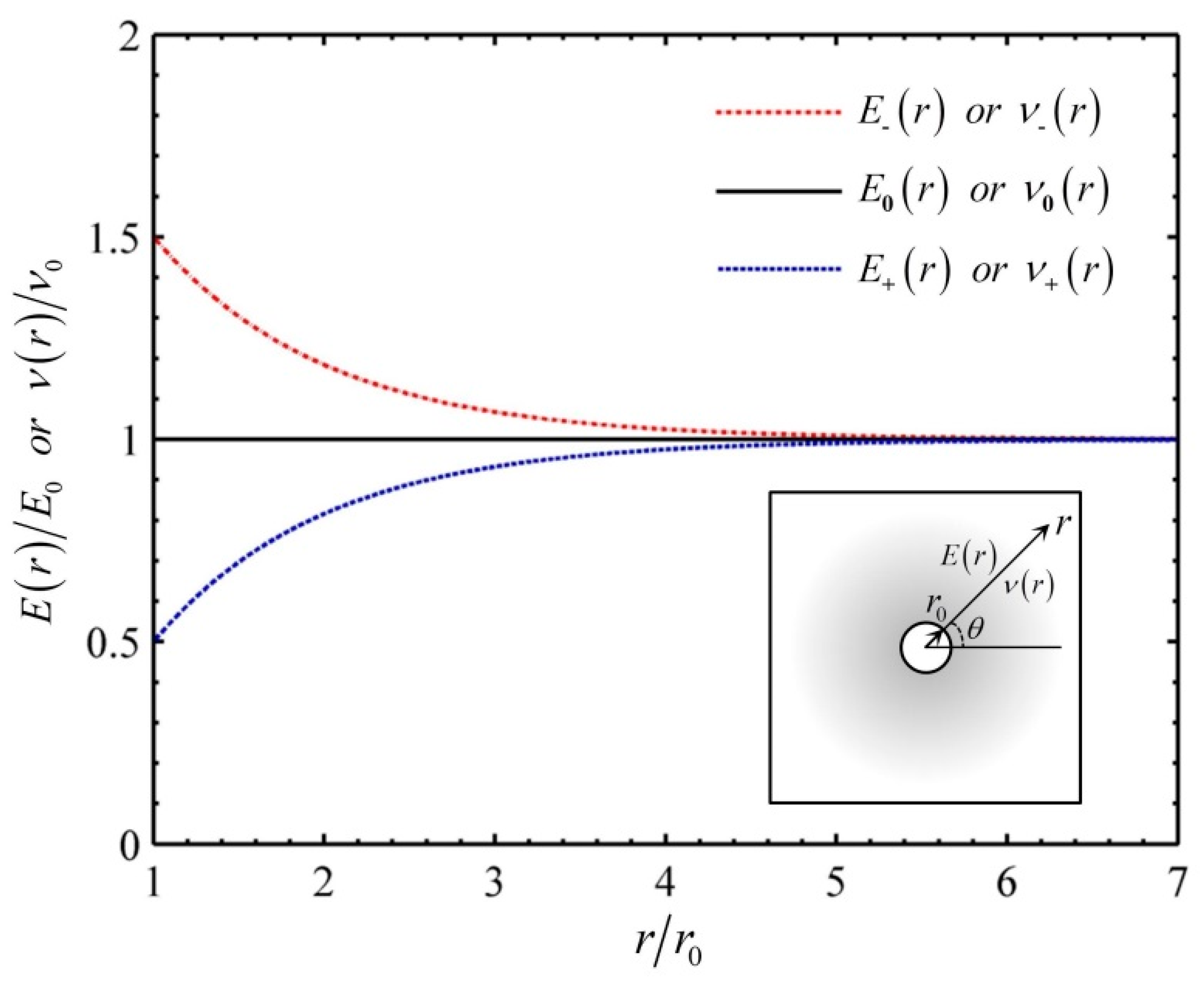
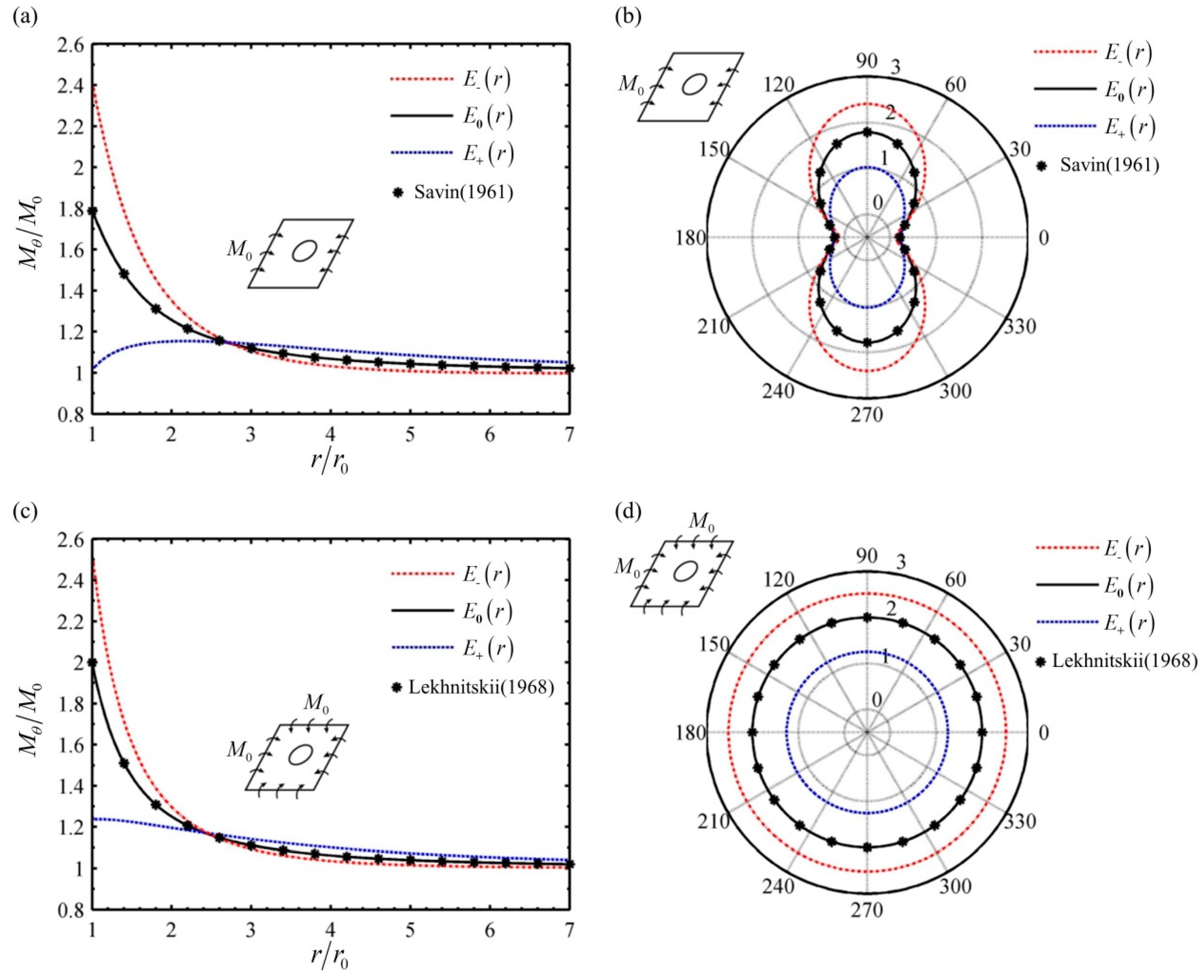
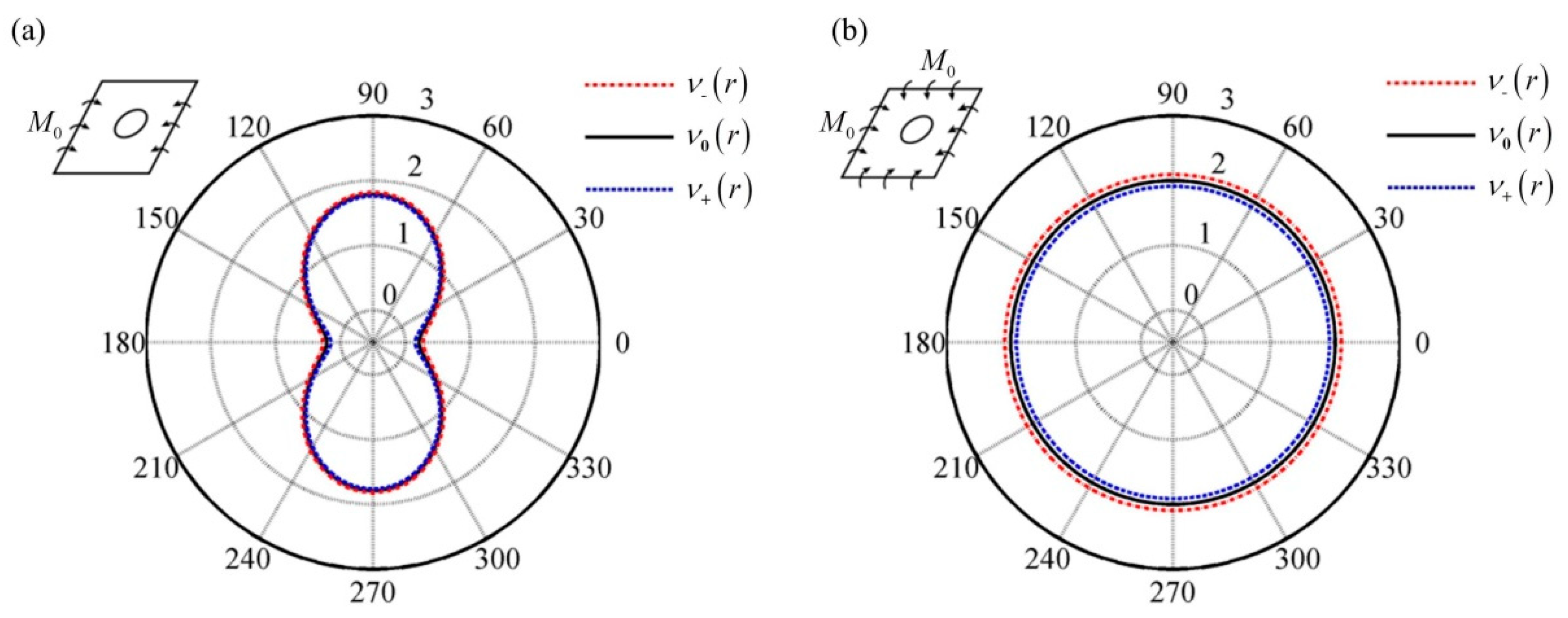
| Varying Forms | The Functions of Young’s Modulus | The Functions of Poisson’s Ratio |
|---|---|---|
| Decreasing | 1 | 1 |
| Unchanged | ||
| Increasing |
| The Types of Ring | The Functions of Young’s Modulus |
|---|---|
| Non-ring | |
| Homo-ring | |
| FGM-ring (linear) | |
| FGM-ring (exponential) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Q.; Cao, H.; Tang, Y.; Yang, B. Out-of-Plane Bending of Functionally Graded Thin Plates with a Circular Hole. Appl. Sci. 2020, 10, 2231. https://doi.org/10.3390/app10072231
Yang Q, Cao H, Tang Y, Yang B. Out-of-Plane Bending of Functionally Graded Thin Plates with a Circular Hole. Applied Sciences. 2020; 10(7):2231. https://doi.org/10.3390/app10072231
Chicago/Turabian StyleYang, Quanquan, He Cao, Youcheng Tang, and Bo Yang. 2020. "Out-of-Plane Bending of Functionally Graded Thin Plates with a Circular Hole" Applied Sciences 10, no. 7: 2231. https://doi.org/10.3390/app10072231
APA StyleYang, Q., Cao, H., Tang, Y., & Yang, B. (2020). Out-of-Plane Bending of Functionally Graded Thin Plates with a Circular Hole. Applied Sciences, 10(7), 2231. https://doi.org/10.3390/app10072231




