Shape Design Optimization of a Robot Arm Using a Surrogate-Based Evolutionary Approach
Abstract
1. Introduction
2. Techniques for Robot Arm Analysis and Design
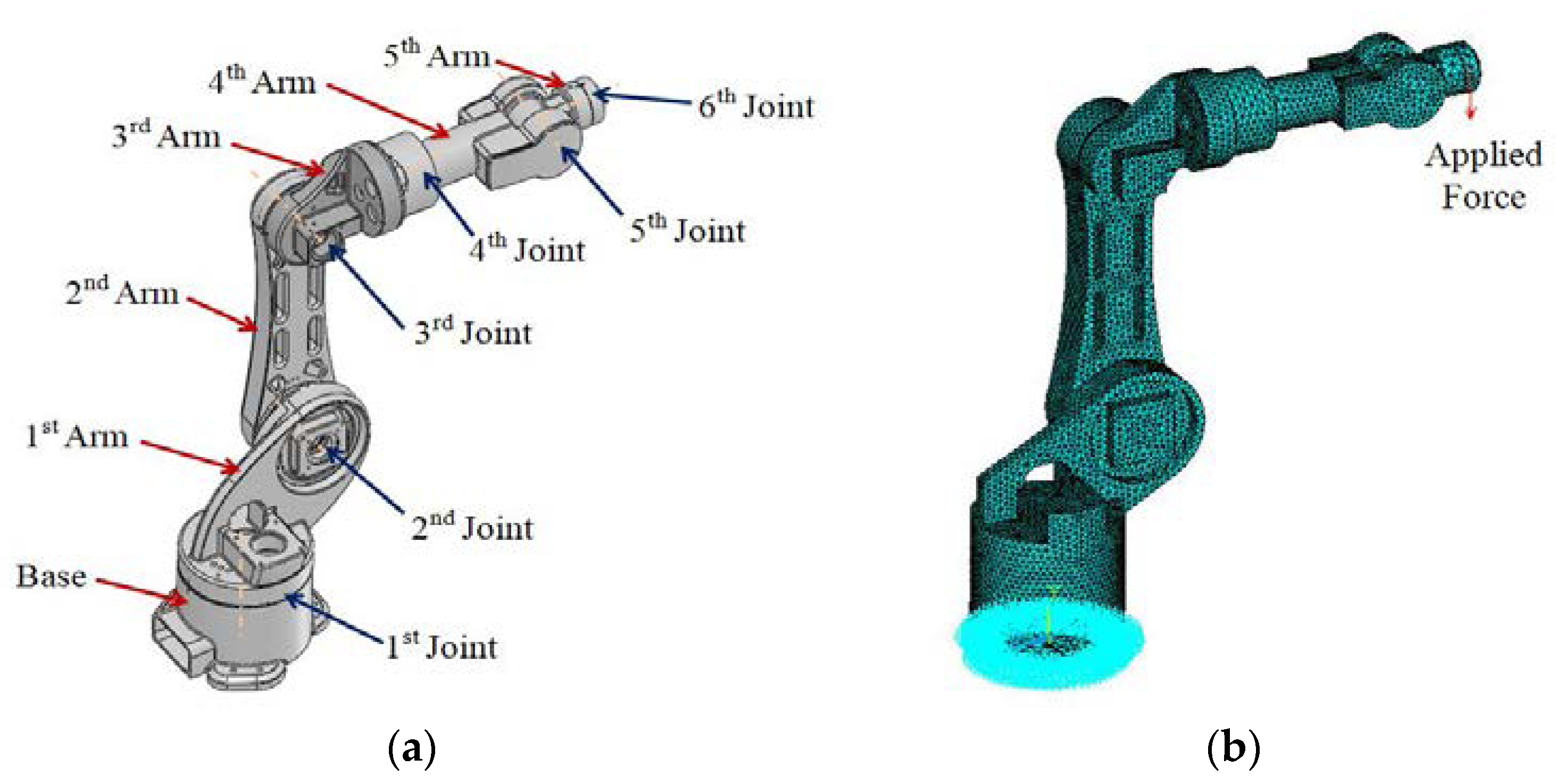
2.1. Architecture of the Industrial Robot
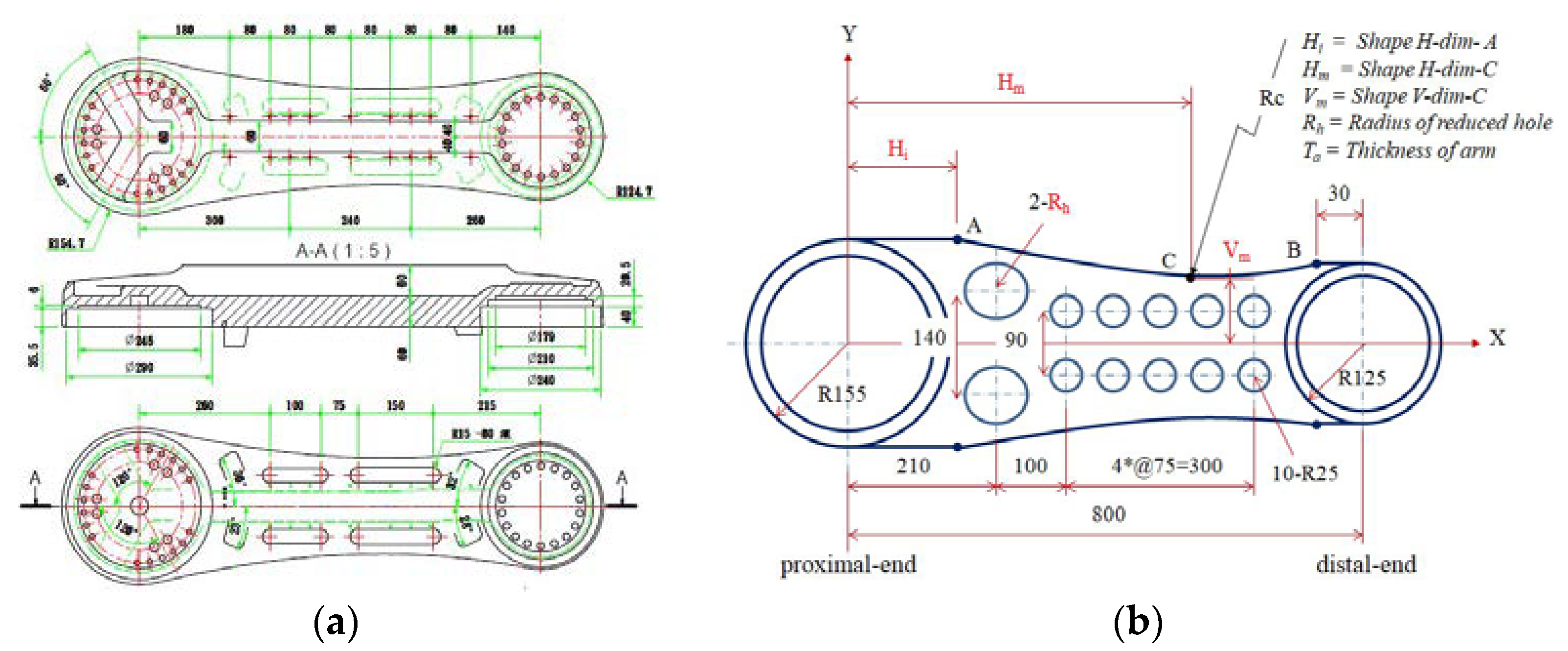
2.2. Problem Description of the Robot Arm
2.2.1. Objective Functions
2.2.2. Design Variables
2.2.3. Design Constraints
- The first set of constraints is the limitation of the feasible design region for design variables based on Table 1.
- The second set of constraints considers the relationship between the radius Rc of the circumcircle and design variables Hi, Hm, and Vm. According to the formulation of the circumcircle, the coordinates (x, y) of the circumcenter of a triangle and its radius Rc can be obtained as follows.Hence, the constraint involving y should be
- One constraint is related to the weight-to-stiffness ratio (W2SR), which is a measure of material mass efficiency used to provide unit resistance to elastic deformation. An improved W2SR enables the realization of longer spans without incurring a significant cost penalty, which is expressed in terms of material usage and deflections due to weight [24]. The W2SR computed from the weight and stiffness of a robot arm can be expressed aswhere Fy is the applied force at the distal-end joint.
- Another constraint is related to the weight-to-moment-of-inertia ratio (W2JR), a measure of a structural property. A higher W2JR will push resonance and anti-resonance peaks to lower frequencies, shrinking the operating bandwidth of the machine. The measure of W2JR in this paper is obtained as
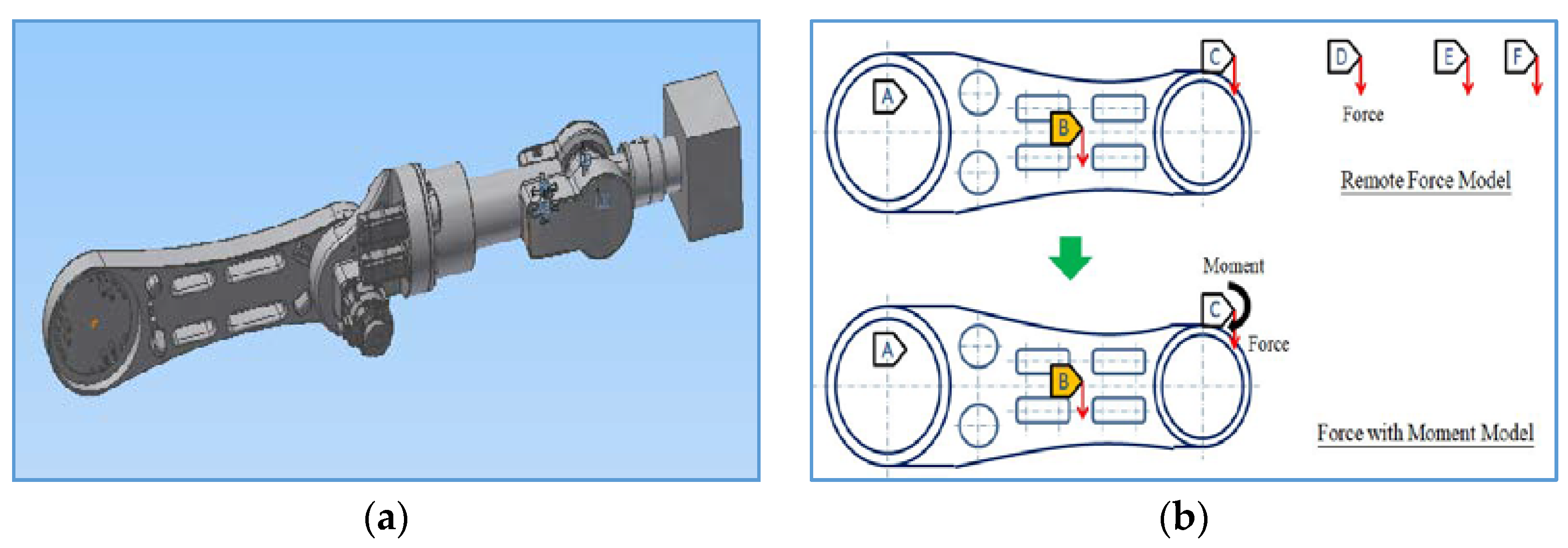
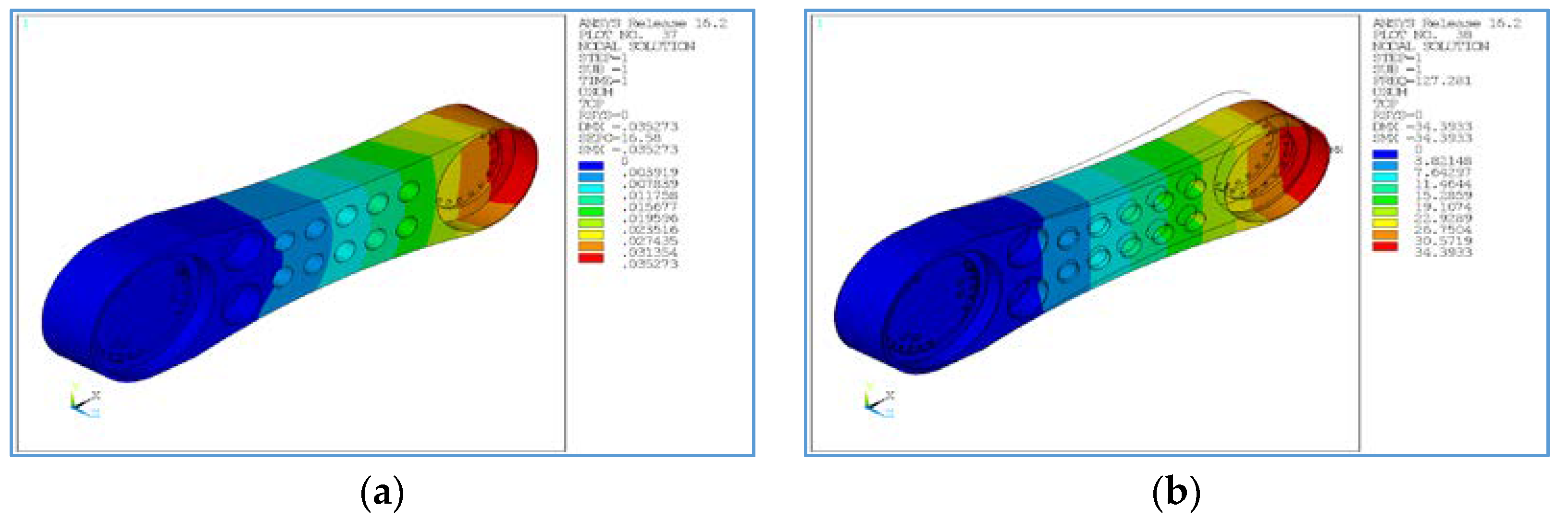
2.3. Performance Analysis Using a CAE Solver
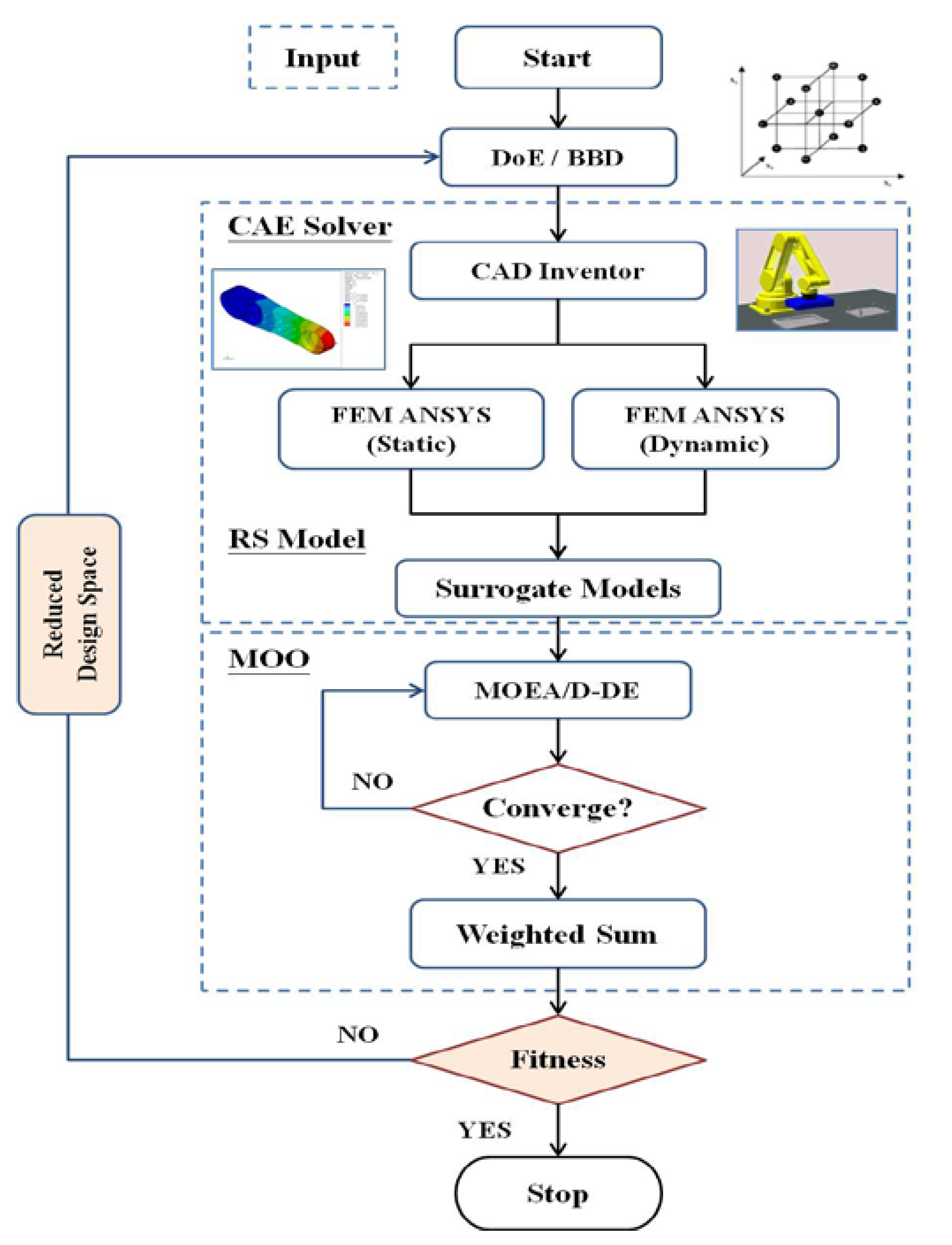
2.4. The Proposed SBEO Approach
2.4.1. The Framework and Procedure
- (1)
- First, a DOE plan is built based on the Box–Behnken design, and initial sample points are chosen according to the plan matrix. The objective (performance) functions are then analyzed and evaluated using the ANSYS solver following the baseline design CAD model of the robot arm.
- (2)
- A quadratic polynomial regression model is defined as the surrogate model for the objective functions based on the sampled dataset. The model parameters are then solved by inverse matrix transformation using Python’s numpy library’s “Polynomial.fit” function.
- (3)
- The surrogate model is used to search for the optimal solution of the objective subjected to the constraint functions in the design space using the MOEA/D-DE algorithm.
- (4)
- The weighted sum method, in which each weighting factor is chosen according to the importance or preference of each objective, is then used to determine the best candidate among the generated population samples. These candidates are used to evaluate the fitness with the termination conditions given in Equations (15)–(17). The reduced design space is thereby found to update the surrogate model.
- (5)
- Steps 3 and 4 are repeated until one of the termination conditions is satisfied.
2.4.2. Criteria of Model Renewal and Termination
3. Shape Design Optimization of the 2nd Robot Arm
3.1. Design Procedure of RSM with BBD
- (1)
- Identify the definition and the value of each variable;
- (2)
- Create a Box–Behnken design matrix;
- (3)
- Define a polynomial regression model;
- (4)
- Set up the X-Table in design of experiment (DOE);
- (5)
- Convert X to physical values x = mean of x + X × standard deviation of x (σx);
- (6)
- Assess y using FEA and the CAD model;
- (7)
- Compute the approximations of mean of y and range of y for scaling Y;
- (8)
- Convert y to scaled Y: Y = (y−mean of y)/(range of y/2);
- (9)
- Solve beta coefficients;
- (10)
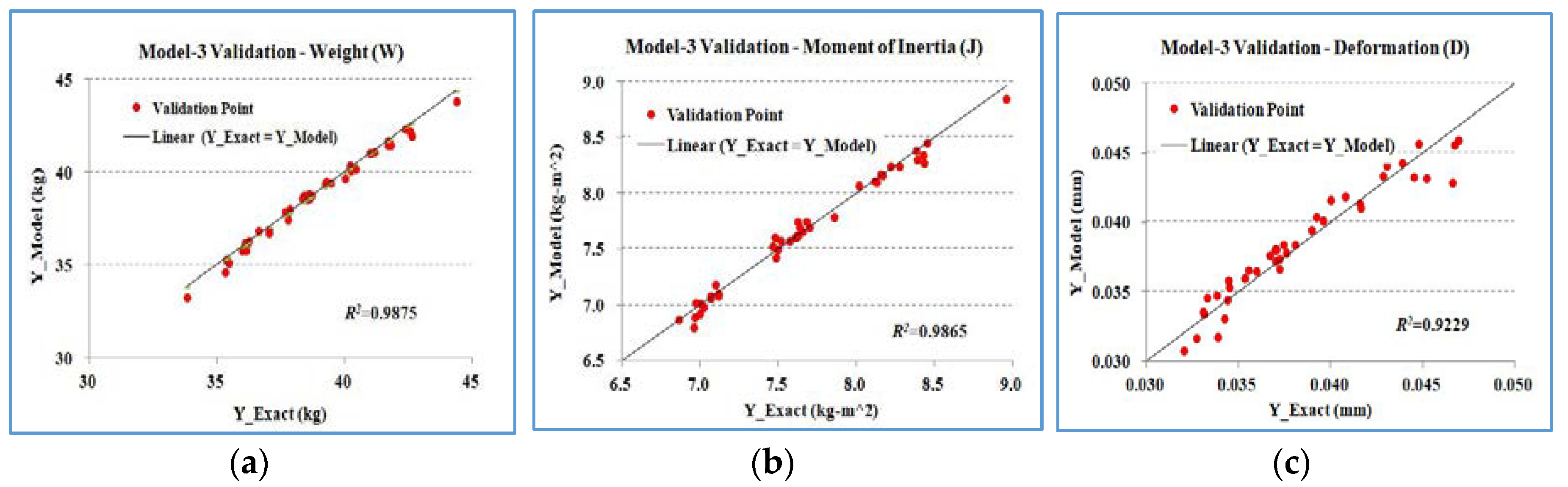
- Compare model y = [x] × {beta Coefficient} with analytical (“exact”) y for validation.
3.2. Construction of the BBD Matrix
3.3. Formulation of the RS Regression Model
3.4. Calculation of the Coefficients of the RS Model
3.5. Validation of the RS Model
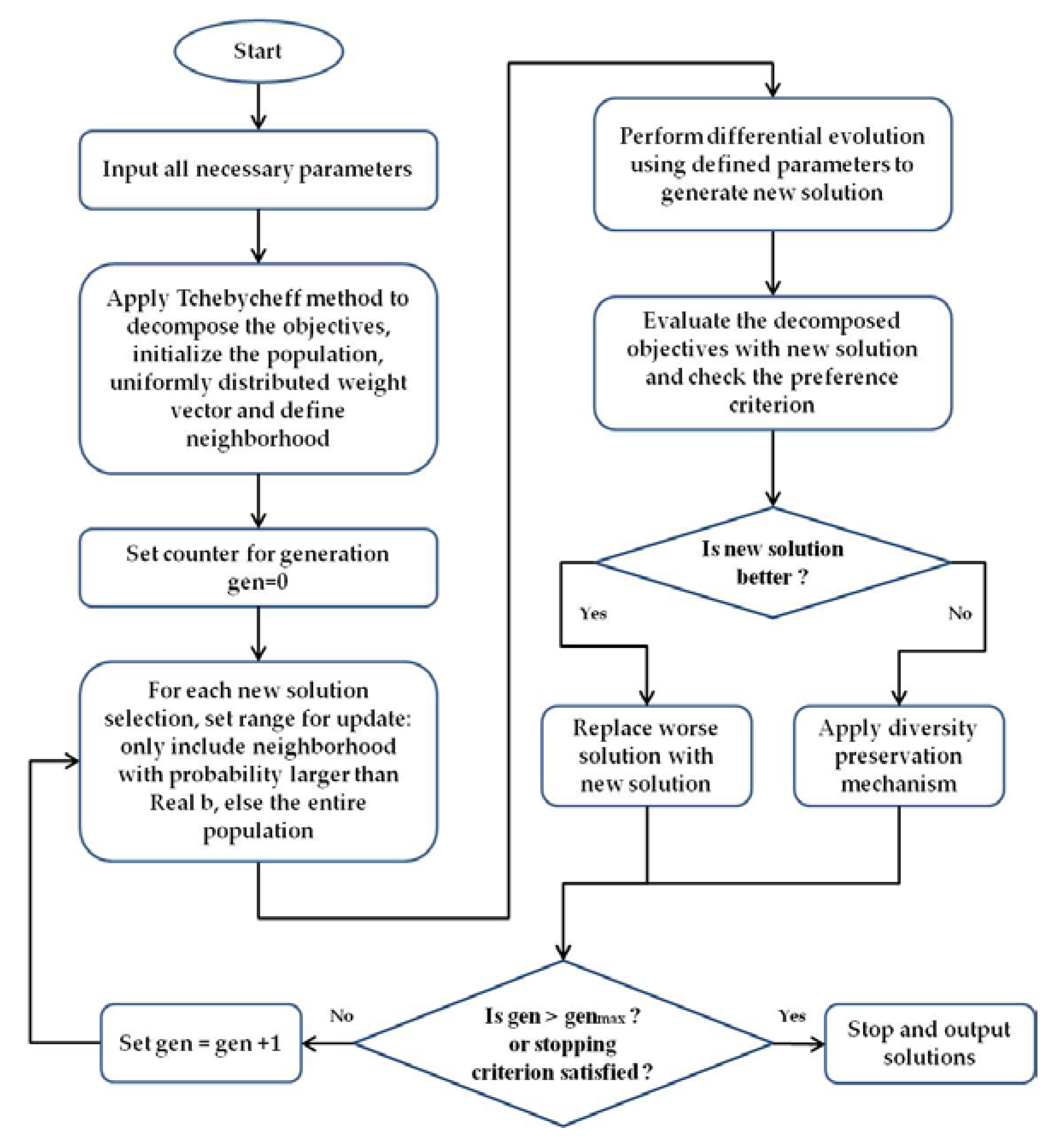
3.6. Multi-objective Evolutionary Optimization
- (1)
- Generations = 300;
- (2)
- Weight generation = grid → method to generate the weights;
- (3)
- Decomposition method = Tchebycheff → method used to decompose the objectives;
- (4)
- Neighbor = 20 → size of weights neighborhood;
- (5)
- Crossover parameter = 0.9;
- (6)
- Differential evolution parameter = 0.5;
- (7)
- Distribution index = 20 → used for polynomial mutation;
- (8)
- Real b = 0.9 → chance that the neighborhood is considered at each generation, rather than the whole population (part of the diversity preservation mechanism);
- (9)
- Limit = 2 → number of copies reinserted in the population (part of the diversity preservation mechanism);
- (10)
- Preserve diversity = True → diversity preservation mechanisms.
4. Simulation Results
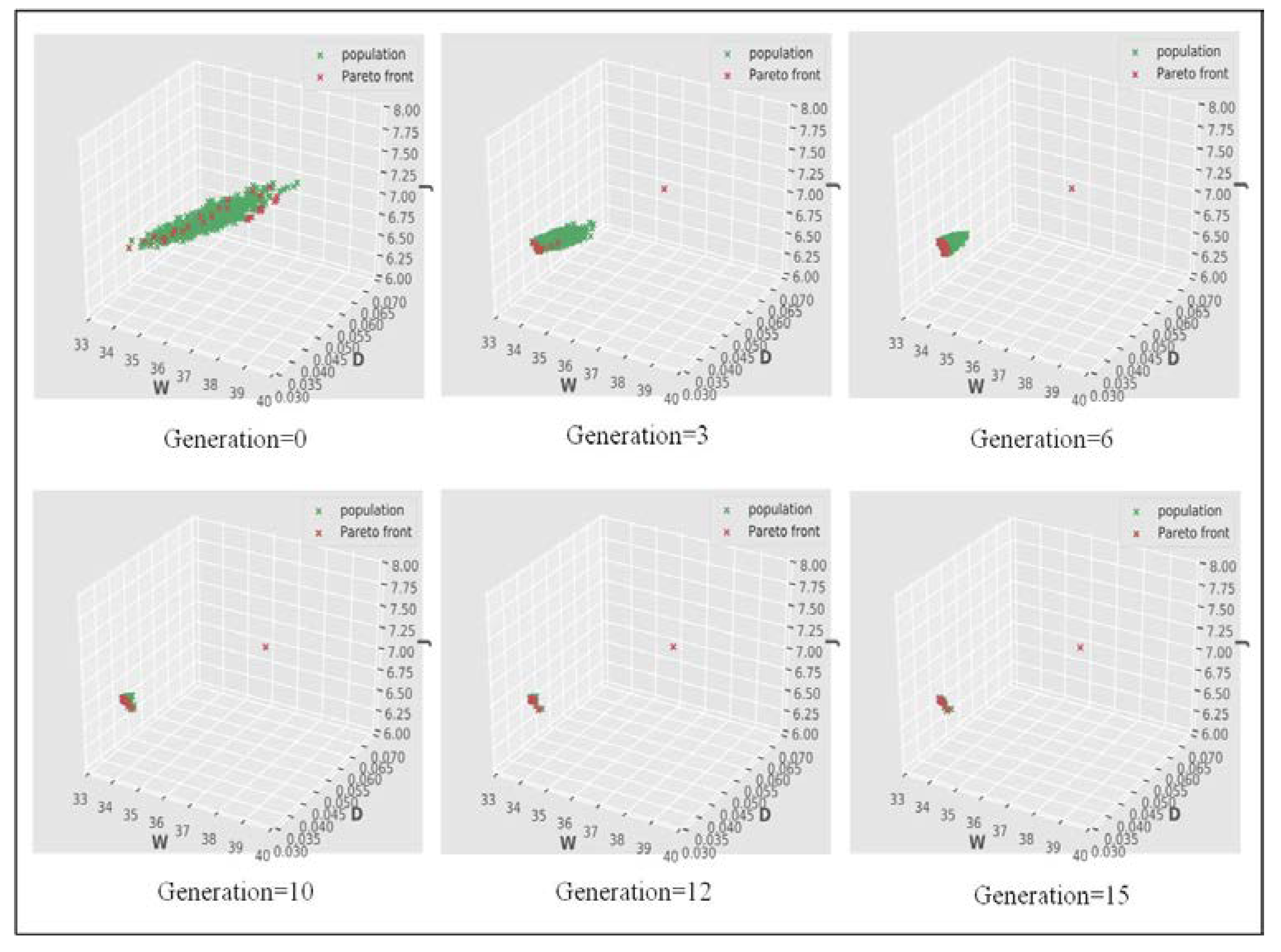
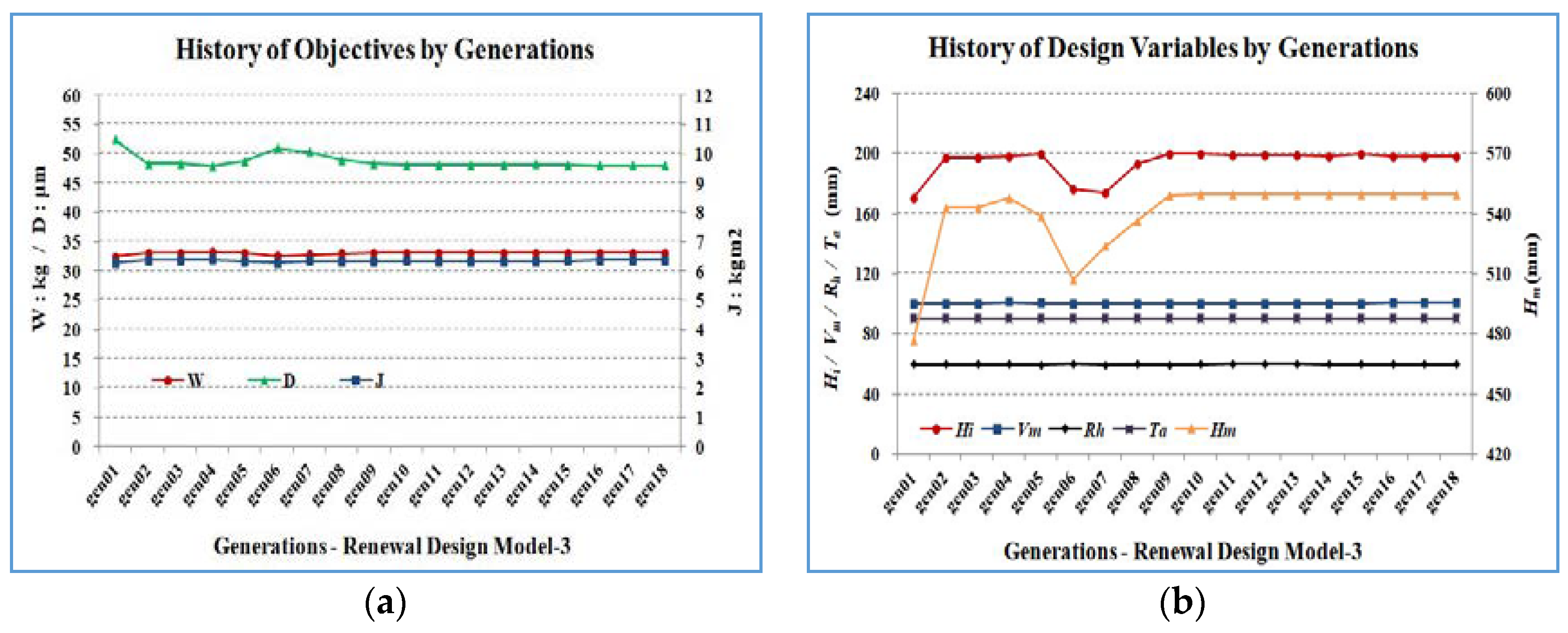
4.1. Pareto Front History
4.2. Weighted Sum History
4.3. The Improvement of Performance
4.4. The Improvement of Computational Efficiency
4.5. The Relationship between Objectives and Design Variables
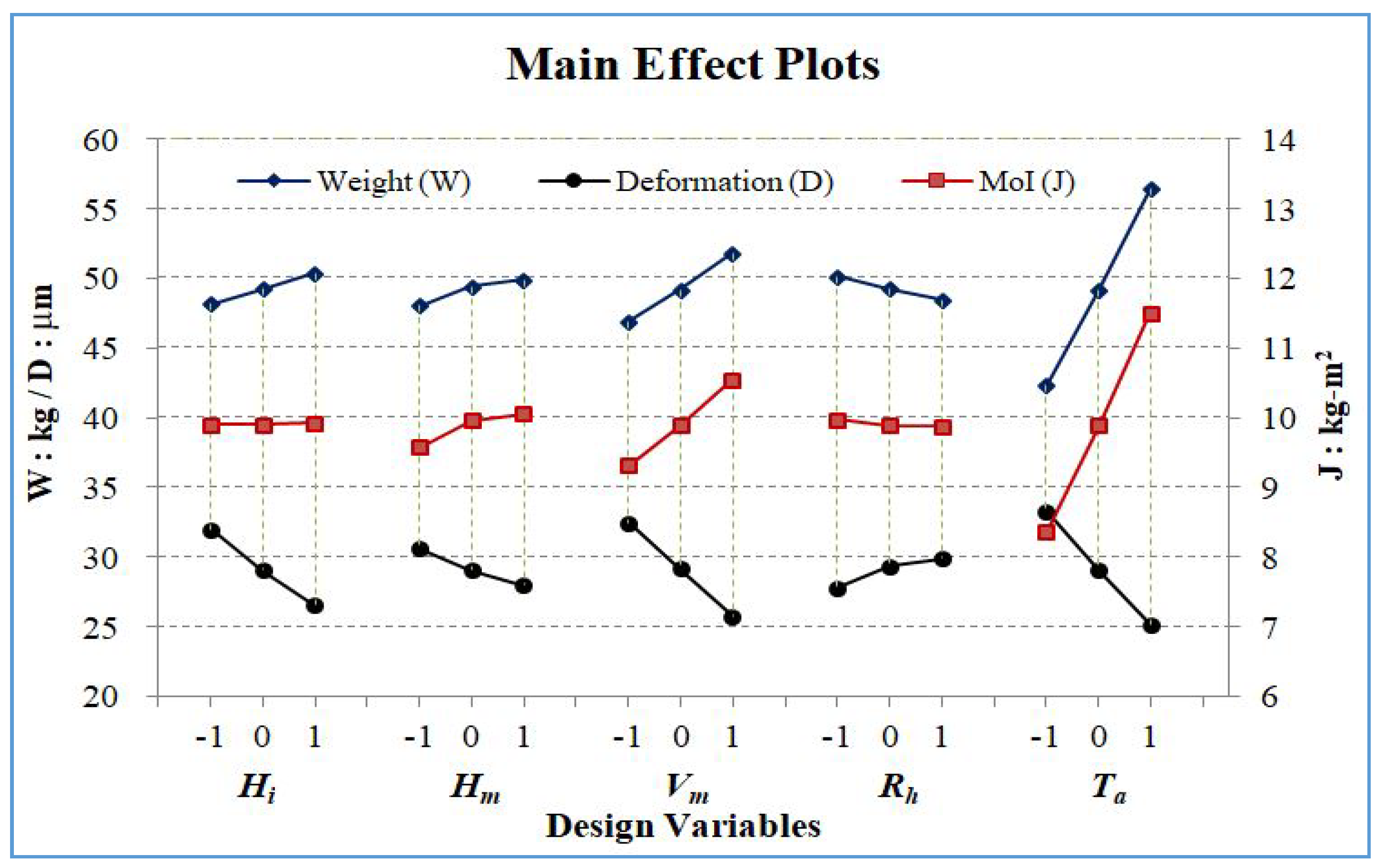
4.5.1. Main Effect Analysis
- (1)
- All factors, except Rh, can cause the response to increase when they move from low level (−1) to high level (+1). While Hi and Hm can only cause the response to increase slightly as the level changes, Vm and Ta can cause the response to increase significantly, especially Ta.
- (2)
- Factor Rh can cause the response to decrease when its level increases, but the slope of the response only changes slightly.
- (3)
- Consequently, all five factors appear to have a main effect on the response W. Among them, Ta is the most important factor because of its high significance.
- (1)
- Factors Hi and Rh present no significant main effects because the response remains nearly the same when they move from low level to high level.
- (2)
- Factors Vm and Ta can cause the response to increase significantly when they move from low level to high level, and the slope of the increased response induced by Ta is the sharpest.
- (3)
- Factor Hm can cause the response to increase sharply when it moves from low level to intermediate level, and after the saddle point, the response remains almost constant until high level.
- (4)
- Consequently, factors Hm, Vm, and Ta appear to cause a main effect on the response J. Among them, Ta is the most important factor because of its high significance.
- (1)
- When the factors move from low level to high level, only Rh causes response D to decrease, while the others cause response D to increase.
- (2)
- Factors Hi, Vm, and Ta cause the response D to decrease sharply when the factors move from low level to high level, and the slopes of the responses remain almost the same.
- (3)
- Consequently, all five factors appear to have main effects on the response. Among them, Ta is the most sensitive and important factor according to the main effect plots.
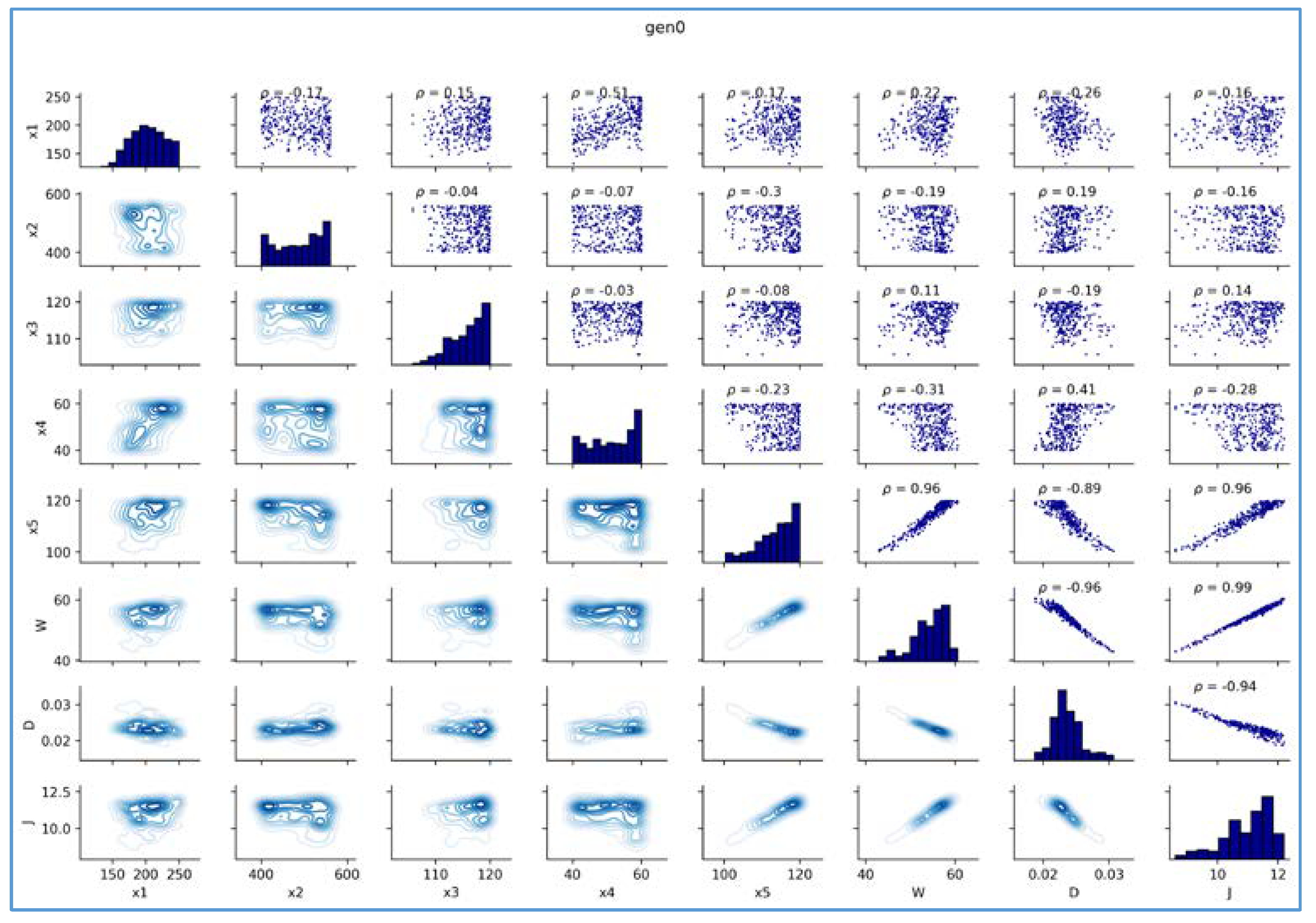
4.5.2. Pairwise Plot Analysis
5. Discussion
- (1)
- The optimal shape design of a robot arm performed in this study showed that shape design optimization is useful to improve the performance of industrial robots with real engineering considerations.
- (2)
- The optimal design of the 2nd robot arm obtained via the multi-objective optimization approach features good performance for conflicting objectives, and a Pareto front was obtained by employing preference sets of weighted factors for the various design objectives.
- (3)
- Compared with the conventional expensive ANSYS-based simulation technique, the proposed SBEO is more practicable and effective for shape optimization of robot arms parameterized with many design variables. In the SBEO, the population samples and Pareto fronts are able to converge quickly to the optimized hot zone of design candidates according to the designer’s preference criteria to obtain better performance.
- (4)
- It was shown that objective W is proportional to J, and both W and J are inversely proportional to D. The objectives are all affected by the five adopted design variables, of which thickness Ta has the most significant effects, which depend on the selected criteria. When Ta, Rh, and Vm are fixed, smaller Hi and Hm at the same time could cause larger deformation in the robot arm design optimization.
Author Contributions
Funding
Conflicts of Interest
References
- Roy, R.; Hinduja, S.; Teti, R. Recent advances in engineering design optimisation: Challenges and future trends. Cirp Ann. 2008, 57, 697–715. [Google Scholar] [CrossRef]
- Christensen, P.W.; Klarbring, A. An Introduction to Structural Optimisation; Springer Science & Business Media B.V: Linköping, Sweeden, 2009. [Google Scholar]
- Van de Straete, H.J.; de Schutter, J.; Belmans, R. An efficient procedure for checking performance limits in servo drive selection and optimization. IEEE/ASME Trans. Mechatron. 1999, 4, 378–386. [Google Scholar] [CrossRef]
- Cusimano, G. A procedure for a suitable selection of laws of motion and electric drive systems under inertial loads. Mech. Mach. Theory 2003, 38, 519–533. [Google Scholar] [CrossRef]
- Tao, W.; Zhang, M.; Liu, M.; Yun, X. Residual vibration analysis and suppression for SCARA robot arm in semiconductor manufacturing. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006. [Google Scholar]
- Roy, J.; Goldberg, R.P.; Whitcomb, L.L. Structural Design, Analysis, and Performance Evaluation of a New Semi-Direct Drive Robotic arm: Theory and Experiment. IEEE/ASME Trans. Mechatron. 2004, 9, 10–19. [Google Scholar] [CrossRef]
- Park, J.-H.; Asada, H. Concurrent design optimization of mechanical structure and control for high speed robots. J. Dyn. Syst. Meas. Control 1994, 116, 344–356. [Google Scholar] [CrossRef]
- Sahu, S.; Choudhury, B.; Biswal, B. A vibration analysis of a 6 axis industrial robot using FEA. Mater. Today Proc. 2017, 4, 2403–2410. [Google Scholar] [CrossRef]
- Sahu, S.; Choudhury, B. Dynamic Behaviour Analysis of an Industrial Robot Using FEM. In Soft Computing in Data Analytics; Springer: Singapore, 2019; Volume 758, pp. 193–202. [Google Scholar]
- Sahu, S.; Choudhury, B. Stress and Modal Analysis of Six-Axis Articulated Robot Using ANSYS. In Information and Communication Technology for Competitive Strategies; Springer: Singapore, 2019; pp. 303–311. [Google Scholar]
- Pupăză, C.; Constantin, G.; NEGRILĂ, Ș. Computer aided engineering of industrial robots. Proc. Manuf. Syst. 2014, 9, 87–92. [Google Scholar]
- Chen, W.; You, D.; Li, R.; Zhang, S. Analysis and optimization of the structure of robot arm. In Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), Beijing, China, 17–19 August 2017. [Google Scholar]
- Han, Z.-H.; Zhang, K.-S. Surrogate-based optimization. In Real-World Applications of Genetic Algorithms; IntechOpen: London, UK, 2012; pp. 343–362. [Google Scholar]
- Yoo, J.; Hyun, M.W.; Choi, J.H.; Kang, S.; Kim, S.J. Optimal Design of a Variable Stiffness Joint in a Robot Manipulator using the Response Surface Method. J. Mech. Sci. Technol. 2009, 23, 2236–2243. [Google Scholar] [CrossRef]
- Qiu, P.; Cui, M.; Kang, K.; Park, B.; Son, Y.; Khim, E.; Jang, M.; Khim, J. Application of Box-Behnken Design with Response Surface Methodology for Modeling and Optimizing Ultrasonic Oxidation of Arsenite with H2O2. Cent. Eurchem. 2014, 12, 164–172. [Google Scholar] [CrossRef]
- Wu, L.; Yick, K.L.; Ng, S.P.; Yip, J. Application of Box-Behnken Design to the Optimization of Process Parameters in Foam Cup Molding. Expert Syst. Appl. 2012, 39, 8059–8065. [Google Scholar] [CrossRef]
- Hsiao, J.C.; Kam, T.Y.; Chou, C.L. Application of FEM-based response surface method with Box–Behnken design for modeling and optimizing multi-objective function in robotic arm design. In Proceedings of the CIE48 International Conference on Computers & Industrial Engineering, Auckland, New Zealand, 2–5 December 2018. [Google Scholar]
- Wang, G.G.; Dong, Z. Design optimization of a complex mechanical system using adaptive response surface method. Trans. Can. Soc. Mech. Eng. 2000, 24, 295–306. [Google Scholar] [CrossRef]
- Wang, G.G. Adaptive response surface method using inherited latin hypercube design points. J. Mech. Des. 2003, 125, 210–220. [Google Scholar] [CrossRef]
- Wang, Y.; Ni, P.; Wen, D.; Lin, Q.; Wang, D.; Ma, C.; Rao, Y.; Wang, H.; Tan, D. Dynamic Performance Optimization of Circular Sawing Machine Gearbox. Appl. Sci. 2019, 9, 4458. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R.; Lin, L. Network Models and Optimization: Multiobjective Genetic Algorithm Approach; Springer Science & Business Media: New York, NY, USA, 2008. [Google Scholar]
- Ghiorghe, A. Optimization design for the structure of an RRR type industrial robot. UPB Sci. Bull. Ser. D 2010, 72, 121–134. [Google Scholar]
- Sadollah, A.; Eskandar, H.; Kim, J.H. Water cycle algorithm for solving constrained multi-objective optimization problems. Appl. Soft Comput. 2015, 7, 279–298. [Google Scholar] [CrossRef]
- Tsavdaridis, K.D.; Kingman, J.J.; Toropov, V.V. Application of structural topology optimisation to perforated steel beams. Comput. Struct. 2015, 158, 108–123. [Google Scholar] [CrossRef]
- Liu, B.; Fernández, F.V.; Zhang, Q.; Pak, M.; Sipahi, S.; Gielen, G. An enhanced MOEA/D-DE and its application to multiobjective analog cell sizing. IEEE Congr. Evol. Comput. 2010, 1–7. [Google Scholar] [CrossRef]
- Biscani, F.; Izzo, D. Optimisation. arXiv 2018, arXiv:1004.3824v1. [Google Scholar]
- Zadeh, L. Optimality and non-scalar-valued performance criteria. IEEE Trans. Automat. Control 1963, 8, 59–60. [Google Scholar] [CrossRef]
- Ferreira, S.C.; Bruns, R.E.; Ferreira, H.S.; Matos, G.D.; David, J.M.; Brandao, G.C.; da Silva, E.P.; Portugal, L.A.; Dos Reis, P.S.; Souza, A.S.; et al. Box–Behnken design: An Alternative for the Optimization of Analytical Methods. Anal. Chim. Acta 2007, 597, 179–186. [Google Scholar] [CrossRef] [PubMed]
- Montgomery, D.C. Design and Analysis of Experiments: Response Surface Method and Designs; John Wiley and Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Joglekar, A.M.; May, A.T. Product excellence through design of experiments. Cereal Food World 1987, 32, 857–868. [Google Scholar]
- Bazgan, C.; Jamain, F.; Vanderpooten, D. Approximate Pareto sets of minimal size for multi-objective optimization problems. Oper. Res. Lett. 2015, 43, 1–6. [Google Scholar] [CrossRef]

| Design Variable | Model-1 | Model-2 | Model-3 | ||||
|---|---|---|---|---|---|---|---|
| xiL | xiU | xiL | xiU | xiL | xiU | ||
| Shape Dimension (point A) | Hi | 100 | 250 | 150 | 200 | 150 | 200 |
| Shape Dimension (point C) | Hm | 400 | 560 | 450 | 550 | 450 | 550 |
| Shape Dimension (point C) | Vm | 100 | 120 | 100 | 120 | 100 | 120 |
| Radius of Reduced Hole | Rh | 40 | 60 | 50 | 60 | 50 | 60 |
| Thickness of Robot Arm | Ta | 100 | 120 | 90 | 110 | 90 | 100 |
| Run | Coded Variables | Uncoded (Real) Variables | Response (FEM) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| X1 | X2 | X3 | X4 | X5 | Hi(x1) | Hm(x2) | HV(x3) | Rh(x4) | Ta(x5) | W(y1) | J(y2) | D(y3) | |
| 1 | −1 | −1 | 0 | 0 | 0 | 150 | 450 | 110 | 55 | 95 | 37.8640 | 7.4954 | 0.03921 |
| 2 | −1 | 1 | 0 | 0 | 0 | 150 | 550 | 110 | 55 | 95 | 38.3861 | 7.6226 | 0.03809 |
| 3 | 1 | −1 | 0 | 0 | 0 | 200 | 450 | 110 | 55 | 95 | 38.4216 | 7.4789 | 0.03700 |
| 4 | 1 | 1 | 0 | 0 | 0 | 200 | 550 | 110 | 55 | 95 | 39.2435 | 7.6958 | 0.03555 |
| 5 | 0 | 0 | −1 | −1 | 0 | 175 | 500 | 100 | 50 | 95 | 37.0219 | 7.1141 | 0.04079 |
| 6 | 0 | 0 | −1 | 1 | 0 | 175 | 500 | 100 | 60 | 95 | 36.0889 | 7.0655 | 0.04287 |
| 7 | 0 | 0 | 1 | −1 | 0 | 175 | 500 | 120 | 50 | 95 | 41.1573 | 8.1635 | 0.03313 |
| 8 | 0 | 0 | 1 | 1 | 0 | 175 | 500 | 120 | 60 | 95 | 40.2243 | 8.1149 | 0.03449 |
| 9 | 0 | −1 | 0 | 0 | −1 | 175 | 450 | 110 | 55 | 90 | 35.3401 | 6.8625 | 0.04671 |
| 10 | 0 | −1 | 0 | 0 | 1 | 175 | 450 | 110 | 55 | 100 | 41.6777 | 8.2743 | 0.03387 |
| 11 | 0 | 1 | 0 | 0 | −1 | 175 | 550 | 110 | 55 | 90 | 35.9760 | 7.0237 | 0.04520 |
| 12 | 0 | 1 | 0 | 0 | 1 | 175 | 550 | 110 | 55 | 100 | 42.3765 | 8.4515 | 0.03272 |
| 13 | −1 | 0 | −1 | 0 | 0 | 150 | 500 | 100 | 55 | 95 | 36.1010 | 7.0679 | 0.04390 |
| 14 | −1 | 0 | 1 | 0 | 0 | 150 | 500 | 120 | 55 | 95 | 40.4444 | 8.1267 | 0.03446 |
| 15 | 1 | 0 | −1 | 0 | 0 | 200 | 500 | 100 | 55 | 95 | 37.0302 | 7.1134 | 0.04001 |
| 16 | 1 | 0 | 1 | 0 | 0 | 200 | 500 | 120 | 55 | 95 | 40.9697 | 8.1538 | 0.03308 |
| 17 | 0 | 0 | 0 | −1 | −1 | 175 | 500 | 110 | 50 | 90 | 36.2567 | 7.0050 | 0.04481 |
| 18 | 0 | 0 | 0 | −1 | 1 | 175 | 500 | 110 | 50 | 100 | 42.6410 | 8.4286 | 0.03238 |
| 19 | 0 | 0 | 0 | 1 | −1 | 175 | 500 | 110 | 60 | 90 | 35.3237 | 6.9565 | 0.04663 |
| 20 | 0 | 0 | 0 | 1 | 1 | 175 | 500 | 110 | 60 | 100 | 41.7079 | 8.3801 | 0.03383 |
| 21 | 0 | −1 | −1 | 0 | 0 | 175 | 450 | 100 | 55 | 95 | 36.0959 | 6.9702 | 0.04304 |
| 22 | 0 | −1 | 1 | 0 | 0 | 175 | 450 | 120 | 55 | 95 | 40.2101 | 8.0121 | 0.03441 |
| 23 | 0 | 1 | −1 | 0 | 0 | 175 | 550 | 100 | 55 | 95 | 36.6138 | 7.1004 | 0.04158 |
| 24 | 0 | 1 | 1 | 0 | 0 | 175 | 550 | 120 | 55 | 95 | 41.0175 | 8.2187 | 0.03330 |
| 25 | −1 | 0 | 0 | −1 | 0 | 150 | 500 | 110 | 50 | 95 | 38.7225 | 7.6191 | 0.03744 |
| 26 | −1 | 0 | 0 | 1 | 0 | 150 | 500 | 110 | 60 | 95 | 37.7895 | 7.5705 | 0.03960 |
| 27 | 1 | 0 | 0 | −1 | 0 | 200 | 500 | 110 | 50 | 95 | 39.4499 | 7.6557 | 0.03535 |
| 28 | 1 | 0 | 0 | 1 | 0 | 200 | 500 | 110 | 60 | 95 | 38.5168 | 7.6072 | 0.03673 |
| 29 | 0 | 0 | −1 | 0 | −1 | 175 | 500 | 100 | 55 | 90 | 33.8264 | 6.4804 | 0.05110 |
| 30 | 0 | 0 | −1 | 0 | 1 | 175 | 500 | 100 | 55 | 100 | 40.0143 | 7.8544 | 0.03724 |
| 31 | 0 | 0 | 1 | 0 | −1 | 175 | 500 | 120 | 55 | 90 | 37.7877 | 7.4856 | 0.04164 |
| 32 | 0 | 0 | 1 | 0 | 1 | 175 | 500 | 120 | 55 | 100 | 44.3674 | 8.9590 | 0.03004 |
| 33 | −1 | 0 | 0 | 0 | −1 | 150 | 500 | 110 | 55 | 90 | 35.4554 | 6.9641 | 0.04696 |
| 34 | −1 | 0 | 0 | 0 | 1 | 150 | 500 | 110 | 55 | 100 | 41.8044 | 8.3859 | 0.03422 |
| 35 | 1 | 0 | 0 | 0 | −1 | 200 | 500 | 110 | 55 | 90 | 36.1521 | 6.9992 | 0.04450 |
| 36 | 1 | 0 | 0 | 0 | 1 | 200 | 500 | 110 | 55 | 100 | 42.5701 | 8.4245 | 0.03202 |
| 37 | 0 | −1 | 0 | −1 | 0 | 175 | 450 | 110 | 50 | 95 | 38.6021 | 7.5130 | 0.03721 |
| 38 | 0 | −1 | 0 | 1 | 0 | 175 | 450 | 110 | 60 | 95 | 37.6691 | 7.4644 | 0.03895 |
| 39 | 0 | 1 | 0 | −1 | 0 | 175 | 550 | 110 | 50 | 95 | 39.2660 | 7.6813 | 0.03599 |
| 40 | 0 | 1 | 0 | 1 | 0 | 175 | 550 | 110 | 60 | 95 | 38.3329 | 7.6328 | 0.03761 |
| 41 | 0 | 0 | 0 | 0 | 0 | 175 | 500 | 110 | 55 | 95 | 38.6488 | 7.6147 | 0.03700 |
| 42 | 0 | 0 | 0 | 0 | 0 | 175 | 500 | 110 | 55 | 95 | 38.6488 | 7.6147 | 0.03700 |
| 43 | 0 | 0 | 0 | 0 | 0 | 175 | 500 | 110 | 55 | 95 | 38.6488 | 7.6147 | 0.03700 |
| 44 | 0 | 0 | 0 | 0 | 0 | 175 | 500 | 110 | 55 | 95 | 38.6488 | 7.6147 | 0.03700 |
| 45 | 0 | 0 | 0 | 0 | 0 | 175 | 500 | 110 | 55 | 95 | 38.6488 | 7.6147 | 0.03700 |
| 46 | 0 | 0 | 0 | 0 | 0 | 175 | 500 | 110 | 55 | 95 | 38.6488 | 7.6147 | 0.03700 |
| Coded Variables | Model-1 | Model-2 | Model-3 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model Coefficients | YW | YJ | YD | YW | YJ | YD | YW | YJ | YD | |
| Beta 0 | Const. | 0.02734 | 0.02496 | −0.15331 | −0.00590 | −0.00610 | −0.15458 | −0.01057 | −0.01064 | −0.01826 |
| Beta 1 | x1 | 0.11596 | 0.00428 | −0.37509 | 0.04264 | 0.00331 | −0.10549 | 0.06862 | 0.01394 | −0.11655 |
| Beta 2 | x2 | 0.09879 | 0.11059 | −0.18021 | 0.03929 | 0.03783 | −0.05495 | 0.06323 | 0.06838 | −0.06151 |
| Beta 3 | x3 | 0.25687 | 0.28164 | −0.46145 | 0.24607 | 0.27069 | −0.32638 | 0.39591 | 0.42706 | −0.39148 |
| Beta 4 | x4 | −0.08976 | −0.02008 | 0.14201 | −0.05228 | −0.01179 | 0.06951 | −0.08852 | −0.01959 | 0.08057 |
| Beta 5 | x5 | 0.74737 | 0.72229 | −0.56288 | 0.75449 | 0.72972 | −0.79298 | 0.60527 | 0.57397 | −0.60071 |
| Beta 6 | x12 | −0.01362 | −0.00941 | 0.10906 | −0.00099 | 0.00532 | 0.01938 | −0.00159 | −0.00037 | 0.01376 |
| Beta 7 | x22 | 0.06079 | 0.08144 | −0.07636 | 0.00885 | 0.03363 | −0.00680 | 0.01422 | 0.01810 | −0.00774 |
| Beta 8 | x32 | −0.03279 | −0.00272 | 0.17937 | −0.01193 | −0.00233 | 0.05312 | −0.01916 | −0.00370 | 0.05953 |
| Beta 9 | x42 | 0.00000 | 0.00000 | −0.08645 | 0.00000 | 0.00000 | −0.01540 | 0.00000 | 0.00000 | −0.01861 |
| Beta 10 | x52 | 0.01099 | 0.00108 | 0.04749 | 0.00410 | 0.00088 | 0.01302 | 0.00327 | 0.00070 | 0.00623 |
| Beta 11 | x1x2 | −0.05798 | −0.06420 | 0.11599 | −0.01896 | −0.01527 | 0.03603 | −0.03051 | −0.03286 | 0.03191 |
| Beta 12 | x1x3 | 0.00505 | 0.00647 | 0.05851 | 0.00853 | 0.00978 | 0.00752 | 0.01373 | 0.01541 | 0.00848 |
| Beta 13 | x1x4 | 0.00000 | 0.00000 | −0.00978 | 0.00000 | −0.00003 | −0.00237 | 0.00000 | 0.00000 | −0.00287 |
| Beta 14 | x1x5 | 0.00865 | 0.00949 | 0.02232 | 0.00373 | 0.00408 | 0.01182 | 0.00298 | 0.00322 | 0.00833 |
| Beta 15 | x2x3 | 0.00033 | 0.00181 | 0.07972 | −0.00051 | −0.00123 | 0.03799 | −0.00081 | 0.00096 | 0.06871 |
| Beta 16 | x2x4 | 0.00000 | 0.00000 | −0.02389 | 0.00000 | 0.00000 | −0.01404 | 0.00000 | 0.00000 | −0.01702 |
| Beta 17 | x2x5 | 0.02283 | 0.02510 | 0.05574 | 0.02318 | 0.02548 | −0.01720 | 0.01858 | 0.02005 | 0.05375 |
| Beta 18 | x3x4 | −0.00816 | −0.00108 | 0.03197 | −0.00234 | −0.00238 | 0.01659 | −0.00398 | −0.00095 | 0.01111 |
| Beta 19 | x3x5 | 0.00000 | 0.00000 | −0.02829 | 0.00003 | 0.00000 | −0.01601 | 0.00000 | 0.00000 | −0.00895 |
| Beta 20 | x4x5 | 0.00082 | 0.00112 | 0.10402 | 0.03974 | 0.03661 | 0.33444 | 0.06728 | 0.06380 | 0.21738 |
| Real Variable yi = Yi× y_Range/2 + y_Mean i = W, J, D | ||||||||||
| y_Mean | 49.29504 | 9.91004 | 0.02896 | 42.24819 | 8.41802 | 0.03467 | 38.70456 | 7.62786 | 0.04325 | |
| y_Range/2 | 9.45013 | 2.17960 | 0.00726 | 8.92588 | 2.05787 | 0.01077 | 5.27049 | 1.23931 | 0.01053 | |
| 2nd Robot Arm | Objectives (Predicted by Model/ANSYS) | ||
|---|---|---|---|
| Weight W (kg) | Moment of Inertia J (kg. m2) | Deformation D (mm) | |
| (0) Baseline Design | --/40.26 | --/8.404 | --/0.0644 |
| (1) First Design Model-1 | 40.75/41.28 | 7.8078/8.0081 | 0.0311/0.0333 |
| (2) Renewal Design Model-2 | 32.69/33.89 | 6.6873/6.5079 | 0.0409/0.0501 |
| (3) Renewal Design Model-3 | 33.02/33.80 | 6.3328/6.4906 | 0.0491/0.0513 |
| Improvement %: ((3)/(0))−(1) | −18.0%/−16.1% | −24.7%/−22.8% | −23.8%/−20.3% |
| Model | Population Size | Time (sec) per Generation | Converge at Generation | Total Time (sec) to Convergence | All Process Time (sec) (Total Time + ANSYS) |
|---|---|---|---|---|---|
| ANSYS | 1035 | 31.050 | 3 | 93.150 | 93.150 |
| Model-1 | 1035 | 0.249 | 25 | 6.225 | 6.225+30 × 25 = 756.225 |
| Model-2 | 1035 | 0.325 | 22 | 7.150 | 7.15+30 × 22 = 667.15 |
| Model-3 | 1035 | 0.299 | 15 | 4.485 | 4.485+30 × 15 = 454.485 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hsiao, J.C.; Shivam, K.; Chou, C.L.; Kam, T.Y. Shape Design Optimization of a Robot Arm Using a Surrogate-Based Evolutionary Approach. Appl. Sci. 2020, 10, 2223. https://doi.org/10.3390/app10072223
Hsiao JC, Shivam K, Chou CL, Kam TY. Shape Design Optimization of a Robot Arm Using a Surrogate-Based Evolutionary Approach. Applied Sciences. 2020; 10(7):2223. https://doi.org/10.3390/app10072223
Chicago/Turabian StyleHsiao, J. C., Kumar Shivam, C. L. Chou, and T. Y. Kam. 2020. "Shape Design Optimization of a Robot Arm Using a Surrogate-Based Evolutionary Approach" Applied Sciences 10, no. 7: 2223. https://doi.org/10.3390/app10072223
APA StyleHsiao, J. C., Shivam, K., Chou, C. L., & Kam, T. Y. (2020). Shape Design Optimization of a Robot Arm Using a Surrogate-Based Evolutionary Approach. Applied Sciences, 10(7), 2223. https://doi.org/10.3390/app10072223






