Computational Characterization of Activities and Learners in a Learning System

Abstract

For a technology-based learning system to be able to personalize its learning process, it must characterize the learners. This can be achieved by storing information about them in a feature vector. The aim of this research is to propose such a system. In our proposal, the students are characterized based on their activity in the system, so learning activities also need to be characterized. The vectors are data structures formed by numerical or categorical variables such as learning style, cognitive level, knowledge type or the history of the learner’s actions in the system. The learner’s feature vector is updated considering the results and the time of the activities performed by the learner. A use case is also presented to illustrate how variables can be used to achieve different effects on the learning of individuals through the use of instructional strategies. The most valuable contribution of this proposal is the fact that students are characterized based on their activity in the system, instead of on self-reporting. Another important contribution is the practical nature of the vectors that will allow them to be computed by an artificial intelligence algorithm.

1. Introduction

In a dynamic digital environment, education needs to focus on models which are capable of facing current challenges and using the potential of the latest Information Technologies. The current environment, where concepts are no longer static and learners present different needs, necessitates changing the way learning is presented, to prepare students for a continuous learning and formation cycle, and to adapt to each of them. With the help of information technologies, we can create learning models that meet those needs, dynamically adapting to each individual situation, called smart learning systems.

To adapt and personalize the learning process to the learners, the system must identify their individual features and behavior, characterizing each individual as a concrete learner with concrete skills and needs. To do so, the system should create a learner model containing all the information needed to characterize each learner, such as their learning skills, their learning style or how they develop different cognitive levels and types of knowledge. Then, in order for the system to gather and understand these features, they must be presented in a computational way, through a set of variables building different feature vectors that characterize each learner. If we want the learner model to be really useful, the feature vector must include meaningful, measurable, discriminating and independent variables describing the individuals.

The aim of this research is to propose a feature vector that characterizes each individual learner, which is then provided to a smart learning system so that it can successfully detect their situation, context and needs along the learning process, and adapt to them.

To fulfill this objective, in Section 2, we first analyze the current background this research is situated in, focusing on describing the concept of smart learning and the different features of learners. Section 3 proposes a learning system that includes the aforementioned requirements and a computational characterization of the learners that are suited to this system. Finally, Section 4 presents the conclusions and future work to be carried out.

Our proposal makes two important contributions. First, it formalizes the characteristics of the learner that other authors have proposed as a computable vector, i.e., learning style, cognitive level and type of knowledge. And second, it proposes a method to calculate the learner’s characteristic vector from the features of the learning activities that the learner performs in the smart learning system.

2. Background

As a first step, to introduce our proposal for a characteristic vector, a review is presented of previous research on the concept of smart learning, the elements that make up such a system and the theories and previous developments that serve as a reference to identify the information that characterizes learners and activities.

A smart learning environment is defined as a learning model based on technology that is able to understand the context, needs and learning styles of the learners, and act dynamically to adapt to them and to improve their learning process [1,2]. This concept is related to those of adaptive learning and personalized learning, which are sometimes confused, although there are some nuances that differentiate them [3,4].

Systems that seek to enhance the learning process by adapting the lessons and activities that students carry out, according to the form and rhythm with which the students learn, are often called adaptive learning systems. Information technologies are now making it possible to develop such learning tools that are adapted to the needs of each learner [5]. In fact, the Horizon 2018 report [6] and the latest Gartner reports [7,8,9] place adaptive learning combined with artificial intelligence at the top of the list of technologies that are having an impact on education.

Personalized learning systems allow students to choose their own learning path. Again, current learning technologies are making possible the sustainable personalization of methodologies and contents; this was impossible in the past with the limited resources that a human teacher can offer [10]. The last smart algorithms are fed from the large set of data that current learning environments can collect and then they can help learners to fulfil their learning needs and to improve their knowledge skills [11].

2.1. Learner Model

A learner model is a compact definition of the features that characterize the individual as a learner. In this section, some of the main theories that attempt to characterize individuals as learners are presented.

The fact that each person has different skills and learns differently seems to be confirmed by different authors [12,13]. Among all the factors that affect the academic performance of a student, some authors consider that the individual characteristics of the person (intelligence, learning style, motivation, character, etc.) are the most important factor [14,15,16,17]. Thus, the intellectual capacity and motivation of the individual account for up to 50% of his/her performance, compared with factors that are considered to be external [16]. When designing a learning process, therefore, it is important to be aware that within the same group, there will be students with different learning styles, distinct types of intelligence and diverse motivations [18,19].

The so-called learning styles refer to a set of theories and methods defined in the literature that propose the classification of students according to the way they learn. Although there are many theories and they are very diverse, there are also many criticisms on this subject. The scientific basis of these theories has been widely criticized, in the sense that they often consider styles as separate compartments. However, learning implies the personal construction of learning strategies involving all our senses and a very diverse set of skills and abilities, and the effectiveness of most learning style models is not supported by sufficient evidence. In spite of these criticisms and without evaluating them, it is interesting to review some of the most renowned theories in order to try to understand the learning processes that students develop, and to try to characterize them. One of the best known theories is that of Gardner’s multiple intelligences [18,20]. This theory considers eight intelligences that imply different ways of learning: linguistic, logical-mathematical, visual-spatial, musical, bodily-kinesthetic, interpersonal, intrapersonal and naturalistic. The triarchic theory of intelligence [19] also classifies intelligence, in this case into three subtypes: componential (mental mechanisms), experimental (relations between the individuals and their experience) and contextual (how the componential processes are put into practice).

The VARK model of Fleming and Mills [21] categorizes the experiences of the students and teachers during learning into four overlapping sensory modalities: visual (the information is preferentially represented as maps, charts or symbols), aural (heard or spoken information is preferred), read/write (information represented by text is preferred) or kinesthetic (a preference of practical elements such as demonstrations, simulations or case studies).

There are other theories that aim to classify the learning style of students in the form of inventories. This is the case of Canfield’s Learning Styles Inventory [22] (comprising four learner styles, namely, social learners, independent learners, conceptual learners and applied learners) and the Approaches and Study Skills Inventory for Students [23] (three possible approaches to learning, namely, deep approach, strategic approach and surface approach). It is also the case of the Kolb Learning Style Inventory [24], with four identified styles, i.e., diverging, assimilating, converging and accommodating. An extension of this theory is the new Kolb Learning Style Inventory 4.0 [25], which is one of the theories considered in the definition of our model. It defines nine styles, i.e., initiating, experiencing, creating, reflecting, analyzing, thinking, deciding, acting and balancing. All the presented inventories collect the information about the learning styles through self-reported questionnaires that evaluate the attitudes of the students about learning and studying.

Learning styles are not the only internal factor that can affect learning. It has also been proved that many processes can strongly be affected by the circadian rhythms of each person [26].

All of this information, set in a structured way, containing every possible data about the learning process, the learner and their characteristics, constitutes a learner model, in order to adapt the system to the learner. The way this information is processed and the kind of information that is stored is what can divide learner models into one or more categories. To decide which type or types or learner models are more appropriate for a given learning system, an analysis of its requirements and practical situations must be carried out. Tadlaoui, Carvalho and Khaldi [27] conducted research aiming to compare the learner models of ten different real educational systems, analyzing each of those systems to define a proper way to build a learner model through a combination of existing ones. This comparison is mainly based on the how the learner model is constructed, its initialization and update. Later in the article, we will compare how these processes are carried out in those learner models with the one we propose.

2.2. Learning Activities and Their Characterization

A learning activity is a task that allows students to develop their learning. The task-centered principle is one of the key aspects of instructional theory [28], which states that instruction is better developed if a progression of increasingly complex, relevant tasks is used. In this section, some research that investigates how those activities should be structured is presented.

In order to model the instruction based on activities with progressive complexity, it is essential to first define the concept of activity difficulty. The concept of difficulty is not easy to define, although intuitively, we all understand that a task is difficult when performing it becomes laborious, requiring a significant effort, and in which skills with a certain complexity must be put into practice [29]. Attempts have been made to measure difficulty from different points of view, such as the analysis of the results of activities carried out by students [30], the estimation of difficulty by means of a linear regression analysis of user data [31] or the automatic generation of exercises with a certain established difficulty [32,33]. Whatever the case, one common factor to all these definitions can be established: difficulty can be considered as an “expense” which students must pay in terms of time and effort to successfully complete an activity; thus, effort is considered to be indirectly related to progress [34,35,36].

Besides difficulty, the other factors that determine the complexity of an activity are mainly the reasoning abilities and the cognitive level necessary for its successful completion. A widespread way of categorizing the levels of reasoning skills required during learning is Bloom’s Taxonomy [37]. It is possible, by extension, to use these levels to categorize learning activities according to the reasoning skills they foster. The six levels of the taxonomy are ordered so that the higher the level, the higher the level of abstraction required from the students. Bloom’s proposal encourages teachers to try to get students to move up the levels of taxonomy as they progress in their knowledge, encouraging complex and abstract thinking in students, as opposed to simple memorization. Bloom’s taxonomy has been revised several times, in particular by Anderson and Krathwohl in 2001 [38]. This review proposes two dimensions: the cognitive process dimension (in which verbs are used to label associated actions) and the knowledge dimension (whose labels are substantives that describe the knowledge students are expected to acquire or construct). These authors identify six categories for the cognitive process dimension (remember, understand, apply, analyze, evaluate and create) and four categories for the knowledge dimension (factual, conceptual, procedural, and metacognitive). A double-entry table is proposed with the categories of each dimension, so that it is possible to place each activity in a cell according to the cognitive process and knowledge to which it refers. Therefore, each activity is labeled with a verb and an object.

In addition to the comprehension and assimilation of concepts, there are other practical factors that have an important impact on effective and meaningful learning, namely, repetition, memorization, practice and application to real or realistic contexts [39,40]. The exercise of knowledge provides more meaningful and deeper learning, promotes autonomy and self-knowledge, and allows the concepts learned to be related to the student’s reality. In addition, it is important to use different types of activities, practice exercises with different levels of difficulty and complexity, encourage students to summarize what they have learned, and include real-world scenarios and simulations. The timing and sequencing of practice also affect learning, so that practice is often more effective when spaced out [41].

3. Proposal

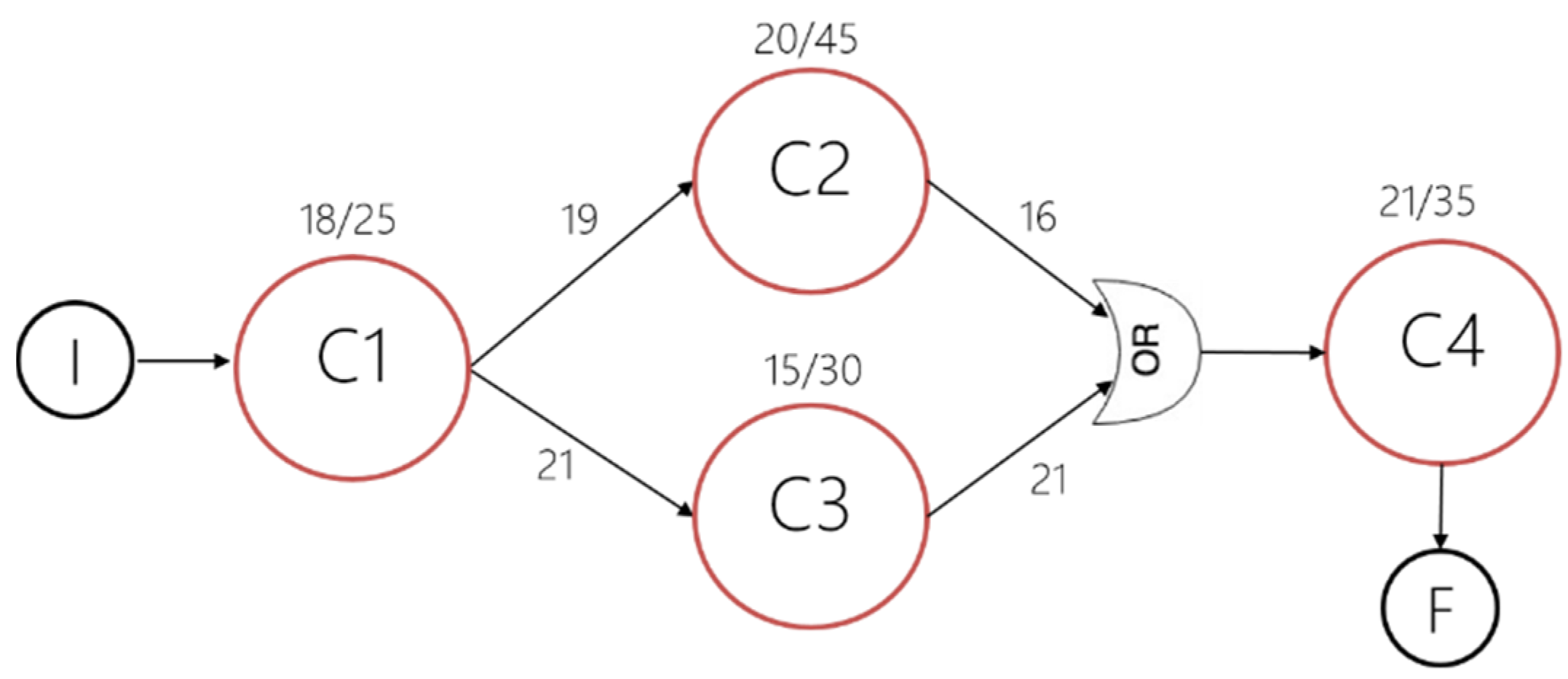
3.1. A smart Learning System

Based on the instructional model, we defined a smart learning system in which our proposal is enclosed. This system is centered around tasks, so that learners will complete different proposed tasks that are suitable for them to progress in the learning process [42,43]. In order to obtain a quality and accurate instructional model system, it must dynamically adapted to each individual [28].

Our proposed system is based on two main concepts, i.e., learning competence and learning activity [44,45,46,47]. The first one is described as the concepts and skills the learners will be achieving along the learning process [48]. In this case, the competences will be acquired progressively to make the student learn a skill before achieving another one, if necessary. Then, the concept of learning activity refers to a task used by the learner to develop one or more skills.

On this basis, our model is composed of three elements, i.e., the set of competences disposed to form a map, the collection of activities and the selection engine.

In the first one, called the competence map, the skills are set as a directed graph, connected between them in one direction only, marking the path the learner can follow from one skill to another (Figure 1). Locked at the beginning, these connections have a threshold associated that depends on the score of the source competence, so when it is reached, the connected skills will be unlocked.

Then, there is the collection of activities called the activity bag. Each of those activities is related to one or more competence, and presents different features depending on its representation and a different difficulty and a concrete learning style. When the learner achieves an activity, a score is obtained; internally, this can be computed in different ways depending on the activity type, and the related competence is updated with this value.

The learner will progress along the map by selecting any of the unlocked skills and completing the corresponding activity given by the system, moving forward along the different learning paths. These will be given by the structure of the map, as set by the teacher, who creates the competences, the relations between them, and therefore, the learning paths to follow, along with the learning activities, which means designing the learning model.

Finally, the selection engine is responsible for choosing a suitable activity any time a competence is selected by the learner, given their state in the learning process and their particular learning features. This means that all the logic of the smart learning process relies on this engine. The selection process will be run by a concrete algorithm which can be changed by the teacher if they deem it necessary, given the inputs of the available activities and their own features, the corresponding learner model containing their individual characteristics, and the chosen instruction strategy that conditions the way that selection is made. This process is shown in Figure 2:

3.2. Characterization of Learners and Activities

Learners and activities, as mentioned above, are characterized by a set of variables that make up the learner model and the activity model. Although each model contains its own variables, many of which are related, as will be explained below.

3.2.1. Definition of a Feature Vector

In a learning system, a learner model is a resource that stores all the learner’s features, such as their preferences or their behavior along the learning process [49]. It is the same for the activity model, which stores all the features of an activity, such as learning style or difficulty level. Both models will be processed by the system and interpreted by the selection engine to perform the corresponding selection at any time. Therefore, these models must be prepared to be correctly read and computed; that is why they are stored as a collection of features in the form of a vector. Each of these features is a measurable variable used to characterize a concrete aspect of an individual or a phenomenon. So, a feature vector will end up being a set of explanatory variables of a phenomenon being observed [50].

As feature vectors are used to characterize the individuals and make decisions by the corresponding algorithm depending on their values, each of those features must be meaningful, discriminating, independent and, as we mentioned before, measurable, so that they will have an interpretable value for the algorithms, which can be quantitative, such as integer or real, or qualitative, also named categorical, containing a value inside a predefined range [51]. A feature is meaningful if it makes sense to a human observer, that is, if the mathematical representation it assumes is interpretable by a person and if it corresponds to what it actually represents. In this case, the features presented are based on models proposed by researchers to explain the complex learning process. Although a mathematical representation is necessary, the basis on which this representation is developed is solid from the point of view of educational research. Those features must also be discriminating to be correctly differentiated into categories, and so to classify the learner. They must also be independent, which means that their values do not depend on other variables, eliminating redundant information and simplifying the task from a computational point of view.

In our model the variables are neither binary nor excluding, meaning that they are configured in the form of weights, so that you can have more or less of each feature, and having one feature does not imply no longer having another. These weights have been normalized and all of them have a value in an interval [0,100], where 0 indicates a total absence of that characteristic, and 100 a maximum value for it.

3.2.2. Learner and Activity Feature Vector

In our proposal, instead of characterizing the learner, e.g., classifying them in one or another concrete learning style, the learner model is built from the activities they do or the actions they perform in the learning system. So, in this case, features apply mainly to activities instead of to learners. As they achieve the proposed learning activities, the system establishes a cycle of updating of the leaner vector according to the corresponding activity vector (Figure 2).

Considering this, some characterization models that are originally defined for individuals have been adapted to be applied correctly to activities. On one hand, the activity feature vector is made up of the learning style applicable to the activity, the cognitive level and knowledge type it belongs to, and its difficulty. From this activity model, the learner model is extracted, built progressively as the student progress in the learning process and interacts with the system, and contains variables representing learning styles, cognitive levels, knowledge type, behavioral data and learning history. Defining both feature vectors in this way makes them ready to be computed automatically.

3.3. Variables Definition

In order for all the aforementioned variables that compose the feature vector to be computed, they must be measurable in order to be interpretable for the algorithms. From all of them, as we are to characterize the learner given the characterization of the activities, we need those variables in the activity vector that can be applied also to the learners, with the exception of difficulty, which is an essential one to be taken into account for each activity. One of them is learning style; among the different theories which seek to categorize learning styles, we will use the Kolb Learning Style Inventory 4.0 [36], due to the fact that this theory is the most suitable to define an activity, and so the learners through the activities they do. The other theories seek to define the learner concretely. There are two more, i.e., the cognitive level and knowledge type, both of which can be measured for learner and activity, respectively taken from the cognitive dimension and knowledge dimension of Bloom’s Taxonomy revision [38].

In the case of the learner model, it will contain all previous variables, with the exception of the activity difficulty, and one of its own, i.e., the time log. This variable will contain the history of the learner’s actions in the system, concretely, referring to the activities they have done, when and how, in order to obtain as much information about the learner as possible.

Finally, we will now analyze each variable and the interpretable value to assign to them.

3.3.1. Activity Vector Definition

Firstly, these variables will describe the activity feature vector, which will be a data structure formed by the following variables and set by the corresponding teacher when an activity is created:

• Activity difficulty. This value needs to be numerical so that it can be measured and leveled at any time. In order to get a high level of accuracy, the format will be an integer. And to assure that every activity has the same activity interval, this value will be normalized between 0 and 100.
• Learning style. In this case we need to use a categorical value, since it will contain the learning style the activity belongs to, according to the different types we defined previously. As it corresponds to the Kolb Learning Style Inventory 4.0 [25], this variable will contain the following subtypes: initiating, experiencing, creating, reflecting, analyzing, thinking, deciding, acting and balancing.
• Cognitive level. This variable will be represented with a categorical value with six subtypes that correspond to the cognitive process dimensions of Bloom’s Taxonomy, i.e., remember, understand, apply, analyze, evaluate and create.
• Knowledge type. As in the cognitive level, the knowledge type is classified into four subtypes using Bloom’s Taxonomy, i.e., factual, conceptual, procedural and metacognitive.

Therefore, we would have an activity feature vector, named A, which may be defined as follows:

A = {

  difficulty: integer,

  learningStyle: { Initiating, Experiencing, Creating, Reflecting, Analyzing, Thinking, Deciding, Acting, Balancing },

  cognitiveLevel: { Remember, Understand, Apply, Analyze, Evaluate, Create },

  knowledgeType: { Factual, Conceptual, Procedural, Metacognitive }

}

3.3.2. Learners’ Vector Definition

Then, the learner is also characterized with a feature vector, containing three of the variables from activity’s vector and some others specifics of the learner, having in total:

• Learning style. In the case of the learner, this variable will be represented with the same categorical values, but each of them will have an associated percentage value, so that instead of belonging just to a concrete subtype, there will be different levels of completion for each learning style subtype. This will be represented using a dictionary in which the keys are the corresponding subtype and the value is a floating point value representing the corresponding percentage.
• Cognitive level. The same happens with this variable, i.e., the learner will have a percentage value for each cognitive level subtype, using a dictionary.
• Knowledge type. Here, it will be a dictionary containing each knowledge type subtype with an associated percentage value.
• Time log. This variable contains the history of the learner’s actions in the system related to the activities. It will be an array of dictionaries, each of which will have the following keys:

  ○

  Starting date: date when the learner started the activity.

  ○

  Finishing date: date when the learner completed the activity.

  ○

  Starting time: the time when the activity started.

  ○

  Finishing time: the time when the activity was completed.

  ○

  Activity id: the id of the corresponding activity, using an integer value.

  ○

  Time spent: the effective time spent completing the activity, represented in seconds using a floating point value.

  ○

  Score: value computed in case the activity is completed. This value needs to be normalized, since every activity’s results are in the same range, despite the fact that each one can be measured in different ways. So, this value will be a floating point between 0.0 and 100.0.

L = {

  learningStyle: {

    initiating: float,

    experiencing: float,

    creating: float,

    reflecting: float,

    analyzing: float,

    thinking: float,

    deciding: float,

    acting: float,

    balancing: float

  },

  cognitiveLevel: {

    remember: float,

    understand: float,

    apply: float,

    analyze: float,

    evaluate: float,

    create: float

  },

  knowledgeType: {

    factual: float,

    conceptual: float,

    procedural: float,

    metacognitive: float

  },

  timeLog: [

    { startingDate: Date },

    { finishingDate: Date },

    { startingtime: Time },

    { finishingtime: Time },

    { activityId: int },

    { timeSpent: float },

    { score: float }

  ]

}

3.3.3. Learners’ Vector Update

When the learner completes an activity, a value is computed, in a way that can vary according to the type of the activity; to be able to measure how the learner has achieved the activity, we need a numerical value. This obtained result is used to update the learner’s feature vector based on the vector if the activity that has just been done. It is, as we said before, a cycle of updating the feature vectors of the learners as they complete the learning activities. In that way, a learner will be characterized by the activities which he/she has done.

In this process, the learner’s feature vector will be updated variable by variable in a different way, since each variable needs to be computed according to different factors. But there will be a common factor that affects all the variables, i.e., the time. While the learner goes forward in the learning process, their skills develop, their experience increases and so their features also change. Therefore, a recently done activity is more relevant than one that was done some time ago.

This is mainly important in the case of variables whose values represent a percentage of completion, such as learningStyle, cognitiveLevel and knowledgeType. These variables are represented by the percentage that each of their own subtypes is developed, so each time a new activity of that concrete subtype is completed, the corresponding value is updated using the resulting evaluation of the new activity, hereafter called e. To take the time aspect into account, we firstly introduce a time-dependent variable which may be understood as the instant an activity has been completed, following a chronological order, called t. An activity at instant t was performed before one at instant t+1. Also, we use a reduction factor λ with a value between 0 and 1, which represents how the weight of older activities decreases.

The computation of the new value for each corresponding subtype is named v_x, where v corresponds to the value of the subtype and x to the subtype affected. This value depends on the instant t in which the current activity was performed, representing v_x^(t) as the value for the subtype x obtained in an instant t, and on all the previous values computed for each activity belonging to the same subtype. It is performed in a recursive way, given e(a_i)^(t) as the value obtained for an activity a_i made in the instant t. In the case of the first instant ( t= 1), the new value v_x is the same as the recently obtained one, so:

$$v_x{}^{\left(1\right)}=e{\left(a_i\right)}^{\left(1\right)}$$

(1)

Then, any v_x computed in the instant t is obtained as follows:

$$v_x{}^{\left(\mathrm{t}\right)}=\frac{v_x{}^{\left(\mathrm{t}-1\right)}·\left(t-1\right)· \lambda +e{\left(a_i\right)}^{\left(t\right)} }{\left(t-1\right)· \lambda +1}$$

(2)

Therefore, when the learner completes an activity, his/her feature vector variables, i.e., learning style, cognitive level and knowledge type, will use this formula to update their values, considering only the subtypes corresponding to the activity’s feature vector. But in order to avoid only one subtype of any of those variables being updated, we use the same formula for the rest of them, but with a value e(a_i)^(t) = 0. In this way, the value of the corresponding subtype will decrease when it is not being developed. As such, besides reducing the weights of all the previously performed activities of a concrete subtype, the value of the other subtypes will be also affected, aiming to take the time factor into account for them.

For example, given an activity a₁ vector A = {difficulty = 5.6, learningStyle = ”Creating”, cognitiveLevel = ”Remember“, knowledgeType = ”Conceptual”}, that has been completed with a result e(a₁) = 76, the following variables of the learner vector L will be modified:

• learningStyle. The value corresponding to Creating subtype will be updated using the previous formula, including the current activity and all the previous ones that have Creating as the value of the learningStyle variable in their feature vector. For the rest of the subtypes, the same formula will be used, but with the value e(a₁) = 0 instead of 76.
• cognitiveLevel. In this case, the Remember subtype will modify its value in the given e(a₁) = 76 and the rest of the subtypes with e(a₁) = 0.
• knowledgeType. As in the previous cases, this variable will update its Conceptual subtype value using the current value of e(a₁) and the rest of the subtypes with e(a₁) = 0.

The variable that is exclusive to the learner’s vector, timeLog, is updated any time the learner performs an activity. It is important to consider that a learner can complete an activity in different periods of time, meaning that they can start on one day, stop, exit the system and return to complete it on another day. That’s why it is important to store starting and finishing dates and times. So, startingDate and startingtime will describe the moment the learner starts an activity, and finishingDate and finishingTime will describe when they complete it. timeSpent will be computed only while the learner is performing the activity, and will be set when they finish it. Finally, given an activity a_i, activityId = i and score = e(a_i).

3.4. Use Case

After defining the variables which make up the activity and learner model, and showing how the last one is updated during the learning process, we explain how those variables intervene in the learning process. Teachers use instructional strategies, which are a set of approaches, models, techniques and methods, to optimize the learning process of their students. These are given to the system so that it can select the right activities to be provided to the learners [52]. An instructional strategy is structured in dimensions which reflect a specific aspect of the strategy from which we want to obtain a result. For this example, we will use the Learning Styles dimension.

This dimension aims to reinforce some or all of the student’s learning styles, or to use them to optimize learning [21,22,23,25]. Within this dimension, there can be a variety tactic to select activities of different leaning styles, an efficiency one to select activities according to the main developed learning styles of the learner, or a reinforcement tactic to select the less developed learning styles.

Considering this dimension, the system will mainly consider two variables inside the feature vectors: the activityDifficulty inside the activity vector and the learningStyle inside both the learner and activity vectors. The teacher can change the selected tactic at any time for a given learner as they progress in the learning process; thereby, the learner model is continuously being updated.

For this example, we will use some simulated data with already computed scores in a concrete point of a learning course. Let’s suppose that a reinforcement tactic is selected, and at some point, the vector of the corresponding learner has the following state for the learningStyle:

learningStyle: {

    initiating: 76.5,

    experiencing: 78.6,

    creating: 85.3,

    reflecting: 51.9,

    analyzing: 68.3,

    thinking: 78.5,

    deciding: 82.25,

    acting: 53.8,

    balancing: 89.3

  }

In this case, the system will prioritize the selection of activities whose feature vector has the value learningStyle = ”Reflecting” or learningStyle = ”Acting”, since they are less developed. If the learner successfully completes activities with this features, their vector will update, and those values will increase. Let’s now suppose that after a while, the learner’s vector variable looks like this:

learningStyle: {

    initiating: 74.4,

    experiencing: 76.6,

    creating: 84.2,

    reflecting: 71.2,

    analyzing: 52.3,

    thinking: 75.8,

    deciding: 79.5,

    acting: 67.8,

    balancing: 83.3

  }

We can see that the values have been updated. Now, the main selected activities will be those with learningStyle = ”Reflecting” as a value in their vector.

3.5. Learner Model Comparison

After explaining the functionality of our learner model, we compared it with the aforementioned alternative learner models, which were applied to ten real educational systems [27], focusing on the initialization and update of the learner model, since these are two crucial steps for the adaptive process in a learning system.

In both cases, the main difference between the proposed model and the others is that our approach is based on learner behavior throughout the learning process, as reflected in the activities or actions that learners perform in the system, instead of classifying them according to a certain style.

Therefore, in the initialization of our learner model, we do not use any preliminary tests to determine the initial level of knowledge of each learner or classify them into some predefined category, like the stereotypes which are applied in the alternative learner models. We simply set a common intermediate value for all learners, which will be modified as the learner progresses, modelling itself to the extracted characteristics. Also, if the learner has completed some previous courses, the system can take the final value of their model in the former course as the initial value for the next one. In

Table 1. Comparison between the initialization process of a learner model between alternative systems and our proposal. The original table and comparison is based on research by Tadlaoui, Carvalho and Khaldi [27].

Initialization	AHA	ADAPTWEB	AVANTI	ANATOMT	AHM	INSPIRE	HYPADAPTER	ELM-ART	HYNECOS	METADOC	PROPOSAL
Pretests		X	X					X
Previous Cases	X						X		X		X
Stereotypes			X	X		X				X
By Default										X
Machine Learning		X				X		X			X
Intermediate Value											X

, a comparison is presented of the different methods for initializing the learner models.

In the case of the update of the learner model, our proposed model and some of the alternatives have one main aspect in common, i.e., that interaction between the learner and the system can change some of the characteristics of the learner. However, most of them classify learners into predefined stereotypes, modifying just some personal aspects. In this respect the proposed learner model is distinct: the whole learner model can change, including both personal and learning characteristics, depending on the learner actions, their behavior within the system or the activities they complete.

4. Conclusions

The aim of this paper was to present a feature vector to characterize activities and learners. This is a crucial step to enable the construction of an Automated Adaptive Learning System, which can provide students with the most suitable learning path according to their characteristics, i.e., learning style and rhythm, behavior and previous performance. There are three main contributions:

Firstly, the proposed feature vectors are computable. The variables included in the vectors are formally defined based on numerical or categorical values that can serve as inputs to an activity selection engine based on artificial intelligence. Therefore, they are measurable variables, the first property that a feature variable must fulfill in order to be treated by a computer. In addition, the selection of features was made based on a detailed study of the literature on the characterization of learners and from instructional designs. This ensures that the features are meaningful, thus guaranteeing usefulness from a pedagogical point of view. The question of whether the variables are discriminant and independent remains to be resolved. However, the variety of types and attributes allows us to assume that these properties will also be met. A further study will focus on these two aspects.

Secondly, the contribution that we consider most valuable is the fact that the students are characterized based on their activity in the system, instead of on self-reporting, which basically collects their opinions. From our point of view, the advantages of this approach are threefold: on the one hand, characterization is somehow objective, since it does not depend on the personal opinion of the learner or of a pedagogical expert, but on the actions of the learner in the system and on observations of their behavior; on the other hand, the criticism that learning style theories have received is avoided, since the learner is not directly characterized, but the characterization is a consequence of his/her behavior; this is objectively collected by the automatic system. Finally, we take a step toward the automation and generalization of the personalization process, making it independent of the action of experts who cannot reach the entire population of learners, and who generally act on very small groups.

The third contribution has to do with the eminently practical nature of the proposed characterization. The vectors are computable, and the mathematical formulation makes it possible to immediately construct the algorithms that put the proposed system into practice.

Finally, a use case was presented to illustrate how variables can be used to achieve different effects on learning among individuals. The instructional strategies as presented, allow the teaching process to be automated in the most routine aspects, but the decisions and the way to guide the student in the process are always the responsibility of the teacher.

Our proposal must still be validated in a real context, i.e., in an automated system with the participation of students and in a specific course. This is our current line of work. Therefore, we consider as future work the incorporation of these vectors and of the instructional strategies to our current learning system and the carrying out of intensive tests, as well as the study of the results.