Survey of Network Coding Based P2P File Sharing in Large Scale Networks
Abstract
1. Introduction
2. BitTorrent-Like Systems and Network Coding Background
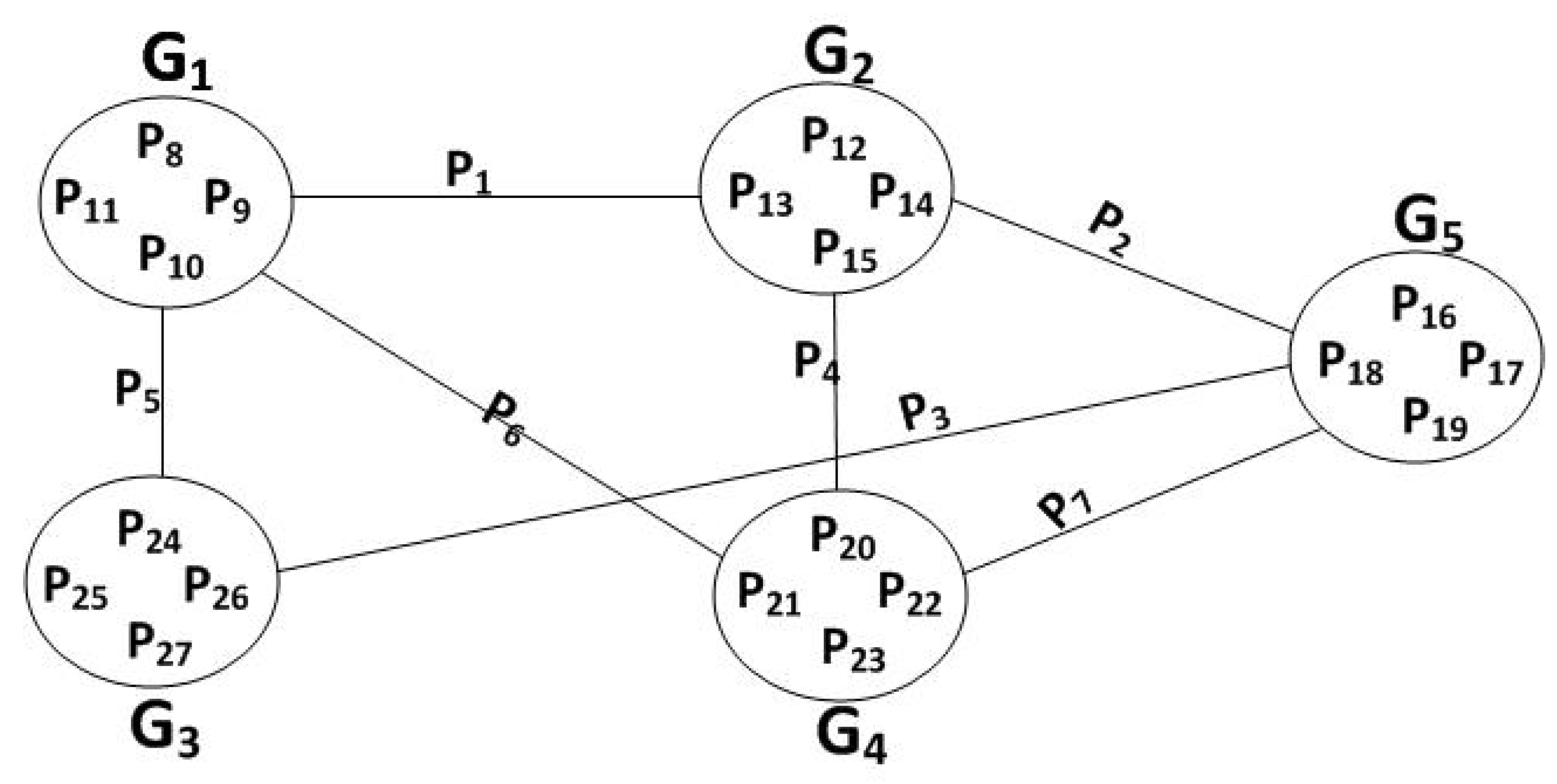
2.1. How BitTorrent-Like Systems Work
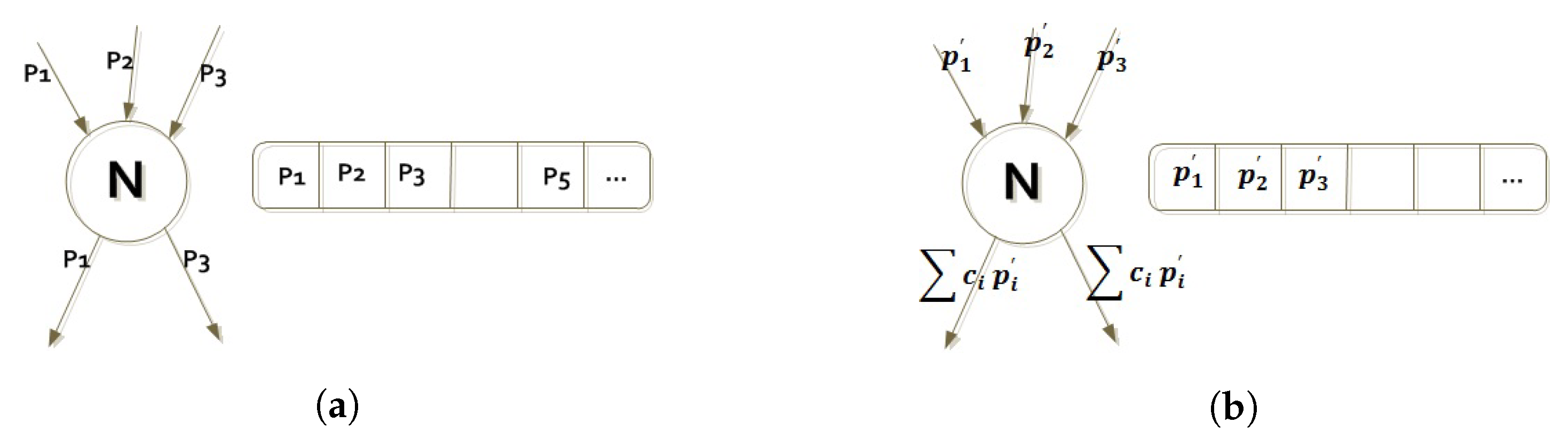
2.2. Network Coding Overview
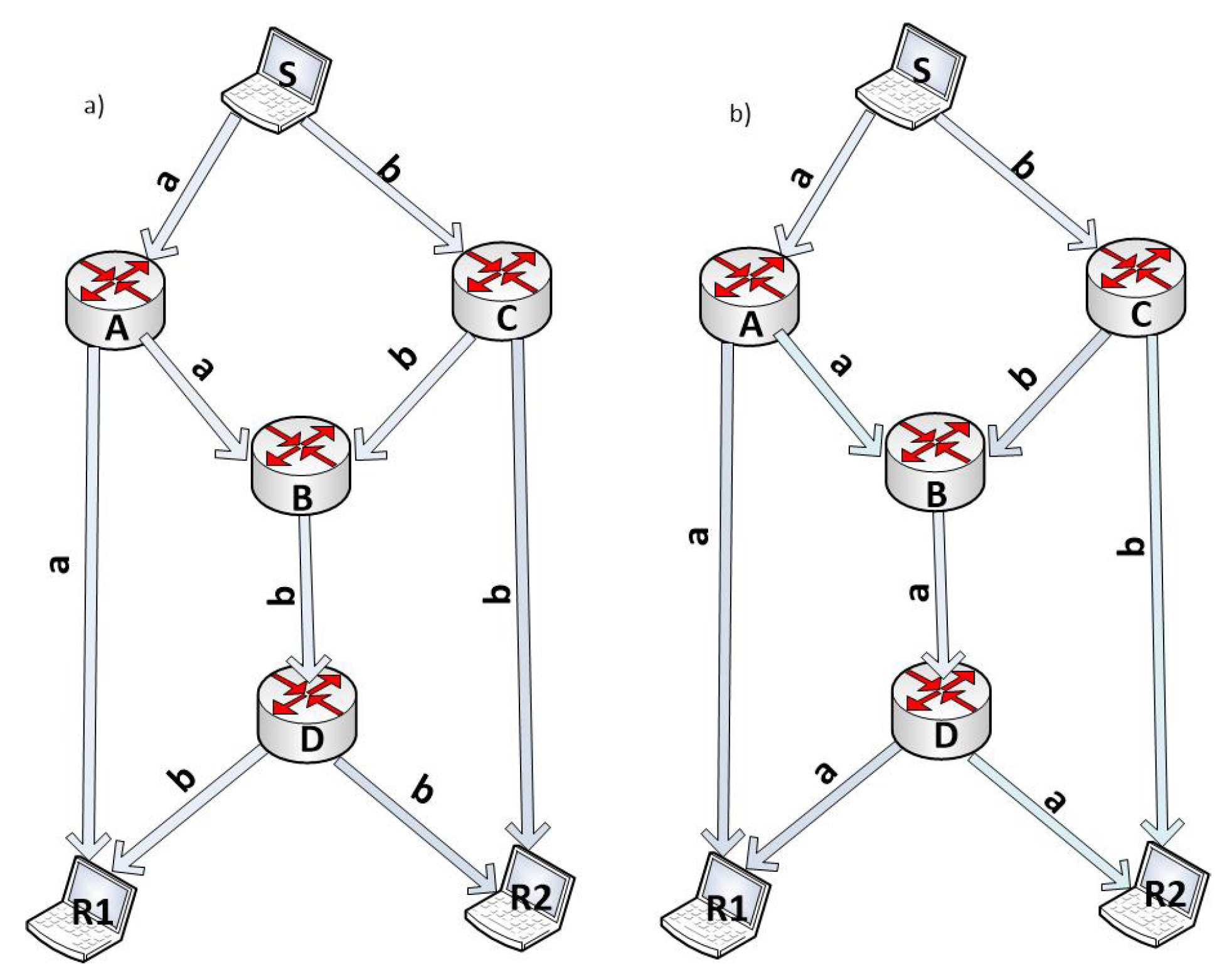
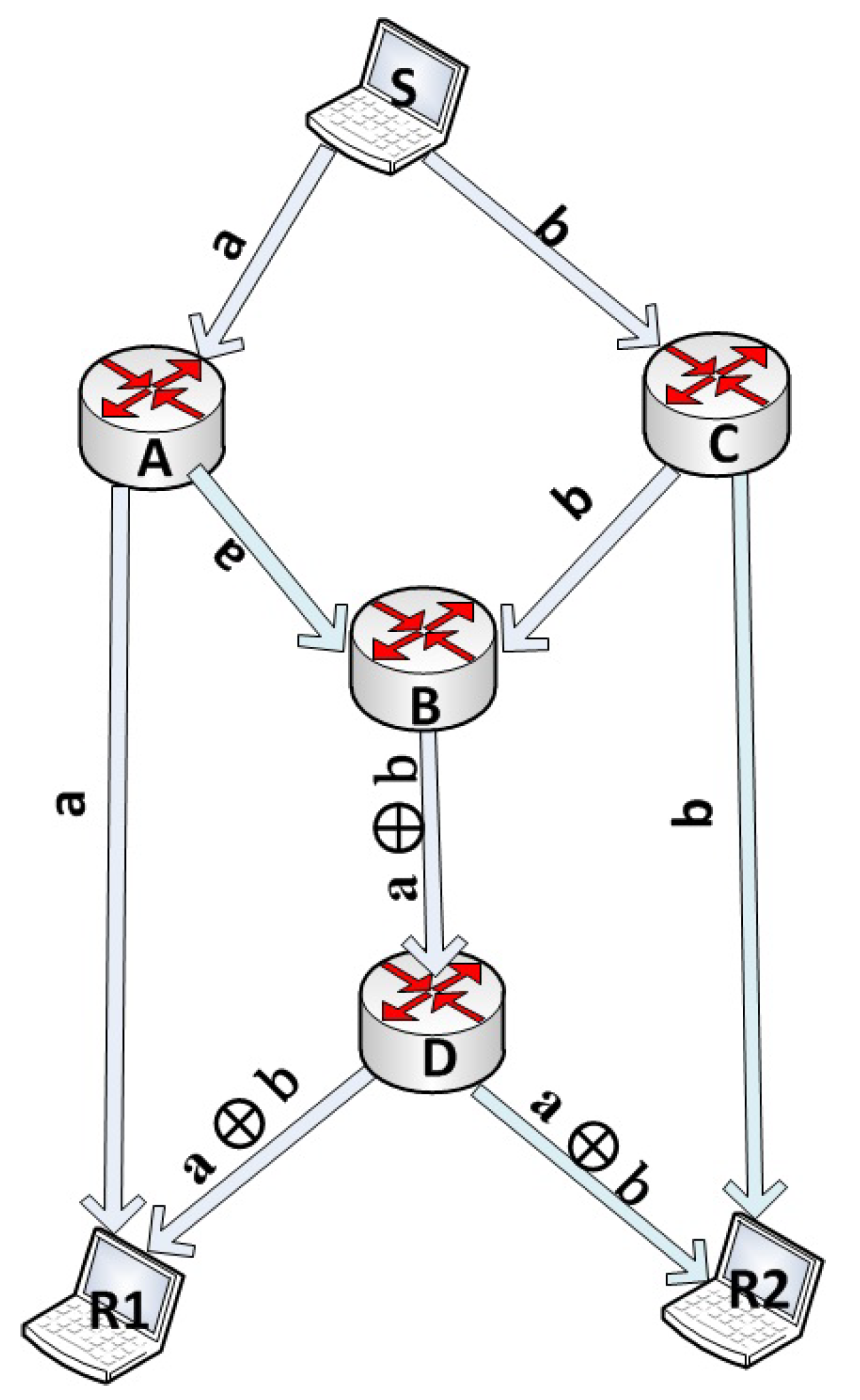
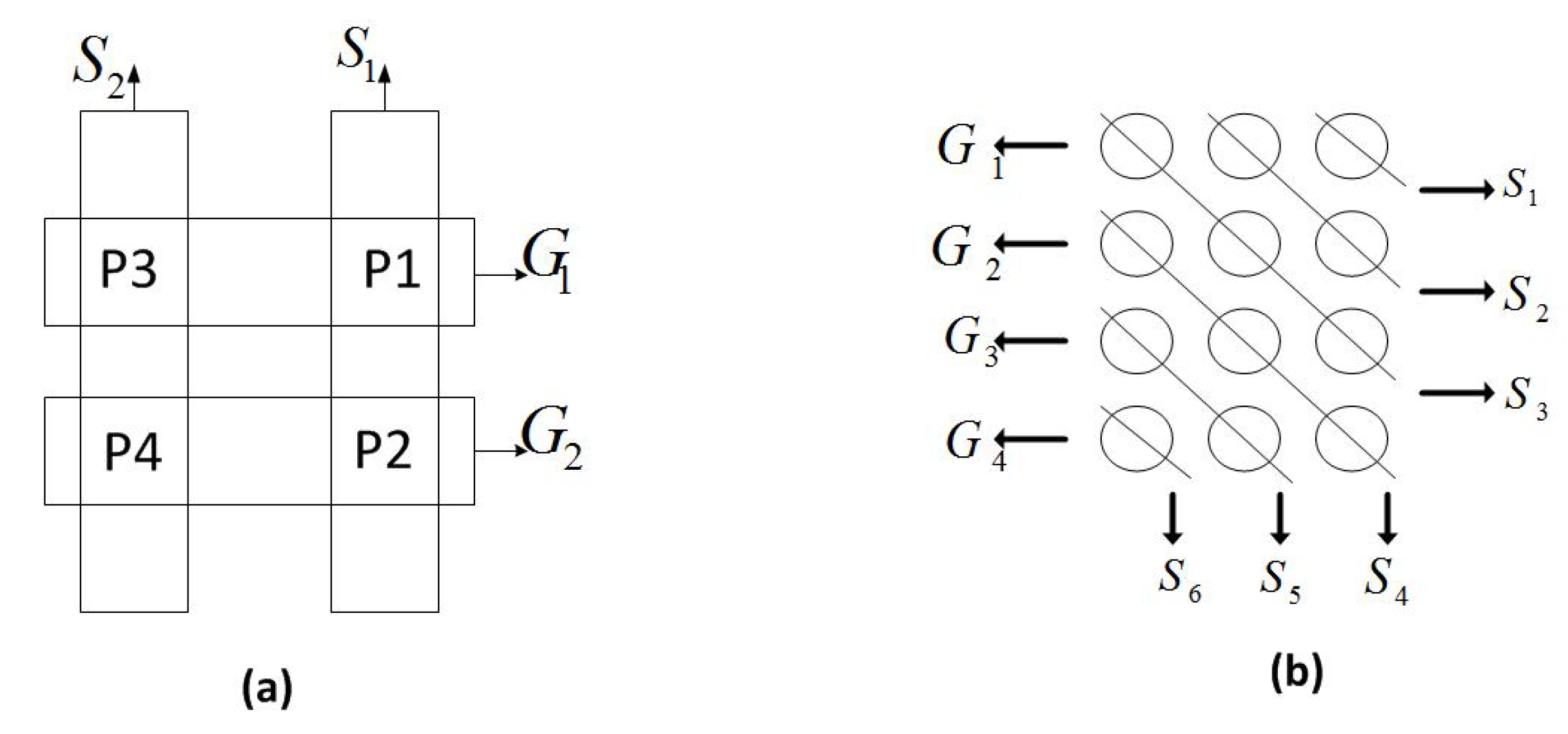
2.3. The Butterfly Example
2.4. Detailed Network Coding Tutorial for P2P File Sharing Systems
- Addition and Subtraction: The sum of two elements is computed according to (2):Addition and subtraction modulo 2 are the same. Moreover, addition modulo 2 is simply equivalent to bitwise XOR.
- Multiplication: two elements of are multiplied using the standard polynomial multiplication rule. However, if the product polynomial has a degree higher than , then it has to be reduced. Irreducible polynomials, which are roughly comparable to prime numbers in such that their only factors are 1 and the polynomial itself, are used for the modulo reduction. Let be an irreducible polynomial over ; then, the multiplication of two elements is done as in (3):To find the product of and in , we begin by doing normal polynomial multiplication: . Since , the irreducible polynomial is needed and thus we calculate .
- Inversion: Every Element (except 0) in has an inverse. The inverse of a nonzero element is defined as in (4):For example, in and , is the inverse of since .
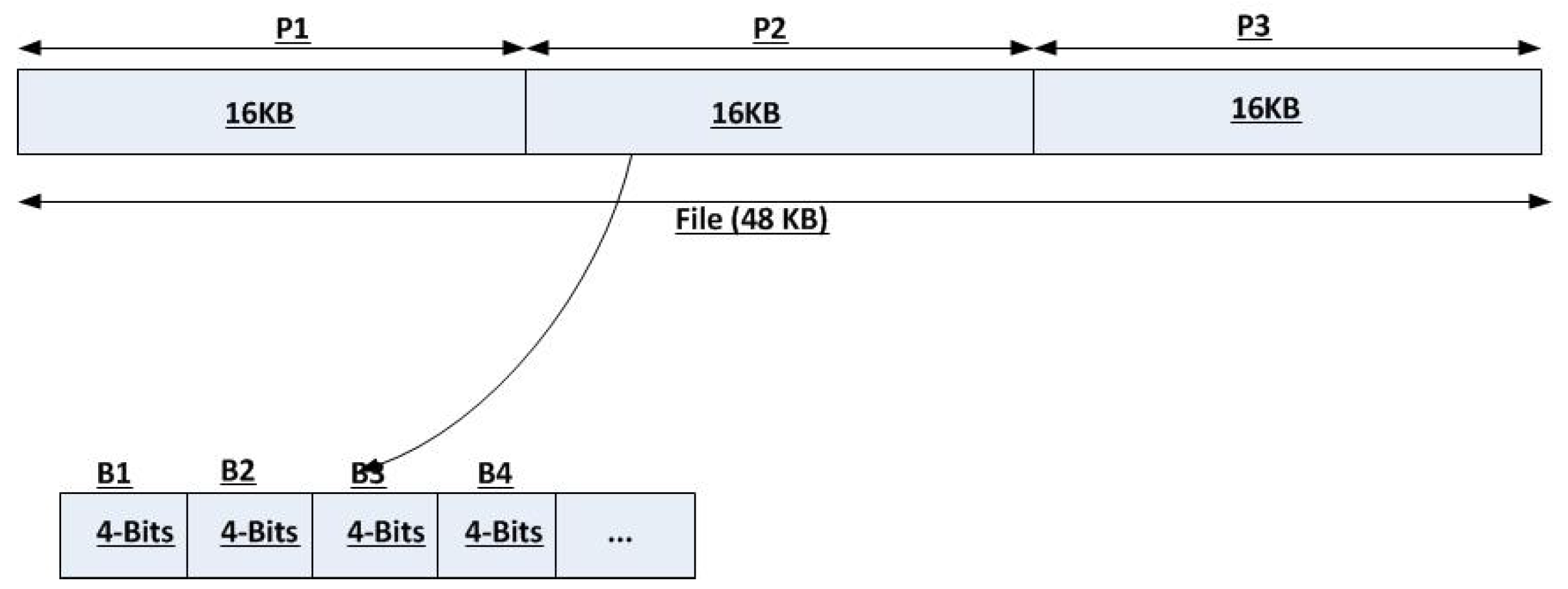
- 1st Step: The seeder decomposes the file into two 6-bit pieces (100011, 110110).
- 2nd Step: For encoding over , we should decompose each piece into two 3-bits blocks: (100, 011), and (110, 110).
- 3rd Step: Interpret each block as element (using (1)); then, we have , and .
- 4th Step: Since we have two plain pieces, we need two coded pieces. Randomly draw coefficients from and multiply them by the blocks. Assuming we first draw , , then the first block of the first encoded piece is (011), and the second block is (000). Now, is completely encoded and ready to be shared. Next, to get the second encoded piece, we randomly draw two additional coefficients, say and generate , and (100). Thus, is completely encoded and ready to be shared.
- 5th Step: The sender shares the encoded pieces along with their coefficients , and . This is algebraically represented as:where A is the coefficients matrix, B is the original blocks vector, and C is the encoded blocks vector.
- 6th Step: Upon receiving the encoded pieces with their coefficients, the receiver should solve the previous matrices system to recover the original blocks and thus the original pieces. This is achieved by using the formula: . First, find the determinant of the coefficients matrix as shown in (8):Since , the system is solvable:This leads to reconstructing the blocks and thus the pieces: and .
- 7th Step: Simply interpret the pieces’ blocks as binary presentation and link the pieces together to reconstruct the original file.
2.5. Network Coding Challenges
3. Related Works
4. Network Coding Based P2P File Sharing Systems
4.1. Full Network Coding
4.2. Sparse Network Coding
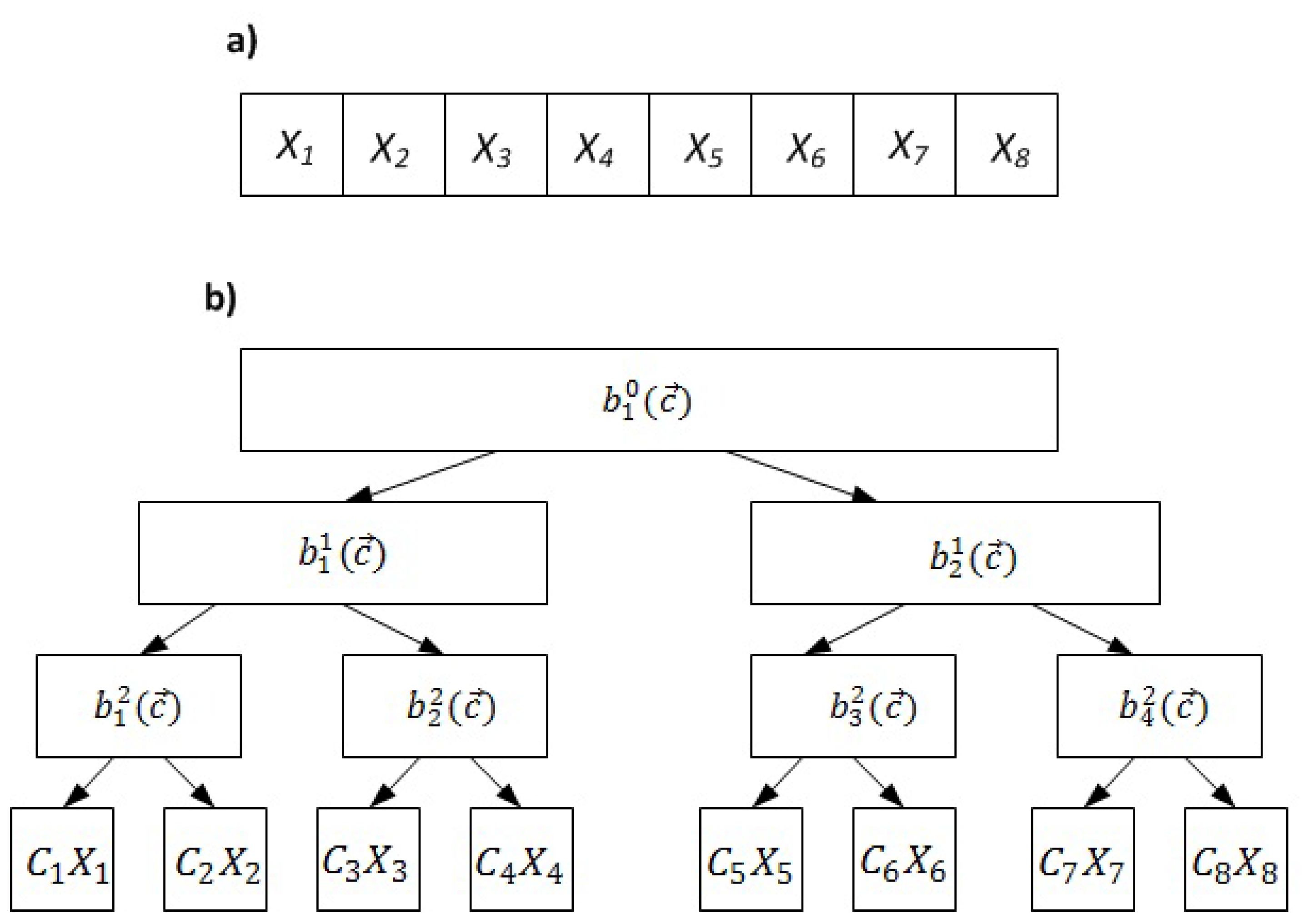
4.3. Generation Based Coding
4.4. Combined Network Coding
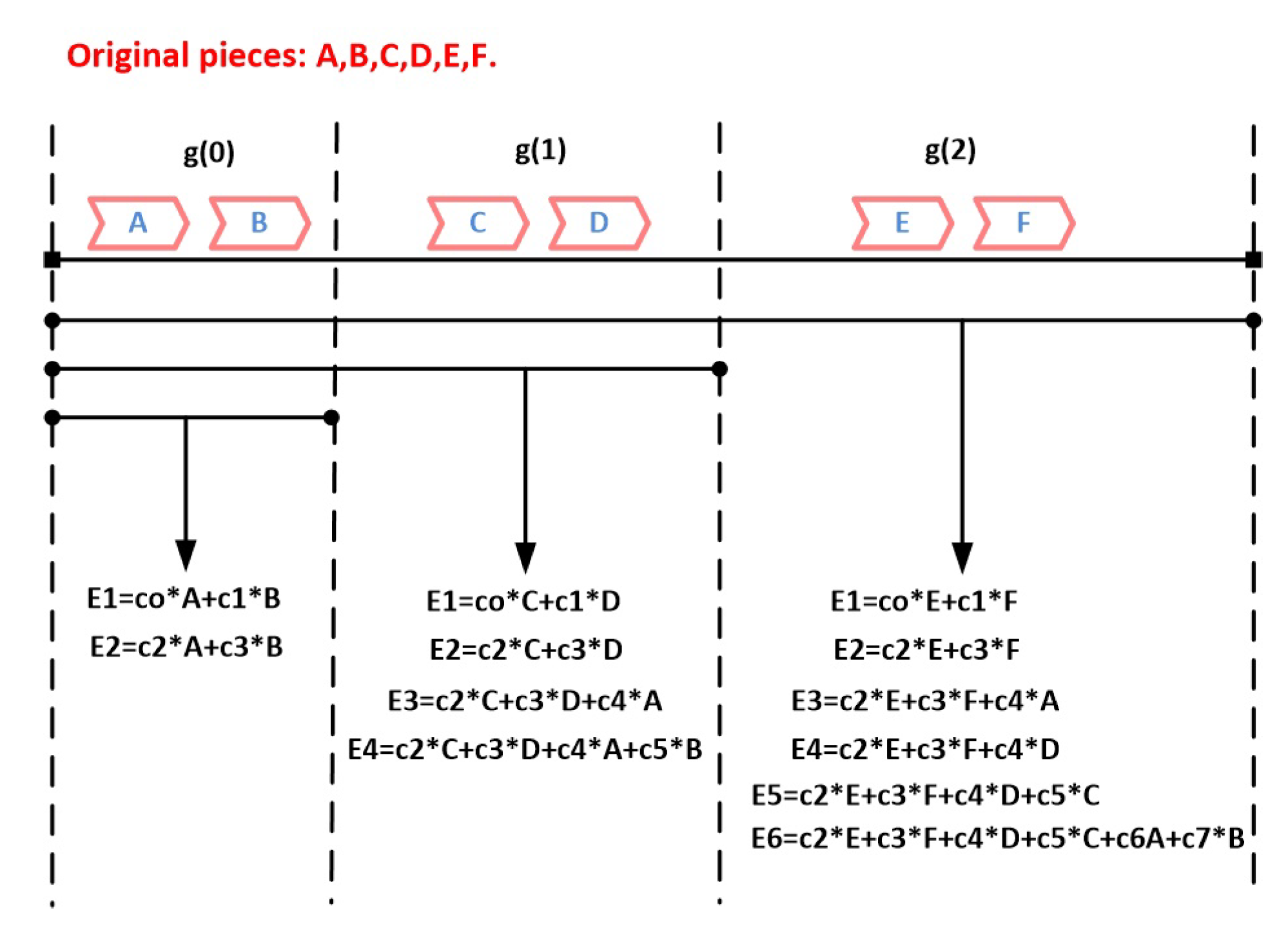
4.5. Multi-Generation Mixing (MGM) and Overlapping Network Coding
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Stoica, I.; Morris, R.; Liben-Nowell, D.; Karger, D.R.; Kaashoek, M.F.; Dabek, F.; Balakrishnan, H. Chord: A scalable peer-to-peer lookup protocol for internet applications. IEEE/ACM Trans. Netw. (TON) 2003, 11, 17–32. [Google Scholar] [CrossRef]
- Nwebonyi, F.N.; Martins, R.; Correia, M.E. Reputation based approach for improved fairness and robustness in P2P protocols. Peer- Netw. Appl. 2019, 12, 951–968. [Google Scholar] [CrossRef]
- Pacifici, V.; Lehrieder, F.; Dán, G. Cache bandwidth allocation for P2P file-sharing systems to minimize inter-ISP traffic. IEEE/ACM Trans. Netw. (TON) 2016, 24, 437–448. [Google Scholar] [CrossRef]
- Cohen, B. The BitTorrent Protocol Specification. 2008. Available online: http://bittorrent.org/beps/bep_0003.html (accessed on 24 March 2020).
- Lareida, A.; Bocek, T.; Waldburger, M.; Stiller, B. RB-tracker: A fully distributed, replicating, network-, and topology-aware P2P CDN. In Proceedings of the IFIP/IEEE International Symposium on Integrated Network Management (IM 2013), Ghent, Belgium, 27–31 May 2013; pp. 1199–1202. [Google Scholar]
- Wu, D.; Dhungel, P.; Hei, X.; Zhang, C.; Ross, K.W. Understanding peer exchange in bittorrent systems. In Proceedings of the IEEE Tenth International Conference on Peer-to-Peer Computing (P2P), Delft, The Netherlands, 25–27 August 2010; pp. 1–8. [Google Scholar]
- Hecht, F.V.; Bocek, T.; Stiller, B. B-tracker: Improving load balancing and efficiency in distributed p2p trackers. In Proceedings of the IEEE International Conference on Peer-to-Peer Computing, Kyoto, Japan, 31 August–2 September 2011; pp. 310–313. [Google Scholar]
- Neglia, G.; Reina, G.; Zhang, H.; Towsley, D.; Venkataramani, A.; Danaher, J. Availability in bittorrent systems. In Proceedings of the IEEE INFOCOM 2007-26th IEEE International Conference on Computer Communications, Barcelona, Spain, 6–12 May 2007; pp. 2216–2224. [Google Scholar]
- Fry, C.P.; Reiter, M.K. Really Truly Trackerless BitTorrent; School of Computer Science, Carnegie Mellon University, Tech. Rep: Pittsburgh, PA, USA, 2006; pp. 6–148. [Google Scholar]
- Navimipour, N.J.; Milani, F.S. A comprehensive study of the resource discovery techniques in Peer-to-Peer networks. Peer- Netw. Appl. 2015, 8, 474–492. [Google Scholar] [CrossRef]
- Luo, J.; Xiao, B.; Bu, K.; Zhou, S. Understanding and improving piece-related algorithms in the BitTorrent protocol. IEEE Trans. Parallel Distrib. Syst. 2013, 24, 2526–2537. [Google Scholar] [CrossRef]
- Hu, Y.; Dong, D.; Li, J.; Wu, F. Efficient and incentive-compatible resource allocation mechanism for P2P-assisted content delivery systems. Future Gener. Comput. Syst. 2013, 29, 1611–1620. [Google Scholar] [CrossRef]
- Chiu, D.M.; Yeung, R.W.; Huang, J.; Fan, B. Can network coding help in P2P networks? In Proceedings of the 4th International Symposium on Modeling and Optimization in Mobile, Ad Hoc and Wireless Networks, Boston, MA, USA, 26 February–2 March 2006; pp. 1–5. [Google Scholar]
- Chiang, J.L.; Tseng, Y.Y.; Chen, W.T. Interest-Intended Piece Selection in BitTorrent-like peer-to-peer file sharing systems. J. Parallel Distrib. Comput. 2011, 71, 879–888. [Google Scholar] [CrossRef]
- Fragouli, C.; Le Boudec, J.Y.; Widmer, J. Network coding: An instant primer. ACM SIGCOMM Comput. Commun. Rev. 2006, 36, 63–68. [Google Scholar] [CrossRef]
- Terelius, H.; Johansson, K.H. Peer-to-peer gradient topologies in networks with churn. IEEE Trans. Control Netw. Syst. 2018, 5, 2085–2095. [Google Scholar] [CrossRef]
- Feng, C.; Li, B. Network coding for content distribution and multimedia streaming in peer-to-peer networks. In Network Coding; Elsevier: Amsterdam, The Netherlands, 2012; pp. 61–86. [Google Scholar]
- Cai, Q.C.; Lo, K.T. Two blocks are enough: On the feasibility of using network coding to ameliorate the content availability of bittorrent swarms. IEEE Trans. Parallel Distrib. Syst. 2012, 24, 1682–1694. [Google Scholar] [CrossRef]
- Huang, K.; Wang, L.; Zhang, D.; Liu, Y. Optimizing the BitTorrent performance using an adaptive peer selection strategy. Future Gener. Comput. Syst. 2008, 24, 621–630. [Google Scholar] [CrossRef]
- Ahlswede, R.; Cai, N.; Li, S.Y.; Yeung, R.W. Network information flow. IEEE Trans. Inf. Theory 2000, 46, 1204–1216. [Google Scholar] [CrossRef]
- Katti, S.; Rahul, H.; Hu, W.; Katabi, D.; Médard, M.; Crowcroft, J. XORs in the air: Practical wireless network coding. In ACM SIGCOMM Computer Communication Review; ACM: New York, NY, USA, 2006; Volume 36, pp. 243–254. [Google Scholar]
- Chen, Y.J.; Wang, L.C.; Wang, K.; Ho, W.L. Topology-aware network coding for wireless multicast. IEEE Syst. J. 2018, 12, 3683–3692. [Google Scholar] [CrossRef]
- Jiang, D.; Xu, Z.; Li, W.; Chen, Z. Network coding-based energy-efficient multicast routing algorithm for multi-hop wireless networks. J. Syst. Softw. 2015, 104, 152–165. [Google Scholar] [CrossRef]
- Czap, L.; Fragouli, C.; Prabhakaran, V.M.; Diggavi, S. Secure network coding with erasures and feedback. IEEE Trans. Inf. Theory 2015, 61, 1667–1686. [Google Scholar] [CrossRef]
- Matsumoto, R.; Hayashi, M. Universal secure multiplex network coding with dependent and non-uniform messages. IEEE Trans. Inf. Theory 2017, 63, 3773–3782. [Google Scholar] [CrossRef]
- He, H.; Li, R.; Xu, Z.; Xiao, W. An efficient ECC-based mechanism for securing network coding-based P2P content distribution. Peer- Netw. Appl. 2014, 7, 572–589. [Google Scholar] [CrossRef]
- He, M.; Gong, Z.; Chen, L.; Wang, H.; Dai, F.; Liu, Z. Securing network coding against pollution attacks in p2p converged ubiquitous networks. Peer- Netw. Appl. 2015, 8, 642–650. [Google Scholar] [CrossRef]
- Xie, D.; Peng, H.; Li, L.; Yang, Y. An efficient privacy-preserving scheme for secure network coding based on compressed sensing. AEU-Int. J. Electron. Commun. 2017, 79, 33–42. [Google Scholar] [CrossRef]
- Li, T.; Chen, W.; Tang, Y.; Yan, H. A homomorphic network coding signature scheme for multiple sources and its application in IoT. Secur. Commun. Netw. 2018, 2018, 6. [Google Scholar] [CrossRef]
- Ho, T.; Médard, M.; Koetter, R.; Karger, D.R.; Effros, M.; Shi, J.; Leong, B. A random linear network coding approach to multicast. IEEE Trans. Inf. Theory 2006, 52, 4413–4430. [Google Scholar] [CrossRef]
- Li, S.Y.; Yeung, R.W.; Cai, N. Linear network coding. IEEE Trans. Inf. Theory 2003, 49, 371–381. [Google Scholar] [CrossRef]
- Etzion, T.; Wachter-Zeh, A. Vector network coding based on subspace codes outperforms scalar linear network coding. IEEE Trans. Inf. Theory 2018, 64, 2460–2473. [Google Scholar] [CrossRef]
- Sun, Q.T.; Yang, X.; Long, K.; Yin, X.; Li, Z. On vector linear solvability of multicast networks. IEEE Trans. Commun. 2016, 64, 5096–5107. [Google Scholar] [CrossRef]
- Ebrahimi, J.; Fragouli, C. Algebraic algorithms for vector network coding. IEEE Trans. Inf. Theory 2011, 57, 996–1007. [Google Scholar] [CrossRef]
- Kafaie, S.; Chen, Y.P.; Dobre, O.A.; Ahmed, M.H. Network coding implementation details: A guidance document. arXiv 2018, arXiv:1801.02120. [Google Scholar]
- Keller, L. Network Coding Utilities. Available online: https://github.com/lokeller/ncutils (accessed on 24 March 2020).
- Matsuda, T.; Noguchi, T.; Takine, T. Survey of network coding and its applications. IEICE Trans. Commun. 2011, 94, 698–717. [Google Scholar] [CrossRef]
- Li, B.; Niu, D. Random network coding in peer-to-peer networks: From theory to practice. Proc. IEEE 2011, 99, 513–523. [Google Scholar]
- Parikh, V.U.; Narmawala, Z. A survey on peer-to-peer file sharing using network coding in delay tolerant networks. Int. J. Comput. Sci. Commun. 2014, 5, 74–79. [Google Scholar]
- Bassoli, R.; Marques, H.; Rodriguez, J.; Shum, K.W.; Tafazolli, R. Network coding theory: A survey. IEEE Commun. Surv. Tutorials 2013, 15, 1950–1978. [Google Scholar] [CrossRef]
- Sanna, M.; Izquierdo, E. A survey of linear network coding and network error correction code constructions and algorithms. Int. J. Digit. Multimed. Broadcast. 2011, 2011, 12. [Google Scholar] [CrossRef]
- Gkantsidis, C.; Rodriguez, P.R. Network coding for large scale content distribution. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005; Volume 4, pp. 2235–2245. [Google Scholar]
- Luby, M.; Vicisano, L.; Gemmell, J.; Rizzo, L.; Handley, M.; Crowcroft, J. The Use of Forward Error Correction (FEC) in Reliable Multicast. Technical Report, RFC 3453. December 2002. Available online: https://dl.acm.org/doi/book/10.17487/RFC3453 (accessed on 24 March 2020).
- Cohen, B. Incentives build robustness in BitTorrent. In Proceedings of the Workshop on Economics of Peer-to-Peer Systems, Berkeley, CA, USA, 5–6 June 2003; Volume 6, pp. 68–72. [Google Scholar]
- Azzedin, F.; Yahaya, M. Modeling BitTorrent choking algorithm using game theory. Future Gener. Comput. Syst. 2016, 55, 255–265. [Google Scholar] [CrossRef]
- Medard, M. How good is random linear coding based distributed networked storage? In Proceedings of the NETCOD’05, Riva del Garda, Italy, 7 April 2005. [Google Scholar]
- Cassuto, Y.; Shokrollahi, A. Online fountain codes with low overhead. IEEE Trans. Inf. Theory 2015, 61, 3137–3149. [Google Scholar] [CrossRef]
- Deb, S.; Médard, M.; Choute, C. Algebraic gossip: A network coding approach to optimal multiple rumor mongering. IEEE/ACM Trans. Netw. (TON) 2006, 14, 2486–2507. [Google Scholar] [CrossRef]
- Karp, R.; Schindelhauer, C.; Shenker, S.; Vocking, B. Randomized rumor spreading. In Proceedings of the 41st Annual Symposium on Foundations of Computer Science, Redondo Beach, CA, USA, 12–14 November 2000; pp. 565–574. [Google Scholar]
- Doerr, B.; Doerr, C.; Moran, S.; Moran, S. Simple and optimal randomized fault-tolerant rumor spreading. Distrib. Comput. 2016, 29, 89–104. [Google Scholar] [CrossRef]
- Wang, N.; Ansari, N. Downloader-initiated random linear network coding for peer-to-peer file sharing. IEEE Syst. J. 2010, 5, 61–69. [Google Scholar] [CrossRef]
- Yeung, R.W. Avalanche: A network coding analysis. Commun. Inf. Syst. 2007, 7, 353–358. [Google Scholar] [CrossRef]
- Soro, A.; Lacan, J. FFT-based Network Coding For Peer-To-Peer Content Delivery. In Proceedings of the 2011 IEEE Global Telecommunications Conference-GLOBECOM 2011, Houston, TX, USA, 5–9 December 2011; pp. 1–5. [Google Scholar]
- Wang, M.; Li, B. How practical is network coding? In Proceedings of the 14th IEEE International Workshop on Quality of Service, New Haven, CT, USA, 19–21 June 2006; pp. 274–278. [Google Scholar]
- Li, T.; Wang, J.; You, J. Using Degree-Based Strategy for Network Coding in Content Distribution Network. In Proceedings of the International Conference on Computer and Electrical Engineering, Phuket, Thailand, 20–22 December 2008; pp. 487–491. [Google Scholar]
- Ma, G.; Xu, Y.; Lin, M.; Xuan, Y. A content distribution system based on sparse linear network coding. In Proceedings of the Third Workshop on Network Coding (Netcod 2007), Miami, FL, USA, 29 July 2007. [Google Scholar]
- Ortolf, C.; Schindelhauer, C.; Vater, A. Paircoding: Improving file sharing using sparse network codes. In Proceedings of the 2009 Fourth International Conference on Internet and Web Applications and Services, Venice, Italy, 24–28 May 2009; pp. 49–57. [Google Scholar]
- Vater, A. Efficient Coding Schemes for File Sharing Networks. Ph.D. Thesis, Albert Ludwig University, Breisgau, Germany, April 2011. [Google Scholar]
- Vater, A.; Schindelhauer, C.; Ortolf, C. Tree network coding for peer-to-peer networks. In Proceedings of the Twenty-Second Annual ACM Symposium on Parallelism in Algorithms and Architectures, Santorini, Greece, 13–15 June 2010; pp. 114–123. [Google Scholar]
- Ortolf, C.; Schindelhauer, C.; Vater, A. Classifying peer-to-peer network coding schemes. In Proceedings of the Twenty-First, Annual Symposium on Parallelism in Algorithms and Architectures, Calgary, AB, Canada, 11–13 August 2009; pp. 310–318. [Google Scholar]
- Shang, T.; Peng, T.; Lei, Q.; Liu, J. Homomorphic Signature for Generation-based Network Coding. In Proceedings of the IEEE International Conference on Smart Cloud (SmartCloud), New York, NY, USA, 18–20 November 2016; pp. 269–273. [Google Scholar]
- Xu, J.; Wang, X.; Zhao, J.; Lim, A.O. I-swifter: Improving chunked network coding for peer-to-peer content distribution. Peer- Netw. Appl. 2012, 5, 30–39. [Google Scholar] [CrossRef]
- Ren, L.Y.; He, H.Y.; Di, Z.; Lei, M. Content distribution system based on segmented network coding. In Proceedings of the International Conference on Apperceiving Computing and Intelligence Analysis, Chengdu, China, 23–25 October 2009; pp. 258–261. [Google Scholar]
- Tao, S.; Huang, J.; Yang, Z.; Cheng, W.; Liu, W. An improved network coding-based cooperative content distribution scheme. In Proceedings of the ICC Workshops-2008 IEEE International Conference on Communications Workshops, Beijing, China, 19–23 May 2008; pp. 360–364. [Google Scholar]
- Chou, P.A.; Wu, Y.; Jain, K. Practical network coding. In Proceedings of the Annual Allerton Conference on Communication Control and Computing, Allerton, IL, USA, 1–3 October 2003; Volume 41, pp. 40–49. [Google Scholar]
- Maymounkov, P.; Harvey, N.J.; Lun, D.S. Methods for efficient network coding. In Proceedings of the 44th Annual Allerton Conference on Communication, Control, and Computing, Allerton, IL, USA, 27–29 September 2006; pp. 482–491. [Google Scholar]
- Xu, J.; Zhao, J.; Wang, X.; Xue, X. Swifter: Chunked network coding for peer-to-peer content distribution. In Proceedings of the IEEE International Conference on Communications, Beijing, China, 19–23 May 2008; pp. 5603–5608. [Google Scholar]
- Hundeboll, M.; Ledet-Pedersen, J.; Sluyterman, G.; Madsen, T.K.; Fitzek, F.H. Peer-assisted content distribution with random linear network coding. In Proceedings of the IEEE 79th Vehicular Technology Conference (VTC Spring), Seoul, Korea, 18–21 May 2014; pp. 1–6. [Google Scholar]
- Niu, D.; Li, B. On the resilience-complexity trade-off of network coding in dynamic P2P networks. In Proceedings of the Fifteenth IEEE International Workshop on Quality of Service, Evanston, IL, USA, 21–22 June 2007; pp. 38–46. [Google Scholar]
- Niu, D.; Li, B. Analyzing the resilience-complexity trade-off of network coding in dynamic P2P networks. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 1842–1850. [Google Scholar] [CrossRef]
- Zhang, X.; Li, B. On the market power of network coding in P2P content distribution systems. In Proceedings of the IEEE INFOCOM, Rio de Janeiro, Brazil, 19–25 April 2009; pp. 334–342. [Google Scholar]
- Zhang, X.; Li, B. On the Market Power of Network Coding in P2P Content Distribution Systems. IEEE Trans. Parallel Distrib. Syst. 2011, 2063–2070. [Google Scholar] [CrossRef]
- Leu, J.S.; Yu, M.C.; Yueh, H.C. Improving network coding based file sharing for unstructured peer-to-peer networks. J. Netw. Syst. Manag. 2015, 23, 803–829. [Google Scholar] [CrossRef]
- Yang, M.; Yang, Y. Applying network coding to peer-to-peer file sharing. IEEE Trans. Comput. 2013, 63, 1938–1950. [Google Scholar] [CrossRef]
- Li, Z.; Li, B.; Jiang, D.; Lau, L.C. On Achieving Optimal End-to-End Throughput in Data Networks: Theoretical and Empirical Studies. ECE Technical Report. 2004. Available online: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.4.6912 (accessed on 24 March 2020).
- Ngai, C.K.; Yeung, R.W. Network coding gain of combination networks. In Proceedings of the IEEE Information Theory Workshop, San Antonio, TX, USA, 24–29 October 2004; pp. 283–287. [Google Scholar]
- Jaggi, S.; Sanders, P.; Chou, P.A.; Effros, M.; Egner, S.; Jain, K.; Tolhuizen, L.M. Polynomial time algorithms for multicast network code construction. IEEE Trans. Inf. Theory 2005, 51, 1973–1982. [Google Scholar] [CrossRef]
- Chu, Y.h.; Rao, S.G.; Seshan, S.; Zhang, H. A case for end system multicast. IEEE J. Sel. Areas Commun. 2002, 20, 1456–1471. [Google Scholar] [CrossRef]
- Braun, P.J.; Sipos, M.; Ekler, P.; Charaf, H. Increasing data distribution in BitTorrent networks by using network coding techniques. In Proceedings of the VDE European Wireless 2015, 21th European Wireless Conference, Budapest, Hungary, 20–22 May 2015; pp. 1–6. [Google Scholar]
- Baumgart, I.; Heep, B.; Krause, S. OverSim: A flexible overlay network simulation framework. In Proceedings of the IEEE Global Internet Symposium, Anchorage, AK, USA, 11 May 2007; pp. 79–84. [Google Scholar]
- Chawathe, Y.; Ratnasamy, S.; Breslau, L.; Lanham, N.; Shenker, S. Making gnutella-like p2p systems scalable. In Proceedings of the 2003 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, Karlsruhe, Germany, 25–29 August 2003; pp. 407–418. [Google Scholar]
- Zeng, H.; Huang, J.; Tao, S.; Cheng, W. A simulation study on network coding parameters in P2P content distribution system. In Proceedings of the Third International Conference on Communications and Networking in China, Hangzhou, China, 25–27 August 2008; pp. 197–201. [Google Scholar]
- Zhang, X.; Liu, J.; Li, B.; Yum, Y.S. CoolStreaming/DONet: A data-driven overlay network for peer-to-peer live media streaming. In Proceedings of the IEEE 24th Annual Joint Conference of the IEEE Computer and Communications Societies, Miami, FL, USA, 13–17 March 2005; Volume 3, pp. 2102–2111. [Google Scholar]
- Kaiqian, O.; Yinlong, X.; Guanjun, M.; Yulin, Z. Dasher: A peer-to-peer content distribution system based on combined network coding. In Proceedings of the 2nd IEEE International Conference on Broadband Network & Multimedia Technology, Beijing, China, 18–20 Ocotber 2009; pp. 687–692. [Google Scholar]
- Su, J.; Deng, Q.; Long, D. PCLNC: A low-cost intra-generation network coding strategy for P2P content distribution. Peer- Netw. Appl. 2019, 12, 177–188. [Google Scholar] [CrossRef]
- Chun, B.; Culler, D.; Roscoe, T.; Bavier, A.; Peterson, L.; Wawrzoniak, M.; Bowman, M. Planetlab: An overlay testbed for broad-coverage services. ACM SIGCOMM Comput. Commun. Rev. 2003, 33, 3–12. [Google Scholar] [CrossRef]
- Montresor, A.; Jelasity, M. PeerSim: A scalable P2P simulator. In Proceedings of the IEEE Ninth International Conference on Peer-to-Peer Computing, Seattle, WA, USA, 9–11 September 2009; pp. 99–100. [Google Scholar]
- Halloush, M.; Radha, H. Network coding with multi-generation mixing. In Proceedings of the 42nd Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 19–21 March 2008; pp. 515–520. [Google Scholar]
- Halloush, M.; Radha, H. Network coding with multi-generation mixing: A generalized framework for practical network coding. IEEE Trans. Wirel. Commun. 2010, 10, 466–473. [Google Scholar] [CrossRef]
- Wei, X.; Long, D.Y. P2P content-propagation mechanism tailored by network coding. In Proceedings of the International Symposium on Computer Network and Multimedia Technology, Wuhan, China, 18–20 January 2009; pp. 1–6. [Google Scholar]
- Silva, D.; Zeng, W.; Kschischang, F.R. Sparse network coding with overlapping classes. In Proceedings of the Workshop on Network Coding, Theory, and Applications, Lausanne, Switzerland, 15–16 June 2009; pp. 74–79. [Google Scholar]
- MacKay, D.J. Fountain codes. IEE Proc.-Commun. 2005, 152, 1062–1068. [Google Scholar] [CrossRef]
- Byers, J.W.; Luby, M.; Mitzenmacher, M.; Rege, A. A digital fountain approach to reliable distribution of bulk data. ACM SIGCOMM Comput. Commun. Rev. 1998, 28, 56–67. [Google Scholar] [CrossRef]
- Luby, M. LT codes. In Proceedings of the 43rd Annual IEEE Symposium on Foundations of Computer Science, Chicago, IL, USA, 27 June–2 July 2002; pp. 271–280. [Google Scholar]
- Shokrollahi, A. Raptor codes. IEEE/ACM Trans. Netw. (TON) 2006, 14, 2551–2567. [Google Scholar] [CrossRef]
- Heidarzadeh, A.; Banihashemi, A.H. Overlapped chunked network coding. In Proceedings of the IEEE Information Theory Workshop on Information Theory (ITW), Cairo, Egypt, 6–8 January 2010; pp. 1–5. [Google Scholar]
- Heidarzadeh, A.; Banihashemi, A.H. Analysis of overlapped chunked codes with small chunks over line networks. In Proceedings of the IEEE International Symposium on Information Theory Proceedings, St. Petersburg, Russia, 31 July–5 August 2011; pp. 801–805. [Google Scholar]
- Li, Y.; Soljanin, E.; Spasojevic, P. Effects of the generation size and overlap on throughput and complexity in randomized linear network coding. IEEE Trans. Inf. Theory 2011, 57, 1111–1123. [Google Scholar] [CrossRef]
- Tang, B.; Yang, S.; Yin, Y.; Ye, B.; Lu, S. Expander graph based overlapped chunked codes. In Proceedings of the IEEE International Symposium on Information Theory Proceedings, Cambridge, MA, USA, 1–6 July 2012; pp. 2451–2455. [Google Scholar]
- Joshi, G.; Soljanin, E. Round-robin overlapping generations coding for fast content download. In Proceedings of the IEEE International Symposium on Information Theory, Istanbul, Turkey, 7–12 July 2013; pp. 2740–2744. [Google Scholar]
- Li, Y.; Chan, W.Y.; Blostein, S.D. Network coding with unequal size overlapping generations. In Proceedings of the International Symposium on Network Coding (NetCod), Cambridge, MA, USA, 29–30 June 2012; pp. 161–166. [Google Scholar]
| Binary | |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | x |
| 011 | |
| 100 | |
| 101 | |
| 110 | |
| 111 |
| Reference | Approach | Main Findings | Verification Method | Network Topology | PerformanceMetrics |
|---|---|---|---|---|---|
| Gkantsidis et al. [42] | Utilizing RNLC on P2P file sharing networks. | - RLNC alleviates the pieces selection problem and churns, and accelerates the downloading process. | Numerical Simulation | Single overlay, and Multi-clusters overlay. | - Download time. - Throughput. |
| Acedanski et al. [46] | Providing extensively theoretical analysis for P2P RNLC-based method. | - RLNC overhead is about % of the file size. - RLNC is highly applicable for uncoordinated P2P networks. | Numerical Simulation | Star. | - Probability of download completion. - Probability of contents availability. |
| Deb et al. [48] | proposing RLNC-based approach for P2P gossip protocols. | - Computational overhead of RNLC to reconstruct the file is rather reasonable for . | Numerical Simulation. | Complete Mesh. | - Download time. |
| Wang et al. [51] | Proposing DRLNC to mitigate unlucky combination problem. | - Unlucky combination problem could be eliminated even with . | Numerical simulation. | Mesh. | - Rounds to complete download. |
| Yeung [52] | Analysis Avalanche using graph theory. | - Avalanche can achieve the theoretical lower bound of the file downloading time. | No experimental work. | Mesh. | —– |
| Chiu et al. [13] | Avalanche is studied by modeling a simple star topology network. | - No advantage of network coding over traditional routing. | No experimental work. | Star. | —– |
| Wang et al. [54] | Justifying the feasibility of RLNC on P2P systems by realistic application layer implementation. | - RNLC performs worse than any conventional store and forward P2P file sharing system. | High performance C++ implementation. | Mesh | - Average downloadtime. - Encoding/ decoding complexity. |
| Reference | Approach | Main Findings | Verification Method | Network Topology | PerformanceMetrics |
|---|---|---|---|---|---|
| M. Guanjun et al. [56] | Proposing sparse network coding based on stochastic formulas. | - Sparse coding encodes/decodes faster than full coding andslightly downloads faster thanbaseline BitTorrent. - Encoding interval anddependency test canminimize the drop rateof dependent coded pieces. | Implementation | Chord overlay | - Encoding/decoding rate. - Download time. |
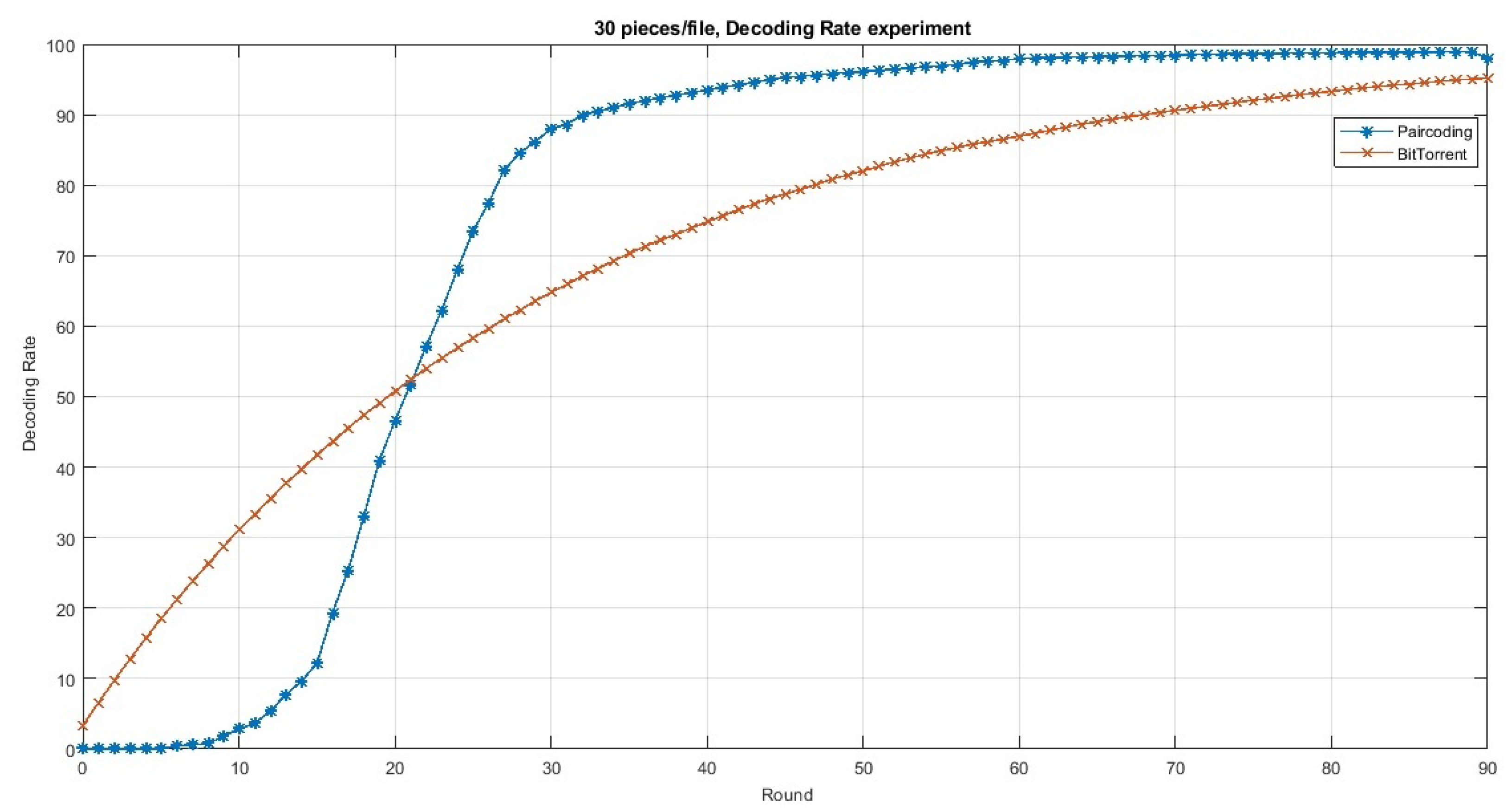
| C. Ortolf et al. [57] | Proposing sparse coding such that each encoded piece is a combination of only tworandomized original pieces. | - Paircoding relatively decodes pieces as good as BitTorrent, and for some scenarios, it achieves the piece diversity of full coding. | Numerical Simulation | Mesh | - Decoding rate. - Content availability. |
| C. Ortolf et al. [60] | Proposing sparse coding such that each encoded piece is a combination of two adjacent original pieces. | - Fixing the choice of the two original pieces yields to faster decoding. yet affects the piece diversity. | No experimental work | —– | —– |
| Q. Cai et al. [18] | Analyze Avalanche and Paircoding, and propose a Fixed-Paircoding with considering the rarest first scheduling policy. | - Achieves both fast decoding opposed to Avalanche and wide piece diversity opposed to Paircoding. - Increases throughput with slightly control overhead. | Numerical Simulation | Mesh | - Content availability. - Control overhead. - Download time. |
| C. Ortolf et al. [55] | Proposing sparse coding by modeling encoded pieces as full binary tree | - allowing encoding only in the seeder, yields to worse pieces availability. On the other hand, dynamic encoding yields to much complexity. | No experimental work | —– | —– |
| Reference | Approach | Main Findings | Verification Method | Network Topology | Performance Metrics |
|---|---|---|---|---|---|
| Xu et al. [67] | Proposing pull-based generation coding system and mixing rarest-first selection policy with generation coding to alleviate the overhead of control messages. | - Swifter can reduce the average download time by 40% compared to push-based generation system with random selection policy. | Implementation over LAN with 30 nodes. | PartiallyMeshed | - Download time. |
| Xu et al. [62] | Proposing push-based generation coding system promising to reduce the requests overhead. | - I-swifter can reduce the average download time by 4% compared to Swifter. | Implementation over LAN with 30 nodes. | PartiallyMeshed | - Download time |
| Hundeboll et al. [68] | Implementing generation coding system to study the parameters of generation coding: generation size, GF size, and piece size. | - BRONCO far outperforms HTTP while it performs almost as good as BitTorrent. - BRONCO consumes almost quarter the CPU utility Avalanche consumes but with extra 9% redundant pieces. | C++ Implementation | PartiallyMeshed | - Download time |
| Niu et al. [69,70] | Modeling generation coding system by Markov process and differential equations and study the optimal generation size. | - The optimal generation size to enjoy network coding is 20–30 pieces. | Numerical simulation | Mesh | - Decoding rate. - Download time. |
| Zhang et al. [71,72] | Proposing a game theory framework to study generation network coding considering a system with many free-riders. | - network coding can enhance the market’s flexibility for urgent peers, but with the high encodingdecoding cost. - network coding can improve the peers’ incentive. Only mathematical and analytical model. | Only mathematical and analytical model | —– | - Robustness to churn. |
| Leu et al. [73] | Proposing a framework based on simulations to deeply analyze and understand generation network coding. | - Network coding outperforms trivial approaches when (1) DRLNC is used, (2) appropriate coding size is selected and, (3) Gauss-Jordan elimination is applied for early decoding. | C++ P2P simulator [80] | GIA [81] overlay | - Encoding/ decoding rates. - Download time. - Network overhead. |
| Yang et al. [74] | Proposing deterministic network coding and utilizing a special network topology “combination network”. | - The overall download time of PPFEED is shorter than Narada and Avalanche by 15-20% and 8-10% respectively. | Simulation | Combination network overlay | - Throughput. - Reliability (to churn). - Link stress (redundancy). - Download time. |
| Braun et al. [79] | Proposing generation coding P2P file sharing system with backward compatibility with standard BitTorrent. | - In some scenarios, NCME can share a file to the network 20% faster than BitTorrent. - The suggested generation size for good level of performance is 43. | Java Implementation | Partially Meshed | - Download time. - Generation size. |
| Reference | Approach | Main Findings | Verification Method | Network Topology | Performance Metrics |
|---|---|---|---|---|---|
| Zeng et al. [82] | Introducing and adjusting new parameters (generation size and encoding size). | - If parameters are well tuned, network coding outperform other traditional P2P schemes. Otherwise, network coding performs worse. | Simulation on NS-2 platform | Partially Meshed | - Download time. - Robustness to churn. |
| Yong et al. [63] | Studying the effect of the generation and encoding sizes on download time and churn. | - The download time is shortened compared with Avalance and BitTorrent by 10% and 20%–30%. - Churn resist can be improved by 12.5%. | Simulation based on CoolStreaming overlay network. | Partially Meshed | - Download time. - Effect of churn. |
| Kaqian et al. [84] | Proposing combined coding with adoption of local rarest first policy for generation scheduling. | - Dasher can download faster than Chunker and BitTorrent as well as decode faster than Sparser. | Implementation. Tested both on Planet-Lab [86] and LAN testbeds. | Mesh | - Download time. - Decoding speed. |
| Su et al. [85] | Proposing (1) adaptive encoding window size and upper triangle matrix to speed-up encoding/decoding and (2) postponement and loop self-checking schemes to minimize linear dependency. | - PCLNC is shortened the download time by 3.17% and 21.0% compared to sparse coding and BitTorrent, respectively. - PCLNC peer can start sharing a piece faster than BitTorrent by 36.8%, and almost as fast as sparse coding. | Simulation based on peerSim [87] | Mesh | - Download time. - Start-up time. - coding degree. |
| Reference | Approach | Main Findings | Verification Method | Network Topology | Performance Metrics |
|---|---|---|---|---|---|
| Silva et al. [91] | Proposing first P2P overlapping coding scheme by introducing grid and diagonal structures. | - The proposed scheme can mainly reduce network overhead by up to 70%. | Simulation | Mesh | - Decoding complexity overhead trade-off. |
| Heidarzadeh et al. [96] | Proposing head-to-toeoverlapping scheme over line network topology | - Overlapping can reduce network overhead for line networks. - Overlapping is appropriate for multimedia streaming. | Numerical Simulation | Line networks overlay | - Decoding probability. |
| Li et al. [98] | Proposing random overlapping by attaching an annex to the base generation. | - The optimal overlap size to achieve the highest throughput is around the half of the generation size. - Random-Annex coding outperforms both head-to-toe and disjoint generations coding. | Numerical Simulation | Point-to-point | - Probability ofDecoding failure. - Throughput. |
| Tang et al. [99] | Proposing and modelinggenerations overlapping as an expander graph (EOC). | - The best number of generations to overlapped varies between 3 to the generation size. - EOC decoder decodes faster than random annex and head-to-toe. | Numerical simulation | Point-to-point | - Throughput. - Decoding rate. |
| Joshi et al. [100] | Proposing deterministicstructures of overlapping and consider round-robin scheduling | - The upper bound limit of the optimal overlapping is . - Deterministic overlapping structures avoid network overhead and index complexity of random structure (EOC). - Proposed schemes minimize the expected download time compared to random annex. | Numerical Simulation | Mesh | -Download time. |
| Li et al. [101] | Proposing overlapping with unequal generations’ sizes based on degree distribution and merge both sequential and random scheduling | - Proposed scheme achieves the minimum overhead whereas independent generations codes achieve the minimum decoding complexity. - Among the overlapping schemes, the best overhead-complexity trade-off is achieved by the proposed scheme. | Numerical Simulation | Point-to-point | - Decoding rate. - Overhead. |
| Robustness to Churn | Decoding Speed | Network Overhead | |
|---|---|---|---|
| Full Coding | Constant: very slow (infeasible) | ↑ | |
| Sparse Coding | Variant: slow at the beginning to quick at the end. | ↑ | |
| Generation Coding | Constant: based on generation size (moderate usually). | ||
| Combined Coding | Variant: moderate at the beginning to quick at the end. | ||
| Overlapping Coding | Variant: moderate at the beginning to very quick at the end. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
AbuDaqa, A.A.; Mahmoud, A.; Abu-Amara, M.; Sheltami, T. Survey of Network Coding Based P2P File Sharing in Large Scale Networks. Appl. Sci. 2020, 10, 2206. https://doi.org/10.3390/app10072206
AbuDaqa AA, Mahmoud A, Abu-Amara M, Sheltami T. Survey of Network Coding Based P2P File Sharing in Large Scale Networks. Applied Sciences. 2020; 10(7):2206. https://doi.org/10.3390/app10072206
Chicago/Turabian StyleAbuDaqa, Anas A., Ashraf Mahmoud, Marwan Abu-Amara, and Tarek Sheltami. 2020. "Survey of Network Coding Based P2P File Sharing in Large Scale Networks" Applied Sciences 10, no. 7: 2206. https://doi.org/10.3390/app10072206
APA StyleAbuDaqa, A. A., Mahmoud, A., Abu-Amara, M., & Sheltami, T. (2020). Survey of Network Coding Based P2P File Sharing in Large Scale Networks. Applied Sciences, 10(7), 2206. https://doi.org/10.3390/app10072206





