Investigation of Ytterbium Incorporation in Lithium Niobate for Active Waveguide Devices

Featured Application

Active waveguide devices, waveguide lasers.

Abstract

In this work, we report on an investigation of the ytterbium diffusion characteristics in lithium niobate. Ytterbium-doped substrates were prepared by in-diffusion of thin metallic layers coated onto x- and z-cut congruent substrates at different temperatures. The ytterbium profiles were investigated in detail by means of secondary neutral mass spectroscopy, optical microscopy, and optical spectroscopy. Diffusion from an infinite source was used to determine the solubility limit of ytterbium in lithium niobate as a function of temperature. The derived diffusion parameters are of importance for the development of active waveguide devices in ytterbium-doped lithium niobate.

1. Introduction

The ferroelectric crystal lithium niobate (LiNbO₃) is a well-known material for various optical applications due to its favorable electro-optical, acousto-optical, piezoelectric, and nonlinear properties. Furthermore, low-loss waveguides can be implemented in rare-earth-doped LiNbO₃ via several fabrication techniques [1,2,3,4,5,6], leading to the development of waveguide amplifiers as well as waveguide lasers. In the past, a variety of efficient erbium- (Er) and neodymium (Nd)-doped LiNbO₃ waveguide lasers have been realized [7,8,9,10]. Another attractive laser material is Yb:LiNbO₃. Due to the simple energy level scheme of ytterbium (Yb) with only one excited state, a small laser quantum defect can be achieved, allowing for the development of highly efficient Yb lasers [11]. Another benefit of Yb is the large gain bandwidth, which allows for wide wavelength tuning and the generation of ultrashort pulses [12,13].

In 1995, Jones et al. reported the demonstration of an Yb:LiNbO₃ waveguide laser with a slope efficiency of 16% [14]. Due to photorefractive damage, the y-propagation Ti-diffused Yb:LiNbO₃ waveguide laser showed unstable laser operation. Later, Fujimura et al. reported continuous-wave lasing with a slope efficiency of 7% in z-cut LiNbO₃ annealed/proton-exchanged (APE) waveguides [15] by using thermally in-diffused Yb. While in the latter works, channel waveguides were used, another method which also reduces photorefractive damage is using ridge waveguides [16]. In such geometry, further improvement of the laser performance can be achieved due to the smaller mode fields and significantly improved overlap of optical pump and laser modes, when compared to their channel counterparts. Recently, a novel fabrication method has been reported comprising ridge definition by diamond blade dicing followed by three-side Er/Nd and Ti in-diffusion for the development of highly efficient rare-earth-doped Ti:LiNbO₃ ridge waveguide lasers [17,18,19]. This fabrication technique is a promising method for increasing the slope efficiency of Yb:LiNbO₃ waveguide lasers, too. For the development of low-loss Yb:Ti:LiNbO₃ ridge waveguides with optimized overlap of the Yb doping profile and the intensity profiles of the guided modes, it is essential to know the diffusion constants and the maximum solubility of Yb in LiNbO₃. Apart from a single value for the diffusivity at 1100 °C in z-direction [20], only a few data regarding the diffusion doping of LiNbO₃ with Yb can be found [14,21].

In this work, we report on an investigation of the incorporation of Yb into LiNbO₃ by in-diffusion. To determine the diffusion constants and the maximum solubility of Yb in LiNbO₃, diffusion profiles measured by SNMS (secondary neutral mass spectrometry) were analyzed. With these data, a first ridge waveguide sample was prepared, and the absorption and emission spectra of the in-diffused Yb ions were measured and compared with literature values.

2. Experimental Methods

2.1. Sample Preparation

For the sample fabrication, optical-grade x- and z-cut wafers of congruent LiNbO₃ (Yamaju Ceramics Co., LTD) were used. Pieces of 10 × 10 × 1 mm³ were prepared by diamond saw dicing. The samples were cleaned using successive baths of acetone, isopropanol and deionized water, and an ultrasonic cleaner. Plasma cleaning in oxygen was applied as the final cleaning step prior to vacuum deposition. The samples were coated with 20 nm thick layers of Yb, with a purity of 99.9%, using electron beam evaporation. For annealing, the samples were placed in a platinum crucible in a high temperature elevator furnace for diffusion time of 30 h at different temperatures between 930 and 1130 °C. The heating and cooling rates were constant for all samples.

One sample with dimensions of 1 × 25 × 8 mm³ (x y z) from the x-cut wafer was also used to prepare Yb-doped ridge waveguides. For this, ridges were prepared in the x surface running parallel to the y-axis by precise diamond blade milling, and these samples were coated with 22 nm of Yb under symmetric angles of ±60°. For diffusion, the coated ridges were annealed at T = 1125 °C for t = 216 h. Afterwards, 85 nm of Ti were deposited under symmetric angles of ±60° and in-diffused to prepare the ridge waveguides as described in [17].

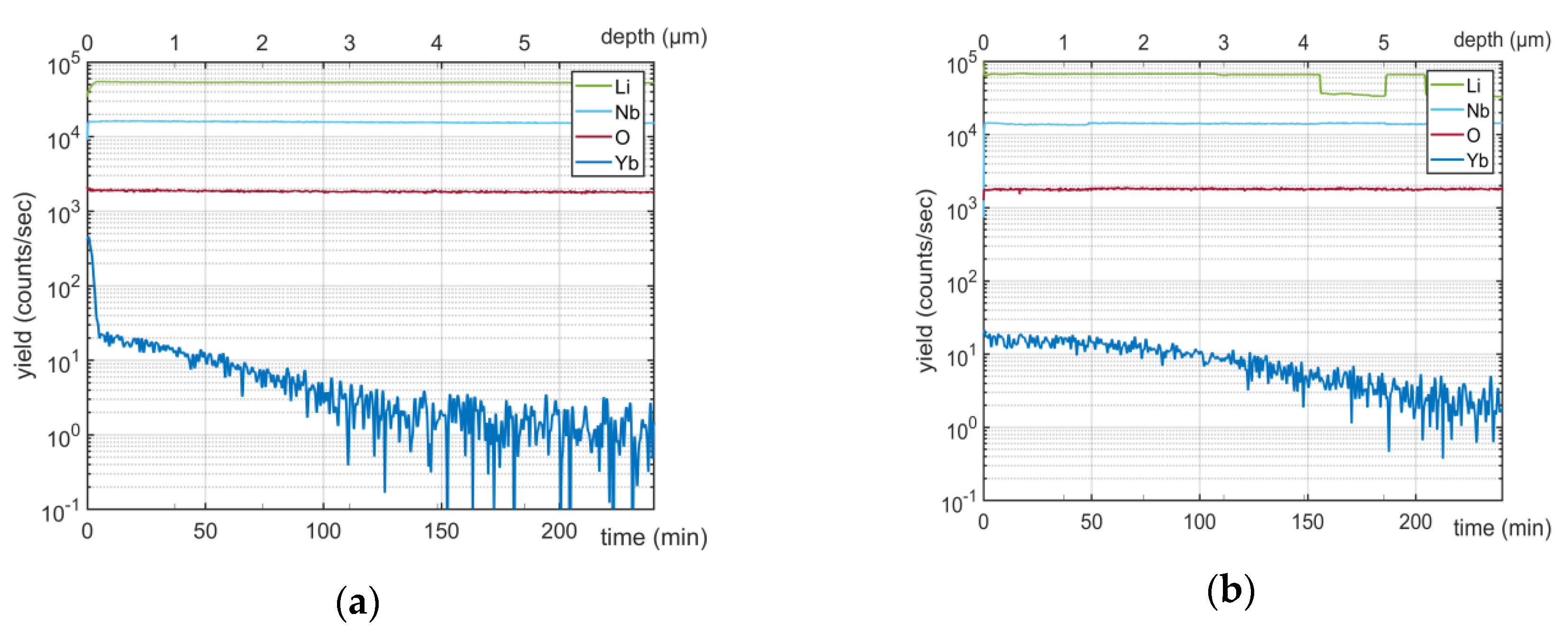
2.2. SNMS Measurements

The SNMS measurements were performed using the Multimethod System with INA-X from SPECS. For the direct bombardment mode during sputtering, an RF-excited Krypton plasma was used. Samples were protected by a copper mask defining a free area with a diameter of 5 mm in the central part of each sample. After SNMS analysis, the sputtered crater was measured using a white light interferometer (WLI from FRT) to determine the sputtering rate. The rate was (0.45 ± 0.02) nm/s for all samples.

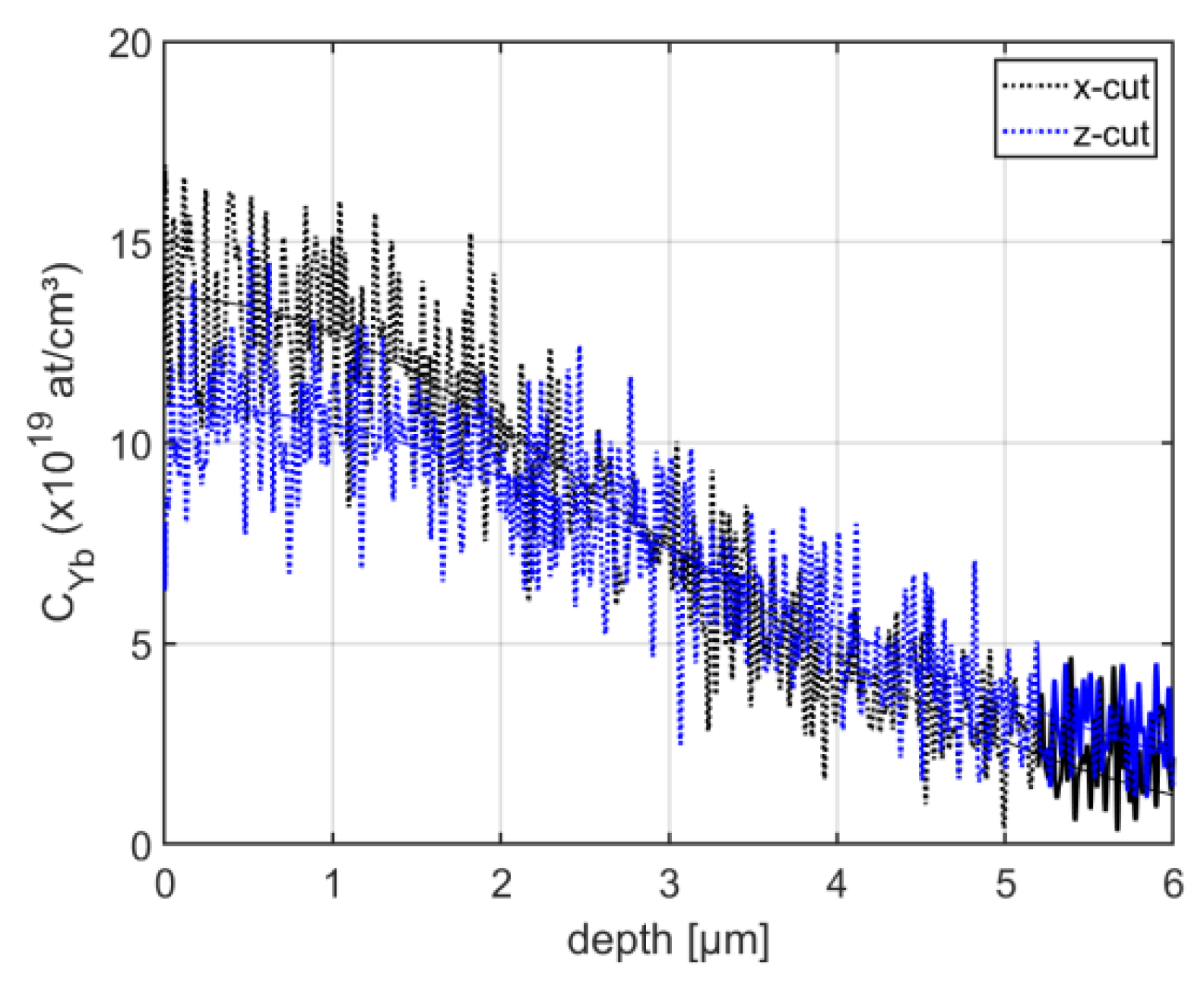
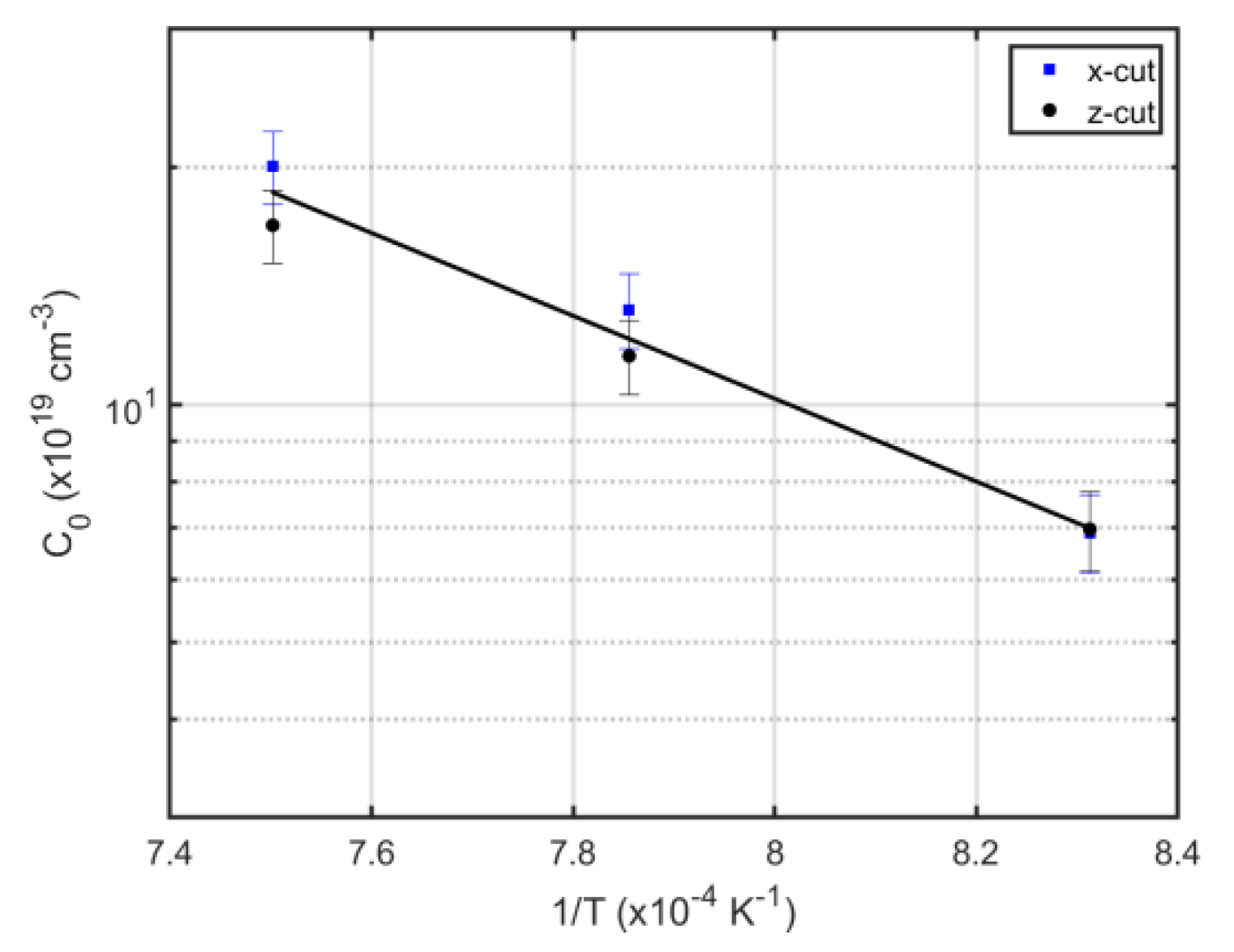
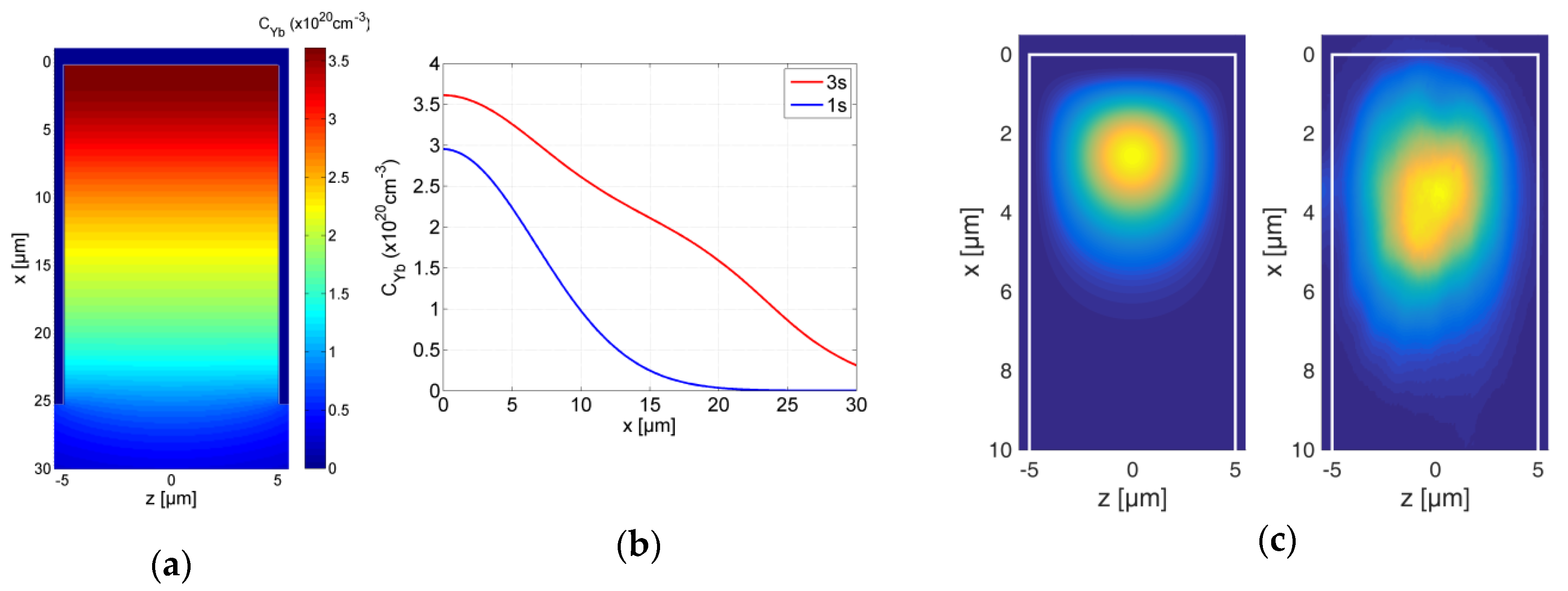
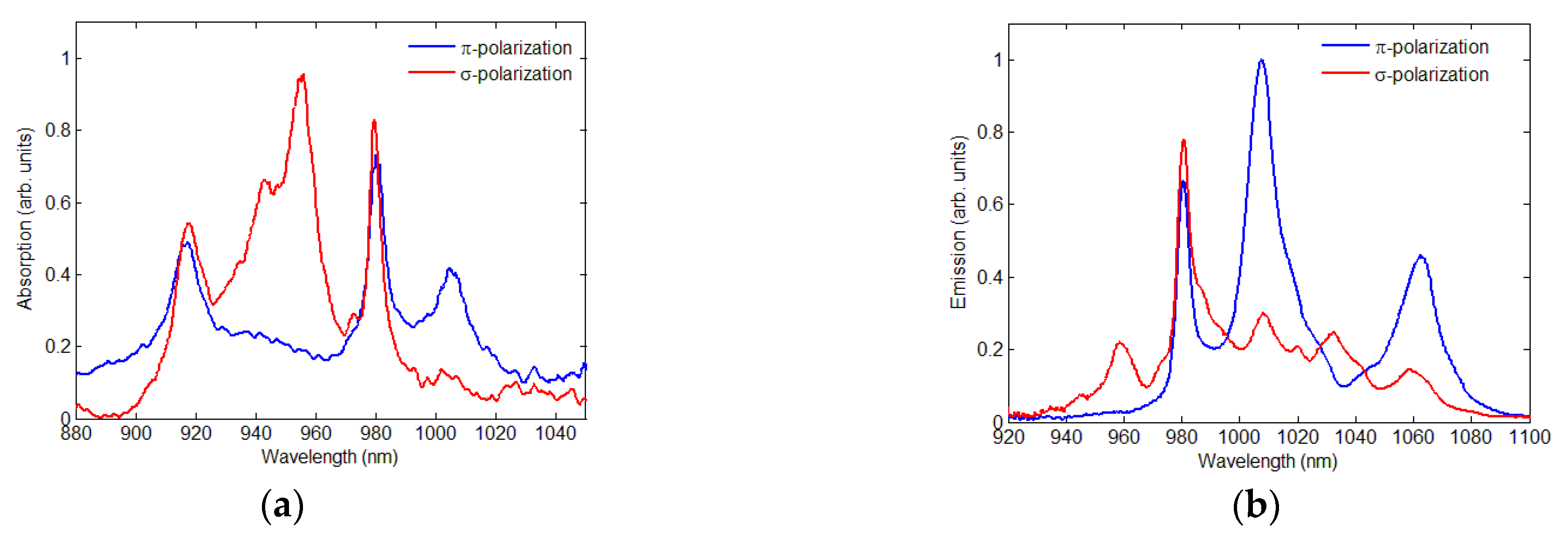
3. Results and Discussion

Figure 1 shows the depth profiles of ⁷Li, ⁹³Nb, ¹⁶O, and ⁷⁰Yb on a semilogarithmic scale giving two examples of SNMS spectra of the Yb-doped LiNbO₃ samples used in this analysis. Figure 1a demonstrates that at lower temperatures, a certain amount of Yb remains in form of a thin film on the surface, indicating that the Yb reservoir has not been exhausted.

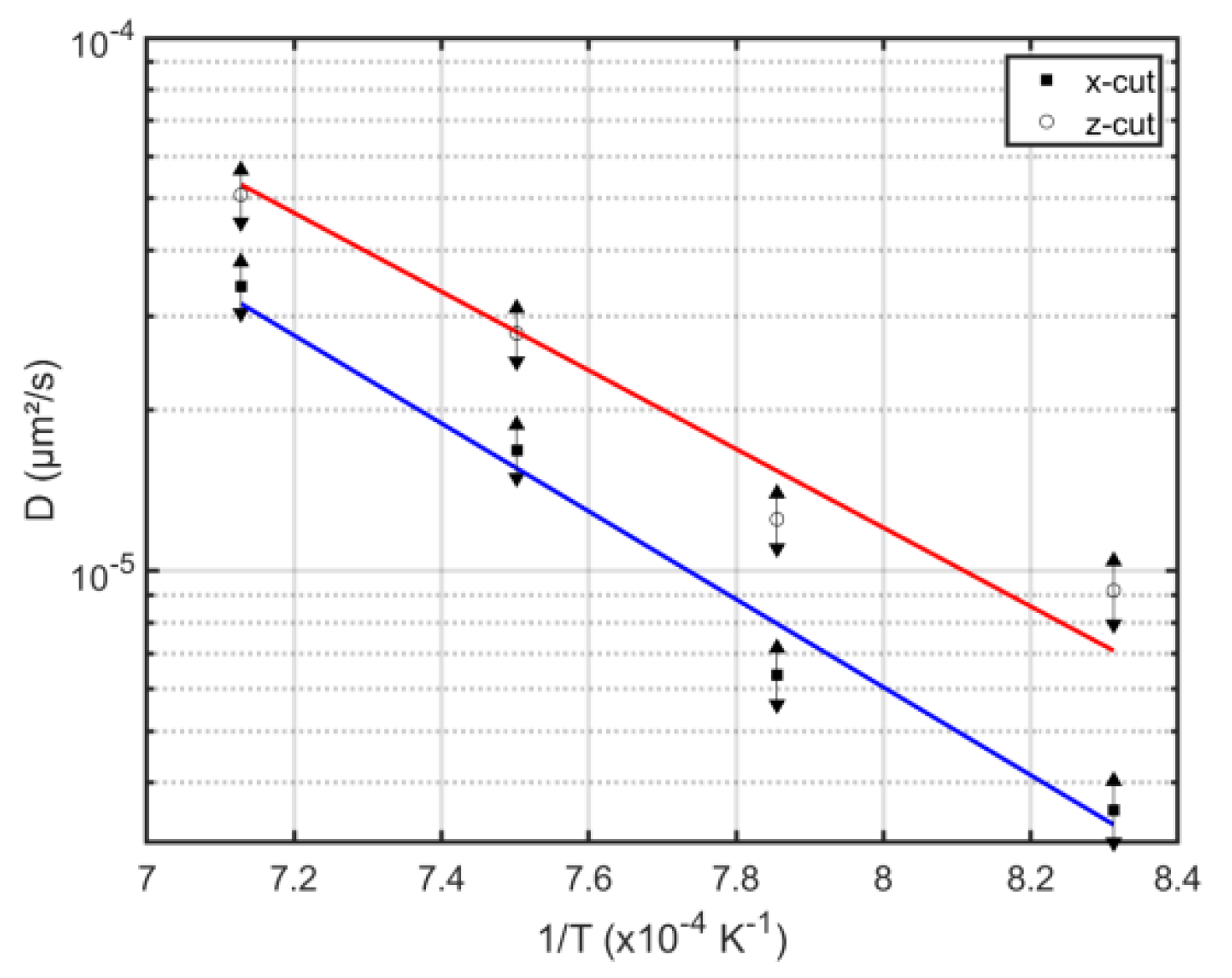
Diffusion Theory

The Yb concentration profiles obtained in this work can be well approximated utilizing the one-dimensional diffusion theory described by Fick’s second law of diffusion.

$$\frac{\partial C}{\partial t}=D\frac{{\partial }^{2}C}{\partial y^2},$$

(1)

where D is the diffusion coefficient and y quantifies the direction normal to the surface. Assuming an inexhaustible source (i.e., a thick film) of Yb on the surface, the solution of Fick’s law (1) can be approximated by

$$C(y)=C_{\max }\mathrm{erfc}(y/d_{erf}),$$

(2)

with C_max being the concentration of Yb at the crystal surface and the diffusion depth $d_{erf}=\sqrt{4Dt}$. In the thick-film diffusion regime. C_max describes the solubility of Yb in LiNbO₃. This value is given by

$$C_{\max }=\sqrt{\frac{\pi }{4Dt}}{\displaystyle \underset{0}{\overset{\infty }{\int }}C(y)dy}.$$

(3)

Using the law of mass conservation, the time needed for the Yb source to be depleted can be calculated with the metallic Yb density ρ, the atomic mass m_Yb, and the thickness τ of the initial Yb layer

$$t_d={\left(\frac{\rho \tau }{2m_{Yb}{C}_{\max }}\right)}^2\frac{\pi }{D}.$$

(4)

For sufficiently thin films and/or sufficiently long in-diffusion times (t > t_d), the Yb source is depleted and the diffusion profile can be approximated by a Gaussian function

$$C(y)=C_0\exp \left(-\frac{y^2}{d_{\exp }^2}\right).$$

(5)

In this case, $d_{\exp }=\sqrt{4Dt}$ describes the 1/e-depth of the profile. The surface concentration C₀ is below the solubility and given by

$$C_0=\frac{\tau C_{\max }}{\sqrt{\pi Dt}}.$$

(6)

The temperature dependence of the diffusion coefficient D is given by the Arrhenius relation

$$D(T)=D_0\exp \left(-\frac{E_A}{k_{B}T}\right).$$

(7)

Here, D₀ is the diffusion constant, E_A the activation energy, k_B the Boltzmann constant, and T is the temperature used for in-diffusion.

As the solubility describes the equilibrium between Yb in LiNbO₃ and the pure metallic Yb on the surface, the concentration at the surface can also be written in terms of an Arrhenius-type equation as

$$C_{\max }(T)=\widehat{C}\exp \left(-\frac{\Delta H}{k_{B}T}\right),$$

(8)

where ∆H is the mixing enthalpy and $\widehat{C}$ is a pre-factor.

Figure 2 shows the high-resolution images of the crystal surfaces obtained using a confocal microscope and applying the differential interference contrast method for the two crystal orientations. When the temperature used for annealing is less than 1130 °C, an increased surface roughness caused by insufficient diffusion is visible. For the x-cut surfaces, the arithmetical mean height (Sa) slightly decreases from 12 to 10 nm when the temperature increases from (a) 1000 to (b) 1060 °C.

For the z-cut surface shown in (d) and (e), the Sa is reduced from 11 to 7 nm. Annealing for 30 h at 1130 °C results in a smooth surface with Sa = 2 nm for both (c) x- and (f) z-cut surfaces, indicating that the Yb ion source at the surface is completely exhausted, and the Yb profile can be described by the thin-film diffusion regime of Equation (5).

For calibration of the SNMS data, the samples annealed at 1130 °C were used assuming a linear relation between ion yield and concentration as well as mass conservation in the diffusion process. For lower temperatures, the experimentally obtained profiles can be best fitted by complementary error functions, as can be seen in Figure 3.

The profiles obtained using the highest temperature were fitted by Gaussian functions; see Figure 4. The results obtained for the surface concentration and for the depths d_erf or d_exp are summarized in

Table 1. Parameters obtained for the Yb diffusion in LiNbO₃.

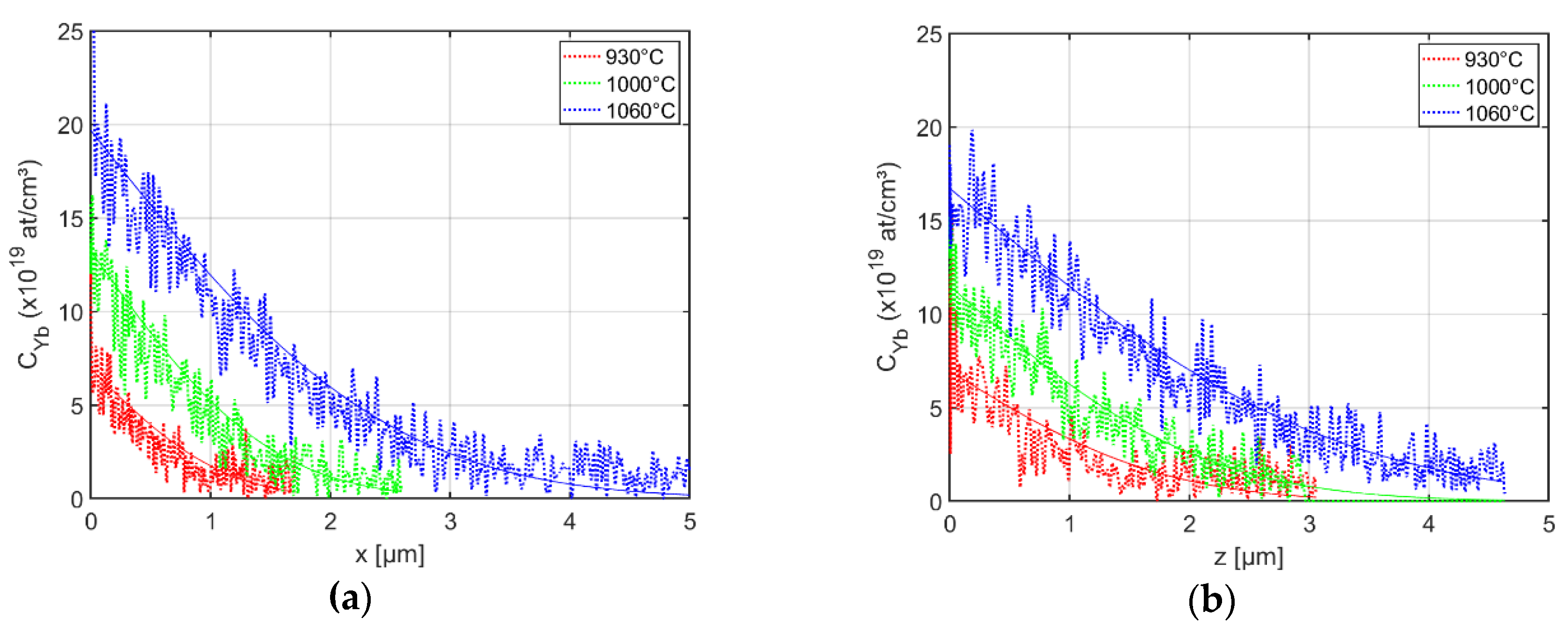
Temperature (°C)	Time (h)	C0 × 1019 (ions/cm3)	Cmax × 1019 (ions/cm3)	derf (µm)	dexp (µm)
z-cut
930	30	6.96 ± 0.10		1.99 ± 0.13
1000	30	11.53 ± 0.09		2.32 ± 0.14
1060	30	16.89 ± 0.10		3.47 ± 0.19
1130	30		10.94 ± 0.05		4.68 ± 0.26
x-cut
930	30	6.89 ± 0.10		1.24 ± 0.08
1000	30	13.21 ± 0.12		1.66 ± 0.10
1060	30	20.06 ± 0.12		2.70 ± 0.15
1130	30		13.62 ± 0.06		3.84 ± 0.21

.

With the values for the diffusion depth, the diffusion coefficients D are calculated. The temperature dependence of the diffusion coefficient is given by Equation (7). Figure 5 shows the corresponding Arrhenius plots for the two crystal-cut directions used. By correlating the fitted lines with Equation (7), the values for the diffusion coefficients and the activation energy for the x- and z-direction were obtained. The results are summarized in

Table 2. Diffusion constants and activation energies for Yb diffusion in LiNbO₃.

	D0 ( × 10-8 cm²/s)	EA (eV)
Diffusion in z-direction	9.7 ± 0.8	1.46 ± 0.07
Diffusion in x-direction	24.1 ± 1.9	1.64 ± 0.07

.

The temperature dependence of the surface concentration is presented in Figure 6. As can be seen, the measured values for the surface concentration of Yb for the three lowest temperatures indicate that, in contrast to the diffusivity, the solubility of Yb in LiNbO₃ shows no anisotropic behavior. The solid line is a fit to the data with Equation (8). This way, the values of ∆H = (1.04 ± 0.23) eV and $\widehat{C}$ = (1.6 ± 0.35) × 10²⁴ cm⁻³ were found.

With these characteristic values for the diffusion of Yb in LiNbO₃, a first test was performed for diffusion doping of a ridge waveguide prepared in an x-cut LiNbO₃ substrate oriented parallel to the y-axis by diamond blade dicing. Figure 7a shows the simulated Yb concentration profile in the ridge for the case of two 22 nm thick Yb layers being coated under ±60° with respect to the x-axis obtained by numerically solving Fick’s second law. For in-diffusion, the sample is annealed for 216 h at 1125 °C. The concentration profile also shows that at the upper right and left corners of the ridge, the expected concentration is below the solubility limit. Thus, no additional surface defects are to be expected. To achieve waveguiding, the upper part of the ridge is additionally doped by in-diffusion of Ti.

Figure 7c shows the expected intensity distribution of the quasi-TE modes at 800 nm and the intensity distribution measured at 796 nm. It is clearly visible that a good overlap between the Yb profile and the intensity distribution of the mode is achieved. The simulated concentration profiles shown in Figure 7a,b prove that ridge waveguides can be almost homogeneously doped by three-side in-diffusion while avoiding any surface damage that might be caused by exceeding the maximum solubility of Yb in LiNbO₃.

The transmission spectrum of such a 10 µm wide and 2.2 cm long ridge waveguide was measured using unpolarized white light coupled into the waveguide by means of a 40× microscope objective. At the output facet, the transmitted light was collected and coupled into a spectrometer. To measure absorption as a function of polarization, a polarizer was placed in front of the collimator of the spectrometer. The measured absorption spectra (π and σ polarization) show three main peaks at 918, 956, and 980 nm (see Figure 8a), which is in good agreement with the absorption spectra reported for bulk-doped Yb:LiNbO₃ [22] and Yb:Ti:LiNbO₃ channel waveguides [14]. The losses of the waveguide of 0.8 dB/cm were determined at 1064 nm using the Fabry–Perot method. Fluorescence spectra (π and σ polarization) were measured for pumping with a titanium-sapphire laser at 918 nm. Figure 8b shows the polarized fluorescence spectrum. In agreement with previously reported results for Yb:LiNbO₃ waveguides [14,20], we observed the expected four main peaks around 960, 980, 1008, and 1062 nm.

4. Summary

The diffusion of Yb in LiNbO₃ can be described by Fick’s law of diffusion. The experimental values determined in this work reveal an anisotropic diffusion coefficient with higher values for the diffusion along the crystallographic c-axis (z-axis). No anisotropy was found for the (maximum) solubility of Yb in LiNbO₃. However, the solubility is temperature-dependent. When the diffusion reservoir is not exhausted, small grains of Yb remain on top of the surface, leading to high surface roughness, which has to be strictly avoided when fabricating optical waveguides. Absorption and fluorescence measurements for Yb diffusion-doped ridge waveguides are in good agreement with results published for volume-doped bulk substrates. These results are essential for the future development of efficient Yb-based laser sources in LiNbO₃ ridge waveguides.