With the increasing popularity of imaging devices as well as the rapid spread of social media and multimedia sharing websites, digital images and videos have become an essential part of daily life, especially in everyday communication. Consequently, there is a growing need for effective systems that are able to monitor the quality of visual signals. Obviously, the most reliable way of assessing image quality is to perform subjective user studies, which involves the gathering of individual quality scores. However, the compilation and evaluation of a subjective user study are very slow and laborious processes. Furthermore, their application in a real-time system is impossible. In contrast, objective image quality assessment (IQA) involves the development of quantitative measures and algorithms for estimating image quality.
Objective IQA is classified based on the availability of the reference image. Full-reference image quality assessment (FR-IQA) methods have full access to the reference image, whereas no-reference image quality assessment (NR-IQA) algorithms possess only the distorted digital image. In contrast, reduced-reference image quality assessment (RR-IQA) methods have partial information about the reference image; for example, as a set of extracted features. Objective IQA algorithms are evaluated on benchmark databases containing the distorted images and their corresponding mean opinion scores (MOSs), which were collected during subjective user studies. The MOS is a real number, typically in the range 1.0–5.0, where 1.0 represents the lowest quality and 5.0 denotes the best quality. Furthermore, the MOS of an image is its arithmetic mean over all collected individual quality ratings. As already mentioned, publicly available IQA databases help researchers to devise and evaluate IQA algorithms and metrics. Existing IQA datasets can be grouped into two categories with respect to the introduced image distortion types. The first category contains images with artificial distortions, while the images of the second category are taken from sources with “natural” degradation without any additional artificial distortions.
1.1. Related Work
Many traditional NR-IQA algorithms rely on the so-called natural scene statistics (NSS) [
1] model. These methods assume that natural images possess a particular regularity that is modified by visual distortion. Further, by quantifying the deviation from the natural statistics, perceptual image quality can be determined. NSS-based feature vectors usually rely on the wavelet transform [
2], discrete cosine transform [
3], curvelet transform [
4], shearlet transform [
5], or transforms to other spatial domains [
6]. DIIVINE [
2] (Distortion Identification-based Image Verity and INtegrity Evaluation) exploits NSS using wavelet transform and consists of two steps. Namely, a probabilistic distortion identification stage is followed by a distortion-specific quality assessment one. In contrast, He et al. [
7] presented a sparse feature representation of NSS using also the wavelet transform. Saad et al. [
3] built a feature vector from DCT coefficients. Subsequently, a Bayesian inference approach was applied for the prediction of perceptual quality scores. In [
8], the authors presented a detailed review about the use of local binary pattern texture descriptors in NR-IQA.
Another line of work focuses on opinion-unaware algorithms that require neither training samples nor human subjective scores. Zhang et al. [
9] introduced the integrated local natural image quality evaluator (IL-NIQE), which combines features of NSS with multivariate Gaussian models of image patches. This evaluator uses several quality-aware NSS features, i.e., the statistics of normalized luminance, mean subtracted and contrast-normalized products of pairs of adjacent coefficients, gradient, log-Gabor filter responses, and color (after the transformation into a logarithmic-scale opponent color space).
Kim et al. [
10] introduced a no-reference image quality predictor called the blind image evaluator based on a convolutional neural network (BIECON), in which the training process is carried out in two steps. First, local metric score regression and then subjective score regression are conducted. During the local metric score regression, non-overlapping image patches are trained independently; FR-IQA methods such as SSIM or GMS are used for the target patches. Then, the CNN trained on image patches is refined by targeting the subjective image score of the complete image. Similarly, the training of a multi-task end-to-end optimized deep neural network [
11] is carried out in two steps. Namely, this architecture contains two sub-networks: a distortion identification network and a quality prediction network. Furthermore, a biologically inspired generalized divisive normalization [
12] is applied as the activation function in the network instead of rectified linear units (ReLUs). Similarly, Fan et al. [
13] introduced a two-stage framework. First, a distortion type classifier identifies the distortion type then a fusion algorithm is applied to aggregate the results of expert networks and produce a perceptual quality score.
In recent years, many algorithms relying on deep learning have been proposed. Because of the small size of many existing image quality benchmark databases, most deep learning based methods employ CNNs as feature extractors or take patches from the training images to increase the database size. The CNN framework of Kang et al. [
14] is trained on non-overlapping image patches extracted from the training images. Furthermore, these patches inherit the MOS of their source images. For preprocessing, local contrast normalization is employed. The applied CNN consists of conventional building blocks, such as convolutional, pooling, and fully connected layers. Bosse et al. [
15] introduced a similar method. Namely, they developed a 12-layer CNN that is trained on
image patches. Furthermore, a weighted average patch aggregation method was introduced in which weights representing the relative importance of image patches in quality assessment are learned by a subnetwork. In contrast, Li et al. [
16] combined a CNN trained on image patches with the Prewitt magnitudes of segmented images to predict perceptual quality.
Li et al. [
17] trained a CNN on
image patches and employed it as a feature extractor. In this method, a feature vector of length 800 represents each image patch of an input image and the sum of image patches’ feature vectors is associated with the original input image. Finally, a support vector regressor (SVR) is trained to evaluate the image quality using the feature vector representing the input image. In contrast, Bianco et al. [
18] utilized a fine-tuned AlexNet [
19] as a feature extractor on the target database. Specifically, image quality is predicted by averaging the quality ratings on multiple randomly sampled image patches. Further, the perceptual quality of each patch is predicted by an SVR trained on deep features extracted with the help of a fine-tuned AlexNet [
19]. Similarly, Gao et al. [
20] employed a pretrained CNN as a feature extractor, but they generate one feature vector for each CNN layer. Furthermore, a quality score is predicted for each feature vector using an SVR. Finally, the overall perceptual quality of the image is determined by averaging these quality scores. In contrast, Zhang et al. [
21] trained first a CNN to identify image distortion types and levels. Furthermore, the authors took another CNN, which was trained on ImageNet, to deal with authentic distortions. To predict perceptual image quality, the features of the last convolutional layers were pooled bi-linearly and mapped onto perceptual quality scores with a fully-connected layer. He et al. [
22] proposed a method containing two steps. In the first step, a sequence of image patches is created from the input image. Subsequently, features are extracted with the help of a CNN and long short-term memory (LSTM) is utilized to evaluate the level of image distortion. In the second stage, the model is trained to predict the patches’ quality score. Finally, a saliency weighted procedure is applied to determine the whole image’s quality from the patch-wise scores. Similarly, Ji et al. [
23] utilized a CNN and LSTM for NR-IQA, but the deep features were extracted from the convolutional layers of a VGG16 [
24] network. In contrast to other algorithms, Zhang et al. [
25] proposed an opinion-unaware deep method. Namely, high-contrast image patches were selected using deep convolutional maps from pristine images which were used to train a multi-variate Gaussian model.
1.2. Contributions
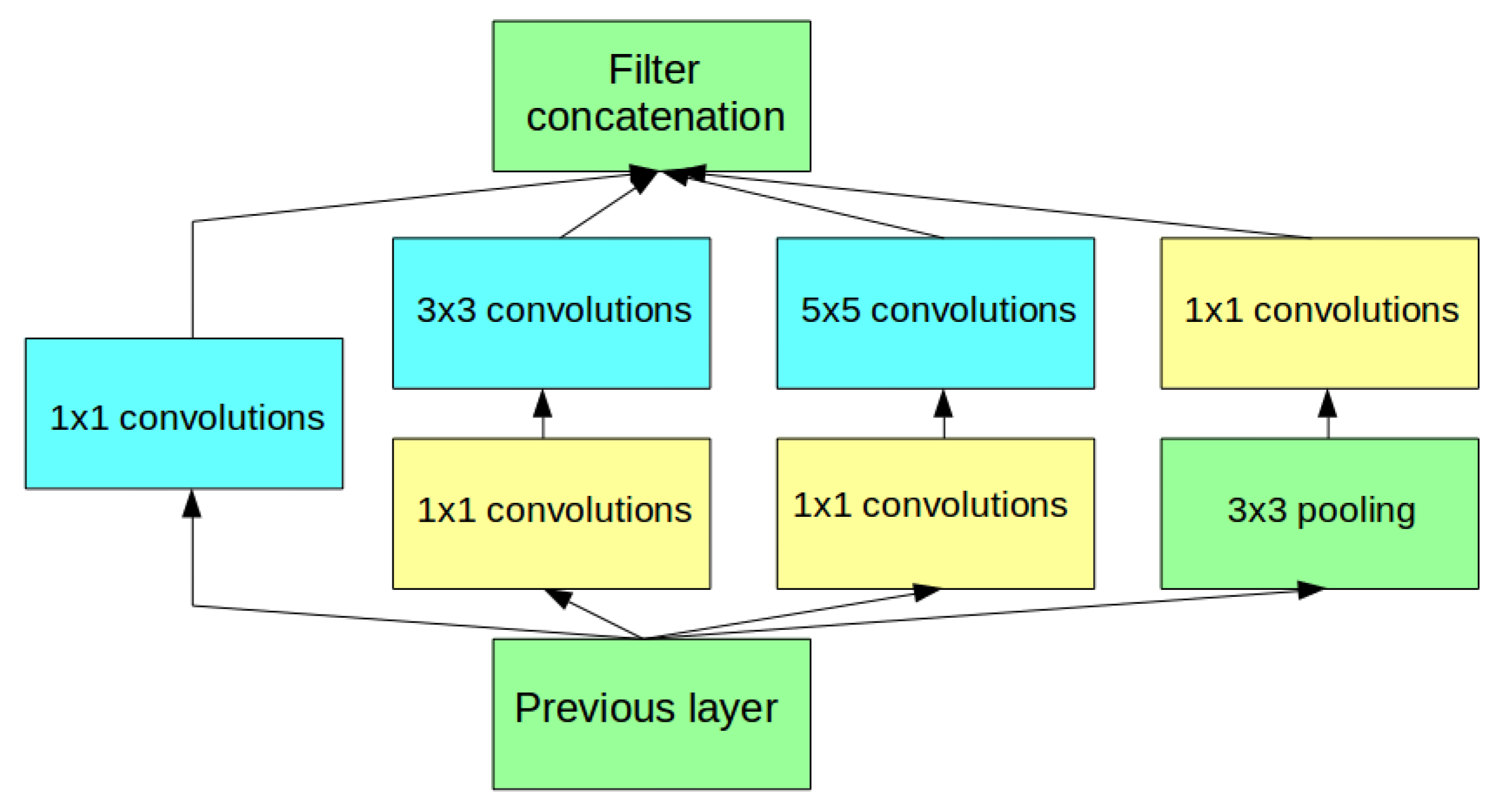
Convolutional neural networks (CNNs) have demonstrated great success in a wide range of computer vision tasks [
26,
27,
28], including NR-IQA [
14,
15,
16,
29]. Furthermore, pretrained CNNs can also provide a useful feature representation for a variety of tasks [
30]. In contrast, employing pretrained CNNs is not straightforward. One major challenge is that CNNs require a fixed input size. To overcome this constraint, previous methods for NR-IQA [
14,
15,
16,
18] take patches from the input image. Furthermore, the evaluation of perceptual quality was based on these image patches or on the features extracted from them. In this paper, we make the following contributions. We introduce a unified and content-preserving architecture that relies on the Inception modules of pretrained CNNs, such as GoogLeNet [
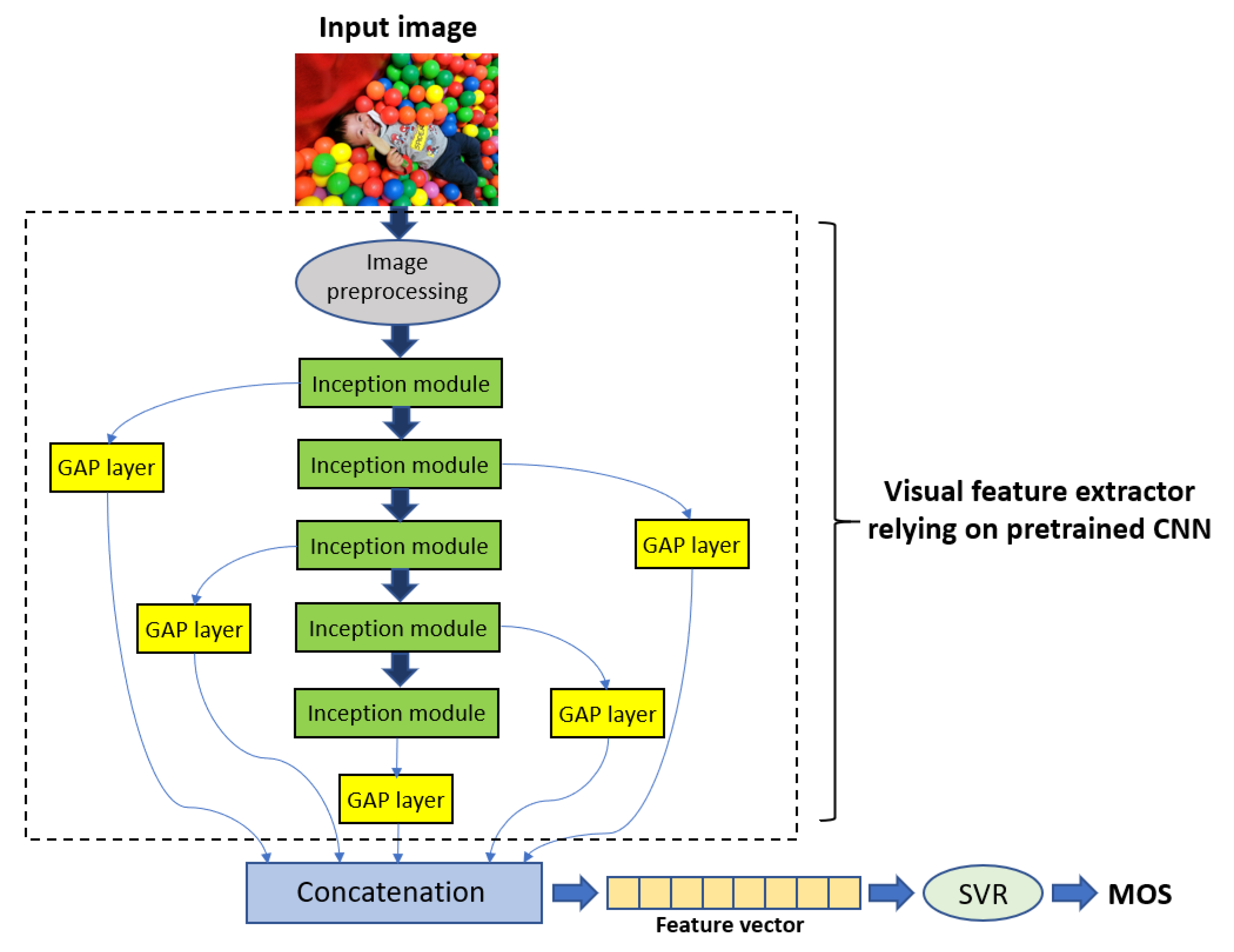
31] or Inception-V3 [
32]. Specifically, this novel architecture applies visual features extracted from multiple Inception modules of pretrained CNNs and pooled by global average pooling (GAP) layers. In this manner, we obtain both intermediate-level and high-level representation from CNNs and each level of representation is considered to predict image quality. Due to this architecture, we do not take patches from the input image as in previous methods [
14,
15,
16,
18]. Unlike previous deep architectures [
15,
18,
22], we do not utilize only the deep features of the last layer of a pretrained CNN. Instead, we carefully examine the effect of different features extracted from different layers on the prediction performance and we point out that the combination of deep features from mid- and high-level layers results in significant prediction performance increase. With experiments on three publicly available benchmark databases, we demonstrate that the proposed method is able to outperform other state-of-the-art methods. Specifically, we utilized KonIQ-10k [
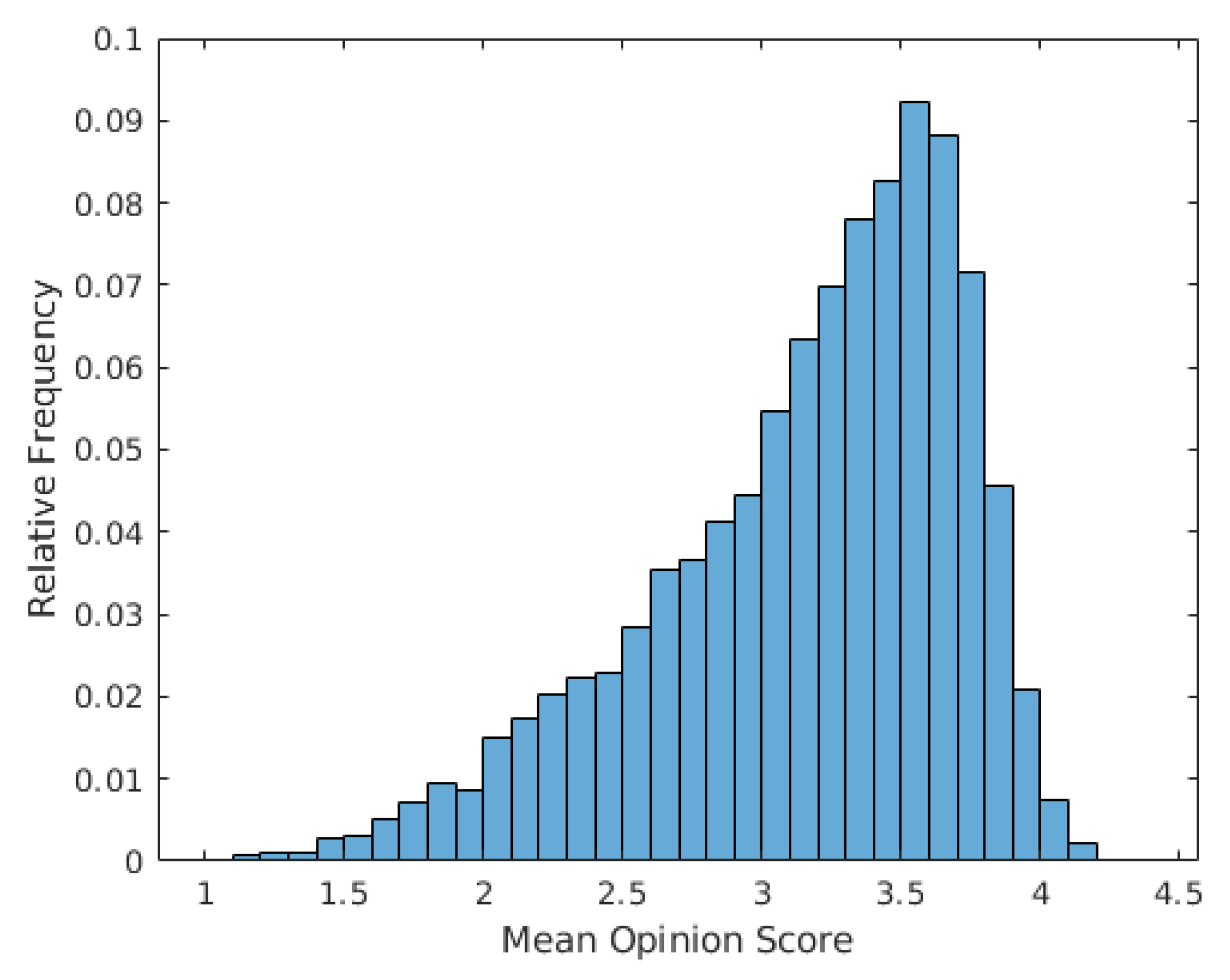
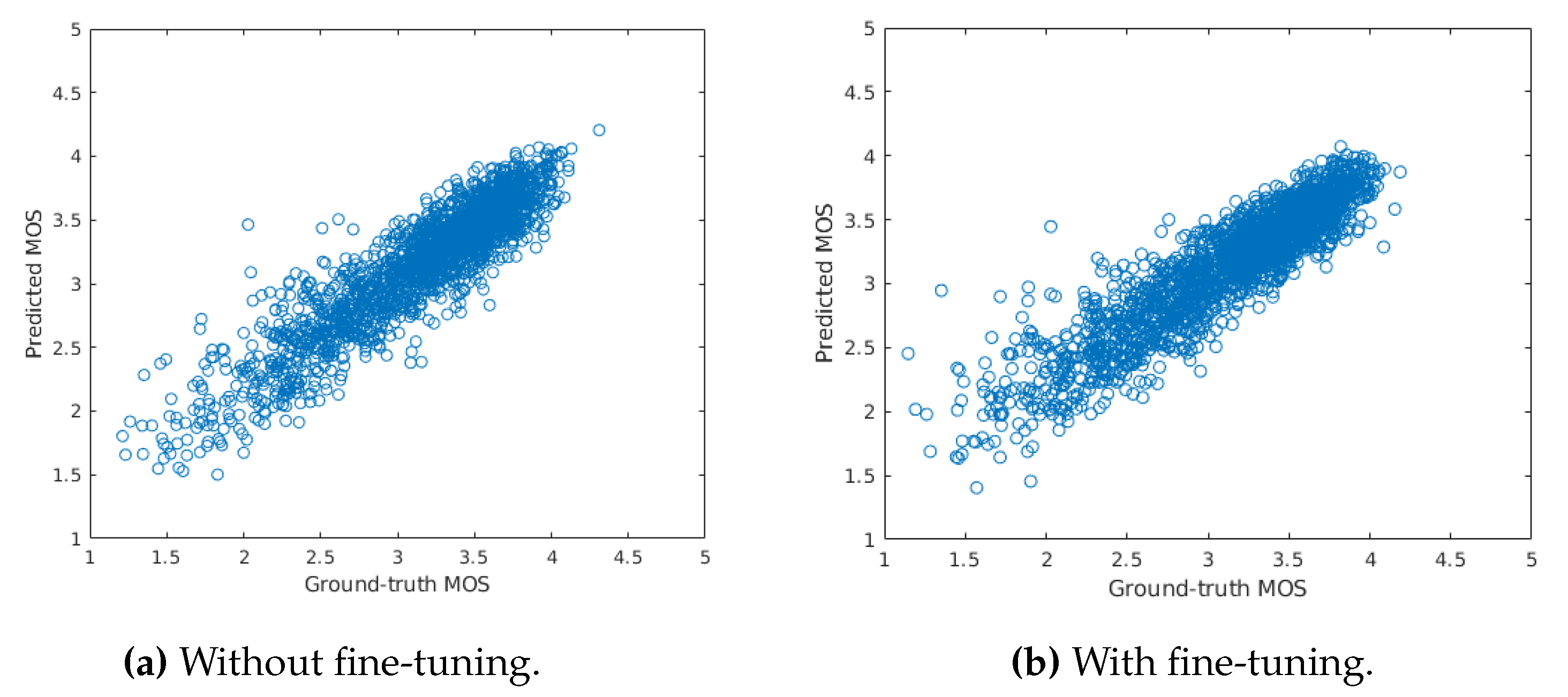
33], KADID-10k [
34], and TID2013 [
35] databases. KonIQ-10k [
33] is the largest publicly available database containing 10,073 images with authentic distortions, while KADID-10k [
34] consists of 81 reference images and 10,125 distorted ones (81 reference images × 25 types of distortions × 5 levels of distortions). TID2013 [
35] is significantly smaller than KonIQ-10k [
33] or KADID-10k [
34] because it contains 25 reference images and 3000 distorted ones (25 reference images × 24 types of distortions × 5 levels of distortions). For a cross database test, LIVE In the Wild Image Quality Challenge Database [
36] was applied, which contains 1162 images with authentic distortions evaluated by over 8100 unique human observers.
The remainder of this paper is organized as follows.
Section 2 introduces our proposed approach. In
Section 3, the experimental results and analysis are presented. A conclusion is drawn in
Section 4.