1. Introduction
The number of young patients with functional impairment of the upper limbs caused by stroke has increased rapidly, as influenced by accelerated pace of life, poor lifestyles and environmental factors [
1,
2]. Limb movement disorder, which is caused by hemiplegia after stroke, not only reduces the quality of life of patients, but also brings great pain to their physiology and psychology. Effective rehabilitation training can improve the defect of patients’ nerve function and maintain the degree of joint activity; it also prevents joint spasms and enhances the final rehabilitation degree of patients’ motor functions significantly [
3]. The traditional rehabilitation training is one-to-one auxiliary exercise for patients by therapists. This method is difficult to develop an effective treatment plan, and it is tough to control accurately [
4]. With the development of rehabilitation robot technology and rehabilitation medicine, the rehabilitation robot has become a novel motor nerve rehabilitation treatment technology. It is of great significance to take advantage of rehabilitation robot technology for rehabilitation training to the recovery of limb function of stroke patients [
5]. The traditional methods of treatment, which are based on the therapist’s clinical experience, have the problems of large staff consumption, long rehabilitation cycles, limited rehabilitation effects, and so on. The research and application of rehabilitation robot system is expected to alleviate the contradiction between supply and demand of rehabilitation medical resources effectively, and improve the quality of life of stroke patients [
6,
7].
The upper limb rehabilitation robot can be divided into two types according to the structural form: terminal traction and exoskeleton type. The terminal traction type mainly provides the rehabilitation training of plane movement. However, the exoskeleton type extends the rehabilitation training range from plane to three-dimensional (3D) space, which can assist the affected limb to complete the rehabilitation training in 3D space. The exoskeleton rehabilitation robot generally drives the movement of the patient’s limbs through the auxiliary device (also known as exoskeleton mechanical structure). The structure of the auxiliary device is similar to the skeleton structure of the human limbs. During the training, the patient’s limbs and the corresponding parts of the auxiliary device are bound together, and the connecting rod of the auxiliary device swings around the corresponding joint, so as to bring the moving limbs into motion. It can make the patient’s limbs train in different postures through controlling the trajectories of power-assist device. At present, the structural design method of exoskeleton rehabilitation robot is one of the hot issues in the research of rehabilitation robot. Owing to different mechanical structures and rehabilitation principles, a variety of exoskeleton rehabilitation robots are developed, e.g., a dynamic exoskeleton system ADEN-7 robot with 7 degrees of freedom [
8], an ARMIN robot with six degrees of freedom (four active and two passive) semi exoskeleton structure [
9], an ARMEO robot providing arm weight reduction support system training, enhancing performance feedback and evaluation tools [
10], etc. In addition, the pneumatic muscle is used as a driver to realize four degrees of freedom active auxiliary motion RUPERT robot [
11], hydraulic drive robot LIMPACT [
12], suspended rope drive robot CAREX [
13]. After that, researchers developed and designed the upper limb rehabilitation robot based on pneumatic muscle drive, unpowered upper limb rehabilitation robot, hybrid drive upper limb rehabilitation robot and under drive exoskeleton upper limb rehabilitation robot [
14,
15,
16,
17,
18,
19,
20,
21,
22]. The exoskeleton rehabilitation robot solves the problem of controlling the motion amplitude and moment of each joint of human body in the process of rehabilitation training, and overcomes the disadvantage that the end guided rehabilitation robot can only perform simple rehabilitation training (linear motion or circular motion) with small motion amplitude. Currently it is a relatively safe and efficient rehabilitation robot structure. However, in the design of exoskeleton prostheses, the matching of mechanical joint motion axis and human joint motion axis is very important. The exoskeleton produces unexpected forces at the patient’s joint under mismatched condition, which not only causes joint pain and injury to the patient, but also limits the movement space of the patient’s limbs, and reduces the effect of rehabilitation training. Therefore, the axis of each pair of motion is matched with the rotation center of each joint of the human body as far as possible in the design of exoskeleton rehabilitation apparatus. The motion of each joint of exoskeleton rehabilitation device is realized mainly by rotating or moving the pair, and good results have been obtained [
23,
24]. Compared with the artificial rehabilitation treatment, the rehabilitation robot system has the advantages of high training accuracy, easy to quantify the amount of exercise, and long-term one-to-one scientific rehabilitation treatment for patients.
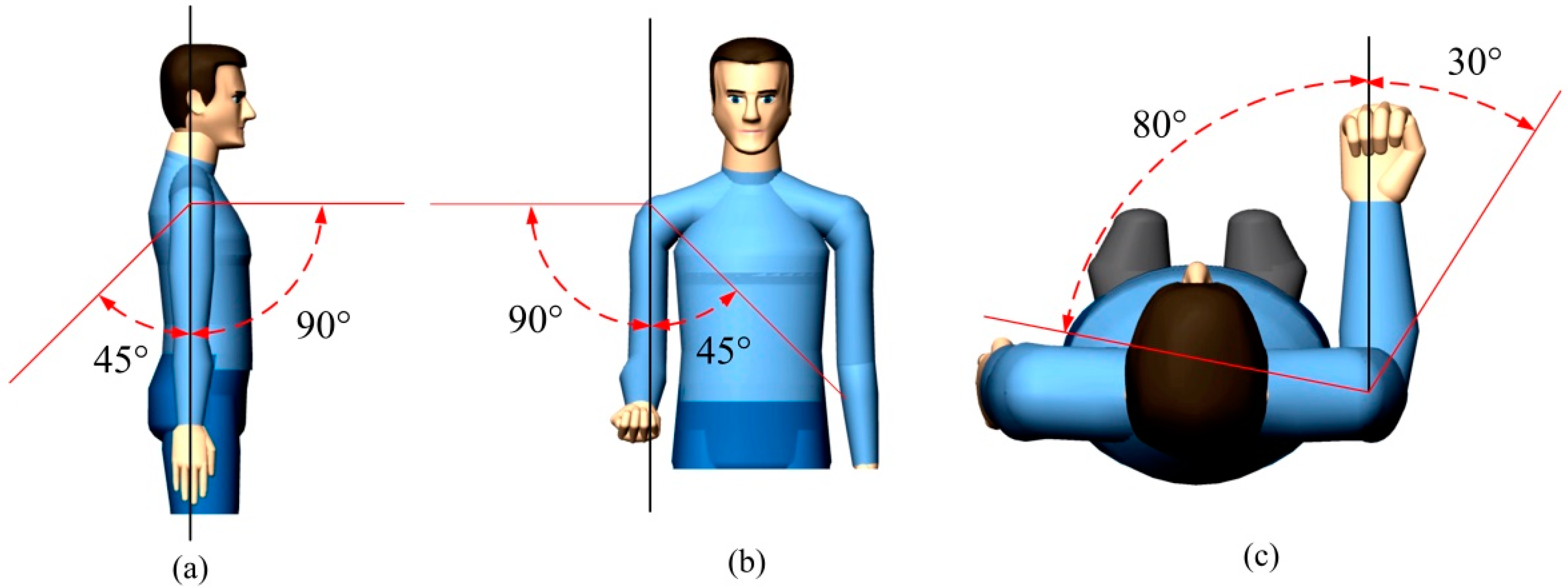
To satisfy the rehabilitation needs of patients with limb disorders, a wearable upper limb rehabilitation robot is designed and developed in this article, which is mainly a device for mid-term semi-active rehabilitation training and post-active rehabilitation training for stroke patients. Owing to understanding the disadvantages of traditional rehabilitation training and the performances of rehabilitation robots, combined with the human upper limb muscle anatomy characteristic and relevant parameters, we determine the arm movement of each joint angle range from all the bones and joints of upper limb movement characteristics, this paper proposes a design scheme of the tensegrity structure wearable upper limbs rehabilitation robot. The wearable upper limb rehabilitation robot is utilized to the exercise rehabilitation treatment of hemiplegic limb to maintain the range of motion of the limb, prevent the muscle atrophy of the limb, enhance the muscle strength of the limb, and promote the recovery of the limb function. Therefore, it can provide an effective rehabilitation equipment for patients with hemiplegia of upper limb caused by stroke.
In this paper, due to the study of anatomy, motion mechanism and motion range of human upper limb, the motion angle range of each joint is determined for human arm, and the mechanical mechanism on each degree of freedom is designed for wearable upper limb rehabilitation robot. First, to establish the spatial pose relationship between each motion component and the end-effector of the wearable upper limb rehabilitation robot, the motion model is established with the Denavit–Hartenberg (D-H) parameter method and the motion space is analyzed for wearable upper limb rehabilitation robot. The kinematics analysis is used to analyze the motion of the wearable upper limb rehabilitation robot. Secondly, to verify whether the wearable upper limb rehabilitation robot can realize the auxiliary upper limb functional rehabilitation training, the working space is analyzed for the wearable upper limb rehabilitation robot. Thirdly, to analyze the output torque of wearable upper limb rehabilitation robot, the dynamic simulation of the robot is carried out. Lastly, the control system of wearable upper limb rehabilitation robot is designed, which obtained the tracking results of robot rehabilitation training. It further verifies that the rationality of the design of wearable upper limb rehabilitation robot.
The main contributions of this paper are summarized as follows:
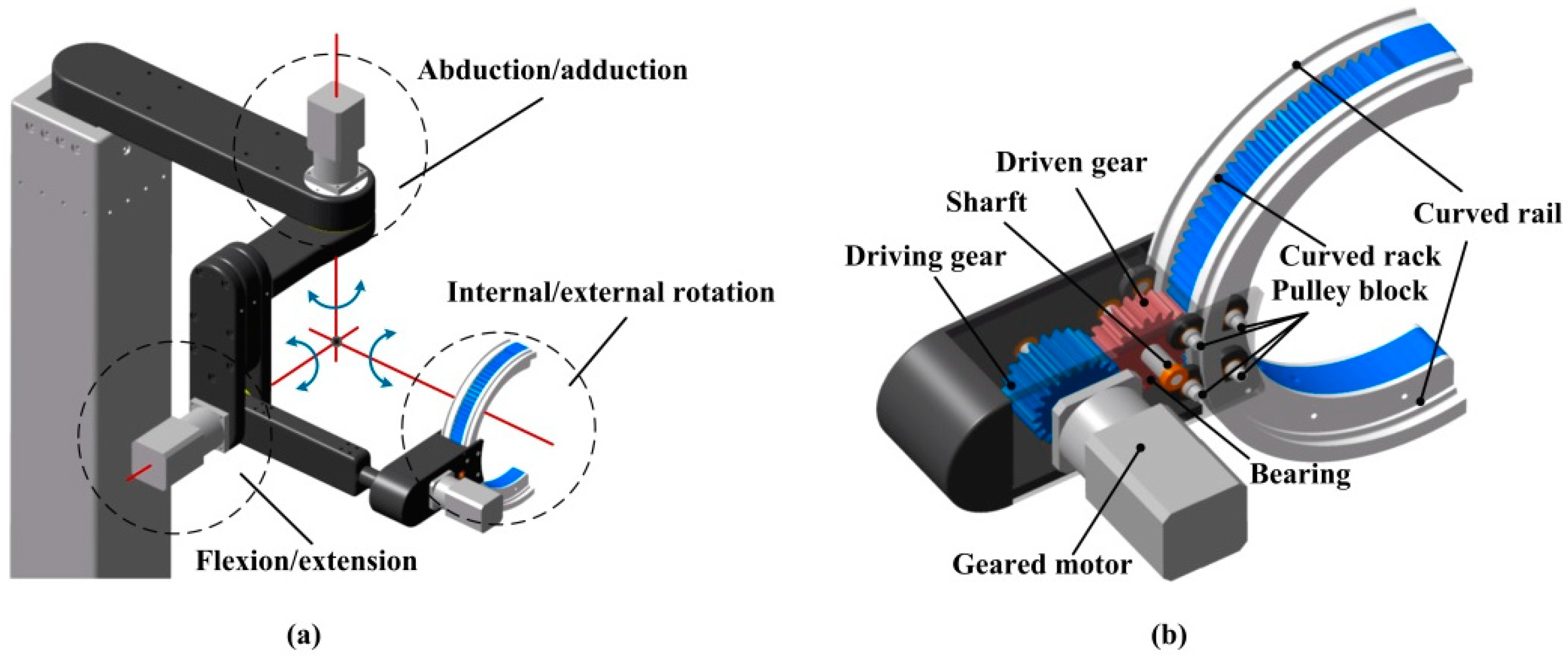
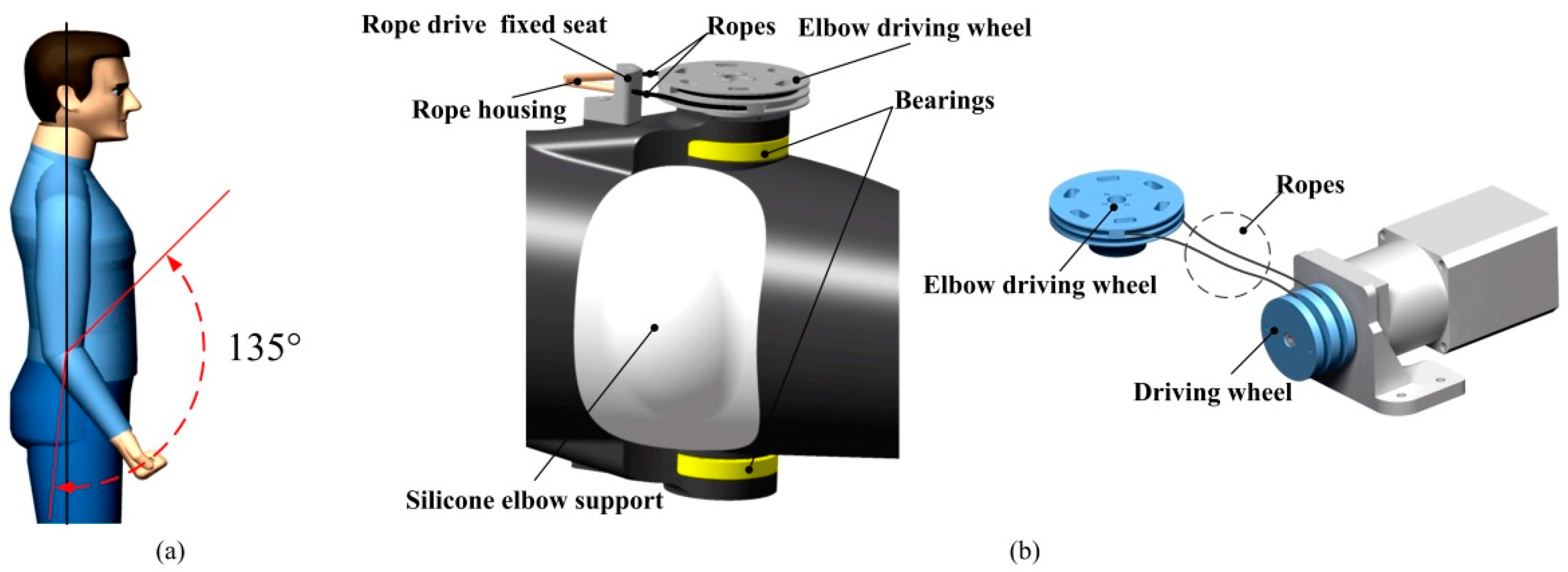
(1) Owing to the anatomy theory, motion mechanism and range of human upper limbs, a novel wearable upper limb rehabilitation robot with tension mechanism is firstly designed, investigated and analyzed for upper limb injured patients based on flexible transmission during rehabilitation training process. A cable-driven modular parallel joints are innovatively designed for elbow/wrist and a shoulder joint driven by a toothed belt. All the cable-driven motors are rear-mounted to achieve long-distance transmission and reduce the drive inertia of the end joints. The gear belt is exploited to drive the joints of a wearable upper limb rehabilitation robot, which realizing high precision meshing. The design approach of the wearable upper limb rehabilitation robot facilitates the rehabilitation training of the joint, effectively reduces the volume, mass and inertia of the actuators, and achieves the lightweight design of the overall structure.
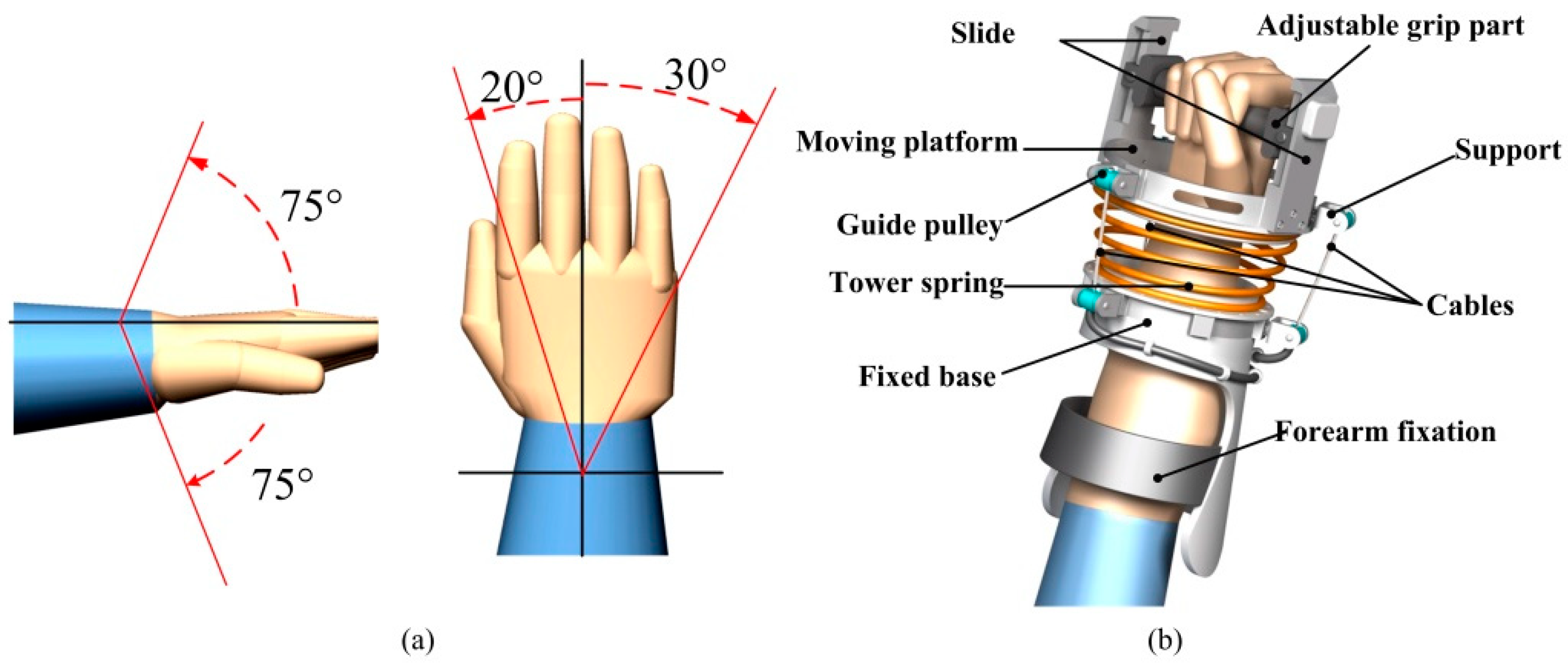
(2) Additionally, this paper proposes a flexibly parallel mechanism of humanoid wrist driven by rope and supported through a compression spring. The fixed base and moving platform of the wearable upper limb rehabilitation robot are connected by three ropes and a conical compression spring. The springs are designed by simulating the human wrist and support the mobile platform to complete the wrist movement, while the ropes are constructed via simulating the wrist muscles to control the wearable upper limb rehabilitation robot. In this paper, the design approach will contribute to the further study of parallel mechanisms with flexible joints. The results will play an important role in reappearing the movement of human wrist and promote the development of rehabilitation robot and rope drive technology.
(3) The kinematics and workspace of the wearable upper limb rehabilitation robot are verified and analyzed based on the D-H method and Monte Carlo method. It demonstrates that the wearable upper limb rehabilitation robot can satisfy the requirements of rehabilitation training through kinematics/dynamics analysis and rehabilitation training experiments. Therefore, it also further verifies that the feasibility and effectiveness of the design method, which provides a valuable idea for improving rehabilitation robot mechanism.
The rest of this paper are organized as follows. From the perspective of bionics,
Section 2 analyzes the joints of the wearable upper limb rehabilitation robot, and designs the mechanical system model of the joints. To obtain the relationship of rotation and translation between adjacent members of the wearable upper limb rehabilitation robot and its terminal pose, the kinematics model is investigated and analyzed for the wearable upper limb rehabilitation robot, and the correctness of the solutions is demonstrated for forward/inverse kinematics of the wearable upper limb rehabilitation robot in
Section 3. Owing to the Monte Carlo method, the workspace and full workspace are analyzed and obtained for the wearable upper limb rehabilitation robot in
Section 3.
Section 4 simulates and analyzes the kinematics/dynamics model of the wearable upper limb rehabilitation robot to demonstrating the stability of the motion state and verifying the output torque of the motor can satisfy the needs of rehabilitation training process. In
Section 5, the control system is designed for the wearable upper limb rehabilitation robot, and the rehabilitation training process is completed for upper limb injured patients, followed by the tracking result of the robot rehabilitation training. Conclusions are drawn in
Section 6.
3. Kinematic Analysis
Because the object of robot’s service is the injured limb, the injured limb wears on the robot and moves together under its traction to achieve rehabilitation training. It is a basis of motion control and execution of rehabilitation training. In order to enable the rehabilitation robot to perform more efficient motion control in the process of rehabilitation training, the movement between the robot’s end and each joint can be coordinated by establishing the spatial pose relationship between the robot’s motion components and the end-effector. The movement variation of each joint of the wearable rehabilitation robot can be appropriately changed, and the movement between the end of the wearable rehabilitation robot and each joint can be adjusted to achieve the expected rehabilitation training requirements.
3.1. Forward Kinematics
The wearable upper limb rehabilitation robot is a typical human-machine cooperation system. The robot is consistent with the movement of the affected limb of the human body. Therefore, to accurately obtain the motion curve of the affected limb, a forward kinematic analysis is required for the wearable upper limb rehabilitation robot. To ensure that the designed wearable upper limb rehabilitation robot has good applicability and practical applications, the D-H parameter model of the wearable upper limb rehabilitation robot based on the D-H coordinate system method needs to set related parameters, which including describing the connecting rod, which used to describe the geometric characteristic parameters of connecting rods, the connection parameter relationship between two connecting rods and the parameters that define the relationship between connecting rods. Lastly, the parameters can be brought into the correlation transformation matrix to get the corresponding results by setting the parameters.
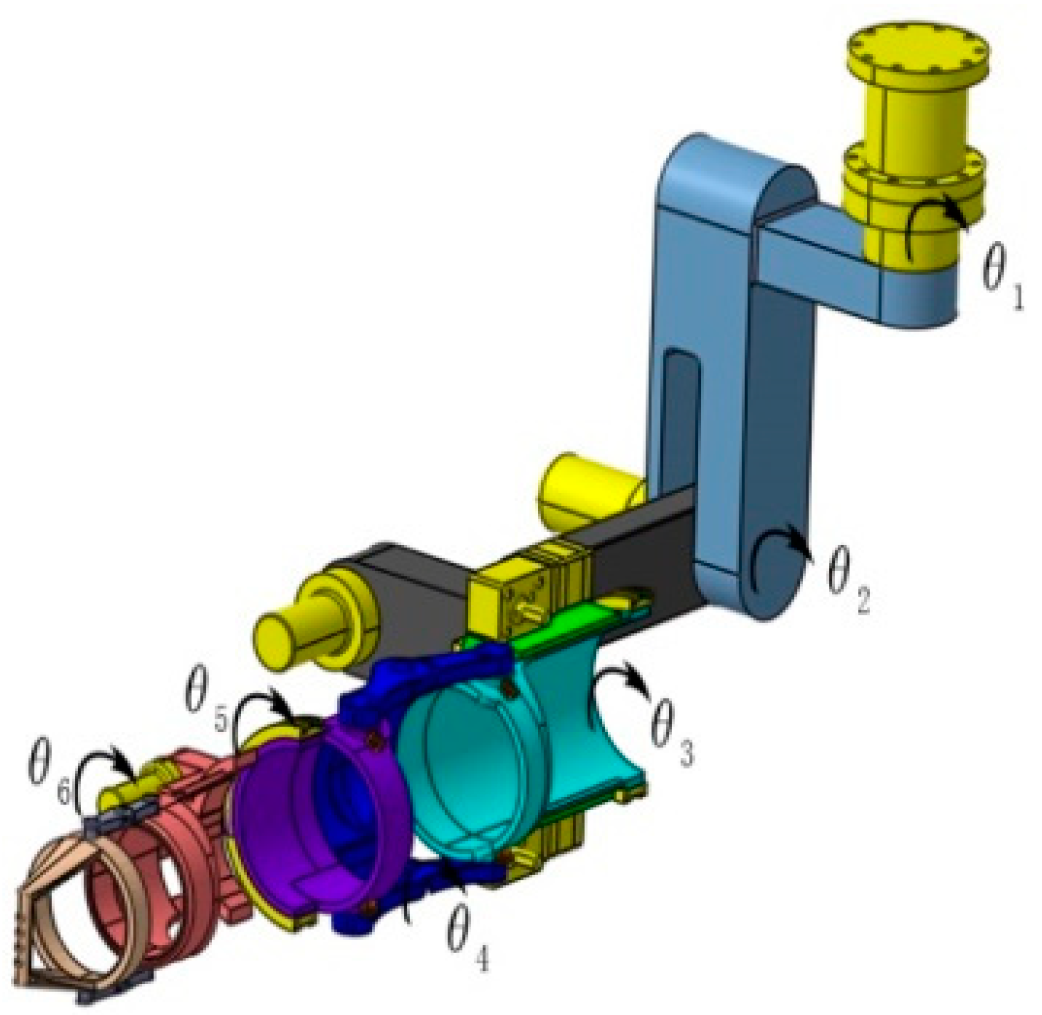
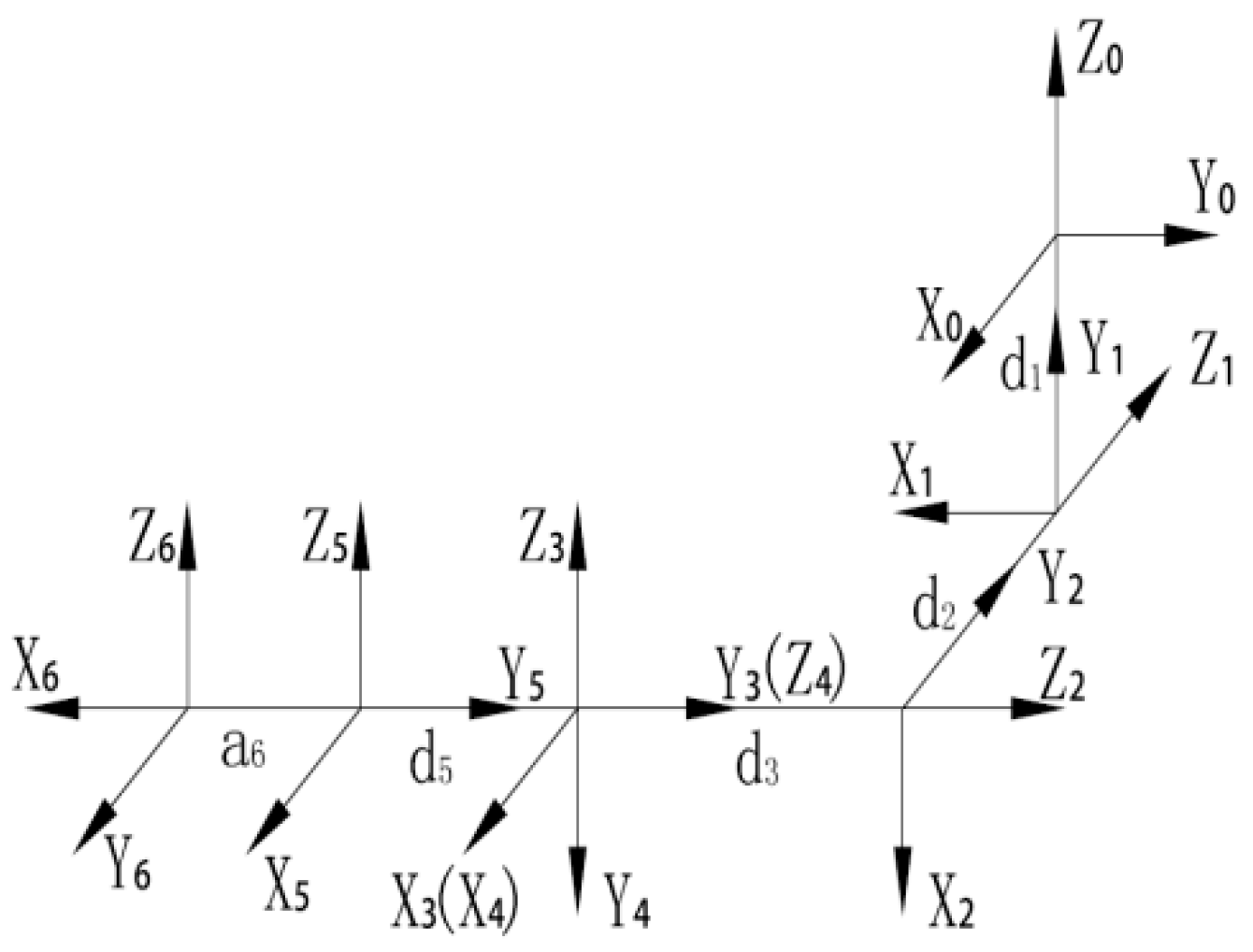
In order to obtain the relationship between the rotation and translation among adjacent members of the wearable upper limb rehabilitation robot and its terminal pose, a reference coordinate system should be assigned to each joint [
36]. In this paper, according to kinematics theory, Denavit–Hartenberg (D-H) coordinate system method is adopted to establish the D-H parameter model of the upper limb rehabilitation robot ontology (see
Figure 6), as shown in
Figure 7. The geometric size of each connecting rod of the rehabilitation robot can be described by four parameters.
and
are used to describe the geometric features of the connecting rod itself. The numerical values are determined by the distance and included angle between the axes
and
The other parameters offset
and joint angle
represent the connection relationship between the two connecting rods, and the values are determined by the distance and included angle between the axes
and
.The parameters of the rehabilitation robot D-H model are listed in
Table 2.
According to the spatial coordinate system established for each joint of the wearable upper limb rehabilitation robot, forward kinematics analysis is carried out, i.e., the coordinate transformation from coordinate system
to coordinate system
. Based on the robotics theory, the vector described in coordinate system
is mapped to coordinate system
by coordinate transformation:
where c means a cosine function and s represents sine function.
For a wearable upper limb rehabilitation robot, when the coordinate system of each link is determined, the parameters of each link can be obtained. According to Formula (1), it can be known that the pose matrix
between the two rods is:
Therefore, the matrix transformation calculation formula can be obtained by the robot’s end handle posture relative to the robot’s base coordinate system:
where
is the direction vector of the terminal, and,
is the position vector of the terminal.
To obtain the solution of positive kinematics, the matrices are multiplied as follows:
3.2. Workspace Analysis
The workspace of the rehabilitation robot is the set of points that the hand reference points can reach in space during the operation of the rehabilitation robot [
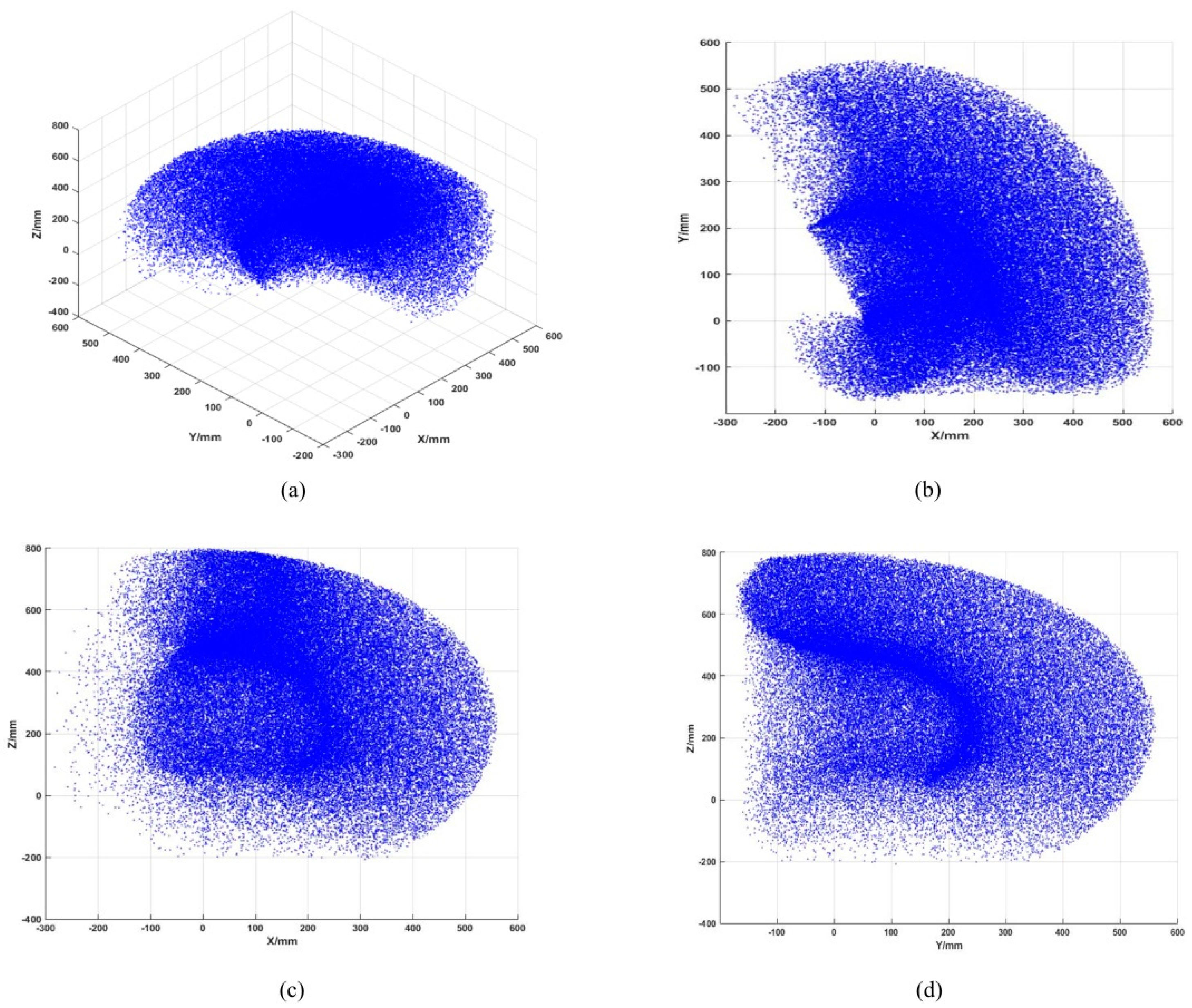
37]. It is a key element to estimate the robot rehabilitation training. Moreover, it provides a key point for evaluating the rationality of machine design. In this paper, the calculation is the set of the end can reach the target point when the rehabilitation robot is given all pose, i.e., the full workspace. The Monte Carlo method is exploited to analyze the workspace of the rehabilitation robot, being a kind of numerical calculation method guided by probability and statistics theory. Taking the end of the wearable upper limb rehabilitation robot as the reference point and combining the position vector in the forward kinematics equation, the set of all random points that generate the reference point constitutes the workspace of the wearable upper limb rehabilitation robot. In the specified range, the angle value of each joint is generated by random sampling method, and then the angle value is substituted into the positive solution calculation program to obtain the corresponding end position point. After 100,000 simulation computations, which can be obtained the terminal spot cloud.
The Programming and Robotics Toolbox of MATLAB software is utilized to adjust the random points. When the sample size is 100,000, the simulation diagram of the wearable upper limb rehabilitation robot’s workspace is obtained, as shown in
Figure 8.
Geometric construction can be calculated more easily to construct the boundary of the maximum range. Due to the linear relationship between the components, the terminal pose corresponding to the joint angles cannot be predicted in extreme cases. However, this design method is to simulate the possible arrival space, and give the relevant probability point cloud.
As can be seen from
Figure 8, the workspace is a sector in XOZ view, and it is approximate in XOY view and YOZ view, which is roughly an ellipse removing part of both ends of the long axis. According to
Figure 8 and kinematic analysis, it concludes that the working radius of the robot’s workspace on the X-axis and Y-axis is 795 mm, and the working radius on the Z-axis is 552 mm. According to ergonomics, the average length of the medium human arm in China is 742 mm [
38], indicating that the limit position of the wearable upper limb rehabilitation robot is very close to the dynamic limit position of the human upper limb. Therefore, the wearable upper limb rehabilitation robot designed to meet the needs of upper limb rehabilitation. Meanwhile, due to the limitation of mechanical structure and its size, a cavity appears near the base of the wearable upper limb rehabilitation robot. The size of the cavity is relevant to the size of the base.
3.3. Inverse Kinematics
Wearable upper limb rehabilitation robots often assist patients with hemiplegia to complete some tasks in daily life, such as eating, holding things, and touching the head, to achieve the purpose of restoring upper limb motor function. If the task is given, the end position is reached by the wearable upper limb rehabilitation robot at this time. In order to determine the parameters of each joint angle under the known position of the end effector, the wearable upper limb rehabilitation robot is solved of inverse kinematics.
The inverse kinematics solution mainly includes two kinds of numerical solutions and closed solutions. When the numerical method is used, the specific value of the joint variable can be obtained by using a recursive algorithm. The result of the numerical calculation can only be used. The independent variable cannot be given at random and the calculated value can be obtained [
39]. On the other hand, the closed solution method can be deduced according to the formula, and the dependent variable can be obtained by giving any independent variable. Because the closed solution is more accurate and faster than the numerical method, and it is easy to distinguish all possible solutions, the wearable upper limb rehabilitation robot designed in this paper satisfies the Pieper criterion in robot kinematics, therefore, this paper uses the closed solution to solve, which provide a basis for subsequent structural optimization and motion control.
Given the parameter values of D-H
can be obtained by inversely solving the following matrices:
Then,
where
means the integer value, and the value of
must be within the range of the value of
at the joint angle;
,
;
,
,
The parameters of a certain number of position points which can be considered as the end of the wearable upper limb rehabilitation robot are substituted into the above formula to obtain the corresponding theoretical rotation angles of each joint. It is consistent with the rotation angle of each joint in the 3D model. Thereby, it verifies the correctness of the inverse kinematics solution of the wearable upper limb rehabilitation robot.
Since there are multiple inverse solutions in the process of solving inverse kinematics, this article introduces three criteria for selecting solutions for robots to avoid singular solutions.
(1) Robot motion range requirements. During the structural design of the wearable upper limb rehabilitation robot, the motion range of each joint is designed according to the requirements of the upper limb motion range of the human body and to avoid mutual interference between mechanisms. Therefore, the joints are required to meet the requirements of the joint motion range during the movement, that is, the following inequality is satisfied:
where
is the minimum limit angle of joint motion, and
is the maximum limit angle of joint motion.
(2) Criterion of motion continuity. The application environment of the wearable upper limb rehabilitation robot is to assist functional rehabilitation training for patients with motor dysfunction. It requires the robot to continuously run smoothly and smoothly during the movement, no joint angle motion mutation, and to avoid the movement of the end effector of the robot. Therefore, in the actual processing, the threshold value m is introduced to provide constraints and restrictions, that is, to check the absolute value of the difference between the next solution and the current joint angle value. If the value is too large, the joint is abruptly changed, then another solution is selected.
where
is the next position angle of joint motion, and
is the current position angle of joint motion.
(3) The principle of minimum end pose error. During the movement of the wearable upper limb rehabilitation robot, the position reached by the end effector and the target pose will inevitably have errors. Therefore, by comparing the final end pose transformation matrix, the end position and attitude error can be compared to achieve the goal of choosing the solution with the smallest error.
During the process of the selection for the inverse solution of the wearable upper limb rehabilitation robot, the constrained conditions will also conflict with each other. At this time, the priority of the constraints should be set according to the actual situation, so as to obtain the optimal solution.
5. Experimental Setup and Results
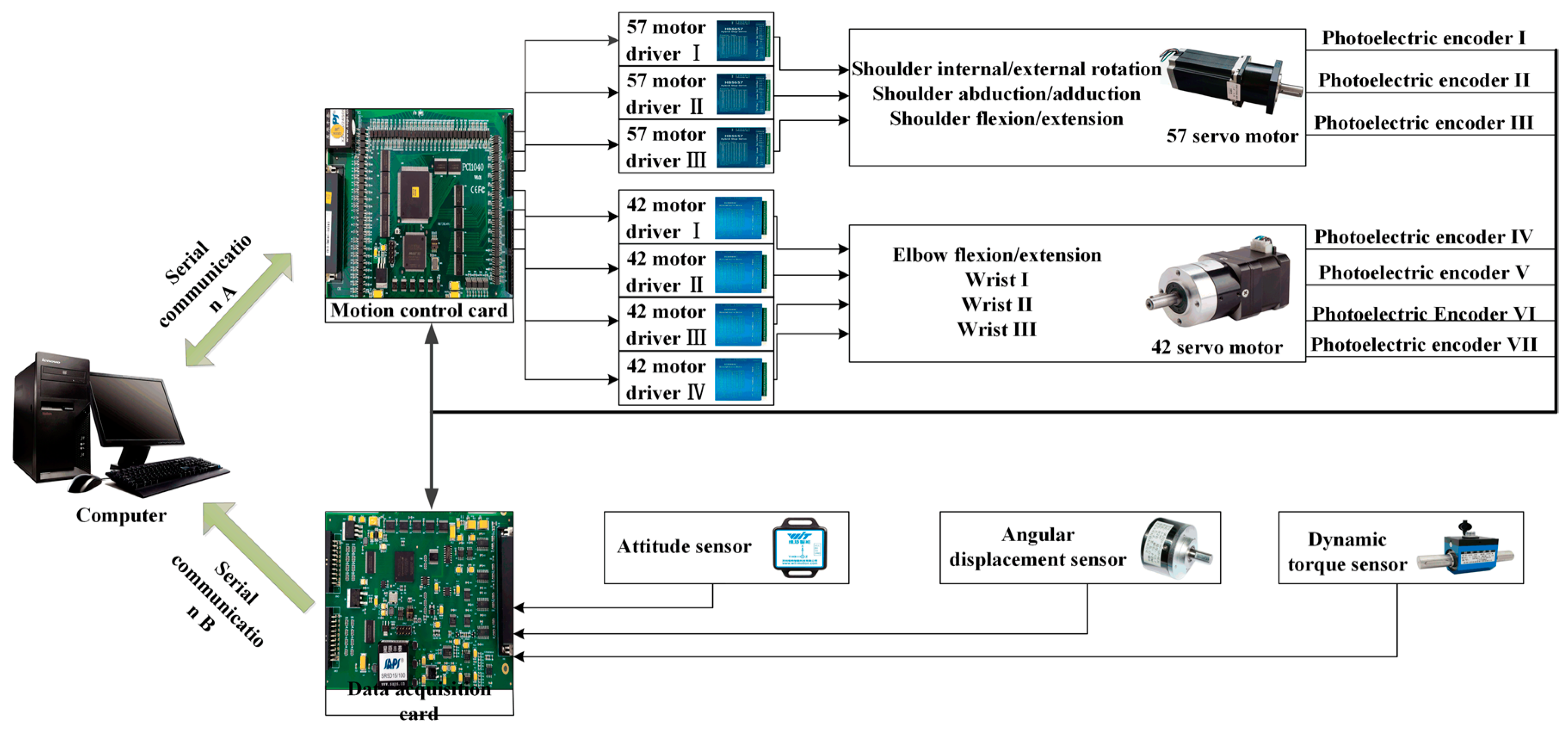
The wearable upper limb rehabilitation robot designed in this paper adopts the upper computer-controlled robot to carry out continuous passive rehabilitation training for the affected limb, and adopts two rehabilitation training methods: independent movement of single joint and combined functional movement of multiple joints. The block diagram of the overall control system is shown in
Figure 12. The lower computer of the control circuit takes the motion control card and data acquisition card as the core. The information acquisition card is used to complete data collection of 3D gyroscope, motion acceleration and other sensors. The upper computer can select the rehabilitation training mode and set the motion parameters of each joint, and then transmit the related parameters to the motion control card. The data collected by each functional sensor will be transmitted to the data acquisition card. After calculation, the data acquisition card converts the collected data into motion parameters, and then passes the motion control card to the motor rotation information, which is output to each motor driver respectively.
To realize the precise control of wearable upper limb rehabilitation robots, and reduce the motor torque error between the actual output torque and the theory, and let patients achieve the best effect of rehabilitation, the torque demand larger shoulder joint is designed in this paper. In addition, the drive motor of bending/stretching exercise and elbow flexion/stretch exercise drive motor installed on the dynamic torque sensor based on the basis of the
Section 4 results, that is to say, wearable upper limbs rehabilitation robot dynamics analysis results of output torque. The dynamic torque sensor transmits the information to the computer through the data acquisition card. The difference between the theoretical torque and the measured torque is input into the PID controller and then the torque of the motor is adjusted in real time to achieve the optimal control.
When designing a control system, it is essential to ensure the stability of the system and the safety of patients. Some control methods and neural network technique have been paid more attention to designing controller for a nonlinear system [
40,
41]. In order to prevent excessive output torque of the motor from causing secondary damage to the affected limb, a current detection circuit is adopted to feed the output current of the driver into the motion control card in real time. Once the detected current exceeds the allowable value, the motor will stop immediately. At the same time, the one-key emergency stop function is set so that the system can be stopped immediately when the patient is uncomfortable. Furthermore, gyroscope and linear velocity sensor are used to detect the real-time position, real-time speed and real-time acceleration of the motor, so as to avoid the adverse effect caused by excessive joint rotation and excessive speed on the rehabilitation training.
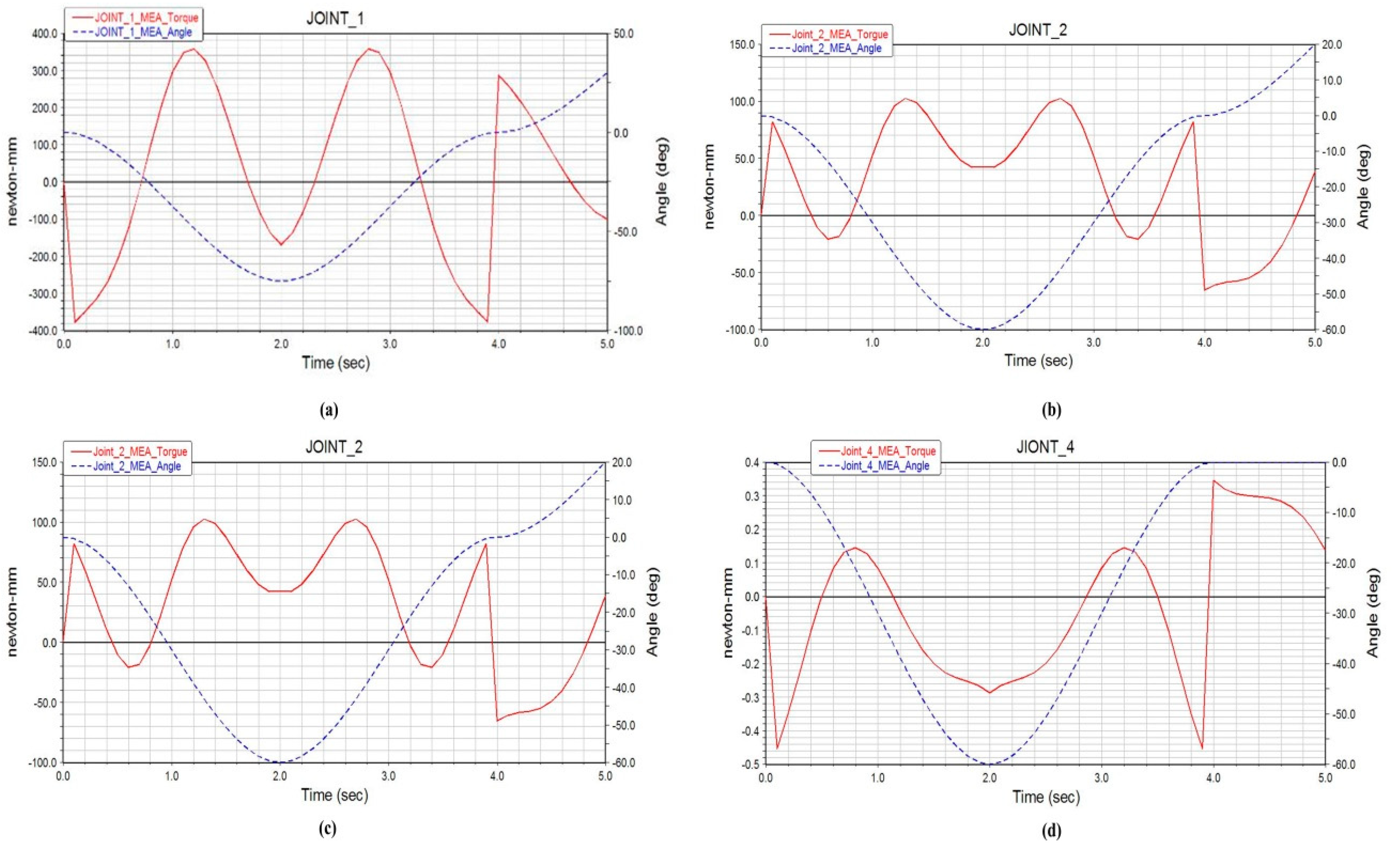
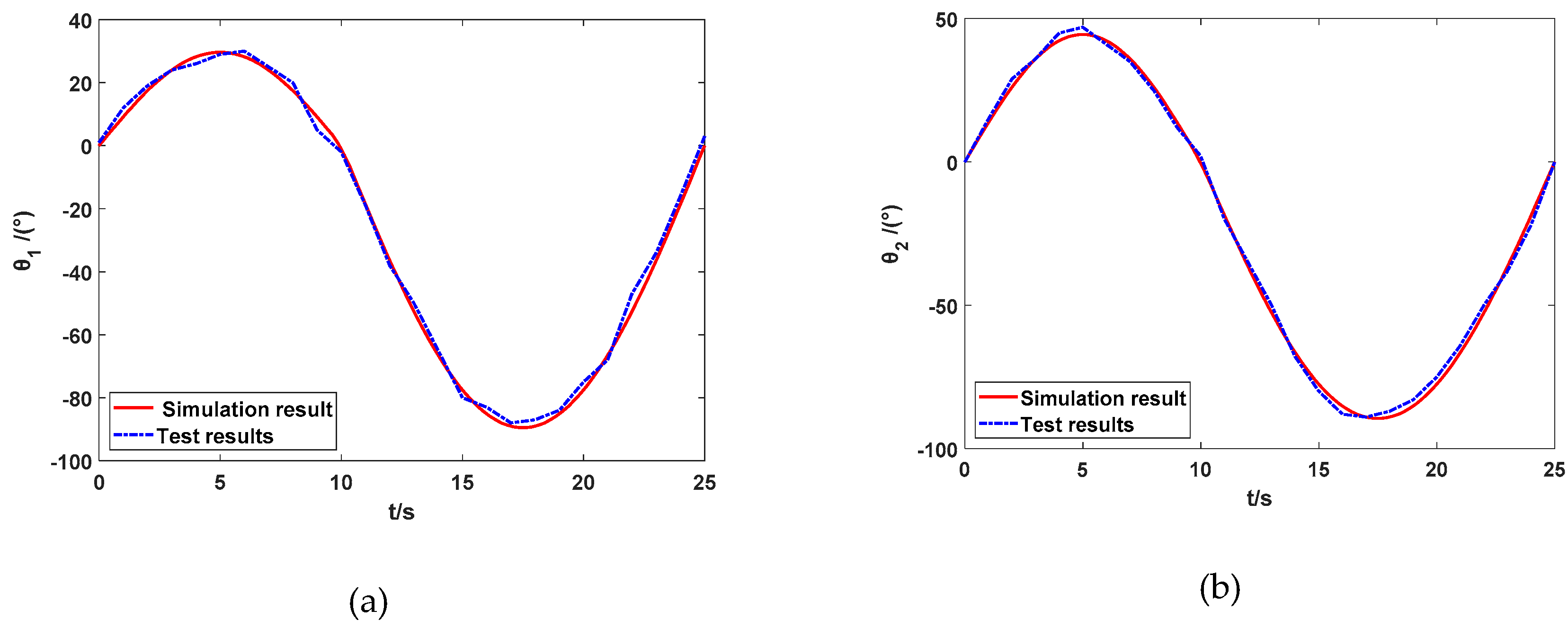
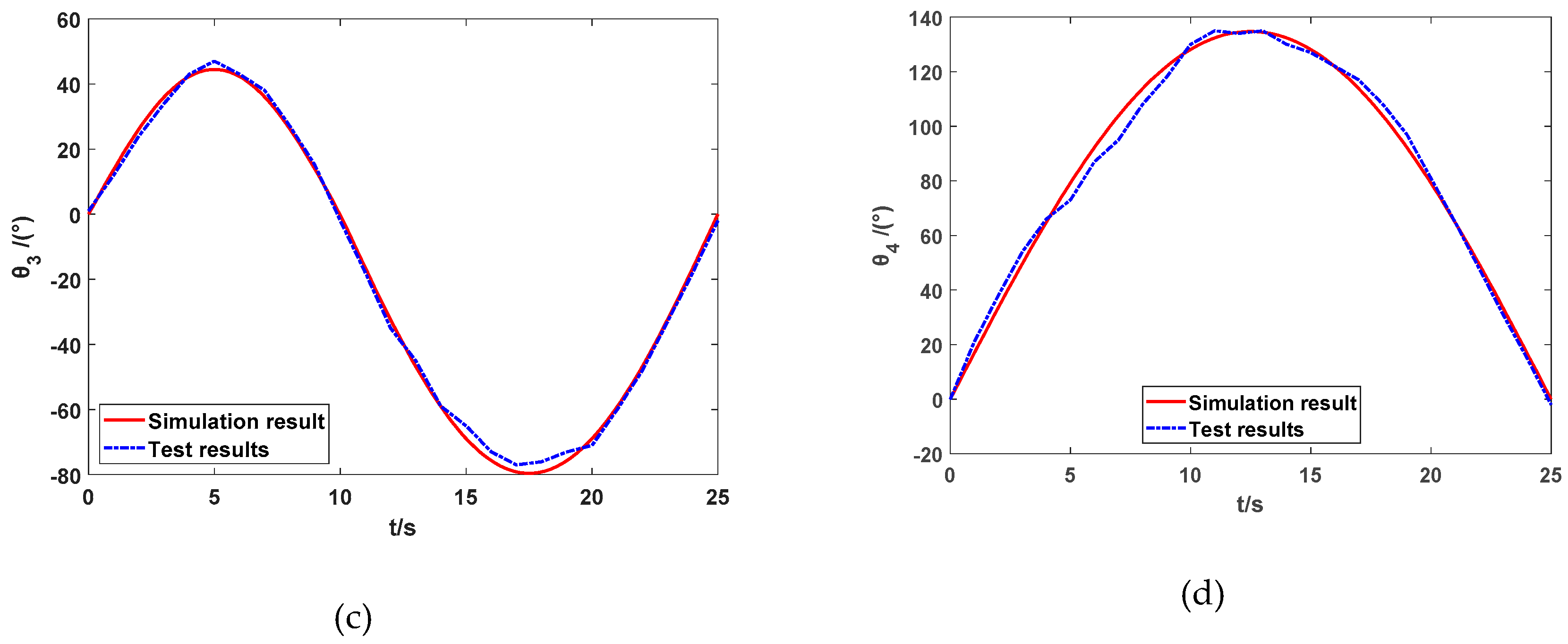
Figure 13 depicts the completed wearable upper limb rehabilitation robot prototype system and rehabilitation training. In the experiment, the time of each degree of freedom of the wearable upper limb rehabilitation robot was set to 25 s, and the range of motion was from the initial position to the extreme position. The test sampling period was 1 s. The experimental results are shown in
Figure 14. Specifically, the experiment curves of horizontal, vertical, rotation, and elbow flexion and extension of the upper limb are plotted respectively. The solid red line in the figure is the simulation result, and the blue dotted line is the test result. It can be observed, the actual angle and simulation angle of each joint of the wearable upper limb rehabilitation robot during the movement have certain deviations. It is mainly due to the error caused by the friction of the mechanical structure itself, and the subject wearing the wearable upper limb rehabilitation robot will also be difficult to avoid rehabilitation. The wearable upper limb rehabilitation robot applies a certain impedance, and one can see that the elbow joint flexion and extension error is relatively large, because this part is driven by rope and the wire rope needs to bear a large load, which increases the error caused by the elastic contraction of the wire rope itself, but these errors do not affect the training characteristics of wearable upper limb rehabilitation robot. The test results of the prototype test are consistent with the simulation results, revealing that the wearable upper limb rehabilitation robot meets the expected design requirements and can complete the motion functions required for passive rehabilitation training of the upper limbs.