Abstract
Work-related low-back disorders (WLBDs) can be caused by manual lifting tasks. Wearable devices used to monitor these tasks can be one possible way to assess the main risk factors for WLBDs. This study aims at analyzing the sensitivity of kinematic data to the risk level changes, and to define an instrument-based tool for risk classification by using kinematic data and artificial neural networks (ANNs). Twenty workers performed lifting tasks, designed by following the rules of the revised NIOSH lifting equation, with an increasing lifting index (LI). From the acquired kinematic data, we computed smoothness parameters together with kinetic, potential and mechanical energy. We used ANNs for mapping different set of features on LI levels to obtain an automatic risk estimation during these tasks. The results show that most of the calculated kinematic indexes are significantly affected by changes in LI and that all the lifting condition pairs can be correctly distinguished. Furthermore, using specific set of features, different topologies of ANNs can lead to a reliable classification of the biomechanical risk related to lifting tasks. In particular, the training sets and numbers of neurons in each hidden layer influence the ANNs performance, which is instead independent from the numbers of hidden layers. Reliable biomechanical risk estimation can be obtained by using training sets combining body and load kinematic features.
1. Introduction
Manual lifting tasks are very common in a variety of workplaces [1] and have been demonstrated to influence the occurrence of musculoskeletal problems such as work-related low-back disorders (WLBDs) [2,3,4]. Over the past three decades, a growing effort has been made to evaluate the effectiveness of ergonomic interventions in preventing and reducing the risk of developing WLBDs. Among the proposed quantitative methods, the revised National Institute for Occupational Safety and Health (NIOSH) lifting equation (RNLE) [3,5,6,7,8,9] is an established means to assess risk of low back pain (LBP) due to manual lifting. More recently, in order to overcome equation and parameter restrictions [10,11,12,13,14,15,16,17], to increase the accuracy and minimize job misidentification [10,18] and to improve the identification of the relationship between WLBDs and risk factors [19], wearable monitoring devices have been proposed for biomechanical risk assessment [20,21]. Among these, inertial measurement units (IMUs), instrumented gloves, surface electromyography (sEMG) sensors, smart footwear-based wearable systems [22,23,24,25] and vision-based tracking systems [26] can monitor workers’ motor behavior if individually placed on the body segments or embedded in elastic suits.
The use of these instrumental techniques has been facilitated by the enormous technological advances that led to increased measurement accuracy, device miniaturization, and more efficient connections via wireless protocols (i.e., WiFi and Bluetooth).
Among the instrumental and quantitative approaches proposed to evaluate different tasks and classify the biomechanical risk, those based on artificial neural networks (ANNs) are particularly promising [27,28,29,30]. An ANN is a model, constituted by elementary processing units (neurons) interconnected in different topologies, mimicking the behavior of real neuronal networks. In layered ANNs, the neurons are arranged in several layers through which information is transmitted in a single direction. The characteristics of each neuron behavior are modified based on the presentation of a number of examples as inputs, through different learning methods. This makes thus ANNs able to respond effectively to generalization, classification and clustering problems, if a sufficient number of examples is provided. For this reason, ANNs’ impact spread over many fields of research, including robotics, biology, psychology, computer science, and ergonomics. For the WLBD problem the predictive capacity of this model has been proven to be greater than that achieved by statistical methods [31]. ANNs with different topologies have been tested to predict the risk of developing WLBDs: Zurada et al. [27] and Chen et al. [28,29] used ANNs to classify the risk (low-risk and high-risk) according to the associated probability of causing WLBDs, by using as input signals some mechanical parameters associated with risk factors (e.g., sagittal angle, lift rate, peak, peak twist velocity average, peak lateral velocity maximum, peak moment).
Not only mechanical features, but also surface electromyography (sEMG) signals recorded from trunk muscles during the performance of lifting tasks can provide risk-related information. Amplitude and coordination parameters calculated from sEMG data (maximum, average rectified value, root mean square, muscle coactivation, [32,33] have been shown to be correlated to the compression and shear forces and moments at L5-S1 joint, and able to detect the risk levels. Recently, Varrecchia and colleagues [30] used ANNs for mapping surface sEMG features on lifting index (LI) levels for biomechanical risk estimation, defined based on the RNLE. They have shown that LI levels during lifting tasks can be reliably estimated through multi-layered ANNs by using a set of combined sEMG time and frequency features obtained only from the erector spinae muscle.
Recently, besides sEMG parameters, kinematic data have been used to calculate indices dealing with mechanical lifting energy consumption; those indices have been proven to be proportional to the LI and also correlated with forces that determine injuries at the L5-S1 joint, so showing an ability in discriminating all the risk condition pairs [34].
Supported by this last study, here we hypothesize that kinematic features as ANN inputs could predict the risk levels while performing controlled lifting tasks with different LI values identified by the NIOSH equation [7,8] in a controlled environment.
The aims of this study were to verify the sensitivity of kinematic data to the risk level and to test the ability of machine-learning techniques (ANNs) to map kinematic features on LI levels so leading to a reliable biomechanical risk estimation.
2. Materials and Methods
In this study we have used data acquired during the experimental procedures detailed in Ranavolo and colleagues [34], briefly described in Section 2.1, Section 2.2, Section 2.3, Section 2.4 and Section 2.5.
2.1. Participants
Twenty male subjects participated to this study. They had the following anthropometric characteristics: age 33.30 ± 7.39 years, body mass index 24.37 ± 2.67 kg/m2. Inclusion criteria were: no history of the following disorders: musculoskeletal disorders; orthopedic or neurological diseases; limbs or trunk surgery; back pain. All participants provided an informed consent that complied with the Declaration of Helsinki.
2.2. Data Recordings
The movement of 33 spherical reflective markers (15 mm in diameter) placed over the cutaneous projections of the spinous processes as in Ranavolo and colleagues [34] were tracked by a optoelectronic system (SMART-DX 6000 System, BTS, Milan, Italy) equipped with eight infrared cameras (sampling frequency, 340 Hz). Four markers were also placed over the four vertexes of a load consisting of a plastic crate [34].
2.3. Experimental Procedures
The calibration procedure was carried on by using a global reference system defined as in the recommendations of the International Society of Biomechanics [35]. Spatial accuracy was 0.2 mm. Before recording the measurement session, each participant underwent a familiarization session with the lifting tasks. The manual material lifting task was performed in a quiet room (humidity 40.60 ± 5.03% and temperature 23.30 ± 0.95 °C) by asking the participants to stand in a neutral posture and lift with both hands a plastic crate with handles; three different lifting conditions, according to the RNLE [8], were recorded for each participant.
Three lifting conditions were included in the protocol each characterized by the values reported in Table 1 [34] for the parameters—load weight (L), horizontal location (H), vertical location (V), vertical travel distance (D), asymmetry angle (A), lifting frequency (F)—and the corresponding multipliers. Nine trials (three repetitions of each of the three lifting conditions) were executed by each participant.

Table 1.
NIOSH protocol values for each lifting task are reported.
2.4. Definition of Lifting Cycle
After acquisition, Smart Analyzer (BTS) and Matlab (version 8.0.0.783; MathWorks, Natick, MA, USA) were used to process the data. The vertical displacement and velocity of one of the four markers placed over the vertexes of the crate (right side in anterior position) were evaluated. By differentiating the marker’s position after a 4-Hz low-pass filter (Butterworth 3rd order), the velocities were obtained. The onset and the end point of the lifting task were defined, respectively, as the time point at which the velocity of the crate marker on the vertical axis exceeded the value of 0.025 m/s [30] and as the time point when the crate marker velocity fell below the same velocity threshold. Kinematic and kinetic data underwent a time normalization procedure so as to be reduced to 101 samples using a polynomial procedure.
2.5. Center of Mass and Lifting Energy Consumption (Lec)
From kinematic data, we calculated CoM values for three different complexes: the load alone (CoML); the complex of the load together with the multi-segment upper body model (hands, forearms, upper arms, trunk, head) defined as CoMUpp+L; the complex of the load together with the whole body model (pelvis, thighs, shanks, feet and multi-segment upper body model) defined as (CoMTot) [29]. The barycentre of the crate was considered the CoML.
For each of the calculated CoMs, the kinetic energy (Ek), the potential energy (Ep) and the mechanical energy (EM) during the lifting tasks were calculated as in [34]. For each CoM, Lifting energy consumption (LEC) values were calculated as the difference between maximum and minimum values of each Ek (LECk), Ep (LECp) and EM (LECM) within the lifting cycle. In particular, we calculated these parameters for the three complexes: LECk_L, LECp_L, and LECM_L for CoML, LECk_Tot, LECp_Tot and LECM_Tot for CoMTot and LECk_Upp+L, LECp_Upp+L and LECM_Upp+L for CoMUpp+L.
2.6. Jerk
The flexion-extension angles of trunk, elbow and knee were evaluated using the kinematic data. The angular jerk, that is the third derivative over time of the angle displacement [degrees/s3]) [36], was calculated for the trunk (Jtrunk), elbow (Jelbow) and knee (Jknee) angles ([degrees/s3]).
For each repetition, we computed the jerk square mean (JSM) values for the trunk (JSMtrunk), the elbow (JSMelbow) and the knee (JSMknee), defined as follows:
where is the instantaneous value of the jerk, and n is the total number of data points (101). The JSM is an index of smoothness of movement: the lower the Jerk is, the smoother the movements are [36].
2.7. Neural Networks Design and Mapping Functions
A neural network model (ANNs) was used to estimate the biomechanical risk in terms of LI on the basis of kinematic features, as schematically described in Figure 1.
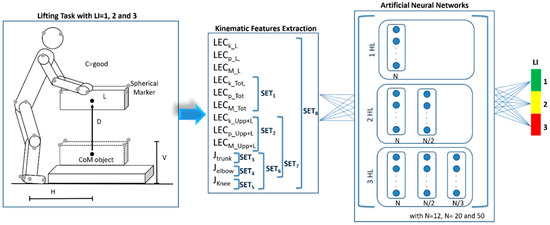
Figure 1.
Schematic diagram of the study. The three boxes of the flowchart represent the lifting task, the feature extraction from recorded data, and the ANN architecture to map kinetic features on the Lifting Index (1, 2, and 3) levels. L: load weight; H: horizontal location; V: vertical location; D: vertical travel distance; C: hand-to-object coupling; N: number of nodes in the first hidden layer (HL).
Particularly, we used a set of feedforwards ANNs trained using different feature combinations, and different network topologies: the latter were implemented by varying the number of Hidden Layers (HL) and the number of Neurons (N) populating each HL. The output set (OS) provided an orthogonal coding of the three LI levels: (1 0 0), (0 1 0) and (0 0 1) representing LI = 1, LI = 2 and LI = 3, respectively. Different features were combined into the eight training sets (SETi, I = 1, …, 8) (Figure 1) constituted as in the following:
- SET1 contained energy data derived from the CoM of the whole body-load complex (LECk_Tot, LECp_Tot and LECM_Tot);
- SET2 contained energy data derived from the CoM of the upper body-load complex (LECk_Upp+L, LECp_Upp+L and LECM_Upp+L);
- SET3 contained jerk data derived from lower limbs (Jknee);
- SET4 contained jerk data derived from upper limbs (Jelbow);
- SET5 contained jerk data derived from trunk (Jtrunk);
- SET6 contained all jerk data (Jknee, Jelbow, Jtrunk);
- SET7 contained both energy and jerk data derived from upper body and load (LECk_Upp+L, LECp_Upp+L, LECM_Upp+L, Jelbow and Jtrunk);
- SET8 contained all energy and jerk data (all extracted features).
In terms of network architecture, we tested nine different network architectures defined by the combination of number of HL and number of N in each layer. Particularly, we tested ANNs with one, two or three HL and different number of neurons in each HL: N was set to 12, 20 and 50 for the first HL (NHL1) and, in the other HL, if defined, was N/2 for the second (NHL2) and N/3 (NHL3) for the third [30].
A Levenberg-Marquardt back-propagation algorithm [37] was used to train the ANNs; the stopping criterion was defined as the occurrence of at least one of the following conditions: number of iterations = 1000, number of consecutive fails on the validation set = 6, mean square error <10−6 [25].
We trained a total of 720 ANNs (10 times × 9 network topologies × 8 training sets) using for each training a random of 80% samples as the training test and 20% as the testing set. A confusion matrix 3 × 3 was calculated for each ANNs considering the actual LI and the one estimated by the ANN on the randomly extracted testing set. Then, the mean confusion matrix was obtained for each network topology and each SET and a performance parameter (P) was calculated as the mean (%) of the elements on the diagonal of these confusion matrices, where 100% indicates the absence of misclassifications [30].
2.8. Statistical Analysis
SPSS 17.0 software (SPSS Inc., Chicago, IL, USA) was used to perform all the statistical analyses. Normality of data distribution was checked using the Shapiro-Walk test. For each LEC and for each J, a one-way repeated-measures ANOVA was performed to check for significant differences between the three risk levels. When significant differences were observed in the ANOVA, post-hoc analyses were performed using a paired t test with Bonferroni’s corrections. A three-way ANOVA test, with SET, L, N as factors, was used to assess the effect of these factors on performance; a post-hoc analysis with Bonferroni’s corrections was performed for ANOVA results showing significant differences. The statistical significance was set for p values at 0.05.
3. Results
3.1. Kinematic Feature Analysis
Figure 2 shows the mean and standard deviation for each lifting condition of each extracted JSM (Figure 2). As reported in [34], the repeated measures ANOVA revealed a significant effect of the lifting condition on LEC. Furthermore, statistically significant effects were also detected for Jtrunk (df = 2, F = 7.12, p = 0.05), Jelbow (df = 2, F = 9.39, p = 0.002) and Jknee (df = 2, F = 15.62, p = 0.001). Post hoc analysis showed significant differences (all p < 0.001) between each pair of lifting conditions for LECp and LECM for all the CoMs considered and also for LECk_Upp+L (see [29]). Furthermore, as regard LECk_Tot, significant differences were found between each pair of lifting conditions (LI = 1 vs. LI = 2: p = 0.001; LI = 1 vs. LI = 3: p = 0.005; LI = 2 vs. LI = 3: p = 0.021; see [34]). As regards J, the following significant differences were found (see Figure 2):
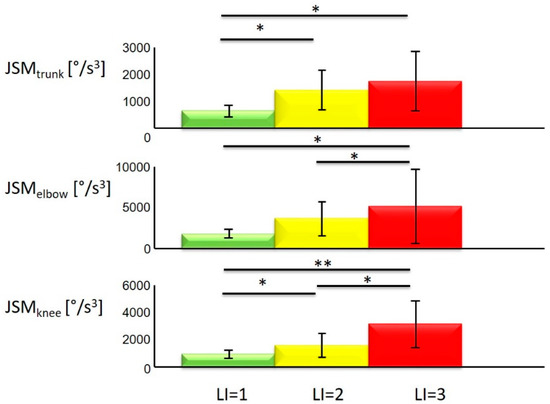
Figure 2.
Jerk square mean (JSM) values. Mean and standard deviation values of the JSM values evaluated considering angles of trunk, elbow and knee while performing manual material lifting tasks in the three different conditions (LI = 1, LI = 2 and LI = 3) and statistical significance (* means p-value < 0.05; ** means p-value < 0.001).
- LI = 1 vs. LI = 2 and LI = vs. LI = 3 (p < 0.05) for Jtrunk
- LI = 1 vs. LI = 3 and LI = 2 vs. LI = 3 (p < 0.05) for Jelbow
- LI = 1 vs. LI = 2and LI = 2 vs. LI = 3 (p < 0.05); LI = 1 vs. LI = 3 (p < 0.001) for Jknee
3.2. Mapping of Kinematic Features on Li Levels
The detection performances are reported in Figure 3; they are expressed as the detection percentage P (mean ± SD) obtained by using the nine different network topologies (in terms of HL and N) when using the eight different training sets. Furthermore, Figure 3 shows also the best confusion matrix for each SET (confusion matrix with highest value of P).
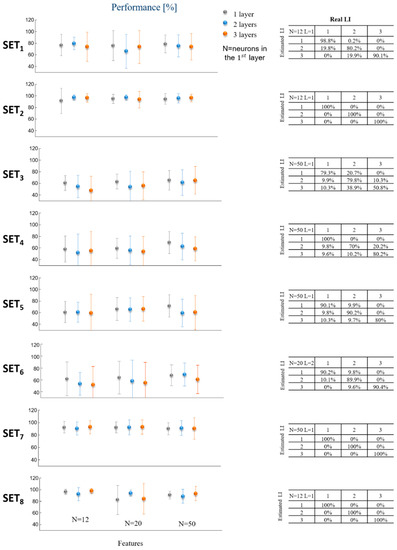
Figure 3.
ANNs performance. The performance are reported on the basis of the different training sets (SETi, i = 1, …, 8) and the nine different architectures (see Section 2.7 for details). The best mean confusion matrix was reported for each SETi.
The training set, as in the outcome of the three-way ANOVA, (df = 7; F = 174.01; p < 0.001), N (df = 2; F = 6.07; p = 0.002) and HL (df = 2; F = 5.2; p = 0.01) resulted to have a significant effect on the ANN performance. Particularly, post-hoc analysis outlined the following significant differences (p < 0.05):
- SET1 vs. all SETi;
- SET2 vs. SET3, SET4, SET5, SET6;
- SET3 vs. SET1, SET2, SET7, SET8;
- SET4 vs. SET1, SET2, SET7, SET8;
- SET5 vs. SET1, SET2, SET7, SET8;
- SET6 vs. SET1, SET2, SET7, SET8;
- SET7 vs. all SETi excepted SET2;
- SET8 vs. all SETi excepted SET2.
As regards N, from post-hoc analysis the following significant differences (p < 0.05) showed up: N = 12 vs. N = 50 and N = 20 vs. N = 50.
As regards HL, post-hoc analysis didn’t show significant differences (p > 0.05). In general, SET2, SET7 and SET8 showed higher mean values of performance with lower standard deviations (Figure 3).
Table 2 shows the sensitivity and specificity (mean ± SD) values obtained when the nine architectures of the ANNs and the different training sets.

Table 2.
Sensitivity and specificity of artificial neural networks (ANNs) considering different features (SETi, i = 1, …, 8) and nine different architectures (see Section 2.7 for details) of ANNs were represented.
.
4. Discussion
In this study, we have used ANNs and kinematic data to classify the biomechanical risk associated with freely performed dynamic lifting tasks with an increasing LI values (LI = 1, LI = 2, and LI = 3) designed using the RNLE [7,8]. The used feed-forward ANNs were trained with different training sets, on different network topologies (numbers of neurons in each hidden layer, numbers of hidden layers,), and different combinations of kinematic features as inputs (from lifting energy consumption and jerk), taken by considering different combinations of the body segments necessary to extract them (i.e., only upper body, only upper limb, total body, etc.).
A proper combination of kinematic features and network architectures can lead to a good classification. Indeed, a machine-learning approach based on ANNs was proven able to predict the biomechanical risk in lifting activities [27,28,29,30] and kinematic data (i.e., mechanical lifting energy consumption) have been proven to be sensitive to the risk level (the higher the risk, the more these parameters increase) and also correlated with forces that determine injuries at the L5-S1 joint [34].
In particular, the training sets, numbers of hidden layers, and numbers of neurons in each hidden layer influence the ANNs performance: the best performances were obtained by using energy consumption data derived from upper body and load, energy and smoothness data derived from the upper body-load complex, and, as expected, by considering all the energy and smoothness features.
ANNs trained by using the configuration of the upper body-load complex and energy data alone, show a high performance. However, this configuration takes into account the kinematic behavior of the multi-segment upper body (head, trunk, upper arms, forearms and hands) and load altogether, and it could thus fail in presence of human-robot collaboration (HRC) technologies, such as wearable assistive devices worn by the workers. For instance, the use of a spinal exoskeleton [38] could strongly reduce the muscle effort without modifying the lifting kinematics, thus implying a misclassification.
This limit linked with the use of HRC technologies could be completely eliminated, or at least greatly reduced, if the other two configurations are used. Both allow the best performance with the advantage of taking into account also information about the smoothness, the only index that could be sensitive to the use of assistive devices. Among these, SET 7 shows a reliable performance also in terms of variability, meaning that biomechanical risk estimation using this specific SET is reliable and repeatable at the same time.
Furthermore, it is worth highlighting that misclassifications between LI = 1 and LI = 3, that represent the lowest and the highest risk classes respectively, are missing. This is a desired and acceptable behavior of an LI classifier.
While complex network architectures (i.e., more than 2 hidden layers) were needed in order to reach suitable performances using ANNs to map sEMG features onto LI levels [30], in this study we have shown that increasing the network complexity does not lead to an increased risk estimation. Indeed, the best performance is almost always obtained with only one hidden layer (see Figure 3 and Table 2). This aspect is of importance when dealing with applications in real scenarios using wearable sensors, since the reduced network complexity lowers the overall computational cost needed to train the ANNs.
Limitations and Future Developments
The results obtained in this study can be applied to the experimental conditions that have been tested but little can be said regarding the applicability of the approach to composite and/or sequential manual lifting jobs characterized by significantly different lifting tasks [8,39].
Possible future developments of this study may be: (i) including, in the range of lifting task types those having the same LI but different multiplier values; (ii) testing also lifting conditions with LI values that are outside the quantized set (i.e., lower than 1, between 1 and 2, and between 2 and 3); (iii) analyzing how environment- and subject-related factors (i.e., temperature and humidity, sex, age, work experience, etc.) affect the results; moreover, while the current sample size was chosen to obtain an appropriate statistical power [40] and to adhere to the requirements given by artificial neural network training [41] increase the sample size to include analysis of gender effects. As regards this latter aspect, women and men show different risks of developing these disorders due to their physiological differences in perception of pain [42], fatigability [43], tendon properties [44], hormonal differences [44], anthropometry and muscular entities [45].
It would be also interesting to test the performance of alternative measuring devices such as wearable inertial sensors and to compare them to the traditional measurements provided by the optoelectronic systems. This evaluation would make it possible to verify the validity of the method, which appears to be much more easily applicable in both indoor and outdoor work environments.
5. Conclusions
In this study, ANNs were used for the prediction of biomechanical risk level from kinematic features during lifting tasks, which are agreed as key determinants of work-related low-back disorders. This approach has been shown able to improve the biomechanical risk estimation, suggesting the use of kinematic features in association with sEMG and kinetic features to evaluate biomechanical risk associated with work activities. These instrumental methods could be a valid integration to the established means to assess biomechanical risk (i.e., NIOSH lifting equation; [7,8]), and they can represent a viable alternative when the standardized methods cannot be used due to the equation and parameters restrictions.
Author Contributions
Conceptualization, T.V.; C.D.M., S.C. and A.R.; methodology, T.V., C.D.M. and A.R.; software, T.V. and C.D.M.; validation, T.V., C.D.M., S.C. and A.R.; formal analysis, T.V. and A.R.; investigation, T.V. and A.R.; resources, F.D., M.S. and A.R.; data curation, T.V. and C.D.M.; writing—original draft preparation, T.V. and A.R.; writing—review and editing, T.V., C.D.M., F.D., M.S., S.C. and A.R.; visualization, T.V. and C.D.M.; supervision, F.D., M.S., S.C. and A.R.; project administration, F.D., M.S. and A.R.; funding acquisition, A.R. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by EU An.Dy Project (An.Dy has received funding from the European Union’s Horizon 2020 Research and Innovation Programme, No. 731540).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Ethical Approval
As our study was considered an observational study on the basis of the definitions of the European Directive 2001/20/EC, therefore, the approval of an Ethic Committee was not requested.
References
- National Research Council (US) and Institute of Medicine (US) Panel on Musculoskeletal Disorders and the Workplace. Musculoskeletal Disorders and the Workplace: Low Back and Upper Extremities. Washington (DC): National Academies Press (US). 2001. Available online: https://www.nap.edu/catalog/10032/musculoskeletal-disorders-and-the-workplace-low-back-and-upper-extremities (accessed on 14 March 2020).
- Griffith, L.E.; Shannon, H.S.; Wells, R.P.; Walter, S.D.; Cole, D.C.; Côté, P.; Frank, J.; Hogg-Johnson, S.; Langlois, L.E. Individual participant data meta-analysis of mechanical workplace risk factors and low back pain. Am. J. Public Health 2012, 102, 309–318. [Google Scholar] [CrossRef]
- Waters, T.R.; Lu, M.; Piacitelli, L.A.; Werren, D.; Deddens, J.A. Efficacy of the revised NIOSH lifting equation to predict low back pain due to manual lifting: Expanded crosssectional analysis. J. Occup. Environ. Med. 2011, 53, 1061–1067. [Google Scholar] [CrossRef]
- Hartvigsen, J.; Bakketeig, L.S.; Leboeuf-Yde, C.; Engberg, M.; Lauritzen, T. The association between physical workload and low back pain clouded by the “healthy worker” effect: Population-based cross-sectional and 5-year prospective questionnaire study. Spine 2001, 26, 1788–1792. [Google Scholar] [CrossRef]
- Garg, A.; Boda, S.; Hegmann, K.T.; Moore, J.S.; Kapellusch, J.M.; Bhoyar, P.; Thiese, M.S.; Merryweather, A.; Deckow-Schaefer, G.; Bloswick, D.; et al. The NIOSH lifting equation and low-back pain, Part 1: Association with low-back pain in the backworks prospective cohort study. Hum. Factors 2014, 56, 6–28. [Google Scholar] [CrossRef]
- Lin, C.J.; Cheng, C.F. Lifting speed preferences and their effects on the maximal lifting capacity. Ind. Health 2017, 55, 27–34. [Google Scholar] [CrossRef]
- Waters, T.R.; Putz-Anderson, V.; Garg, A.; Fine, L.J. Revised NIOSH Equation for the Design and Evaluation of Manual Lifting Tasks. Ergonomics 1993, 36, 749–776. [Google Scholar] [CrossRef]
- Waters, T.R.; Putz-Anderson, V.; Garg, A. Applications Manual for the Revised NIOSH Lifting Equation. Cincinnati, OH: U.S. Department of Health and Human Services Public Health Service, Centers for Disease Control and Prevention. Natl. Inst. Occup. Saf. Health Div. Biomed. Behav. Sci. 1994, 94–110. Available online: https://stacks.cdc.gov/view/cdc/5434 (accessed on 20 January 2020).
- Waters, T.R.; Baron, S.L.; Piacitelli, L.; Anderson, V.; Skov, T.; Haring-Sweeney, M.; Walk, D.K.; Fine, L.J. Evaluation of the Revised NIOSH Lifting Equation. Spine 1999, 24, 386–395. [Google Scholar] [CrossRef]
- Marras, W.S.; Fine, L.J.; Ferguson, S.A.; Waters, T.R. The effectiveness of commonly used lifting assessment methods to identify industrial jobs associated with elevated risk of low-back disorders. Ergonomics 1999, 42, 229–245. [Google Scholar] [CrossRef] [PubMed]
- Lavender, S.A.; Li, Y.C.; Natarajan, R.N.; Andersson, G.B. Does the asymmetry multiplier in the 1991 NIOSH lifting equation adequately control the biomechanical loading of the spine? Ergonomics 2009, 52, 71–79. [Google Scholar] [CrossRef] [PubMed]
- Dempsey, P.G. Usability of the revised NIOSH lifting equation. Ergonomics 2002, 45, 817–828. [Google Scholar] [CrossRef] [PubMed]
- Elfeituri, F.E.; Taboun, S.M. An evaluation of the NIOSH Lifting Equation: A psychophysical and biomechanical investigation. Int. J. Occup. Saf. Ergon. 2002, 8, 243–258. [Google Scholar] [CrossRef] [PubMed]
- Dempsey, P.G.; Fathallah, F.A. Application issues and theoretical concerns regarding the 1991 NIOSH equation asymmetry multiplier. Int. J. Ind. Ergon. 1999, 23, 181–191. [Google Scholar] [CrossRef]
- Wang, M.; Garg, A.; Chang, Y.; Shin, Y.; Yeh, W.; Lee, C. The relationship between low back discomfort ratings and the NIOSH lifting index. Hum. Factors 1998, 40, 509–515. [Google Scholar] [CrossRef]
- Nussbaum, M.; Chaffin, D.; Page, G. A biomechanical investigation of the asymmetric multiplier in the revised NIOSH lifting equation. In Proceedings of the Human Factors and Ergonomics Society 39th Annual Meeting (709–713), Santa Monica, CA, USA, 19–21 April 2018. [Google Scholar]
- Karwowski, W.; Brokaw, N. Implications of the proposed revisions in a draft of the revised NIOSH lifting guide (1991) for job redesign: A field study. In Proceedings of the 36th Annual Meeting of the Human Factors Society, Atlanta, GA, USA, 12–16 October 1992; Human Factors Society: Santa Monica, CA, USA, 1995; pp. 659–663. [Google Scholar]
- Sesek, R.; Gilkey, D.; Drinkaus, P.; Bloswick, D.S.; Herron, R. Evaluation and quantification of manual materials handling risk factors. Int. J. Occup. Saf. Ergon. 2003, 9, 271–287. [Google Scholar] [CrossRef] [PubMed]
- Dempsey, P.G.; Burdorf, A.; Fathallah, F.A.; Sorock, G.S.; Hashemi, L. Influence of measurement accuracy on the application of the 1991 NIOSH equation. Appl. Ergon. 2001, 32, 91–99. [Google Scholar] [CrossRef]
- Ranavolo, A.; Draicchio, F.; Varrecchia, T.; Silvetti, A.; Iavicoli, S. Erratum: Alberto, R. Wearable Monitoring Devices for Biomechanical Risk Assessment at Work: Current Status and Future Challenges—A Systematic Review. Int. J. Environ. Res. Public Health 2018, 15, 2569. [Google Scholar] [CrossRef]
- Alberto, R.; Draicchio, F.; Varrecchia, T.; Silvetti, A.; Iavicoli, S. Wearable Monitoring Devices for Biomechanical Risk Assessment at Work: Current Status and Future Challenges-A Systematic Review. Int. J. Environ. Res. Public Health 2018, 15, 2001. [Google Scholar] [CrossRef]
- Hegde, N.; Bries, M.; Sazonov, E. A Comparative Review of Footwear-BasedWearable Systems. Electronics 2016, 5, 48. [Google Scholar] [CrossRef]
- Moufawad, E.L.; Achkar, C.; Lenbole-Hoskovec, C.; Paraschiv-Ionescu, A.; Major, K.; Büla, C.; Aminian, K. Classification and characterization of postural transitions using instrumented shoes. Med. Biol. Eng. Comput. 2018, 56, 1403–1412. [Google Scholar] [CrossRef]
- Liu, K.; Liu, Y.; Yan, J.; Sun, Z. Nondestructive Estimation of Muscle Contributions to STS Training with Different Loadings Based onWearable Sensor System. Sensors 2018, 18, 971. [Google Scholar]
- Liu, T.; Inoue, Y.; Shibata, K. A wearable ground reaction force sensor system and its application to the measurement of extrinsic gait variability. Sensors 2010, 10, 10240–10255. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Buckle, P. Evaluating Change in Exposure to Risk for Musculoskeletal Disordersea Practical Tool. HSE Books, Suffolk [Online]. 1999; 74p, CRR251. Available online: http://www.hse.gov.uk/research/crr_pdf/1999/crr99251.pdf (accessed on 27 October 2005).
- Zurada, J.; Karwowski, W.; Marras, W.S. A neural network-based system for classification of industrial jobs with respect to risk of low back disorders due to workplace design. Appl. Ergon. 1997, 28, 49–58. [Google Scholar] [CrossRef]
- Chen, C.L.; Kaber, D.B.; Dempsey, P.G. A new approach to applying feedforward neural networks to the prediction of musculoskeletal disorder risk. Appl. Ergon. 2000, 31, 269–282. [Google Scholar] [CrossRef]
- Chen, C.L.; Kaber, D.B.; Dempsey, P.G. Using feedforward neural networks and forward selection of input variables for an ergonomics data classification problem. Hum. Factors Ergon. Manuf. 2004, 14, 31–49. [Google Scholar] [CrossRef]
- Varrecchia, T.; De Marchis, C.; Rinaldi, M.; Draicchio, F.; Serrao, M.; Schmid, M.; Conforto, S.; Ranavolo, A. Lifting activity assessment using surface electromyographic features and neural networks. Int. J. Ind. Ergon. 2018, 66, 1–9. [Google Scholar] [CrossRef]
- Asensio-Cuesta, S.; Diego-Mas, J.A.; Alcaide-Marzal, J. Applying generalised feedforward neural networks to classifying industrial jobs in terms of risk of low back disorders. Int. J. Ind. Ergon. 2010, 40, 629–635. [Google Scholar] [CrossRef]
- Ranavolo, A.; Mari, S.; Conte, C.; Serrao, M.; Silvetti, A.; Iavicoli, S.; Draicchio, F. A new muscle co-activation index for biomechanical load evaluation in work activities. Ergonomics 2015, 58, 966–979. [Google Scholar] [CrossRef]
- Ranavolo, A.; Varrecchia, T.; Iavicoli, S.; Marchesi, A.; Rinaldi, M.; Serrao, M.; Conforto, S.; Cesarelli, M.; Draicchio, F. Surface electromyography for risk assessment in work activities designed using the “revised NIOSH lifting equation”. Int. J. Ind. Ergon. 2018, 68, 34–45. [Google Scholar] [CrossRef]
- Ranavolo, A.; Varrecchia, T.; Rinaldi, M.; Silvetti, A.; Serrao, M.; Conforto, S.; Draicchio, F. Mechanical lifting energy consumption in work activities designed by means of the “revised NIOSH lifting equation”. Ind. Health 2017, 55, 444–454. [Google Scholar] [CrossRef]
- Wu, G.; van der Helm, F.C.; Veeger, H.E.; Makhsous, M.; Van Roy, P.; Anglin, C.; Nagels, J.; Karduna, A.R.; McQuade, K.; Wang, X.; et al. International Society of Biomechanics. ISB Recommendation on Definitions of Joint Coordinate Systems of Various Joints for the Reporting of Human Joint Motion. Part II.; Shoulder, Elbow, Wrist and Hand. J. Biomech. 2005, 38, 981–992. [Google Scholar] [CrossRef] [PubMed]
- Sakata, K.; Kogure, A.; Hosoda, M.; Isozaki, K.; Masuda, T.; Morita, S. Evaluation of the age-related changes in movement smoothness in the lower extremity joints during lifting. Gait Posture 2010, 31, 27–31. [Google Scholar] [CrossRef] [PubMed]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning internal representations by error propagation. In Parallel Distributed Processing; MIT Press: Cambridge, MA, USA, 1986; Volume 1, pp. 318–362. [Google Scholar]
- De Looze, M.P.; Bosch, T.; Krause, F.; Stadler, K.S.; O’Sullivan, L.W. Exoskeletons for industrial application and their potential effects on physical work load. Ergonomics 2016, 59, 671–681. [Google Scholar] [CrossRef] [PubMed]
- Waters, T.R.; Dick, R.B.; Davis-Barkley, J.; Krieg, E.F. A cross-sectional study of risk factors for musculoskeletal symptoms in the workplace using data from the General Social Survey (GSS). J. Occup. Environ. Med. 2007, 49, 172–184. [Google Scholar] [CrossRef]
- Naing, L.; Winn, T.; Rusli, B.N. Practical issues in calculating the sample size for prevalence studies. Arch. Orofac. Sci. 2006, 1, 9–14. [Google Scholar]
- Markham, I.S.; Rakes, T.R. The effect of sample size and variability of data on the comparative performance of artificial neural networks and regression. Comput. Oper. Res. 1998, 25, 251–263. [Google Scholar] [CrossRef]
- Fillingim, R.B.; King, C.D.; Ribeiro-Dasilva, M.C.; Rahim-Williams, B.; Riley, J.L. Sex, gender, and pain: A review of recent clinical and experimental findings. J. Pain 2009, 10, 447–485. [Google Scholar] [CrossRef]
- Hunter, S.K. Sex differences in human fatigability: Mechanisms and insight to physiological responses. Acta Physiol. (Oxf.) 2014, 210, 768–789. [Google Scholar] [CrossRef]
- Sullivan, B.E.; Carroll, C.C.; Jemiolo, B.; Trappe, S.W.; Magnusson, S.P.; Dossing, S.; Kjaer, M.; Trappe, T.A. Effect of acute resistance exercise and sex on human patellar tendon structural and regulatory mRNA expression. J. Appl. Physiol. (1985) 2009, 106, 468–475. [Google Scholar] [CrossRef][Green Version]
- Johansen, T.; Samani, A.; Antle, D.; Côté, J.N.; Madeleine, P. Gender effects on the coordination of subdivisions of the trapezius muscle during a repetitive box-folding task. Eur. J. Appl. Physiol. 2013, 113, 175–182. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).