1. Introduction
In the past two decades, the interest in the research related to metaheuristic algorithms has increased significantly due to the fact that existing numerical methods do not allow for solving a number of complex optimization problems, such as discrete structural optimization [
1], design of water distribution networks [
2], and vehicle routing [
3]. A metaheuristic algorithm is applied to simulate the randomness and rules in natural phenomena. For example, the genetic algorithm (GA) [
4] imitates the process of the biological evolutionary and natural selection. The particle swarm optimization (PSO) [
5] was inspired by the animal behavior, namely, the foraging behavior of bird flocking. In addition, there are many algorithms extending PSO and GA, such as the harmony search (HS) algorithm [
6] and the honey bee mating optimization (HBMO) [
7]. These algorithms have proved their ability to search for better solutions than numerical methods in extensive optimization problems [
8,
9,
10]. However, compared with theses algorithms, the HS algorithm which imitates an improvisation process of a harmony has two features. Firstly, it has fewer mathematical requirements and is easy to implement. Secondly, each decision variable in a new solution vector could be generated independently by considering all of the existing solution vectors [
11]. Due to these two features, the HS algorithm has stronger adaptability for many engineering problems and could generate competition results compared with the GA [
11]. In addition, based on the above advantages, many modified versions of the HS algorithm are proposed to further improve the searching ability of the HS algorithm, such as the improved harmony search (IHS) algorithm [
11], the self-adaptive global best harmony search (SGHS) algorithm [
12], and the novel global harmony search (NGHS) algorithm [
13]. These modified versions of the HS algorithm have better search ability than the original HS algorithm.
It is worth noting that, among these HS algorithms, the mechanism that is used to decide whether a new generated harmony (solution vector) is accepted and replaces the worst harmony in the harmony memory (HM) or not is different. The HM is a storage of the harmony. Specifically, the HS, IHS, and SGHS algorithms accept a new generated harmony only when it is better than the worst harmony in the current HM. This mechanism, we call it accept-the-better-only mechanism, reminded us of the tabu search (TS) algorithm [
14] which also only accepts the better solution vector in the searching process. Conversely, in the NGHS algorithm, a new generated harmony is accepted and replaced the worst harmony in the HM without preconditions in each iteration. This mechanism, we call it accept-everything mechanism, is the same one used in the PSO and GA. In the PSO algorithm, in each iteration, after calculating the velocity of the particle, the particle will fly to the new position according to its velocity whether the fitness of the new position is better than the current position or not. However, while we were discussing these two acceptance mechanisms, we suddenly came up with an old algorithm, the simulated annealing (SA) algorithm [
15]. In the SA algorithm, in each iteration, the new solution vector is accepted or not according to the acceptable probability (AP), which is calculated by the Boltzmann distribution. Thus, the SA algorithm inspired us to investigate whether the AP affects the search ability or not in the NGHS algorithm. Therefore, in this paper, we proposed the selective acceptance novel global harmony search (SANGHS) algorithm, which combined the selective acceptance mechanism with the NGHS algorithm. Moreover, we proposed a proportion formula to calculate the AP according to the convergence degree. To verify the searching performance of the SANGHS algorithm, we used the SANGHS algorithms in ten well-known optimization problems and two engineering problems and compared the experimental results with other 15 algorithms. The results revealed that the SANGHS algorithm outperformed other 15 algorithms.
The remainder of this paper is organized as follows. In
Section 2, the HS, IHS, SGHS, and the NGHS algorithms are introduced.
Section 3 describes the SANGHS algorithm. A considerable number of experiments were conducted to test the search ability of the proposed SANGHS algorithm, and the corresponding experiments results are analyzed in
Section 4. Conclusions and future research directions are provided in
Section 5.
2. HS, IHS, SGHS, and NGHS Algorithms
2.1. Harmony Search Algorithm
The harmony search was proposed by Geem in 2001 [
6]. Unlike other metaheuristic algorithms used to simulate the reproductive or foraging processes in the biological world, such as PSO and GA, the harmony search algorithm is inspired by a jazz trio and simulates its improvisation process [
6]. The HS algorithm introduces musical notes to represent decision variables in practical problems. The number of musical notes is determined by the number of decision variables. Each note is played by a musician. Harmony requires two or more notes to be played at the same time. Thereby, each harmony represents a set of decision values. The HS algorithm simulates this in an improvisation process; hence, if the new harmony is better than the worst harmony, the new harmony will be saved to the harmony memory, and the worst harmony will be discarded from the harmony memory. Conversely, the new harmony will not be committed, and the worst harmony will not be discarded.
The HS algorithm is superior to other heuristic algorithms in terms of solving continuous variable problems and combinatorial problems; for example, it is deemed to be more applicable that GA [
6]. The HS algorithm works as follows [
16].
• Step 1: Initialize the algorithm and problem parameters
The main parameters of the harmony search algorithm include the harmony memory size (HMS), the harmony memory considering rate (HMCR), the pitch adjusting rate (PAR), and the bandwidth (BW). HMS is the total number of harmonies, which can be stored in the harmony memory (HM). HMCR determines whether musicians create a new harmony based on a harmony in the HM or not. PAR determines whether musicians fine-tune the musical note of a harmony that was selected in the HM or not. The bandwidth BW is the range, in which musicians fine-tune the selected harmony. Another parameter is the maximum number of iterations (NI), which denotes how many improvisations musicians have made to define the best harmony.
In this step, the above parameters in the HS algorithm are determined. In addition, the current iteration (k) is set to 1. The HS algorithm is usually used in the D-dimensional optimization problem defined as minimization of subject to . Here, and are the lower and upper bounds for the decision variable .
• Step 2: Initialize the harmony memory (HM)
The number of harmony vectors stored in the HM is equal to HMS. A harmony vector is a set of decision variables. The initial values of the decision variable
are generated by Equation (1). In Equation (1),
is a random number in the range [0,1]. Here,
represents the
jth decision variable in the
ith harmony vector, when the current iteration is
. The harmony memory (HM) is shown in Equation (2):
• Step 3: Improvise a new harmony
A new harmony vector
is improvised by three mechanisms: memory consideration, pitch adjustment, and random selections. It is defined as in Algorithm 1.
| Algorithm 1 The Improvisation of New Harmony in HS |
| 1: For to do |
| 2: If then |
| 3: %memory consideration |
| 4: If then |
| 5: %pitch adjustment |
| 6: If then |
| 7: |
| 8: Else if then |
| 9: |
| 10: End |
| 11: End |
| 12: Else |
| 13: % random selection |
| 14: End |
| 15: End |
Here, is the jth decision variable of the new harmony improvised in the current iteration . In the memory consideration mechanism, of the is an integer random selected in the range of [1, HMS]; , , , and are random numbers in the region of [0,1].
• Step 4: Update the harmony memory
If the new harmony vector has better fitness compared with the worse fitness in the harmony memory, the new harmony vector will replace the worse harmony vector.
• Step 5: Check the stopping iteration
If the current iteration is equal to the stopping iteration (the maximum number of iterations is NI), the computation is terminated. Otherwise, set and go back to step 3.
2.2. Improved Harmony Search Algorithm
In the HS algorithm, the pitch adjustment mechanism is designed to improve the local search ability. However, the PAR and the BW are fixed in the search process, which means that the local search ability does not change in the early iteration and the final iteration. This is a reason why the HS algorithm has a limit to balance the global search ability and local search ability in the different stages of the search process. To mitigate this deficiency, Mahdavi et al. [
11] proposed a new strategy to dynamically adjust PAR and BW. At the early stage of optimization, the small PAR values with the large BW enhance the ability of the global search and increase the diversity of the solution vectors. The large PAR and the small BW values improve the ability of the local search and make the algorithm converge to the optimal solution vector in the late stage of optimization. Therefore, PAR and BW are adjusted according to Equations (3) and (4), respectively:
In Equation (3), represents the pitch adjusting rate, when the current iteration is . and are the minimum and maximum pitch adjusting rates in the process of optimization, respectively. Additionally, in Equation (4), represents the bandwidth, when the current iteration is . and are the maximum and the minimum bandwidth in the process of optimization.
2.3. Self-Adaptive Global Best Harmony Search Algorithm
In 2010, the SGHS algorithm was proposed by Pan et al. [
12]. The SGHS algorithm and the HS algorithm differ between each other in three aspects. Firstly, the SGHS algorithm implies that the pitch adjusting mechanism should be computed before the memory consideration mechanism. In addition, the memory consideration mechanism only selects the best harmony in the HM other than selecting randomly. Thereby, the new harmony is improvised using Algorithm 2. Secondly, the parameters HMCR and PAR are dynamically adjusted by the normal distribution, and BW is adjusted in each iteration according to Equation (5). Furthermore, HMCR is generated by the mean
that is in the range of [0.9, 1.0] and the static standard deviation (0.01). PAR is generated by the mean
that is in the region of [0.0, 1.0] and the static standard deviation (0.05). Finally, the SGHS algorithm introduces another parameter named the learning period (LP) to determine
and
. In a learning period, if the new harmony replaces the worse harmony in the HM, when the iteration is
,
and
are recorded. When the learning period is satisfied,
and
are recalculated by averaging the recorded
and
, respectively, then the recorded
and
are discarded, and another new learning period will begin.
| Algorithm 2 The Improvisation of New Harmony in SGHS |
| 1: For to do |
| 2: If then |
| 3: %pitch adjustment |
| 4: If then |
| 5: |
| 6: Else if then |
| 7: |
| 8: End |
| 9: If then |
| 10: %memory consideration |
| 11: End |
| 12: Else |
| 13: % random selection |
| 14: End |
| 15: End |
Here,
represents the
jth decision variable of the best harmony in the HM, when the iteration is
. The meaning of other variables in Algorithm 2 is the same as in Algorithm 1:
2.4. Noval Global Harmony Search Algorithm
In 2010, the NGHS algorithm was proposed by Zou et al. [
13,
17,
18]. The algorithm proposed in their study combines the HS algorithm, GA, and the particle swarm optimization (PSO) algorithm. GA imitates a process of the biological evolution [
4]. The genetic mutation probability (
) in GA was introduced to escape from the local optimum. Particle swarm optimization (PSO) imitates the foraging process of bird flocking [
5]. The position update in the NGHS algorithm was inspired by the main characteristic of PSO implying that the position of the particles is affected by the best position of all particles [
13].
Figure 1 illustrates the principle of the position update.
is an adaptive step of the
jth decision variable in the current iteration
. The range between P and R is referred to as a truth region, which is centered at the global best harmony. In other words, the
jth decision variable is generated randomly in a range of the truth region. In the early iteration, all solution vectors in the harmony memory are sporadic, and the truth region is wide, which means that the new harmony is generated randomly in a large range. It is beneficial to enhance the global search ability. In the late iteration, all solution vectors in the HM are inclined to move to the global optimum. Therefore, all solution vectors are concentrated within a small solution space, and the truth region is narrow, which enhances the local search ability of NGHS [
13,
17,
18]. The NGHS algorithm works as follows.
• Step 1: Initialize the algorithm and problem parameters
The genetic mutation probability (), the current iteration , and the maximum number of iterations (NI) are set in this step. However, the harmony memory considering rate (HMCR), pitch adjusting rate (PAR), and the bandwidth (BW) are excluded from the NGHS algorithm.
• Step 2: Initialize the harmony memory (HM)
The initial values of the decision variable are generated by Equation (1). The harmony memory (HM) is shown in Equation (2).
• Step 3: Improvise a new harmony
A new harmony vector
is improvised by Algorithm 3.
| Algorithm 3 The Improvisation of New Harmony in NGHS |
| 1: For to do |
| 2: |
| 3: If then |
| 4: |
| 5: Else if then |
| 6: |
| 7: End |
| 8: %position update |
| 9: If then |
| 10: % genetic mutation |
| 11: End |
| 12: End |
Here, and are the best harmony and the worse harmony in the harmony memory, when the current iteration is , respectively. , , and are random numbers in the range of [0,1]:
• Step 4: Update the harmony memory
The new harmony replaces the worse harmony in the HM, even if the worse harmony in the HM has better fitness than the new harmony.
• Step 5: Check the stopping iteration
If the current iteration is equal to the stopping iteration (the maximum number of iterations is NI), the algorithm is terminated. Otherwise, set and go back to step 3.
3. Selective Acceptance Novel Global Harmony Search Algorithm
Assad et al. [
19] pointed that the effectiveness of evolutionary algorithms relies on the extent of balance between diversification, which implies the ability of an algorithm to explore the high performance regions of the search space, and intensification, which is the ability of an algorithm to search for better solution in the high performance regions during the optimizing process. In other words, the key to improving the searching ability of evolutionary algorithms is to enhance the extent of balance between diversification and intensification capabilities. It can be seen that, in
Section 2, Step 3 (Improvise a new harmony) in the IHS, SGHS, or NGHS algorithm is gradually improved to balance the diversification and intensification capabilities. However, in Step 4, the mechanism of updating the HM is different in these algorithms. Accept-the-better-only mechanism is used in the HS, IHS, and the SGHS algorithm. The accept-everything mechanism is used in the NGHS algorithm. This difference inspired us to explore whether the mechanism in Step 4 could affect the balance of diversification and intensification capabilities and improve the searching ability of the NGHS algorithm. However, in the process of finding a good mechanism in Step 4, the mechanism that is used in the SA algorithm attracted our attention. The SA algorithm used Boltzmann distribution to calculate the acceptable probability dynamically in each iteration and determine to accept the new solution or not by the value of acceptable probability. Therefore, in this paper, we proposed the selective acceptance novel global harmony search (SANGHS) algorithm, which combined the selective acceptance mechanism with the NGHS algorithm.
The main difference between the SANGHS and the NGHS algorithms is that the SANGHS algorithm will accept and replace the worst harmony in the HM with the new harmony according to the selective acceptance mechanism. In this mechanism, the selective acceptance formula as shown in Equation (6), which is also dynamically adjusted in the optimization process as in the SA algorithm, is used to further balance the diversification and intensification capabilities. However, the selective acceptance formula is different from the Boltzmann distribution in the SA algorithm and does not need to use additional parameters. In Equation (6),
represents the acceptable probability in the current iteration
.
represents the fitness value of the new harmony in the current iteration
.
and
represent the fitness values of the best and the worst harmonies in the HM in the current iteration
, respectively. According to the selective acceptance formula in the SANGHS algorithm, if the fitness of the new harmony is better than the worst harmony in the HM, the AP is equal to 1. It means that the worst harmony will be replaced by the new harmony in the HM. However, if the fitness of the new harmony is worse than the worst harmony in the HM, the SANGHS algorithm will accept the new harmony according to the AP, which is calculated by the proportion formula. Proportion formula is the most important part of the selective acceptance formula. In proportion formula,
represents the convergence degree of all harmonies in the HM. In the early iterations, all harmonies in the HM are dispersed in a large solution space, and the value of
is a large value. Thus, it is more likely to accept a worse harmony and thereby expand the range of truth region in the SANGHS algorithm, which would contribute to improve the diversification capabilities. Conversely, in the late iterations, all harmonies in the HM have converged in a small solution space; the value of
is a small value. The HM is less likely to accept a worse harmony and thereby reduce the range of truth region, which makes the SANGHS algorithm have strong intensification capabilities:
In general, the SANGHS algorithm contains the following steps:
• Step 1: Initialize the algorithm and problem parameters
The genetic mutation probability (), the current iteration , and the maximum iteration (NI) are set in this step.
• Step 2: Initialize the harmony memory (HM)
The initial values of the decision variable are generated by Equation (1). The harmony memory (HM) is shown in Equation (2).
• Step 3: Improvise a new harmony
A new harmony vector is improvised by Algorithm 3. This step is the same as in the NGHS algorithm.
• Step 4: Calculate AP
If the new harmony has a better fitness value than the worst harmony in the HM, AP is set to 1. Otherwise, AP is calculated by Equation (6).
• Step 5: Update the harmony memory
Firstly, generate a random number in [0,1]. If the random number is smaller than the AP, the new harmony replaces the worst harmony in the HM. Otherwise, the new harmony is discarded.
• Step 6: Check the stopping iteration
If the current iteration is equal to the stopping iteration (the maximum number of iterations is NI), the algorithm is terminated. Otherwise, set and go back to Step 3.
5. Conclusions
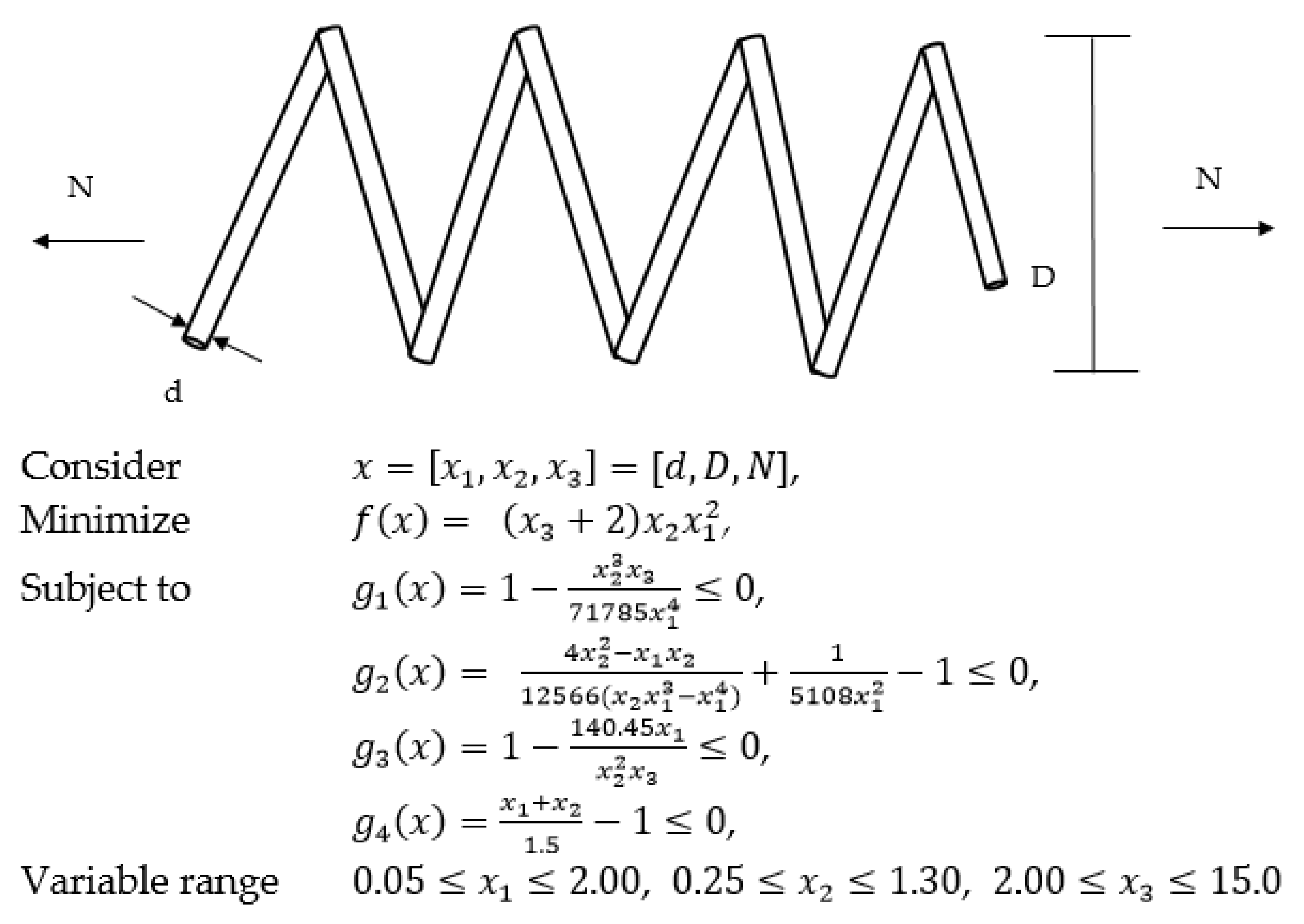
In this paper, we presented a novel algorithm, called the SANGHS algorithm, which combines the NGHS algorithm with a selective acceptance mechanism. In the SANGHS algorithm, the acceptable probability (AP) is generated by a selective acceptance formula in each iteration. Based on the value of AP, the SANGHS algorithm will determine whether to accept the worse trial solution or not. Moreover, to verify the searching performance of the SANGHS algorithm, we used the SANGHS algorithm in ten well-known benchmark continuous optimization problems and two engineering problems and compared the experimental results with other state-of-the-art metaheuristic algorithms. The experimental results provide two findings that are worth noting.
Firstly, it was found that the SANGHS algorithm could result in improved searching performance as opposed to the NGHS algorithm. In the SANGHS algorithm, the selective acceptance mechanism dynamically adjusts the acceptable probability according to the selective acceptance formula. The most important part of the selective acceptance formula is proportion formula, and the main concept of the proportion formula is convergence degree in the HM. Hence, in Equation (6), represents the convergence degree of all harmonies in the HM. In the early iterations, all solutions have not yet converged in the HM. Therefore, the value of will be a larger value, and then there is a larger acceptable probability to accept a worse harmony. In the next iteration, there is a higher probability to generate a new harmony in a larger truth region. In other words, there is a strong global exploration ability in the early iterations. However, in the late iterations, the value of will be a smaller value while all solutions have converged in the HM. Therefore, there is a smaller acceptable probability to accept a worse harmony. In the next iteration, there is a higher probability to generate a new harmony in a smaller truth region. In other words, there is a strong local exploitation ability in the later iterations. According to the experimental results, the proposed proportion mechanism can balance the global exploration and local exploitation ability in the NGHS algorithm.
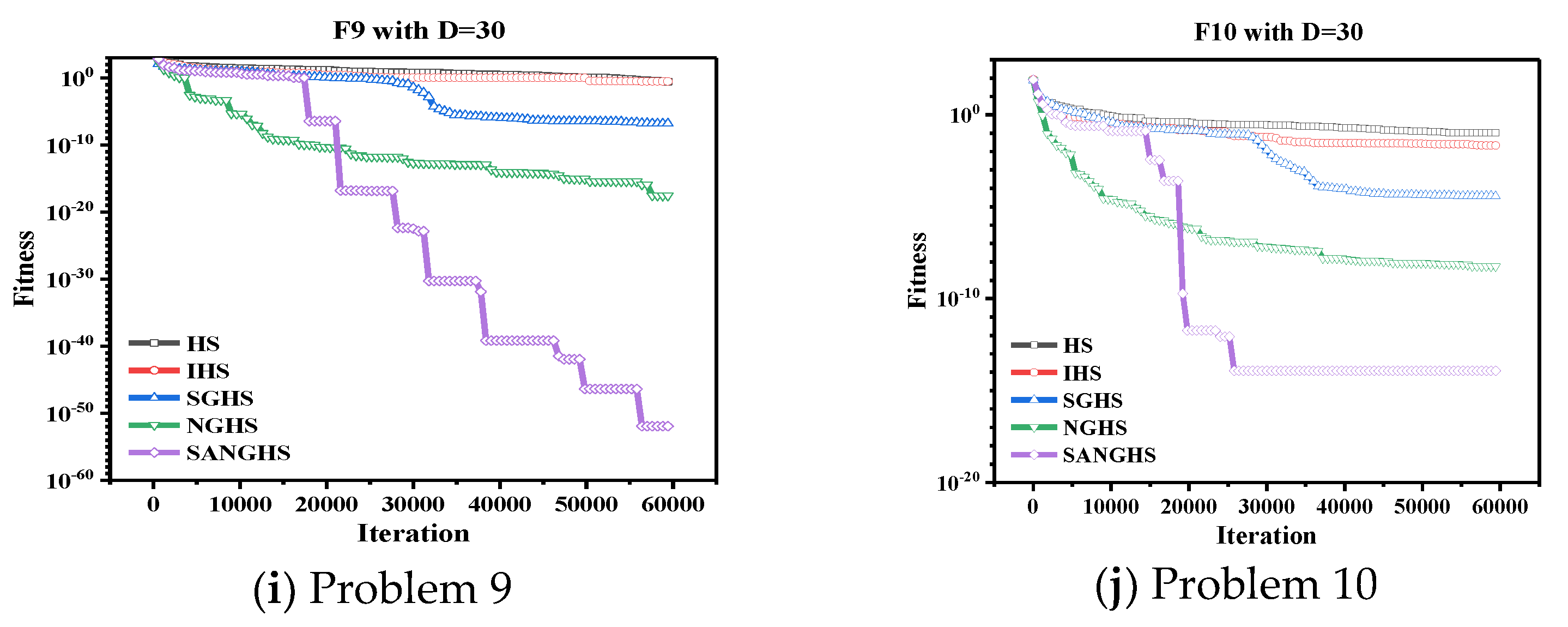
Finally, in ten considered benchmark optimization problems with three different dimensions, based on the results of the Wilcoxon rank-sum test and the convergence graphs, the searching performance of the SANGHS algorithm was better than other four HS algorithms significantly. Especially in
Figure 2, we can easily observe that the SANGHS algorithm had the better searching performance and convergence ability than other algorithms in all problems. Conversely, the HS, IHS, and the SGHS algorithms easily fall within the local optimum, and unlikely escape it. Moreover, in two engineering optimization problems, the SANGHS algorithm could not only search for a better solution compared with other four HS algorithms, but also could provide a competition result to compare with other state-of-the-art algorithms. In conclusion, the SANGHS algorithm is a more efficient and effective algorithm.