Insights into the Effect of WJ-7 Fastener Rubber Pad to Vehicle-Rail-Viaduct Coupled Dynamics
Abstract
1. Introduction
2. Fundamentals of Dynamic Flexibility Method
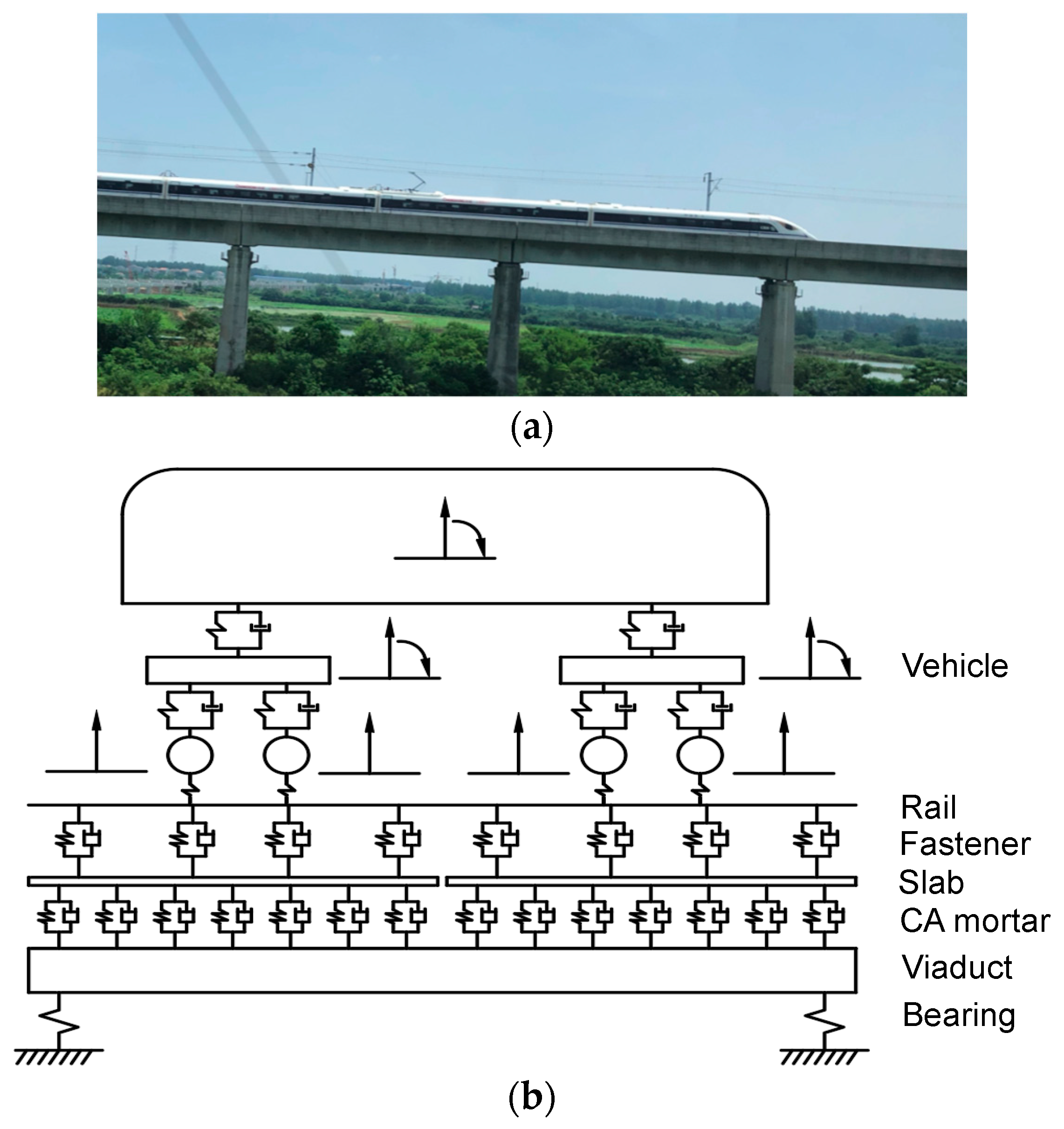
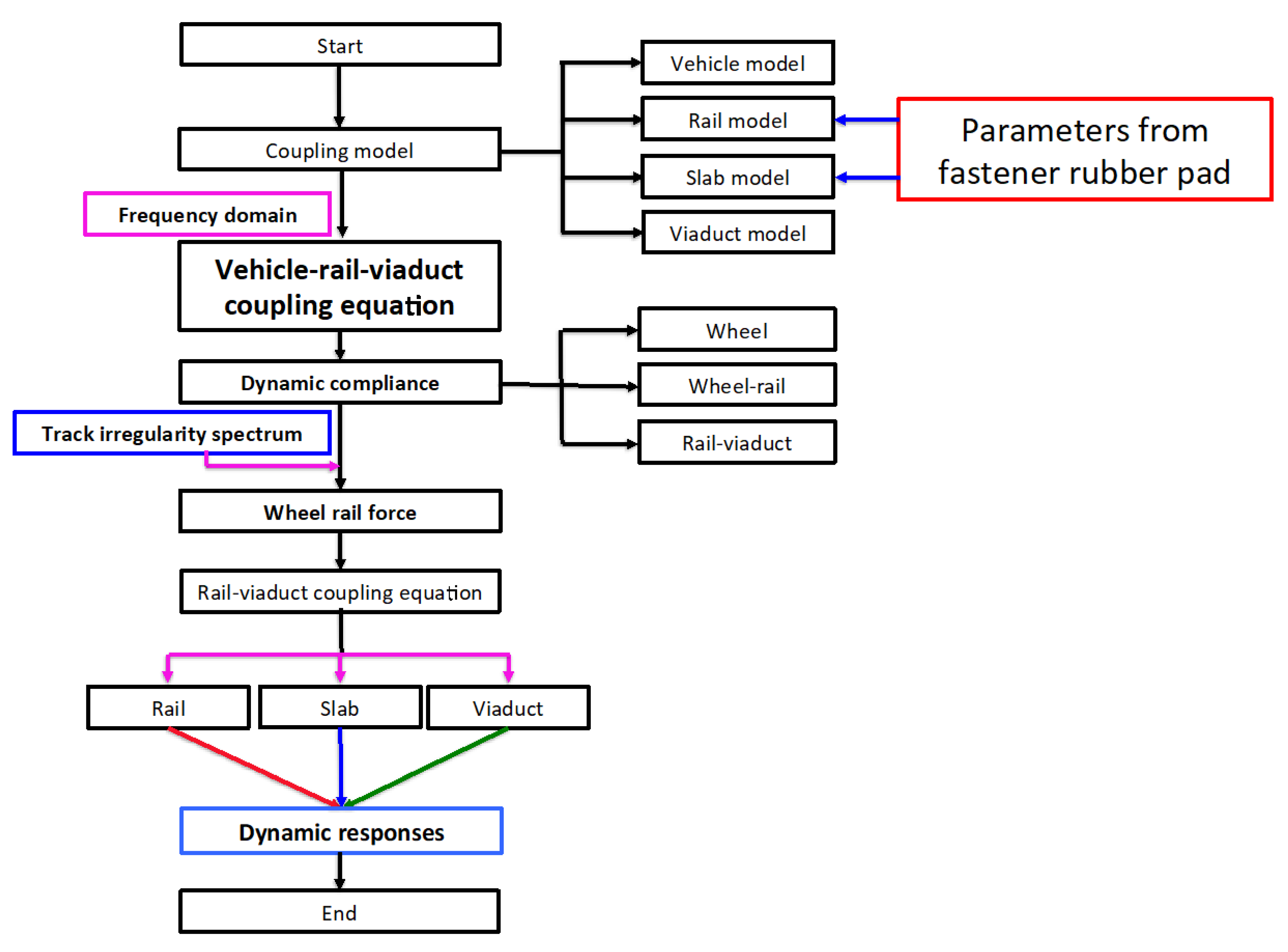
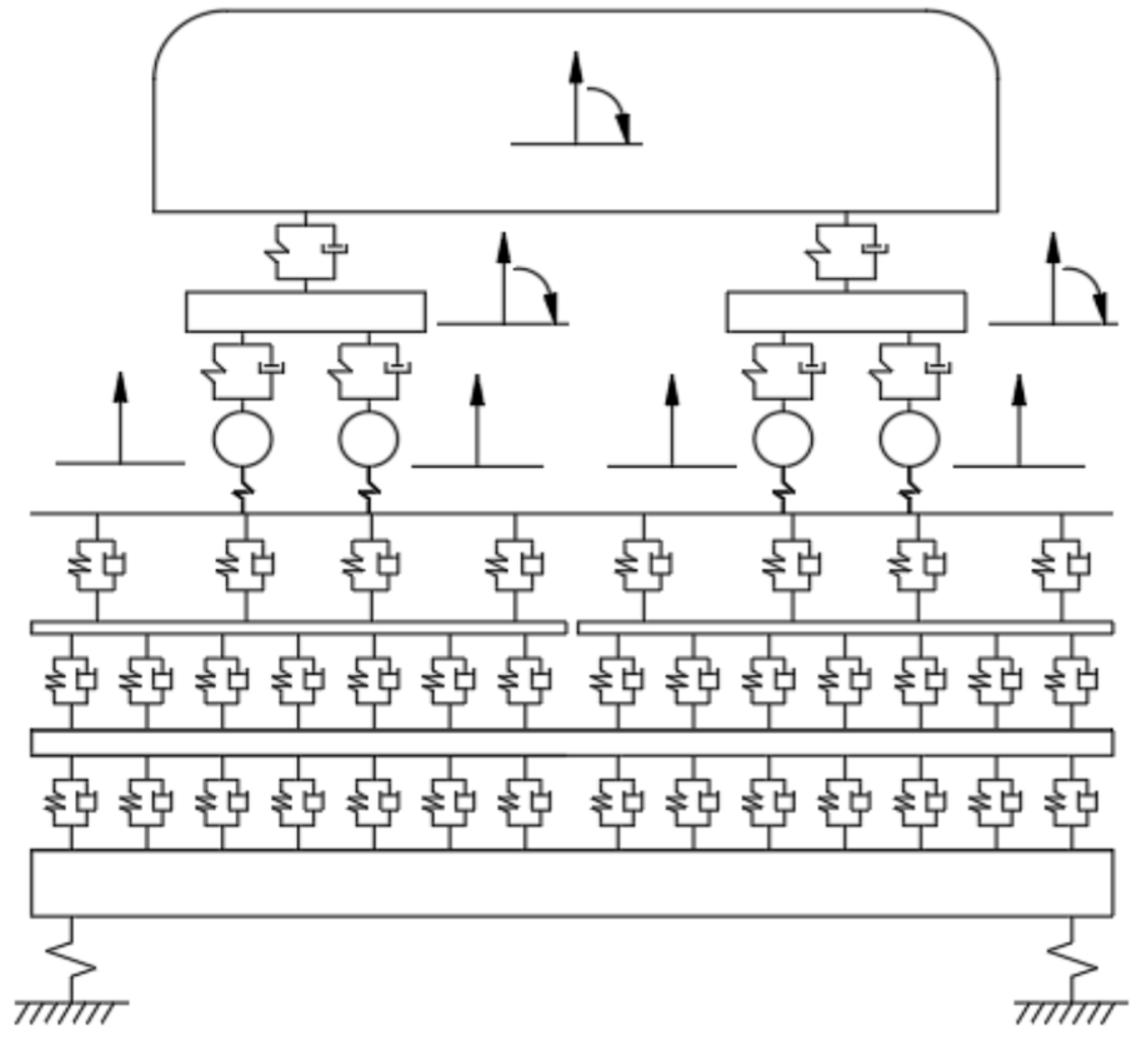
2.1. Vehicle-Rail-Viaduct Coupling Model via Dynamic Flexibility Method
2.2. Dynamic Flexibility Calculation for the Wheel
2.3. Dynamic Flexibility for the Wheel Rail Interaction
2.4. The Dynamic Flexibility of the Rail-Viaduct Coupling System
2.5. Harmonic Analysis for the Vehicle-Rail-Viaduct Coupling System
3. Experimental Tests
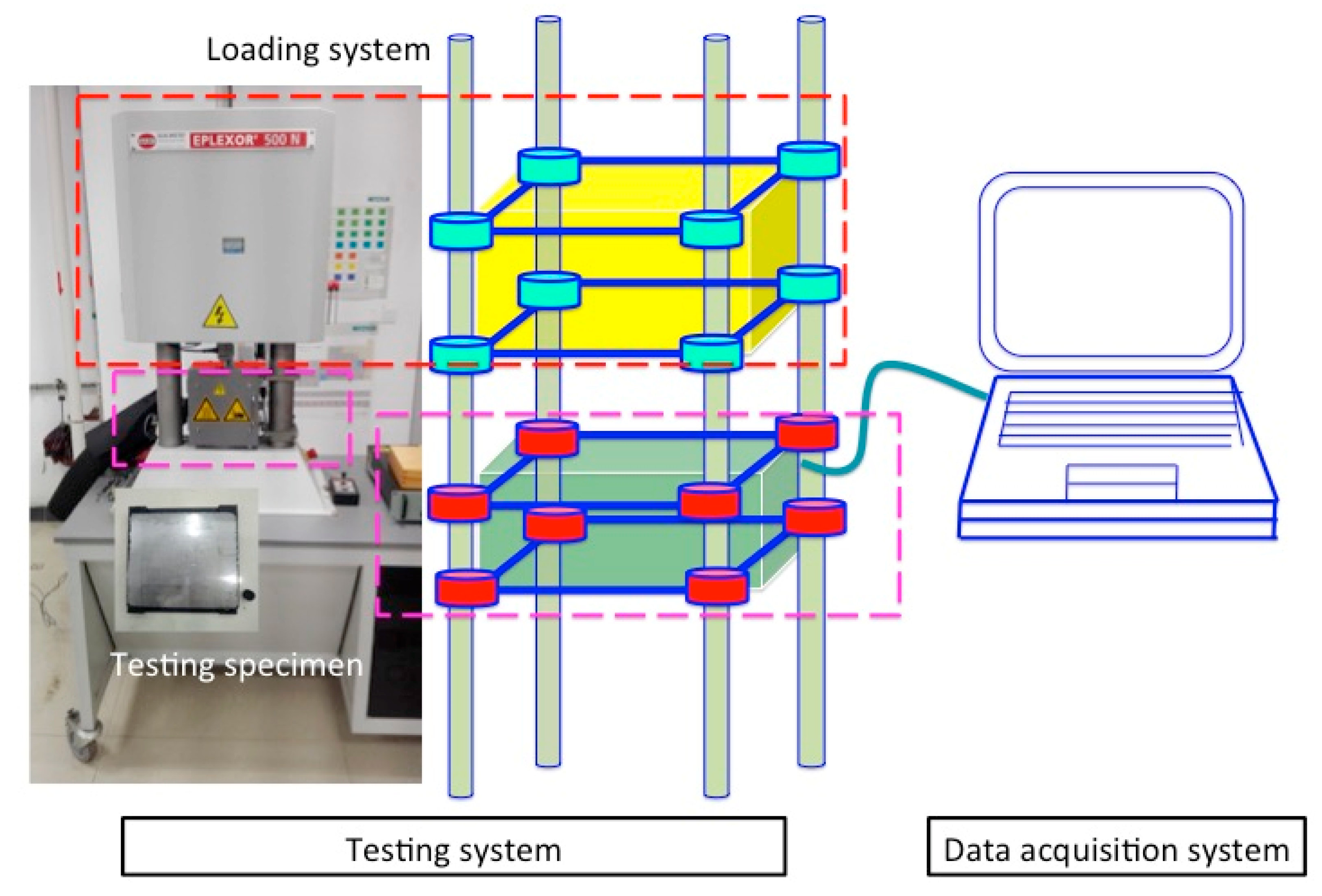
3.1. General information for the tests
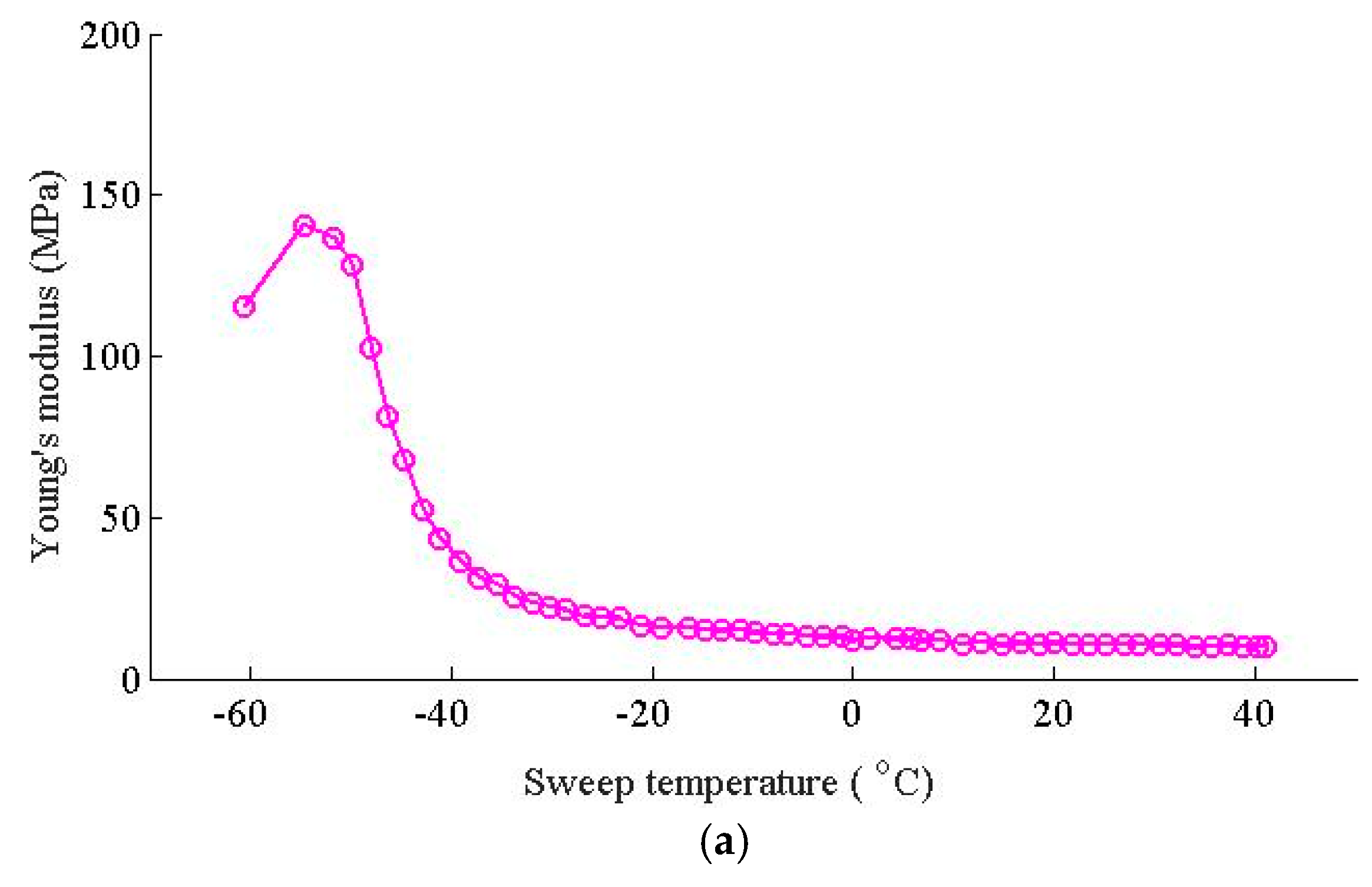
3.1.1. Dynamic Mechanical Tests for the Fastener Rubber Pad
3.1.2. Testing Configuration
3.2. Model Description
3.2.1. Model Properties
3.2.2. Track Irregularity Spectrum of the Rail
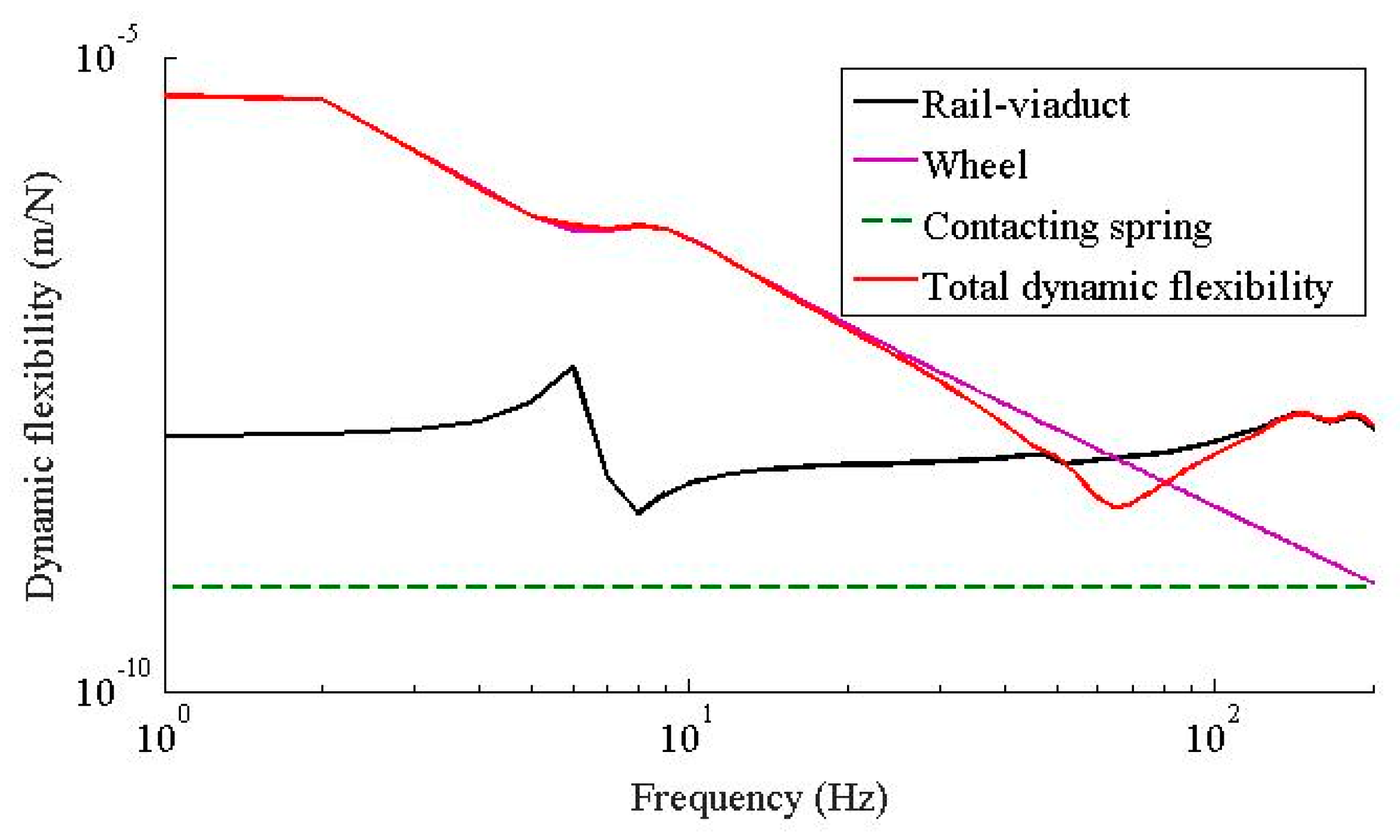
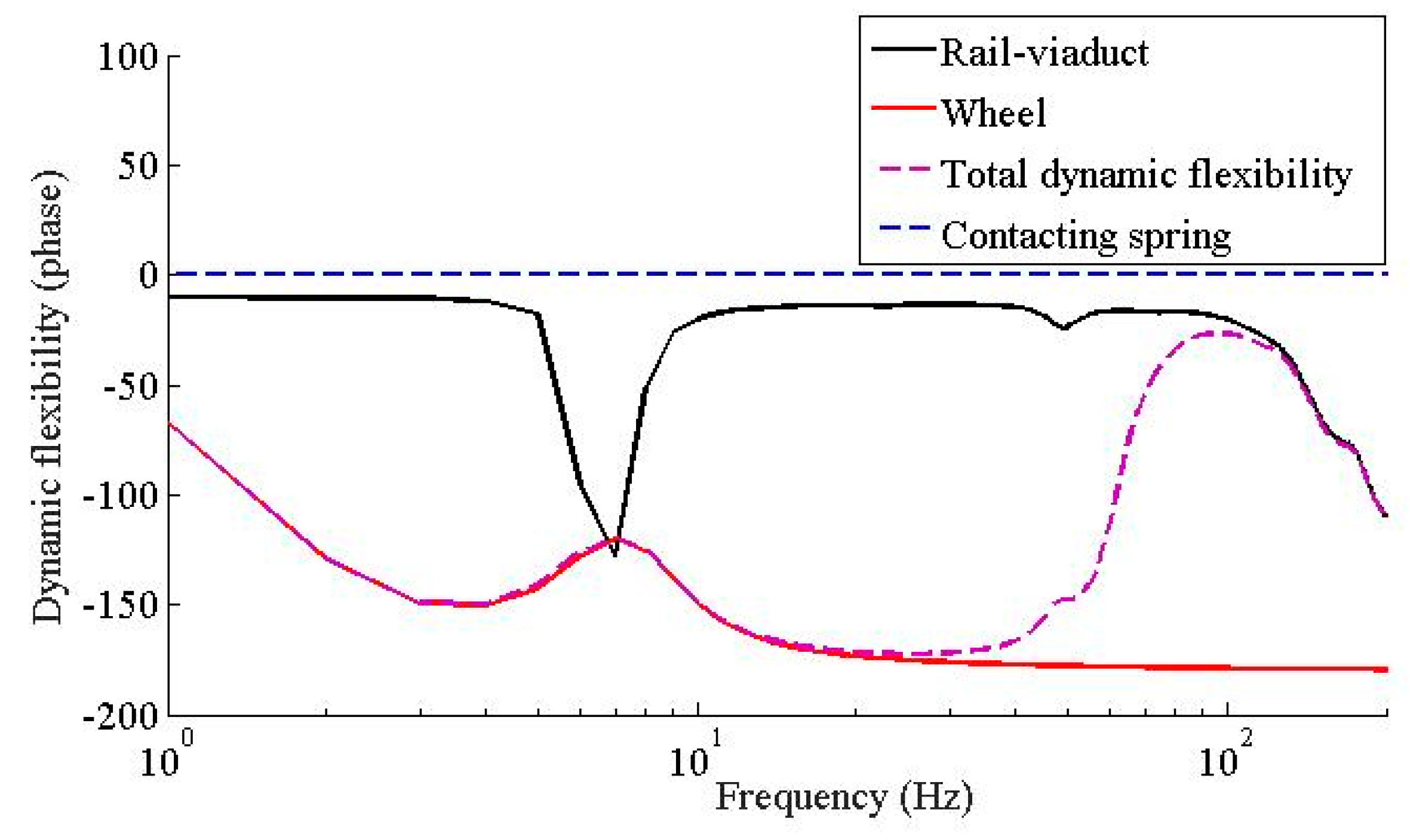
4. Results Analysis
5. Comparison of Proposed Method with Conventional Method
5.1. Case I: Three-Span Bridge
5.2. Case II: Multi-Layer Model for Ballastless Track
6. Concluding Remarks
- The WJ-7B small resistance fastener rubber pad behaves sensitive at low temperatures, while stable at high temperatures. The WJ-7B small resistance fastener rubber pad has relatively high stiffness at low temperatures; during the transition period from a glassy state to a rubbery state, the stiffness of the WJ-7B small resistance fasteners declines sharply; while at relatively high temperatures, the stiffness of the WJ-7B small resistance fasteners keeps stable, with little change versus the temperature change.
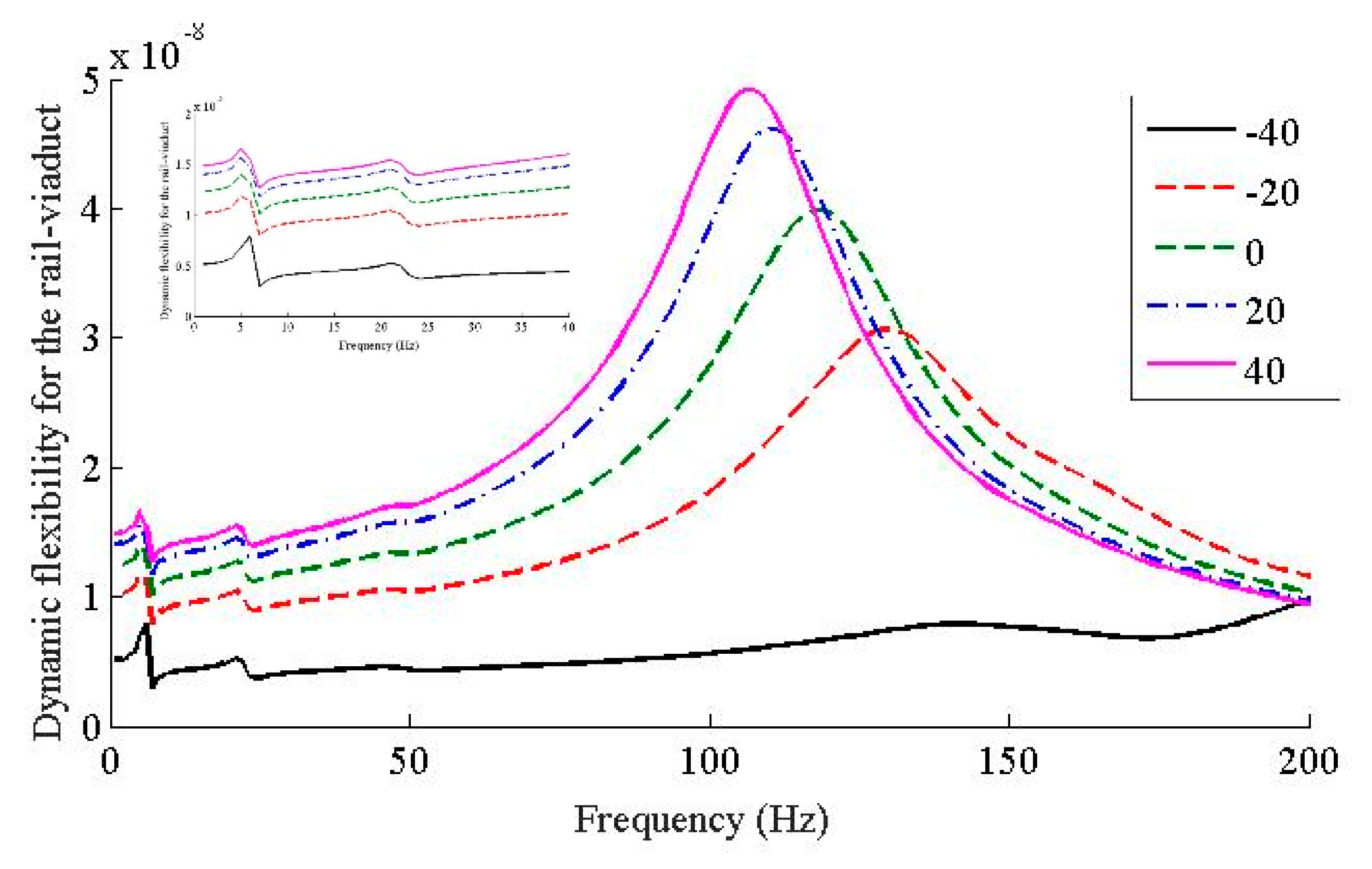
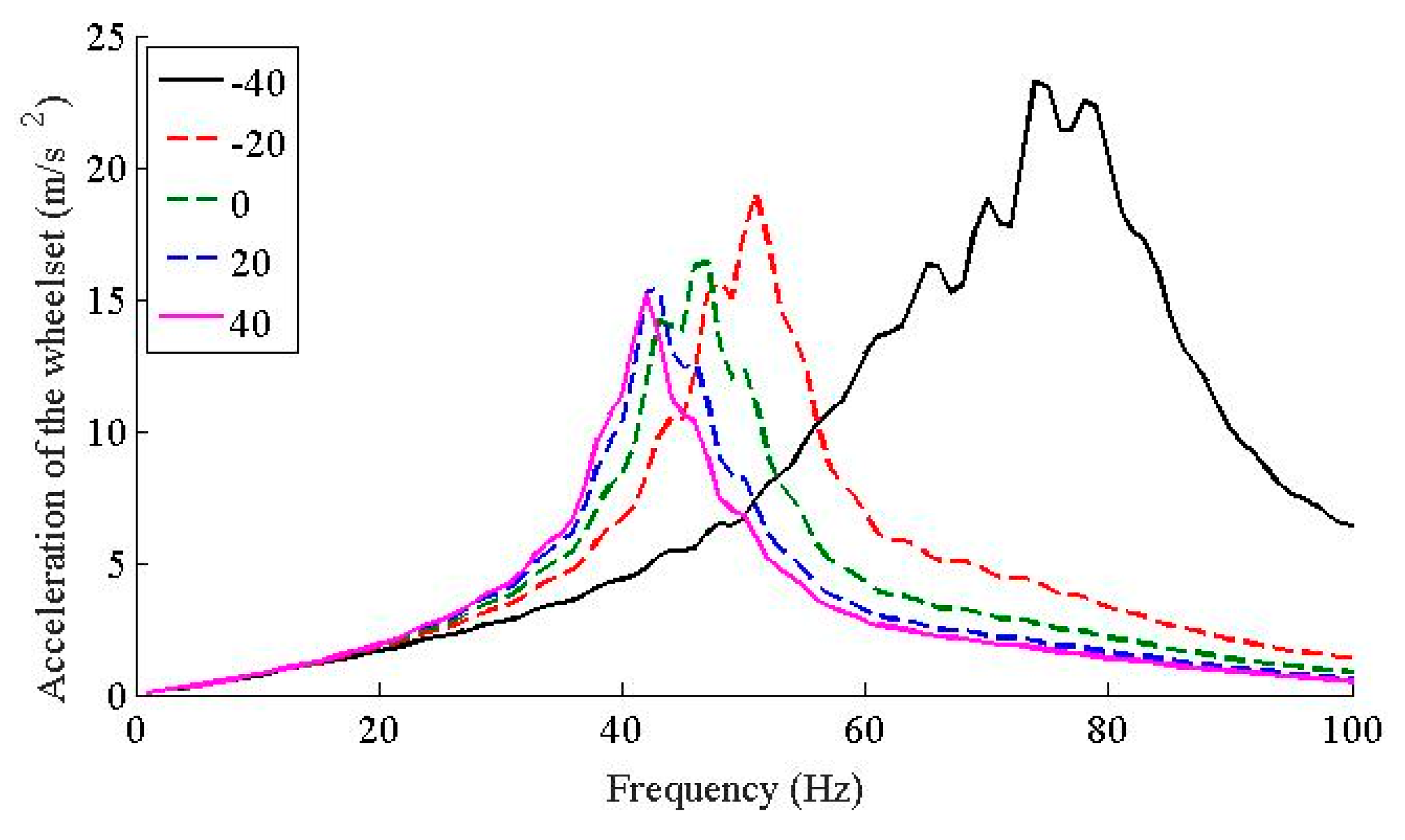
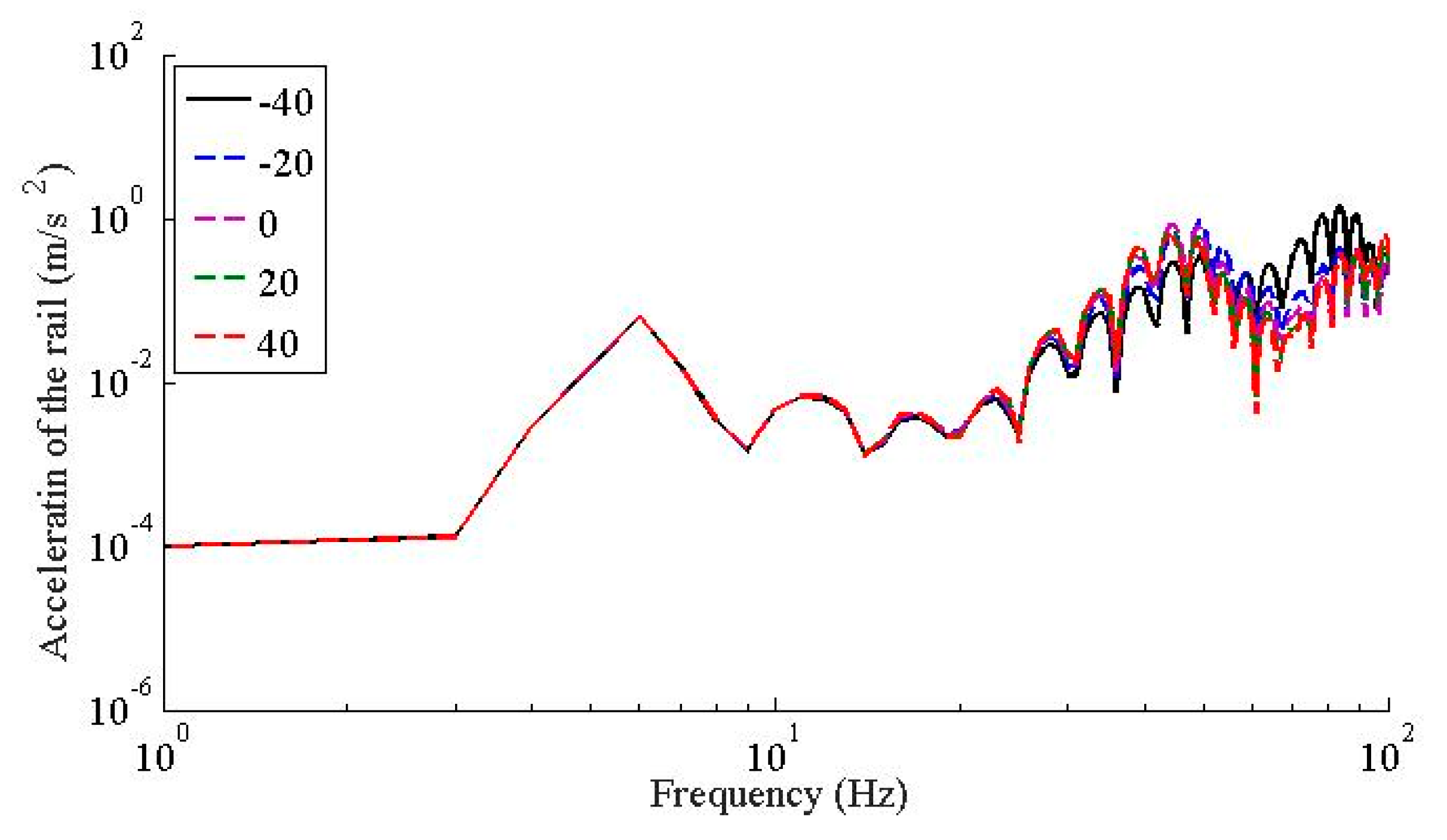
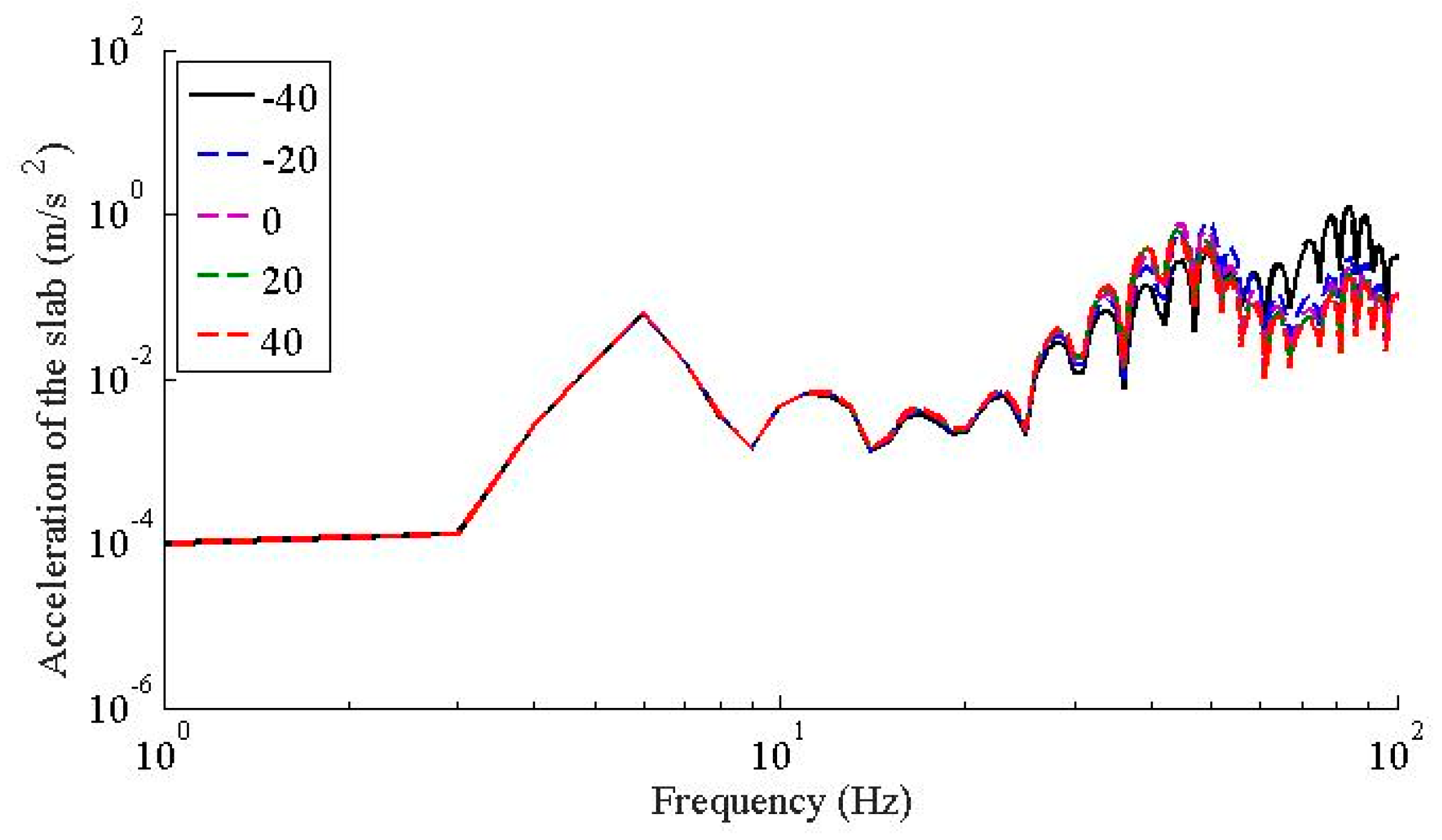
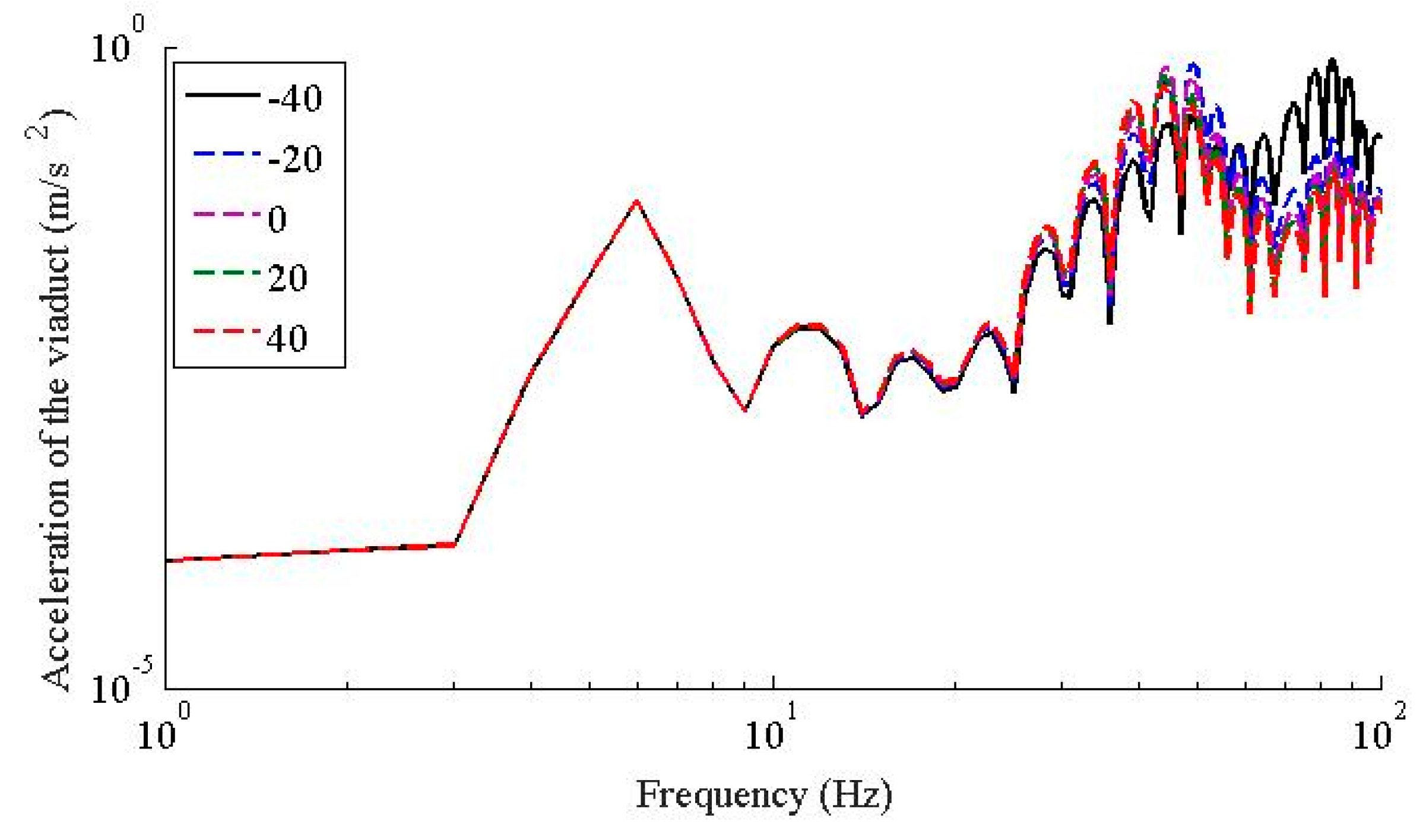
- The temperature dependent stiffness of the WJ-7B small resistance fastener rubber pad has little effect to the vertical vibration responses of the vehicle; as the temperature increases, the dynamic flexibility of the rail-viaduct increases, the amplitudes increases, but the resonant frequencies decrease especially when the frequency is higher than 30 Hz.
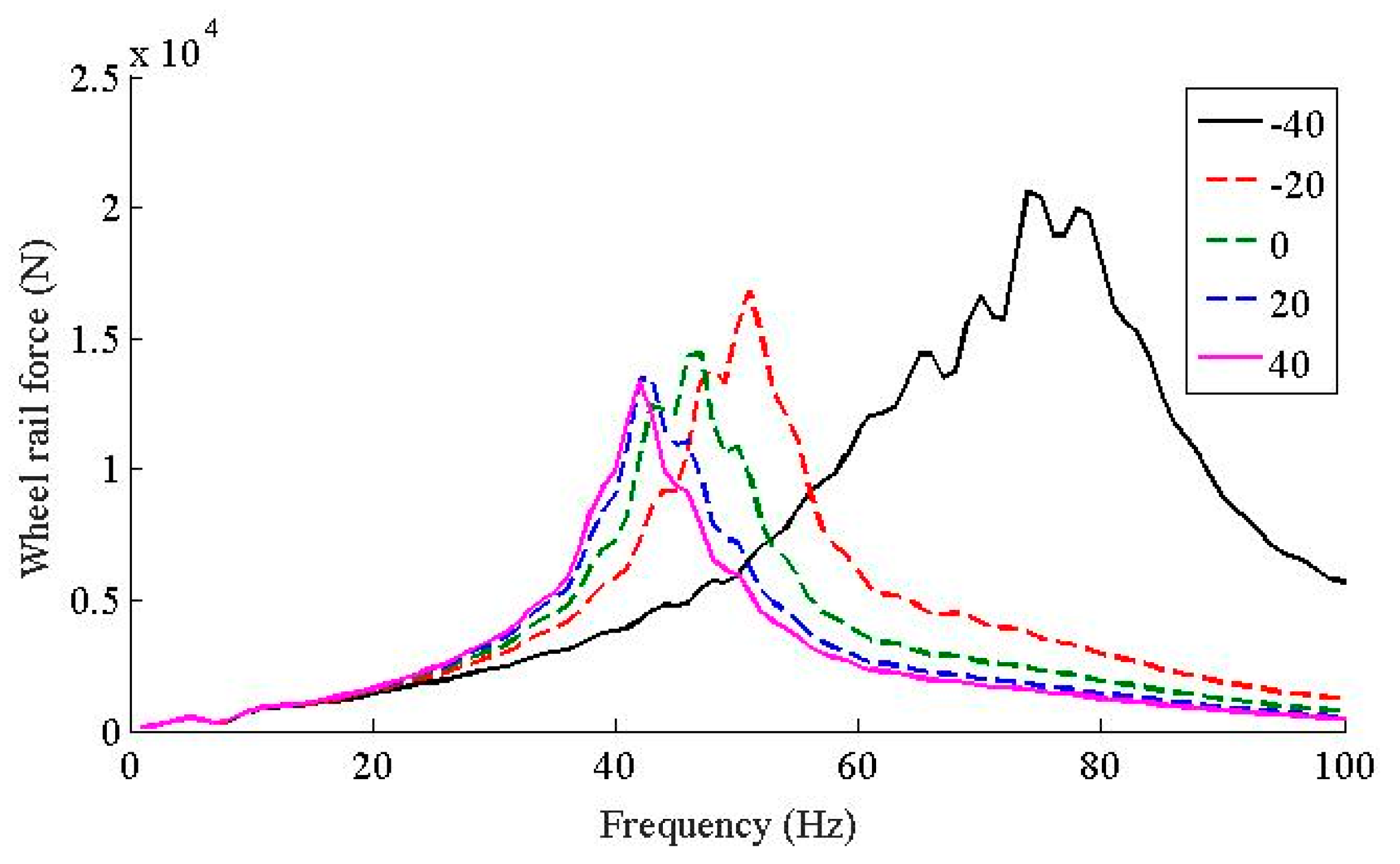
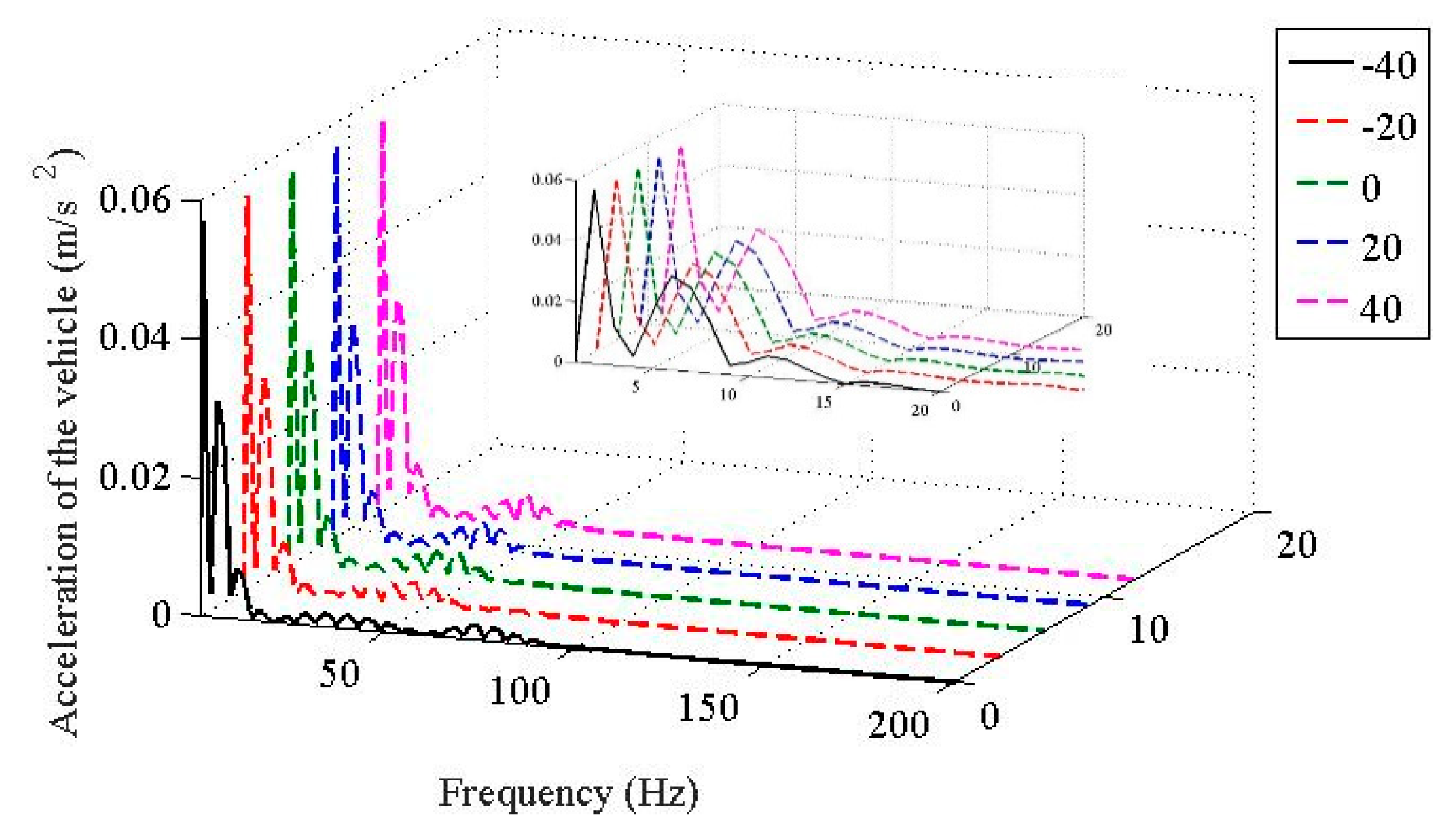
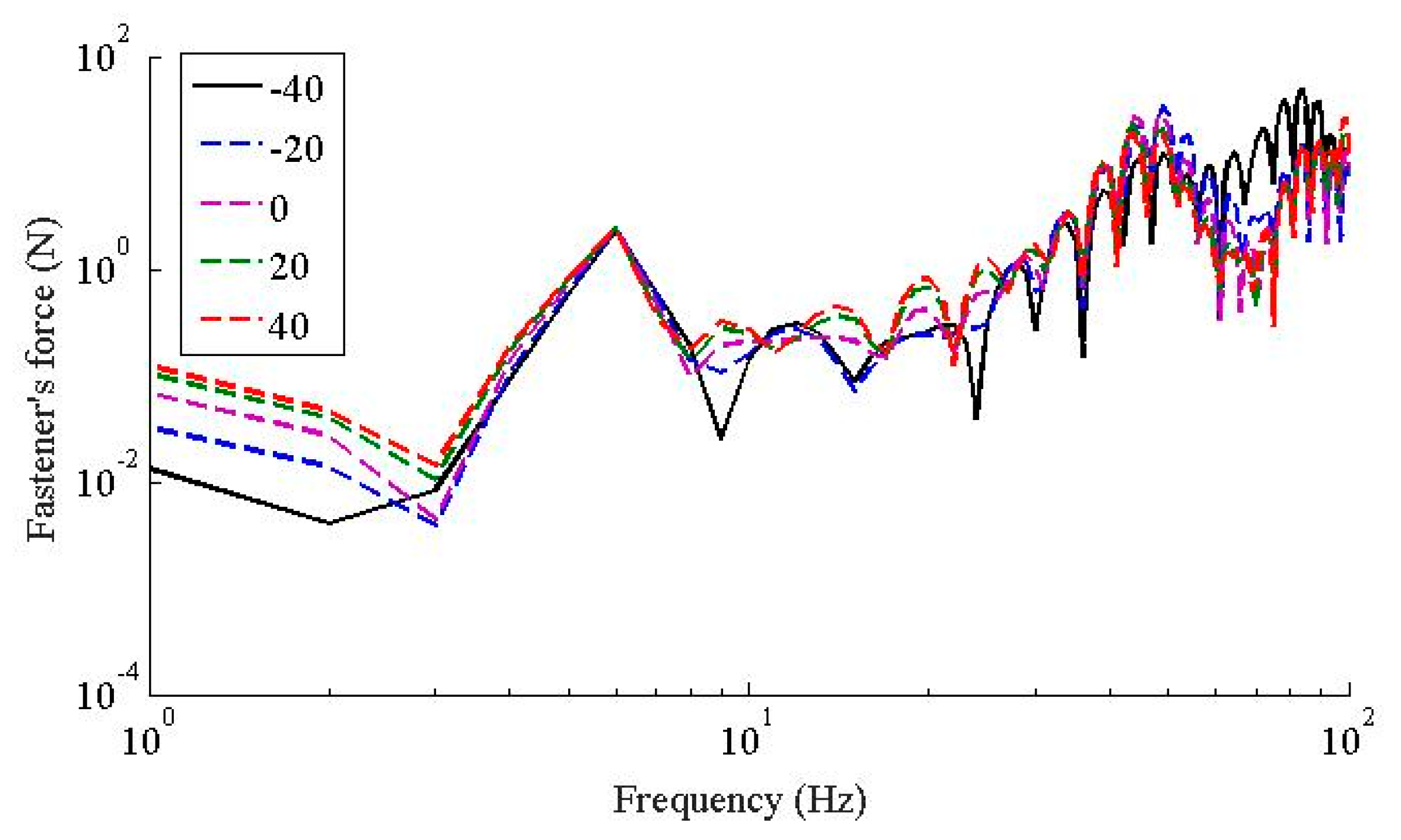
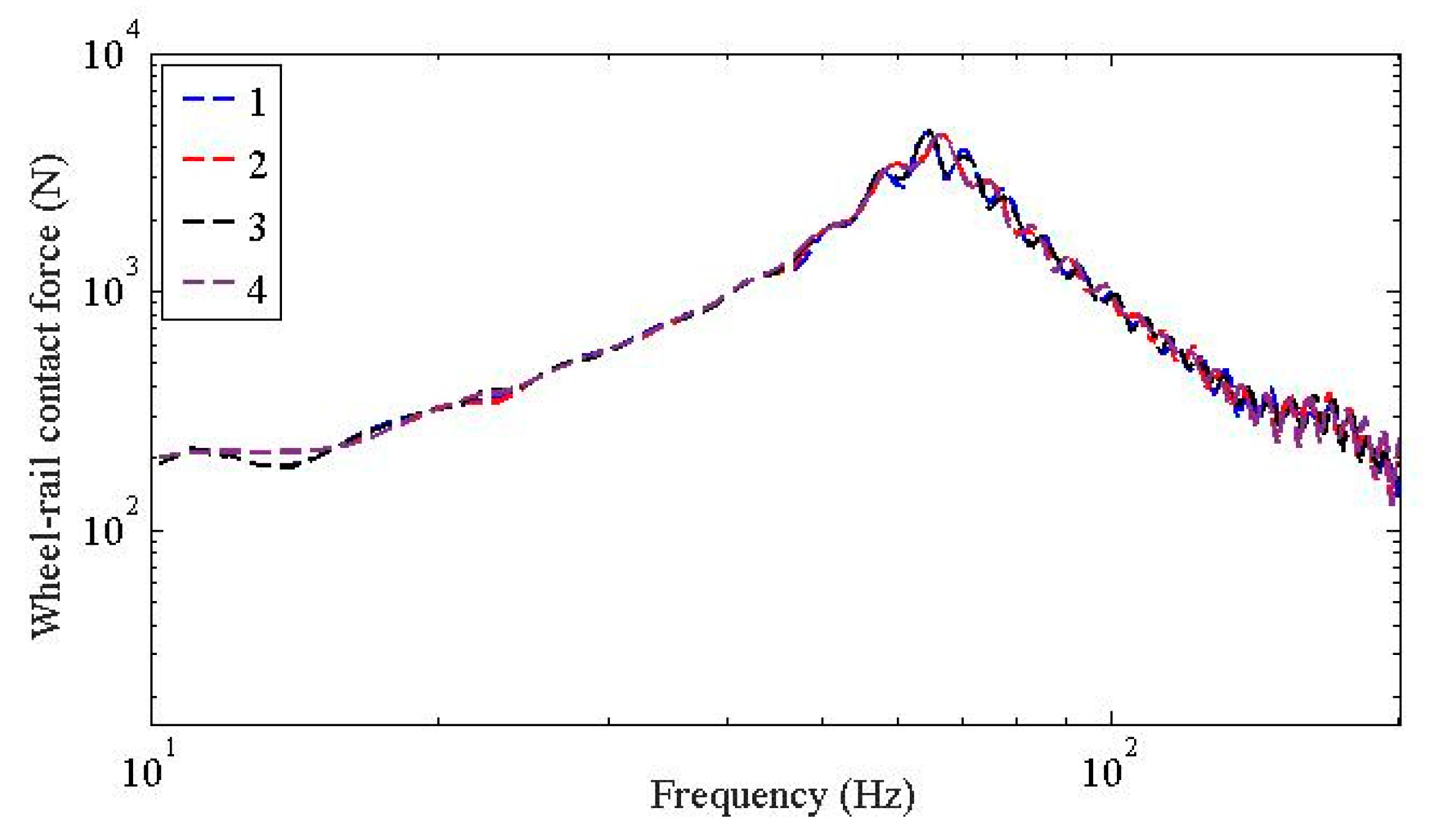
- In terms of the temperature dependent stiffness to wheel rail force and the dynamic responses of the wheelsets, they share similar characteristics; i.e., in frequency range below 20 Hz, the temperature dependent stiffness of the WJ-7B small resistance fastener rubber pad has little influence on the wheel-rail contact force and the accelerations of the wheelsets; the peaks of the wheel-rail contact force and the accelerations of the wheelsets decrease as the temperature increases, and the dominant frequencies also decrease as the temperature increases; considering the fact that the temperature dependent stiffness of the WJ-7B fastener rubber pad enables the resonant frequencies of the coupled wheel-rail to decrease as the temperature increases, the peak of the acceleration of the viaduct also decreases, and the dominant frequencies shift leftward.
- In terms of further investigation, the extension of such work to the real engineering tests would be desirable to optimize the proposed methodology. As to engineering application, in the low temperature areas and sudden temperature changing areas, the stiffness of the WJ-7B fastener rubber pad changes sharply, which further affects the vehicle-rail-viaduct coupling analysis. Such an effect has to be considered in certain areas in the engineering projects.
Author Contributions
Funding
Conflicts of Interest
References
- Thompson, D.J.; Verheij, J.W. The dynamic behavior of rail fasteners at high frequencies. Appl. Acoust. 1997, 52, 1–17. [Google Scholar] [CrossRef]
- Maes, J.; Sol, H.; Guillaume, P. Measurements of the dynamic railpad properties. J. Sound Vib. 2006, 293, 557–565. [Google Scholar] [CrossRef]
- Li, Q.; Wu, D.J. Analysis of the dominant vibration frequencies of rail bridges for structure-born noise using a power flow method. J. Sound Vib. 2013, 300, 4153–4163. [Google Scholar] [CrossRef]
- Liu, L.; Qin, J.; Zhou, Y.L.; Xi, R.; Peng, S. Structural noise mitigation for viaduct box girder using acoustic modal contribution analysis. Struct. Eng. Mech. 2019, 72, 421–432. [Google Scholar]
- Bezin, Y.; Iwnicki, S.D. An invetigation of sleeper viods using a flexible track model integrated with railway muti-body dynamics. J. Rail Rapid Transit 2009, 223, 597–607. [Google Scholar] [CrossRef]
- Zhang, X.; Su, B.; Li, X.Z. Effects of fastener stiffness and damping on structure-borne noise of railway box-girders. J. Vib. Shock 2015, 34, 150–155. [Google Scholar]
- Wei, K.; Zhang, P.; Wang, P.; Xiao, J.; Luo, Z. Influence of amplitude-and frequency-dependent stiffness of rail pads on the frequency-domain random vibration of vehicle-track coupled system. Eng. Mech. 2017, 34, 108–115. [Google Scholar]
- Liu, Z. Study on the Influence of Amplitude-Dependent and Frequency-Dependent Dynamic Characteristics of Rubber Pads on Wheel-Rail Dynamic Response in High Speed. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2017. [Google Scholar]
- Ahmad, N.; Thompson, D.; Jones, C.; Muhr, A. Predicting the effect of temperature on the performance of elastomer-based rail damping devices. J. Sound Vib. 2009, 322, 674–689. [Google Scholar] [CrossRef]
- Zhao, Y.; Hou, Z. Two viscoelastic constitutive models of rubber materials using fractional derivations. J. Tsinghua Univ. 2013, 53, 378–383. [Google Scholar]
- Wei, K.; Zhou, C.; Wang, P.; Zhang, P. Influence of Temperature-dependent Stiffness of Rail Pads on the Frequency-domain Random Vibration of Vehicle-track Coupled System. J. China Railw. Soc. 2016, 38, 111–116. [Google Scholar]
- Wei, K.; Wang, F.; Zhao, Z.; Hu, X.; Jiang, W. The methodology research on the test and evaluation of static stiffness of elastic pads in elastic separated fastener. J. Railw. Soc. 2018, 35, 32–36+86. [Google Scholar]
- Wei, K.; Dou, Y.; Wang, F.; Niu, P.; Wang, P.; Luo, Z. High-frequency random vibration analysis of a high-speed vehicle–track system with the frequency-dependent dynamic properties of rail pads using a hybrid SEM–SM method. Veh. Syst. Dyn. 2018, 1–26. [Google Scholar] [CrossRef]
- Liu, L.; Lu, P.; Qin, J. Random Vibration Analysis of Vehicle-track Coupling System Based on Fastener FVMP Model. J. China Railw. Soc. 2019, 41, 93–100. [Google Scholar]
- Chang, G. Viscoelastic Damping Materials; National Defense Industry Press: Beijing, China, 2012. [Google Scholar]
- Li, L.; Thompson, D.; Xie, Y.; Zhu, Q.; Luo, Y.; Lei, Z. Influence of rail fastener stiffness on railway vehicle interior noise. Appl. Acoust. 2019, 145, 69–81. [Google Scholar] [CrossRef]
- Sheng, X.W.; Zheng, W.Q.; Zhu, Z.H.; Luo, T.J.; Zheng, Y.H. Properties of rubber under-ballast mat used as ballastless track isolation layer in high-speed railway. Constr. Build. Mater. 2020, 240, 117822. [Google Scholar] [CrossRef]
- Wei, K.; Yang, Q.; Dou, Y.; Wang, F.; Wang, P. Experimental investigation into temperature- and frequency-dependent dynamic properties of high-speed rail pads. Constr. Build. Mater. 2017, 151, 848–858. [Google Scholar] [CrossRef]
- Liang, L.; Li, X.; Zheng, J.; Lei, K.; Gou, H. Structure-borne noise from long-span steel truss cable-stayed bridge under damping pad floating slab: Experimental and numerical analysis. Appl. Acoust. 2020, 157, 106988. [Google Scholar] [CrossRef]
- Liu, L.; Wang, X.; Zhou, Y.L.; Qin, J. Vibration Mitigation Effect Investigation of a New Slab Track Plate Design. Sensors 2019, 19, 168. [Google Scholar] [CrossRef]
- Liu, L.; Song, R.; Zhou, Y.-L.; Qin, J. Noise and Vibration Mitigation Performance of Damping Pad under CRTS-III Ballastless Track in High Speed Rail Viaduct. KSCE J. Civ. Eng. 2019, 23, 3525–3534. [Google Scholar] [CrossRef]
- Lei, X. High Speed Railway Track Dynamics: Model, Algorithm and Application; Science Press: Beijing, China, 2015. [Google Scholar]
- Shi, G.; Yang, J.; Yang, X.; Zhang, X. Vertical vehicle-track-bridge coupling vibration based on dynamic flexibility method. J. Central South Univ. 2017, 48, 1119–1126. [Google Scholar]
- Xin, T.; Zhang, Q.; Gao, L.; Zhao, L.; Qu, J. Dynamic effects and structure optimization of damping layers of CRTSIII slab ballastless track for high speed railway. China Railw. Sci. 2016, 37, 1–7. [Google Scholar]
- International Organization for Standardization. ISO 3095:2005: Railway Applications-Acoustics-Measurement of Noise Emitted by Rail Bound Vehicles. 2005. Available online: https://www.iso.org/standard/41669.html (accessed on 10 March 2020).
- Zhang, Z. Semi-analytical analysis and experimental study of ground vibration induced by trains moving over high-speed railway bridges. Ph.D. Thesis, Southwest Jiaotong University, Chengdu, China, 2016. (In Chinese). [Google Scholar]


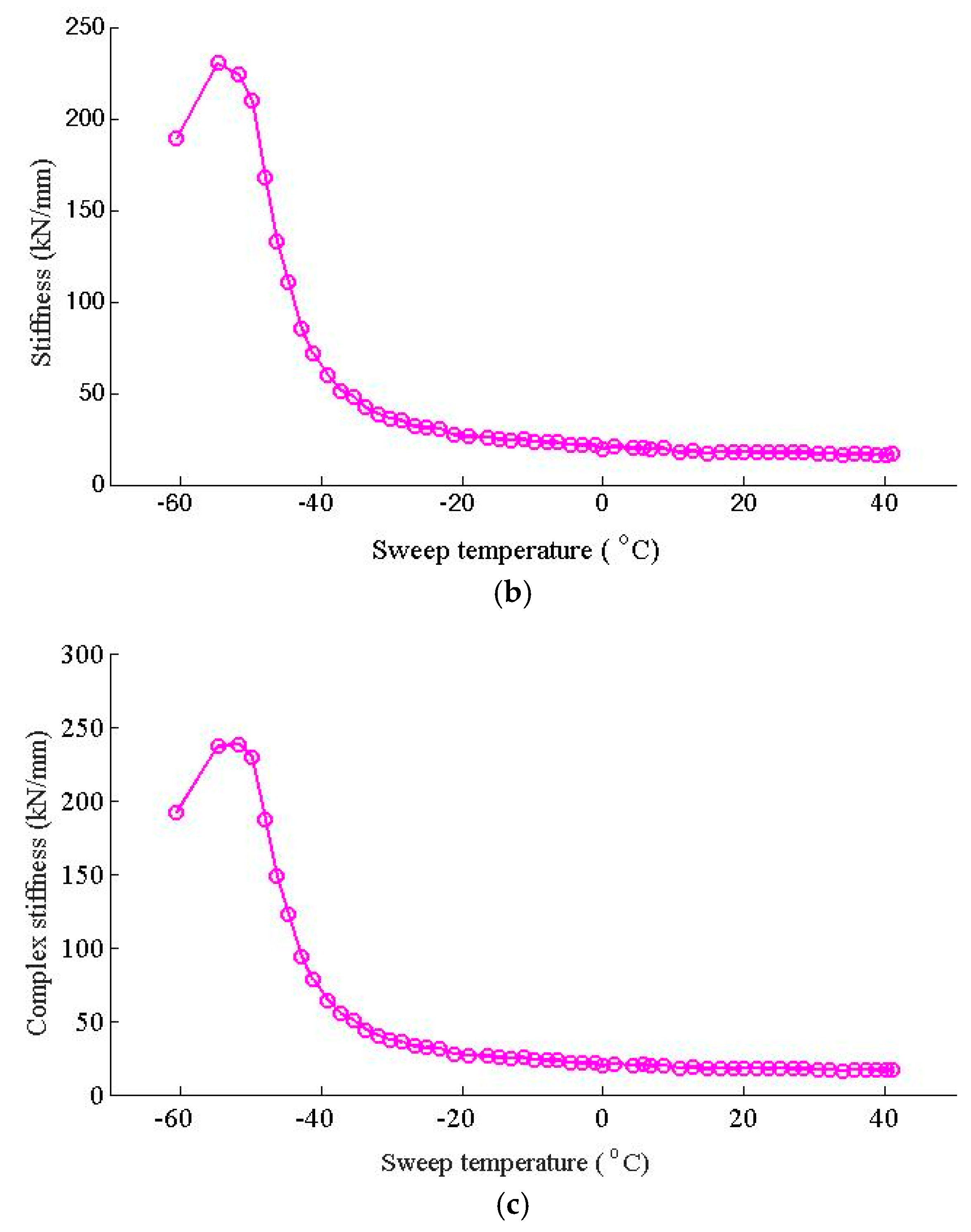
| Cases | Temperature (°C) | Stiffness (MN/m) |
|---|---|---|
| #1 | −40 | 64.71 |
| #2 | −20 | 26.66 |
| #3 | 0 | 21.00 |
| #4 | 20 | 17.94 |
| #5 | 40 | 16.65 |
| Parameter, Symbol (Unit) | Value |
|---|---|
| Vehicle’s weight under rated load (kg) | 42,934 |
| Bogie weight (kg) | 3300 |
| Wheelset weight (kg) | 1780 |
| Rotary of inertia for vehicle’s nod (kg m2) | 1.712 × 106 |
| Rotary of inertia for bogie’s nod (kg m2) | 1807 |
| Vertical stiffness of primary suspension (N m−1) | 1.176 × 106 |
| Damping of primary suspension (N s/m) | 1.0 × 104 |
| Stiffness of secondary suspension (N m−1) | 2.4 × 105 |
| Damping of secondary suspension (N s/m) | 2.0 × 104 |
| Length of train (m) | 25 |
| Fixed distance of carriage (m) | 17.5 |
| Fixed distance between axles (m) | 2.5 |
| Component | Symbol, Unit | Value |
|---|---|---|
| Rail | Stiffness (N/m2) | 2.059 × 1011 |
| Sectional inertia moment (m4) | 3.217 × 10−5 | |
| Density (kg/m3) | 7850 | |
| Section area (m2) | 7.745 × 10−3 | |
| Shear modulus (N/m2) | 7.7 × 1010 | |
| Section coefficient (κ) | 0.45 | |
| Loss factor (ηr) | 0.01 | |
| Fastener | Loss factor | 0.25 |
| Distance between fasteners (m) | 0.625 | |
| Slab | Stiffness (N/m2) | 3.6 × 1010 |
| Sectional inertia moment (m4) | 1.7 × 10−3 | |
| Density (kg/m3) | 2750 | |
| Section area (m2) | 0.51 | |
| Loss factor | 0.1 | |
| CA mortar | Equivalent stiffness (N/m) | 0.78 × 109 |
| Loss factor | 0.2 | |
| Viaduct | Length (m) | 32 |
| Stiffness (N/m2) | 3.45 × 1010 | |
| Sectional inertia moment (m4) | 5.757 | |
| Density (kg/m3) | 2650 | |
| Section area (m2) | 4.416 | |
| Loss factor | 0.1 | |
| Bearing for the viaduct | Stiffness (MN/m) | 6 × 109 |
| Distance between bearings (m) | 32 | |
| Loss factor | 0.25 |
| Scenarios | First Order and Dominant Resonant Frequencies | |||||
|---|---|---|---|---|---|---|
| First Order Resonant Frequency | Dominant Resonant Frequency | |||||
| (Hz) | ∆(#-#1) (Hz) | ∆(#1-#) (%) | (Hz) | ∆(#-#1) (Hz) | ∆(#1-#) (%) | |
| #1 | 6 | 0 | 0 | 142 | 0 | 0 |
| #2 | 5 | 1 | 16.67 | 130 | 12 | 8.45 |
| #3 | 5 | 1 | 16.67 | 118 | 24 | 16.90 |
| #4 | 5 | 1 | 16.67 | 110 | 32 | 22.53 |
| #5 | 5 | 1 | 16.67 | 107 | 35 | 24.65 |
| Scenarios | Peak Value and Dominant Frequency | |||
|---|---|---|---|---|
| Peak Value | Dominant Frequency | |||
| (kN) | ∆(#1-#) (%) | (Hz) | ∆(#1-#) (%) | |
| #1 | 20.62 | 0 | 74 | 0 |
| #2 | 16.79 | 18.57 | 51 | 31.08 |
| #3 | 14.41 | 30.12 | 47 | 36.49 |
| #4 | 13.50 | 34.53 | 43 | 41.89 |
| #5 | 13.35 | 35.26 | 42 | 43.24 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, L.; Zuo, Z.; Zhou, Y.; Qin, J. Insights into the Effect of WJ-7 Fastener Rubber Pad to Vehicle-Rail-Viaduct Coupled Dynamics. Appl. Sci. 2020, 10, 1889. https://doi.org/10.3390/app10051889
Liu L, Zuo Z, Zhou Y, Qin J. Insights into the Effect of WJ-7 Fastener Rubber Pad to Vehicle-Rail-Viaduct Coupled Dynamics. Applied Sciences. 2020; 10(5):1889. https://doi.org/10.3390/app10051889
Chicago/Turabian StyleLiu, Linya, Zhiyuan Zuo, Yunlai Zhou, and Jialiang Qin. 2020. "Insights into the Effect of WJ-7 Fastener Rubber Pad to Vehicle-Rail-Viaduct Coupled Dynamics" Applied Sciences 10, no. 5: 1889. https://doi.org/10.3390/app10051889
APA StyleLiu, L., Zuo, Z., Zhou, Y., & Qin, J. (2020). Insights into the Effect of WJ-7 Fastener Rubber Pad to Vehicle-Rail-Viaduct Coupled Dynamics. Applied Sciences, 10(5), 1889. https://doi.org/10.3390/app10051889






