Monte Carlo Optimization for Sliding Window Size in Dixon Quality Control of Environmental Monitoring Time Series Data
Abstract
1. Introduction
2. Dixon Quality Control Method
- (1)
- In a short period of time, environmental monitoring factors have similar physical and chemical properties;
- (2)
- the monitoring value in a short time window has the same significance as the parallel repeated observation experiment in outlier detection;
- (3)
- the time series of environmental monitoring that needs quality control treatment should meet the assumption of stationarity.
- (1)
- If Q > Q0.01, then the dubious values are outliers that must processed;
- (2)
- If Q0.05 < Q < Q0.01, then the dubious values are deviant values that can be retained or processed;
- (3)
- If Q < Q0.05, then the dubious values are normal values and should be retained;
- (4)
- If it is necessary to address a dubious value, the median of the remaining valid data is commonly used in lieu of the abnormal data. However, an appropriate interpolation method such as spline interpolation may be more reasonable. In this paper, the inverse distance weighted average method is used instead of the median.
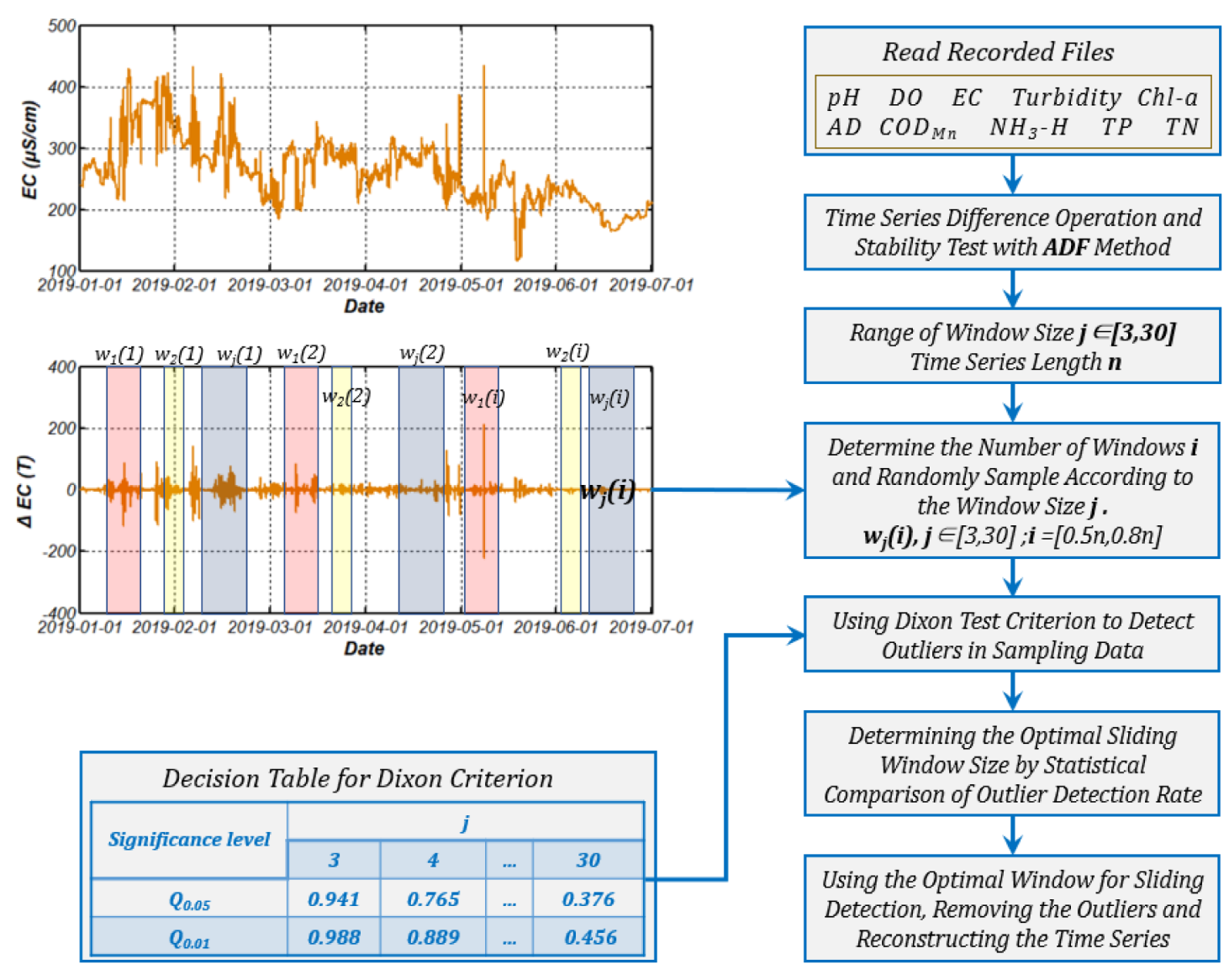
3. Optimization Algorithms for Sliding Window Size
| Algorithm 1:Monte Carlo Search Method (MCSM). |
| Input: |
|
| Preprocess: |
|
| Main Procedure: |
| for kk=1:k |
| for ii=1:i |
| for jj=3:30 |
| do Calculate the Q value according to the formula in Table 1 and using Dixon criterion to detect outliers |
| end |
| end |
| end odr(J,i) Calculate maximum detection ratio of outlier data according to Equation (1) |
| Output: |
| ow = J |
4. Experimental Studies
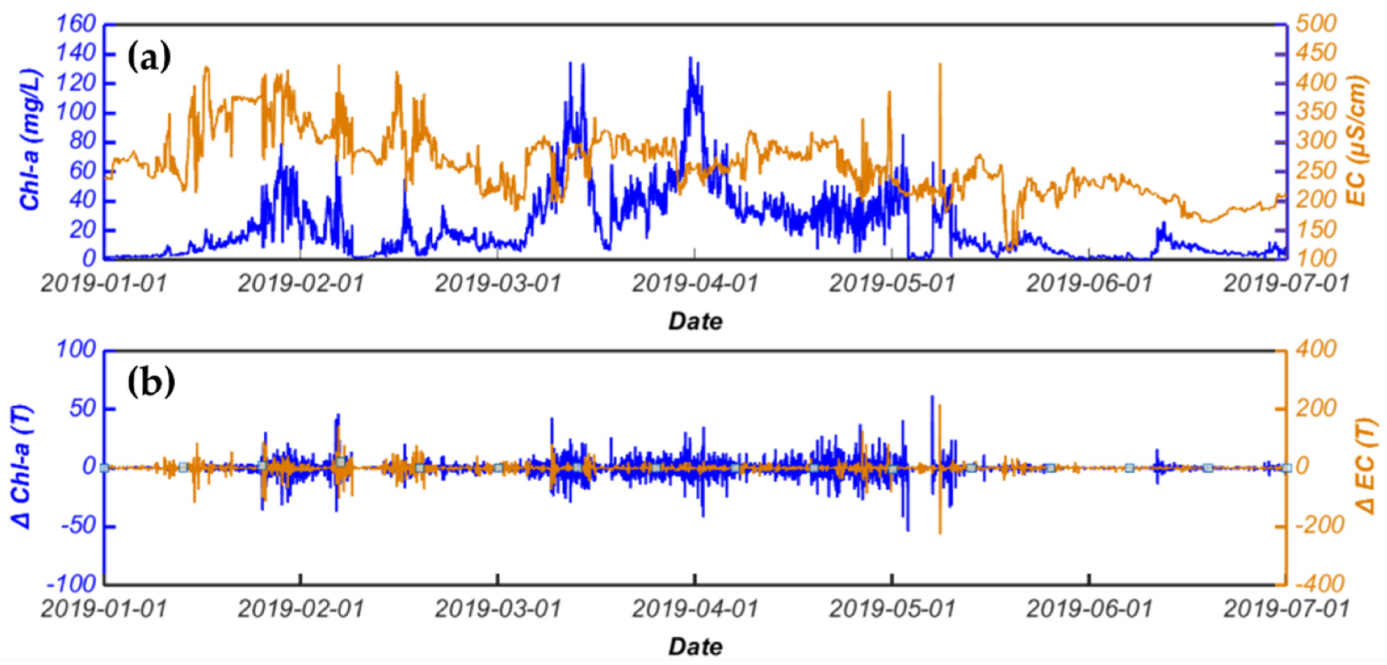
4.1. Data Sources
4.2. Experiment Platform and Initial Conditions
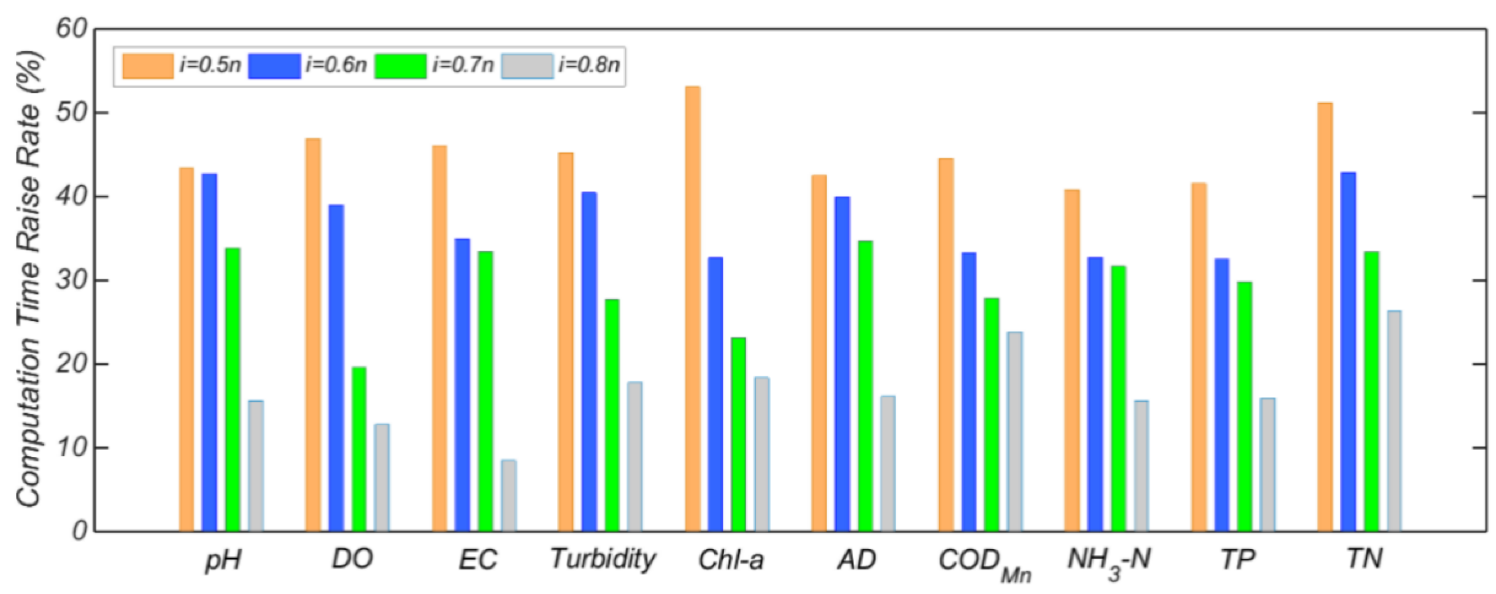
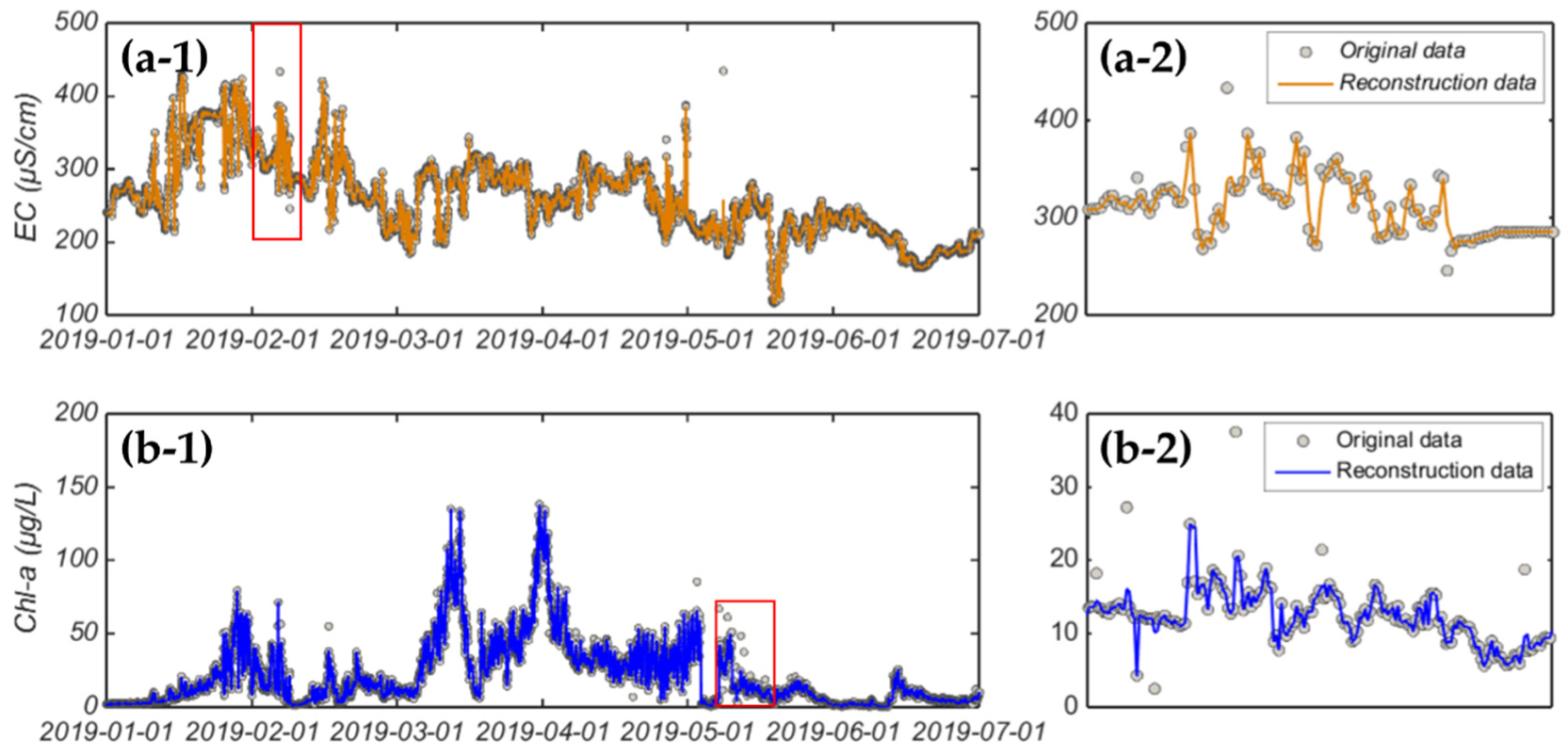
4.3. Results and Comparative Analysis
5. Discussion and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sun, A.Y.; Zhong, Z.; Jeong, H.; Yang, Q. Building complex event processing capability for intelligent environmental monitoring. Environ. Model. Softw. 2019, 116, 1–6. [Google Scholar] [CrossRef]
- Huang, Q.; Rodriguez, K. A Software Framework for Heterogeneous Wireless Sensor Network Towards Environmental Monitoring. Appl. Sci. 2019, 9, 867. [Google Scholar] [CrossRef]
- Cucina, D.; Di Salvatore, A.; Protopapas, M.K. Outliers detection in multivariate time series using genetic algorithms. Chemom. Intell. Lab. Syst. 2014, 132, 103–110. [Google Scholar] [CrossRef]
- Garces, H.; Sbarbaro, D. Outliers detection in environmental monitoring databases. Eng. Appl. Artif. Intell. 2011, 24, 341–349. [Google Scholar] [CrossRef]
- Doong, D.J.; Chen, S.H.; Kao, C.C.; Lee, B.C.; Yeh, S.P. Data quality check procedures of an operational coastal ocean monitoring network. Ocean Eng. 2007, 34, 234–246. [Google Scholar] [CrossRef]
- Ghallab, H.; Fahmy, H.; Nasr, M. Detection outliers on internet of things using big data technology. Egypt. Inform. J. 2019. [Google Scholar] [CrossRef]
- Teegavarapu, R.S.V. Chapter 1 -Methods for Analysis of Trends and Changes in Hydroclimatological Time-Series. In Trends and Changes in Hydroclimatic Variables; Teegavarapu, R., Ed.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 1–89. [Google Scholar] [CrossRef]
- Dou, W.; Jiang, J.; Zhou, B.; Bai, Y. An algorithm for the difference correlation filter for multi-parameter marine timing observation data. Acta Oceanolgica Sin. 2012, 34, 51–58. [Google Scholar]
- Tiwari, R.C.; Dienes, T.P. The Kalman filter model and Bayesian outlier detection for time series analysis of BOD data. Ecol. Model. 1994, 73, 159–165. [Google Scholar] [CrossRef]
- Čampulová, M.; Michálek, J.; Moučka, J. Generalised linear model-based algorithm for detection of outliers in environmental data and comparison with semi-parametric outlier detection methods. Atmos. Pollut. Res. 2019, 10, 1015–1023. [Google Scholar] [CrossRef]
- Fox, A.J. Outliers in Time Series. J. R. Stat. Soc. 1972, 34, 350–363. [Google Scholar] [CrossRef]
- Choy, K. Outlier detection for stationary time series. J. Stat. Plan. Inference 2001, 99, 111–127. [Google Scholar] [CrossRef]
- Arumugam, P.; Saranya, R. Outlier Detection and Missing Value in Seasonal ARIMA Model Using Rainfall Data*. Mater. Today Proc. 2018, 5, 1791–1799. [Google Scholar] [CrossRef]
- Salles, R.; Belloze, K.; Porto, F.; Gonzalez, P.H.; Ogasawara, E. Nonstationary time series transformation methods: An experimental review. Knowl. Based Syst. 2019, 164, 274–291. [Google Scholar] [CrossRef]
- Giménez, E.; Crespi, M.; Garrido, M.S.; Gil, A.J. Multivariate outlier detection based on robust computation of Mahalanobis distances. Application to positioning assisted by RTK GNSS Networks. Int. J. Appl. Earth Obs. Geoinf. 2012, 16, 94–100. [Google Scholar] [CrossRef]
- Angiulli, F.; Basta, S.; Lodi, S.; Sartori, C. Reducing distance computations for distance-based outliers. Expert Syst. Appl. 2020, 147, 113215. [Google Scholar] [CrossRef]
- Tang, B.; He, H. A local density-based approach for outlier detection. Neurocomputing 2017, 241, 171–180. [Google Scholar] [CrossRef]
- Christy, A.; Gandhi, G.M.; Vaithyasubramanian, S. Cluster Based Outlier Detection Algorithm for Healthcare Data. Procedia Comput. Sci. 2015, 50, 209–215. [Google Scholar] [CrossRef]
- Wang, B.; Yang, X.-C.; Wang, G.-R.; Yu, G. Outlier Detection over Sliding Windows for Probabilistic Data Streams. J. Comput. Sci. Technol. 2010, 25, 389–400. [Google Scholar] [CrossRef][Green Version]
- Bauer, M.E. Remote Sensing of Environment: History, Philosophy, Approach and Contributions, 1969–2019. Remote Sens. Environ. 2020, 237, 111522. [Google Scholar] [CrossRef]
- de Araujo Barbosa, C.C.; Atkinson, P.M.; Dearing, J.A. Remote sensing of ecosystem services: A systematic review. Ecol. Indic. 2015, 52, 430–443. [Google Scholar] [CrossRef]
- Turner, W.; Spector, S.; Gardiner, N.; Fladeland, M.; Sterling, E.; Steininger, M. Remote sensing for biodiversity science and conservation. Trends Ecol. Evol. 2003, 18, 306–314. [Google Scholar] [CrossRef]
- Malche, T.; Maheshwary, P.; Kumar, R. Environmental Monitoring System for Smart City Based on Secure Internet of Things (IoT) Architecture. Wirel. Pers. Commun. 2019, 107, 2143–2172. [Google Scholar] [CrossRef]
- Pijanowski, B.C.; Farina, A.; Gage, S.H.; Dumyahn, S.L.; Krause, B.L. What is soundscape ecology? An introduction and overview of an emerging new science. Landsc. Ecol. 2011, 26, 1213–1232. [Google Scholar] [CrossRef]
- Luque, A.; Gómez-Bellido, J.; Carrasco, A.; Barbancho, J. Optimal Representation of Anuran Call Spectrum in Environmental Monitoring Systems Using Wireless Sensor Networks. Sensors 2018, 18, 1803. [Google Scholar] [CrossRef]
- Li, X.; Yang, X.; Wei, Q.; Zhang, B. Authoritarian environmentalism and environmental policy implementation in china. Resour. Conserv. Recycl. 2019, 145, 86–93. [Google Scholar] [CrossRef]
- Jingang, J.; Lu, S.; Zhongya, F.; Jiaguo, Q. Outlier detection and sequence reconstruction in continuous time series of ocean observation data based on difference analysis and the Dixon criterion. Limnol. Oceanogr. Methods 2017, 15, 916–927. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.B.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econom. 1992, 54, 159–178. [Google Scholar] [CrossRef]
- Mills, T.C. (Ed.) Chapter 5 -Unit Roots, Difference and Trend Stationarity, and Fractional Differencing. In Applied Time Series Analysis; Academic Press: Cambridge, MA, USA, 2019; pp. 71–101. [Google Scholar] [CrossRef]
- Dixon, W.J. Analysis of Extreme Values. Ann. Math. Stat. 1950, 21, 488–506. [Google Scholar] [CrossRef]
- Dixon, W.J. Ratios Involving Extreme Values. Ann. Math. Stat. 1951, 22, 68–78. [Google Scholar] [CrossRef]
- Dixon, W.J. Processing Data for Outliers. Biometrics 1953, 9, 74–89. [Google Scholar] [CrossRef]
- Efstathiou, C.E. Estimation of type I error probability from experimental Dixon’s “Q” parameter on testing for outliers within small size data sets. Talanta 2006, 69, 1068–1071. [Google Scholar] [CrossRef] [PubMed]
- González, J.; Tuerlinckx, F.; De Boeck, P.; Cools, R. Numerical integration in logistic-normal models. Comput. Stat. Data Anal. 2006, 51, 1535–1548. [Google Scholar] [CrossRef]
- Jank, W. Quasi-Monte Carlo sampling to improve the efficiency of Monte Carlo EM. Comput. Stat. Data Anal. 2005, 48, 685–701. [Google Scholar] [CrossRef]
- Lesaffre, E.; Spiessens, B. On the Effect of the Number of Quadrature Points in a Logistic Random-Effects Model: An Example. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2001, 50, 325–335. [Google Scholar] [CrossRef]

| Sliding Window Size (w) | Δy(t + w)′ Is a Dubious Value | Δy(t + 1)′ Is a Dubious Value |
|---|---|---|
| 3–7 | ||
| 8–10 | ||
| 11–13 | ||
| 14–30 |
| Significance Level | w | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | |
| Q0.05 | 0.941 | 0.765 | 0.642 | 0.560 | 0.507 | 0.554 | 0.512 | 0.477 | 0.576 | 0.546 | 0.521 | 0.546 | 0.525 | 0.507 |
| Q0.01 | 0.988 | 0.889 | 0.780 | 0.698 | 0.637 | 0.683 | 0.635 | 0.597 | 0.679 | 0.642 | 0.615 | 0.641 | 0.616 | 0.595 |
| Significance Level | w | |||||||||||||
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | |
| Q0.05 | 0.490 | 0.475 | 0.462 | 0.450 | 0.440 | 0.431 | 0.422 | 0.413 | 0.406 | 0.399 | 0.393 | 0.387 | 0.381 | 0.376 |
| Q0.01 | 0.577 | 0.561 | 0.547 | 0.535 | 0.526 | 0.516 | 0.507 | 0.497 | 0.489 | 0.482 | 0.474 | 0.468 | 0.462 | 0.456 |
| Water Factors | Sampling Period | Time Series Length | Instrument Accuracy | Unit | Mean Value | Standard Deviation | Coefficient of Variation |
|---|---|---|---|---|---|---|---|
| pH | 1 h | 4723 | ±0.2 pH | − | 8.29 | 0.73 | 0.09 |
| Dissolved Oxygen | 1 h | 4723 | ±0.2 mg/L (≤20 mg/L) ±0.6 mg/L (>20 mg/L) | mg/L | 10.43 | 3.02 | 0.29 |
| Electronic Conductivity | 1 h | 4723 | ±0.01% | μS/cm | 261.00 | 53.90 | 0.21 |
| Turbidity | 1 h | 4723 | ±0.01NTU | NTU (Nephelometric Turbidity Unit) | 99.20 | 118.51 | 1.19 |
| Chlorophyll-a | 1 h | 4723 | ±3% | μg/L | 21.81 | 22.46 | 1.03 |
| Algal Density | 1 h | 4723 | ±3% | cells/ml | 14,906 | 19,221 | 1.29 |
| Permanganate Index | 4 h | 1187 | ±5% | mg/L | 8.80 | 4.86 | 0.55 |
| Ammonia-Nitrogen | 4 h | 1187 | ±10% | mg/L | 0.12 | 0.17 | 1.42 |
| Total Phosphorus | 4 h | 1187 | ±10% | mg/L | 0.17 | 0.11 | 0.65 |
| Total Nitrogen | 4 h | 1187 | ±10% | mg/L | 1.37 | 0.65 | 0.47 |
| Water Factors | Full Time Series Sliding Search Method | Monte Carlo Search Method | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 0.5n | 0.6n | 0.7n | 0.8n | |||||||
| Run Time (s) | Optimal Sliding Window Size | Run Time (s) | Optimal Window Accuracy (%) | Run Time (s) | Optimal Window Accuracy (%) | Run Time (s) | Optimal Window Accuracy (%) | Run Time (s) | Optimal Window Accuracy (%) | |
| pH | 1.0508 | 14 | 0.5950 | 62 | 0.6023 | 65 | 0.6949 | 70 | 0.8867 | 77.5 |
| Dissolved Oxygen | 1.0701 | 12, 14 | 0.5687 | 65 | 0.6527 | 72.5 | 0.8605 | 77.5 | 0.9332 | 80 |
| Electronic Conductivity | 1.1270 | 16 | 0.6074 | 62.5 | 0.7332 | 67.5 | 0.7504 | 75 | 1.0313 | 85 |
| Turbidity | 1.1163 | 16, 17, 18 | 0.6113 | 60 | 0.6648 | 67.5 | 0.8070 | 72.5 | 0.9176 | 80 |
| Chlorophyll-a | 1.1410 | 17 | 0.5352 | 57.5 | 0.7680 | 65 | 0.8770 | 67.5 | 0.9316 | 75 |
| Algal Density | 1.1251 | 14 | 0.6469 | 55 | 0.6754 | 65 | 0.7352 | 72.5 | 0.9437 | 75 |
| Permanganate Index | 0.2606 | 9 | 0.1445 | 57.5 | 0.1738 | 62.5 | 0.1879 | 65 | 0.1984 | 75 |
| Ammonia–Nitrogen | 0.2658 | 8 | 0.1574 | 52.5 | 0.1789 | 60 | 0.1816 | 67.5 | 0.2242 | 70 |
| Total Phosphorus | 0.2426 | 12 | 0.1418 | 55 | 0.1637 | 57.5 | 0.1703 | 65 | 0.2039 | 67.5 |
| Total Nitrogen | 0.2586 | 14 | 0.1262 | 60 | 0.1477 | 62.5 | 0.1723 | 65 | 0.1906 | 72.5 |
| Water Factors | Optimal Window Sizes | Suboptimal Window Sizes | Worst Window Sizes | |||
|---|---|---|---|---|---|---|
| Window Size | Outliers Detection Rate (%) | Window Size | Outliers Detection Rate (%) | Window Size | Outliers Detection Rate (%) | |
| pH | 14 | 5.25 | 12 | 5.23 | 23 | 3.01 |
| Dissolved Oxygen | 12,14 | 3.09 | 11 | 2.99 | 29 | 1.80 |
| Electronic Conductivity | 16 | 6.69 | 15 | 6.58 | 5 | 3.47 |
| Turbidity | 16, 17, 18 | 5.99 | 15 | 5.95 | 7 | 3.56 |
| Chlorophyll-a | 17 | 3.05 | 16 | 3.02 | 6 | 2.10 |
| Algal Density | 14 | 3.22 | 16 | 2.90 | 7 | 2.10 |
| Permanganate Index | 9 | 6.23 | 12 | 5.81 | 30 | 4.04 |
| Ammonia–Nitrogen | 8 | 12.47 | 14 | 12.13 | 28 | 6.66 |
| Total Phosphorus | 12 | 7.16 | 14 | 6.99 | 5 | 4.04 |
| Total Nitrogen | 14 | 7.92 | 9 | 7.58 | 30 | 4.80 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, Z.; Feng, H.; Jiang, J.; Zhao, C.; Jiang, N.; Wang, W.; Zeng, F. Monte Carlo Optimization for Sliding Window Size in Dixon Quality Control of Environmental Monitoring Time Series Data. Appl. Sci. 2020, 10, 1876. https://doi.org/10.3390/app10051876
Fan Z, Feng H, Jiang J, Zhao C, Jiang N, Wang W, Zeng F. Monte Carlo Optimization for Sliding Window Size in Dixon Quality Control of Environmental Monitoring Time Series Data. Applied Sciences. 2020; 10(5):1876. https://doi.org/10.3390/app10051876
Chicago/Turabian StyleFan, Zhongya, Huiyun Feng, Jingang Jiang, Changjin Zhao, Ni Jiang, Wencai Wang, and Fantang Zeng. 2020. "Monte Carlo Optimization for Sliding Window Size in Dixon Quality Control of Environmental Monitoring Time Series Data" Applied Sciences 10, no. 5: 1876. https://doi.org/10.3390/app10051876
APA StyleFan, Z., Feng, H., Jiang, J., Zhao, C., Jiang, N., Wang, W., & Zeng, F. (2020). Monte Carlo Optimization for Sliding Window Size in Dixon Quality Control of Environmental Monitoring Time Series Data. Applied Sciences, 10(5), 1876. https://doi.org/10.3390/app10051876





