Numerical and Experimental Investigations of Composite Solar Walls Integrating Sensible or Latent Heat Thermal Storage
Abstract
1. Introduction
- Present the specific features and experimental set-up of a composite Trombe wall containing PCM;
- Explain how the numerical method, with the help of the Dymola/Modelica software, performs in determining the thermal behavior of the composite solar walls;
- Validate this numerical model based on a comparison between simulation and measurement;
- Compare the efficiency of sensible vs. latent storage of composite solar walls.
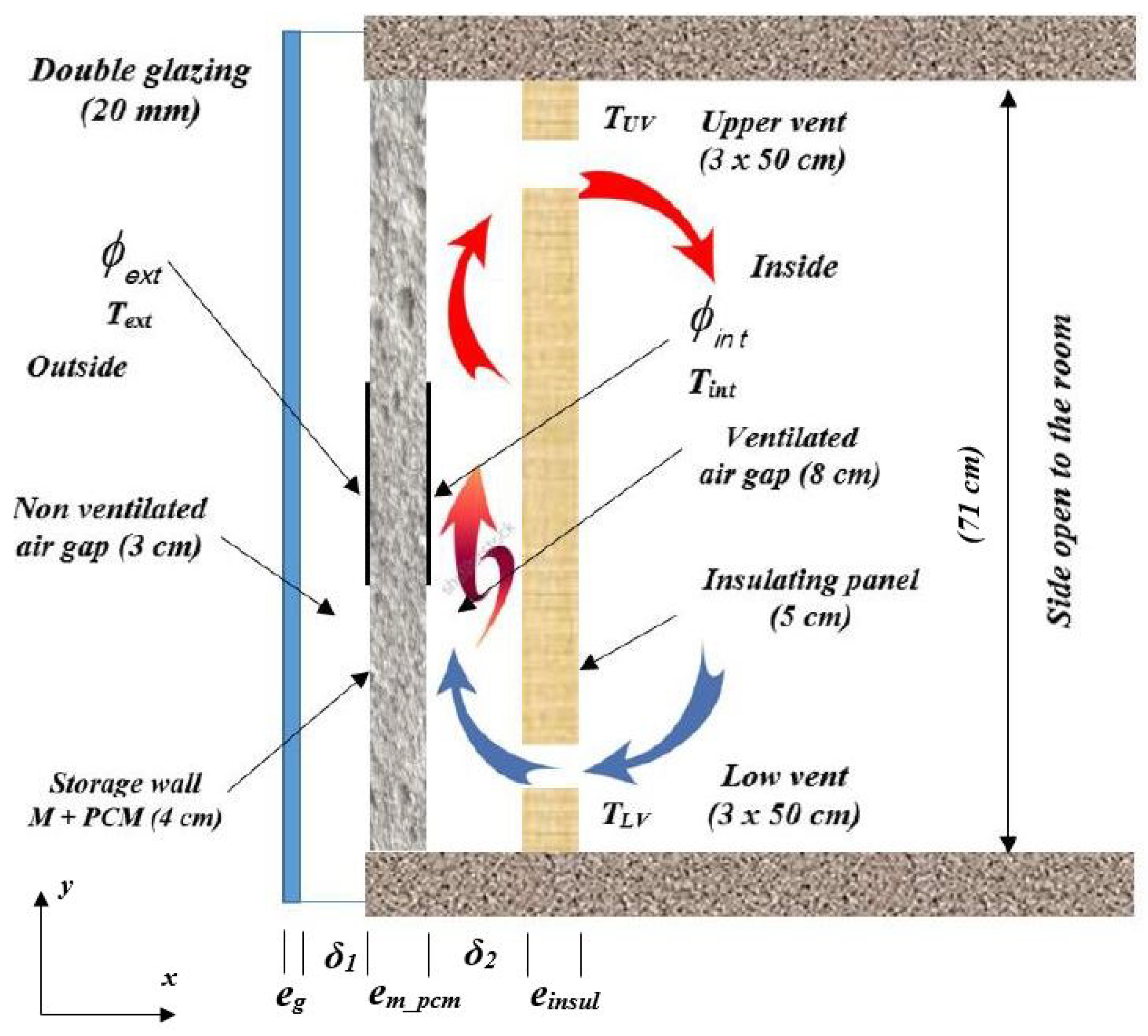
2. Composite Solar Wall and Experimental Set-Up
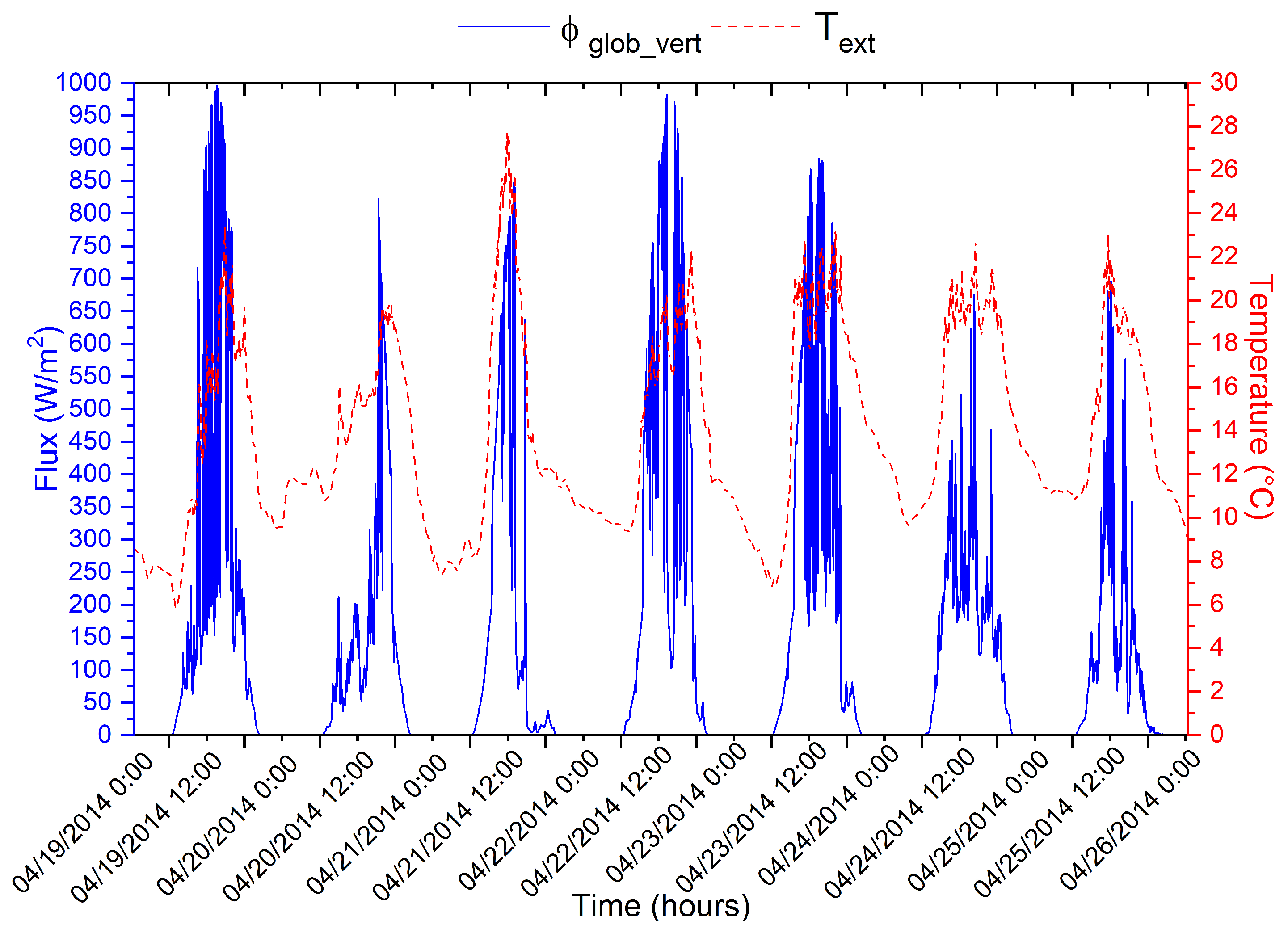
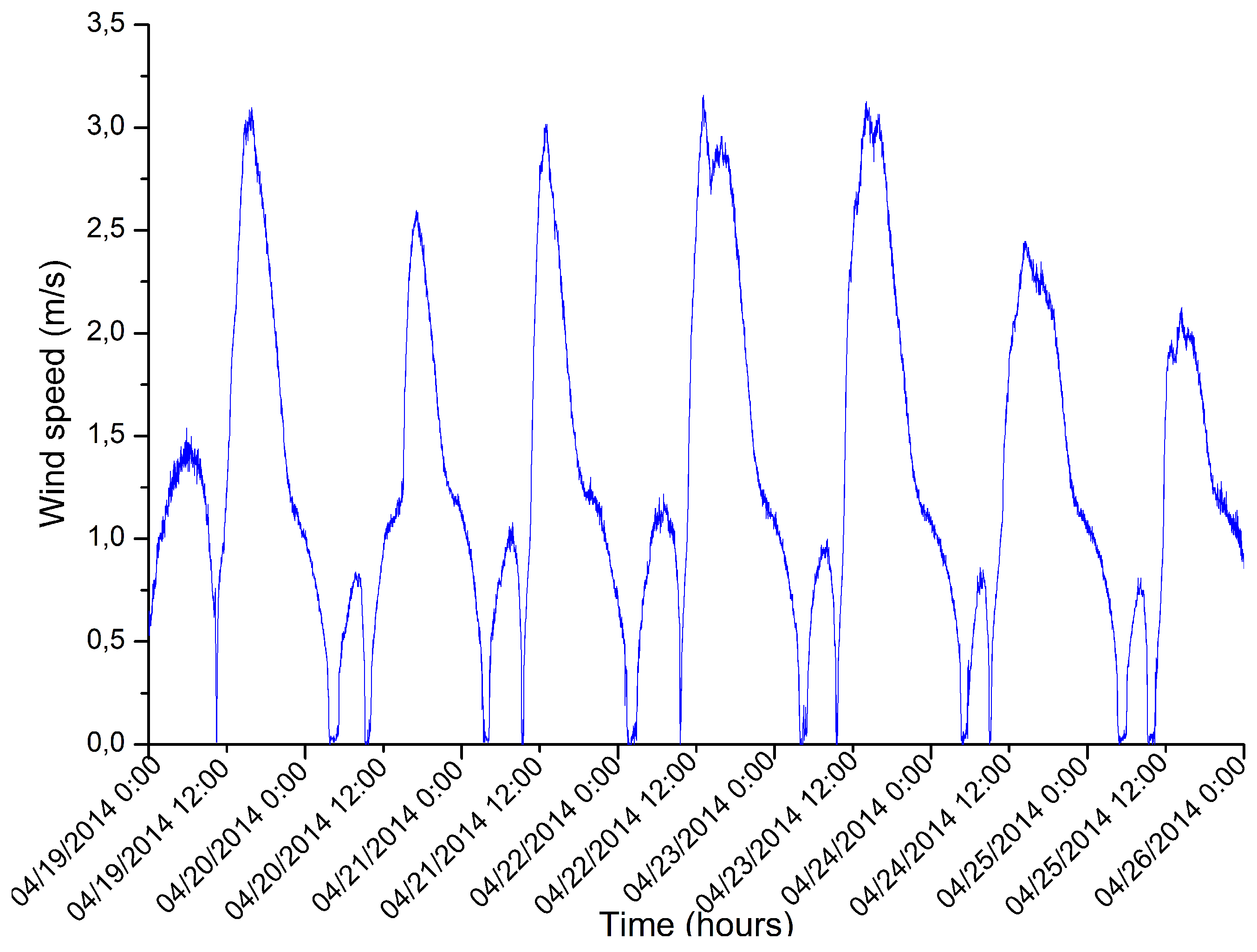
3. Meteorological Data
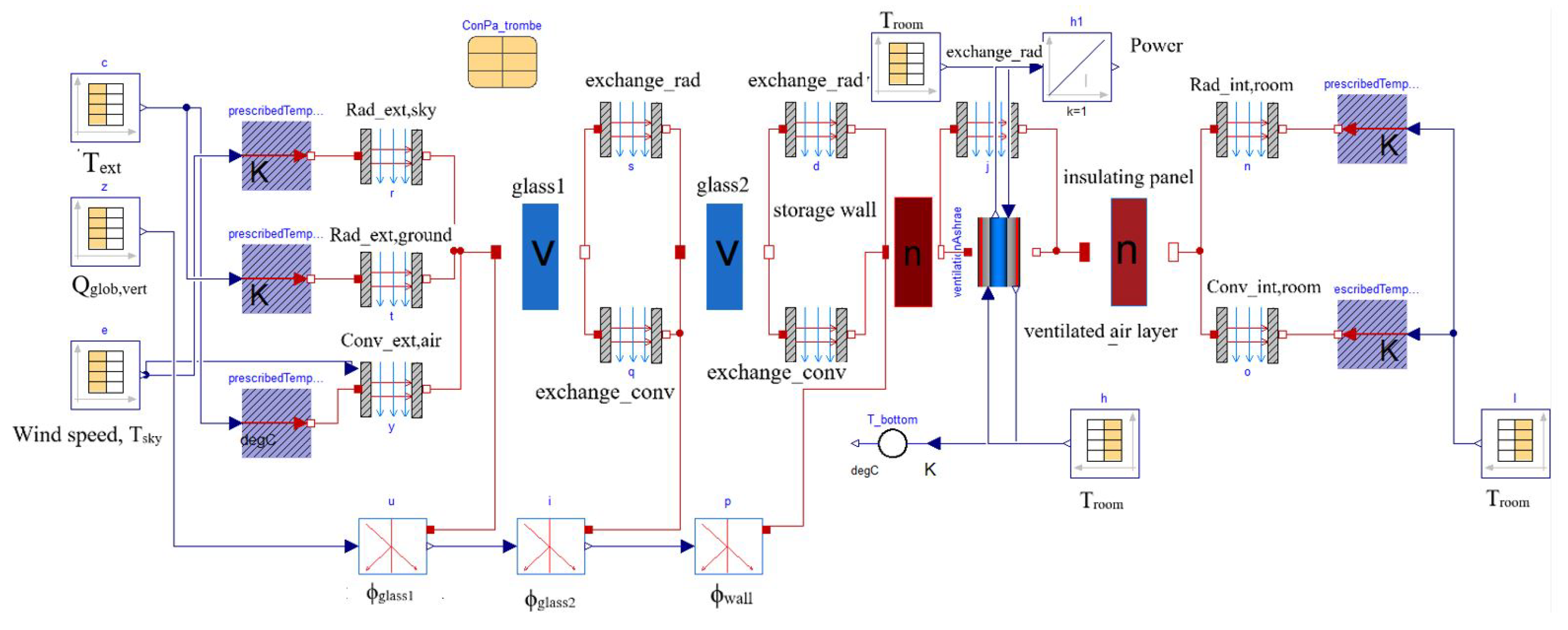
4. Mathematical Model
- glass: evaluate the solar heat flux absorbed by glazing and the direct flux transmitted to the outer storage wall surface M+PCM Equation (14);
- wall: evaluate the total energy absorbed by the wall in considering the heat flux transmitted from the glazing and multi-reflections in the non-ventilated air gap Equation (15);
- Conv_ext: evaluate the total heat transfers by convection between the composite Trombe wall and the outside. This step depends on the outdoor air temperature as well as the wind velocity and direction Equation (6);
- Rad_int: evaluate the inside longwave radiative heat transfer between the inner wall facade and the indoor environment Equation (35);
4.1. Thermal Balance on the External Glazing Surface
4.2. Thermal Balance on the Inner Surface of the Glazing (Non-Ventilated Air Gap)
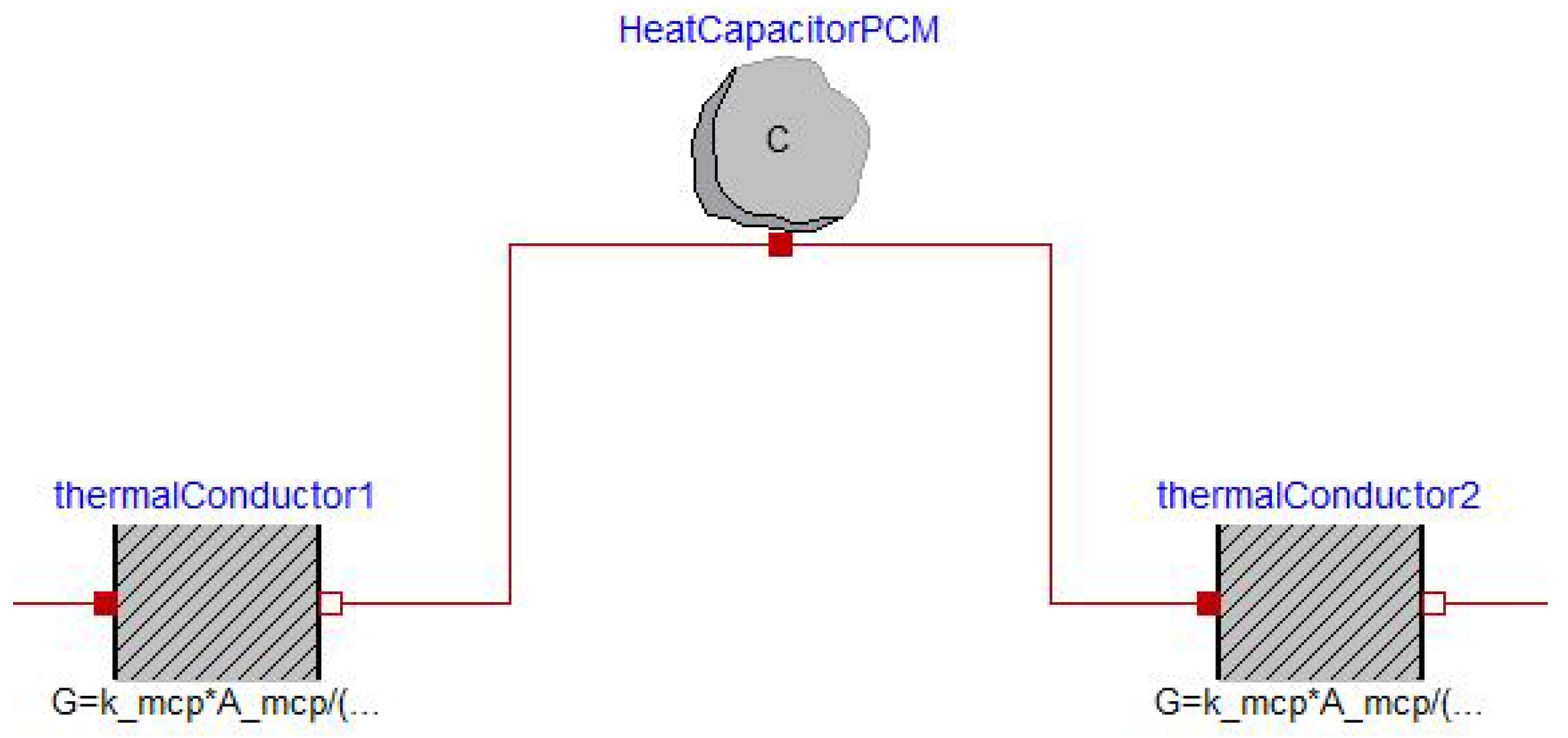
4.3. Thermal Transfer by Conduction on the Storage Wall
4.4. Thermal Balance in the Ventilated-Air Layer
4.5. Thermal Balance towards the Interior Atmosphere
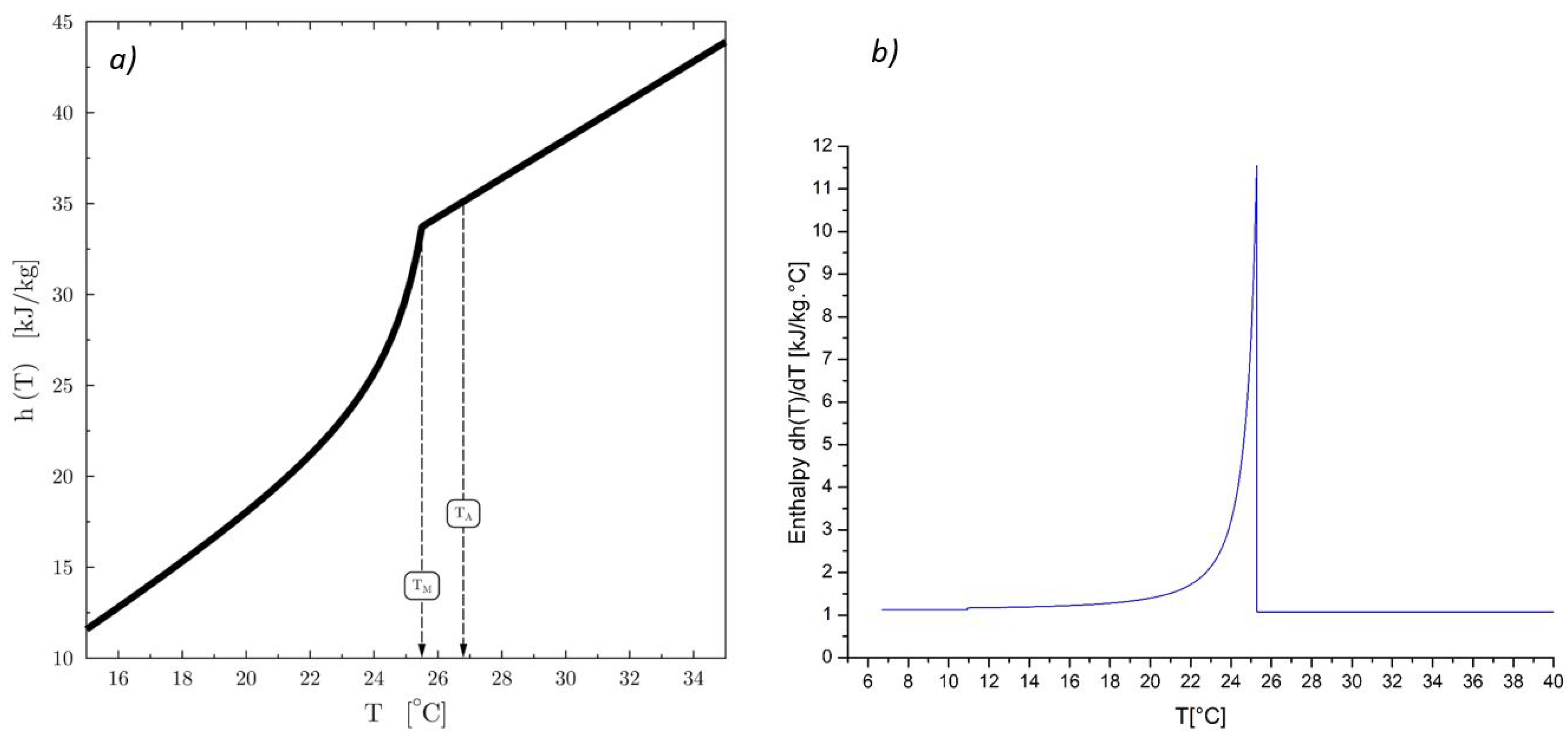
4.6. Material Properties
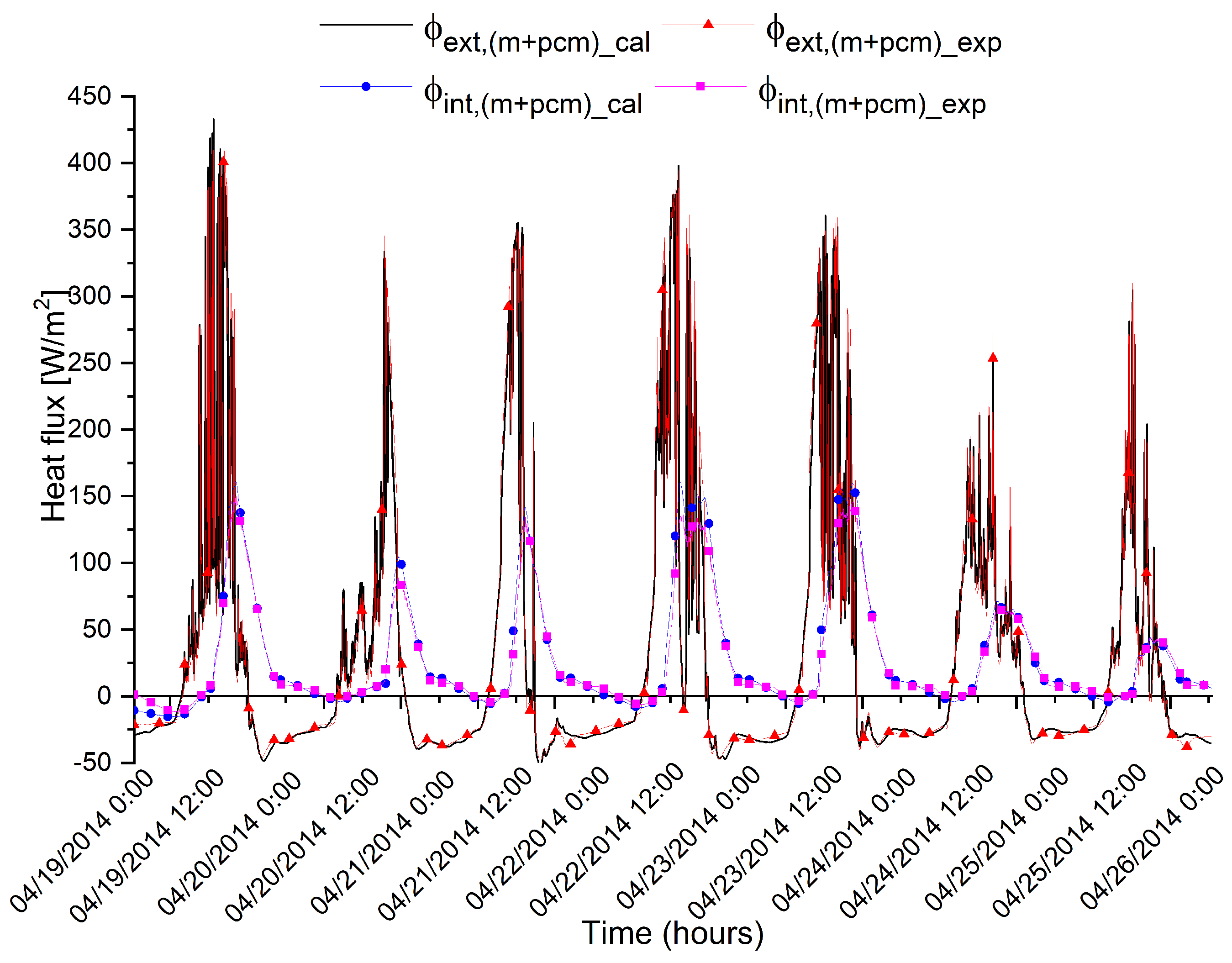
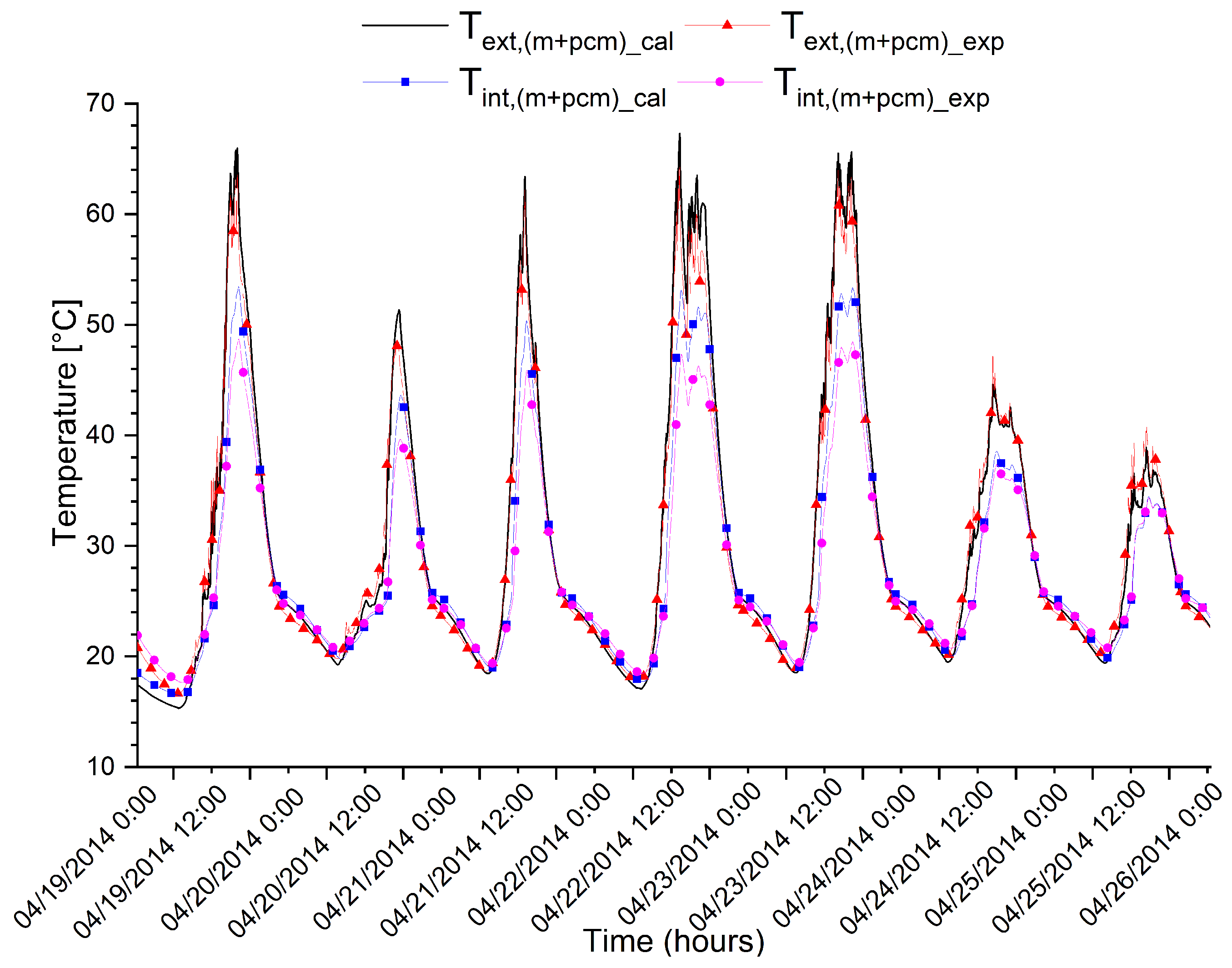
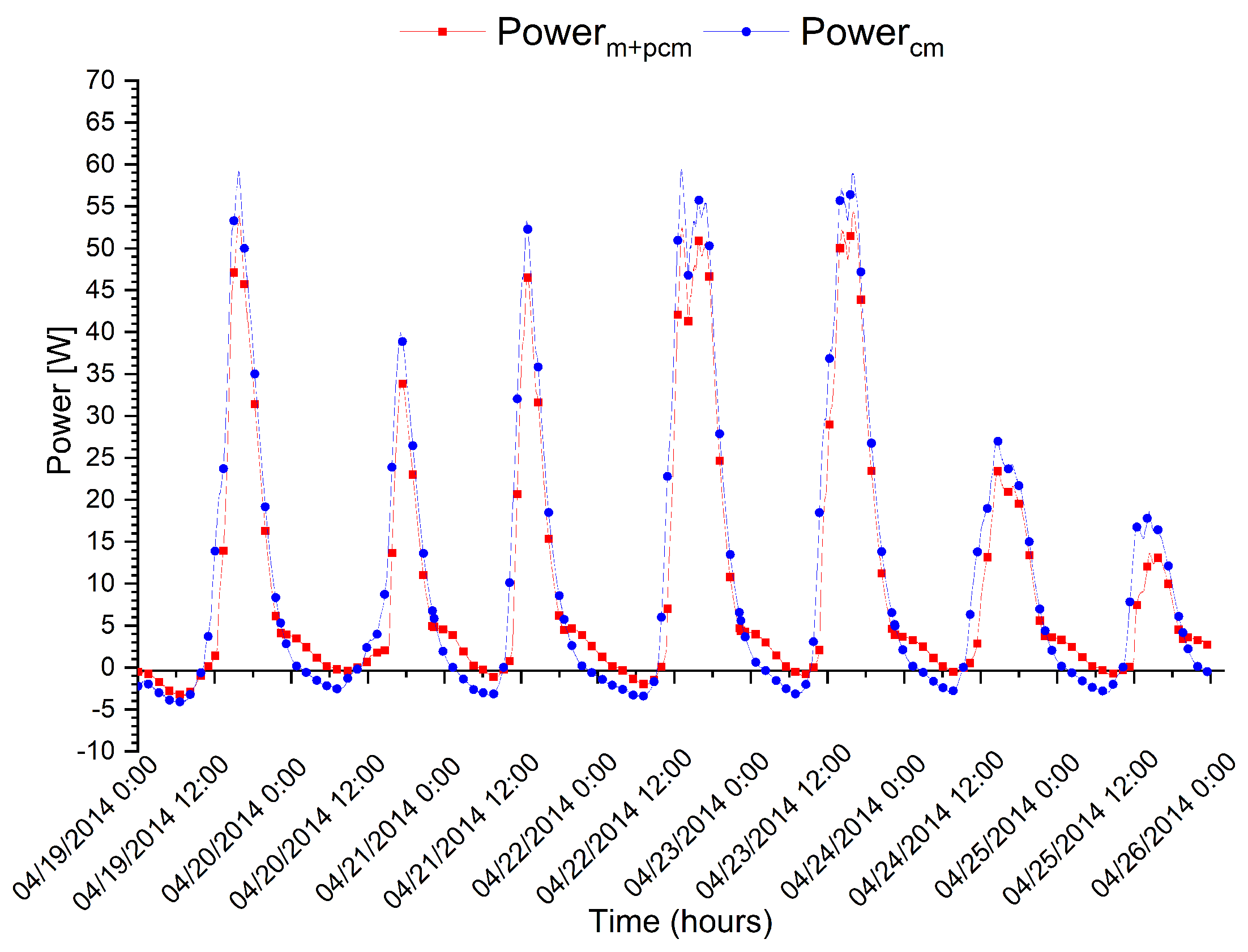
5. Model Validation, Results and Discussion
6. Comparing Performance of Composite Solar Walls with Sensible vs. Latent Heat Storage
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| Symbols: | |
| A | area, m2 |
| Aexch | exchange surface, m2 |
| C | heat capacity, J/K |
| c | specific heat capacity, J/kg K |
| cf | specific heat capacity of fluid, J/kg K |
| csolid | specific heat capacity when PCM is in the solid state, J/kg K |
| cliquid | specific heat capacity when PCM is in the liquid state, J/kg K |
| E | thermal energy, J |
| e | thickness, m |
| Gr | Grashof number |
| H | height, m |
| h | specific enthalpy, J/kg |
| hc | convective heat transfer coefficient, W/m2 K |
| hc1 | convective heat transfer coefficient in non-ventilated air layer, W/m2 K |
| hc2 | convective heat transfer coefficient in ventilated air layer, W/m2 K |
| hr | radiative heat transfer coefficient, W/m2 K |
| hr1 | radiant heat transfer coefficient between glazing and wall, W/m2 K |
| hr2 | radiant heat transfer coefficient between wall and insulating panel, W/m2 K |
| LA | latent heat, J/kg |
| air mass flow rate, kg/s | |
| Nu | Nusselt number |
| P | power supplied by air layer, W |
| Pr | Prandtl number |
| Qsol | solar radiation intensity, W/m2 |
| Ra | Rayleigh number |
| Re | Reynolds number |
| T | temperature, °C |
| t | time, s |
| V | velocity of wind, m/s |
| W | width, m |
| Greek symbols | |
| absorptivity | |
| dilatation coefficient at constant pressure, K−1 | |
| non ventilated air gap width, m | |
| ventilated air gap width, m | |
| emissivity | |
| thermal conductivity, W/m K | |
| dynamic viscosity of air, kg/m s | |
| kinematic viscosity of air, m2/s | |
| g | absorptivity of multi-reflection radiation intensity to glazing |
| w | global absorptivity of wall (including multi-reflection) |
| density, kg/m3 | |
| Stefan-Boltzmann constant, 5.67 × 10 W/m2 K4 | |
| transmissivity | |
| heat flux, W | |
| Subscripts | |
| A | pure substance |
| amb | ambient |
| cal | calculation |
| env | environment |
| exp | experimentation |
| ext | exterior surface |
| f | fluid |
| f1 | fluid circulating in non-ventilated |
| f2 | fluid circulating in ventilated air layer |
| g | glazing |
| gro | ground |
| i | initial |
| ins | insulating |
| int | interior surface |
| lv | lower vent |
| M | melting |
| uv | upper vent |
| w | wall (storage wall) |
| Abbreviations | |
| CM | cement mortar |
| M_PCM | composite material: mortar + PCM |
| PCM | phase change material |
| Q_cm | internal capacity of CM |
| Q_pcm | internal capacity of M_PCM |
References
- Buzzoni, L.; Dall’Olio, R.; Spiga, M. Energy analysis of a passive solar system. Rev. Générale Therm. 1998, 37, 411–416. [Google Scholar] [CrossRef]
- Chan, H.Y.; Riffat, S.B.; Zhu, J. Review of passive solar heating and cooling technologies. Renew. Sustain. Energy Rev. 2010, 14, 781–789. [Google Scholar] [CrossRef]
- Dabaieh, M.; Elbably, A. Ventilated Trombe wall as a passive solar heating and cooling retrofitting approach; a low-tech design for off-grid settlements in semi-arid climates. Sol. Energy 2015, 122, 820–833. [Google Scholar] [CrossRef]
- Hassanain, A.A.; Hokam, E.M.; Mallick, T.K. Effect of solar storage wall on the passive solar heating constructions. Energy Build. 2011, 43, 737–747. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.; Jiang, J.; Liu, J. The Optimized Matching of Passive Solar Energy supply and Classroom Thermal Demand of Rural Primary and Secondary School in Northwest China. Procedia Eng. 2015, 121, 1089–1095. [Google Scholar] [CrossRef]
- Castell, A.; Martorell, I.; Medrano, M.; Pérez, G.; Cabeza, L.F. Experimental study of using PCM in brick constructive solutions for passive cooling. Energy Build. 2010, 42, 534–540. [Google Scholar] [CrossRef]
- Rekstad, J.; Meir, M.; Murtnes, E.; Dursun, A. A comparison of the energy consumption in two passive houses, one with a solar heating system and one with an air–water heat pump. Energy Build. 2015, 96, 149–161. [Google Scholar] [CrossRef]
- Santamouris, M.; Argiriou, A.; Vallindras, M. Design and operation of a low energy consumption passive solar agricultural greenhouse. Sol. Energy 1994, 52, 371–378. [Google Scholar] [CrossRef]
- Taleb, H.M. Using passive cooling strategies to improve thermal performance and reduce energy consumption of residential buildings in U.A.E. buildings. Front. Archit. Res. 2014, 3, 154–165. [Google Scholar] [CrossRef]
- Tyagi, V.V.; Buddhi, D. PCM thermal storage in buildings: A state of art. Renew. Sustain. Energy Rev. 2007, 11, 1146–1166. [Google Scholar] [CrossRef]
- Mazria, E. Passive Solar Energy Book; Rodale Press: Emmaus, PA, USA, 1979. [Google Scholar]
- Trombe, F. Maisons solaires. Techniques de l’ingenieur 1974, 3, 375–382. [Google Scholar]
- Smolec, W.; Thomas, A. Theoretical and experimental investigations of heat transfer in a trombe wall. Energy Convers. Manag. 1993, 34, 385–400. [Google Scholar] [CrossRef]
- Utzinger, D.M.; Klein, S.A.; Mitchell, J.W. The effect of air flow rate in collector-storage walls. Sol. Energy 1980, 25, 511–519. [Google Scholar] [CrossRef]
- Yedder, R.B.; Bilgen, E. Natural convection and conduction in Trombe wall systems. Int. J. Heat Mass Transf. 1991, 34, 1237–1248. [Google Scholar] [CrossRef]
- Gracia, A.d.; Cabeza, L.F. Phase change materials and thermal energy storage for buildings. Energy Build. 2015, 103, 414–419. [Google Scholar] [CrossRef]
- Fiorito, F. Trombe Walls for Lightweight Buildings in Temperate and Hot Climates. Exploring the Use of Phase-change Materials for Performances Improvement. Energy Procedia 2012, 30, 1110–1119. [Google Scholar] [CrossRef]
- Ghoneim, A.A.; Klein, S.A.; Duffie, J.A. Analysis of collector-storage building walls using phase-change materials. Sol. Energy 1991, 47, 237–242. [Google Scholar] [CrossRef]
- Sharma, A.; Tyagi, V.V.; Chen, C.R.; Buddhi, D. Review on thermal energy storage with phase change materials and applications. Renew. Sustain. Energy Rev. 2009, 13, 318–345. [Google Scholar] [CrossRef]
- Stritih, U.; Novak, P. Solar heat storage wall for building ventilation. Renew. Energy 1996, 8, 268–271. [Google Scholar] [CrossRef]
- Zhou, G.; Pang, M. Experimental investigations on thermal performance of phase change material—Trombe wall system enhanced by delta winglet vortex generators. Energy 2015, 93, 758–769. [Google Scholar] [CrossRef]
- Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Numerical study of a composite Trombe solar wall integrating microencapsulated PCM. Energy Procedia 2017, 122, 1009–1014. [Google Scholar] [CrossRef]
- Shen, J.; Lassue, S.; Zalewski, L.; Huang, D. Numerical study on thermal behavior of classical or composite Trombe solar walls. Energy Build. 2007, 39, 962–974. [Google Scholar] [CrossRef]
- Zalewski, L.; Chantant, M.; Lassue, S.; Duthoit, B. Experimental thermal study of a solar wall of composite type. Energy Build. 1997, 25, 7–18. [Google Scholar] [CrossRef]
- Zalewski, L.; Joulin, A.; Lassue, S.; Dutil, Y.; Rousse, D. Experimental study of small-scale solar wall integrating phase change material. Sol. Energy 2012, 86, 208–219. [Google Scholar] [CrossRef]
- Zrikem, Z.; Bilgen, E. Theoretical study of a composite Trombe-Michel wall solar collector system. Sol. Energy 1987, 39, 409–419. [Google Scholar] [CrossRef]
- Irshad, K.; Habib, K.; Thirumalaiswamy, N. Performance Evaluation of PV-trombe Wall for Sustainable Building Development. Procedia CIRP 2015, 26, 624–629. [Google Scholar] [CrossRef]
- Irshad, K.; Habib, K.; Thirumalaiswamy, N. Energy and Cost Analysis of Photo Voltaic Trombe Wall System in Tropical Climate. Energy Procedia 2014, 50, 71–78. [Google Scholar] [CrossRef]
- Jiang, B.; Ji, J.; Yi, H. The influence of PV coverage ratio on thermal and electrical performance of photovoltaic-Trombe wall. Renew. Energy 2008, 33, 2491–2498. [Google Scholar] [CrossRef]
- Jie, J.; Hua, Y.; Gang, P.; Bin, J.; Wei, H. Study of PV-Trombe wall assisted with DC fan. Build. Environ. 2007, 42, 3529–3539. [Google Scholar] [CrossRef]
- Jie, J.; Hua, Y.; Wei, H.; Gang, P.; Jianping, L.; Bin, J. Modeling of a novel Trombe wall with PV cells. Build. Environ. 2007, 42, 1544–1552. [Google Scholar] [CrossRef]
- Jie, J.; Hua, Y.; Gang, P.; Jianping, L. Study of PV-Trombe wall installed in a fenestrated room with heat storage. Appl. Therm. Eng. 2007, 27, 1507–1515. [Google Scholar] [CrossRef]
- Koyunbaba, B.K.; Yilmaz, Z.; Ulgen, K. An approach for energy modeling of a building integrated photovoltaic (BIPV) Trombe wall system. Energy Build. 2013, 67, 680–688. [Google Scholar] [CrossRef]
- Koyunbaba, B.K.; Yilmaz, Z. The comparison of Trombe wall systems with single glass, double glass and PV panels. Renew. Energy 2012, 45, 111–118. [Google Scholar] [CrossRef]
- Sun, W.; Ji, J.; Luo, C.; He, W. Performance of PV-Trombe wall in winter correlated with south façade design. Appl. Energy 2011, 88, 224–231. [Google Scholar] [CrossRef]
- Taffesse, F.; Verma, A.; Singh, S.; Tiwari, G.N. Periodic modeling of semi-transparent photovoltaic thermal-trombe wall (SPVT-TW). Sol. Energy 2016, 135, 265–273. [Google Scholar] [CrossRef]
- Saadatian, O.; Sopian, K.; Lim, C.H.; Asim, N.; Sulaiman, M.Y. Trombe walls: A review of opportunities and challenges in research and development. Renew. Sustain. Energy Rev. 2012, 16, 6340–6351. [Google Scholar] [CrossRef]
- Gan, G. A parametric study of Trombe walls for passive cooling of buildings. Energy Build. 1998, 27, 37–43. [Google Scholar] [CrossRef]
- Hu, Z.; He, W.; Ji, J.; Zhang, S. A review on the application of Trombe wall system in buildings. Renew. Sustain. Energy Rev. 2017, 70, 976–987. [Google Scholar] [CrossRef]
- Stazi, F.; Mastrucci, A.; di Perna, C. The behaviour of solar walls in residential buildings with different insulation levels: An experimental and numerical study. Energy Build. 2012, 47, 217–229. [Google Scholar] [CrossRef]
- Dutil, Y.; Rousse, D.; Lassue, S.; Zalewski, L.; Joulin, A.; Virgone, J.; Kuznik, F.; Johannes, K.; Dumas, J.P.; Bédécarrats, J.P.; et al. Modeling phase change materials behavior in building applications: Comments on material characterization and model validation. Renew. Energy 2014, 61, 132–135. [Google Scholar] [CrossRef]
- Khudhair, A.M.; Farid, M.M. A review on energy conservation in building applications with thermal storage by latent heat using phase change materials. Energy Convers. Manag. 2004, 45, 263–275. [Google Scholar] [CrossRef]
- Zalba, B.; Marin, J.M.; Cabeza, L.F.; Mehling, H. Review on thermal energy storage with phase change: Materials, heat transfer analysis and applications. Appl. Therm. Eng. 2003, 23, 251–283. [Google Scholar] [CrossRef]
- Swet, C. Phase change storage in passive solar architecture. Proc. Annu. Meet. Am. Sect. Int. Sol. Energy Soc. 1980, 5, 282–286. [Google Scholar]
- Bourdeau, L. Utilisation d’un matériau à changement de phase dans un mur Trombe sans thermocirculation. Rev. Phys. Appl. 1982, 17, 633–642. [Google Scholar] [CrossRef][Green Version]
- Khalifa, A.J.N.; Abbas, E.F. A comparative performance study of some thermal storage materials used for solar space heating. Energy Build. 2009, 41, 407–415. [Google Scholar] [CrossRef]
- Li, Y.; Liu, S. Experimental study on thermal performance of a solar chimney combined with PCM. Appl. Energy 2014, 114, 172–178. [Google Scholar] [CrossRef]
- Zhou, Y.; Yu, C.W.F.; Zhang, G. Study on heat-transfer mechanism of wallboards containing active phase change material and parameter optimization with ventilation. Appl. Therm. Eng. 2018, 144, 1091–1108. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, Y.; Zhang, G. Numerical study on cooling performance of a ventilated Trombe wall with phase change materials. Build. Simul. 2018, 11, 677–694. [Google Scholar] [CrossRef]
- Baetens, R.; De Coninck, R.; Jorissen, F.; Picard, D.; Helsen, L.; Saelens, D. Openideas-an open framework for integrated district energy simulations. In Proceedings of the 14th International Conference of IBPSA—Building Simulation, Hyderabad, India, 7–9 December 2015; pp. 347–354. [Google Scholar]
- Wetter, M.; Bonvini, M.; Nouidui, T.S.; Tian, W.; Zuo, W. Modelica buildings library 2.0. In Proceedings of the 14th International Conference of IBPSA—Building Simulation, Hyderabad, India, 7–9 December 2015; pp. 387–394. [Google Scholar]
- Zhou, Y.; Zheng, S.; Zhang, G. Study on the energy performance enhancement of a new PCMs integrated hybrid system with the active cooling and hybrid ventilations. Energy 2019, 179, 111–128. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Machine-learning based study on the on-site renewable electrical performance of an optimal hybrid PCMs integrated renewable system with high-level parameters’ uncertainties. Renew. Energy 2019. [Google Scholar] [CrossRef]
- Zhou, Y.; Zheng, S.; Zhang, G. Artificial neural network based multivariable optimization of a hybrid system integrated with phase change materials, active cooling and hybrid ventilations. Energy Convers. Manag. 2019, 197, 111859. [Google Scholar] [CrossRef]
- Tang, L.; Zhou, Y.; Zheng, S.; Zhang, G. Exergy-based optimisation of a phase change materials integrated hybrid renewable system for active cooling applications using supervised machine learning method. Sol. Energy 2020, 195, 514–526. [Google Scholar] [CrossRef]
- Liu, X.; Zhou, Y.; Li, C.Q.; Lin, Y.; Yang, W.; Zhang, G. Optimization of a New Phase Change Material Integrated Photovoltaic/Thermal Panel with The Active Cooling Technique Using Taguchi Method. Energies 2019, 12, 1022. [Google Scholar] [CrossRef]
- Zalewski, L. Etude Thermique Expérimentale et Simulation Numérique d’un mur Solaire Composite. Optimisation des Performances énergétiques. Ph.D. Thesis, Univ. Artois, Arras, France, 1996. [Google Scholar]
- Leclercq, D.; Thery, P. Apparatus for simultaneous temperature and heat-flow measurements under transient conditions. Rev. Sci. Instrum. 1983, 54, 374–380. [Google Scholar] [CrossRef]
- Cherif, Y.; Joulin, A.; Zalewski, L.; Lassue, S. Superficial heat transfer by forced convection and radiation in a horizontal channel. Int. J. Therm. Sci. 2009, 48, 1696–1706. [Google Scholar] [CrossRef]
- Sparrow, E.M.; Ramsey, J.W.; Mass, E.A. Effect of Finite Width on Heat Transfer and Fluid Flow about an Inclined Rectangular Plate. J. Heat Transf. 1979, 101, 199–204. [Google Scholar] [CrossRef]
- Buchberg, H.; Catton, I.; Edwards, D.K. Natural Convection in Enclosed Spaces—A Review of Application to Solar Energy Collection. J. Heat Transf. 1976, 98, 182–188. [Google Scholar] [CrossRef]
- Hollands, K.G.T.; Unny, T.E.; Raithby, G.D.; Konicek, L. Free Convective Heat Transfer Across Inclined Air Layers. J. Heat Transf. 1976, 98, 189–193. [Google Scholar] [CrossRef]
- Franquet, E.; Gibout, S.; Tittelein, P.; Zalewski, L.; Dumas, J.P. Experimental and theoretical analysis of a cement mortar containing microencapsulated PCM. Appl. Therm. Eng. 2014, 73, 32–40. [Google Scholar] [CrossRef]
- Tittelein, P.; Gibout, S.; Franquet, E.; Zalewski, L.; Defer, D. Identification of Thermal Properties and Thermodynamic Model for a Cement Mortar Containing PCM by Using Inverse Method. Energy Procedia 2015, 78, 1696–1701. [Google Scholar] [CrossRef]
- Zalewski, L.; Franquet, E.; Gibout, S.; Tittelein, P.; Defer, D. Efficient Characterization of Macroscopic Composite Cement Mortars with Various Contents of Phase Change Material. Appl. Sci. 2019, 9, 1104. [Google Scholar] [CrossRef]
- Tittelein, P.; Gibout, S.; Franquet, E.; Johannes, K.; Zalewski, L.; Kuznik, F.; Dumas, J.P.; Lassue, S.; Bédécarrats, J.P.; David, D. Simulation of the thermal and energy behaviour of a composite material containing encapsulated-PCM: Influence of the thermodynamical modelling. Appl. Energy 2015, 140, 269–274. [Google Scholar] [CrossRef]
- Churchill, S.W.; Chu, H.H.S. Correlating equations for laminar and turbulent free convection from a vertical plate. Int. J. Heat Mass Transf. 1975, 18, 1323–1329. [Google Scholar] [CrossRef]
- McAdams, W.H. Transmission de la Chaleur; Dunod: Paris, France, 1961. [Google Scholar]
- Joulin, A.; Zalewski, L.; Lassue, S.; Naji, H. Experimental investigation of thermal characteristics of a mortar with or without a micro-encapsulated phase change material. Appl. Therm. Eng. 2014, 66, 171–180. [Google Scholar] [CrossRef]



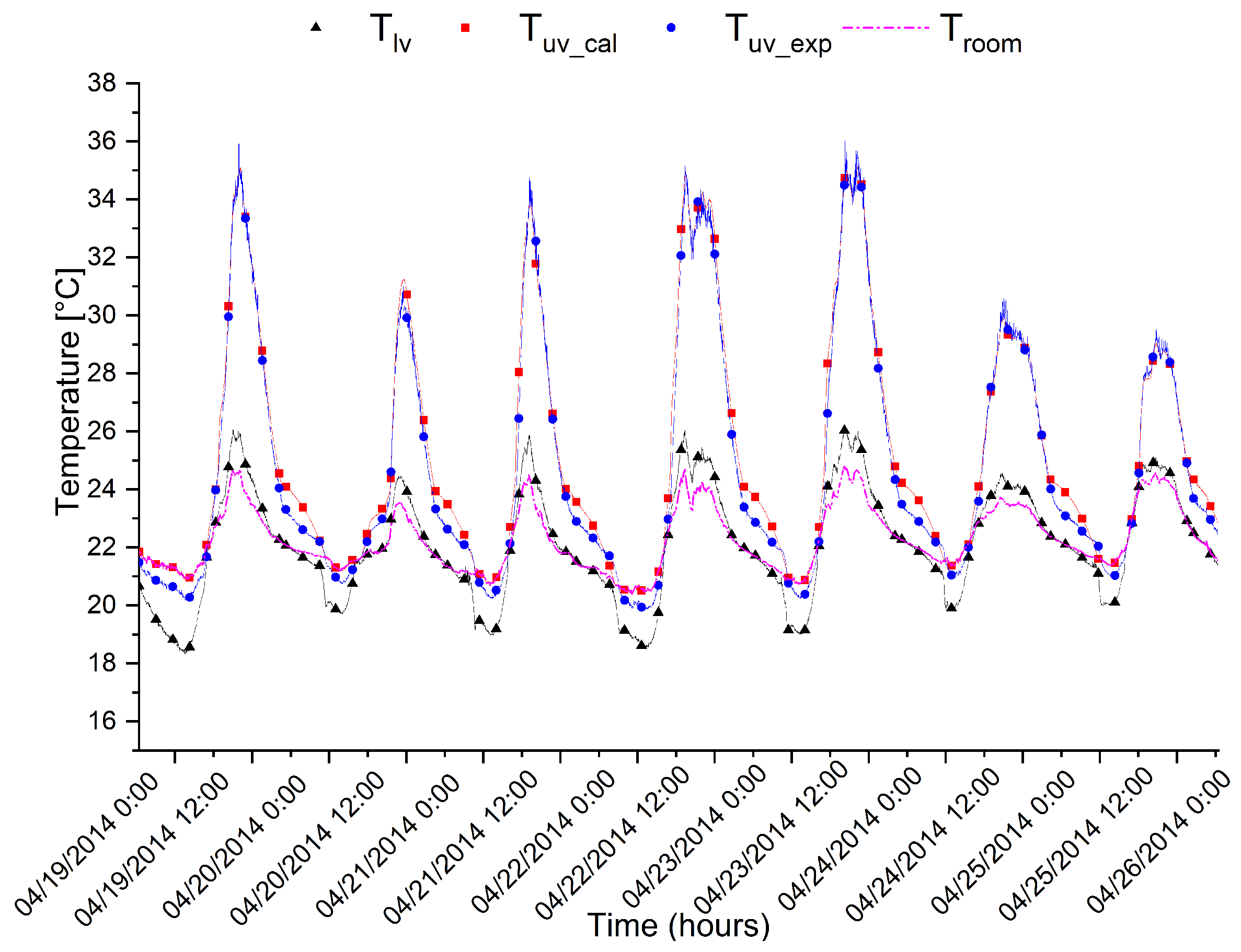
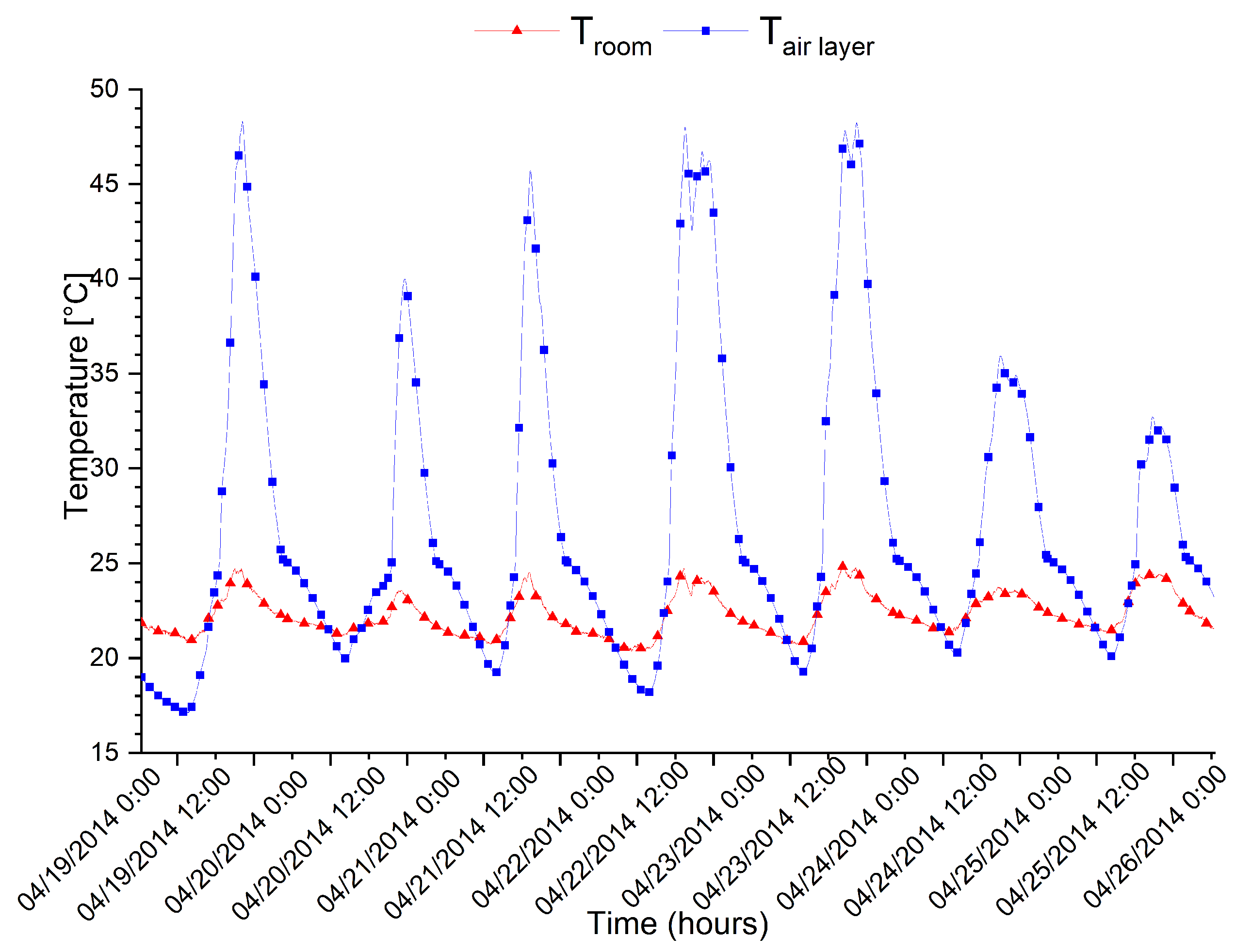
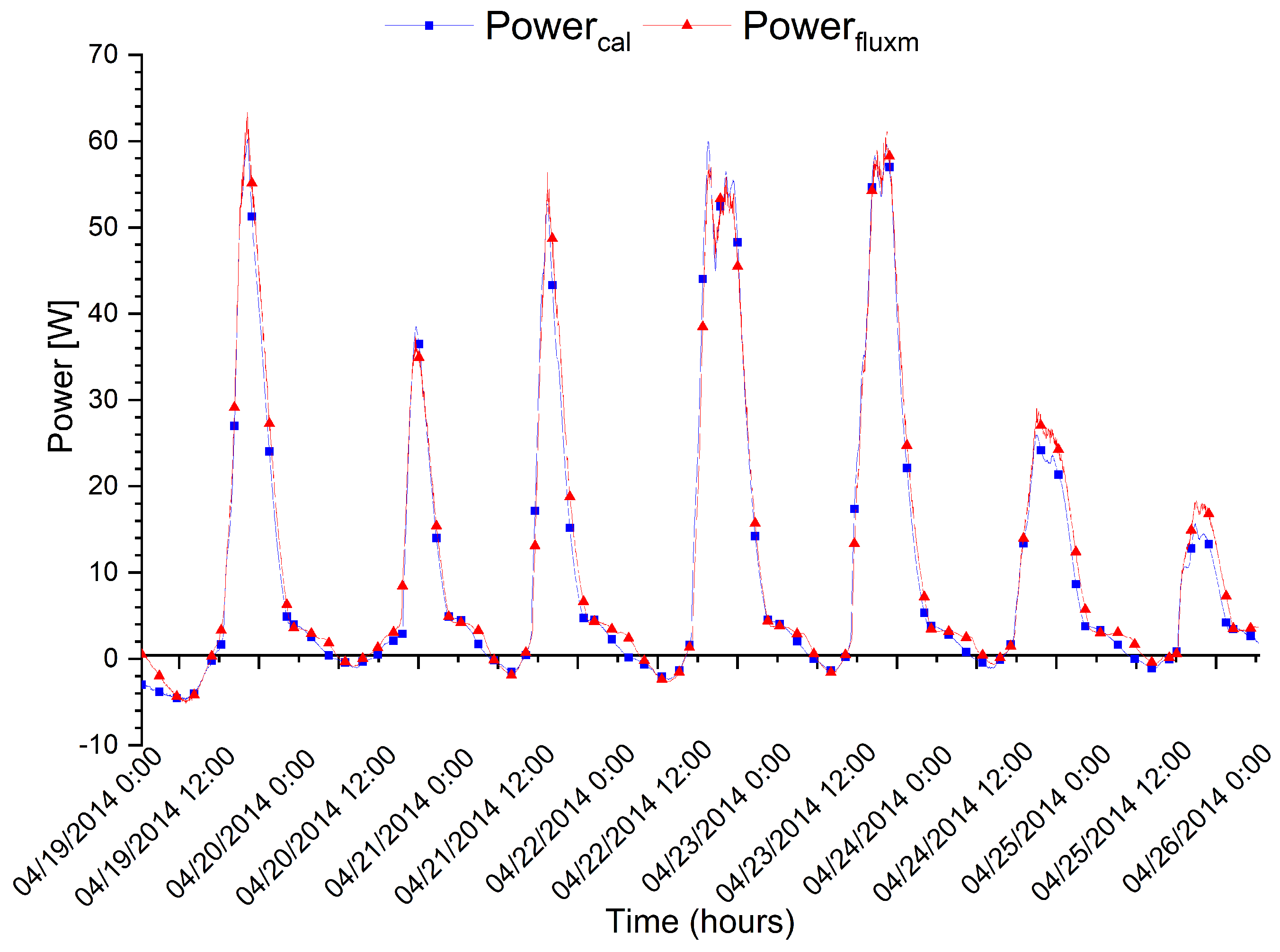
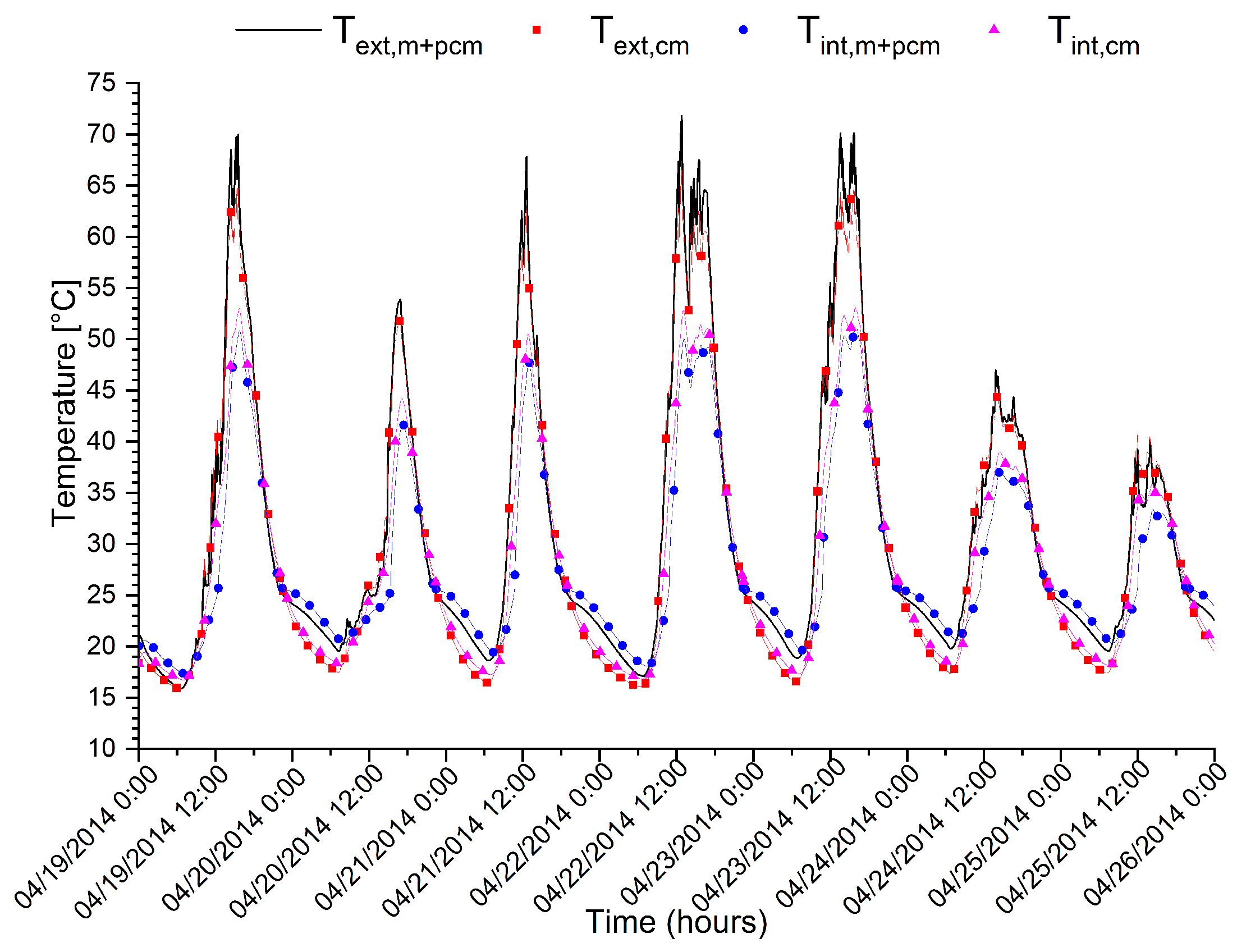
| Cement-Sand Mass Ratio | Water to Cement Ratio | PCM/(Cement + Sand) Mass Ratio |
|---|---|---|
| 1/2.6 | 1/1.1 | 1/4.1 |
| Material | Symbol | Explanation | Unit | Value |
|---|---|---|---|---|
| Glazing | density | kg/m | 2500 | |
| specific heat capacity | J/(kg.K) | 830 | ||
| thermal conductivity | W/(m.K) | 1.47 | ||
| absorptivity | - | 0.84 | ||
| transmissivity | - | 0.76 | ||
| emissivity | - | 0.84 | ||
| Mortar + PCM | density | kg/m | 1329 | |
| specific heat at solid state | J/(kg.K) | 1178 | ||
| specific heat at liquid state | J/(kg.K) | 1150 | ||
| latent heat | J/kg | 17,100 | ||
| pure substance temperature | °C | 27.37 | ||
| melting temperature | °C | 25.83 | ||
| thermal conductivity | W/(m.K) | 0.62 | ||
| absorptivity | - | 0.9 | ||
| emissivity | - | 0.9 | ||
| Insulating wall | density | kg/m | 30 | |
| specific heat capacity | J/(kg.K) | 880 | ||
| thermal conductivity | W/(m.K) | 0.041 | ||
| absorptivity | - | 0.9 | ||
| emissivity | - | 0.9 |
| Symbol | Explanation | Unit | Value | |
|---|---|---|---|---|
| Solar energy | Esol | energy | kWh/m2 | 21.4 |
| Energy absorbed | Epcm,ext_cal | energy | kWh/m2 | 7.8 |
| Epcm,ext_exp | energy | kWh/m2 | 7.7 | |
| - | variance | % | 1.3 | |
| Solar release | Epcm,int_cal | energy | kWh/m2 | 5.1 |
| Epcm,int_exp | energy | kWh/m2 | 4.7 | |
| - | variance | % | 7.8 |
| Material | Mortar | PCM-M |
|---|---|---|
| Solid State | Liquid State | ||
| Thermal Conductivity (W.m−1.K−1) | 0.65 | 0.37 |
| Heat Capacity (J.kg−1.K−1) | 925 | 1255; 1238 |
| Latent Heat (J.kg−1) | — | 19,520 |
| Density (kg.m−3) | 2001 | 1248 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Numerical and Experimental Investigations of Composite Solar Walls Integrating Sensible or Latent Heat Thermal Storage. Appl. Sci. 2020, 10, 1854. https://doi.org/10.3390/app10051854
Leang E, Tittelein P, Zalewski L, Lassue S. Numerical and Experimental Investigations of Composite Solar Walls Integrating Sensible or Latent Heat Thermal Storage. Applied Sciences. 2020; 10(5):1854. https://doi.org/10.3390/app10051854
Chicago/Turabian StyleLeang, Enghok, Pierre Tittelein, Laurent Zalewski, and Stéphane Lassue. 2020. "Numerical and Experimental Investigations of Composite Solar Walls Integrating Sensible or Latent Heat Thermal Storage" Applied Sciences 10, no. 5: 1854. https://doi.org/10.3390/app10051854
APA StyleLeang, E., Tittelein, P., Zalewski, L., & Lassue, S. (2020). Numerical and Experimental Investigations of Composite Solar Walls Integrating Sensible or Latent Heat Thermal Storage. Applied Sciences, 10(5), 1854. https://doi.org/10.3390/app10051854






