Distributed Adaptive Neural Network Control Applied to a Formation Tracking of a Group of Low-Cost Underwater Drones in Hazardous Environments
Abstract
Featured Application
Abstract
1. Introduction
- We have proposed an incorporation of distributed adaptive neural networks control and collision-obstacle avoidance so that a group of the underwater drones is able to operate independently and autonomously in hazardous environments.
- The desired formation is proposed as a time-variant function, so that a group of UUVs can quickly change their shape between them to cross a narrow area.
- The implementation of algorithms is integrated on the Gazebo underwater drone models. The results show that the control framework can be applicable to low-cost UUVs.
2. Preliminaries and Problem Formulation
2.1. Preliminaries
2.1.1. Graph Theory
2.1.2. Radial Basis Functions
2.1.3. Low-Cost Underwater Drone Modeling
2.2. Problem Formulation
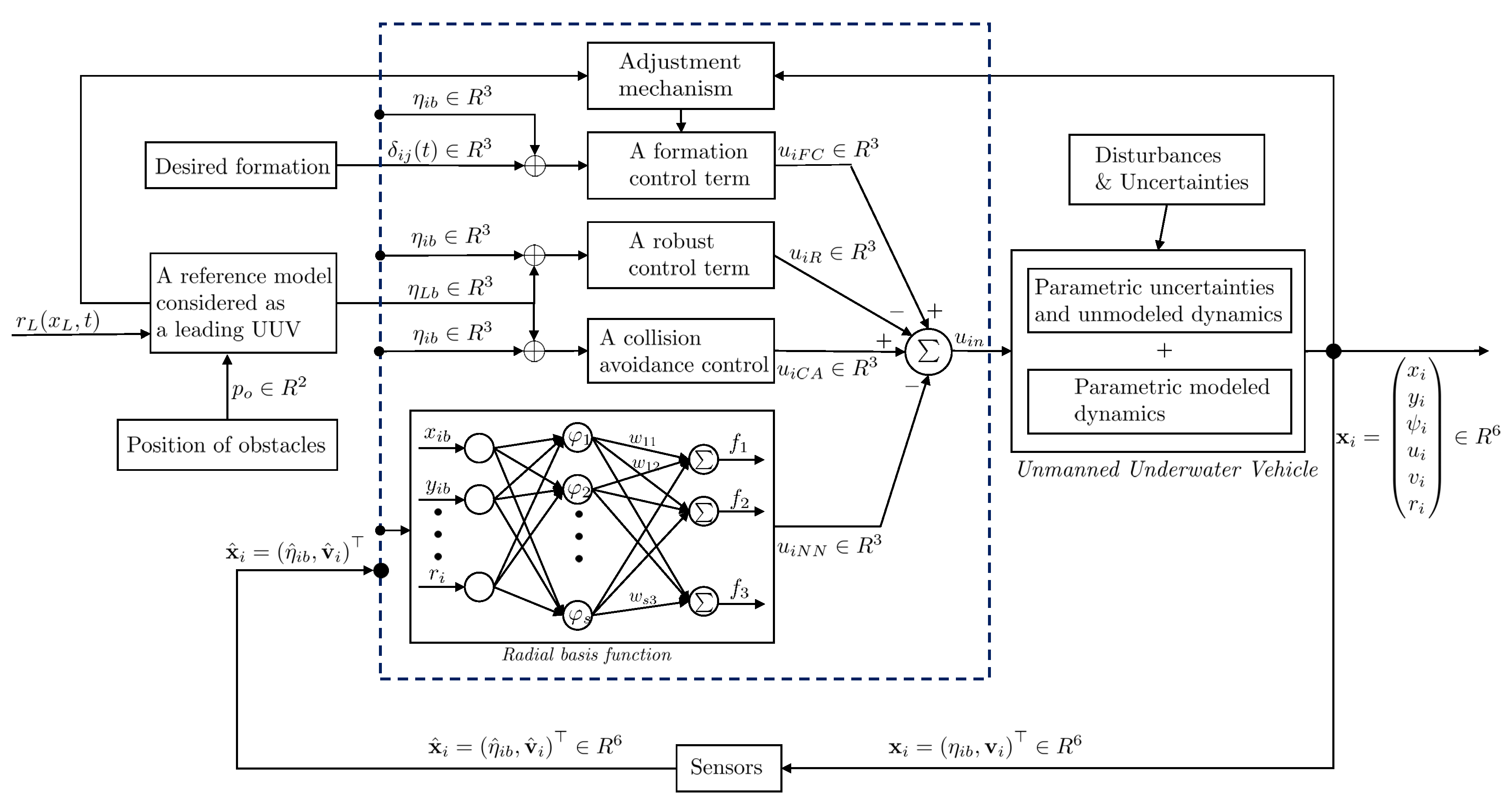
3. Incorporation of DANNC and Collision-Obstacle Avoidance for a Group of UUVs
3.1. Leader-Follower Formation Tracking
3.1.1. Formation Control Term
3.1.2. Neural Network Control Term
3.1.3. Robust Control Term
3.2. Collision Avoidance for a Group of Multiple UUVs
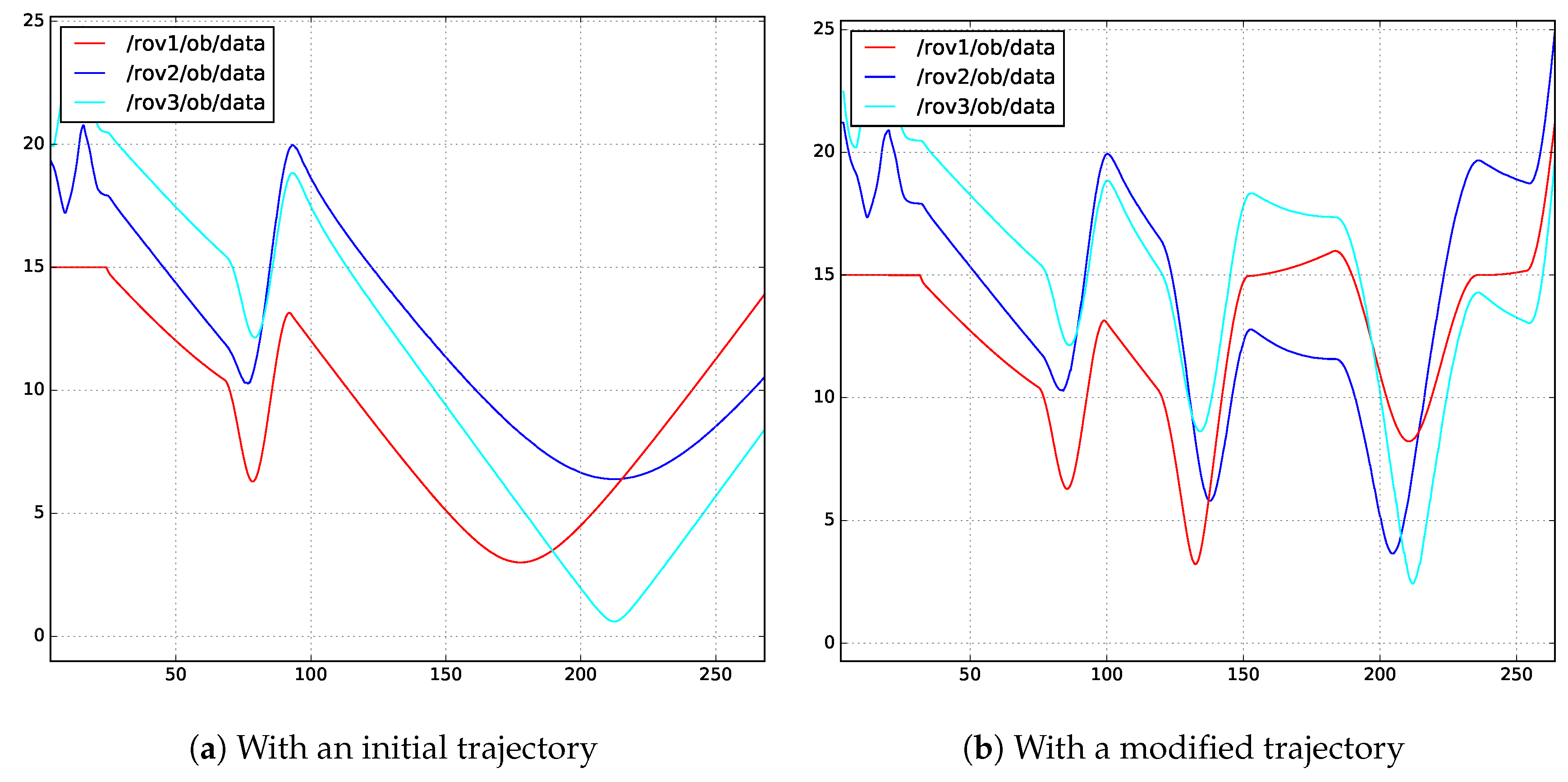
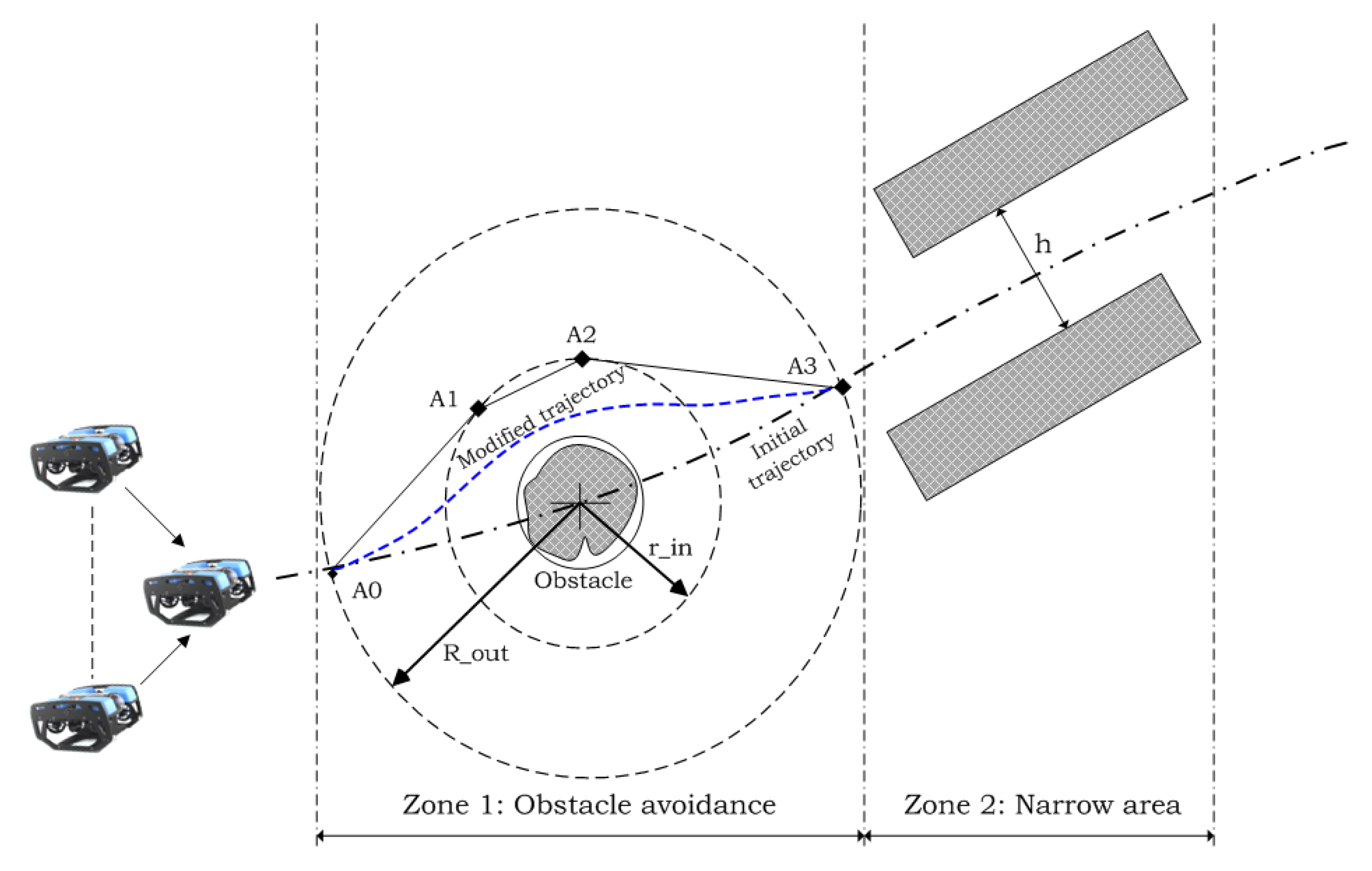
3.3. Obstacle Avoidance for a Group of Multiple UUVs
| Algorithm 1: Propose to make a modified trajectory for obstacle avoidance. |
 |
4. Experiments with a Group of Low-Cost UUVs
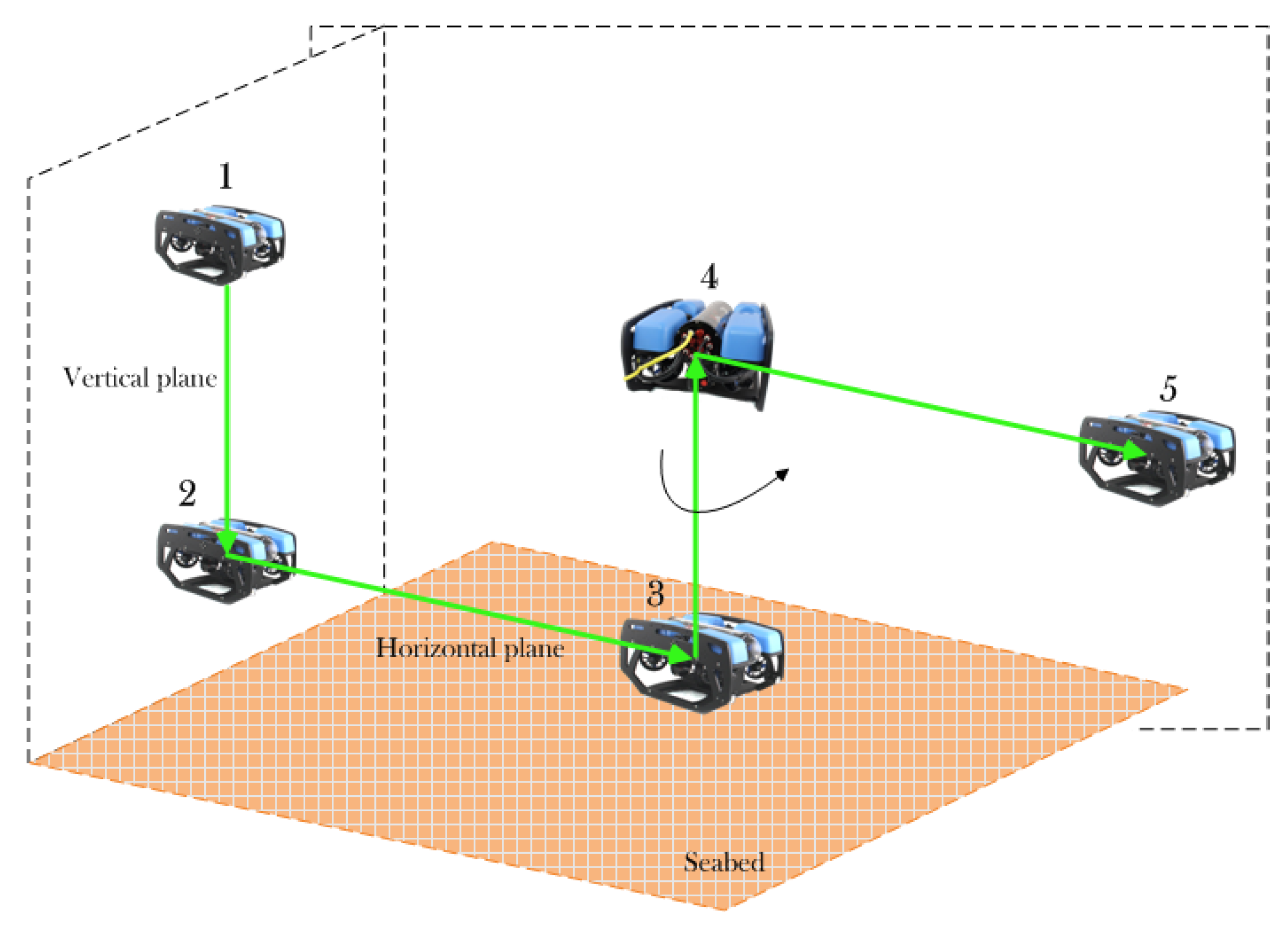
4.1. Experimental Setup
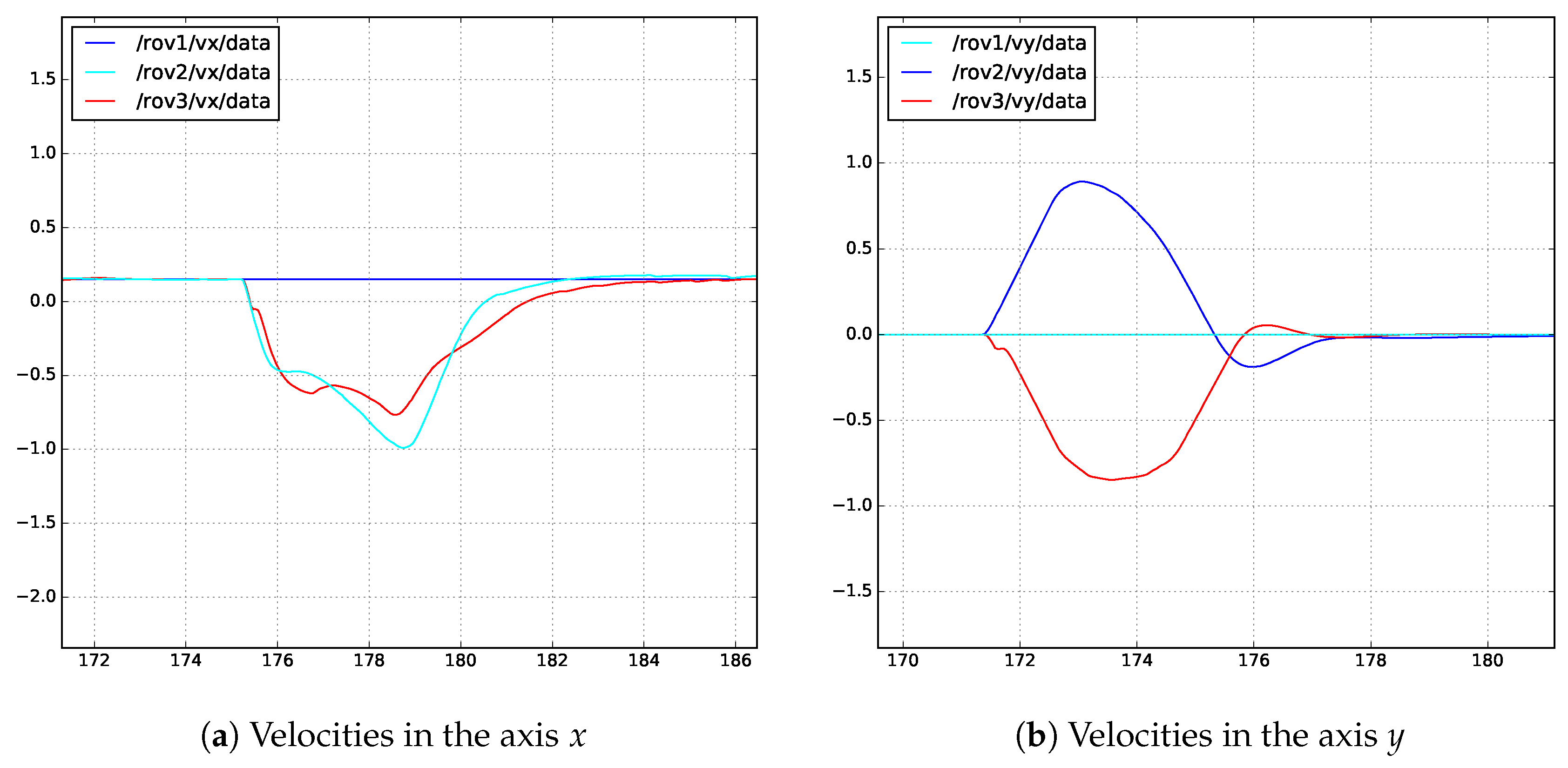
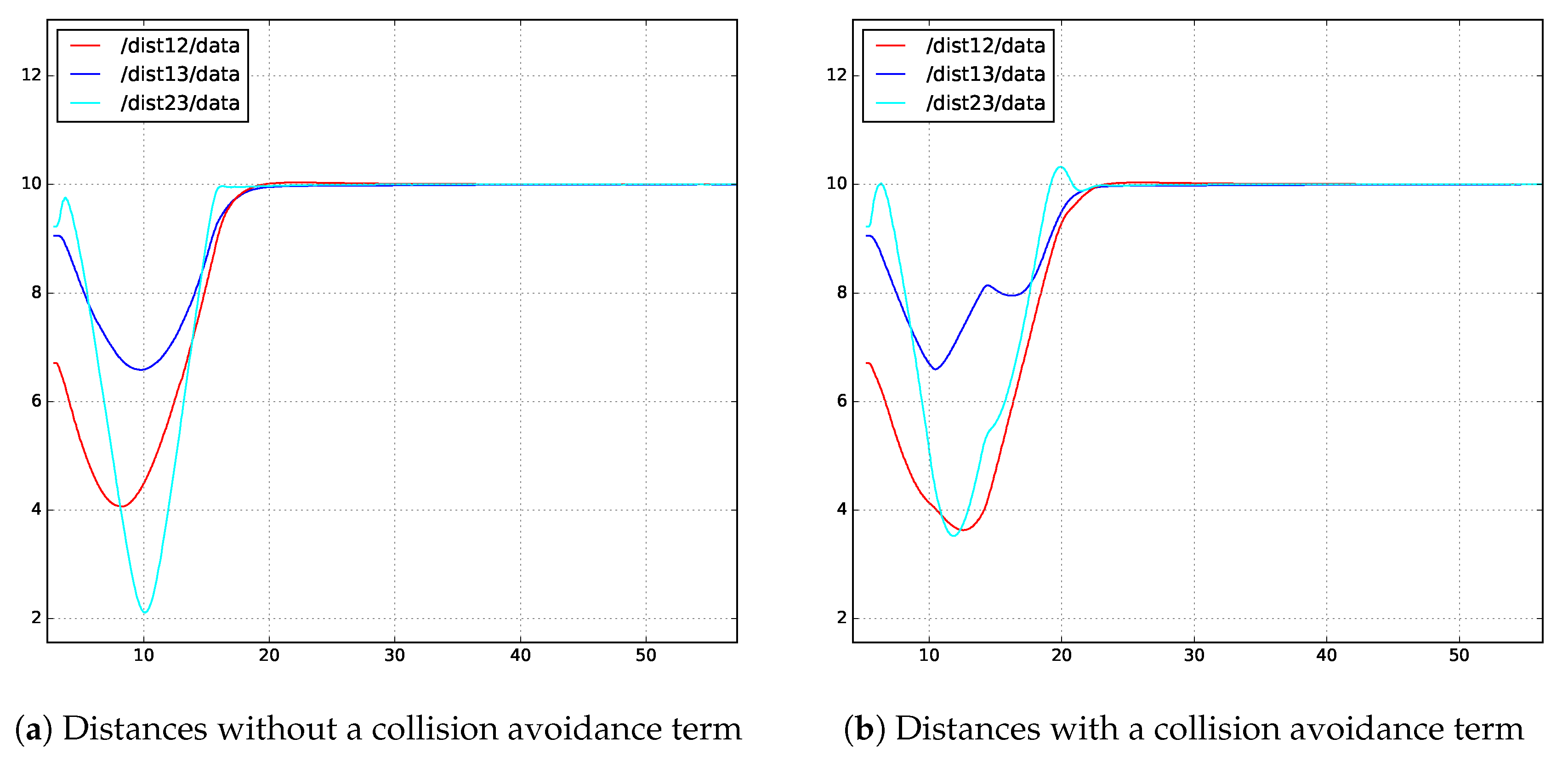
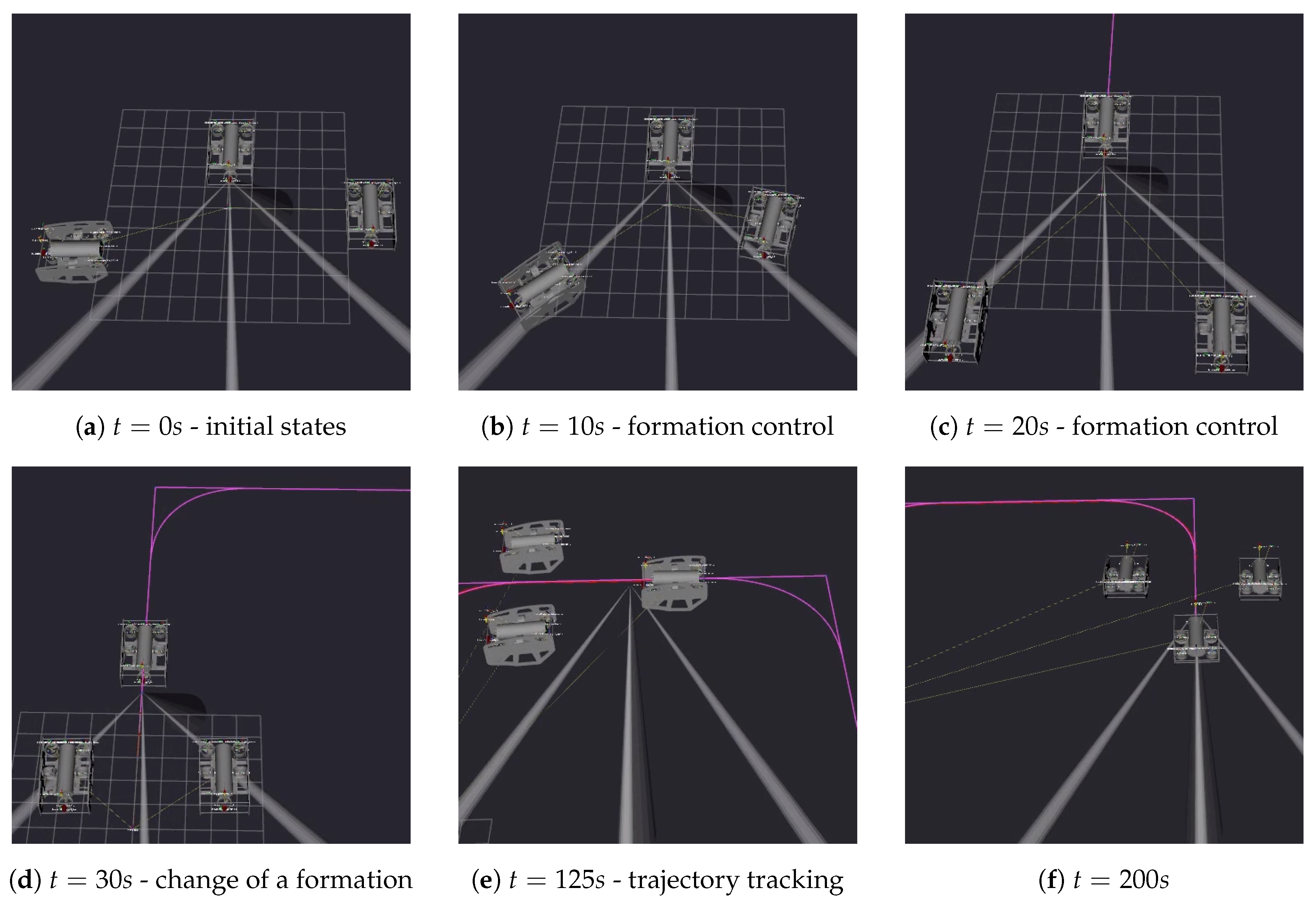
4.2. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AUV | Autonomous Underwater Vehicle |
| DANNC | Distributed Adaptive Neural Network Control |
| LiDAR | Light Detection and Ranging |
| NN | Neural Network |
| ROS | Robot Operating System |
| ROV | Remotely Operated Underwater Vehicle |
| UUV | Unmanned Underwater Vehicle |
| UWSim | UnderWater Simulator |
Appendix A

References
- Liu, H.; Wang, Y.; Lewis, F.L. Robust Distributed Formation Controller Design for a Group of Unmanned Underwater Vehicles. IEEE Trans. Syst. Man Cybern. Syst. 2019, 1–9. [Google Scholar] [CrossRef]
- Bechlioulis, C.P.; Giagkas, F.; Karras, G.C.; Kyriakopoulos, K.J. Robust Formation Control for Multiple Underwater Vehicles. Front. Robot. AI 2019, 6. [Google Scholar] [CrossRef]
- Yuan, C.; Licht, S.; He, H. Formation Learning Control of Multiple Autonomous Underwater Vehicles With Heterogeneous Nonlinear Uncertain Dynamics. IEEE Trans. Cybern. 2018, 48, 2920–2934. [Google Scholar] [CrossRef] [PubMed]
- Elhaki, O.; Shojaei, K. Neural network-based target tracking control of underactuated autonomous underwater vehicles with a prescribed performance. Ocean Eng. 2018, 167, 239–256. [Google Scholar] [CrossRef]
- Liu, Y.; Huang, P.; Zhang, F.; Zhao, Y. Distributed Formation Control Using Artificial Potentials and Neural Network for Constrained Multiagent Systems. IEEE Trans. Control Syst. Technol. 2018, 1–8. [Google Scholar] [CrossRef]
- Cui, R.; Yang, C.; Li, Y.; Sharma, S. Adaptive Neural Network Control of AUVs With Control Input Nonlinearities Using Reinforcement Learning. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 1019–1029. [Google Scholar] [CrossRef]
- Peng, Z.; Wang, H.; Wang, D.; Sun, G.; Zhang, H. Distributed model reference adaptive control for cooperative tracking of uncertain dynamical multi-agent systems. IET Control Theory Appl. 2013, 7, 1079–1087. [Google Scholar] [CrossRef]
- Yoo, S.J. Distributed Consensus Tracking for Multiple Uncertain Nonlinear Strict-Feedback Systems Under a Directed Graph. IEEE Trans. Neural Netw. Learn. Syst. 2013, 24, 666–672. [Google Scholar] [CrossRef]
- Hou, Z.G.; Cheng, L.; Tan, M. Decentralized Robust Adaptive Control for the Multiagent System Consensus Problem Using Neural Networks. IEEE Trans. Syst. Man. Cybern. Part B (Cybern.) 2009, 39, 636–647. [Google Scholar] [CrossRef]
- Abreu, P.C.; Pascoal, A.M. Formation Control in the scope of the MORPH project. Part I: Theoretical Foundations. IFAC-PapersOnLine 2015, 48, 244–249. [Google Scholar] [CrossRef]
- Shi, H.; Hou, M.; Wu, Y. Distributed Control for Leader-Following Consensus Problem of Second-Order Multi-Agent Systems and Its Application to Motion Synchronization. Appl. Sci. 2019, 9, 4208. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, L.; Yu, J.; Ai, X. Distributed adaptive neural networks leader-following formation control for quadrotors with directed switching topologies. ISA Trans. 2019. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Zong, Q.; Tian, B.; Shao, S.; Zhang, X.; Zhao, X. Neural network disturbance observer-based distributed finite-time formation tracking control for multiple unmanned helicopters. ISA Trans. 2018, 73, 208–226. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Wen, G.; Yang, S.; Rahmani, A. Distributed consensus-based formation control for nonholonomic wheeled mobile robots using adaptive neural network. Nonlinear Dyn. 2016, 86, 605–622. [Google Scholar] [CrossRef]
- Li, Y.; Wang, C.; Cai, X.; Li, L.; Wang, G. Neural-network-based distributed adaptive asymptotically consensus tracking control for nonlinear multiagent systems with input quantization and actuator faults. Neurocomputing 2019, 349, 64–76. [Google Scholar] [CrossRef]
- Yang, Q.; Cao, M.; de Marina, H.G.; Fang, H.; Chen, J. Distributed formation tracking using local coordinate systems. Syst. Control Lett. 2018, 111, 70–78. [Google Scholar] [CrossRef]
- Yuan, C.; Zeng, W.; Dai, S.L. Distributed model reference adaptive containment control of heterogeneous uncertain multi-agent systems. ISA Trans. 2019, 86, 73–86. [Google Scholar] [CrossRef]
- Mondal, A.; Behera, L.; Sahoo, S.R.; Shukla, A. A novel multi-agent formation control law with collision avoidance. IEEE/CAA J. Autom. Sin. 2017, 4, 558–568. [Google Scholar] [CrossRef]
- Xia, Y.; Na, X.; Sun, Z.; Chen, J. Formation control and collision avoidance for multi-agent systems based on position estimation. ISA Trans. 2016, 61, 287–296. [Google Scholar] [CrossRef]
- Yu, J.; Ji, J.; Miao, Z.; Zhou, J. Formation control with collision avoidance for uncertain networked Lagrangian systems via adaptive gain techniques. IET Control Theory Appl. 2018. [Google Scholar] [CrossRef]
- Soriano-Asensi, D.C.A.; Avilés, J.V.M.; Prades, R.M.; Valero, P.J.S. Underwater Wireless Communications for Cooperative Robotics with UWSim-NET. Appl. Sci. 2019, 9, 3526. [Google Scholar]
- Prats, M.; Pérez, J.; Fernández, J.J.; Sanz, P.J. An open source tool for simulation and supervision of underwater intervention missions. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Portugal, 7–12 October 2012; pp. 2577–2582. [Google Scholar] [CrossRef]
- Manhães, M.M.M.; Scherer, S.A.; Voss, M.; Douat, L.R.; Rauschenbach, T. UUV Simulator: A Gazebo-based package for underwater intervention and multi-robot simulation. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–8. [Google Scholar] [CrossRef]
- Martínez, N.L.; Martínez-Ortega, J.F.; Castillejo, P.; Martínez, V.B. Survey of Mission Planning and Management Architectures for Underwater Cooperative Robotics Operations. Appl. Sci. 2020, 10, 1086. [Google Scholar] [CrossRef]
- Martínez, N.L.; Martínez-Ortega, J.F.; Rodríguez-Molina, J.; Zhai, Z. Proposal of an Automated Mission Manager for Cooperative Autonomous Underwater Vehicles. Appl. Sci. 2020, 10, 855. [Google Scholar] [CrossRef]
- Fossen, T.I. Handbook of Marine Craft Hydrodynamics and Motion Control; John Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Fossen, T.I.; Perez, T. Kalman Filtering for Positioning and Heading Control of Ships and Offshore Rigs. In IEEE Control Systems Magazine; IEEE: Piscataway, NJ, USA, 2009. [Google Scholar]
- Lavretsky, E.; Gibson, T.E.; Annaswamy, A.M. Projection Operator in Adaptive Systems. arXiv 2012, arXiv:1112.4232. [Google Scholar]
- Pham, H.A.; Soriano, T.; Ngo, V.H. Integrated scenarios of formation tracking and collision avoidance of multi-vehicles. In Proceedings of the 2018 13th Annual Conference on System of Systems Engineering (SoSE), Paris, France, 19–22 June 2018; pp. 313–318. [Google Scholar] [CrossRef]
- Skaalvik, S.S. System Identification and State Estimation for ROV uDrone. Master’s Thesis, Norwegian University of Science and Technology, Trondheim, Norway, 2016. [Google Scholar]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pham, H.A.; Soriano, T.; Ngo, V.H.; Gies, V. Distributed Adaptive Neural Network Control Applied to a Formation Tracking of a Group of Low-Cost Underwater Drones in Hazardous Environments. Appl. Sci. 2020, 10, 1732. https://doi.org/10.3390/app10051732
Pham HA, Soriano T, Ngo VH, Gies V. Distributed Adaptive Neural Network Control Applied to a Formation Tracking of a Group of Low-Cost Underwater Drones in Hazardous Environments. Applied Sciences. 2020; 10(5):1732. https://doi.org/10.3390/app10051732
Chicago/Turabian StylePham, Hoang Anh, Thierry Soriano, Van Hien Ngo, and Valentin Gies. 2020. "Distributed Adaptive Neural Network Control Applied to a Formation Tracking of a Group of Low-Cost Underwater Drones in Hazardous Environments" Applied Sciences 10, no. 5: 1732. https://doi.org/10.3390/app10051732
APA StylePham, H. A., Soriano, T., Ngo, V. H., & Gies, V. (2020). Distributed Adaptive Neural Network Control Applied to a Formation Tracking of a Group of Low-Cost Underwater Drones in Hazardous Environments. Applied Sciences, 10(5), 1732. https://doi.org/10.3390/app10051732




