Abstract
As in many countries, the rise of nanosciences in Belgium has been triggered in the eighties in the one hand, by the development of scanning tunneling and atomic force microscopes offering an unprecedented possibility to visualize and manipulate the atoms, and in the other hand, by the synthesis of nano-objects in particular carbon nanostructures such as fullerene and nanotubes. Concomitantly, the increasing calculating power and the emergence of computing facilities together with the development of DFT-based ab initio softwares have brought to nanosciences field powerful simulation tools to analyse and predict properties of nano-objects. Starting with 0D and 1D nanostructures, the floor is now occupied by the 2D materials with graphene being the bow of this 2D ship. In this review article, some specific examples of 2D systems has been chosen to illustrate how not only density functional theory (DFT) but also tight-binding (TB) techniques can be daily used to investigate theoretically the electronic, phononic, magnetic, and transport properties of these atomically thin layered materials.
1. Introduction
The invention of the scanning tunneling microscope (STM) in 1981 [1,2], winning of the Nobel Prize in Physics by the inventors in 1986, and the invention of the atomic force microscope (AFM) in the same year [3], opened the doors to the Small World described by Richard Feynman in his visionary lecture There’s Plenty of Room at the Bottom [4]. This new ability to see and eventually manipulate individual atoms was soon complemented by other prominent experimental achievements—the discovery of fullerenes in 1985 [5], the development of nanoscale transistors, the structural assignement of carbon nanotubes in 1991 [6]—that definitely established nanosciences as the major research field that we know today. Around the same time, the first quantum-simulation codes were developed based on different flavors of theory such as Hartree-Fock (HF), Density Functional Theory (DFT), Møller-Plesset perturbation (MP2), Configuration Interaction (CI), Coupled Cluster (CC), or multi-reference methods [7,8,9,10,11], facilitating the theoretical investigation of materials and nanostructures at the atomic scale. A major advantage of these quantum-mechanical modelling methods compared for example to the semi-emirical tight-binding (TB) techniques [12] is their ab initio, i.e. parameter-free, character. Nevertheless, the computational cost of ab initio methods remains much higher than the one of TB techniques. In UCLouvain, all these new exciting tools for nanosciences arrived in the nineties. The first AFM and STM were acquired in 1994 [13,14]. The first DFT and TB simulators were developed and used in the early nineties [15,16,17,18] and the ABINIT project was launched officially in 1997 [19].
The exfoliation of graphene in 2004 [20], and the early measurements of its superlative properties shed light on a new class of nanomaterials—two-dimensional (2D) crystals—that exhibits peculiar properties due to the quantum confinement of their electrons in the flatland [21]. Presently, the existence and the stability under ambient conditions of more than a few dozens of different 2D crystals have been reported, including hexagonal boron nitride (h-BN), transition metal dichalcogenides (MoS, MoSe, WS, WSe, NbSe, …), thin oxide layers (TiO, MoO, WO, …), silicene, germanene, phosphorene, borophene, arsenene, stanene, MXenes, and many others.
In this review article, published in the special issue entitled ’State of the art of nanosciences in Belgium’, a small country being sometimes called the flatland [22], the predictive power of DFT and TB techniques for various properties of 2D materials is illustrated. Through a selection of monolayered systems, namely graphene, borophene, MXene, and h-BN, the potential use of 2D materials in many fields of applications including electronics, electron optics, valleytronics, phononics, and spintronics, will be exposed. The article includes four sections, each investigating a property of a given 2D system using a specific modeling technique. The first section describes the electronic transport properties in polycrystalline graphene using the Green’s function approach within the Landauer-Büttiker formalism. The second section presents the optical properties of borophene and graphene monolayers including optical Hall effect. The third section introduces the recent and large family of MXenes and in particular their versatile electronic and phononic properties. Last but not least, the genuine use of h-BN in innovative magnetic tunnel junctions is discussed in the fourth section. With the present review paper, we wish you an exciting modeling experience in a quite localized region of the still hugely unexplored Flatlands!
2. Electronic Transport in Polycrystalline Graphene
Although graphene was first isolated by mechanical exfoliation [20], it is currently synthesized for the most part by chemical vapor deposition (CVD) techniques. This approach is presently by far the most viable and industry-compatible production method [23,24]. Importantly, CVD yields polycrystalline graphene (PG) where single-crystal domains are separated by graphene grain boundaries (GBs) of irregular shapes. Grains have a roughness comparable to the substrate and a lateral size ranging from a few hundred nanometers to several centimeters [25]. At the grains interface, topological defects accommodate for the lattice misorientation between domains. Those GBs consist of non-hexagonal rings (mostly pentagon-heptagon pairs) randomly distributed along the interface [26,27]. It was revealed by scanning probe microscopy that such extended structural defects induce major perturbations in the electronic structure of graphene [28,29]. The transport of charge carriers is degraded on the one hand by structural defects acting as scattering sites [30,31,32] and on the other hand by electrical potential barriers formed at GBs which tend to be negativey-doped (n-doped) [33,34]. A strong correlation was demonstrated between the quality and the resistivity of GBs [30,32,35]. Macroscopically, the carrier mobility of wafer-scale graphene is drastically limited by GBs [36,37,38]. Nonetheless, Banszerus et al. measured mobilities for CVD graphene rivaling those reported for similar devices based on exfoliated graphene [39]. This suggests that CVD samples are comparable in quality to large-area exfoliated single-crystals that contain intragranular line defects and other structural imperfections [40].
In this context, an atomic-scale analysis of the GBs detrimental effects on the transport properties of PG is required, with so far only a few first-principles studies characterizing charge transport through GBs. Importantly, Yazyev et al. [41] showed that GBs degrading role could be alleviated through atomically precise manufacturing. A transport gap was also demonstrated to appear for specific types of GBs. However, experimentally-observed GBs exhibit more complicated arrangements of non-hexagonal rings [42] than atomic structures of ref. [41]. This necessarily leads to discrepancies between experimental measurements in PG and theoretical predictions of transport properties of “ideal” GBs. Our researches focus on the systematic study of the electronic transport through realistic graphene grain boundaries [43,44] and on the exploration of novel phenomena such as valley-dependent transport, electron optics effects, Aharonov-Bohm interferences and spin-diffusion lengths in polycrystalline graphene [45,46,47].
Graphene GBs atomic structures were obtained using classical molecular dynamics with optimized Tersoff potentials [48]. This empirical potential model has been shown to accurately describe the structural properties of defective graphene [49]. The electronic properties of defective graphene systems under study were calculated using either the first-principles approach [44] or the -orbital TB technique [43,45,46]. First-principles calculations were performed using DFT within the OPENMX code [50,51,52], a software package based on norm-conserving pseudo-potentials and pseudo-atomic localized basis functions. Parametrized TB models are very effective to model the electronic properties of graphene at low energies, i.e., around the Fermi level. The good agreement between these two approaches was demonstrated in refs. [41,45].
Charge transport through GBs was simulated using the Landauer-Büttiker formalism implemented within the Green’s function approach. In this framework, the zero-temperature linear conductance is given by the Landauer formula:
where W is the transverse width of the system, is the transmission probability across the system, a function of carrier energy E and transverse momentum . The function is calculated through a fully quantum-mechanical approach:
where the retarded Green’s function is determined in terms of the device Hamiltonian as:
In Equation (3), represents the left (right) self-energy, describing the left (right) lead-to-device coupling. in Equation (2) is the transfer rate at the left (right) contact determined as .
To investigate quantum transport in PG, GBs are modeled as periodic lines of defects with a periodicity that is expressed in terms of two translation vectors and in the left and right domains, respectively. Yazyev et al. [41] demonstrated that GBs exhibit either metallic or semi-conducting transport regime depending on the interface nature. If but (or vice versa; ), a transport gap appears as the allowed momentum-energy manifolds of the two crystalline domains are significantly misaligned. In the case of massless Dirac fermions, this transport gap is given by:
where is the Fermi velocity, and the common GB period (after applying possibly strain to obtain matching of both domains). Interestingly, the transport gap depends only on the GB periodicity.
GBs are subsequently classified as either transparent (class-I) or reflective (class-II) to electronic transport. First, a symmetric GB with and Å is investigated as illustrated in Figure 1. The system is transparent, as expected from its symmetry, with a conductance comparable to pristine graphene despite the large concentration of pentagon-heptagon pairs (see Figure 1a,c). In the asymmetric case (see Figure 1b,d), a transport gap of 0.92 eV appears when , and Å, in relative accordance with Equation (4). Outside the transport gap, transmissions are considerably smaller compared to pristine graphene. However, systems considered in Figure 1a,b have short periodicities and are not representative of real GBs which exhibit a more complicated atomic structure. Consequently, more realistic GBs constructed from more complicated arrangements of polygons are studied hereafter. First, an asymmetric class-I GB is examined. This system is defined by , and Å, as illustrated in Figure 1e. The corresponding transmissions are significantly lower than pristine graphene, indicating an increased scattering due to the presence of dangling bonds. An asymmetric class-II GB is then considered, with , and Å (see Figure 1f). The interface was constructed by creating a vacancy after repeating n times an initial pattern (here ), which corresponds to applying a perturbation approach to the periodicity assumption. The related transmissions depicted in Figure 1d show a transport gap of 0.76 eV. However, a logarithmic scale plot analysis reveals non-zero conductance as large as G nm in the transport-forbidden energy range. This implies that the transport gap depends on the smallest perceptible periodicity while perturbations in periodicity induce leakage currents.
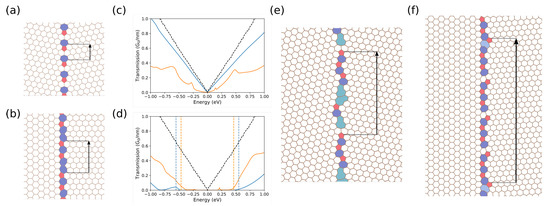
Figure 1.
Electronic transport through graphene grain boundaries (GBs). Atomic structures of (a) the class-I GB, (b) the class-II GB, (e) the class-I GB and (f) the class-II GB. The zero-bias conductances are given in (c,d) for class-I and class-II systems, respectively. Conductances through the smallest (blue lines) and largest (orange lines) GBs are compared to pristine graphene (black dashed lines). Reprinted and adapted with permission from reference [44].
In a nutshell, disorder is found to normalize the transport properties of PG (metallic or semi-conducting) [44]. On the one hand, the disordered nature of GBs increases scattering, reducing the overall transmissions in transparent systems, on the other hand, it induces leakage currents which damage the transport gap for reflective configurations.
Owing to the misorientation between grains, the transport through GBs has been also shown to be highly sensitive to the effect of strains [43]. This is essentially due to the fact that even though the metallicity of graphene is still conserved, its Brillouin zone is strongly deformed and Dirac cones can be displaced in the momentum space when strains are applied. Moreover, such displacements of the Dirac cones are strongly dependent of the crystallographic orientation of graphene with respect to the strain direction. On this basis, the strain effects in PG can result in different momentum displacements of Dirac cones in two graphene grains surrounding a given GB, thus strongly modifying the low-energy transport properties through the system. In particular, while the transport gap in the boundary of class-II is modifiable, a uniaxial strain applied in proper directions can always open a gap in the boundary of class-I as illustrated in Figure 2. Interestingly, a large gap of a few hundred meV can be achieved with a small strain of a few percents only. The value of this gap has been shown to depend on three main parameters: the uniaxial strain magnitude, the uniaxial strain direction, and the lattice symmetry of graphene grains [43].
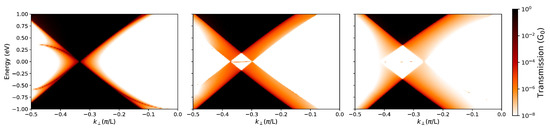
Figure 2.
Strain effects on the electronic transport through graphene grain boundaries. () maps of transmission obtained for the class-I GB in Figure 1a with different uniaxial strain magnitudes: 0% (left), 3% (middle) and 6% (right), oriented with 45 with respect to BG axis. Reprinted and adapted with permission from reference [43].
In addition to its dependence on the GBs and crystallographic orientation of grains, the transport through PG also represents interesting magnetotransport phenomena. For instance, it has been shown in ref. [53] that the formation of Landau levels is limited by the grain size and cannot be observed until the magnetic length is smaller than the average grain radius. The electron localization is also found to be unusual. In particular, strongly localized states and extended electronic states are at the center and between Landau levels, respectively. These extended states are developed along the network of GBs, explaining a finite value for the bulk dissipative conductivity and suppression of the quantized Hall conductance.
A novel fascinating magnetotransport feature has been recently predicted in polycrystalline graphene [46]. In particular, the extended states strongly localized along the grain boundaries can be exploited to create tunneling paths connecting quantum Hall edge channels in CVD graphene samples. Consequently, strong Aharonov–Bohm (AB) interferences in the quantum Hall regime can be achieved in the PG systems schematized in Figure 3a. The AB oscillations in the conductance in a typical system are indeed illustrated in Figure 3b. These predicted AB oscillations are clarified by the pictures of the local density of left-injected electronic states in Figure 3c,d and can be essentially explained as follows. First, under a strong magnetic field, electrons in the internal graphene grain have to propagate following quantum Hall edge states. Second, because of defect scattering at the GBs, these electrons can circulate inside such graphene grain (i.e., along its edge). Therefore, depending on the accumulated phase of electron wave in such circulating trajectories, constructive/destructive states are created and tuned when varying the magnetic field. These constructive (see Figure 3c) and destructive (see Figure 3d) states explain the obtained high and low values of conductance, respectively, and the conductance oscillations presented in Figure 3b.
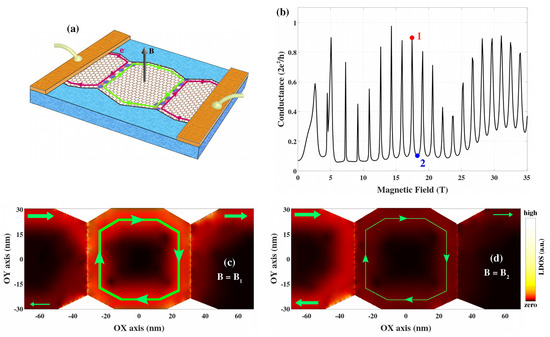
Figure 3.
Aharonov–Bohm interferences in polycrystalline graphene in the quantum Hall regime: (a) Schematic of considered systems, (b) computed conductance as a function of the magnetic field, and (c,d) images of the local density of left-injected electronic states at magnetic fields (c) (conductance peak), marked in red in (b,d) (conductance valley) marked in blue in (b). Reprinted and adapted with permission from reference [46].
At last, graphene grain boundaries have also been suggested to be used to explore other novel phenomena, e.g., valley filtering [45,54], creating 1D topologically conducting states [28,55], for electron optics [45], for electronic waveguides [56], and for the detection of chemical analytes [57].
3. Optical Absorption in Graphene and Borophene
Owing to their extreme thinness, 2D materials are expected to absorb only a small amount of light. Therefore, even metallic 2D layers can be almost transparent in particular in the visible range. Such transparent conducting layers are of broad interest for various applications, e.g., as front current collector in solar panels. To assess the optical properties of 2D materials, a key quantity is the optical conductivity , whose real part is related to the imaginary part of the dielectric function (Equation (5)). Based on vertical interband electronic transitions, can be routinely computed with both TB and DFT approaches using the Kubo formula (Equation (6)).
where are the principal in-plane directions (x and y), S is the cell surface, is the Fermi-Dirac distribution function, , and are the eigenenergies and eigenstates, is the velocity operator along a given direction, and is a small broadening. The longitudinal optical conductivity components are and while is the optical Hall conductivity. Both are given in units of the universal value of ( with , and c the fine-structure, the vacuum electric permittivity and the speed of light constants, respectively). As a consequence of intraband transitions in metallic systems, Drude corrections are added to (The real part of can also be corrected by the Drude term with )
where ( with n the electron density and m an effective mass. In practise, is computed through Kramers-Kronig relation) and = are the plasmon frequency and the inverse scattering time of the Drude model, respectively. Light propagation is considered orthogonal to the 2D layers and the associated linearly oscillating electric field is thus in-plane along the direction.
Photon absorption is therefore by essence a 3D phenomenon and to account for the 2D nature of the atomically-thin structure within DFT calculation, the computed dielectric function has to be renormalized [58,59] (including both interband transitions and Drude terms), as = with H the total height of the DFT 3D periodic cell which includes the vacuum distance introduced to separate the periodic images of the layer, and h the polarizable electronic thickness which can be estimated e.g., from van der Waals atomic radii [59]. To compute the transmittance T, general Fresnel equations should be used or at least their limit for (ultra-)thin film which include secondary reflections at top and back side interfaces with external media [59,60,61], here vacuum:
where is the complex refractive index.
The synthesis of monolayers of boron atoms, so-called borophene, has been reported in 2015–2016 [62,63] showing a rich structural polytype. In particular three important structures have been reported, including a buckled triangular lattice and two flat layers named and (Figure 4a). These three borophene layers are (semi-)metallic as clearly shown by their electronic bandstructure and density of states (Figure 4b). Nevertheless and interestingly, the buckled triangular borophene layer displays a zero optical conductivity up to 3 eV (Figure 4c) and, hence, absorbs light only in the UV range or for higher photon energy (with a strong anisotropic character between and ) [59]. In contrast, and borophene layers absorb light in the visible range starting from ∼0.5 and ∼1.0 eV, respectively, with a value varying between and . For comparison, graphene exhibits a value slowly increasing from up to roughly at the end of the visible range. This value of for graphene corresponds to the well-known absorbance of % of light, which gives, with reflectance being nearly zero (∼0.05%), the high transmittance displayed in Figure 5. Again, buckled triangular borophene is fully transparent in this visible region neglecting the Drude corrections which, depending on the scattering time , can give rise, at most, to a decrease of transmittance down to 96% in the visible range, i.e., comparable to graphene.
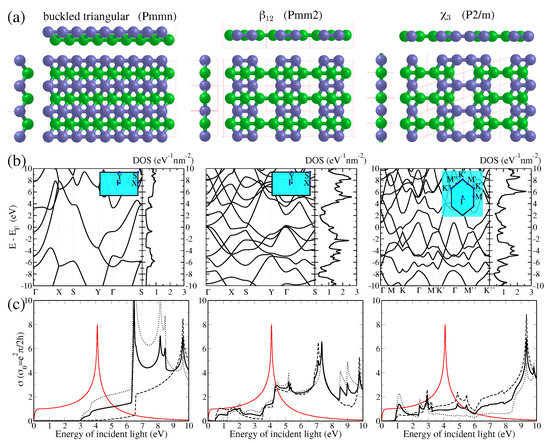
Figure 4.
Electronic and optical properties of borophene monolayers: (a) Three 2D crystal polytype structures of borophene with increasing boron vacancies, i.e., buckled triangular, , and , with in (b) the corresponding electronic band structures and in (c) the corresponding longitudinal optical conductivities , , and their averaged in dotted, dashed, and thick black line, respectively. Graphene optical conductivity is also given in red line.
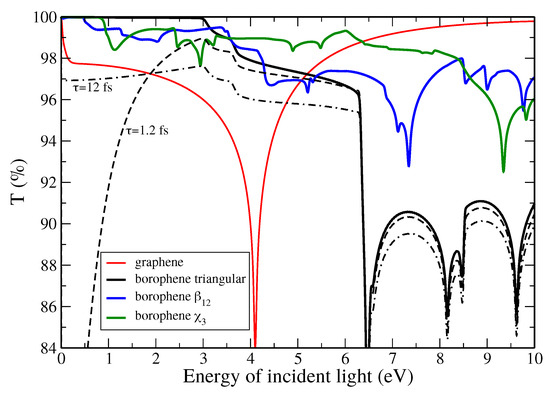
Figure 5.
Optical transmittance T of graphene and borophene monolayers (electric field in oblique direction) without Drude corrections (thick lines). To illustrate the effect of Drude corrections, two representative values of scattering time and 12 fs (dashed and dotted-dahsed black lines) are also displayed for the case of buckled triangular borophene.
Linearly polarized light can be rotated when going through a material in the presence of a magnetic field. This phenomenon is known as Faraday rotation and originates from the optical Hall effect (OHE) for which . The OHE has been investigated in thin films and more recently in 2D materials. Strain engineering has been proposed as an alternative to magnetic fields to induce finite optical Hall conductivity [64]. Indeed, without any symmetry breaking mechanisms, is normally zero after integrating over the whole Brillouin zone (BZ). Uniaxial strain in graphene, but also shear strain, allows to split in energy the van Hove singularities and the related optical absorption peaks (see in Figure 6). Because of this strain-induced asymmetry, the BZ integration at a given energy yields a positive or negative (see in Figure 6 for light linearly polarized along oblique direction and for two strain directions and corresponding to armchair and zigzag respectively) which are responsible for clockwise or anti-clockwise Faraday rotation (Figure 6(inset)). The Faraday rotation angle is however limited to a few degrees for a strained monolayer and its exact value depends on the strain amplitude and the orientation with respect to light polarization. Additionally, the effect can be amplified using a few layers although at the cost of more absorption and, hence, a reduction of the transmitted light intensity.
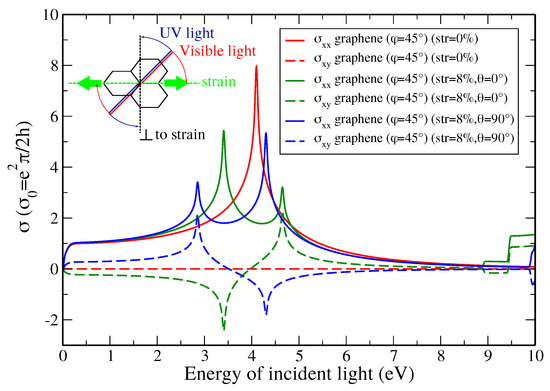
Figure 6.
Optical Hall conductivity of unstrained and 8% strained graphene along armchair () and zigzag () direction for incoming light polarized obliquely (). Inset: Sketch illustrating the Faraday rotation mechanism of linearly polarized light (red and blue lines) in uniaxially strained graphene (green line). Visible (UV) light rotates (anti-)clockwise when strain is applied along the armchair direction.
4. Electronic Structure and Vibrational Properties of MXenes
Among the recently discovered 2D systems, the emerging family of 2D transition metal carbides and nitrides, known as MXenes [65,66,67], stands out because of the wide chemical diversity allowing for materials property tuning. In contrast to graphite-like layered materials which can be mechanically exfoliated to obtain 2D flakes, MXenes are obtained from the chemical treatment of three-dimensional MAX phases [65]. MAX phases are layered ceramics with the general formula MAX, where M represents an early transition metal, A an element from groups 13 to 16, X either a carbon or a nitrogen atom, and n varies from 1 to 3 [68,69]. Due to the use of etching agents, MXenes are always terminated with functional surface groups, such as –F, =O, and –OH, that are randomly distributed [67]. Since the discovery of the first MXene, TiCT, at Drexel University in 2011 [65], more than 30 MXenes have been synthesized, and the stability and properties of dozens more have been investigated using ab initio calculations [70]. The exploration of new MAX phases and derivative MXenes is of great interest to further control materials properties and highlight potential applications, such as catalysis, energy storage and related electrochemical applications [70]. Up to now, most of the research has been devoted to the first MXene TiCT and consists in experimental works [70]. However, given the wide chemical versatility on both M and T sites, ab initio calculations are powerful to investigate the structural and functional properties of the resulting huge variety of MXenes compositions.
The geometries and electronic properties of the VCT systems are investigated using DFT calculations. The ground-state structure of the pristine VC shows a hexagonal lattice with the space group (Figure 7a). Based on the unit cell of VC, functionalized VCT MXene structures with terminations are constructed. Two types of hollow sites on the surface of VC can be distinguished (Figure 7a), leading to different functionalization models [71]. The energetically favorable model for functionalized VCT corresponds to MD2 where the two functional groups are located on fcc sites for which no C atom is present under the V atom (Figure 7b). Similarly to graphene and other 2D materials with hexagonal symmetry, an armchair direction and a zigzag direction can be identified, as depicted in Figure 7c. Moreover, moving to the reciprocal space, the –M and –K high-symmetry paths in the Brillouin zone respectively correspond to the armchair and zigzag direction (Figure 7c). The electronic band structure of pristine VC and fully-terminated VCT with T = –F and/or –OH are presented in Figure 8. The metallic character of VC is ensured by the presence of V- orbitals at the Fermi level, and is not affected by any kind of terminations [72]. This is not always verified since Khazaei et al. showed that the metallic pristine TiC could turn into a semiconductor upon functionalization, depending on the nature of the terminal groups [71]. In general, all pristine MXenes are metallic, while terminated MXenes can be either metallic or semiconducting, depending on the configuration and nature of the terminal groups. This is a powerful property that allows to tune MXenes electronic properties playing on their composition.
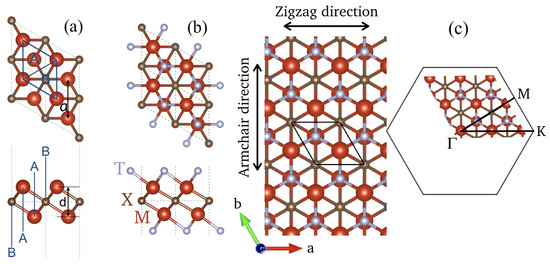
Figure 7.
Atomic structure of (a) pristine VC and (b) terminated VCT with MD2, and (c) high-symmetry armchair and zigzag directions in both real and reciprocal space.
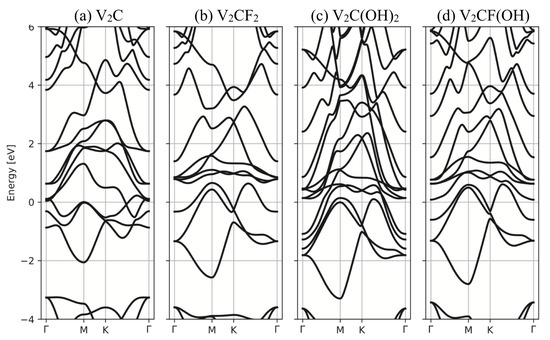
Figure 8.
Electronic band structure of (a) pristine VC, and terminated (b) VCF, (c) VC(OH), (d) VCF(OH). The Fermi level is fixed as the reference of zero energy.
The vibrational properties of the VCT systems are investigated using density functional perturbation theory (DFPT). The three atoms of the primitive cell of the VC monosheet give rise to nine phonon modes at the point of the Brillouin zone. Similarly, the five, seven, and six atoms respectively in the VCF, VC(OH), and VCF(OH) primitive cells lead to 15, 21, and 18 phonon modes at the point of the Brillouin zone. The phonon spectra of VC-based systems along the armchair (M) and zigzag (K) directions are presented in Figure 9. The stability of all systems is verified since all phonon frequencies are positive in the whole Brillouin zone. The phonon dispersions have three acoustic modes. Two of them exhibit a linear dispersion near and correspond to in-plane rigid-body motions. In contrast, the third acoustic mode corresponding to out-of-plane vibration has a quadratic dispersion close to and a lower energy in the rest of the spectrum. This quadratic dependence is analogous to the one observed in graphene [73] and MoS [74]. In Figure 9a, the first three optical branches in the phonon spectrum of pristine VC demonstrate significantly lower frequencies close to the three acoustic phonon branches, thus inducing a phonon gap of about 250 cm between the lower three and the upper three optical branches. Upon functionalization, this phonon gap between optical phonons is filled by additional optical phonon branches (Figure 9b–d). This makes the most noticeable difference between pristine and terminated MXene systems.
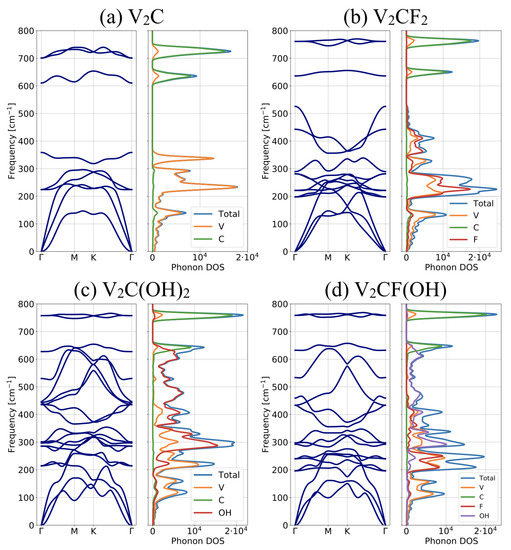
Figure 9.
Phonon spectra and projected density of states of (a) pristine VC, and terminated (b) VCF, (c) VC(OH), (d) VCF(OH).
Using the group theory, one can have access to the Raman and infrared activity of the phonon modes, hence allowing for an accurate analysis of both Raman and infrared experimental spectra, presented in ref. [72]. Additionally, the knowledge of the phonon spectrum of a material is essential to understand a wide set of macroscopic properties, including the electrical and thermal conductivities.
5. Magnetoresistance in 2D Tunnel Junctions
Since the isolation of graphene, the library of synthesizable two-dimensional materials has been enriched with several hundreds items featuring versatile electronic properties. This catalog offers unprecedented design opportunities for the rapidly growing field of spintronic where the structural quality of interfaces often plays an instrumental role in determining the functionality and performance of devices. A prototypical spintronic device is the magnetic tunnel junction (MTJ) consisting of two ferromagnetic (FM) layers separated by a thin insulating (I) barrier.
The instrumental property of MTJs is the modulation of their resistance by individually switching the magnetization of the FM electrodes via the application of an external magnetic field. MTJs are thus characterized by two states of electrical resistance associated with the parallel and anti-parallel magnetizations of the electrodes. This is quantified by the tunnel magnetoresistance (TMR) defined as:
where and correspond to the resistance and conductance of the junction in the anti-parallel and parallel configurations. This effect was discovered by Julliere in 1975 [75] who proposed a simple model to rationalize the measured TMR signal based on the assumption that (i) the carriers spin is conserved upon tunneling and (ii) the conductance of a given spin channel is proportional to the product of the density of conducting states in the FM electrodes,
Here, () denotes the density of conducting states of majority (minority) spin in the left and right electrodes. Within this framework, the TMR can be expressed as:
where are the spin polarization of the conducting electrons in the left and right electrodes defined as .
The spin polarization of the tunneling electrons ultimately depends on the electronic structure of the interfaces. Over the last decade, significant research efforts have been dedicated to introduce 2D materials to control and tailor the magnetoresistive response of the interfaces [76]. Boosted by the theoretical prediction of perfect spin filtering by few of its layers [77,78,79,80], graphene has been the first 2D material to be investigated [81,82,83], rapidly followed by insulating h-BN [84,85,86] and semi-conducting transition metal dichalcogenides (TMDCs) [87,88,89,90]. While very promising experimental results have yet been reported, first-principles simulations provide a complementary tool to unravel the full potential of 2DMs in tunneling junctions. This is illustrated here with the theoretical investigation of a MTJ consisting of a monolayer h-BN sandwiched between two Co ferromagnet electrodes. The in-plane lattice constant of the hcp Co matches almost perfectly the lattice constant of h-BN. This suggests that epitaxial Co/h-BN interface can be realized experimentally by CVD technique [91,92]. As a consequence, the interface may be perfectly commensurate or not depending on the integration pathway. The epitaxial interface is illustrated in Figure 10 along with a misaligned configuration obtained by twisting the h-BN monolayer by 21.78. First-principles calculations reveal strikingly different spin behaviours for these two geometries.
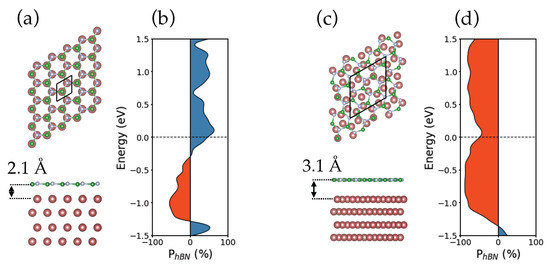
Figure 10.
(a,c) Ball and stick representation of monolayer h-BN on Co (hcp ) within the (a) aligned and (c) misaligned () configurations. Boron and nitrogen atoms are colored respectively in green and white. Cobalt atoms are depicted in red. (b,d) Spin polarization of the density of states projected on h-BN. The excess of majority spins is colored in blue, and the excess of minority spins is colored in red.
Structural optimization of the aforementioned interfaces indicates a stronger bonding of h-BN with Co in the aligned configuration with respect to the misaligned one. The average distance between h-BN and the FM is of 2.1 Å for the epitaxial structure and of 3.1 Å for the misaligned one. The charge transfer from the ferromagnet to the monolayer and the hybridization of h-BN are consequently affected by the relative crystallographic orientation across the interface. As a result, the computed spin polarization of h-BN (see Figure 10a,c) exhibits opposite sign at the Fermi energy for the two considered geometries. Straight application of the Julliere model, see Equation (10), predicts radically different magnetoresistive behaviour for the aligned and misaligned configurations.
Further calculations of the electronic transmission functions by means of the Green’s function formalism, see Equation (2), confirm the dependence of the spin-polarized tunneling current on the relative crystallographic orientation of the interfaces. The electronic transmission functions computed for a fully epitaxial Co/h-BN/Co junction (i.e., with Co, h-BN, and Co aligned) is reported in Figure 11a for the parallel and anti-parallel magnetizations of the electrodes. In the anti-parallel configuration the transmission functions associated with majority and minority spins are degenerated as expected for a symmetric junction. At equilibrium, the computed TMR is of 36%. The case of an asymmetric junction, where one electrode has been twisted by 21.78°, is considered in Figure 11b. In this configuration, the global amplitude of the transmission is reduced with respect to the epitaxial junction and the spin symmetry of the transmission in the anti-parallel configuration is lifted. The computed TMR at equilibrium is reduced to 15%. This illustrates the strong dependence of the magnetoresistive behaviour of 2D-MTJs on the atomic configuration of interfaces. The calculations were performed within the DFT framework as implemented in the SIESTA electronic structure package [93,94]. Converged k-point grids and a basis set of double- plus polarization quality were used.
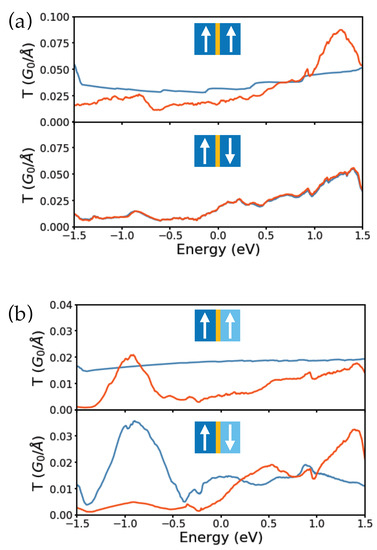
Figure 11.
The spin dependent electronic transmission function of a (a) symmetric and (b) asymmetric Co/h-BN/Co junction with both the parallel and anti-parallel relative orientation of FM magnetization. The transmission functions of the majority and minority spins are depicted in blue and red respectively. In the symmetric junction, Co, h-BN and Co are exactly aligned hence giving rise to two epitaxial interfaces (see Figure 10b). In the asymmetric case, Co and h-BN are aligned but Co has been twisted by an angle of 21.78° hence corresponding to a less strongly bonded interface (see Figure 10d).
6. Conclusions
In this review article covering the state-of-the-art of DFT and TB methods devoted to the prediction of 2D materials properties, a particular emphasis was put on the electrical, optical, vibrational, and magnetic properties. Physical quantities such as the charge and spin transmission (across GBs and MJTs), the optical conductivity and normal transmittance, and the influence of chemical terminations on electronic states and phonon modes, are key parameters used to understand the response of 2D metallic materials (i.e., graphene, borophene, MXenes, and h-BN) and hetero-junctions, to fundamental excitations, such as non-oscillating and oscillating electric fields and thermal gradients.
The tremendous properties of 2D materials have proven their outstanding capability to bring new paradigms in the vast field of nanosciences… and the family of 2D crystals is continuously growing, both in terms of variety and number of materials. Indeed, theoretical search for novel 2D materials has been proposed, focusing on how easily the monolayers can be exfoliated from their parent layered compounds [95]. Starting from 108,423 unique, experimentally known 3D compounds, high-throughput calculations using van der Waals DFT allowed the identification of 1825 compounds that are either easily or potentially exfoliable. Since the physical properties of monolayers can often dramatically change from those of their parent 3D materials, these ab initio predicted 2D systems provide a new degree of freedom for applications while also unveiling novel physics. Thanks to this huge number of potentially new 2D layers, computational atomistic modelling will still have a major role to play in the accurate prediction of the corresponding and possibly promising properties using state-of-the-art quantum simulations.
Author Contributions
All the authors contributed equally to this work and should thus be considered as co-first authors. Consequently, the authors are listed in alphabetic order, except for our esteemed supervisor reported as last author. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the FRS-FNRS through the “3D nanoarchitecturing of 2D crystals” project (ARC 16/21-077), the Région Wallonne through the BATWAL project (N1318146), the European Union’s Horizon 2020 research and innovation program (GrapheneFlagship Core1—N696656 and Core2—N785219), and the Flag-ERA JTC 2017 project entitled “MORE-MXenes”. Computational resources were provided by the supercomputing facilities of the Université catholique de Louvain (CISM/UCL) and the Consortium des Équipements de Calcul Intensif en Fédération Wallonie Bruxelles (CÉCI) funded by the Fond de la Recherche Scientifique de Belgique (F.R.S.-FNRS) under convention 2.5020.11. The present research also benefited from computational resources made available on the Tier-1 supercomputer of the Fédération Wallonie-Bruxelles, infrastructure funded by the Région Wallonne under the grant agreement n1117545.
Acknowledgments
The authors acknowledge technical help from J.-M. Beuken and M. Giantomassi. The authors thank all former members of the Equipe des Charbonniers for stimulating discussions, bowlings and beers during all these years!
Conflicts of Interest
The authors declare no conflict of interest.
References
- Binnig, G.; Rohrer, H.; Gerber, C.; Weibel, E. Tunneling through a controllable vacuum gap. Appl. Phys. Lett. 1982, 40, 178–180. [Google Scholar] [CrossRef]
- Binnig, G.; Rohrer, H.; Gerber, C.; Weibel, E. Surface Studies by Scanning Tunneling Microscopy. Phys. Rev. Lett. 1982, 49, 57–61. [Google Scholar] [CrossRef]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef] [PubMed]
- Feynman, R.P. There’s Plenty of Room at the Bottom. Eng. Sci. 1960, 23, 22–36. [Google Scholar]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Iijima, S. Helical microtubules of graphitic carbon. Nature 1991, 354, 56–58. [Google Scholar] [CrossRef]
- Martin, R.M. Electronic Structure: Basic Theory and Practical Methods; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar] [CrossRef]
- Friesner, R.A. Ab initio quantum chemistry: Methodology and applications. Proc. Natl. Acad. Sci. USA 2005, 102, 6648–6653. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous Electron Gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Gonze, X.; Michenaud, J.P.; Vigneron, J.P. Ab initiocalculations of bismuth properties, including spin–orbit coupling. Phys. Scr. 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO Method for the Periodic Potential Problem. Phys. Rev. 1954, 94, 1498–1524. [Google Scholar] [CrossRef]
- Nysten, B.; Verfaillie, G.; Ferain, E.; Legras, R.; Lhoest, J.B.; Poleunis, C.; Bertrand, P. SEM, ToF-SIMS and LFM morphological study of an heterogeneous polymeric surface. Microsc. Microanal. Microstruct. 1994, 5, 373–380. [Google Scholar] [CrossRef]
- Nysten, B.; Legras, R.; Costa, J. Atomic force microscopy imaging of viscoelastic properties in toughened polypropylene resins. J. Appl. Phys. 1995, 78, 5953–5958. [Google Scholar] [CrossRef]
- Charlier, J.C.; Gonze, X.; Michenaud, J.P. First-principles study of the electronic properties of graphite. Phys. Rev. B 1991, 43, 4579–4589. [Google Scholar] [CrossRef] [PubMed]
- Charlier, J.C.; Michenaud, J.P.; Gonze, X.; Vigneron, J.P. Tight-binding model for the electronic properties of simple hexagonal graphite. Phys. Rev. B 1991, 44, 13237–13249. [Google Scholar] [CrossRef] [PubMed]
- Charlier, J.C.; Michenaud, J.P.; Gonze, X. First-principles study of the electronic properties of simple hexagonal graphite. Phys. Rev. B 1992, 46, 4531–4539. [Google Scholar] [CrossRef]
- Charlier, J.C.; Michenaud, J.P.; Lambin, P. Tight-binding density of electronic states of pregraphitic carbon. Phys. Rev. B 1992, 46, 4540–4543. [Google Scholar] [CrossRef]
- Gonze, X.; Beuken, J.M.; Caracas, R.; Detraux, F.; Fuchs, M.; Rignanese, G.M.; Sindic, L.; Verstraete, M.; Zerah, G.; Jollet, F.; et al. First-principles computation of material properties: The ABINIT software project. Comput. Mater. Sci. 2002, 25, 478–492. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Geim, A.K.; Morozov, S.V.; Jiang, D.; Zhang, Y.; Dubonos, S.V.; Grigorieva, I.V.; Firsov, A.A. Electric field effect in atomically thin carbon films. Science 2004, 306, 666–669. [Google Scholar] [CrossRef]
- Novoselov, K.S. Graphene: Materials in the Flatland (Nobel Lecture). Angew. Chem. Int. Ed. 2011, 50, 6986–7002. [Google Scholar] [CrossRef]
- Brel, J. Le Plat Pays. In Les Bourgeois; Barclay: Paris, France, 1962. [Google Scholar]
- Bhuyan, M.S.A.; Uddin, M.N.; Islam, M.M.; Bipasha, F.A.; Hossain, S.S. Synthesis of graphene. Int. Nano Lett. 2016, 6, 65–83. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal, V.; Colombo, L.; Gellert, P.; Schwab, M.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192–200. [Google Scholar] [CrossRef] [PubMed]
- Isacsson, A.; Cummings, A.W.; Colombo, L.; Colombo, L.; Kinaret, J.M.; Roche, S. Scaling properties of polycrystalline graphene: A review. 2D Mater. 2016, 4, 012002. [Google Scholar] [CrossRef]
- Kim, K.; Lee, Z.; Regan, W.; Kisielowski, C.; Crommie, M.; Zettl, A. Grain boundary mapping in polycrystalline graphene. ACS Nano 2011, 5, 2142–2146. [Google Scholar] [CrossRef]
- Huang, P.Y.; Ruiz-Vargas, C.S.; van der Zande, A.M.; Whitney, W.S.; Levendorf, M.P.; Kevek, J.W.; Garg, S.; Alden, J.S.; Hustedt, C.J.; Zhu, Y.; et al. Grains and grain boundaries in single-layer graphene atomic patchwork quilts. Nature 2011, 469, 389–392. [Google Scholar] [CrossRef]
- Lahiri, J.; Lin, Y.; Bozkurt, P.; Oleynik, I.I.; Batzill, M. An extended defect in graphene as a metallic wire. Nat. Nanotechnol. 2010, 5, 326–329. [Google Scholar] [CrossRef]
- Luican-Mayer, A.; Barrios-Vargas, J.E.; Falkenberg, J.T.; Autès, G.; Cummings, A.W.; Soriano, D.; Li, G.; Brandbyge, M.; Yazyev, O.V.; Roche, S.; et al. Localized electronic states at grain boundaries on the surface of graphene and graphite. 2D Mater. 2016, 3, 031005. [Google Scholar] [CrossRef]
- Tsen, A.W.; Brown, L.; Levendorf, M.P.; Ghahari, F.; Huang, P.Y.; Havener, R.W.; Ruiz-Vargas, C.S.; Muller, D.A.; Kim, P.; Park, J. Tailoring electrical transport across grain boundaries in polycrystalline graphene. Science 2012, 336, 1143–1146. [Google Scholar] [CrossRef]
- Ogawa, Y.; Komatsu, K.; Kawahara, K.; Tsuji, M.; Tsukagoshi, K.; Ago, H. Structure and transport properties of the interface between CVD-grown graphene domains. Nanoscale 2014, 6, 7288–7294. [Google Scholar] [CrossRef]
- Kochat, V.; Tiwary, C.S.; Biswas, T.; Ramalingam, G.; Hsieh, K.; Chattopadhyay, K.; Raghavan, S.; Jain, M.; Ghosh, A. Magnitude and origin of electrical noise at individual grain boundaries in graphene. Nano Lett. 2015, 16, 562–567. [Google Scholar] [CrossRef]
- Koepke, J.C.; Wood, J.D.; Estrada, D.; Ong, Z.Y.; He, K.T.; Pop, E.; Lyding, J.W. Atomic-scale evidence for potential barriers and strong carrier scattering at graphene grain boundaries: A scanning tunneling microscopy study. ACS Nano 2013, 7, 75–86. [Google Scholar] [CrossRef] [PubMed]
- Song, H.; Li, S.; Miyazaki, H.; Sato, S.; Hayashi, K.; Yamada, A.; Yokoyama, N.; Tsukagoshi, K. Origin of the relatively low transport mobility of graphene grown through chemical vapor deposition. Sci. Rep. 2012, 2, 337. [Google Scholar] [CrossRef] [PubMed]
- Park, S.; Shehzad, M.A.; Khan, M.F.; Nazir, G.; Eom, J.; Noh, H.; Seo, Y. Effect of grain boundaries on electrical properties of polycrystalline graphene. Carbon 2017, 112, 142–148. [Google Scholar] [CrossRef]
- Cummings, A.W.; Duong, D.L.; Nguyen, V.L.; Van Tuan, D.; Kotakoski, J.; Barrios Vargas, J.E.; Lee, Y.H.; Roche, S. Charge transport in polycrystalline graphene: Challenges and opportunities. Adv. Mater. 2014, 26, 5079–5094. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Jauregui, L.A.; Wu, W.; Colby, R.; Tian, J.; Su, Z.; Cao, H.; Liu, Z.; Pandey, D.; Wei, D.; et al. Control and characterization of individual grains and grain boundaries in graphene grown by chemical vapour deposition. Nat. Mater. 2011, 10, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Kumari, A.; Prasad, N.; Bhatnagar, P.; Mathur, P.; Yadav, A.K.; Tomy, C.; Bhatia, C. Electrical transport properties of polycrystalline CVD graphene on SiO2/Si substrate. Diam. Relat. Mater. 2014, 45, 28–33. [Google Scholar] [CrossRef]
- Banszerus, L.; Schmitz, M.; Engels, S.; Dauber, J.; Oellers, M.; Haupt, F.; Watanabe, K.; Taniguchi, T.; Beschoten, B.; Stampfer, C. Ultrahigh-mobility graphene devices from chemical vapor deposition on reusable copper. Sci. Adv. 2015, 1, e1500222. [Google Scholar] [CrossRef]
- Zhou, H.; Yu, W.J.; Liu, L.; Cheng, R.; Chen, Y.; Huang, X.; Liu, Y.; Wang, Y.; Huang, Y.; Duan, X. Chemical vapour deposition growth of large single crystals of monolayer and bilayer graphene. Nat. Commun. 2013, 4, 1–8. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Louie, S.G. Electronic transport in polycrystalline graphene. Nat. Mater. 2010, 9, 806–809. [Google Scholar] [CrossRef]
- Tapasztó, L.; Nemes-Incze, P.; Dobrik, G.; Jae Yoo, K.; Hwang, C.; Biró, L.P. Mapping the electronic properties of individual graphene grain boundaries. Appl. Phys. Lett. 2012, 100, 053114. [Google Scholar] [CrossRef]
- Nguyen, V.H.; Hoang, T.X.; Dollfus, P.; Charlier, J.C. Transport properties through graphene grain boundaries: Strain effects versus lattice symmetry. Nanoscale 2016, 8, 11658–11673. [Google Scholar] [CrossRef] [PubMed]
- Dechamps, S.; Nguyen, V.H.; Charlier, J.C. Ab initio quantum transport in polycrystalline graphene. Nanoscale 2018, 10, 7759–7768. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.H.; Dechamps, S.; Dollfus, P.; Charlier, J.C. Valley filtering and electronic optics using polycrystalline graphene. Phys. Rev. Lett. 2016, 117, 247702. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.H.; Charlier, J.C. Aharonov–Bohm interferences in polycrystalline graphene. Nanoscale Adv. 2020, 2, 256–263. [Google Scholar] [CrossRef]
- Cummings, A.W.; Dubois, S.M.-M.; Charlier, J.-C.; Roche, S. Universal Spin Diffusion Length in Polycrystalline Graphene. Nano Lett. 2019, 19, 7418–7426. [Google Scholar] [CrossRef] [PubMed]
- Lindsay, L.; Broido, D.A. Optimized Tersoff and Brenner empirical potential parameters for lattice dynamics and phonon thermal transport in carbon nanotubes and graphene. Phys. Rev. B 2010, 81, 205441. [Google Scholar] [CrossRef]
- Jiang, J.W.; Wang, B.S.; Wang, J.S.; Park, H.S. A review on the flexural mode of graphene: Lattice dynamics, thermal conduction, thermal expansion, elasticity and nanomechanical resonance. J. Phys. Condens. Matter 2015, 27, 083001. [Google Scholar] [CrossRef]
- Ozaki, T. Variationally optimized atomic orbitals for large-scale electronic structures. Phys. Rev. B 2003, 67, 155108. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Numerical atomic basis orbitals from H to Kr. Phys. Rev. B 2004, 69, 195113. [Google Scholar] [CrossRef]
- Ozaki, T.; Kino, H. Efficient projector expansion for the ab initio LCAO method. Phys. Rev. B 2005, 72, 045121. [Google Scholar] [CrossRef]
- Cummings, A.W.; Cresti, A.; Roche, S. Quantum Hall effect in polycrystalline graphene: The role of grain boundaries. Phys. Rev. B 2014, 90, 161401. [Google Scholar] [CrossRef]
- Gunlycke, D.; White, C.T. Graphene Valley Filter Using a Line Defect. Phys. Rev. Lett. 2011, 106, 136806. [Google Scholar] [CrossRef] [PubMed]
- Ma, C.; Sun, H.; Zhao, Y.; Li, B.; Li, Q.; Zhao, A.; Wang, X.; Luo, Y.; Yang, J.; Wang, B.; et al. Evidence of van Hove Singularities in Ordered Grain Boundaries of Graphene. Phys. Rev. Lett. 2014, 112, 226802. [Google Scholar] [CrossRef] [PubMed]
- Márk, G.I.; Vancsó, P.; Lambin, P.; Hwang, C.; Biro, L.P. Forming electronic waveguides from graphene grain boundaries. J. Nanophotonics 2012, 6, 1–6. [Google Scholar] [CrossRef]
- Yasaei, P.; Kumar, B.; Hantehzadeh, R.; Kayyalha, M.; Baskin, A.; Repnin, N.; Wang, C.; Klie, R.F.; Chen, Y.P.; Král, P.; et al. Chemical sensing with switchable transport channels in graphene grain boundaries. Nat. Commun. 2014, 5, 4911. [Google Scholar] [CrossRef] [PubMed]
- Machón, M.; Reich, S.; Thomsen, C.; Sánchez-Portal, D.; Ordejón, P. Ab initio calculations of the optical properties of 4-Å-diameter single-walled nanotubes. Phys. Rev. B 2002, 66, 155410. [Google Scholar] [CrossRef]
- Lherbier, A.; Botello-Méndez, A.R.; Charlier, J.C. Electronic and optical properties of pristine and oxidized borophene. 2D Mater. 2016, 3, 045006. [Google Scholar] [CrossRef]
- Holovský, J.; Ballif, C. Thin-film limit formalism applied to surface defect absorption. Opt. Express 2014, 22, 31466–31472. [Google Scholar] [CrossRef]
- Holovský, J.; Nicolay, S.; De Wolf, S.; Ballif, C. Effect of the thin-film limit on the measurable optical properties of graphene. Sci. Rep. 2015, 5, 15684. [Google Scholar] [CrossRef]
- Mannix, A.J.; Zhou, X.F.; Kiraly, B.; Wood, J.D.; Alducin, D.; Myers, B.D.; Liu, X.; Fisher, B.L.; Santiago, U.; Guest, J.R.; et al. Synthesis of borophenes: Anisotropic, two-dimensional boron polymorphs. Science 2015, 350, 1513–1516. [Google Scholar] [CrossRef]
- Feng, B.; Zhang, J.; Zhong, Q.; Li, W.; Li, S.; Li, H.; Cheng, P.; Meng, S.; Chen, L.; Wu, K. Experimental realization of two-dimensional boron sheets. Nat. Chem. 2016, 8, 563–568. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, V.H.; Lherbier, A.; Charlier, J.C. Optical Hall effect in strained graphene. 2D Mater. 2017, 4, 025041. [Google Scholar] [CrossRef]
- Naguib, M.; Kurtoglu, M.; Presser, V.; Lu, J.; Niu, J.; Heon, M.; Hultman, L.; Gogotsi, Y.; Barsoum, M.W. Two-Dimensional Nanocrystals Produced by Exfoliation of Ti3AlC2. Adv. Mater. 2011, 23, 4248–4253. [Google Scholar] [CrossRef]
- Naguib, M.; Mashtalir, O.; Carle, J.; Presser, V.; Lu, J.; Hultman, L.; Gogotsi, Y.; Barsoum, M.W. Two-Dimensional Transition Metal Carbides. ACS Nano 2012, 6, 1322–1331. [Google Scholar] [CrossRef] [PubMed]
- Naguib, M.; Mochalin, V.N.; Barsoum, M.W.; Gogotsi, Y. 25th Anniversary Article: MXenes: A New Family of Two-Dimensional Materials. Adv. Mater. 2014, 26, 992–1005. [Google Scholar] [CrossRef] [PubMed]
- Barsoum, M.W. The MN+1AXN phases: A new class of solids: Thermodynamically stable nanolaminates. Prog. Solid State Chem. 2000, 201–281. [Google Scholar] [CrossRef]
- Sokol, M.; Natu, V.; Kota, S.; Barsoum, M.W. On the Chemical Diversity of the MAX Phases. Trends Chem. 2019, 210–223. [Google Scholar] [CrossRef]
- Gogotsi, Y.; Anasori, B. The Rise of MXenes. ACS Nano 2019, 13, 8491–8494. [Google Scholar] [CrossRef]
- Khazaei, M.; Arai, M.; Sasaki, T.; Chung, C.Y.; Venkataramanan, N.S.; Estili, M.; Sakka, Y.; Kawazoe, Y. Novel Electronic and Magnetic Properties of Two-Dimensional Transition Metal Carbides and Nitrides. Adv. Funct. Mater. 2013, 23, 2185–2192. [Google Scholar] [CrossRef]
- Champagne, A.; Shi, L.; Ouisse, T.; Hackens, B.; Charlier, J.C. Electronic and vibrational properties of V2C-based MXenes: From experiments to first-principles modeling. Phys. Rev. B 2018, 97, 115439. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Eklund, P.C. Phonons in carbon nanotubes. Adv. Phys. 2000, 49, 705–814. [Google Scholar] [CrossRef]
- Molina-Sánchez, A.; Wirtz, L. Phonons in single-layer and few-layer MoS2 and WS2. Phys. Rev. B 2011, 84, 155413. [Google Scholar] [CrossRef]
- Julliere, M. Tunneling between ferromagnetic films. Phys. Lett. A 1975, 54, 225–226. [Google Scholar] [CrossRef]
- Piquemal-Banci, M.; Galceran, R.; Martin, M.B.; Godel, F.; Anane, A.; Petroff, F.; Dlubak, B.; Seneor, P. 2D-MTJs: Introducing 2D materials in magnetic tunnel junctions. J. Phys. D Appl. Phys. 2017, 50, 203002. [Google Scholar] [CrossRef]
- Karpan, V.M.; Giovannetti, G.; Khomyakov, P.A.; Talanana, M.; Starikov, A.A.; Zwierzycki, M.; van den Brink, J.; Brocks, G.; Kelly, P.J. Graphite and Graphene as Perfect Spin Filters. Phys. Rev. Lett. 2007, 99, 176602. [Google Scholar] [CrossRef] [PubMed]
- Karpan, V.M.; Khomyakov, P.A.; Starikov, A.A.; Giovannetti, G.; Zwierzycki, M.; Talanana, M.; Brocks, G.; van den Brink, J.; Kelly, P.J. Theoretical prediction of perfect spin filtering at interfaces between close-packed surfaces of Ni or Co and graphite or graphene. Phys. Rev. B 2008, 78, 195419. [Google Scholar] [CrossRef]
- Yazyev, O.V.; Pasquarello, A. Magnetoresistive junctions based on epitaxial graphene and hexagonal boron nitride. Phys. Rev. B 2009, 80, 035408. [Google Scholar] [CrossRef]
- Karpan, V.M.; Khomyakov, P.A.; Giovannetti, G.; Starikov, A.A.; Kelly, P.J. Ni(111) | graphene | h -BN junctions as ideal spin injectors. Phys. Rev. B 2011, 84. [Google Scholar] [CrossRef]
- Cobas, E.; Friedman, A.L.; van’t Erve, O.M.J.; Robinson, J.T.; Jonker, B.T. Graphene As a Tunnel Barrier: Graphene-Based Magnetic Tunnel Junctions. Nano Lett. 2012, 12, 3000–3004. [Google Scholar] [CrossRef]
- Chen, J.J.; Meng, J.; Zhou, Y.B.; Wu, H.C.; Bie, Y.Q.; Liao, Z.M.; Yu, D.P. Layer-by-layer assembly of vertically conducting graphene devices. Nat. Commun. 2013, 4. [Google Scholar] [CrossRef]
- Martin, M.B.; Dlubak, B.; Weatherup, R.S.; Piquemal-Banci, M.; Yang, H.; Blume, R.; Schloegl, R.; Collin, S.; Petroff, F.; Hofmann, S.; et al. Protecting nickel with graphene spin-filtering membranes: A single layer is enough. Appl. Phys. Lett. 2015, 107, 012408. [Google Scholar] [CrossRef]
- Dankert, A.; Venkata Kamalakar, M.; Wajid, A.; Patel, R.S.; Dash, S.P. Tunnel magnetoresistance with atomically thin two-dimensional hexagonal boron nitride barriers. Nano Res. 2015, 8, 1357–1364. [Google Scholar] [CrossRef]
- Piquemal-Banci, M.; Galceran, R.; Caneva, S.; Martin, M.B.; Weatherup, R.S.; Kidambi, P.R.; Bouzehouane, K.; Xavier, S.; Anane, A.; Petroff, F.; et al. Magnetic tunnel junctions with monolayer hexagonal boron nitride tunnel barriers. Appl. Phys. Lett. 2016, 108, 102404. [Google Scholar] [CrossRef]
- Piquemal-Banci, M.; Galceran, R.; Godel, F.; Caneva, S.; Martin, M.B.; Weatherup, R.S.; Kidambi, P.R.; Bouzehouane, K.; Xavier, S.; Anane, A.; et al. Insulator-to-Metallic Spin-Filtering in 2D-Magnetic Tunnel Junctions Based on Hexagonal Boron Nitride. ACS Nano 2018, 12, 4712–4718. [Google Scholar] [CrossRef]
- Iqbal, M.Z.; Iqbal, M.W.; Siddique, S.; Khan, M.F.; Ramay, S.M. Room temperature spin valve effect in NiFe/WS2/Co junctions. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Dankert, A.; Pashaei, P.; Kamalakar, M.V.; Gaur, A.P.S.; Sahoo, S.; Rungger, I.; Narayan, A.; Dolui, K.; Hoque, M.A.; Patel, R.S.; et al. Spin-Polarized Tunneling through Chemical Vapor Deposited Multilayer Molybdenum Disulfide. ACS Nano 2017, 11, 6389–6395. [Google Scholar] [CrossRef]
- Zatko, V.; Galbiati, M.; Dubois, S.M.M.; Och, M.; Palczynski, P.; Mattevi, C.; Brus, P.; Bezencenet, O.; Martin, M.B.; Servet, B.; et al. Band-Structure Spin-Filtering in Vertical Spin Valves Based on Chemical Vapor Deposited WS2. ACS Nano 2019, 13, 14468–14476. [Google Scholar] [CrossRef]
- Galbiati, M.; Tatay, S.; Dubois, S.M.M.; Godel, F.; Galceran, R.; Mañas-Valero, S.; Piquemal-Banci, M.; Vecchiola, A.; Charlier, J.C.; Forment-Aliaga, A.; et al. Path to Overcome Material and Fundamental Obstacles in Spin Valves Based on MoS2 and Other Transition-Metal Dichalcogenides. Phys. Rev. Appl. 2019, 12. [Google Scholar] [CrossRef]
- Caneva, S.; Weatherup, R.S.; Bayer, B.C.; Brennan, B.; Spencer, S.J.; Mingard, K.; Cabrero-Vilatela, A.; Baehtz, C.; Pollard, A.J.; Hofmann, S. Nucleation Control for Large, Single Crystalline Domains of Monolayer Hexagonal Boron Nitride via Si-Doped Fe Catalysts. Nano Lett. 2015, 15, 1867–1875. [Google Scholar] [CrossRef]
- Tonkikh, A.A.; Voloshina, E.N.; Werner, P.; Blumtritt, H.; Senkovskiy, B.; Güntherodt, G.; Parkin, S.S.P.; Dedkov, Y.S. Structural and electronic properties of epitaxial multilayer h-BN on Ni(111) for spintronics applications. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA method for ab initio order- N materials simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Papior, N.; Lorente, N.; Frederiksen, T.; García, A.; Brandbyge, M. Improvements on non-equilibrium and transport Green function techniques: The next-generation transiesta. Comput. Phys. Commun. 2017, 212, 8–24. [Google Scholar] [CrossRef]
- Mounet, N.; Gibertini, M.; Schwaller, P.; Campi, D.; Merkys, A.; Marrazzo, A.; Sohier, T.; Castelli, I.E.; Cepellotti, A.; Pizzi, G.; et al. Two-dimensional materials from high-throughput computational exfoliation of experimentally known compounds. Nat. Nanotechnol. 2018, 13, 246–252. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).