Regulation Principles of Power Flow Gradients to Multiple Characteristic Independent Variables in UPFC Embedded Power System
Abstract
1. Introduction
2. Modelling and Theoretical Analysis for Power Flow Gradients
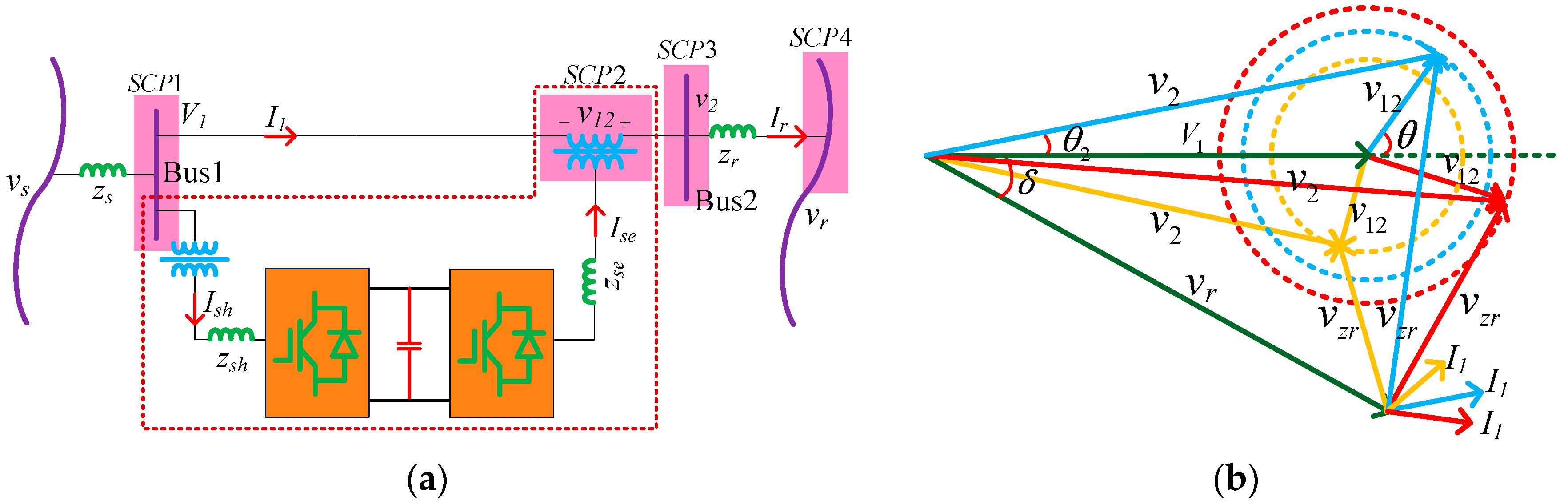
2.1. Power Flow Regulation Theories by the OSIV of UPFC
2.2. Mathematical Model for all the PFG to CIVs
2.3. Theoretical Analysis for Regulation Principles of the PFG to CIVs
3. Case Studies and Analysis
3.1. Settings of the System Operation Conditions and the Regulation Modes and Scenarios of CIVs
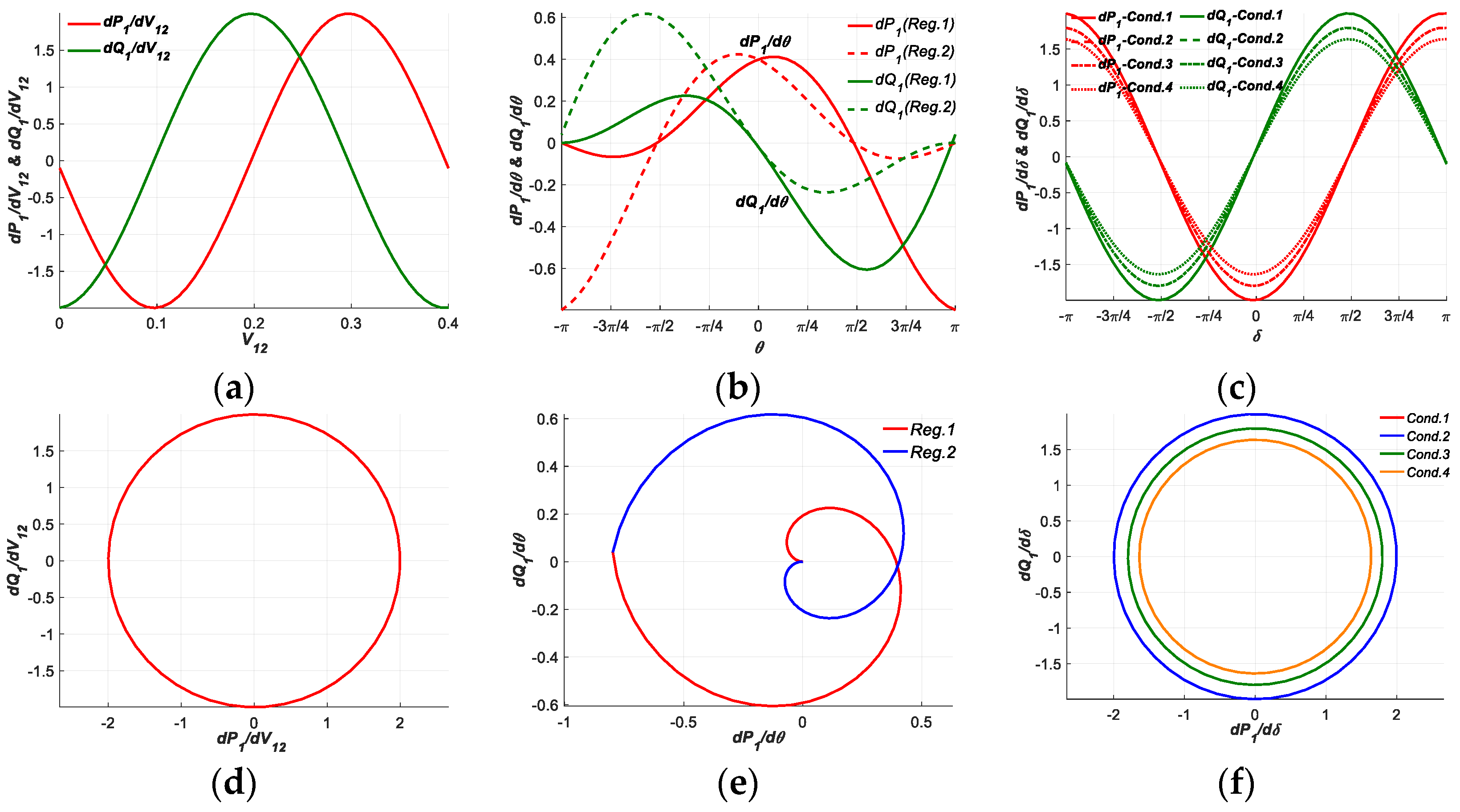
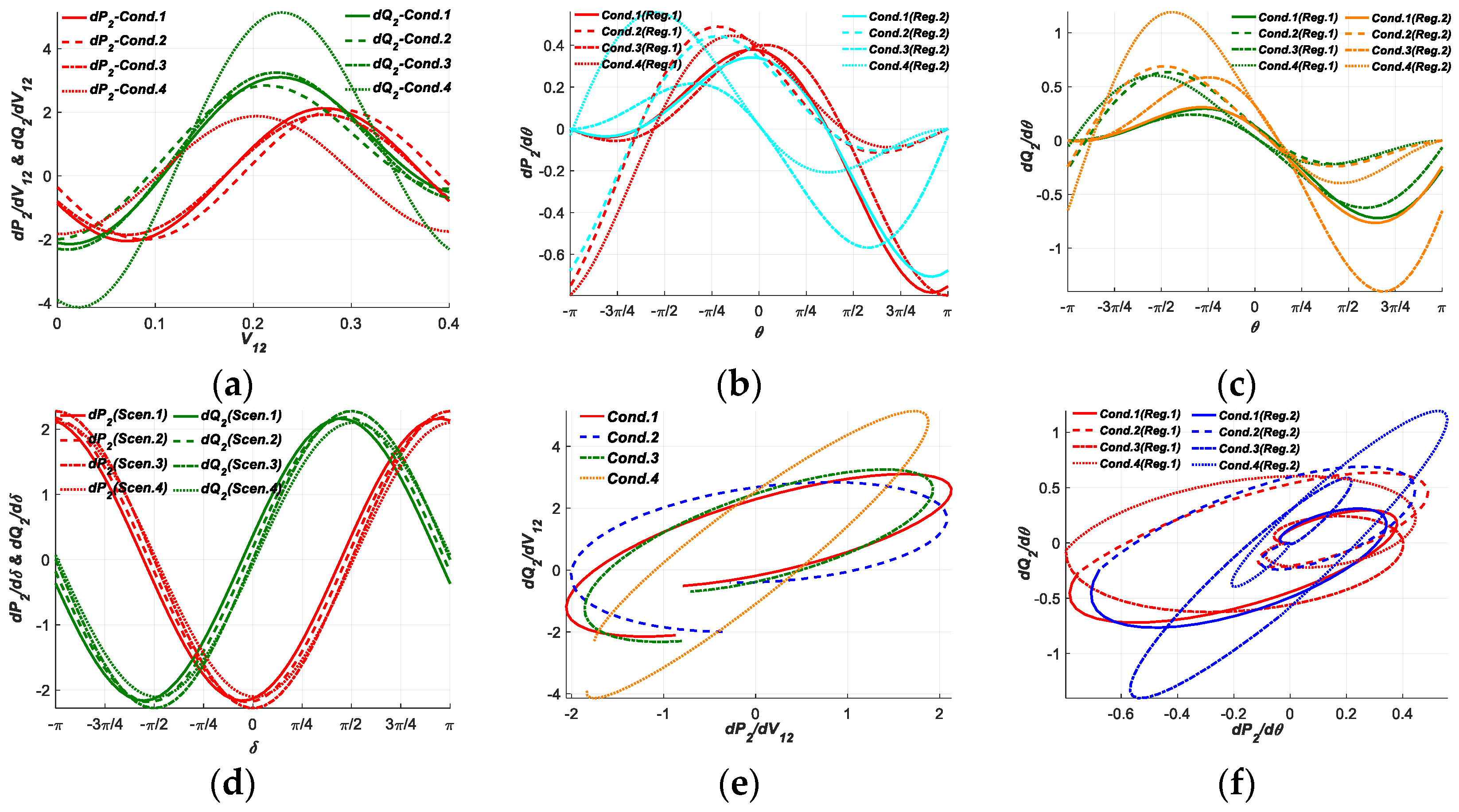
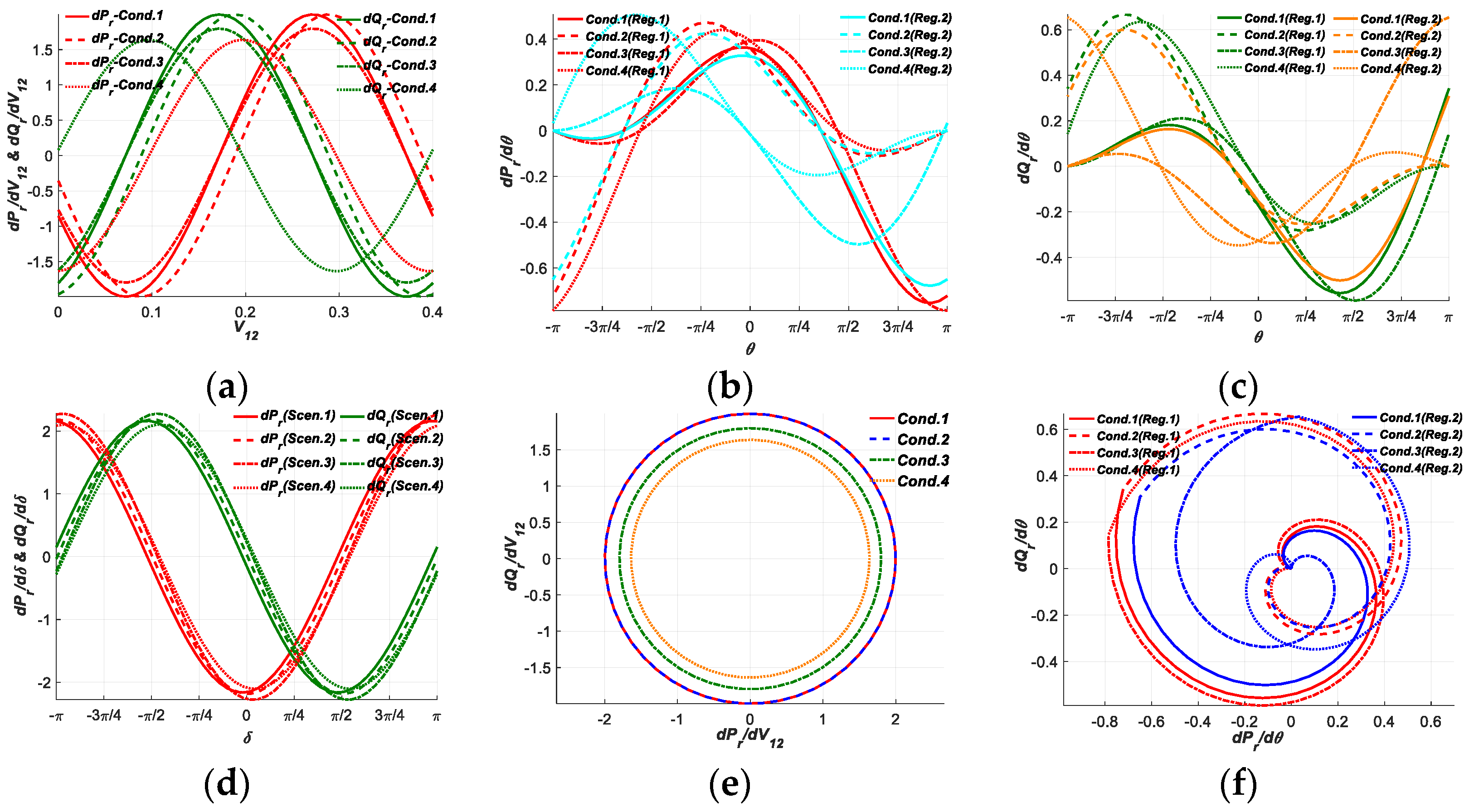
3.2. Test Results and Analysis for PFG at SCP1
3.2.1. Test Results and Analysis in Two-Dimensional Planes
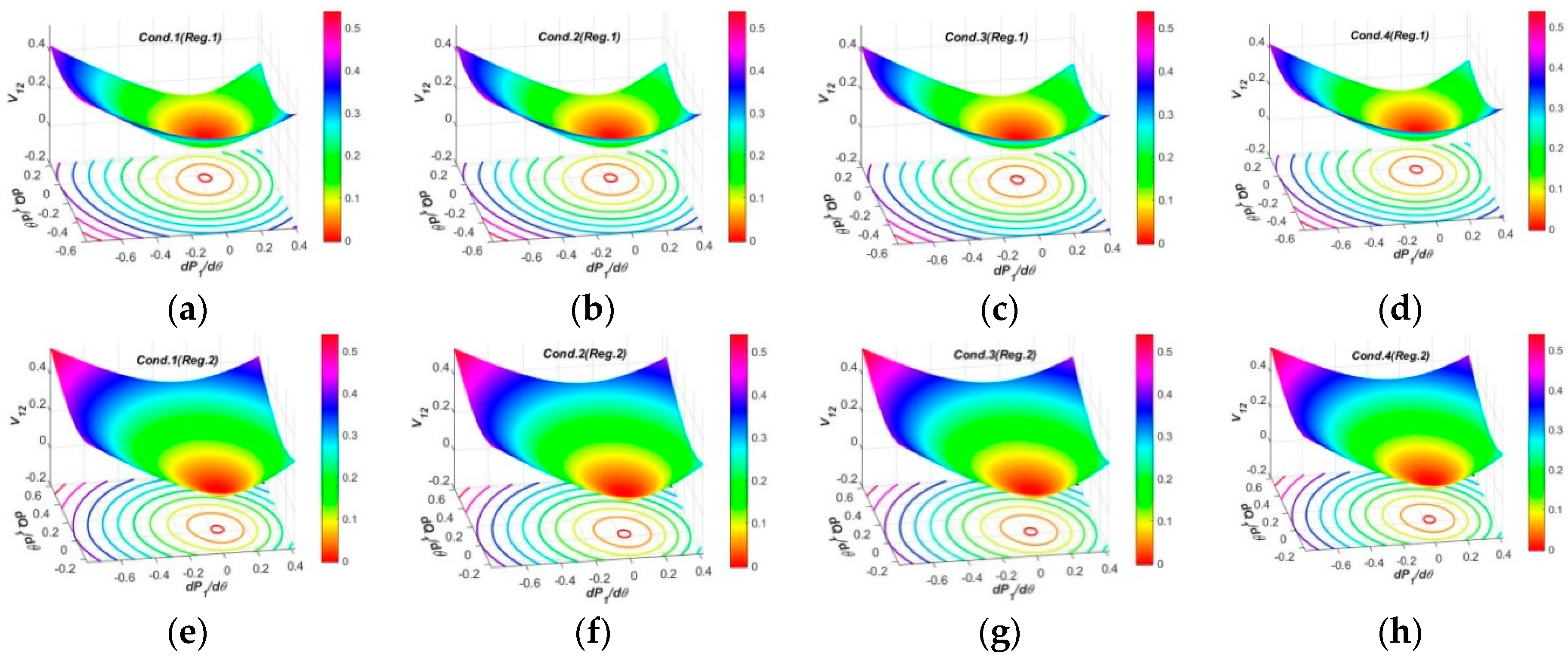
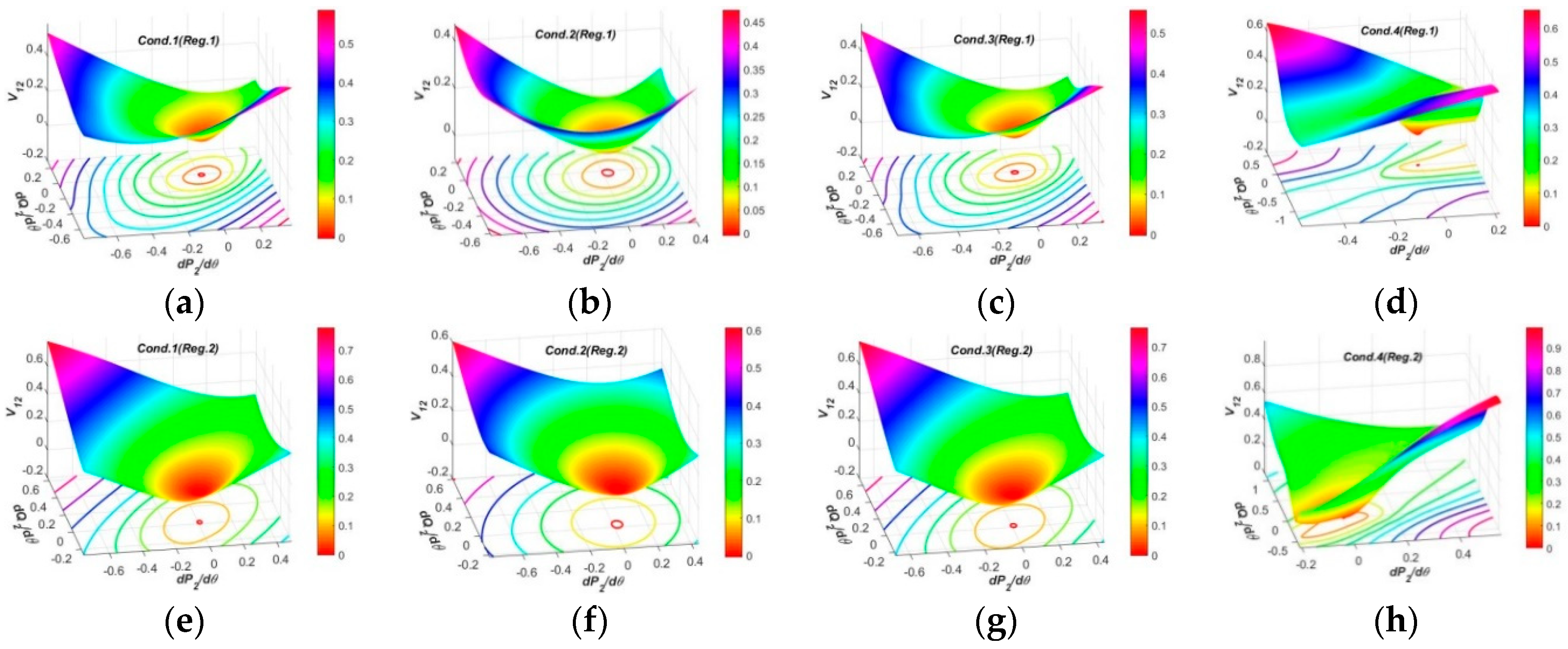
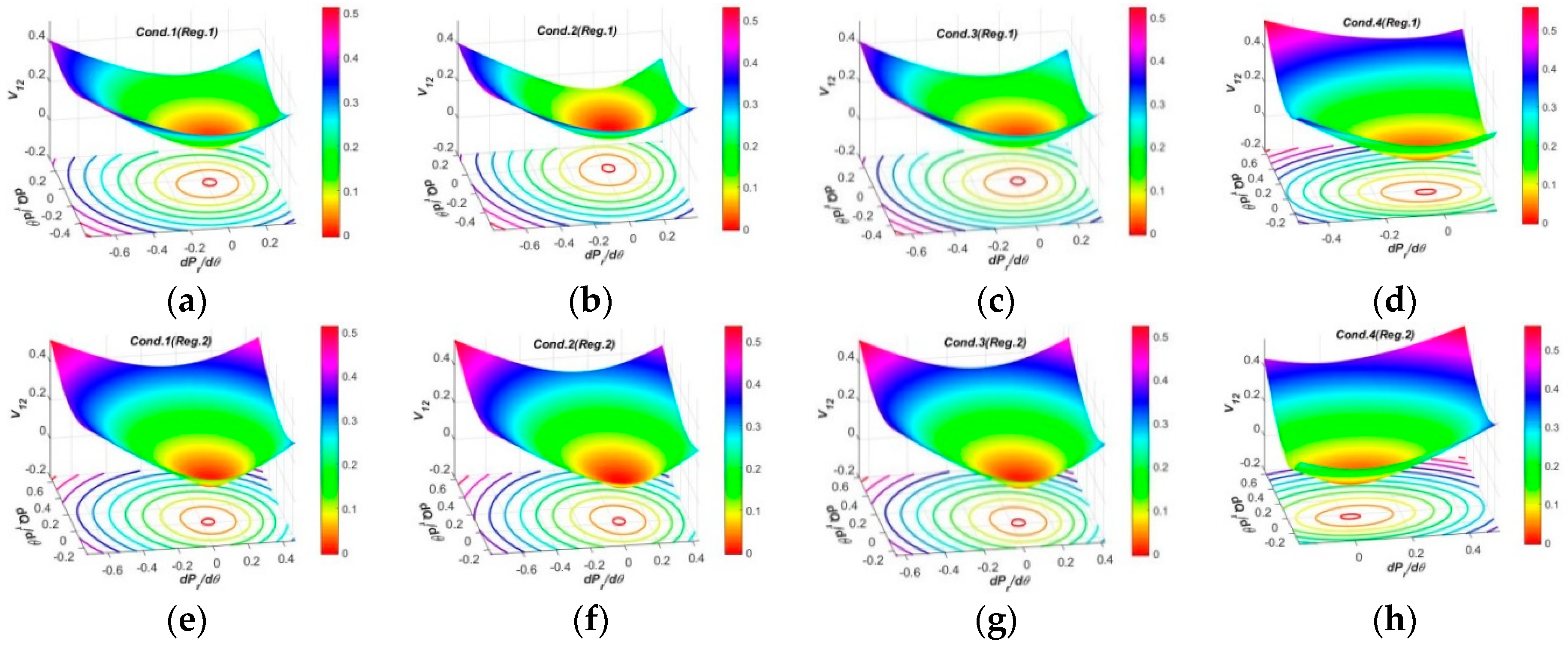
3.2.2. Test Results and Analysis in Three-Dimensional Spaces
3.3. Test Results and Analysis for PFG at SCP2
3.3.1. Test Results and Analysis in Two-Dimensional Planes
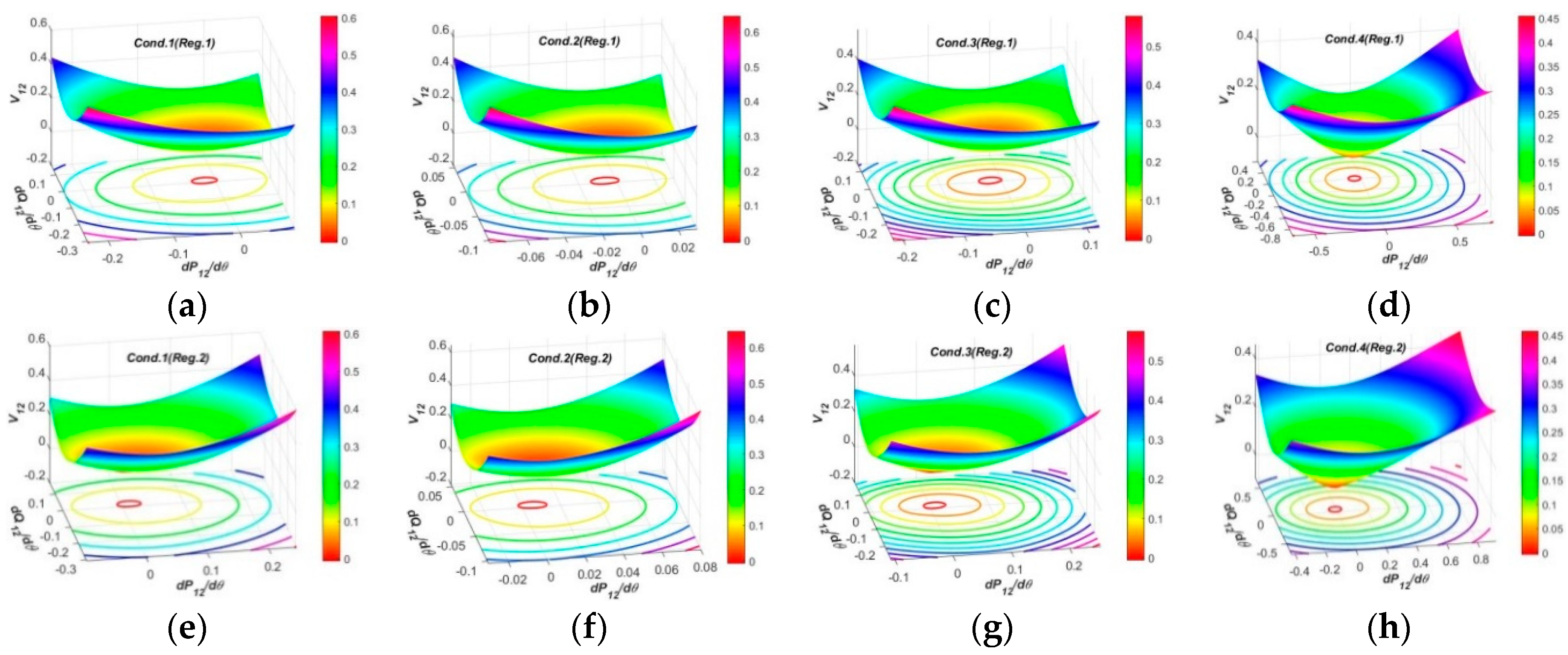
3.3.2. Test Results and Analysis in Three-Dimensional Spaces
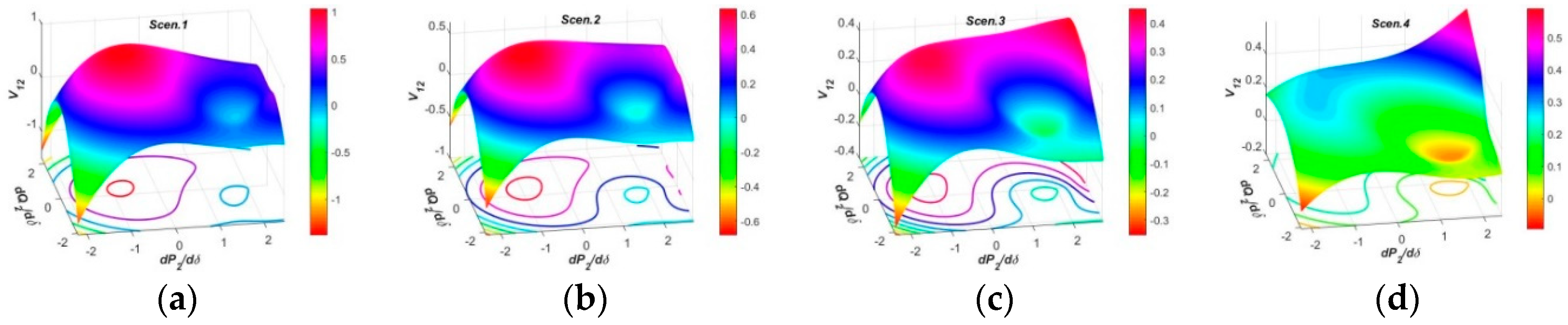
3.4. Test Results and Analysis for PFG at SCP3
3.4.1. Test Results and Analysis in Two-Dimensional Planes
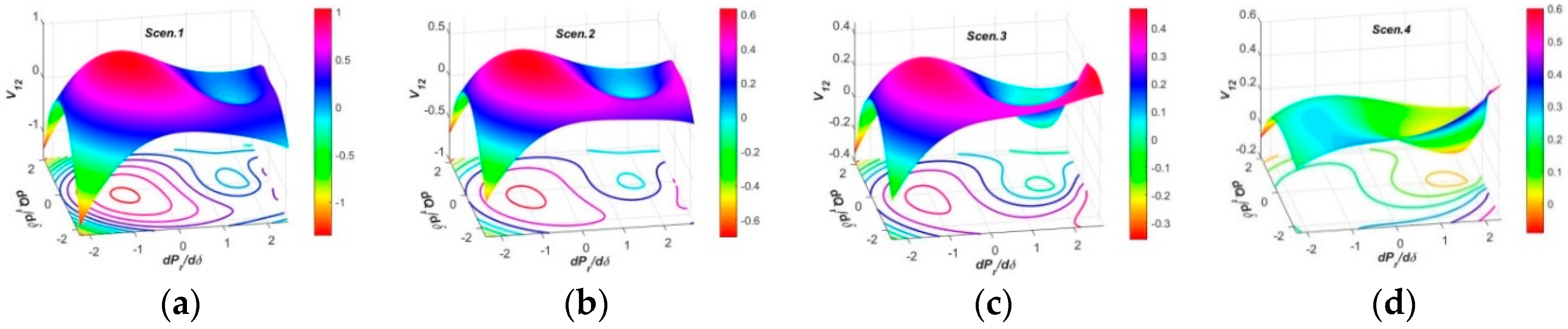
3.4.2. Test Results and Analysis in Three-Dimensional Spaces
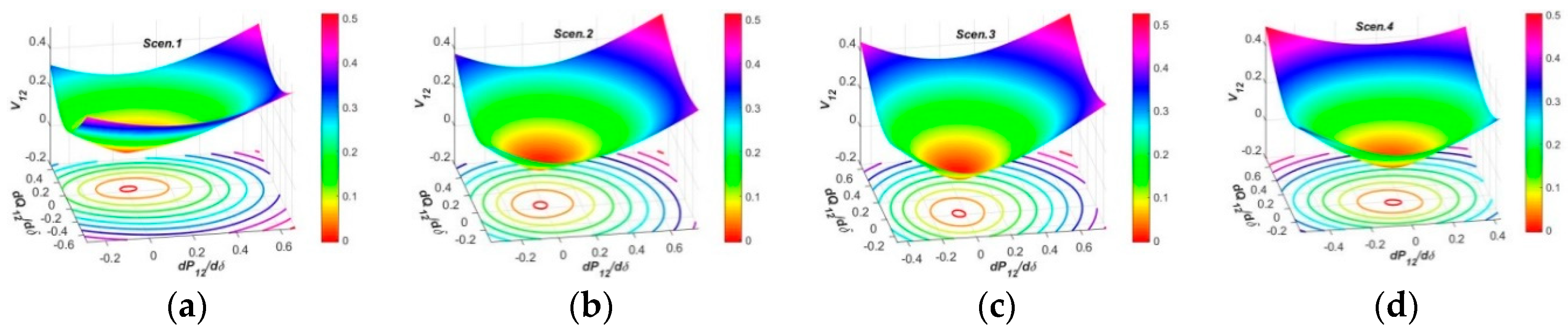
3.5. Test Results and Analysis for PFG at SCP4
3.5.1. Test Results and Analysis in Two-Dimensional Planes
3.5.2. Test Results and Analysis in Three-Dimensional Spaces
4. Conclusions
- (1)
- The PFG to each CIV at different SCP have different degrees of freedom for regulations. The PFG at SCP1 have the fewest degrees of freedom and the simplest regulation principles for regulations by UPFC-. The PFG at SCP2 and SCP4 have the similar degrees of freedom for regulations by UPFC, and the PFG at SCP3 owns the most degrees of freedom and the most complicated regulation principles for regulations for regulations by UPFC, indicating that the PFG of the power system can be regulated by UPFC efficiently after the insertion of OSIV at SCP2.
- (2)
- In the two-dimensional planes, the APFG and RPFG to CIV1 at SCP3 and SCP4 in the normal operation conditions have the similar curves and focus within their individual certain regions, while the curves of APFG and RPFG in the severe operation condition stay at different regions with the curves in the normal operation conditions. The PFG to CIV2 at each SCP can be regulated to larger or smaller required amplitudes in different regions by Reg.1 and Reg.2 modes, the curves of APFG to CIV2 against RPFG to CIV2 by Reg.1 and Reg.2 modes can form special axial or rotational symmetrical closed shapes, the regulation ranges and areas by Reg.2 mode in the third and fourth operation condition are much larger than others, which are beneficial to be regulated throughout an overall closed region and adaptive to different operation conditions. Both the curves of PFG to CIV3 at SCP1, SCP3 and SCP4 show nearly the same shapes with the similar magnitudes and phases in different regulation scenarios, while those at SCP2 are with different magnitudes and phases, indicating the regulations of PFG by UPFC at SCP2 can be efficiently adaptive to different operation conditions.
- (3)
- In the three-dimensional spaces, the spatial surfaces of PFG to CIV1 at SCP3 have non-uniform dome shapes humping upwards, and nearly the same regulation efficiencies by Reg.1 and Reg.2 modes which are larger than SCP1 and SCP2. The spatial surfaces of PFG to CIV2 at each SCP present similar funnel shapes in all operation conditions, and the surface curvatures and areas by Reg.1 mode at each SCP are similar, but those by Reg.2 mode at SCP1, SCP3 and SCP4 are larger than SCP2, revealing the OSIV of UPFC at SCP2 has enough large efficiencies to regulate the power flows at other SCP. The spatial surfaces of PFG to CIV3 at SCP2 present similar funnel shapes, while those at SCP3 and SCP4 have two funnel peaks and inverse varying tendencies within different regulation regions, which is more beneficial to occupy larger surface areas and adaptive to different regulation requirements.
- (4)
- When the PFG to CIVs have larger regulation efficiencies, the resulting impulses or shocks to the power system during the regulation processes may also be more intense, and the requirements for suppressing the resulting shocks need to be more rigorous at the same time, so as to maintain the stability and normal operations of the power system.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| UPFC | unified power flow controller |
| V1 | the voltage of Bus1 |
| v2 | the voltage of Bus2 |
| zr | the impendence of the receiving end transmission line |
| rr | the resistance of zr |
| I1 | the current through the transmission line of the system |
| δ | the phase difference between V1 and vr |
| APFG | active power flow gradients |
| SCP | selected critical points |
| SCP2 | the voltage v12 of OSIV |
| SCP4 | the voltage vr of the receiving end |
| CIV1 | the magnitude of OSIV |
| CIV3 | the phase difference δ |
| Reg.1 | the first regulations mode of OSIV |
| Cond.1 | the first normal operation condition |
| Cond.3 | the third normal operation condition |
| Scen.1 | the first regulation scenarios for CIV3 |
| Scen.3 | the third regulation scenarios for CIV3 |
| dPj/dv12 | the APFG to CIV1 at SCPj |
| dPj/dθ | the APFG to CIV1 at SCPj |
| dPj/dδ | the APFG to CIV1 at SCPj |
| OSIV | output series inserted voltage |
| v12 | the voltage of OSIV |
| vr | the voltage of the receiving end |
| vzr | the voltage drop on the zr |
| xr | the reactance of zr |
| θ | the phase angle of OSIV |
| RFG | power flow gradients |
| RPFG | reactive power flow gradients |
| SCP1 | the voltage of Bus1 |
| SCP3 | the voltage of Bus2 |
| CIVs | characteristic independent variables |
| CIV2 | the phase angle θ of OSIV |
| j | stands for the number of SCP |
| Reg.2 | the second regulations mode of OSIV |
| Cond.2 | the second normal operation condition |
| Cond.4 | the severe operation condition |
| Scen.2 | the second regulation scenarios for CIV3 |
| Scen.4 | the fourth regulation scenarios for CIV3 |
| dQj/dv12 | the RPFG to CIV1 at SCPj |
| dQj/dθ | the RPFG to CIV1 at SCPj |
| dPj/dδ | the RPFG to CIV1 at SCPj |
Appendix A
References
- Gyugyi, L.; Schauder, C.D.; Williams, S.L. The unified power flow controller: A new approach to power transmission control. IEEE Trans. Power Del. 1995, 10, 1085–1097. [Google Scholar] [CrossRef]
- Bulac, C.; Eremia, M.; Balaurescu, R.; Stefanescu, V. Load flow management in the interconnected power systems using UPFC devices. In Proceedings of the IEEE Bologna Power Tech Conference, Bologna, Italy, 23–26 June 2003. [Google Scholar]
- Stefanov, P.C.; Stankovic, A.M. Modeling of UPFC operation under unbalanced conditions with dynamic phasors. IEEE Trans. Power Syst. 2002, 17, 395–403. [Google Scholar] [CrossRef]
- Mete, A.; Mehmet, T. Mathematical modeling and analysis of a unified power flow controller: A comparison of two approaches in power flow studies and effects of UPFC location. Electr. Power Energy Syst. 2007, 29, 617–629. [Google Scholar]
- Shahgholian, G.; Mahdavian, M.; Janghorbani, M.; Eshaghpour, I.; Ganji, E. Analysis and Simulation of UPFC in Electrical Power System for Power Flow Control. In Proceedings of the 2017 14th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology (ECTI-CON), Phuket, Thailand, 27–30 June 2017. [Google Scholar]
- Hamache, A.; Bensidhoum, M.O.; Ouslimani, A. UPFC Power Flow Tracking using Decentralized Discrete-Time Quasi-Sliding Mode Control. In Proceedings of the 2019 8th International Conference on Systems and Control (ICSC), Marrakesh, Morocco, 23–25 October 2019. [Google Scholar]
- Ebeed, M.; Kamel, S.; Yu, J.; Jurado, F. Development of UPFC operating constraints enforcement approach for power flow control. IET Gener. Trans. Distri. 2019, 13, 4579–4591. [Google Scholar] [CrossRef]
- Papic, I. Mathematical analysis of FACTS devices based on a voltage source converter Part 1: Mathematical models. Electr. Power Energy Syst. 2000, 56, 139–148. [Google Scholar] [CrossRef]
- Parvathy, S.; Thampatty, K.S. Dynamic Modelling and Control of UPFC for Power Flow Control. Procedia Technol. 2015, 21, 581–588. [Google Scholar] [CrossRef][Green Version]
- Tomasz, O.; Kazimierz, W. Consideration of Different Operation Modes of UPFC in Power System State Estimation. In Proceedings of the International Conference on Environment and Electrical Engineering, Rome, Italy, 8–11 May 2011. [Google Scholar]
- Nabavi, A.; Iravani, R. Steady State and Dynamic Models of UPFC for Power System Studies. IEEE Trans. Power Syst. 1996, 11, 1937–1943. [Google Scholar] [CrossRef]
- Marcos, P.; Luiz, C. A current based model for load flow studies with UPFC. IEEE Trans. Power Syst. 2013, 28, 677–682. [Google Scholar]
- Alomoush, M.I. Impacts of UPFC on line flows and transmission usage. Electr. Power Syst. Res. 2004, 71, 223–234. [Google Scholar] [CrossRef]
- Wu, X.; Zhou, Z.; Liu, G.; Qi, W.; Xie, Z. Preventive security-constrained optimal power flow considering UPFC control modes. Energies 2017, 10, 1199. [Google Scholar] [CrossRef]
- Abbas, R.; Mahmud, F.; Muhammad, O. Optimal unified power flow controller application to enhance total transfer capability. IET Gener. Trans. Distr. 2015, 9, 358–368. [Google Scholar]
- Hasan, R.; Salman, S.; Saleem, N. Control system design of UPFC for optimal power flow control. In Proceedings of the International Conference on Open Source Systems and Technologies, Lahore, Pakistan, 16–18 December 2019. [Google Scholar]
- Yuan, J.; Liu, L.; Fei, W. Hybrid electromagnetic unified power flow controller: A novel flexible and effective approach to control power flow. IEEE Trans. Power Deliv. 2018, 33, 2061–2069. [Google Scholar] [CrossRef]
- Monteiro, J.; Pinto, S.; Martin, A.D. A new real time Lyapunov based controller for power quality improvement in unified power flow controllers using direct matrix converters. Energies 2017, 10, 779. [Google Scholar] [CrossRef]
- Ilango, G.S.; Nagamani, C.; Sai, A.V.; Aravindan, D. Control algorithms for control of real and reactive power flows and power oscillation damping using UPFC. Electr. Power Syst. Res. 2009, 79, 595–605. [Google Scholar] [CrossRef]
- Wilson, D.G.; Robinett, R.D. Nonlinear power flow control applications to conventional generator swing equations subject to variable generation. In Proceedings of the International Symposium on Power Electronics, Pisa, Italy, 14–16 June 2010. [Google Scholar]
- Zahid, M.; Chen, J.; Li, Y.; Duan, X.; Lei, Q.; Bo, W.; Mohy, G.; Waqar, A. New approach for optimal location and parameters setting of UPFC for enhancing power systems stability under contingency analysis. Energies 2017, 10, 1738. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z.; Xiao, L. Comprehensive power flow analyses and novel feedforward coordination control strategy for MMC-Based UPFC. Energies 2019, 12, 824. [Google Scholar] [CrossRef]


| Conditions | Voltage Vr | Phase Difference δ | Magnitude of v12 | Phase Angle θ |
|---|---|---|---|---|
| Cond.1 | 1 | −π/8 | 0 p.u. to 4.0 p.u. | −π to π |
| Cond.2 | 1 | −π/24 | ||
| Cond.3 | 0.9 | −π/8 | ||
| Cond.4 | 0.82 | −π/2 |
| Scenarios | phase Angle θ | Magnitude of v12 | Phase Difference δ |
|---|---|---|---|
| Scen.1 | −π/3 | 0 p.u. to 4.0 p.u. | −π to π |
| Scen.2 | −π/8 | ||
| Scen.3 | π/8 | ||
| Scen.4 | π/3 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Yang, J.; Xu, Z.; Zhang, Z.; Song, P. Regulation Principles of Power Flow Gradients to Multiple Characteristic Independent Variables in UPFC Embedded Power System. Appl. Sci. 2020, 10, 1720. https://doi.org/10.3390/app10051720
Liu J, Yang J, Xu Z, Zhang Z, Song P. Regulation Principles of Power Flow Gradients to Multiple Characteristic Independent Variables in UPFC Embedded Power System. Applied Sciences. 2020; 10(5):1720. https://doi.org/10.3390/app10051720
Chicago/Turabian StyleLiu, Jinlian, Jian Yang, Zheng Xu, Zheren Zhang, and Pengcheng Song. 2020. "Regulation Principles of Power Flow Gradients to Multiple Characteristic Independent Variables in UPFC Embedded Power System" Applied Sciences 10, no. 5: 1720. https://doi.org/10.3390/app10051720
APA StyleLiu, J., Yang, J., Xu, Z., Zhang, Z., & Song, P. (2020). Regulation Principles of Power Flow Gradients to Multiple Characteristic Independent Variables in UPFC Embedded Power System. Applied Sciences, 10(5), 1720. https://doi.org/10.3390/app10051720







