Aerodynamic Characteristics of Different Airfoils under Varied Turbulence Intensities at Low Reynolds Numbers
Abstract
:Featured Application
Abstract
1. Introduction
2. Numerical Approach
2.1. Estimation Method of Turbulence Intensity
2.2. Transition Model
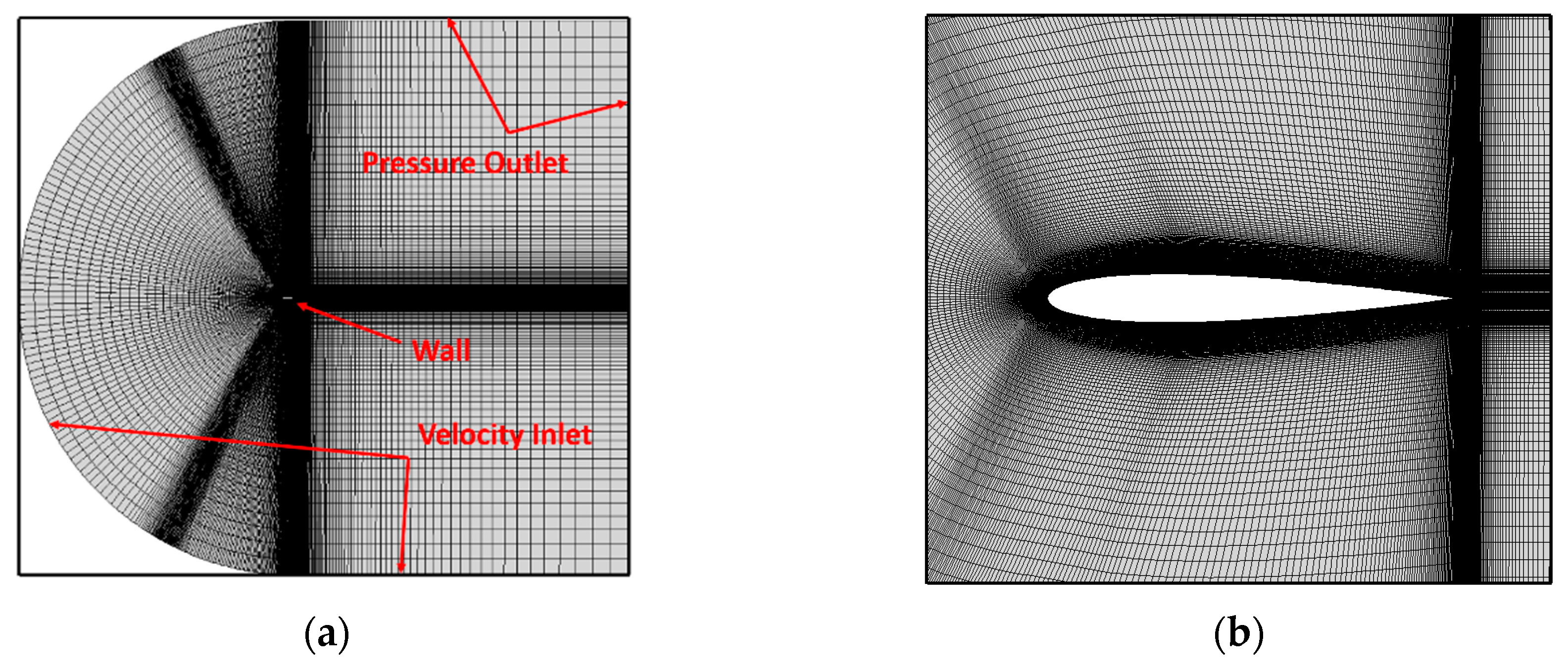
3. Validation of Numerical Simulation Method
3.1. Validation of Pressure Distribution
3.2. Validation of Aerodynamic Force
4. Effect of Turbulence Intensity on Airfoil at Different Reynolds Numbers
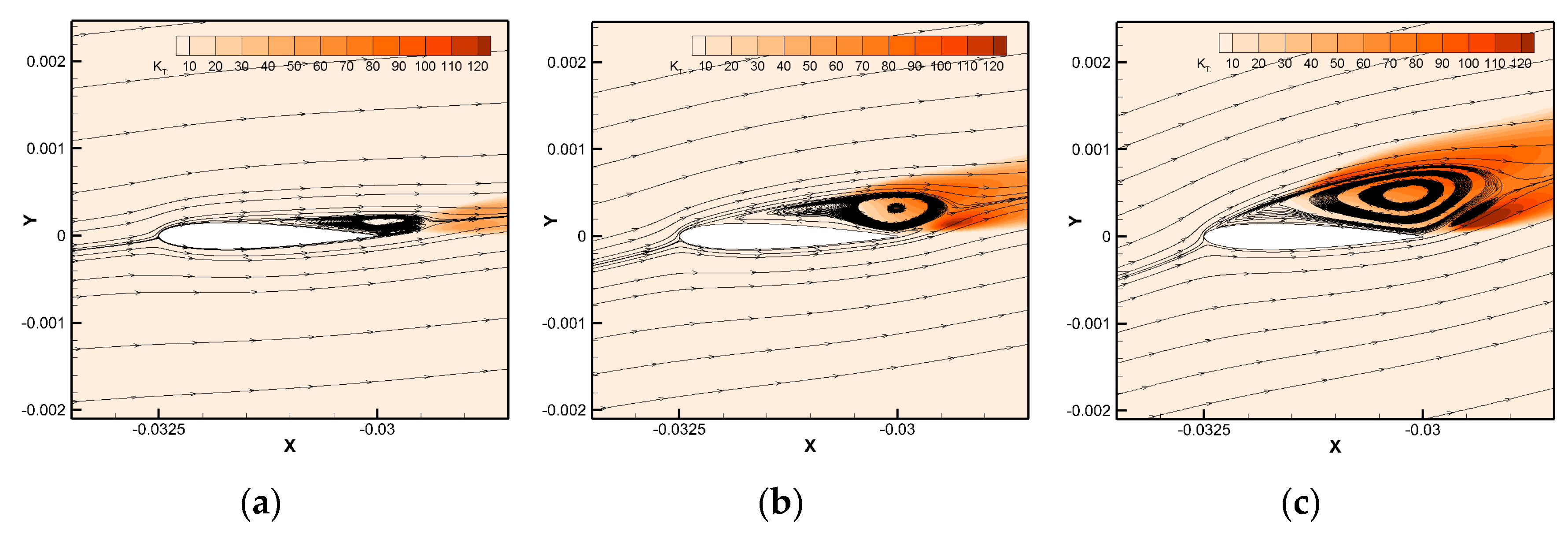
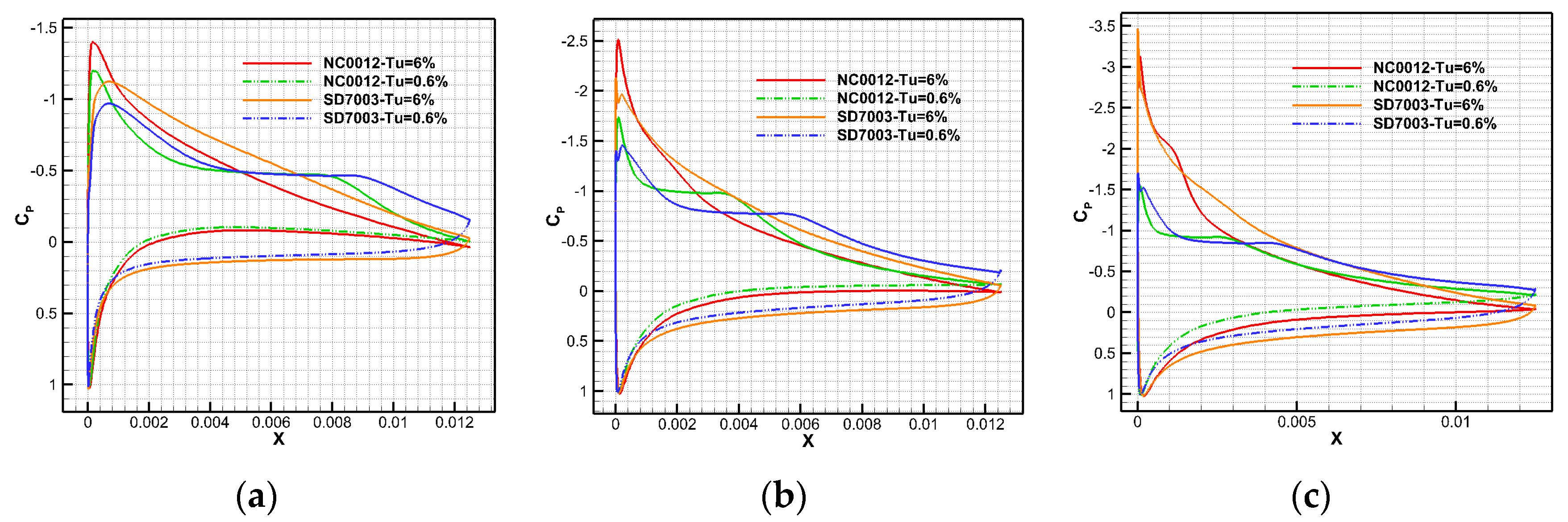
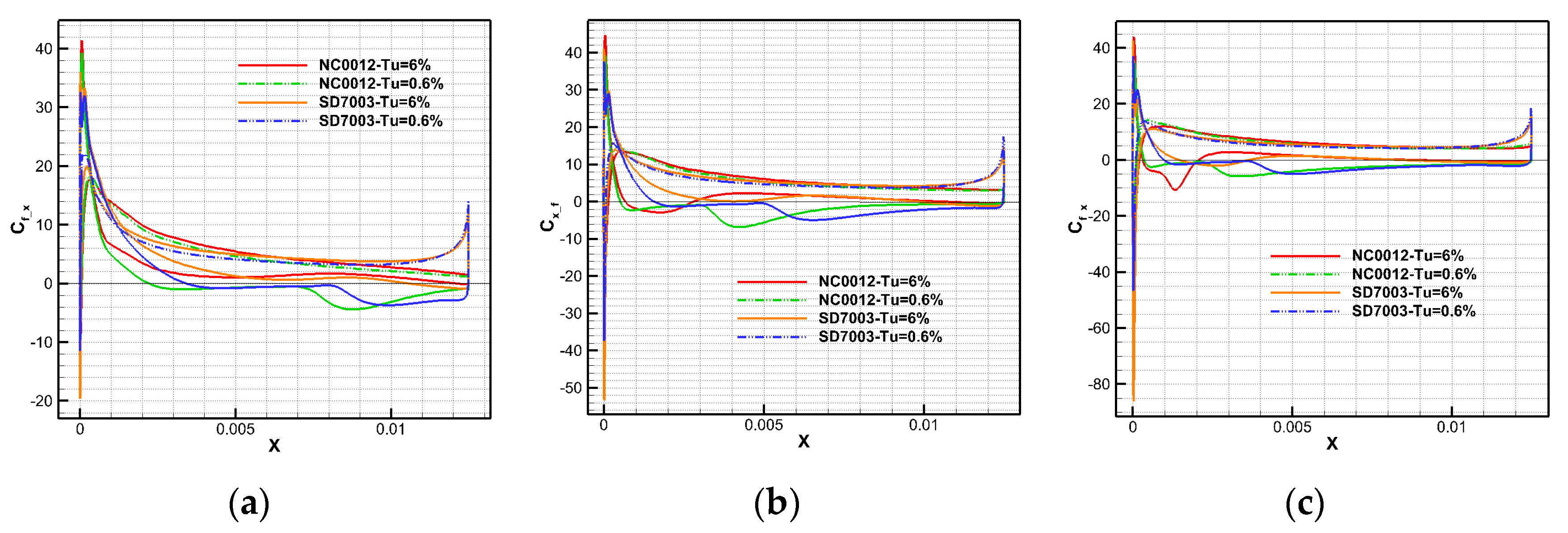
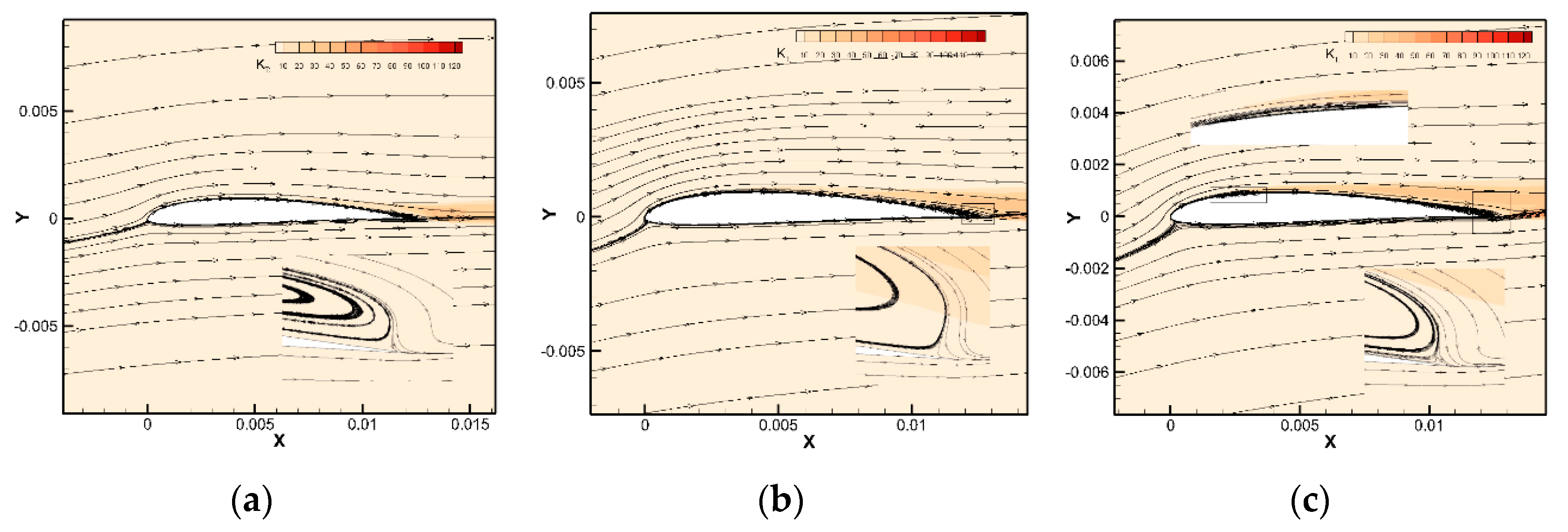
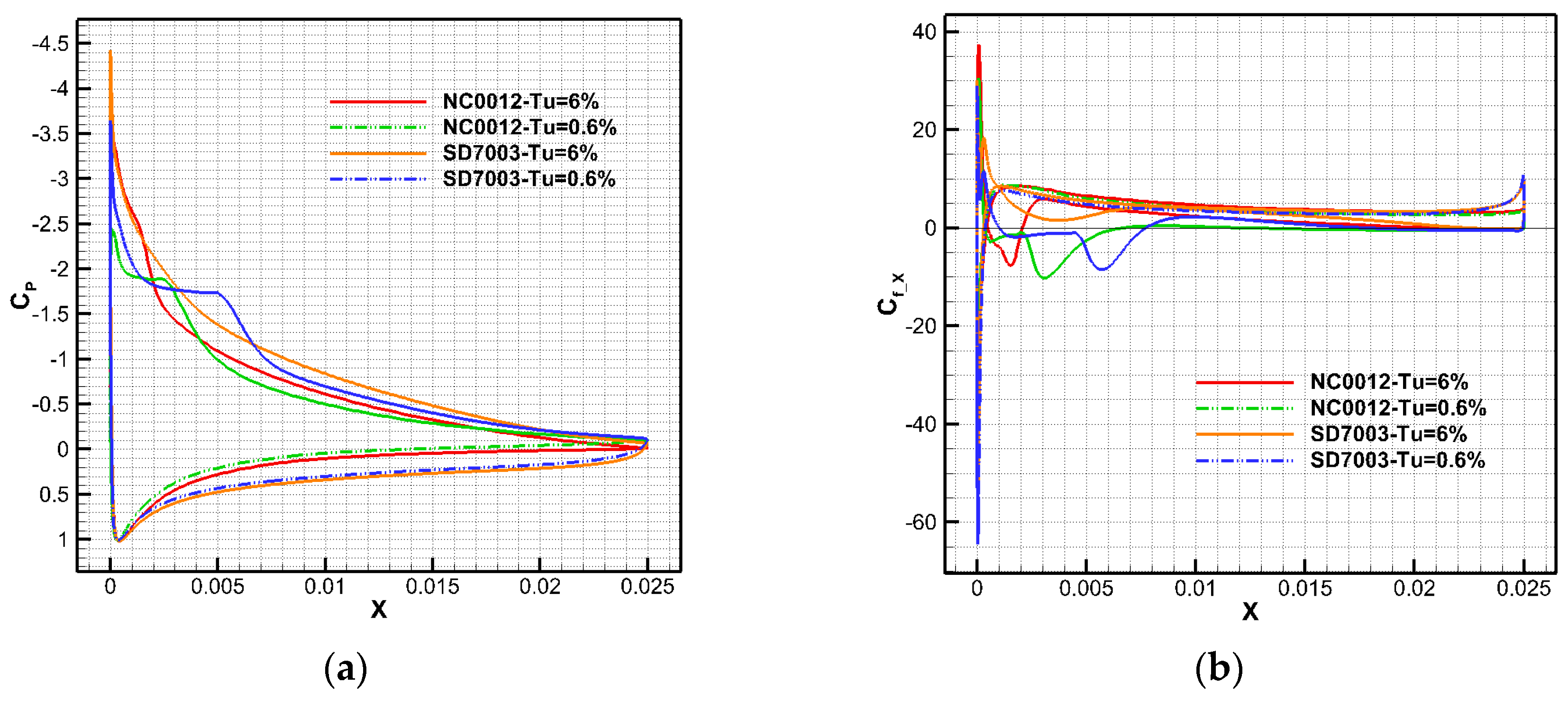
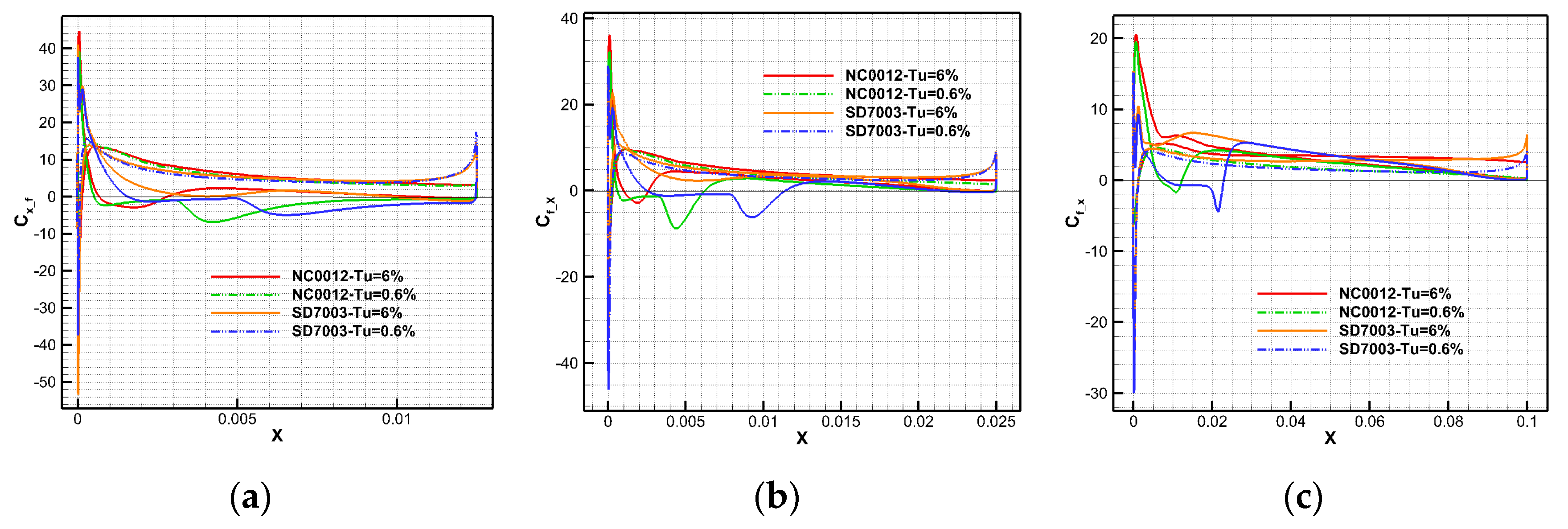
4.1. The Influence of Turbulence Intensity Upon Airfoils at Re1 = 26,500
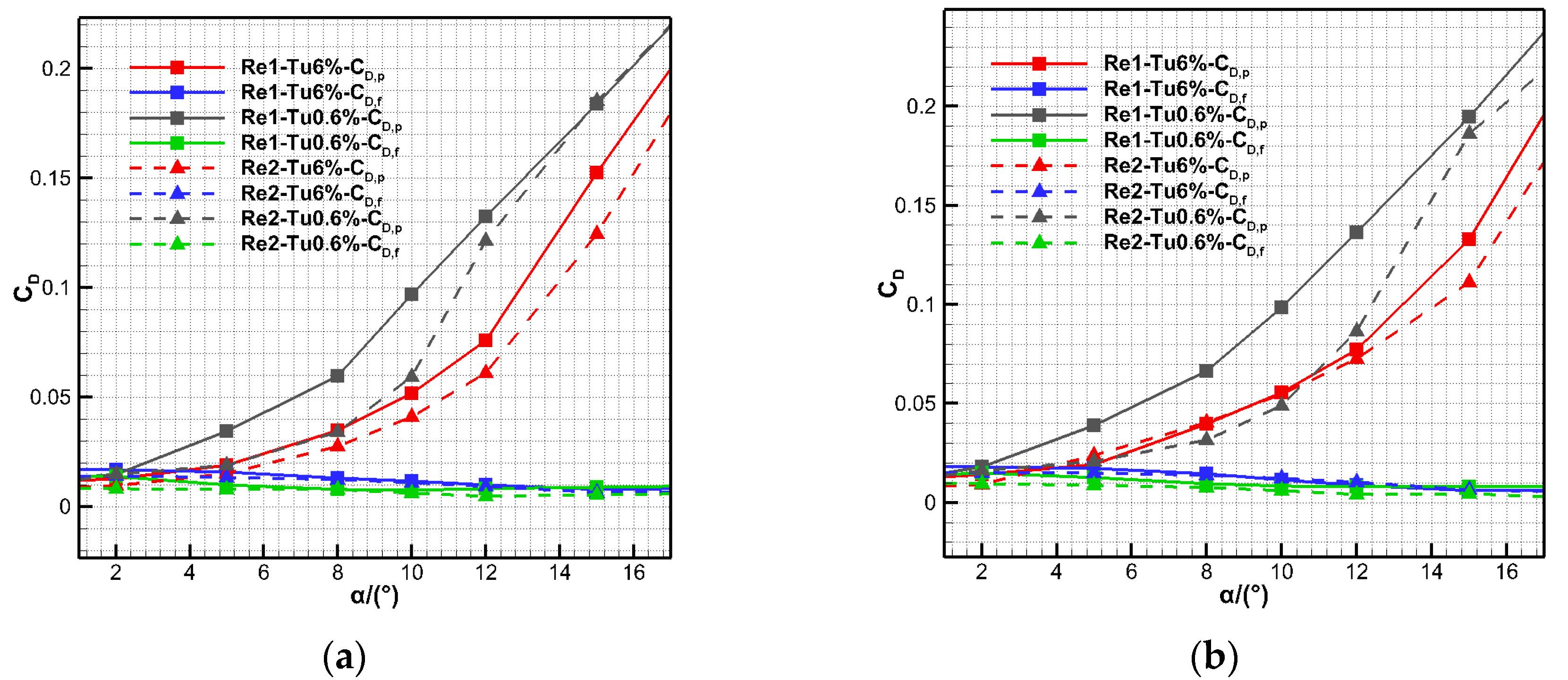
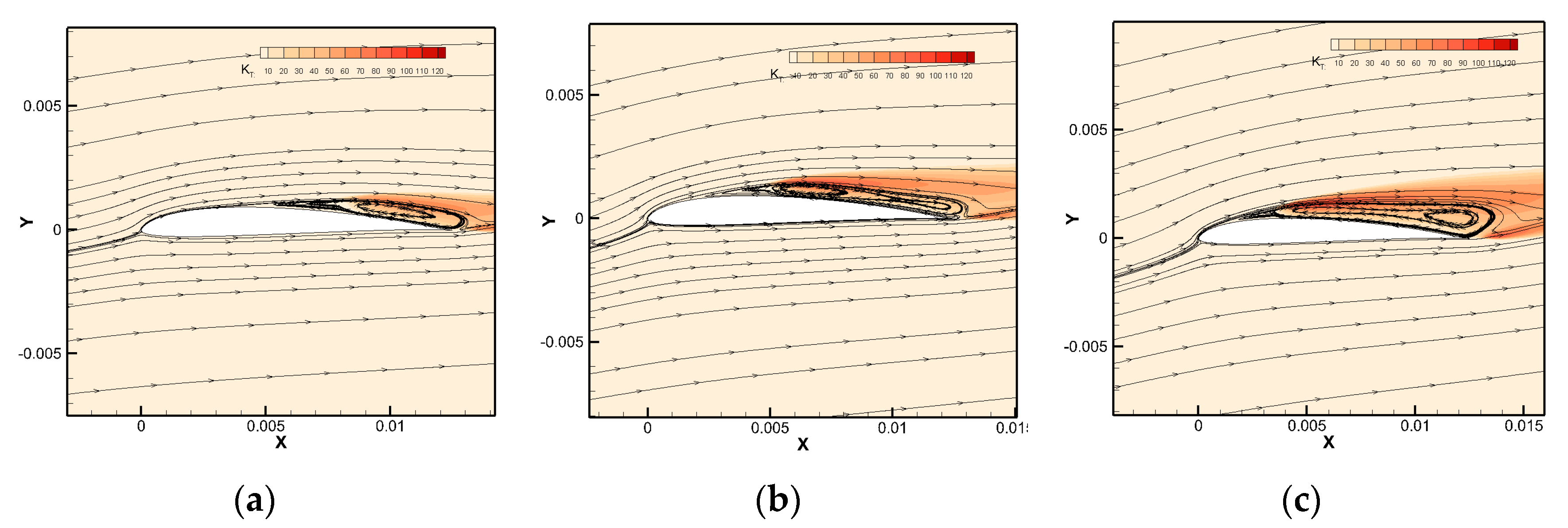
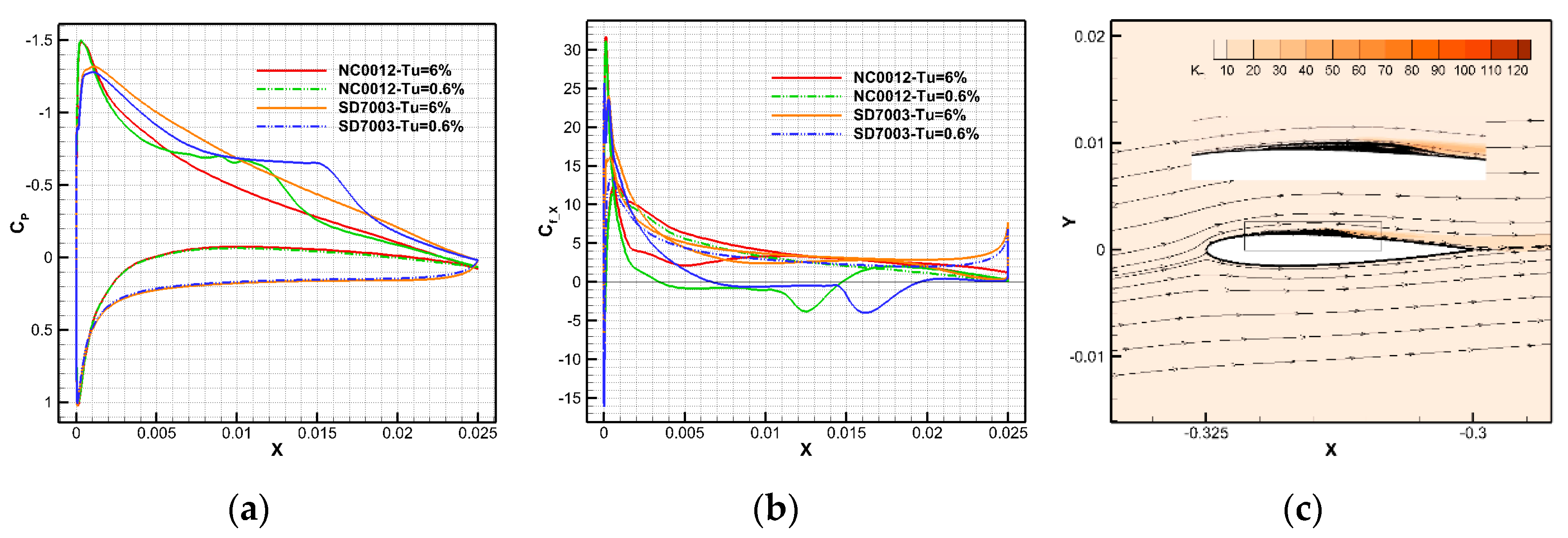
4.2. The Influence of Reynolds Number on the Airfoil
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| CD | Coefficient of drag |
| CL | Coefficient of lift |
| CP | Coefficient of pressure |
| CD,p | Coefficient of pressure drag |
| CD,f | Coefficient of friction drag |
| Cf,X | Coefficient of friction in X direction |
| Tu | Turbulence intensity |
| l | Turbulence length scale |
| RT | Ratio of turbulence viscosity to laminar viscosity |
| Tuinlet | Turbulence intensity at the inlet of wind tunnel |
| ε | Turbulence dissipation rate |
| k | Turbulent kinetic energy |
| γ | Intermittence factor |
| Rev | Vorticity Reynolds number |
| Sr | Strouhal number |
| d1 | First layer grid element to wall distance |
| TeDP | Turboelectric distributed propulsion |
| URANS | Unsteady Reynolds-averaged Navier-Stokes |
| Transition momentum thickness Reynolds number | |
| LSB | Laminar separation bubble |
| FSTI | Freestream turbulence intensity |
| SST | Shear stress transport |
References
- Kong, X.; Zhang, Z. Review of electric power system of distributed electric propulsion aircraft. Acta Aeronaut. Astronaut. Sin. 2018, 39, 51–67. [Google Scholar]
- Nalianda, D.; Singh, R. Turbo-electric distributed propulsion—Opportunities, benefits and challenges. Aircr. Eng. Aerosp. Technol. 2014, 86, 543–549. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, X.; Zhou, Z. Distributed electric propulsion slipstream aerodynamic effects at low Reynolds number. Acta Aeronaut. Astronaut. Sin. 2016, 37, 2669–2678. [Google Scholar]
- Lee, B.J.; Liou, M.F.; Kim, H. Design of distributed mail-slot propulsion system on a hybrid wingbody air-craft, AIAA-2018-3954. In Proceedings of the 2018 Applied Aerodynamics Conference, Atlanta, GA, USA, 25–29 June 2018. [Google Scholar]
- Gibson, A.; Green, M.; Schiltgen, B. TurboElectric Distributed Propulsion (TeDP) Design, Performance, Bene-fits, Concerns and Considerations for both Conventional Non-Superconducting and Cryogenically Cooled Super-conducting Machines in a Propulsion System Architecture for Conventional Tube-and-Wing Configuration; ISABE: Busan, Korea, 2013. [Google Scholar]
- Winslow, J.; Otsuka, H. Basic understanding of airfoil characteristics at low reynolds numbers (104–105). J. Aircr. 2017, 55, 1050–1061. [Google Scholar] [CrossRef]
- Mueller, T.J.; Pohlen, L.J.; Conigliaro, P.E.; Jansen, B.J. The influence of freestream disturbances on low reynolds number airfoil experiments. Exp. Fluids 1983, 1, 3–14. [Google Scholar] [CrossRef]
- Boiko, A.V.; Grek, G.R.; Dovgal, A.V.; Kozlov, V.V.; Dowling, D.R. Origin of turbulence in near-wall flows. Appl. Mech. Rev. 2003, 56, B13. [Google Scholar] [CrossRef]
- Argyropoulos, C.D.; Markatos, N.C. Recent advances on the numerical modelling of turbulent flows. Appl. Math. Model. 2015, 39, 693–732. [Google Scholar] [CrossRef]
- Lengani, D.; Simoni, D. Recognition of coherent structures in the boundary layer of a low-pressure-turbine blade for different freestream turbulence intensity levels. Int. J. Heat Fluid Flow 2015, 54, 1–13. [Google Scholar] [CrossRef]
- Porté-Agel, F.; Wu, Y.T.; Lu, H. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms. J. Wind Eng. Ind. Aerodyn. 2011, 99, 154–168. [Google Scholar] [CrossRef]
- Gramespacher, C.; Albiez, H. The generation of grid turbulence with continuously adjustable intensity and length scales. Exp. Fluids 2019, 60, 85. [Google Scholar] [CrossRef]
- Grzelak, J. Influence of freestream turbulence intensity on bypass transition parameters in a boundary layer. J. Fluids Eng. 2017, 139, 051201. [Google Scholar] [CrossRef]
- Hancock, P.E.; Bradshaw, P. The effect of freestream turbulence on turbine boundary layers. J. Fluids Eng. 1983, 105, 284–294. [Google Scholar] [CrossRef]
- Hillier, R.; Cherry, N.J. The effects of stream turbulence on separation bubbles. J. Wind Eng. Ind. Aerodyn. 1981, 8, 49–58. [Google Scholar] [CrossRef]
- Fransson, J.H.M.; Matsubara, M. Transition induced by free-stream turbulence. J. Fluids Mech. 2005, 527, 1–25. [Google Scholar] [CrossRef]
- Jacobs, R.G.; Durbin, P. Simulations of bypass transition. J. Fluids Mech. 2001, 428, 185–212. [Google Scholar] [CrossRef]
- Marxen, O.; Lang, M.; Rist, U. A Combined experimental/numerical study of unsteady phenomena in a laminar separation bubble. Flow Turbul. Combust. 2003, 71, 133–146. [Google Scholar] [CrossRef]
- McAuliffe, B.R.; Yaras, M.I. Transition mechanisms in separation bubbles under low- and elevated-freestream turbulence. J. Turbomach. 2010, 132, 011004. [Google Scholar] [CrossRef]
- Cao, N.; Ting, D.S. The Performance of a high-lift airfoil in turbulent wind. Wind Eng. 2011, 35, 179–196. [Google Scholar] [CrossRef]
- Mistf, P. Mean loading effects on the surface pressure fluctuations on an airfoil in turbulence: AIAA-2001-2211. In Proceedings of the 7th AIAA/CEAS Aeroacoustics Conference and Exhibit, AIAA, Maastricht, The Netherlands, 28–30 May 2001. [Google Scholar]
- Istvan, M. Turbulence intensity effects on laminar separation bubbles formed over an airfoil. AIAA J. 2018, 56, 335–1347. [Google Scholar] [CrossRef]
- Istvan, M.S.; Yarusevych, S. Effects of free-stream turbulence intensity on transition in a laminar separation bubble formed over an airfoil. Exp. Fluids 2018, 59, 52. [Google Scholar] [CrossRef]
- Bryan, D.; McGranahan, M.; Selig, S. Surface oil flow measurements on several airfoils at low reynolds numbers. AIAA-2003-4067. In Proceedings of the 21st AIAA Applied Aerodynamics Conference, Orlando, FL, USA, 23–26 June 2003. [Google Scholar]
- Wang, S.; Mi, J. Effect of large turbulence intensity on airfoil load and flow. Acta Aeronaut. Astronaut. Sin. 2011, 32, 41–48. [Google Scholar]
- Li, S.; Wang, S. Effect of turbulence intensity on airfoil flow: Numerical simulations and experimental measurements. Appl. Math. Mech. 2011, 32, 964–972. [Google Scholar] [CrossRef]
- Arunvinthan, S.; Nadaraja, S. Aerodynamic characteristics of unsymmetrical aerofoil at various turbulence intensities. Chin. J. Aeronaut. 2019, 32, 2395–2407. [Google Scholar] [CrossRef]
- Simoni, D.; Lengani, D. Inspection of the dynamic properties of laminar separation bubbles: Free-stream turbulence intensity effects for different Reynolds numbers. Exp. Fluids 2017, 58, 66. [Google Scholar] [CrossRef]
- Chen, Y. On the Transition Prediction for Aeronautical Application; Northwestern Polytechnical University. Press: Xi’an, China, 2008; Volume 23–35, pp. 44–46. [Google Scholar]
- Menter, F.R.; Langtry, R.B.; Likki, S.R.; Suzen, Y.B.; Huang, P.G.; Völker, S. A correlation based transition model using local variables Part 1—Model formulation: ASME 2004-GT-53452. In Proceedings of the Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar]
- Langtry, R.B.; Menter, F.R.; Likki, S.R. A Correlation based transition model using local variables Part 2-Test cases and industrial applications, ASME 2004-GT-53434. In Proceedings of the Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004. [Google Scholar]
- Mistf, M.T.; Obayashi, S. Application of local correlation-based transition model to flows around wings, AIAA-2006-918. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reston, VA, USA, 9–12 January 2006. [Google Scholar]
- Jang, D.S.; Jetli, R. Comparison of the PISO, SIMPLER, and SIMPLEC algorithms for the treatment of the pressure-velocity coupling in steady flow promblems. Numer. Heat Transf. 1986, 10, 209–228. [Google Scholar] [CrossRef]
- Shen, W.; Michelsen, J.A. An improved SIMPLEC method on collocated grids for steady and unsteady flow computations. Numer. Heat Transf. 2003, 43, 221–239. [Google Scholar] [CrossRef]
- Wahidi, R.; Bridges, D. Experimental Investigation of the Boundary Layer and Pressure Measurements on Airfoils with Laminar Separation Bubbles. AIAA-2009-4278. In Proceedings of the 39th AIAA Fluid Dynamics Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar]
- Counsil, J.N.N.; Goni Boulama, K. Validating the URANS shear stress transport γ −Reθ model for low-Reynolds-number external aerodynamics. Int. J. Numer. Meth. Fluids 2012, 69, 1411–1432. [Google Scholar] [CrossRef]
- Selig, M.S.; Guglielmo, J.J.; Broeren, A.P.; Giguere, P. Summary of Low-Speed Airfoil Data; SoarTech Publications: Virginia Beach, VA, USA, 1995; Volume 1. [Google Scholar]
- Zhang, Y.; Zhao, K. The influence of Reynolds number on boundary layer development and stall characteristics of airfoil. Adv. Aeronaut. Sci. Eng. 2019, 10, 319–329. [Google Scholar]
- Mayle, R.E. The role of laminar-turbulent transition in gas turbine engines. ASME J. Turbomach. 1991, 113, 509–537. [Google Scholar] [CrossRef]
- Carmichael, B.H. Low Reynolds Number Airfoil Survey: NASA CR 1165803; NASA: Washington, DC, USA, 1981. [Google Scholar]

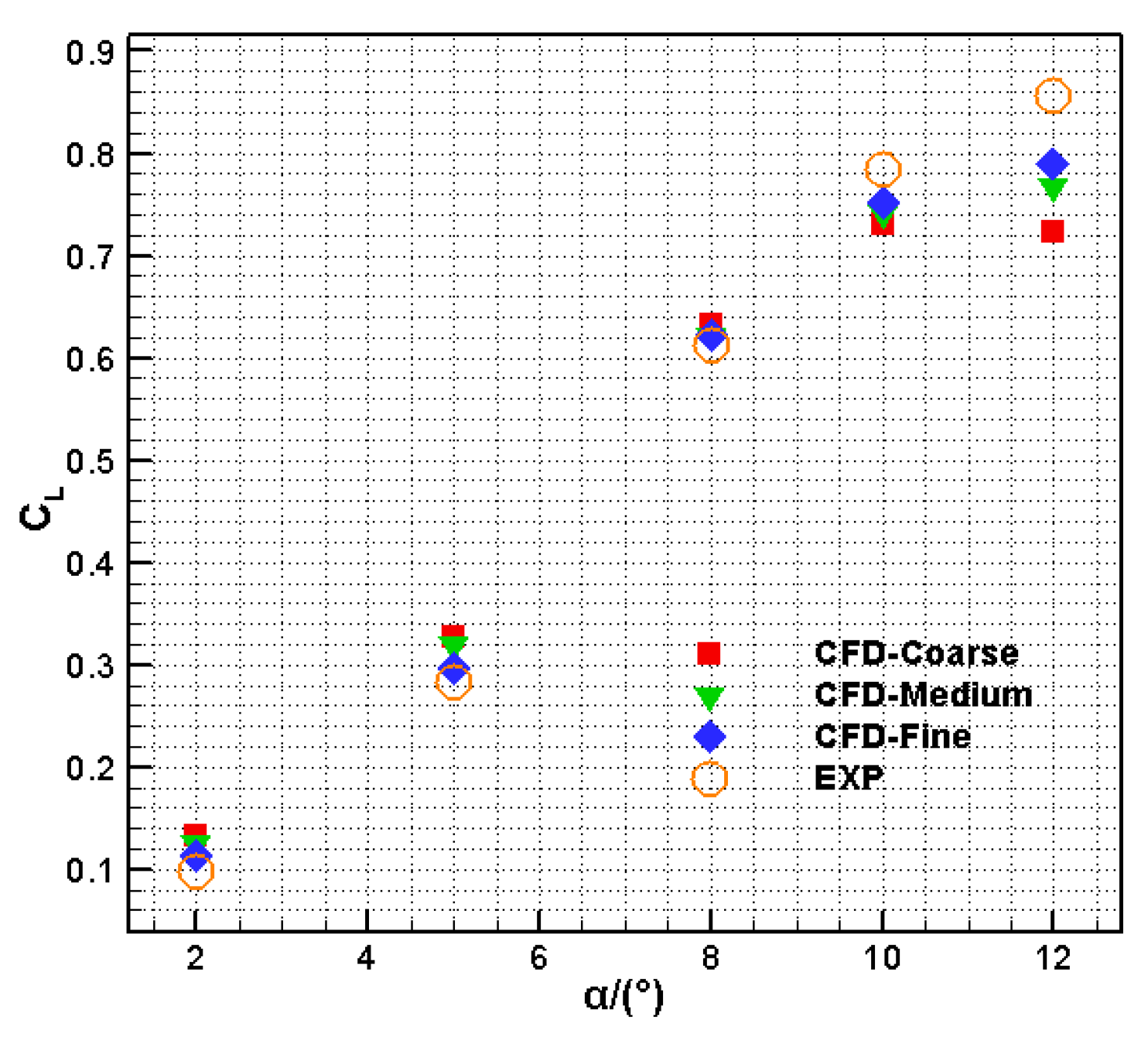








| AOA | Coarse | Medium | Fine | Exp | R |
|---|---|---|---|---|---|
| 2 | 0.1324 | 0.1256 | 0.1123 | 0.098 | 0.146 |
| 5 | 0.3276 | 0.3207 | 0.2950 | 0.282 | 0.046 |
| 8 | 0.6323 | 0.6218 | 0.6224 | 0.612 | 0.017 |
| 10 | 0.7314 | 0.7421 | 0.7507 | 0.785 | 0.044 |
| 12 | 0.7231 | 0.7748 | 0.7893 | 0.856 | 0.078 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Zhou, Z.; Wang, K.; Li, X. Aerodynamic Characteristics of Different Airfoils under Varied Turbulence Intensities at Low Reynolds Numbers. Appl. Sci. 2020, 10, 1706. https://doi.org/10.3390/app10051706
Zhang Y, Zhou Z, Wang K, Li X. Aerodynamic Characteristics of Different Airfoils under Varied Turbulence Intensities at Low Reynolds Numbers. Applied Sciences. 2020; 10(5):1706. https://doi.org/10.3390/app10051706
Chicago/Turabian StyleZhang, Yang, Zhou Zhou, Kelei Wang, and Xu Li. 2020. "Aerodynamic Characteristics of Different Airfoils under Varied Turbulence Intensities at Low Reynolds Numbers" Applied Sciences 10, no. 5: 1706. https://doi.org/10.3390/app10051706
APA StyleZhang, Y., Zhou, Z., Wang, K., & Li, X. (2020). Aerodynamic Characteristics of Different Airfoils under Varied Turbulence Intensities at Low Reynolds Numbers. Applied Sciences, 10(5), 1706. https://doi.org/10.3390/app10051706






