3.1. Waveform Matching Extension
In the waveform matching extension, we first look for all available similar waveforms, then pick out the best matching waveform within them. Last, we connect the waveband before/after the best matching waveform to both left and right ends of the raw waveform to finish the task of boundary processing.
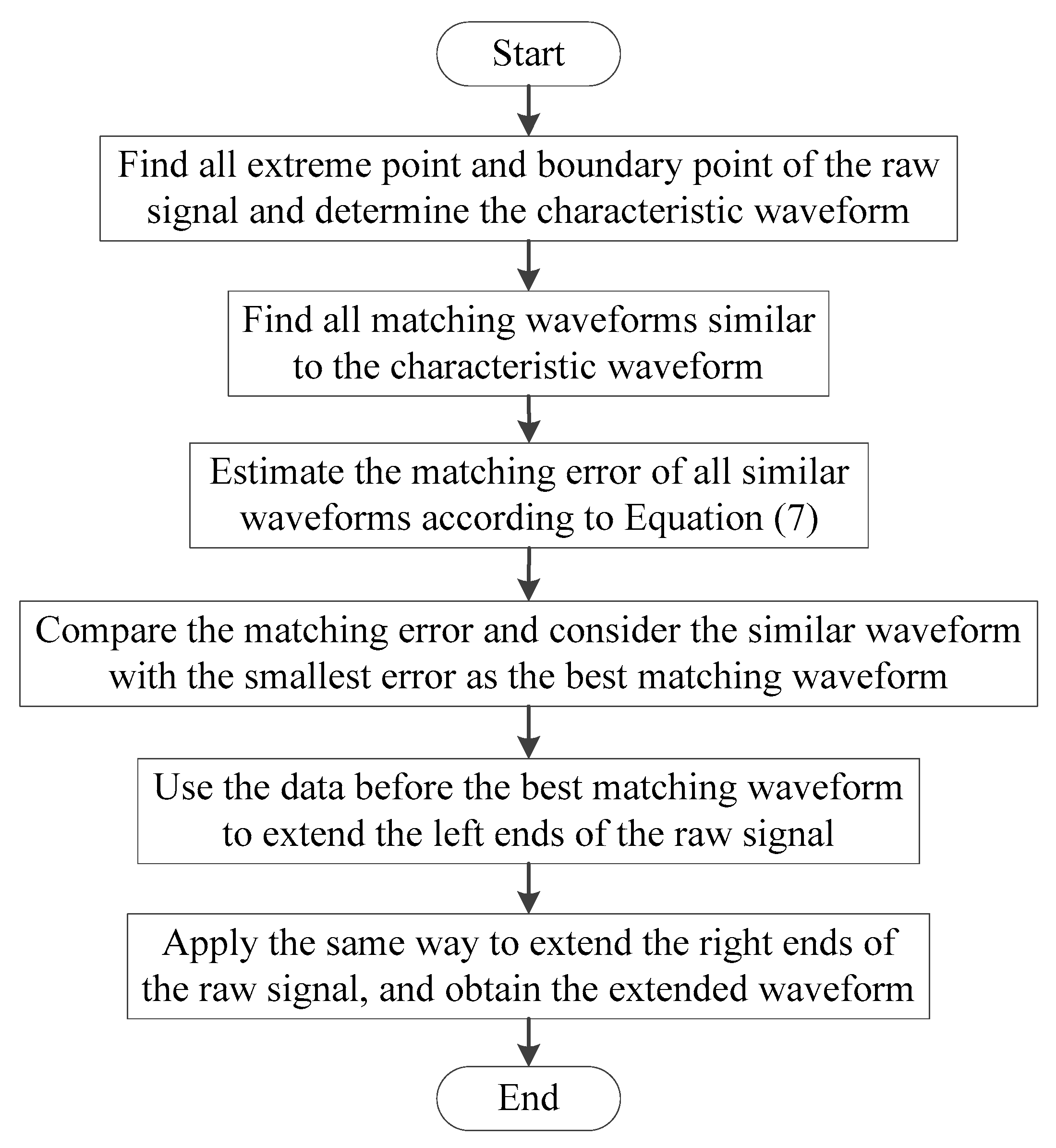
Figure 1 shows the flowchart of the waveform matching extension. For one compound waveform
x(
t), the waveform matching extension procedure is described below [
56].
(1) Find all extreme points and boundary points of the original signal
x(
t) through the peak searching method, and determine the characteristic waveform. Take
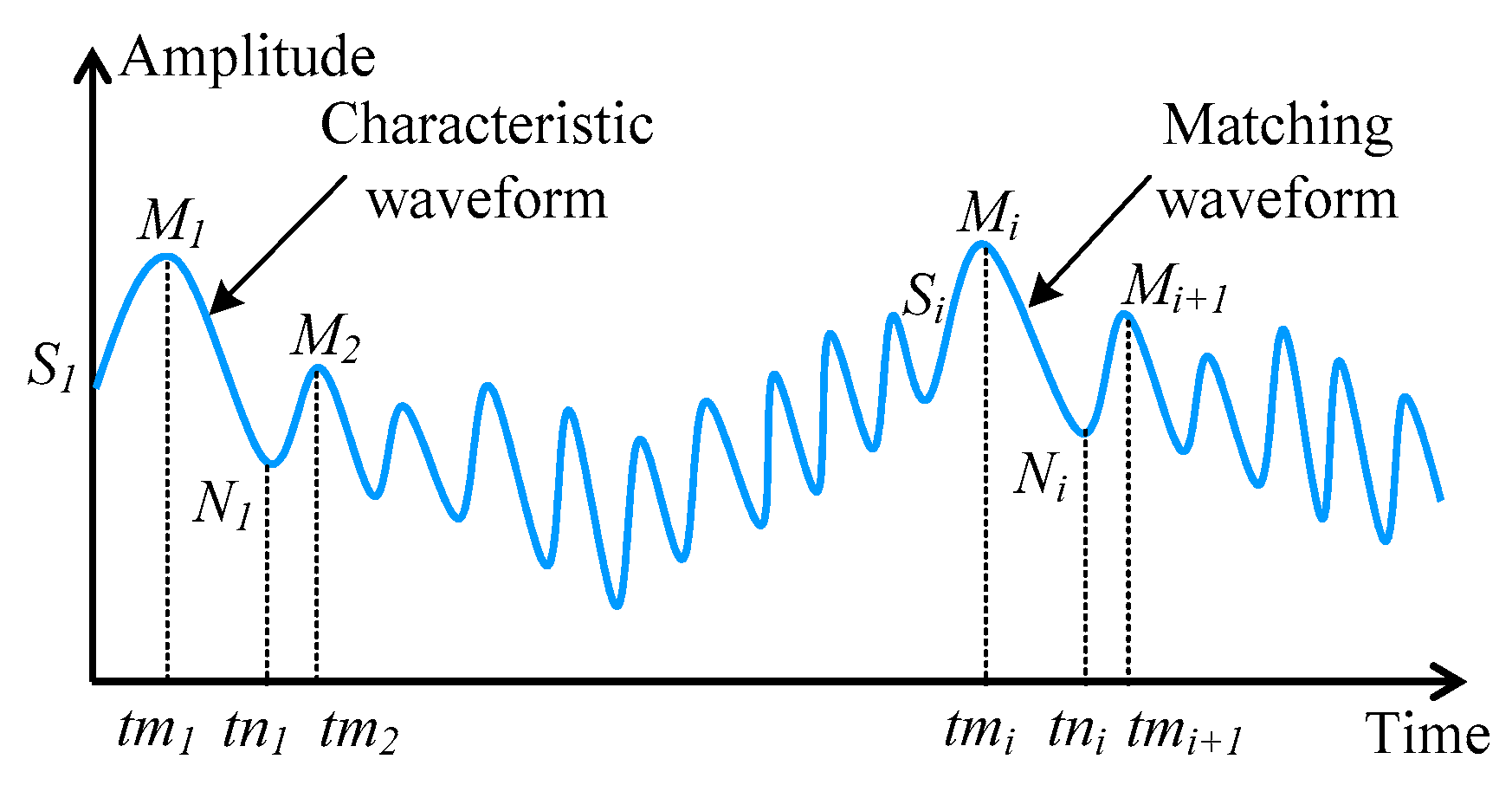
Figure 2 for an example,
is the maximum value of
x(
t), corresponding to the time
,
is the minimum value of
x(
t), corresponding to the time
, and
is the left boundary point of the signal
x(
t). We regard the triangular waveform
of the original signal
x(
t) as the characteristic waveform to search the optimum matching waveform.
(2) Seek for all matching waveforms resembling the characteristic waveform
on the basis of the time
corresponding to the starting value
of the matching waveforms, where the time
of the horizontal axis is achieved by the linear interpolation, which is expressed as:
(3) Estimate the matching error generated in searching all similar waveforms according to the following Equation (7):
where
represents the trend term of the similar waveforms, which can reveal the relative extremum position of all similar waveforms.
(4) Compare the matching error, determine the smallest error, and consider the similar waveform containing the smallest error as the best matching waveform.
(5) Use the data before the best matching waveform to extend the left ends of the raw waveform x(t).
(6) Apply the same way to extend the right ends of the raw waveform x(t), and finally obtain the extended waveform. This indicates that the waveform matching extension procedure of the original signal x(t) is finished in this stage. That is, the left and right boundaries of the original signal x(t) have been processed thoroughly.
Here, two representative examples for a signal with an abrupt change are utilized to describe intuitively the procedure of waveform matching extension. Without loss of generality, the number of data points extended in both left and right ends are selected as 100 points.
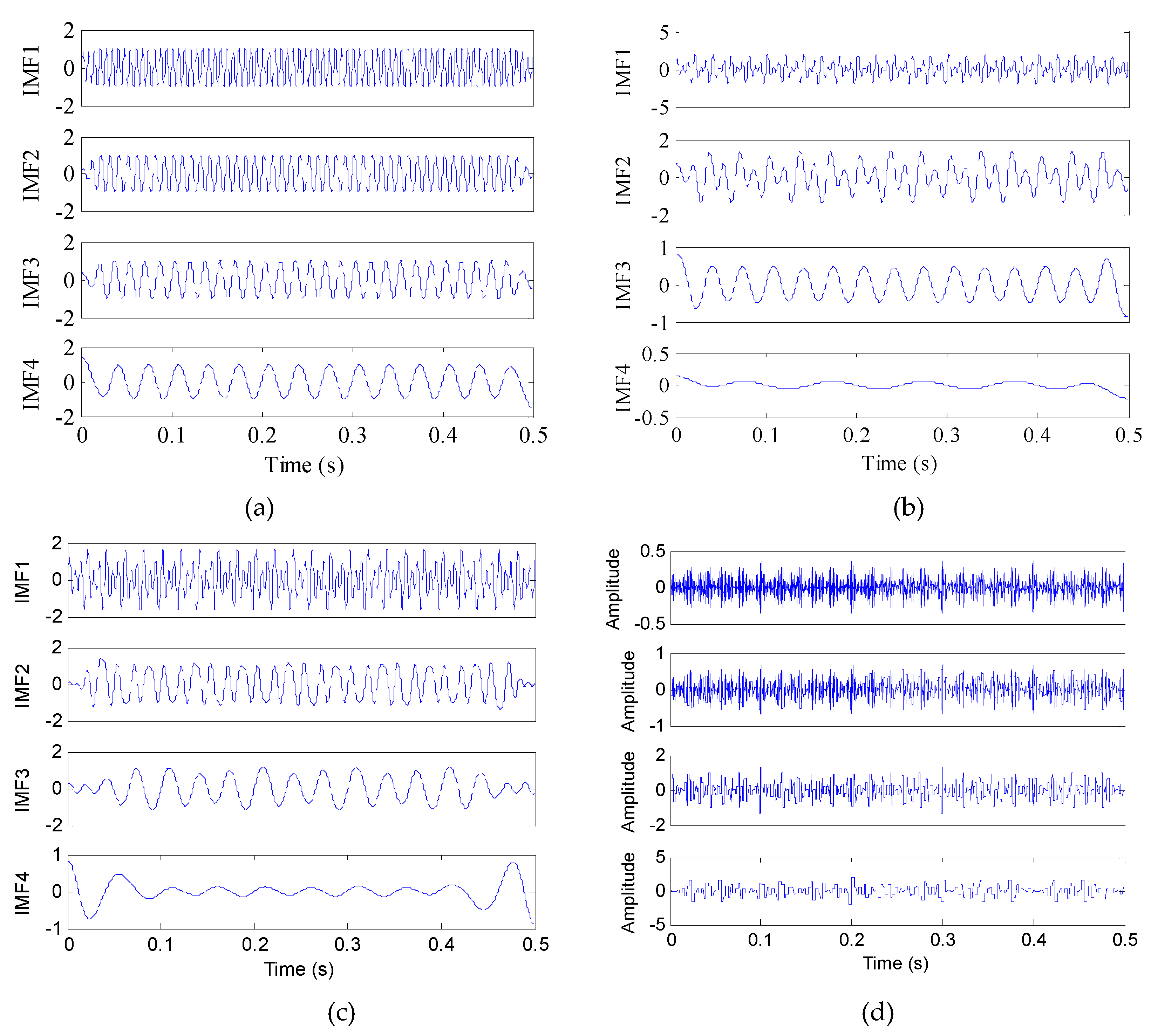
Figure 3a,b shows the processing results achieved when applying the waveform matching extension for a cycle shock pulse signal and a modulated compound signal, respectively. Obviously, the waveform extended in both the left and right ends is in line with the variation trend of the raw signal, which indicates that the waveform matching extension is feasible in analyzing the modulated compound signal.
3.2. Parameter Optimization of VMD Using GWO
Two important variables (i.e., the penalty factor
and mode number
K) are required to define in advance when we employ VMD to a process complex compound signal. Some previous studies have shown that the two variables (
and
K) have a great influence on the decomposition performance of VMD. On the one hand, the bigger
represents the smaller bandwidth of modes. Otherwise, the smaller
represents the greater bandwidth of modes. On the other hand, if the mode number
K is too big, it easily leads to the over decomposition phenomenon (i.e., information redundancy), while this will cause the under-decomposition phenomenon (i.e., information loss) when the mode number
K is too small. Hence, how to pick out the appropriate variables (
,
K), is a challenge when applying VMD to deal with complex compound signals. To address this issue, a new nature-inspired algorithm called GWO is introduced to determine and select automatically the combination parameters (
,
K) of VMD in this subsection due to its excellent global optimization performance. Obviously, the objective function should be constructed when we use GWO to optimize the parameters of VMD. At present, there are many indicators (e.g., smoothness index, entropy, sparseness, kurtosis, and correlation coefficient) in the analysis of the mechanical vibration signal, but it is not optimal to use any of their single indicators to measure vibration signal characteristics. This indicates that the combination of two or more of their single indicators is valuable for practical vibration detection. Zhang et al. [
57] presented a new combination index named weighted kurtosis (WK) as the objective function of their method to optimize the key parameters of VMD, but the proposed weighted kurtosis does not consider some abnormal impacts (i.e., the outlier) with disperse distributions. Hence, to solve this problem, a comprehensive evaluation indicator named weighted sparseness kurtosis (WSK) is formulated in this paper to work as the objective function of the parameter optimization process of VMD, which is defined by:
where
S is the sparseness of the signal
x(
n),
N is the length of the signal
x(
n),
represents the Pearson correlation coefficient between two signals (i.e.,
x and
y) and satisfies
, and
denotes the expectation operator. This indicates that the correlation coefficient
amounts to the weight of the sparseness kurtosis indicator. That is, Equation (8) is reputed essentially as the weighted sparseness kurtosis indicator in this paper. Note that in Equation (8) the sparseness is a statistical indicator reflecting the amplitude distribution of the signal, especially for an abnormal impact amplitude with discrete distribution, while kurtosis is very sensitive to the periodic impulse series of vibration signals. Besides, the correlation coefficient can measure the similarity between two vibration signals.
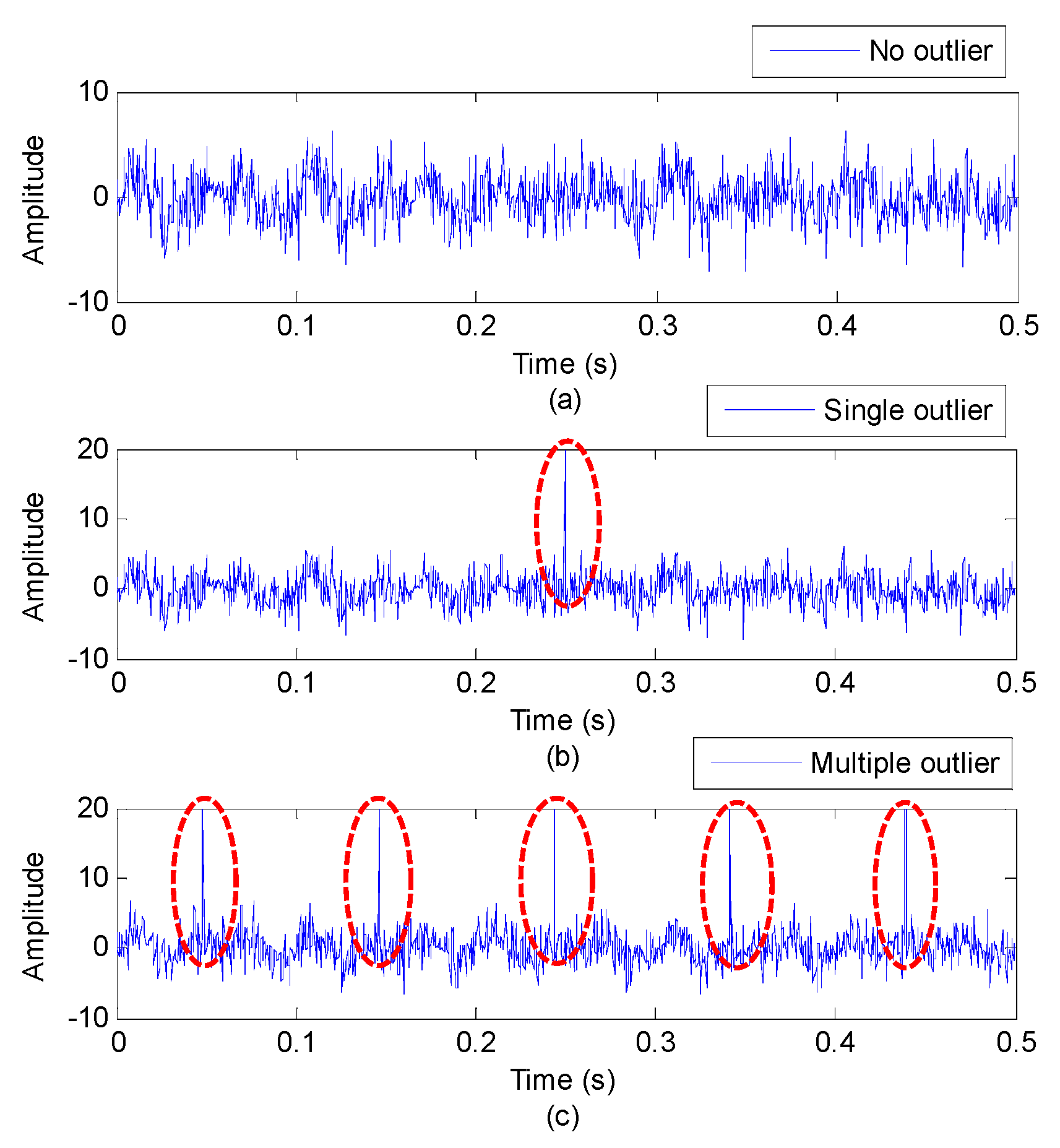
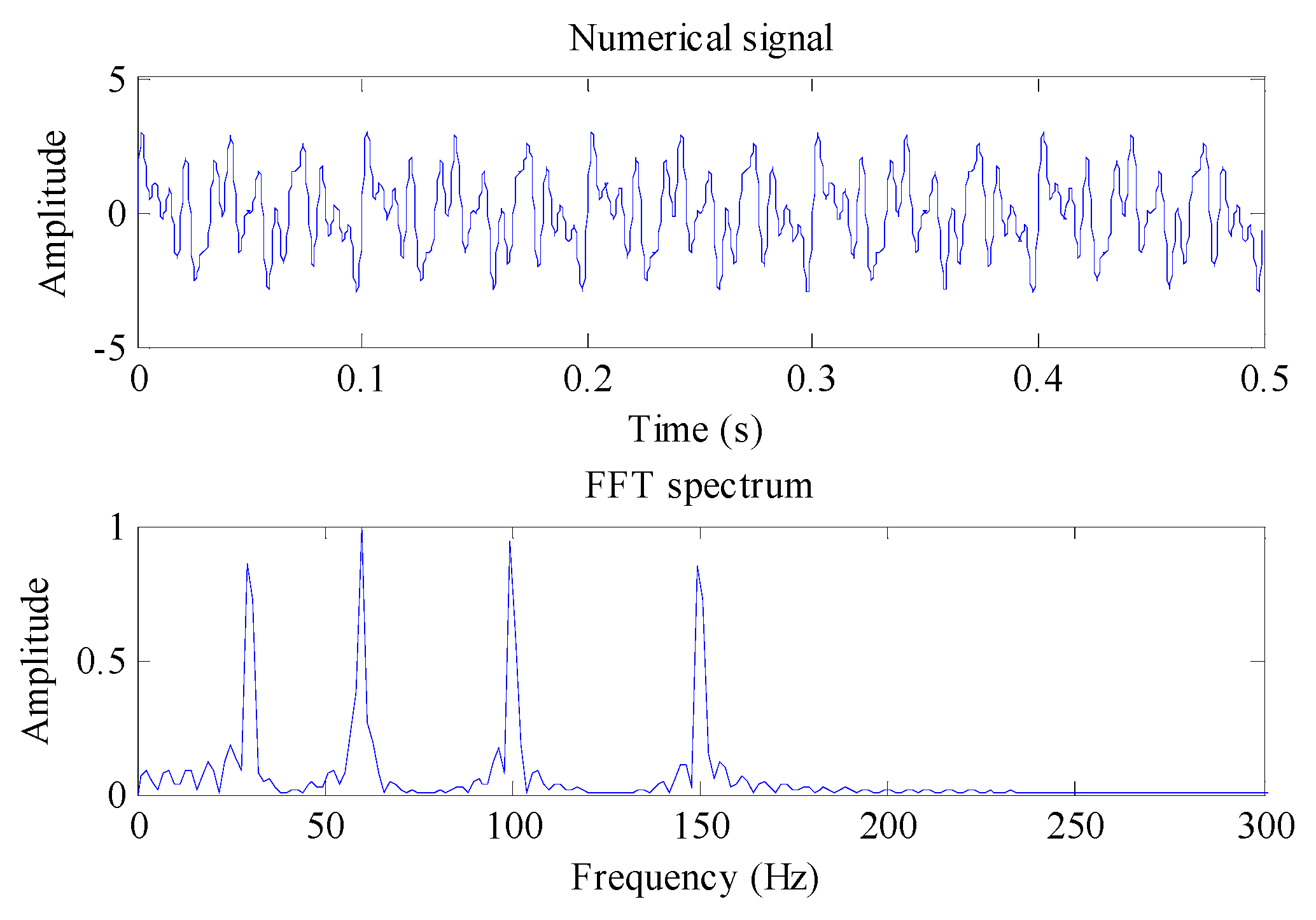
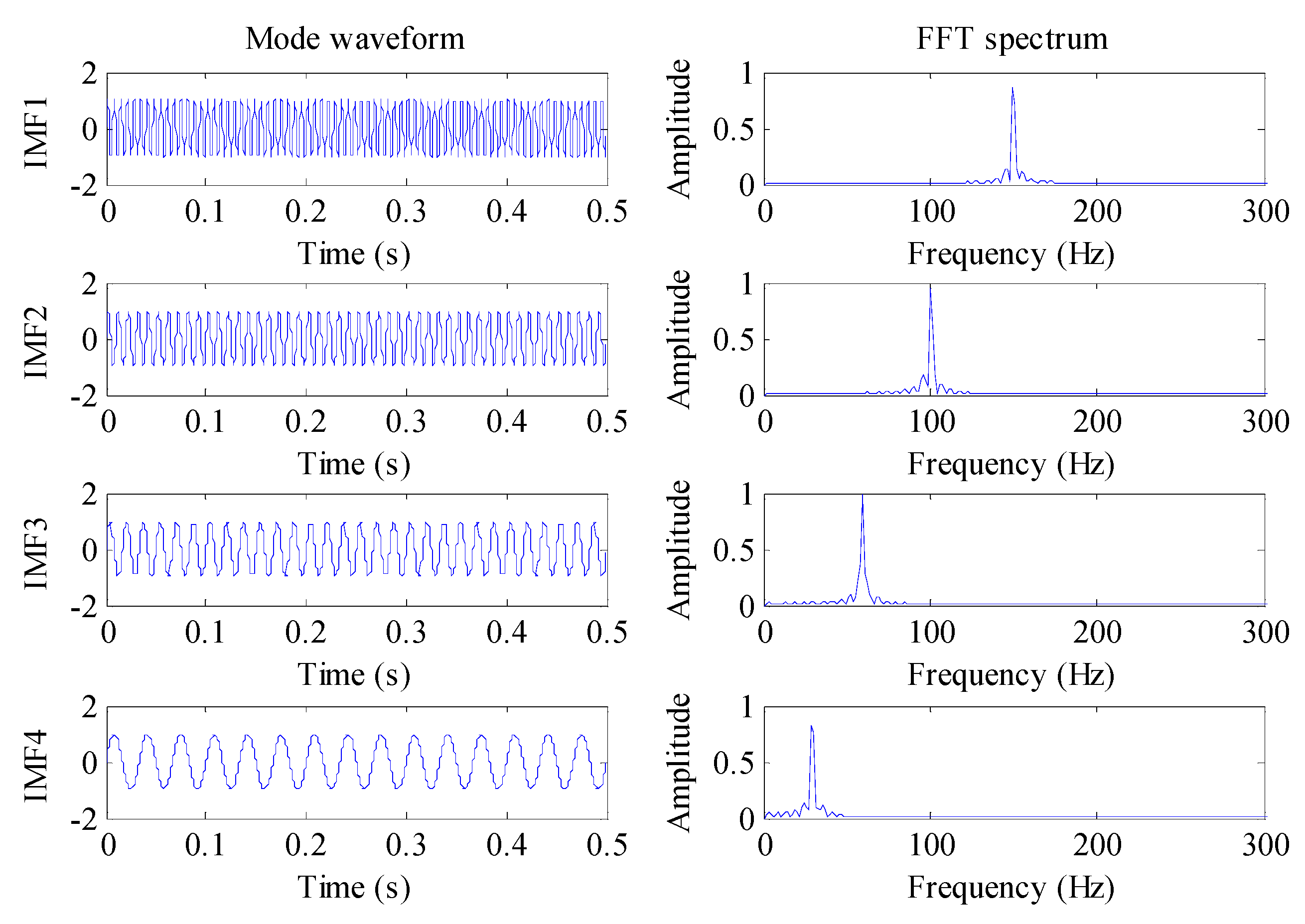
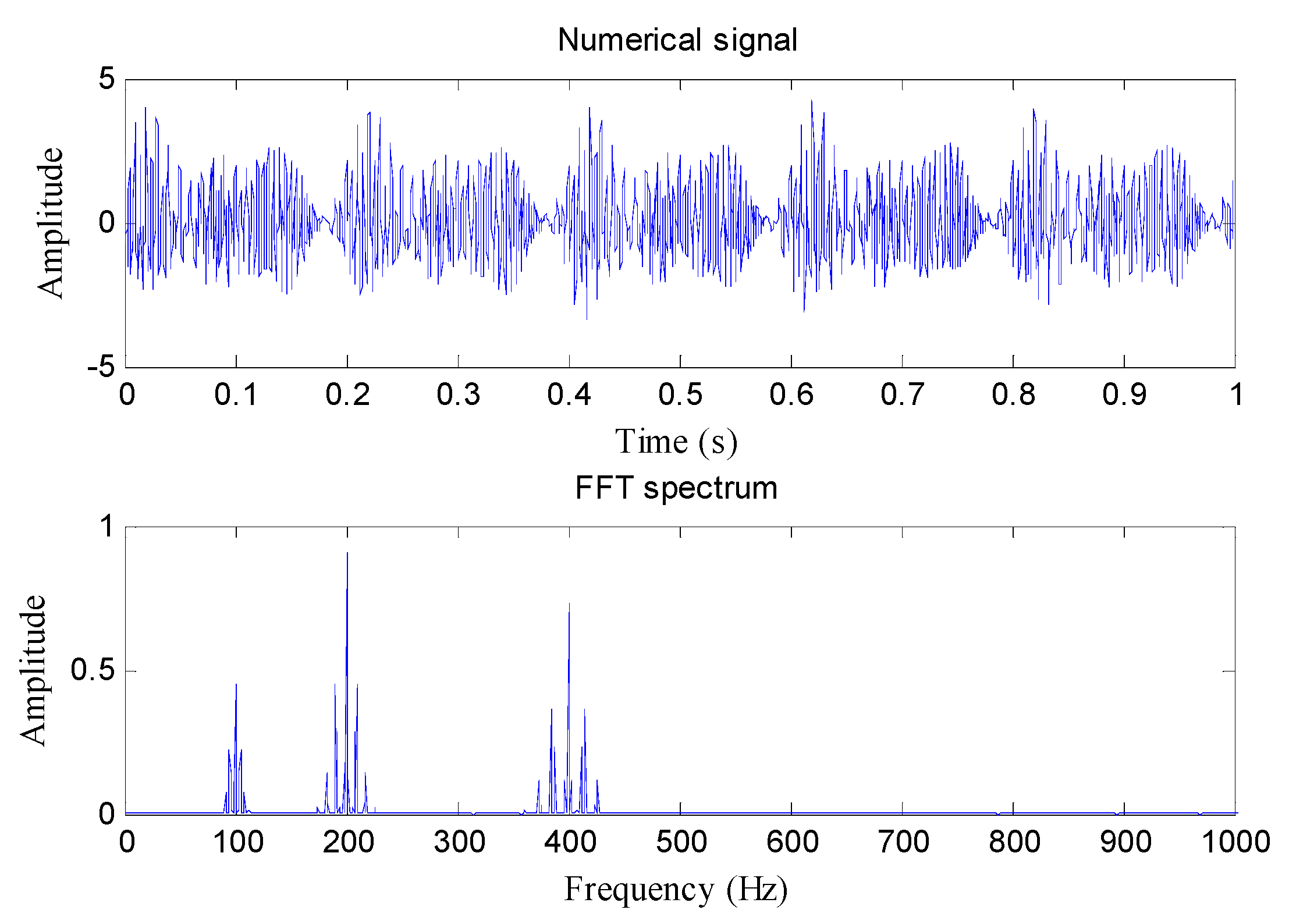
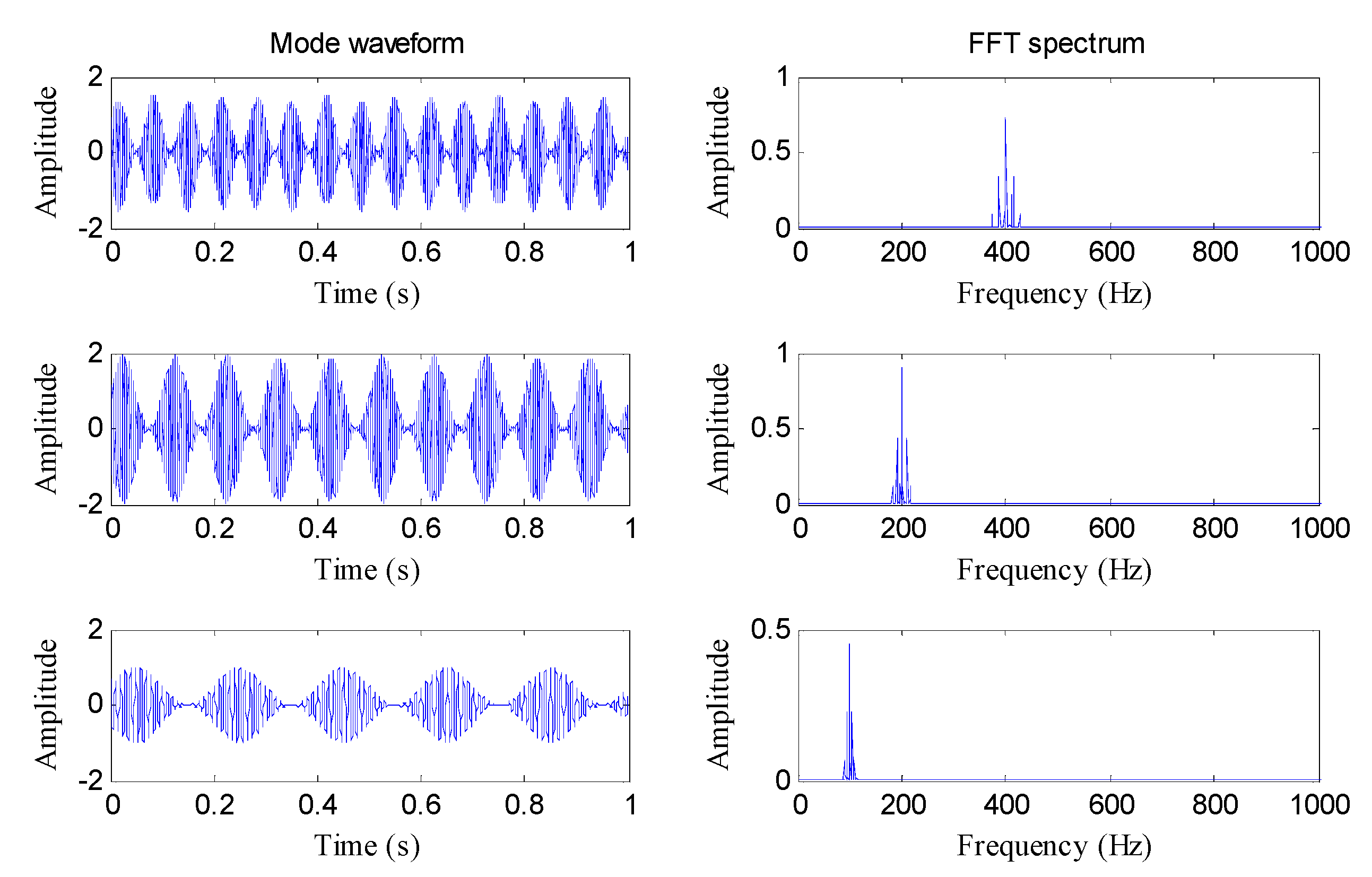
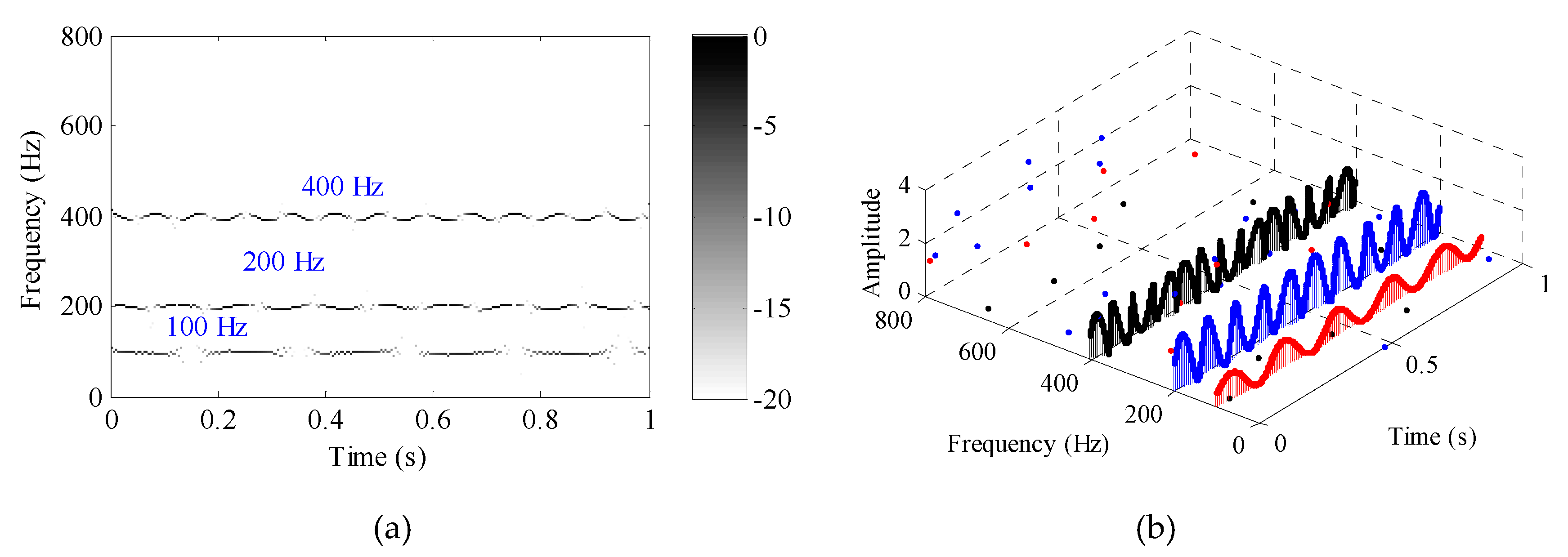
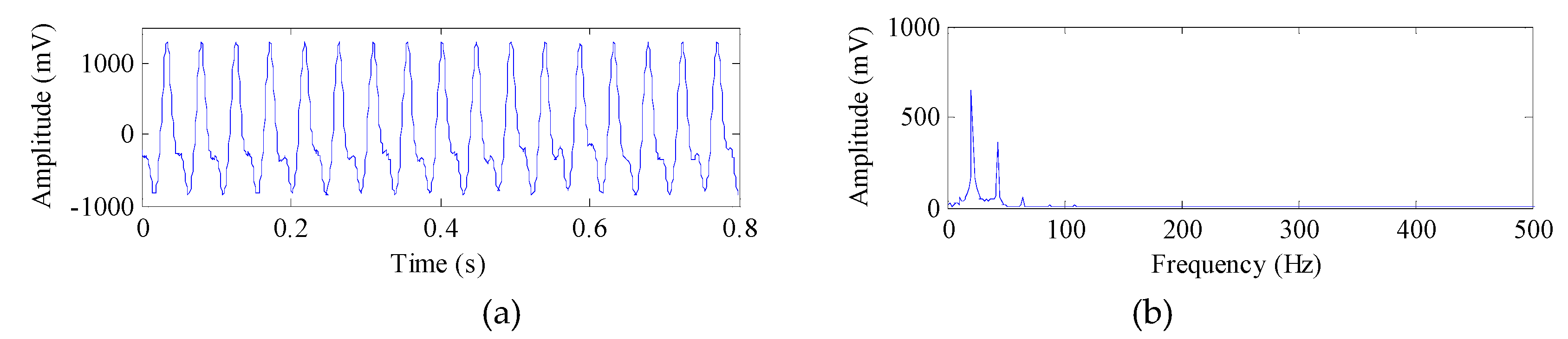
To prove the efficacy of the presented WSK indicator, comparisons between four indicators (i.e., kurtosis, entropy, WK, and WSK) are conducted by analyzing a simulation signal. The simulation signal shown in
Figure 4a is composed of the periodic impulse, harmonic signal, and random noise.
Figure 4b,c shows the simulation signal containing a single outlier and multiple outlier, respectively.
Table 1 gives the comparison results of different indicators for the simulation signal. From the chart we know that the proposed WSK indicator has the smallest change when the outlier of the signal increases gradually. This implies that the proposed WSK indicator is more reliable and robust to the outlier of the signal compared with the single indicator and WK. Hence, through the combination of three indicators (i.e., the sparseness, kurtosis, and correlation coefficient), the WSK indicator is more comprehensive and has more advantages in measuring vibration features.
Obviously, a larger WSK implies a richer impact feature and a better signal sparseness and decomposition results. Here, to further ensure a global optimal solution, we deem the mean of the WSK of modes acquired by VMD as an objective function of the optimization procedure. Concretely, the goal of the parameter optimization process of VMD using GWO is visually interpreted as an effective search for the minimum value of the opposite of the objective function, as shown in Equation (12):
where
K denotes the mode number,
denotes the penalty factor,
is the mean value of WSK, and
is the WSK corresponding to the
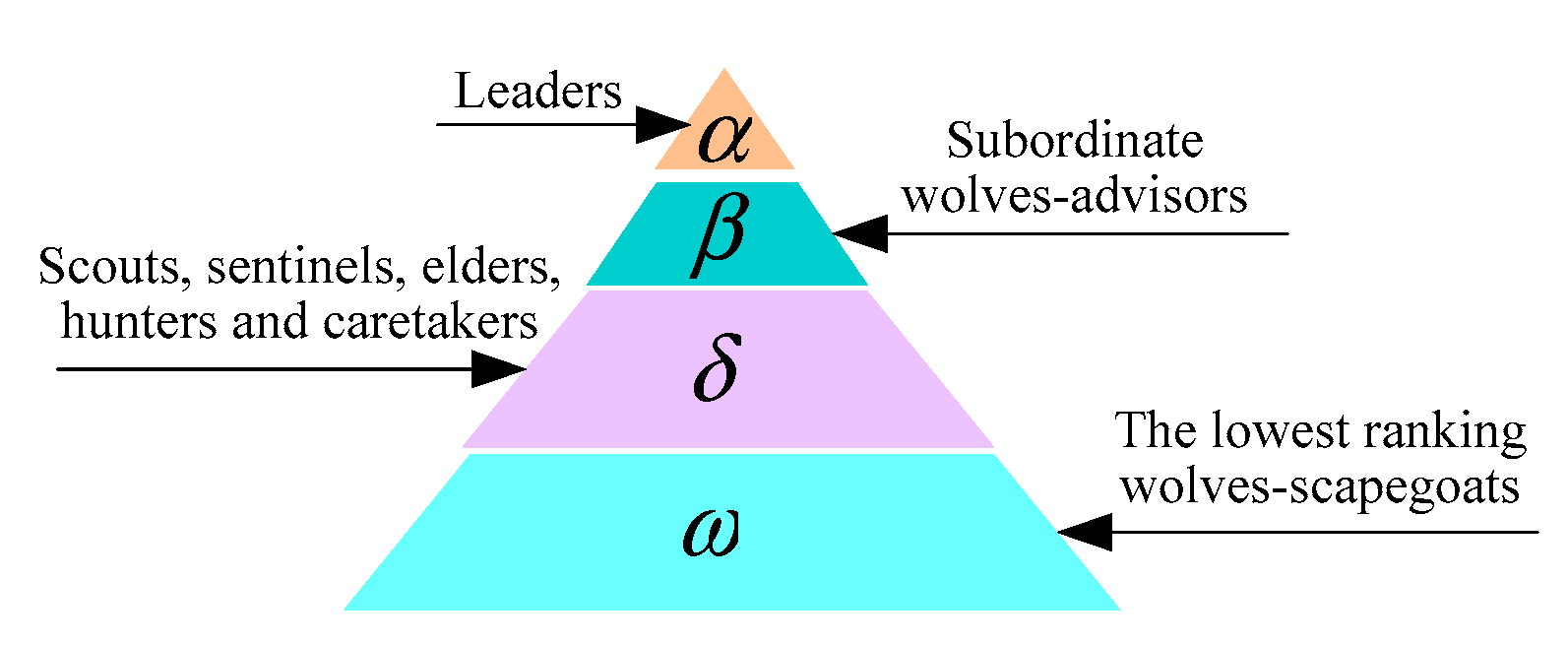
i-th mode. GWO has a strict population hierarchy, which is mainly divided into four layers (see
Figure 5), where the first layer is
(i.e., leaders/the optimal solution), the second layer is
(i.e., subordinate wolves-advisors/the suboptimal solution), the third layer is
(i.e., scouts, sentinels, elders, hunters, and caretakers/the third optimal solution), and the last layer is
(i.e., lowest ranking wolves-scapegoats/other solutions). Moreover, GWO is applied for parameter optimization by implementing several steps (e.g., hunting, searching for prey, encircling prey, and attacking prey).
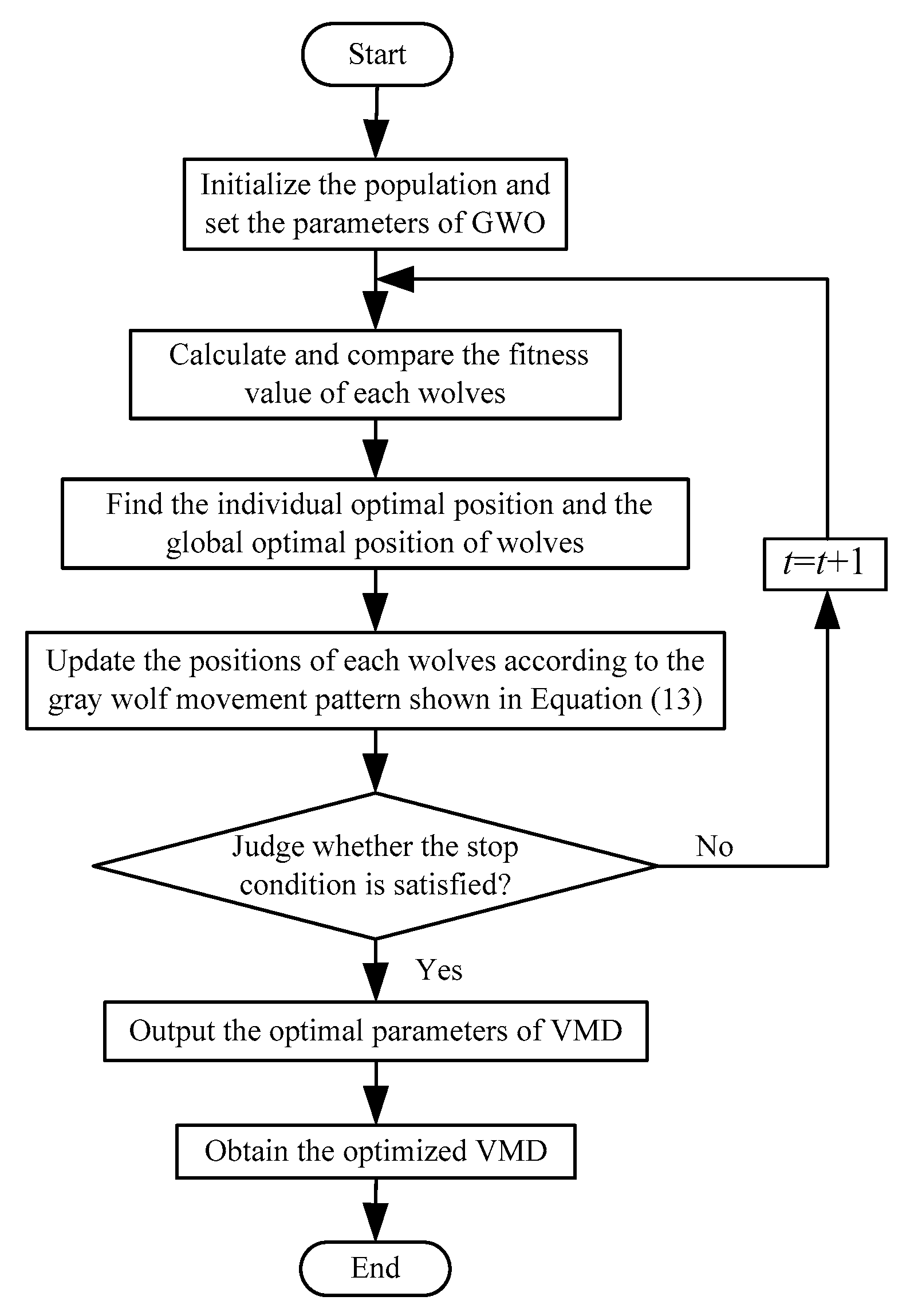
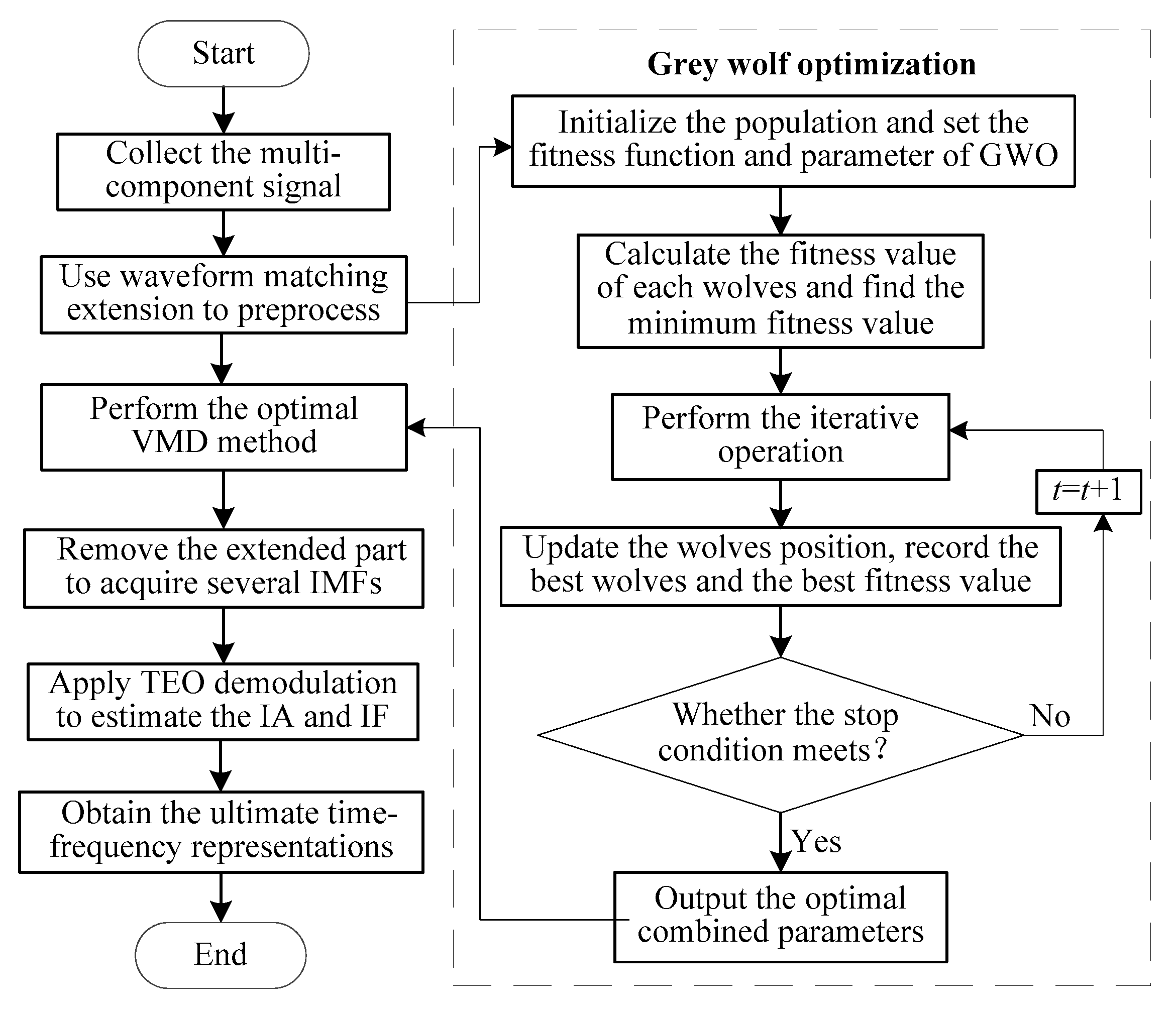
Figure 6 shows the flowchart of the parameter optimization of VMD using the GWO method. The general procedure of VMD parameter optimization is elaborated in detail below:
(1) Initialize the grey wolf population
, and set the fitness function and the parameters of the GWO algorithm. Generally speaking, the higher the number of wolves and iterations is, the better the optimization results are, but the longer the computation time is; thus, according to Ref. [
42], we define the maximum number of wolves
m = 30 and maximum iterations
T = 10, which is aimed at achieving a tradeoff between the optimization results and computational efficiency. Besides, due to the pre-optimization, the objective only involves two variables (
,
K), and thus each wolf is expressed as
,
, where
and
represent the penalty factor and mode number, respectively. Due to fault feature information of the practical signal usually spread over the first few high-frequency components obtained by VMD, the first two to eight components are usually selected and analyzed. Besides, the feature information of the main components obtained by VMD is distributed over an appropriate bandwidth, which means that the parameter
is supposed to stay within an empirical range and is neither too big nor too small compared to the default of VMD. For all those reasons, here the search ranges of the two parameters
and
K are empirically set as [2, 8] and [100, 2000], respectively.
(2) Calculate the fitness value of each wolf , look for the minimum fitness value (i.e., ) between the four agents (i.e., the fitness value of the individual grey wolf , , , and ) and record the current best wolves .
(3) Update the position of wolves in terms of the gray wolf movement pattern shown in Equation (13):
where
A is the convergence factor and meets
,
C is the swing factor and meets
,
d is the range control parameter which linearly decays from 2 to 0 over the whole iteration, and
and
are the random numbers between 0 and 1.
(4) Calculate the fitness value of new wolves, and record the best wolves through the comparison of the fitness value. That is, if the fitness value of the updated wolves overmatches that of the previous wolves, the updated wolves will take the place of the previous wolves . Otherwise, retain the previous wolves .
(5) Determine whether the stopping condition is satisfied. Concretely, decide whether the current iterations are lower than the maximum iterations (i.e., ) or whether the opposite of the fitness value is small enough. If that is the case, stop the iteration and output the best wolves (i.e., the best parameters and of VMD). Otherwise, let t = t + 1, back to step (2) to keep working.
In short, this section has two contributions. First, the WSK indicator is proposed and is more reliable and robust to the outlier of the signal compared with the previous WK and three single indicators (i.e., the sparseness, kurtosis, and correlation coefficient). Second, two key parameters (, K) of VMD can be determined automatically by using the GWO method, where the mean of the proposed WSK for all modes is regarded as the objective function of the optimization procedure.