Sound Absorption and Diffusion by 2D Arrays of Helmholtz Resonators
Abstract
1. Introduction
2. Model
2.1. 2D Helmholtz Resonator
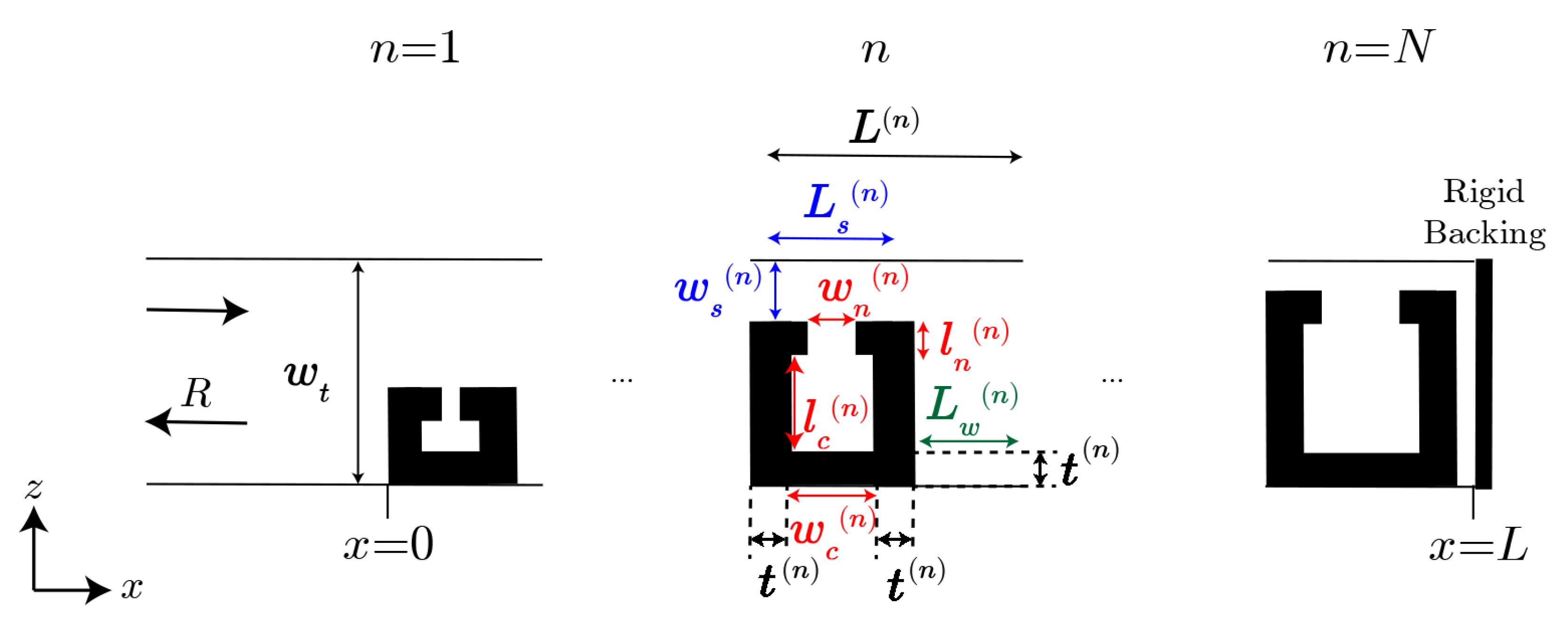
2.2. 1D Array of Helmholtz Resonators
- The transfer matrix for each step in the slit of the n-th building block, , reads aswhere , are the wavenumber and the impedance in the slit. As it was previously mentioned, the term Ms is applied along a distance . Thus, this term must be considered twice in the transfer matrix of the building block (before and after the one corresponding to the Helmholtz resonator).
- The transfer matrix for each resonator, , is defined asbeing the acoustic impedance of the Helmholtz resonator. Notice that this definition is valid when , where the Helmholtz resonators can be considered as point resonators.
- The transfer matrix for the radiation correction of the slit to the free space, , can be defined aswith the characteristic radiation impedance, where is the angular frequency, is the total porosity and . is the length correction, where is the length correction given by the pressure radiation at the discontinuity from the neck duct to the cavity of the Helmholtz resonator, and comes from the radiation at the discontinuity from the neck to the principal waveguide (see reference [38]) given by Equation (4) and Equation (5). It is important to note that, due to the symmetry of each resonator, the radiation correction of the slit to the free space must be applied at both sides of the structure.
- The transfer matrix for the air cavity placed behind the Helmholtz resonator, , is defined in the following formwhere and are the wavenumber and the acoustic impedance of the air. In this part of the system we consider that the width of the tube is large enough to neglect the effect of viscothermal losses.
2.3. 2D Finite Array of Helmholtz Resonators
2.4. Noise Control Parameters
2.4.1. Insertion Loss in Reflection
2.4.2. Diffusion Coefficient
3. Experimental Setups
3.1. Impedance Tube: 1D System
3.2. Anechoic Chamber: 2D System
4. Results
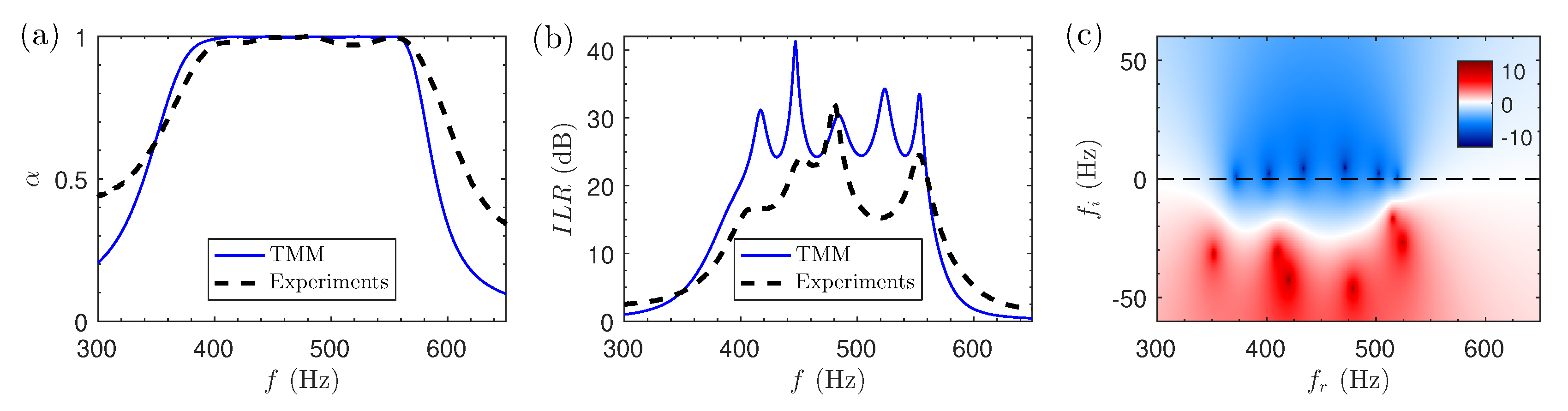
4.1. Results for the 1D Problem: Sound Absorption and ILR
4.2. Results for the 2D Problem
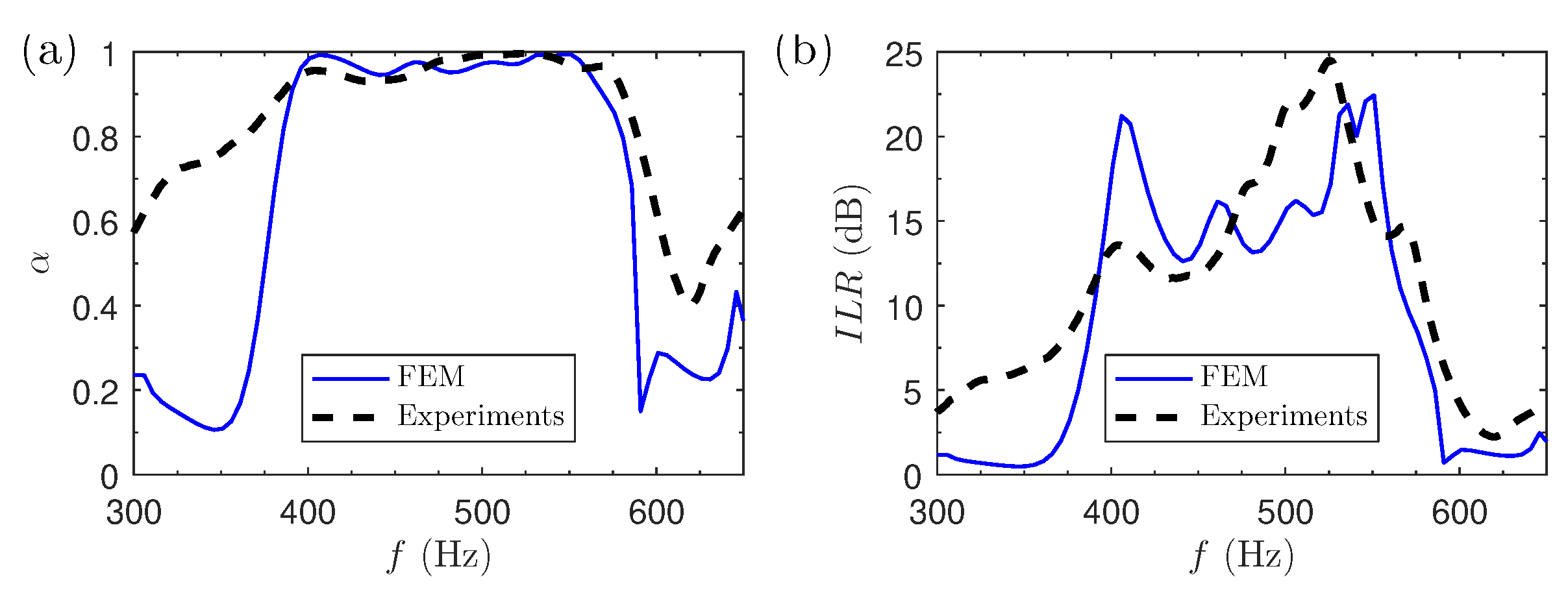
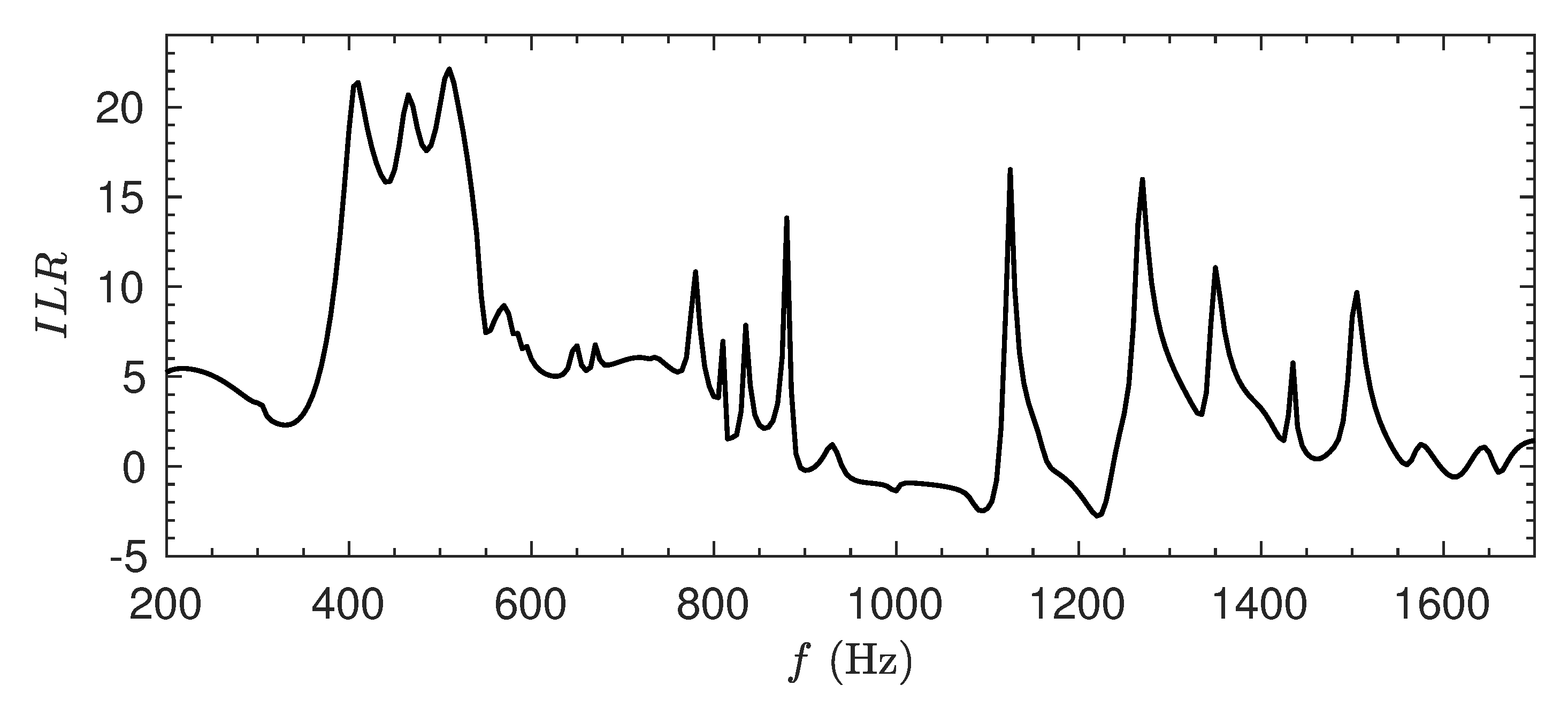
4.2.1. Sound Absorption and ILR
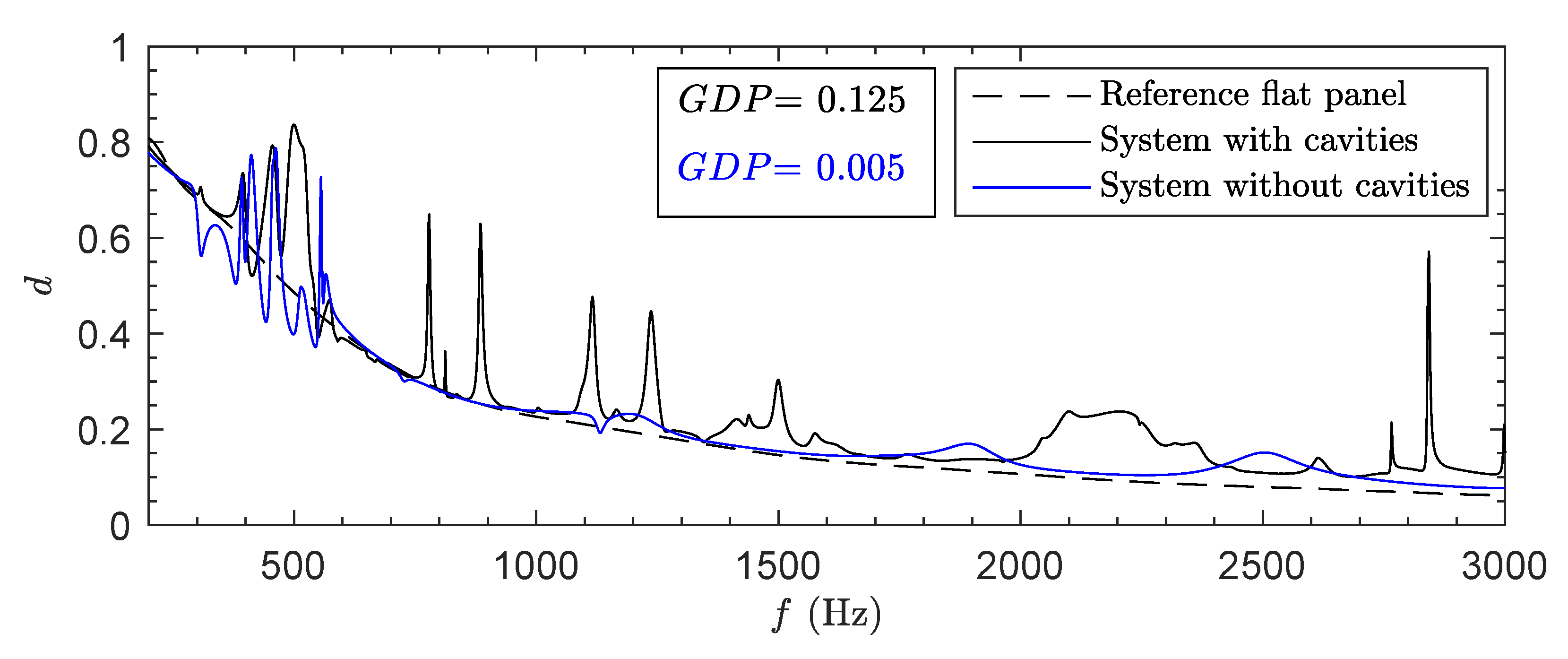
4.2.2. Diffusion Coefficient
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Romero-García, V.; Hladky-Hennion, A.C. (Eds.) Fundamentals and Applications of Acoustic Metamaterials: From Seismic to Radio Frequency; Wiley-ISTE: London, UK, 2019. [Google Scholar]
- Deymier, P. (Ed.) Acoustic Metamaterials and Phononic Crystals; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Sigalas, M.; Economou, E. Elastic and acoustic wave band structure. J. Sound Vib. 1992, 158, 377. [Google Scholar] [CrossRef]
- Matlack, K.H.; Bauhofer, A.; Krödel, S.; Palermo, A.; Daraio, C. Composite 3D-printed metastructures for low-frequency and broadband vibration absorption. Proc. Natl. Acad. Sci. USA 2016, 113, 8386–8390. [Google Scholar] [CrossRef]
- Wormser, M.; Wein, F.; Stingl, M.; Körner, C. Design and Additive Manufacturing of 3D Phononic Band Gap Structures Based on Gradient Based Optimization. Materials 2017, 10, 1125. [Google Scholar] [CrossRef] [PubMed]
- Lucklum, F.; Vellekoop, M.J. Bandgap engineering of three-dimensional phononic crystals in a simple cubic lattice. Appl. Phys. Lett. 2018, 113, 201902. [Google Scholar] [CrossRef]
- D’Alessandro, L.; Ardito, R.; Braghin, F.; Corigliano, A. Low frequency 3D ultra-wide vibration attenuation via elastic metamaterial. Sci. Rep. 2019, 9, 8039. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Sala, R.; Sancho, J.; Sánchez, J.V.; Gómez, V.; Llinares, J.; Meseguer, F. Sound Attenuation by sculpture. Nature 1995, 378, 241. [Google Scholar] [CrossRef]
- Cebrecos, A.; Krattiger, D.; Sánchez-Morcillo, V.J.; Romero-García, V.; Hussein, M.I. The finite-element time-domain method for elastic band-structure calculations. Comput. Phys. Commun. 2019, 238, 77–87. [Google Scholar] [CrossRef]
- Cebrecos, A.; Romero-García, V.; Groby, J.P. Complex Dispersion Relation Recovery from 2D Periodic Resonant Systems of Finite Size. Appl. Sci. 2019, 9, 478. [Google Scholar] [CrossRef]
- Hussein, M.I.; Leamy, M.J.; Ruzzene, M. Dynamics of phononic materials and structures: Historical origins, recent progress, and future outlook. Appl. Mech. Rev. 2014, 66, 040802. [Google Scholar] [CrossRef]
- Sánchez-Pérez, J.; Rubio, C.; Martínez-Sala, R.; Sánchez-Grandia, R.; Gómez, V. Acoustic barriers based on periodic arrays of scatterers. Appl. Phys. Lett. 2002, 81, 5240. [Google Scholar] [CrossRef]
- Martńez-Sala, R.; Rubio, C.; Garcia-Raffi, L.; Sánchez-Pérez, J.; Sánchez-Pérez, E.; Llinares, J. Control of noise by trees arranged like sonic crystals. Jour. Sound Vib. 2006, 291, 100. [Google Scholar] [CrossRef]
- Garcia-Raffi, L.; Salmerón-Contreras, L.; Herrero-Durá, I.; Picó, R.; Redondo, J.; Sánchez-Morcillo, V.; Staliunas, K.; Adkins, N.; Cebrecos, A.; Jiménez, N.; et al. Broadband reduction of the specular reflections by using sonic crystals: A proof of concept for noise mitigation in aerospace applications. Aerosp. Sci. Technol. 2018, 73, 300–308. [Google Scholar] [CrossRef]
- Castiñeira Ibáñez, S.; Romero-García, V.; Sánchez-Pérez, J.V.; García-Raffi, L. Periodic systems as road traffic noise reducing devices: Prototype and standardization. Environ. Eng. Manag. J. 2015, 14, 2759–2769. [Google Scholar]
- Kandula, M. Broadband shock noise reduction in turbulent jets by water injection. Appl. Acoust. 2009, 70, 1009–1014. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, X.; Mao, Y.; Zhu, Y.Y.; Yang, Z.; Chan, C.T.; Sheng, P. Locally Resonant Sonic Materials. Science 2000, 289, 1734–1736. [Google Scholar] [CrossRef]
- Fang, N.; Xi, D.; Xu, J.; Ambati, M.; Srituravanich, W.; Sun, C.; Zhang, X. Ultrasonic metamaterials with negative modulus. Nat. Mater. 2006, 5, 452–456. [Google Scholar] [CrossRef]
- Sugimoto, N.; Horioka, T. Dispersion characteristics of sound waves in a tunnel with an array of Helmholtz resonators. J. Acoust. Soc. Am. 1995, 97, 1446. [Google Scholar] [CrossRef]
- Bradley, C.E. Acoustic Bloch Wave Propagation in a Periodic Waveguide; Technical Report, Technical Report of Applied Research Laboratories, Report No. ARL-TR-91-19 (July); The University of Texas at Austin: Austin, TX, USA, 1991. [Google Scholar]
- Theocharis, G.; Richoux, O.; Romero-García, V.; Merkel, A.; Tournat, V. Limits of slow sound and transparency in lossy locally resonant periodic structures. New J. Phys. 2014, 16, 093017. [Google Scholar] [CrossRef]
- Jiménez, N.; Cox, T.J.; Romero-García, V.; Groby, J.P. Metadiffusers: Deep-subwavelength sound diffusers. Sci. Rep. 2017, 7, 5389. [Google Scholar] [CrossRef]
- Ballestero, E.; Jiménez, N.; Groby, J.P.; Dance, S.; Aygun, H.; Romero-García, V. Experimental validation of deep-subwavelength diffusion by acoustic metadiffusers. Appl. Phys. Lett. 2019, 115, 081901. [Google Scholar] [CrossRef]
- Romero-García, V.; Sánchez-Pérez, J.V.; Garcia-Raffi, L.M. Tunable wideband bandstop acoustic filter based on two-dimensionalmultiphysical phenomena periodic systems. J. Appl. Phys. 2011, 110, 149041. [Google Scholar] [CrossRef]
- Lagarrigue, C.; Groby, J.P.; Tournat, V. Sustainable sonic crystal made of resonating bamboo rods. J. Acoust. Soc. Am. 2013, 133, 247. [Google Scholar] [CrossRef] [PubMed]
- Krynkin, A.; Umnova, O.; Chong, A.Y.B.; Taherzadeh, S.; Attenborough, K. Predictions and measurements of sound transmission through a periodic array of elastic shells in air. J. Acoust. Soc. Am. 2010, 128, 3496–3506. [Google Scholar] [CrossRef] [PubMed]
- Koussa, F.; Defrance, J.; Jean, P.; Blanc-Benon, P. Acoustical Efficiency of a Sonic Crystal Assisted Noise Barrier. Acta Acust. United Acust. 2013, 99, 399–409. [Google Scholar] [CrossRef]
- Castiñeira-Ibáñez, S.; Romero-García, V.; Sánchez-Pérez, J.V.; Garcia-Raffi, L.M. Overlapping of acoustic bandgaps using fractal geometries. EPL 2010, 92, 24007. [Google Scholar] [CrossRef]
- García-Chocano, V.; Cabrera, S.; Sánchez-Dehesa, J. Broadband sound absorption by lattices of microperforated cylindical shells. Appl. Phys. Lett. 2012, 101, 184101. [Google Scholar] [CrossRef]
- Lardeau, A.; Groby, J.; Romero-García, V. Broadband Transmission Loss Using the Overlap of Resonances in 3D Sonic Crystals. Crystals 2015, 6, 51. [Google Scholar] [CrossRef]
- Cavalieri, T.; Cebrecos, A.; Groby, J.P.; Chaufour, C.; Romero-García, V. Three-dimensional multiresonant lossy sonic crystal for broadband acoustic attenuation: Application to train noise reduction. Appl. Acoust. 2019, 146, 1–8. [Google Scholar] [CrossRef]
- Dimitrijević, S.M.; García-Chocano, V.M.; Cervera, F.; Roth, E.; Sánchez-Dehesa, J. Sound Insulation and Reflection Properties of Sonic Crystal Barrier Based on Micro-Perforated Cylinders. Materials 2019, 12, 2806. [Google Scholar] [CrossRef]
- Zwikker, C.; Kosten, C. Sound Absorbing Materials; Elsevier Publishing Company, Inc.: Amsterdam, The Netherlands, 1949. [Google Scholar]
- Stinson, M.R. The propagation of plane sound waves in narrow and wide circular tubes, and generalization to uniform tubes of arbitrary cross-sectional shape. J. Acoust. Soc. Am. 1991, 89, 550–558. [Google Scholar] [CrossRef]
- Duclos, A.; Lafarge, D.; Pagneux, V. Transmission of acoustic waves through 2D phononic crystal: Visco-thermal and multiple scattering effects. Eur. Phys. J. Appl. Phys. 2009, 45, 11302. [Google Scholar] [CrossRef]
- Romero-García, V.; Theocharis, G.; Richoux, O.; Pagneux, V. Use of complex frequency plane to design broadband and sub-wavelength absorbers. J. Acoust. Soc. Am. 2016, 139, 3395–3403. [Google Scholar] [CrossRef] [PubMed]
- Romero-García, V.; Theocharis, G.; Richoux, O.; Merkel, A.; Tournat, V.; Pagneux, V. Perfect and broadband acoustic absorption by critically coupled sub-wavelength resonators. Sci. Rep. 2016, 6, 19519. [Google Scholar] [CrossRef]
- Jiménez, N.; Huang, W.; Romero-García, V.; Pagneux, V.; Groby, J.P. Ultra-thin metamaterial for perfect and quasi-omnidirectional sound absorption. Appl. Phys. Lett. 2016, 109, 121902. [Google Scholar] [CrossRef]
- Jiménez, N.; Romero-García, V.; Pagneux, V.; Groby, J.P. Quasiperfect absorption by subwavelength acoustic panels in transmission using accumulation of resonances due to slow sound. Phys. Rev. B 2017, 95, 014205. [Google Scholar] [CrossRef]
- Jiménez, N.; Romero-García, V.; Pagneux, V.; Groby, J.P. Rainbow-trapping absorbers: Broadband, perfect and asymmetric sound absorption by subwavelength panels for transmission problems. Sci. Rep. 2017, 7, 13595. [Google Scholar] [CrossRef] [PubMed]
- Merkel, A.; Theocharis, G.; Richoux, O.; Romero-García, V.; Pagneux, V. Control of acoustic absorption in one-dimensional scattering by resonant scatterers. Appl. Phys. Lett. 2015, 107, 244102. [Google Scholar] [CrossRef]
- Kergomard, J.; Garcia, A. Simple discontinuities in acoustic waveguides at low frequencies: Critical analysis and formulae. J. Sound Vib. 1987, 114, 465–479. [Google Scholar] [CrossRef]
- Dubos, V.; Kergomard, J.; Khettabi, A.; Dalmont, J.P.; Keefe, D.; Nederveen, C. Theory of sound propagation in a duct with a branched tube using modal decomposition. Acta Acust. United Acust. 1999, 85, 153–169. [Google Scholar]
- International Organization for Standards. Acoustics - Sound Scattering Properties of Surfaces. Part 2: Measurement of the Directional Diffusion Coefficient in a Free Field; ISO 17497-2:2012; International Organization for Standardization (ISO): Geneva, Switzerland, 2012. [Google Scholar]
- International Organization for Standards. Acoustics - Determination of Sound Absorption and Impedance in Impedances Tubes. Part 2: Transfer-Function Method; ISO 10534-2:2002; International Organization for Standardization (ISO): Geneva, Switzerland, 2002. [Google Scholar]
- Sánchez-Dehesa, J.; Garcia-Chocano, V.M.; Torrent, D.; Cervera, F.; Cabrera, S.; Simon, F. Noise control by sonic crystal barriers made of recycled materials. J. Acoust. Soc. Am. 2011, 129, 1173–1183. [Google Scholar] [CrossRef]
- Christensen, J.; Romero-García, V.; Picó, R.; Cebrecos, A.; de Abajo, F.J.G.; Mortensen, N.A.; Willatzen, M.; Sánchez-Morcillo, V.J. Extraordinary absorption of sound in porous lamella-crystals. Sci. Rep. 2014, 4, 4674. [Google Scholar] [CrossRef] [PubMed]
- Sonic Crystals for Noise Reduction at the Launch Pad; Technical Report, European Space Agency under Contract ITT 1-7094 (ITI); Universitat Politècnica de València (UPV): Gandia, Spain, 2014.



| Parameter (mm) | HR1 | HR2 | HR3 | HR4 | HR5 |
|---|---|---|---|---|---|
| 5.20 | 32.39 | 38.61 | 24.78 | 10.46 | |
| 4.63 | 1.00 | 1.00 | 1.00 | 1.67 | |
| 49.77 | 34.92 | 42.06 | 47.13 | 75.52 | |
| 46.34 | 10.00 | 10.00 | 10.00 | 16.74 | |
| 36.03 | 23.69 | 10.34 | 19.09 | 5.02 | |
| 66.35 | 30.00 | 30.00 | 30.00 | 36.74 | |
| 25.00 | 25.00 | 25.00 | 23.00 | 20.00 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Herrero-Durá, I.; Cebrecos, A.; Picó, R.; Romero-García, V.; García-Raffi, L.M.; Sánchez-Morcillo, V.J. Sound Absorption and Diffusion by 2D Arrays of Helmholtz Resonators. Appl. Sci. 2020, 10, 1690. https://doi.org/10.3390/app10051690
Herrero-Durá I, Cebrecos A, Picó R, Romero-García V, García-Raffi LM, Sánchez-Morcillo VJ. Sound Absorption and Diffusion by 2D Arrays of Helmholtz Resonators. Applied Sciences. 2020; 10(5):1690. https://doi.org/10.3390/app10051690
Chicago/Turabian StyleHerrero-Durá, Iván, Alejandro Cebrecos, Rubén Picó, Vicente Romero-García, Luis Miguel García-Raffi, and Víctor José Sánchez-Morcillo. 2020. "Sound Absorption and Diffusion by 2D Arrays of Helmholtz Resonators" Applied Sciences 10, no. 5: 1690. https://doi.org/10.3390/app10051690
APA StyleHerrero-Durá, I., Cebrecos, A., Picó, R., Romero-García, V., García-Raffi, L. M., & Sánchez-Morcillo, V. J. (2020). Sound Absorption and Diffusion by 2D Arrays of Helmholtz Resonators. Applied Sciences, 10(5), 1690. https://doi.org/10.3390/app10051690










